Sub-Compartment Variation in Tree Height, Stem Diameter and Stocking in a Pinus radiata D. Don Plantation Examined Using Airborne LiDAR Data
Abstract
: Better information regarding the spatial variability of height, Diameter at Breast Height (DBH) and stocking could improve inventory estimates at the operational Planning Unit since these parameters are used extensively in allometric equations, including stem volume, biomass and carbon calculations. In this study, the influence of stand stocking on height and DBH of two even aged radiata pine (Pinus radiata D. Don) stands were investigated using airborne Light Detection and Ranging (LiDAR) data at a study site in New South Wales, Australia. Both stands were characterized by irregular stocking due to patchy establishment and self-thinning in the absence of any silvicultural thinning events. For the purpose of this study, a total of 34 plots from a 34 year old site and 43 plots from a nine year old site were established, from which a total of 447 trees were sampled. Within these plots, DBH and height measurements were measured and their relationships with stocking were evaluated. LiDAR was used for height estimation as well as stem counts in fixed plots (stocking). The results showed a significant relationship between stem DBH and stocking. At both locations, trees with larger diameters were found on lower stocking sites. Height values were also significantly correlated with stocking, with taller trees associated with high stocking. These results were further verified of additional tree samples, with independent field surveys for DBH and LiDAR-derived metrics for height analysis. This study confirmed the relationship between P. radiata tree heights and stem diameter with stocking and demonstrated the capacity of LiDAR to capture sub-compartment variation in these tree-level attributes.1. Introduction
Tree Diameter at Breast Height (DBH), height and stocking (number of tree stems per ha) are the most common variables used in forest inventory. Spatial variability of these inventory attributes directly influences the precision of growth and yield estimates. Various environmental factors such as water and nutrient availability, climatic variables and soil nutrition, texture and depth have been reported to affect the growth and canopy structure of radiata pine [1–3].
Silvicultural practices, in particular the manipulation of stocking, are commonly used by plantation growers to optimize stand growth and structure. Stand density influences both internal and external characteristics of trees between and within a stand by altering competition between trees for water, nutrients and solar radiation [4,5]. Considerable research has focused on the impact of stocking on radiata pine (Pinus radiata D. Don) growth patterns [6], wood quality and stiffness [7], breeding [8], genotype [9] and product yields [10]. Moreover, Klitscher [11] reported a reduction in mortality percentage of this species within lower stand densities.
Stocking has been linked to diameter growth in several studies. Mason [12] reported that individual tree diameters were unrelated to stocking (620 to 12,000 stems per ha) in young P. radiata plantations up to age four, however a decrease of diameter growth was seen with an increase of stocking during the fifth growing season. In another study by Beets and Kimberley [13] a comparison of diameter development showed greater diameters in low density stands (less than 180 stems per ha). Stocking has also been reported to influence the structural patterns of height in radiata pine, although with conflicting results. The influence of stocking on height growth has been reported to be less marked than diameter growth [14], although several studies have shown the increase of height to be influenced by increased stocking [12,15]. In contrast, Whiteside [16] reported an increase in height with a reduction in stocking (from 1250 to 250 stems per ha).
Although individual tree variables (e.g., height, diameter) can be measured directly in the field, stocking has been somewhat harder to measure accurately as in some situations it is difficult to locate individual trees reliably [17]. In recent years, with the development of remote sensing technology, such as airborne Light Detection and Ranging (LiDAR, also known as Airborne Laser Scanning), the retrieval of forest structural attributes across different scales has become more efficient and accurate (e.g., [18]). LiDAR data has been shown to capture detailed information on P. radiata plot-level metrics and area-based modeling [19–21], and more recently at the tree-level modeling with improved tree detection techniques [22–24]. Once individual trees are identified and delineated, the tree structural parameters, as well as stand density, can be derived from LiDAR data. For the purpose of identifying trees, a number of studies have counted crown maximas or delineated individual crowns using the LiDAR Canopy Height Model (CHM) [25–28] or the LiDAR point cloud [29], while several others have developed area-based models based on the distribution of LiDAR metrics for plot-level estimates [18]. Although LiDAR is widely used in Europe and North America to provide estimates of a range of stand and canopy attributes, it is often noted that more research is required for accurate estimates of stand density [30,31].
In this study, despite the similar initial stocking rate, similar genetic sources as well as similar climatic (temperature and rainfall) and edaphic (geology and soil type) conditions, the trees displayed significant height and DBH variation within even-aged stands. The effect of topography and solar radiation on tree height and DBH were revealed in earlier work by authors and exhibited significant relationships with the variables [32,33]. This study concentrated on examining the effect of stand stocking on tree height and DBH variation in two stands. For this aim, height and stocking were extracted from LiDAR and correlated with measurements of DBH (field) and height. Prior to the main investigation, relationships between field measured tree height with LiDAR-derived height and field stocking with LiDAR-derived stocking (tree counts per plot) were conducted to demonstrate the accuracy of LiDAR. This study not only confirms the relationship between tree stem structure and stocking but also demonstrates the value of LiDAR data for improved inventory estimates for locally variable stands of P. radiata.
2. Methods
2.1. Study Area Description
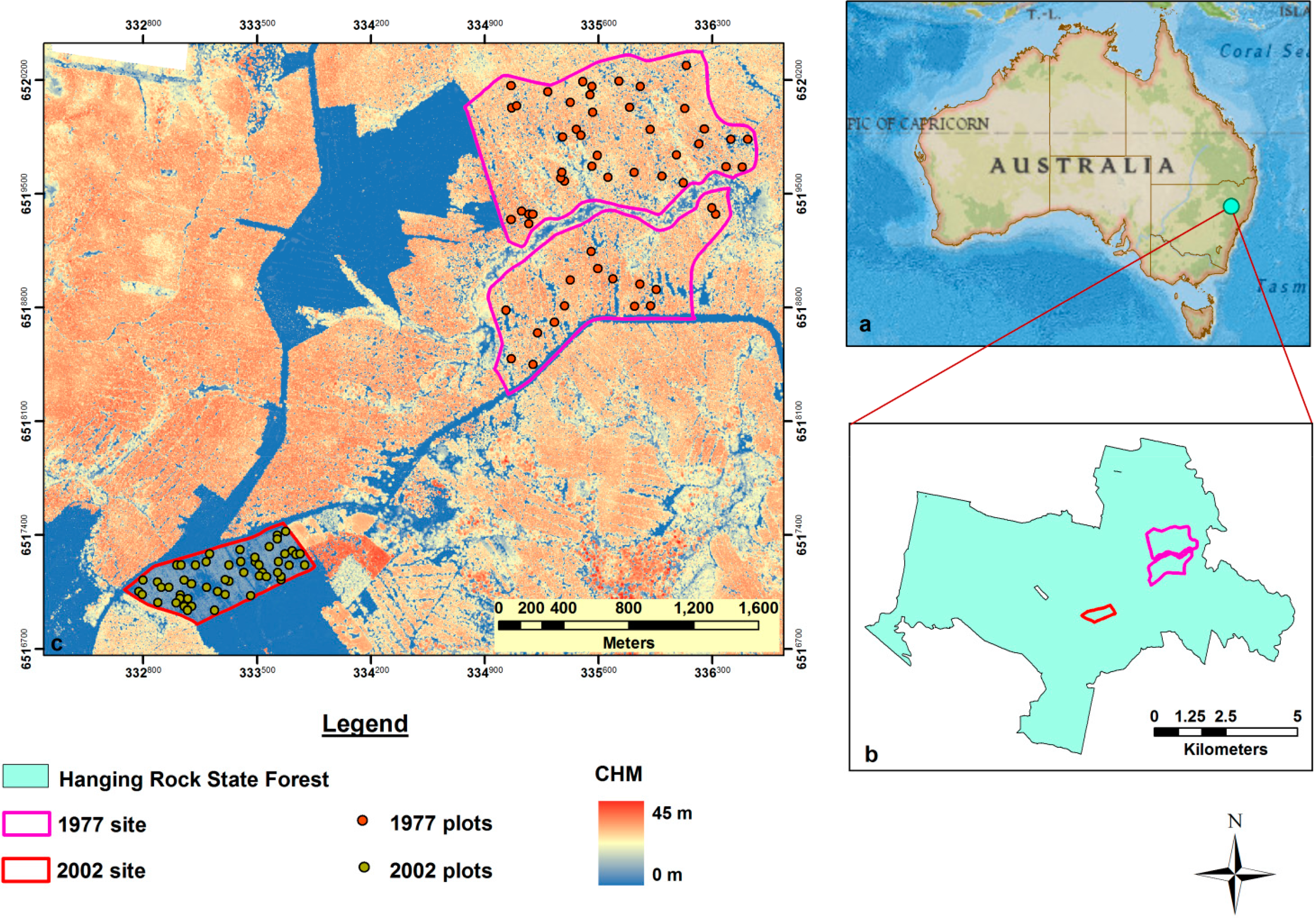
The study area is located within Hanging Rock State Forest, a 7000 ha radiata pine plantation near the town of Nundle in the northern tablelands of New South Wales, Australia (Figure 1). An undulating plateau characterized by hilly topography underlies this plantation, which is comprised of largely basalt rock and fertile Tertiary basalt soils [34]. The mean elevation and the annual rainfall are approximately 1090 m asl and 1050 mm, respectively, as calculated by BIOCLIM variables using ANUCLIM 6.1 software [35]. The commercial plantation estate contains over 100 compartments, representing a range of age classes and silvicultural practices, however, due to financial constraints; only two even-aged stands were evaluated. The two stands included the 34 year old age (at the time of assessment-July 2011) class established in 1977 and the 9 year old age class planted in 2002. According to local historical records, the initial stocking rate of these stands was approximately 1300 stems per ha for the 1977 stand and 1000 stems per ha for the 2002 stand; however self-thinning processes resulted in irregular stem density within the study sites over the years following plantation establishment.
2.2. Field Survey Data
The field survey plots used in this study were originally established for another study by the New South Wales Department of Primary Industries and the Forestry Corporation NSW (FCNSW). The plots were initially stratified using focal-based stand level metrics extracted from a LiDAR-derived CHM with 1 m resolution. Two metrics were used for the stratification process, Mean Dominant Height (MDH) and local stocking. A total of 55 plots in the 1977 stand and 53 plots in the 2002 stand were initially established. The plot centers were provided as GPS waypoints and A4 size color prints. Two GPS units were used to locate plot centers in the field, the ScoutPak GPS system (Juniper Systems and OnPOZ Precision Positioning, Logan, UT, USA) and the Garmin Oregon® 550 (Garmin International, Olathe, KS, USA), while color print images were manually interpreted as a secondary location check. The 1977 plots ranged in size from 11.28 to 19.96 m radius and in the 2002 stand from 7.98 to 17.84 m radius, depending on the density of trees. The DBH (at 1.3 m) of all the trees in these plots was measured with diameter tape. Moreover, from each plot an average of 5 to 6 trees were selected and their heights measured (using an average of three readings recorded with a digital hypsometer (Haglöf Vertex IV Hypsometer, Sweden). These trees were selected based on the diameter range observed across each plot and represented a subsample of the variability present in all trees across the plot. Stocking rate values were calculated for each plot by counting the number of trees in the plot and dividing by the known area (area of circular plot = π × radius2). Table 1 shows additional information relating to the study sites.
2.3. LiDAR Data Acquisition
Over the Hanging Rock State Forest, discrete return airborne LiDAR data was collected using a Trimble Harrier 68i system mounted on a Cessna U206G airplane with a flying altitude of 1000 m and a swath width of approximately 1 km. The acquisition occurred in June 2011. The Trimble Harrier 68i had a scan rate of 81 Hz, pulse rate of 200 kHz, a footprint size of 50 cm, an average sampling interval of 70 cm and an average posting density of 3.65 points per square meter (including 40% overlap). The airplane was further equipped with the Applanix POS/AV 410 navigational system and a dual frequency GPS base station. The LiDAR points were captured, processed, geo-referenced and classified by Terranean Mapping Technologies Pty Ltd into ground and non-ground categories using MARSÒ software (Merrick & Company, Merrick, NY, USA).
2.4. Visual Tree Counts Using LiDAR Point Cloud and WorldView-2 Imagery
Although the number of trees in each plot was recorded in the field, to validate the LiDAR prediction accuracy the tree counts per plot from LiDAR (manual detection) were compared to the field data. FUSION software and LiDAR data viewer (LDV) visualizing system created from the US Forest Service [36] were used for processing the LiDAR data. As mentioned previously, the radius values of each field plot varied within the study areas. Using the GPS waypoint of the plot center together with the plot radius, virtual boundaries were created for each plot using ArcGIS software (ArcGIS 10, ESRI). To increase the reliability of plot boundaries, FUSION “plot mode” was also used, which defines a buffer around the specific area, in this case plot center coordinates, and includes data from the buffer in a data subset. This option facilitates the alignment of LiDAR data subsets with field plots and eases the tree identification process as well as attributes measurements for trees whose stem is within the plot [36]. A WorldView-2 (2011) satellite image was also used as background image to provide accurate estimation of tree numbers. Therefore, based on these functions, stems in each virtual boundary (plots) were counted manually and correlated with the sum of all stems within each field plot.
2.5. Diameter at Breast Height (DBH) and Height Relationship with Stocking
Relationships between LiDAR height and stocking and DBH and stocking were examined. To achieve this objective, only those trees in the field that could be exactly identified and matched within the LiDAR data were selected. This was possible with the aid of GPS locations, color hardcopy image prints and visual interpretation of crown and canopy gap arrangements. A total of 193 trees within 34 plots (out of 55 plots established by FCNSW) in the 1977 stand and 254 trees within 43 plots (out of 53 plots established by FCNSW) in the 2002 stand were identified. These plots were denoted as “experimental plots”. The heights of these 447 trees were individually calculated in LDV using the LiDAR point cloud. The LiDAR estimated heights and measured field height were compared with each other and the results revealed a significant correlation (R2 = 0.90 and relative RMSE = 0.66 for 2002 and R2 = 0.87 and relative RMSE = 1.49 for 1977 stands) within the two study sites. Therefore, given the similarity of these two measures, LiDAR extracted heights were used instead of field measured heights in all subsequent analyses. Following this examination, the relationships between LiDAR height and stocking and DBH and stocking were evaluated.
Multivariate Mixed Linear Model
For the primary analysis, a multivariate mixed linear model was used, in which tree DBH and height were modeled simultaneously. The basic assumption in this modeling approach was that the DBH and height of the trees are correlated variables. Multivariate mixed effects models define a relationship between the response variables (DBH and height) and the covariate (stocking) that has been measured or observed along with the response, and allow for the inclusion of Plot and Stratum as random terms in the model [37]. The use of plots and strata as random terms in the model accounts for much of the variation and allows the relationship between DBH/height and stocking to be better estimated.
The multivariate model was written in the following form:
2.6. Verification Process
2.6.1. Field Measured Diameter at Breast Height (DBH) and Field Measured Tree Counts
To further support the analysis between height-stocking and DBH-stocking, two separate examinations were undertaken. For the DBH-stocking relationship, the field measured DBH of the remaining trees, besides the ones located within the LiDAR data (447 trees), were used. Within the 55 plots in the 1977 stand, 1071 trees were selected and the DBHs measured, while in the 53 plots in the 2002 stand, 1009 trees were selected and the DBHs measured. These DBH values were used to assess the relationship between DBH and plot density. The exact locations of these trees were not identified in field or LiDAR data, therefore their height could not be manually extracted from LiDAR; as a result a separate analysis was considered to verify the height-stocking relationship.
2.6.2. LiDAR-Derived Tree Counts and Height
Specifically for height-stocking relationship an additional desk-top examination was undertaken, based on randomly selected trees across the sites. For this purpose a CHM was generated in FUSION as the difference in elevation between the upper canopy surface or Digital Surface Model (DSM) and the Digital Elevation Model (DEM) values. A CHM, based on 3 m and 2 m resolution pixels was produced (due to the differences in crown size) for the 1977 and 2002 stands respectively. Based on the average radius of the field plots established by FCNSW, virtual plots were randomly created across the study sites. The average radius for the 1977 and 2002 stands was calculated as 17 and 12 m respectively. The virtual plots were randomly spread across the sites representing a range of different stocking rates. In the older stand, 125 virtual plots, and in the younger stand, 100 virtual plots were established. From each plot 15 trees (some plots had less than 15 trees) were selected randomly and their heights were determined from the CHM (with tree heights >5 m in the young forest stand and >15 m in the older forest stand), bringing the total sample to 1789 trees in the 1977 stand and 1382 trees in the 2002 stand. The local maxima method was performed for detecting the tree tops in a fixed 3 × 3 search window across the 2 m and 3 m CHMs. The local maxima method is based on the assumption that the highest elevation data (local high intensity maxima) contained in individual pixels, represent a tree and the surrounding pixels are assumed to represent laser hits of the same tree crown [40]. This method has been widely used in the literature with satisfactory results (e.g., [25,41]). For detecting the exact position of the trees in order to verify the local maxima height calculation, as well as measuring the tree numbers in each virtual plot, the LiDAR point cloud in LDV (3D) and the WorldView-2 image were also used. The integration of tree positions in the CHM along with LDV and satellite imagery provided a useful way of assessing the accuracy of the local maxima method at the single tree-level. The LiDAR-derived heights were later correlated with LiDAR-derived stocking.
The verification process for DBH-stocking and height-stocking was performed with univariate linear mixed models fitted separately since the DBH and height measurements were not from the same trees. In order to reduce estimation bias, linear mixed models were fitted using the REML method. Similar to the experimental plots, the statistical software package R was used for verification. Since the virtual plots were not stratified, strata were not included as a random effect in the height-stocking model.
3. Results
3.1. The Accuracy of Tree Counts from LiDAR
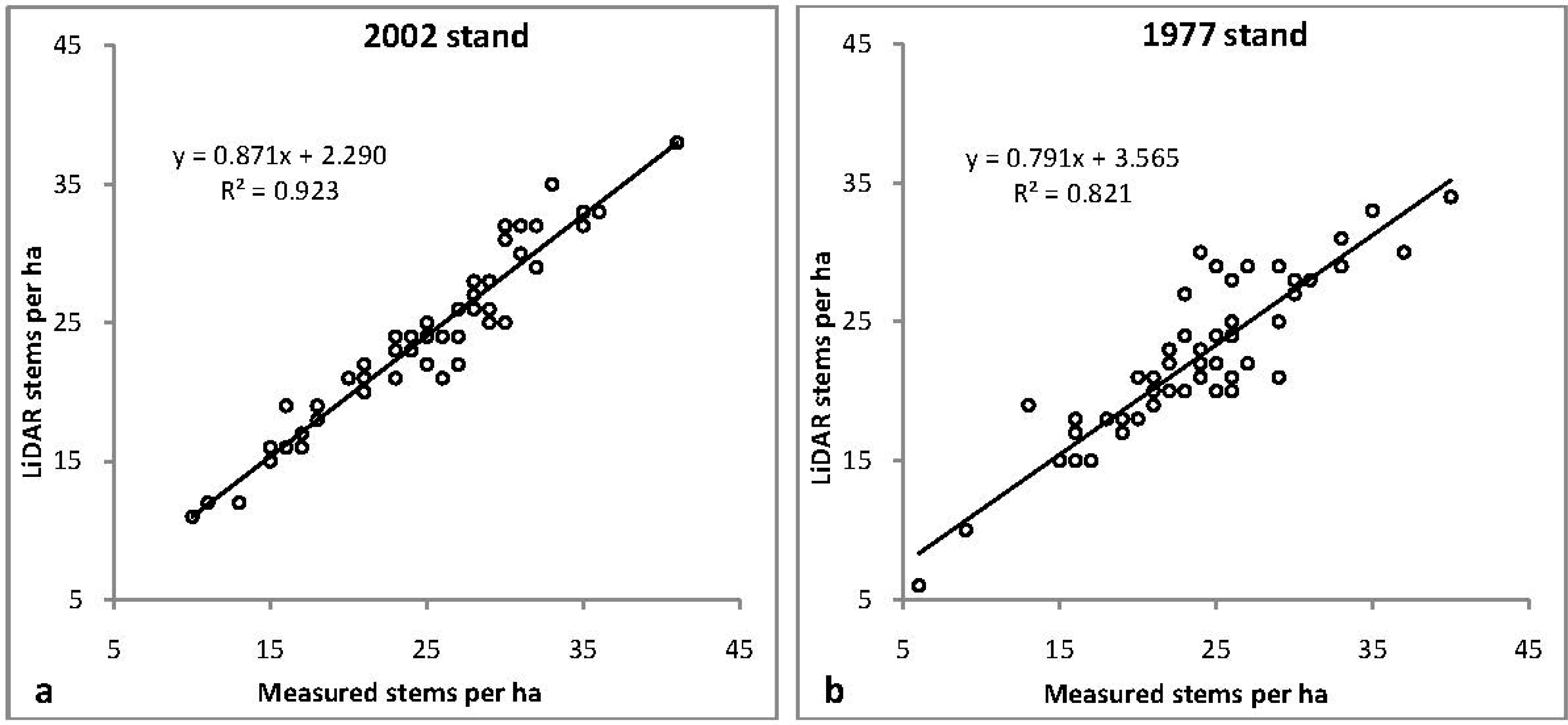
Figure 2 illustrates the high correlation between the density of stems observed in the field and the density of stems manually estimated from the LiDAR point cloud at both study sites. The values of R2 for 2002 and 1977 stands were 0.92 and 0.82 and the root mean square error (RMSE) values for the stands were 4.13 and 9.47 respectively.
3.2. Effect of Stocking on Diameter at Breast Height (DBH) and Height
3.2.1. The 1977 Stand
The DBH and height (derived from LiDAR) of the 193 trees in the older stand were fitted to stocking using the multivariate mixed linear model (Equation (2)).
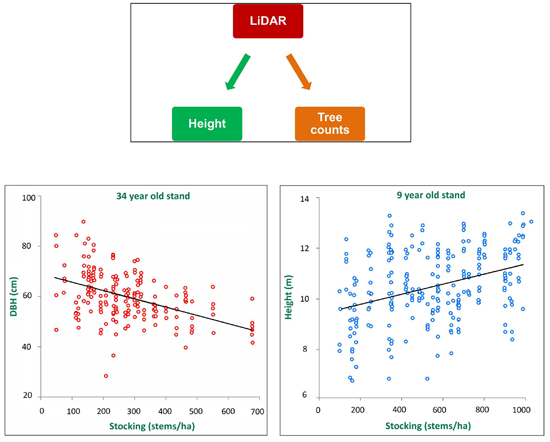
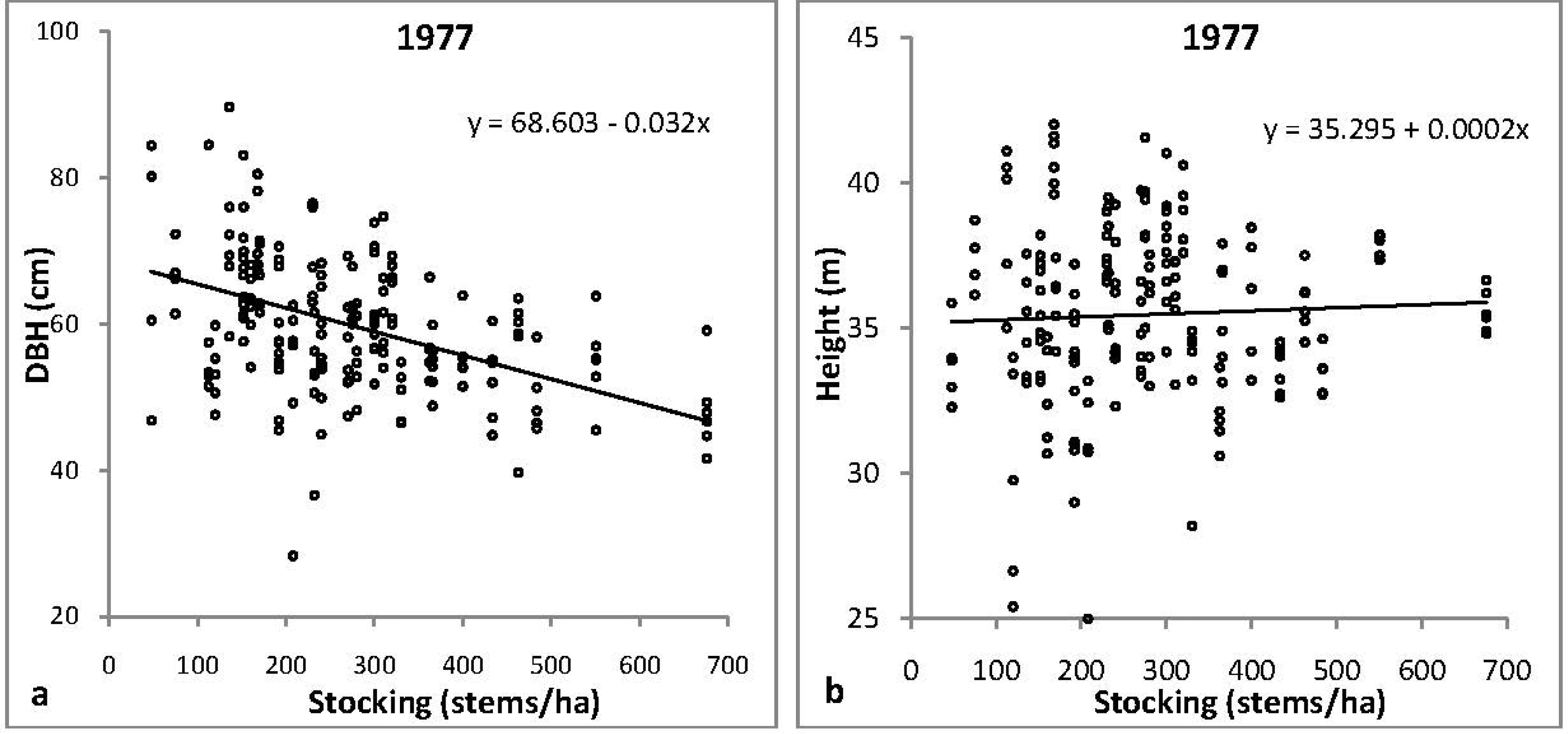
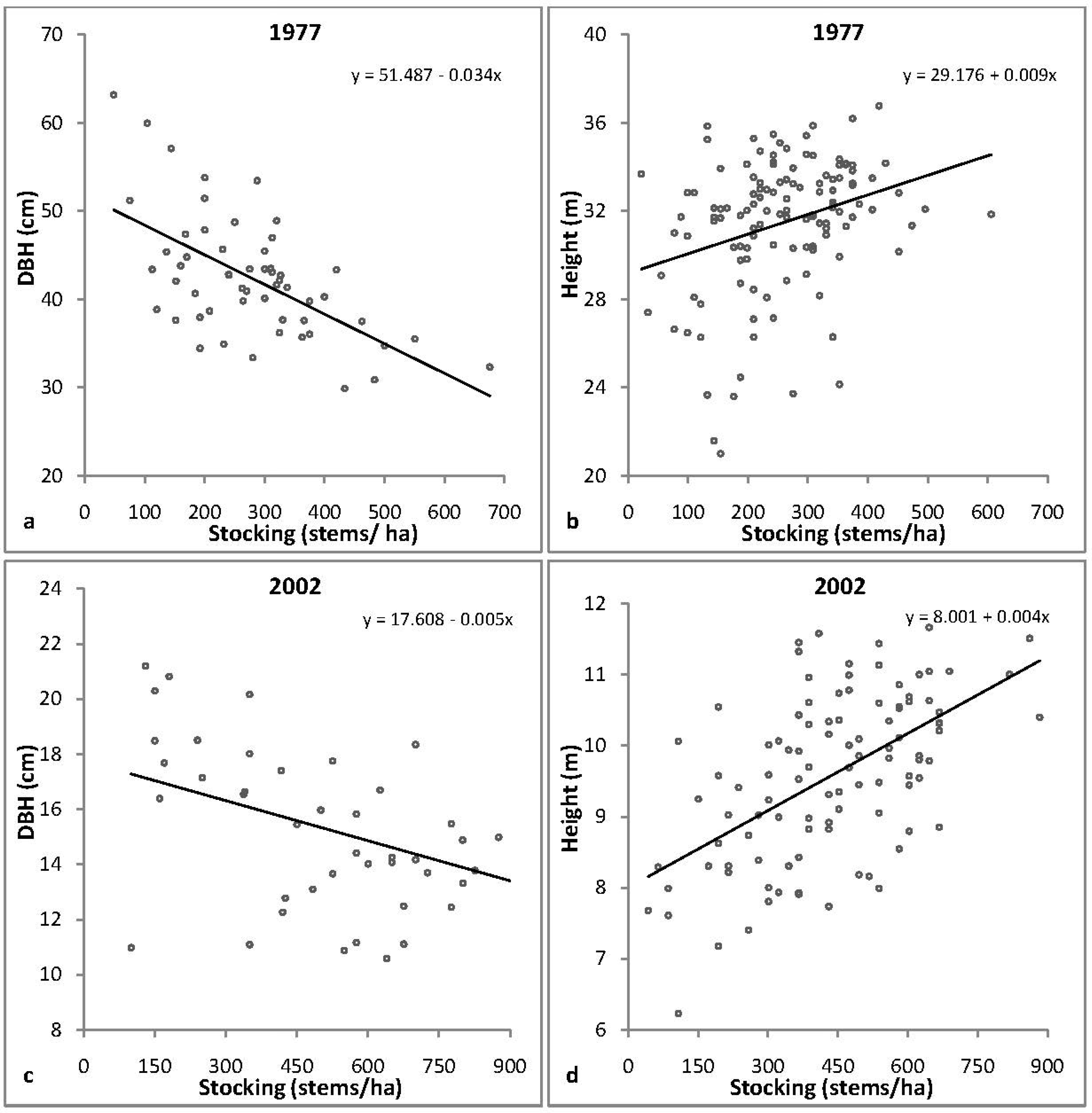
The Wald statistics and P values (probabilities of exceeding the Wald statistics) are presented in Table 2. The relationship between the DBH and height of the trees in the older stand and stocking were highly significant (p < 0.001). Figure 3a illustrates the relationship between DBH and stocking, suggesting a decrease in DBH with increased stocking in the 1977 stand. However unlike DBH, Figure 3b illustrates an increase in height with a reduction in stocking.
3.2.2. The 2002 Stand
A similar process was carried out for the 2002 stand, where the DBH and height (derived from LiDAR) of the younger trees were fitted to the stocking (Equation (2)). The analysis of variance (ANOVA) results in Table 3 showed a significant relationship between the height and DBH of the 254 trees and the stocking (p < 0.01), with random plots and strata also showing a highly significant correlation.
Figure 4 presents the relationship between the tree variables and stocking for the 2002 stand. Similar to the older stand, in lower density plots larger DBH values were seen but as the density increased smaller diameter trees were more evident. However, taller trees were found in areas with higher stocking, while shorter trees were seen in areas with lower stocking.
3.3. Independent Verification of the Effect of Stocking on Diameter at Breast Height (DBH) and LiDAR Height
Mixed linear models were constructed separately for the DBH-stocking and height-stocking relationships at both sites. Due to the uncoupling of height and DBH measurements (derived from different trees); the model parameters of these components could not be estimated simultaneously. Based on the results presented in Table 4, the DBH and height of both sites showed significant relationships with stocking (p < 0.001 and p < 0.01). The linear model of the DBH-stocking and height-stocking is illustrated in Figure 5. The DBH-stocking relationship at both sites displayed a similar trend, where larger DBHs are associated with lower stocking. However in contrast to DBH results, trees tended to grow taller with increased stocking rate at both sites.
The verification results presented here were similar to the experimental plots (Figures 3 and 4). The additional analysis confirmed the significant relationships between the DBH and height with stocking (Figure 5).
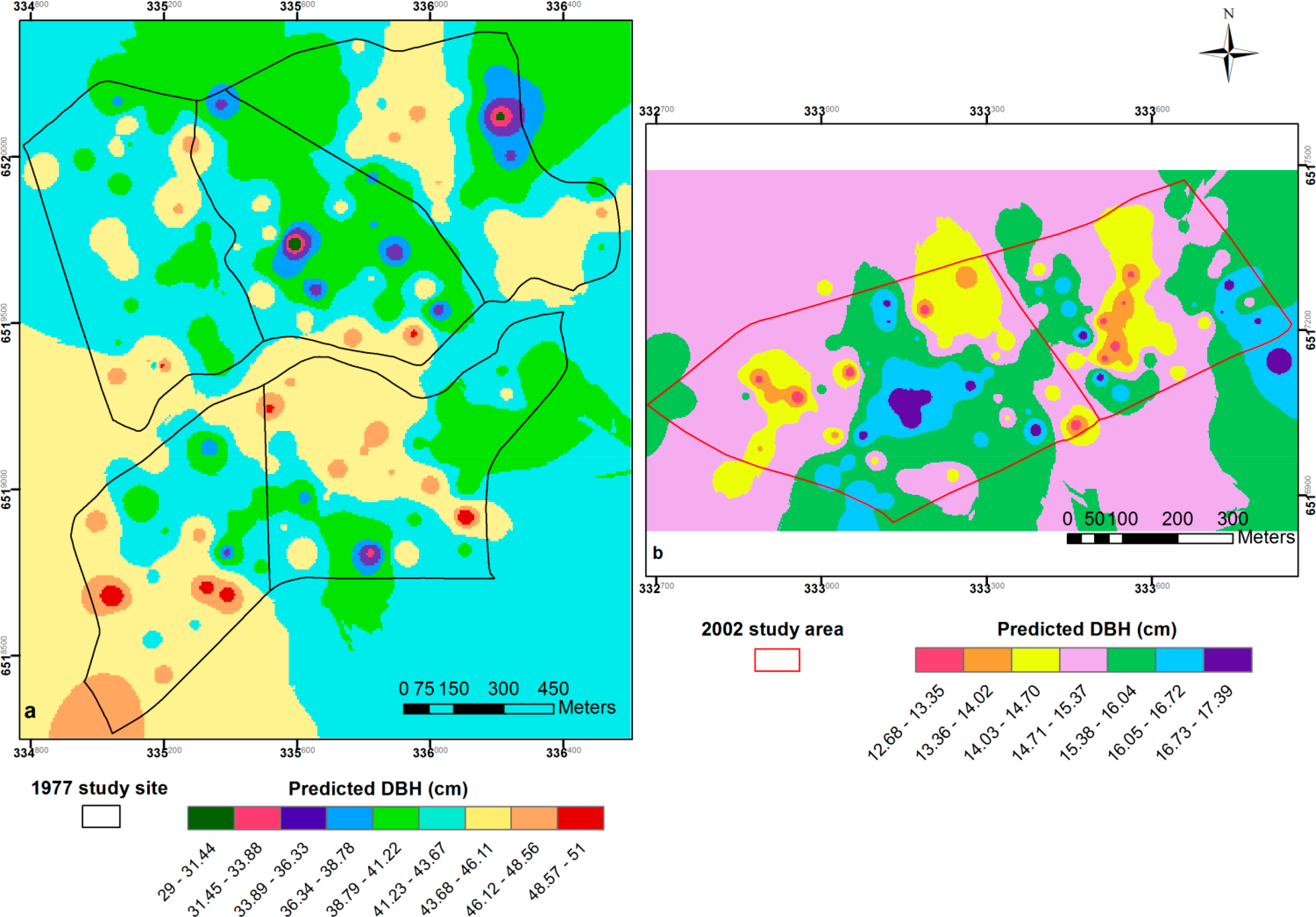
Figure 6 illustrates the spatial distributions of the predicted DBH derived from the equations in Figure 5 at both study sites.
4. Discussion
Stocking (stems/ha) is an important inventory metric and is a critical parameter used in forest management decisions. Effective stocking, for example, is a measure of minimum stocking at particular critical ages and silvicultural stages that are required to support current or future commercial thinning and harvesting operations. In this study, a combination of plot field data and LiDAR data was used to confirm the relationship of variable stocking on tree DBH and height within stands of P. radiata. The results from the 2002 and 1977 age class stands demonstrate the strong relationship between tree DBH and heights with stocking rate, wherein taller and smaller diameter trees (i.e., more slender trees) were found in areas with higher stocking. The additional independent verification process confirmed these results. Maclaren et al. [42], in New Zealand, observed an increase in height of radiata pine trees with stocking rate at very young ages (4 to 5 years). They also compared the height of trees at 50 stems/ha stocking with those at 400 stems/ha and their results revealed that the majority of trees in higher stocking areas were taller than the lower stocking areas. The negative linear relationship between stand density and DBH in the experimental plots in both the 1977 and 2002 stands revealed that larger diameter trees were found in areas with lower stocking. These findings are consistent with other studies which have reported that tree height appears to be relatively unaffected by stand stocking, except in younger stands, while tree diameter exhibits a strong negative relationship with stand stocking (e.g., [9,13,42]). Rapid height growth in competition with other young trees is advantageous to access a greater share of solar radiation, however once the size structure is determined (mature age), trees tend to grow laterally (DBH growth) not vertically (height growth). This arises in part, because the initial preferential carbon allocation to height becomes limited by hydraulic and mechanical considerations [43]. In addition, Watt and Kirschbaum [44] have shown that the relationship between P. radiata height and diameter is influenced by the soil carbon to nitrogen (CN) ratio, although the two sites in this study had relatively uniform fertile Tertiary basalt soils [34].
The manipulation of stocking through initial planting densities and subsequent thinning operations is commonly practiced to control growth rates and tree form, with the aim to maintaining uniformity in these attributes throughout the management unit (i.e., compartment). However, even in well-managed stands, significant variation in stand stocking can occur for a range of reasons, for example, drought, animal browsing or strong winds [45–47]. Falling trees expose gaps between trees, giving the remaining trees better access to light, nutrients, and soil moisture. In our study area, however, the lack of prescribed thinning events has likely been the cause of the irregular stocking rates, which in turn has contributed to the variation observed in height and DBH.
In operational planning, knowledge of stand variability is highly desirable as it can directly affect operational scheduling and costs. LiDAR technology has proven to be an effective tool for estimating mean values as well as the spatial variation of inventory parameters for P. radiata plantations such as stand height, basal area and volume [19,20,48]. In this study, a comparison of the number of stems counted from LiDAR data (average posting density of 3.6 points m−2) and stem numbers counted in field plots in two age class stands also confirmed the feasibility of using LiDAR data for tree detection in commercial P. radiata plantations. Two previous studies also revealed acceptable levels of accuracy in detecting P. radiata tree crowns [21,48]. Chen and Zhu [48] applied a marker-controlled watershed segmentation technique to identify local maxima representing radiata tree tops. Their approach has the advantage in that it does not require a priori knowledge of the relationship between tree height and crown size. González-Ferreiro et al. [24] compared the manual detection of radiata trees in the LiDAR point cloud with an automatic approach using Definiens®Developer 7.0 software. They reported that the manual method performed slightly better, as 71.9% of the trees were correctly located in the manual process compared to 63.5% in the automated procedure. However, they suggested the use of the automated approach over the manual method since it allows large-scale automation of the tree identification process without substantial loss of accuracy with less processing time. Nevertheless, in our study, the fusion of the WorldView-2 imagery with the 3D display of LiDAR point clouds was instrumental in achieving a high correlation with the number of stems in the field plots. Although not applied in this study, numerous automatic algorithms for detecting and delineating individual tree crowns from LiDAR data are routinely being presented with improving performance and computational efficiencies (e.g., [29,49]). The challenge is now for to the integration of these routines into operational plantation management information systems.
It should be noted that LiDAR studies, similar to other remote sensing studies of individual tree properties, are sensitive to positional error of both field data and remote sensed data [28]. Potential sources of errors derived from ground-based survey measurements, scanning configuration, position of the tree within the canopy, ground slope effects and crown shape and spacing might affect the predictors extracted from LiDAR such as height [22,28]. LiDAR tree height measurement methods rely on ground surface elevation model. The spatial accuracy of DEMs can also be influenced by the surface modeling approach used in processing the raw data points which can also transfer to height estimates. Although the accuracy of DEM was not calculated in this study, the RMSE derived from the LiDAR height and field heights (0.66 for 2002 and 1.49 for 1977 stands) indicate the terrain error is likely to be small. The LiDAR derived DEMs with higher spatial resolution are better able to describe small-scale landscape with moderately dense canopy variations than low resolution DEMs [50]. Many researchers have indicated that LiDAR-derived elevation were highly accurate with similar elevation predictions (e.g., [28,51,52]). Moreover, the field survey was designed to prevent potential errors (tree height and DBH precision were measured to 10–30 cm and 1 cm, respectively); however, it is likely that slight errors may have occurred in the field measurements.
5. Conclusions
Radiata tree height and Diameter at Breast Height (DBH) can be influenced by a range of stand and local environmental conditions. In this research the interrelationship between stem diameter, height and stocking were investigated with the use of LiDAR for the case of two large even-aged radiata pine stands in Australia. Significant relationships existed between both height and DBH variables with stocking (p < 0.001), wherein an increase in DBH and a decrease in height were found to be associated with decreased stocking. Moreover LiDAR data showed a good performance in detecting individual trees in the plots (average R2 = 0.87). In addition to providing a good estimation of stocking based on the accurate detection of tree crown maximas, the successful use of LiDAR to estimate stand and individual tree heights illustrates its effectiveness in forest inventory applications. The relationships between stocking density and DBH and height are of interest for understanding the influence of environmental factors on the growth of forests as well as silvicultural planning. Since field inventory is time consuming and costly, this study showed that airborne LiDAR data with sufficient point density, allows for estimating a range of forest biophysical attributes with high accuracy, especially when there is considerable variation within compartments or there are accessibility issues such as steep slopes or dense undergrowth (e.g., see [53]). It should also be noted that the recommended sampling intensity for inventory plots prescribed by radiata plantation growers in Australia is 1 plot per 4 ha; however, it is unlikely that this sampling strategy would accurately capture the observed variation in these stands. Further work needs to be done to find suitable explicit attributes in sampling designs.
Acknowledgments
The authors would like to thank Forestry Corporation New South Wales for providing the LiDAR data, and the New South Wales Department of Primary Industries for help in conducting the field surveys used in this study.
Author Contributions
Hanieh Saremi designed the experiment and processed the data. Lalit Kumar coordinated the research project and gave technical support and conceptual advice. Christine Stone served as scientific advisor. Hanieh Saremi and Christine Stone wrote the paper. Hanieh Saremi, Russell Turner and Christine Stone collected the data. Gavin Melville performed experiments and analyzed the data. Hanieh Saremi, Lalit Kumar, Christine Stone, Gavin Melville and Russell Turner helped in preparation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Álvarez, J.; Allen, H.L.; Albaugh, T.J.; Stape, J.L.; Bullock, B.P.; Song, C. Factors influencing the growth of radiata pine plantations in chile. Forestry 2013, 86, 13–26. [Google Scholar]
- Forrest, W.G. Variations in the Accumulation, Distribution and Movement of Mineral Nutrients in Radiata Pine Plantations. Ph.D. Thesis. Australian National University, Canberra, Australia, 1969. [Google Scholar]
- McCallum, D.J.; Mason, E.G.; Whitley, B. Influence of exposure and elevation on radiata pine branch size, log velocity, sweep, taper and value. N. Z. J. For. Sci 2007, 52, 10–16. [Google Scholar]
- Lasserre, J.P.; Mason, E.G.; Watt, M. The influence of initial stocking on corewood stiffness in a clonal experiment of 11-year-old. Pinus radiata D. Don. N. Z. J. For. Sci 2004, 49, 18–23. [Google Scholar]
- Kumar, L.; Skidmore, A.K. Radiation—Vegetation relationships in an eucalyptus forest. Photogramm. Eng. Remote Sens 2000, 66, 193–204. [Google Scholar]
- Castedo-Dorado, F.; Crecente-Campo, F.; Álvarez-Álvarez, P.; Barrio-Anta, M. Development of a stand density management diagram for radiata pine stands including assessment of stand stability. Forestry 2009, 82, 1–16. [Google Scholar]
- Lasserre, J.-P.; Mason, E.G.; Watt, M.S. The effects of genotype and spacing on Pinus radiata [D. Don] corewood stiffness in an 11-year old experiment. For. Ecol. Manag 2005, 205, 375–383. [Google Scholar]
- James, R.N. The influence of tree breeding and stocking rate on tree crop quality. N. Z. J. For. Sci 1979, 24, 230–240. [Google Scholar]
- Waghorn, M.J.; Mason, E.G.; Watt, M.S. Assessing interactions between initial stand stocking and genotype on growth and form of 17 year old Pinus radiata in Canterbury. N. Z. J. For. Sci 2007, 52, 24–30. [Google Scholar]
- Mead, D.J. Sustainable Management of Pinus Radiata Plantations; FAO Forestry Paper: Rome, Italy, 2013. [Google Scholar]
- Klitscher, J.A. Mortality trends in Pinus radiata in the rotorua region. N. Z. J. For. Sci 1987, 31, 23–25. [Google Scholar]
- Mason, E.G. Decision-Support Systems for Establishing Radiata Pine Plantations in the Central North Island of New Zealand. Ph.D. Thesis. University of Canterbury, Christchurch, New Zealand, 1992. [Google Scholar]
- Beets, P.N.; Kimberley, M.O. Genotype x stocking interactions in Pinus radiata: Productivity and yield implications. In Management of Structure and Productivity of Borealand Subalpine Forests; Linder, S., Kellomaki, S., Eds.; Studia Forestalia Suecica: Uppsala, Sweden, 1993; pp. 11–194. [Google Scholar]
- Hocker, H.W. Introduction to Forest Biology; John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Menzies, M.I.; Klomp, B.K.; Holden, D.G.; Hong, S.O. The effect of initial spacing on growth and crop selection of radiata pine seedlings and cuttings. In Efficiency of Stand Establishment Operations; Menzies, M.I., Parrot, G.E., Whitehouse, L.J., Eds.; New Zealand Forest Research Institute Bulletin: Rotorua, New Zealand, 1989; Volume 156, pp. 152–164. [Google Scholar]
- Whiteside, I.D. Silvicultural characteristics of radiata pine in Tapanui district. N. Z. J. For. Sci 1962, 594–607. [Google Scholar]
- Bortolot, Z.J. Using tree clusters to derive forest properties from small footprint lidar data. Photogramm. Eng. Remote Sens 2006, 72, 1389–1397. [Google Scholar]
- Næsset, E. Practical large-scale forest stand inventory using small-footprint airborne scanning laser. Scand. J. For. Res 2004, 19, 164–179. [Google Scholar]
- Stone, C.; Penman, T.; Turner, R. Determining an optimal model for processing lidar data at the plot level: Results for a Pinus radiata plantation in New South Wales. N. Z. J. For. Sci 2011, 41, 191–205. [Google Scholar]
- Rombouts, J.; Ferguson, I.S.; Leech, J.W. Campaign and site effects in lidar prediction models for site-quality assessment of radiata pine plantations in South Australia. Int. J. Remote Sens 2010, 31, 1155–1173. [Google Scholar]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Miranda, D. Estimation of stand variables in Pinus radiata D. Don plantations using different lidar pulse densities. Forestry 2012, 85, 281–292. [Google Scholar]
- Edson, C.; Wing, M.G. Airborne light detection and ranging (Lidar) for individual tree stem location, height, and biomass measurements. Remote Sens 2011, 3, 2494–2528. [Google Scholar]
- Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on the random forests technique. ISPRS J. Photogramm. Remote Sens 2011, 66, 28–37. [Google Scholar]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Barreiro-Fernández, L.; Buján, S.; Barbosa, M.; Suárez, J.C.; Bye, I.J.; Miranda, D. A mixed pixel- and region-based approach for using airborne laser scanning data for individual tree crown delineation in Pinus radiata D. Don plantations. Int. J. Remote Sens 2013, 34, 7671–7690. [Google Scholar]
- Hyyppä, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens 2001, 39, 969–975. [Google Scholar]
- Leckie, D.; Gougeon, F.; Hill, D.; Quinn, R.; Armstrong, L.; Shreenan, R. Combined high-density lidar and multispectral imagery for individual tree crown analysis. Can. J. Remote Sens 2003, 29, 633–649. [Google Scholar]
- Jakubowski, M.K.; Li, W.; Guo, Q.; Kelly, M. Delineating individual trees from Lidar data: A comparison of vector- and raster-based segmentation approaches. Remote Sens 2013, 5, 4163–4186. [Google Scholar]
- Turner, R.S. An Airborne Lidar Canopy Segmentation Approach for Estimating Above-Ground Biomass in Coastal Eucalypt Forests. Ph.D. Thesis. University of New South Wales, Sydney, Australia, 2006. [Google Scholar]
- Li, W.; Guo, Q.; Jakubowski, M.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens 2012, 78, 75–84. [Google Scholar]
- Watt, M.; Meredith, A.; Watt, P.; Gunn, A. Use of lidar to estimate stand characteristics for thinning operations in young Douglas-fir plantations. N. Z. J. For. Sci 2013, 43. [Google Scholar] [CrossRef]
- Woods, M.; Pitt, D.; Penner, M.; Lim, K.; Nesbitt, D.; Treitz, P. Operational implementation of a lidar inventory in Boreal Ontario. Forest. Chron 2010, 87, 512–528. [Google Scholar]
- Saremi, H.; Kumar, L.; Turner, R.; Stone, C. Airborne lidar derived canopy height model reveals a significant difference in radiata pine (Pinus radiata D. Don) heights based on slope and aspect of sites. Trees 2014, 28, 733–744. [Google Scholar]
- Saremi, H.; Kumar, L.; Turner, R.; Stone, C.; Melville, G. Impact of local slope and aspect assessed from LiDAR records on tree diameter in radiata pine (Pinus radiata D. Don) plantations. Ann. For. Sci 2014. [Google Scholar] [CrossRef]
- Ryan, P.J.; Holmes, G.I. Geology of Hanging Rock and Nundle State Forests; Soils and Nutrition Group, Forestry Commission of New South Wales: Sydney, Australia, 1986. [Google Scholar]
- Xu, T.; Hutchinson, M.F. Anuclim Version 6.1 User Guide; The Australian National University, Fenner School of Environment and Society: Canberra, Australia, 2011. [Google Scholar]
- Fusion Manual Version 2.90. Available online: http://www.fs.fed.us/ (accessed on 20 May 2012).
- Gilmour, A.R.; Cullis, B.R.; Verbyla, A.P. Accounting for natural extraneous variation in the analysis of field experiments. JABES J. Agric. Biol. Environ. Stat 1997, 2, 269–273. [Google Scholar]
- Butler, D.; Cullis, B.R.; Gilmour, A.R.; Gogel, B.J. Asreml-R Reference Manual, Release 3; Department of Primary Industries and Fisheries: Queensland, Australia, 2009. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2011. [Google Scholar]
- Kini, A.U.; Popescu, S.C. Treevaw: A versatile tool for analyzing forest canopy lidar data—A preview with an eye towards future. Proceedings of the American Society for Photogrammetry and Remote Sensing (ASPRS) Fall Conference, Kansas City, MO, USA, 12–16 September 2004; pp. 1–10.
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint lidar data. Photogramm. Eng. Remote Sens 2006, 72, 923–932. [Google Scholar]
- Maclaren, J.P.; Grace, J.C.; Kimberley, M.O.; Knowles, R.L.; West, G.G. Height growth of Pinus radiata as affected by stocking. N. Z. J. For. Sci 1995, 25, 73–90. [Google Scholar]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the structure and allometry of plant vascular systems. Nature 1999, 400, 664–667. [Google Scholar]
- Watt, M.S.; Kirschbaum, M.U.F. Moving beyond simple linear allometric relationships between tree height and diameter. Ecol. Model 2011, 222, 3910–3916. [Google Scholar]
- Moore, J.R.; Tombleson, J.D.; Turner, J.A.; van der Colff, M. Wind effects on juvenile trees: A review with special reference to toppling of radiata pine growing in new zealand. Forestry 2008, 81, 377–387. [Google Scholar]
- Cremer, K.W.; Borough, C.J.; McKinnell, F.H.; Carter, P.R. Effects of stocking and thinning on wind damage in plantations. N. Z. J. For. Sci 1982, 12, 244–268. [Google Scholar]
- Stone, C.; Penman, T.; Turner, R. Managing drought-induced mortality in Pinus radiata plantations under climate change conditions: A local approach using digital camera data. For. Ecol. Manag 2012, 265, 94–101. [Google Scholar]
- Chen, Y.; Zhu, X. Site quality assessment of a Pinus radiata plantation in Victoria, Australia, using lidar technology. South. For 2012, 74, 217–227. [Google Scholar]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkänen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2011, 85, 27–40. [Google Scholar]
- Venzin, C. Analyzing the Impact of High Resolution DEM Uncertainty on Hydrological Models Using a Parallel Computing Approach. M.Sc. Thesis. University of Zurich, Zurich, Switzerland, 31 January 2013. [Google Scholar]
- Reutebuch, S.E.; McGaughey, R.J.; Andersen, H.-E.; Carson, W.W. Accuracy of a high-resolution lidar terrain model under a conifer forest canopy. Can. J. Remote Sens 2003, 29, 527–535. [Google Scholar]
- Watt, M.; Adams, T.; Gonzalez Aracil, S.; Marshall, H.; Watt, P. The influence of lidar pulse density and plot size on the accuracy of New Zealand plantation stand volume equations. N. Z. J. For. Sci 2013, 43, 15. [Google Scholar]
- Wolf, J.A.; Fricker, G.A.; Meyer, V.; Hubbell, S.P.; Gillespie, T.W.; Saatchi, S.S. Plant species richness is associated with canopy height and topography in a neotropical forest. Remote Sens 2012, 4, 4010–4021. [Google Scholar]

| Study Site | Land Cover type | Elevation Range (m) | Area (ha) | No of Initial Plots | Mean Stocking in 2011 (stems/ha) | Plot Size Radius Range (m) | Mean Tree DBH (cm) | Mean Tree Height (m) |
|---|---|---|---|---|---|---|---|---|
| 2002 | 9-year old forest | 1256–1280 | 36 | 53 | 560 | 7.98–17.84 | 16.33 | 10.96 |
| 1977 | 34-year old forest | 1200–1253 | 215 | 55 | 285 | 11.28–19.96 | 43.9 | 35.0 |
| Dependent Variable | Parameter | Degrees of Freedom | Wald Statistic | p a (Chisq) |
|---|---|---|---|---|
| DBH/Height | Mean | 1 | 6390.5 | p < 0.001 |
| Stocking | 1 | 22.3 | p < 0.001 |
aSignificance level at p < 0.001 (***).
| Dependent Variable | Parameter | Degrees of Freedom | Wald Statistic | p a (Chisq) |
|---|---|---|---|---|
| DBH/Height | Mean | 1 | 2588.7 | p < 0.001 |
| Stocking | 1 | 10.9 | p < 0.01 |
aSignificance level at p < 0.001 (***).
| Sites | Dependent Variable | Parameter | Degrees of Freedom | Wald Statistic | p a (Chisq) |
|---|---|---|---|---|---|
| 1977 stand | DBH | Mean | 1 | 1630.8 | p < 0.001 |
| Stocking | 1 | 30.0 | p < 0.001 | ||
| Height | Mean | 1 | 14,483.6 | p < 0.001 | |
| Stocking | 1 | 12.1 | p < 0.001 | ||
| 2002 stand | DBH | Mean | 1 | 905.1 | p < 0.001 |
| Stocking | 1 | 9.8 | p < 0.01 | ||
| Height | Mean | 1 | 10,135.6 | p < 0.001 | |
| Stocking | 1 | 39.6 | p < 0.001 | ||
aSignificance level at p < 0.001 (***).
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Saremi, H.; Kumar, L.; Stone, C.; Melville, G.; Turner, R. Sub-Compartment Variation in Tree Height, Stem Diameter and Stocking in a Pinus radiata D. Don Plantation Examined Using Airborne LiDAR Data. Remote Sens. 2014, 6, 7592-7609. https://doi.org/10.3390/rs6087592
Saremi H, Kumar L, Stone C, Melville G, Turner R. Sub-Compartment Variation in Tree Height, Stem Diameter and Stocking in a Pinus radiata D. Don Plantation Examined Using Airborne LiDAR Data. Remote Sensing. 2014; 6(8):7592-7609. https://doi.org/10.3390/rs6087592
Chicago/Turabian StyleSaremi, Hanieh, Lalit Kumar, Christine Stone, Gavin Melville, and Russell Turner. 2014. "Sub-Compartment Variation in Tree Height, Stem Diameter and Stocking in a Pinus radiata D. Don Plantation Examined Using Airborne LiDAR Data" Remote Sensing 6, no. 8: 7592-7609. https://doi.org/10.3390/rs6087592
APA StyleSaremi, H., Kumar, L., Stone, C., Melville, G., & Turner, R. (2014). Sub-Compartment Variation in Tree Height, Stem Diameter and Stocking in a Pinus radiata D. Don Plantation Examined Using Airborne LiDAR Data. Remote Sensing, 6(8), 7592-7609. https://doi.org/10.3390/rs6087592