Soil Surface Sealing Effect on Soil Moisture at a Semiarid Hillslope: Implications for Remote Sensing Estimation
Abstract
: Robust estimation of soil moisture using microwave remote sensing depends on extensive ground sampling for calibration and validation of the data. Soil surface sealing is a frequent phenomenon in dry environments. It modulates soil moisture close to the soil surface and, thus, has the potential to affect the retrieval of soil moisture from microwave remote sensing and the validation of these data based on ground observations. We addressed this issue using a physically-based modeling approach that accounts explicitly for surface sealing at the hillslope scale. Simulated mean soil moisture at the respective layers corresponding to both the ground validation probe and the radar beam’s typical effective penetration depth were considered. A cyclic pattern was found in which, as compared to an unsealed profile, the seal layer intensifies the bias in validation during rainfall events and substantially reduces it during subsequent drying periods. The analysis of this cyclic pattern showed that, accounting for soil moisture dynamics at the soil surface, the optimal time for soil sampling following a rainfall event is a few hours in the case of an unsealed system and a few days in the case of a sealed one. Surface sealing was found to increase the temporal stability of soil moisture. In both sealed and unsealed systems, the greatest temporal stability was observed at positions with moderate slope inclination. Soil porosity was the best predictor of soil moisture temporal stability, indicating that prior knowledge regarding the soil texture distribution is crucial for the application of remote sensing validation schemes.1. Introduction
Soil moisture at the surface vicinity affects the partitioning of rainfall into infiltration and runoff and modulates soil-atmosphere feedback interactions [1,2]. It also affects groundwater recharge, the movement of contaminants and crop growth [1], and therefore, it has been the focus of many studies that have addressed soil moisture dynamics across different climatic regions and spatial and temporal scales [3–6].
Due to advances in sensor technologies over the last two decades, spaceborne microwave instruments have become efficient tools for indirectly estimating soil moisture in the top few centimeters of soils at different spatial and temporal scales [7–13]. The effective penetration depth of the microwave beam depends upon several factors, including soil moisture [14] and soil properties [15]. Consequently, the effective penetration depth of the sensors ranges from ≈0.5 to 5 cm [14,16,17]. A common need for all remote-sensing (RS) missions, regardless of the spatial scale of interest, is intensive ground soil moisture sampling for the calibration of retrieval algorithms and the validation of the data [18]. These field campaigns are usually conducted using a network of soil moisture probes that monitor changes in the soil moisture of the upper soil layer [19,20]. Due to technical constraints [14] and field conditions, these probes usually measure the moisture in a layer 5 to 10 cm thick [21–24]. Therefore, when these probes are used for the calibration or validation of remotely sensed soil moisture, the depth of the sampled soil layer on the ground is generally deeper than the sensor’s effective penetration depth, a bias that can affect the estimates [14,16,25].
This issue can become even more complex when a physical seal layer has formed at the soil surface. Surface sealing is a widespread phenomenon that occurs in bare agricultural soils (after seed bed preparation, for example) and between patches of vegetation in natural landscapes [26]. The seal layer develops due to the pounding of raindrops on the soil surface and the destruction of soil aggregates. This, in turn, leads to the washing-in of fine material and the formation of a distinct compacted soil layer at the surface [27–29]. The difference in bulk density between the seal layer and the underlying undisturbed soil is greatest at the soil surface and decreases exponentially with depth at a rate that depends on soil and rainfall properties [26,30]. Therefore, the seal layer is characterized by hydraulic properties that differ significantly from those of the underlying soil and by a thickness that can reach a few centimeters [26]. Consequently, the seal layer was found to affect infiltration [31,32], evaporation fluxes [33–36] and runoff [32,37,38]. The presence of a seal layer at the surface can complicate the calibration or the validation of RS missions, since the sensor’s effective penetration depth lies mostly within the seal layer, whereas the soil moisture probe uses average soil moisture readings from both the seal layer and the undisturbed soil in the much thicker layer underneath. The way in which the seal layer on top of undisturbed soil affects the bias in the calibration and validation of RS data has not been investigated.
A second issue related to the validation procedure applied to RS data that could also be affected by soil surface sealing is the optimal location of soil moisture sampling sites on the ground. Regardless of the spatial scale of interest, field soil moisture data are required for the validation of the RS sensor footprint [5,18]. Conducting simultaneous multi-point soil-moisture validation campaigns can be unfeasible, due to time and cost restrictions, and an optimization method is highly sought to reduce the number of ground samples [39]. While many statistical optimization methods were presented (see the review by Hu et al. [40]), one of the promising methods for approaching this task that has been widely applied [4,41–43] is the time stability analysis, described by Vachaud et al. [44]. In that study, it was shown that soil moisture in particular individual locations conserves the property to represent the mean soil moisture value of the field and, thus, could be referred to as temporally stable.
To avoid an exhaustive review of the literature regarding factors affecting soil moisture temporal stability, only a concise summary is presented here (a detailed review can be found in Vanderlinden et al. [45]). Topography has a strong effect on soil moisture temporal stability (SMTS), with locations within mid-slopes or elevation [41,46] and locations with mild slope inclinations [43] exhibiting greater temporal stability. Vegetation was found to decrease SMTS [47]. Contradictory results were published regarding the effect of soil texture, where SMTS either increases [43,48] or decreases [2] with finer soil texture. Contradictory results were also published regarding the effect of soil depth on SMTS, with studies concluding that SMTS increases [42,49–51], decreases [52–54] or is unaffected by soil depth [55,56]. SMTS is affected by both spatial (e.g., maximal distance between measurements) and temporal (e.g., the frequency and duration of data acquisition) scales, with only a few studies spanning a period of several rainfall seasons or longer [45].
Modeling could be a step forward to address the complex interactions between the factors that affect soil moisture and its temporal stability [45]. This was demonstrated recently by Martinez et al. [48], who used a 1D physically-based model and a synthetic dataset of soil and climatic parameters to study how local controls, such as soil texture, regulate SMTS. However, soil surface sealing was disregarded in that study. Moreover, to the best of our knowledge, no attempt was made to study how the presence of a seal layer affects bare soil SMTS patterns at the hillslope scale and, consequently, optimal soil-moisture sampling locations.
This paper applies a physically-based model and uses long-term climatic records to reconstruct soil moisture realizations at the hillslope scale of a semiarid experimental site in central Israel, accounting explicitly for soil surface sealing. We addressed two questions:
- (1)
How does the presence of a seal layer affect soil moisture at the top soil? What are the implications for the validation of close range and remotely sensed data?
- (2)
Which factors control SMTS under sealed and unsealed conditions and how does the presence of a seal layer affect the sampling locations that best represent the hillslope mean soil moisture?
2. Material and Methods
2.1. The Study Site
The LTER (long-term ecological research) Lehavim site (31°20′N, 34°45′E) is located in the Negev Desert in the center of Israel (Figure 1). The climate is characterized as semiarid, with an annual rainfall of 290 mm, usually falling between November and March. Within the LTER, a typical hillslope was chosen (0.075 km2) composed of east- and west-facing slopes. The soils are brown lithosols and arid brown loess, which are prone to surface sealing, with a mean soil texture of 23% sand, 56% silt and 21% clay. The hillslope soil depth ranges from 0 to 55 cm, with a mean value of 22 cm. Rock outcroppings cover 11% of the entire hillslope and are concentrated mainly in the interfluvial area. The vegetation (24% cover) is characterized by scattered dwarf shrubs (the dominant species is Sarcopoterium spinosum) and patches of herbaceous plants [57].
2.2. Methodological Approach
A physically-based modeling approach relying on the numerical solution of the flow equations using Hydrus 1D [58] and measured climatic data was applied to simulate the mean soil moisture dynamics across a hillslope represented by 8240 cells (3 × 3 m). Two cases of bare soil profiles were considered: (1) uniform (unsealed case); (2) topped by a completely formed seal layer (sealed case). An extensive validation of this approach for the upper 15 cm of the soil profile was performed previously [59]. The characterization of the hillslope as an amalgamation of 1D cells was compared with a 2D approach for a subset of the data and was found suitable in reconstructing soil moisture measured in the field (see Appendix A).
To corroborate the model’s ability to reconstruct the soil moisture dynamics at shallower soil depths, the simulated soil moisture was compared with gravimetric soil-moisture data repeatedly collected from the 0–10 cm-deep upper layer at 7 to 13 different locations on the hillslope (Figure 1B), during nine field campaigns spanning the 2010–2011 rainy season (for a total of 82 samples). For each sampling date, each gravimetric sample, in each location, was averaged over three replicates. Details regarding the 2010–2011 rainfall season and sampling dates can be found in Sela et al. [59]. Gravimetric soil moisture data were converted to volumetric soil moisture using soil bulk density calculated following Saxton et al. [60], using soil texture at each sampling site as the input.
To address the objectives of the study, two datasets of soil moisture were created by averaging the simulated data for the hillslope in two different ways: the first dataset represents the soil layer, which corresponds to satellite observations. While in reality, the thickness of this layer is affected by soil moisture, this is neglected at this stage, and the layer thickness is assumed to be 0–2 cm (spatially uniform and constant in time). The second simulated soil moisture dataset represents the soil layer that is usually sampled by soil moisture probes used to validate satellite observations. In this study, the thickness of this layer was assumed to be 0–10 cm and to be spatially uniform. Using a soil moisture dataset created by a hydrological model allows more flexibility in studying near-surface soil moisture dynamics at various temporal scales, from a single rainfall event to the multi-seasonal scale, than if real RS data were used.
The use of model-based soil moisture realizations enables the study of SMTS dynamics at any prescribed spatial scale, both with and without accounting for a seal layer at the surface, thus allowing the quantitative evaluation of its specific effect. In this study, all analyses were applied to a 30 × 30-m spatial scale, corresponding to the scale of synthetic aperture radar (SAR) satellites, such as RadarSat-1 [61]. Consequently, the studied hillslope was mapped to a 30 × 30-m grid, resulting in 69 cells (Figure 1B).
The initial soil moisture conditions at the beginning of each simulation were assumed uniform, both spatially and with depth, and consisted of a soil moisture value of . For each of the simulated seasons, mean soil moisture values for the 0–2 cm (representing the penetration depth of the RS sensor) and 0–10 cm (representing the sampled depth of the ground sensors) layers were computed on an hourly basis in each 3 × 3-m model cell and extracted every 6 h for both the sealed and the unsealed conditions. The known discrepancy between the point scale of the ground validation measurements and the RS sensor footprint scale was not addressed here, and the comparison between the 0–2 cm and 0–10-cm soil depths was conducted directly at the RS sensor footprint scale of 30 × 30 m to emphasize the net effect of the seal layer. Therefore, simulated soil moisture data were upscaled from the 3 × 3-m model cell to the 30 × 30-m RS sensor cells by averaging all respective 3 × 3-m cells contained within each RS sensor cell, for each time step. Finally, to study the factors controlling the bias between mean soil moisture at the 0–2 cm and 0–10 cm depths, the mean difference between the simulated soil moisture at these depths during all seasons was computed for each RS sensor cell and was used as an input for a multi-parameter, stepwise regression (SPSS version 20, IBM, Inc. Armonk, NY, USA).
To study how surface sealing affects the sampling locations that best represent the hillslope mean soil-moisture, a temporal stability analysis [44] was applied using simulated soil moisture data for the 0–2-cm layer, representing the RS sensor output. A long-term dataset of measured climate records was used for this analysis, and both sealed and unsealed conditions were considered. Finally, to study the factors affecting the spatial distribution of temporally stable cells, an analysis of variance (ANOVA) was applied.
2.3. Modeling Approach
For a detailed description of the modeling approach, the reader is referred to Sela et al. [59]. In short, the Hydrus 1D software [58] is used to solve numerically the flow equations in the 8240 independent cells (3 × 3 m) that represent the hillslope study site. MATLAB (Release 2012b, The MathWorks, Inc., Natick, MA, USA) code was used to automate the simulations on an hourly basis during the rainfall season. The 8240 bare soil cells were characterized using an extensive database of topographic and soil-hydraulic parameters collected in the field. Assuming that potential evaporation (PE) is mainly controlled by solar radiation, the model accounts for the spatial variability of PE at the study site using a correction index, Ei [59]. This index adjusts the applied PE values in each cell according to aspect and hillslope location, using the ratio between solar radiation in each model cell and the respective radiation of a flat surface. Using the ratio between the rock and soil covers in each cell, rainfall intensity over all cells was corrected to account for the contribution from local rock outcrops. Boundary conditions consist of an atmospheric condition for the top (open to rainfall and evaporation fluxes) and free drainage for the bottom of the solution domain, reflecting the high level of uncertainty regarding the local bedrock permeability, which was found to be highly disintegrated [62]. In the unsealed case, a uniform soil profile was assumed. When a seal layer was accounted for, a two-layer soil profile was assumed, with the seal having a thickness of 2 cm based on observations of a similar soil type [63,64]. Under field conditions, the thickness of the seal layer is expected to depend on local factors, such as slope inclination and the percentage of fine material in the soil. However, no such relations had been established yet for the study site. Therefore, in this analysis, the seal layer thickness is assumed to be spatially uniform throughout the hillslope.
The hydraulic parameters of the seal layer were directly related to the underlying soil using the Mualem and Assouline [30] approach. The model simulates soil moisture dynamics at the bare soil between vegetation patches and, thus, neglects vegetation effect on infiltration and water redistribution. This approach could be justified at the study site, as the dominant shrubs (Sarcopoterium Spinosum) were found to have mainly vertical roots, extracting water from fissures at the bedrock [65]. Surface water ponding was not allowed in the Hydrus 1D model simulations. Rainfall excess was recorded, but no runoff routing was considered between the cells, based on very limited runoff connectivity, which was measured at the site [66]. Subsurface flow between the cells was not accounted for. Considering all the above-mentioned assumptions, the simulated results were verified extensively in the field. Several sampling campaigns of the 2–15-cm layer for soil gravimetric soil moisture measurements were carried out in the bare soil areas between vegetation patches during the 2010–2011 rainfall season. A comparison between simulated and measured mean soil moisture values has resulted in a satisfactory Nash and Sutcliffe [67] efficiency index of 0.7, indicating that the modeling approach and the assumptions were able to represent soil moisture dynamics in the top soil of the experimental hillslope.
2.4. Climate Data
A 20-y dataset (1993–2013) of daily rainfall measured at the Lahav meteorological station, located 4 km north of the study site, was used for the analysis. All precipitation from a particular rain event was assumed to fall during a 3-h period, the average duration of rainfall events at the study site. Potential evaporation for the years 1993–2009 was measured using a Class A pan at the Lahav station. For the period of 2010–2013, potential evaporation was calculated using the Penman–Monteith equation [68], based on data from the Beer Sheva meteorological station located 10 km south of the study site.
2.5. Time Stability Analysis
In this study, SMTS was analyzed using the mean relative difference (MRD) method [44]. The mean relative difference (δ̄1) for each 30 × 30 m RS cell (i) was calculated using Equation (1):
The combination of these two indices leads to the root mean square error (RMSE) of the relative difference for each cell (Equation (3)) [43].
Lower RMSE values indicate locations with a higher time stability of soil moisture. These locations are considered to represent the best the mean soil moisture of the hillslope [43].
2.6. Statistical Analysis
To study the factors that affect the bias in validation, two statistical methods were applied: linear multiple parameter step-wise regression and analysis of variance (one way ANOVA). Five topographic and soil hydraulic variables (all of them serve also as model inputs) were chosen for the analysis: (1) soil depth; (2) rock cover; (3) the correction index, Ei for PE [59]; (4) the saturated water content value (θs) of the soil layer, which is equivalent to soil porosity; and (5) slope inclination. A moderate correlation (R = 0.53) was found between the relations of the soil depth-rock cover and the soil depth-slope inclination. A weak correlation was found for all other combinations of the regression parameters. For the regression analysis, we have used dimensionless standardized regression coefficients, calculated by scaling the sample mean value to zero and the sample variance to one [69]. Using standardized regression coefficients allows us to compare, with necessary caution, the relative importance of each explanatory parameter. One-way ANOVA can be used to test for significant differences between the means of multiple populations [70]. Here, it is applied to study if significant differences are found between populations grouped by topography or soil hydraulic parameters [43], highlighting variables that could be good predictors of SMTS. For this analysis, each of the five variables mentioned above was discretized into four groups, based on an equal interval classification.
3. Results and Discussion
3.1. Corroboration of the Model with Field Data
The comparison between simulated and measured mean soil moisture data for the 0–10 cm upper layer is depicted in Figure 2. Accounting for soil surface sealing improved model predictions for the lower soil moisture levels and increased the Nash and Sutcliffe [67] efficiency index from 0.59 for the unsealed case to 0.66 for the sealed case. This latter value is considered a satisfactory agreement according to the guidelines presented in Moriasi et al. [71]. Based on these results, we conclude that the modeling approach accurately simulates soil moisture dynamics in the upper soil layer and that the sealed case is better at representing soil moisture in the field than the unsealed case.
3.2. Differences between Simulated Soil Moisture for the RS Sensor Penetration Depth and Ground Validation Depth
To investigate the bias induced by using soil moisture measured at the 0–10-cm layer to validate soil moisture sensed at the 0–2-cm layer, the model was forced with the climatic data from three representative seasons: 2004–2005 (407 mm rainfall), 2006–2007 (275 mm rainfall) and 2007–2008 (203 mm rainfall), representing above average, average and less than average rainfall seasons, respectively. For each model cell, soil moisture data from all three seasons were combined to a continuous dataset and the difference between the mean soil moisture in the two layers was compared for both the sealed and unsealed systems (Equations (4) and (5), respectively):
3.3. Temporal Variation in the Error between the 0–2 and 0–10 Layers
The computed Diff values for Equations (4) and (5) for the 2006–2007 rainfall season are depicted in Figure 4. This season was chosen, because the seasonal cumulative rainfall depth during that year is similar to the long-term mean value of the rainfall data for the study site. A cyclic pattern for the difference between the mean soil moisture within the two layers was observed under the sealed and the unsealed conditions. Negative values were found to characterize the rainfall events (e.g., higher soil moisture at the 0–2-cm compared to the 0–10-cm layer) and positive values to characterize drying periods (e.g., higher soil moisture at the 0–10-cm compared to the 0–2-cm layer). The bias associated with the validation of remotely sensed soil moisture during rainfall events due to the different RS penetration and ground sampling depths in unsealed systems is a known issue that was addressed previously [21]. The seal layer was found to intensify this bias, especially during low-intensity rainfall events where, in the absence of runoff initiation, the percolation of water through the seal layer is impeded by the seal layer’s lower hydraulic conductivity. Interestingly, the difference in soil moisture values between the 0–2 and 0–10-cm layers during the drying periods was substantially smaller in the sealed system. This is attributed to the seal layer’s suppression of evaporation during the drying periods [33,59], which reduces the difference between the two layers over time. Conversely, in the unsealed system, the progression of a drying front through the soil profile led to an increase in the differences in soil moisture between the 0–2 and 0–10-cm soil layers over time. Figure 4C summarizes the net contribution of the seal layer to the difference in soil moisture between the 0–2 and 0–10-cm soil layers. The seal was found to add up to 10%–15% of the difference between the 0–2 and the 0–10-cm layers during rainfall events. However, immediately following a rainfall event, the seal layer starts to compensate for this increased difference, and by the time the drying period ends, the difference in moisture between the two layers can be reduced by 10%–15%.
The cyclic pattern in the differences in soil moisture between the 0–2 and 0–10-cm soil layers, driven by the rainfall events and drying periods (Figure 4), suggests that there might be a characteristic duration until the difference in soil moisture between these layers vanishes. To test this hypothesis, this duration was computed following each of the rainfall events of the three representative seasons (a total of 40 rainfall events). The results are summarized in Figure 5, which shows a histogram of the computed durations. In most of the cases, the difference in soil moisture between the layers vanished 10 h for the unsealed system and 30 h for the sealed system after rainfall, representing an ideal duration for sampling. In reality, validation ground sampling schemes is designed to coincide with the timing of satellite overpass and not according to the local climatic conditions. However, since the bias between the layers was found to follow a cyclic pattern, using these calculated durations can assist validation schemes by indicating whether a positive or negative bias in soil moisture validation could be expected during the actual satellite overpass.
3.4. Effects of a Seal Layer on SMTS and the Determination of Optimal Hillslope-Scale Sampling Locations
To study the effect a seal layer has on SMTS patterns at the hillslope scale, the model was forced with 20 years of measured climate data (1993–2013), and MRD and RMSE values (Equations (1)–(3)) were calculated for each 30-m cell based on the entire period. Figure 6 presents the MRD and RMSE values of the sealed and unsealed systems, ranked from the smallest to the largest, according to the MRD values. Sixteen percent and 14% of the cells in the sealed and unsealed systems, respectively, estimated the hillslope mean soil moisture within ±2%, thus exhibiting a relatively high SMTS. Fifty five percent and 39% of the cells captured up to ±5% of the mean hillslope soil moisture, while 87% and 78% of the cells captured up to ±10% of the mean hillslope soil moisture (for the sealed and unsealed systems, respectively). Overall, soil surface sealing improves SMTS, reduces the RMSE by 26%, the mean absolute MRD by 20% and its variance by 46%. In both the sealed and unsealed systems, the variance of the MRD values was greater in cells with soil moisture that is consistently higher than the mean value (positive values of the MRD) than in cells that were consistently drier then the hillslope mean. This result agrees with those of several previous studies [1,2,43,52,72]. The MRD values calculated in this study were lower than the values reported in other studies conducted on similar semiarid hillslopes or small catchments [47,72,73]. This could be related to the fact that we considered soil moisture data averaged over the 30-m footprint, while those studies used data originating from a network of point measurements.
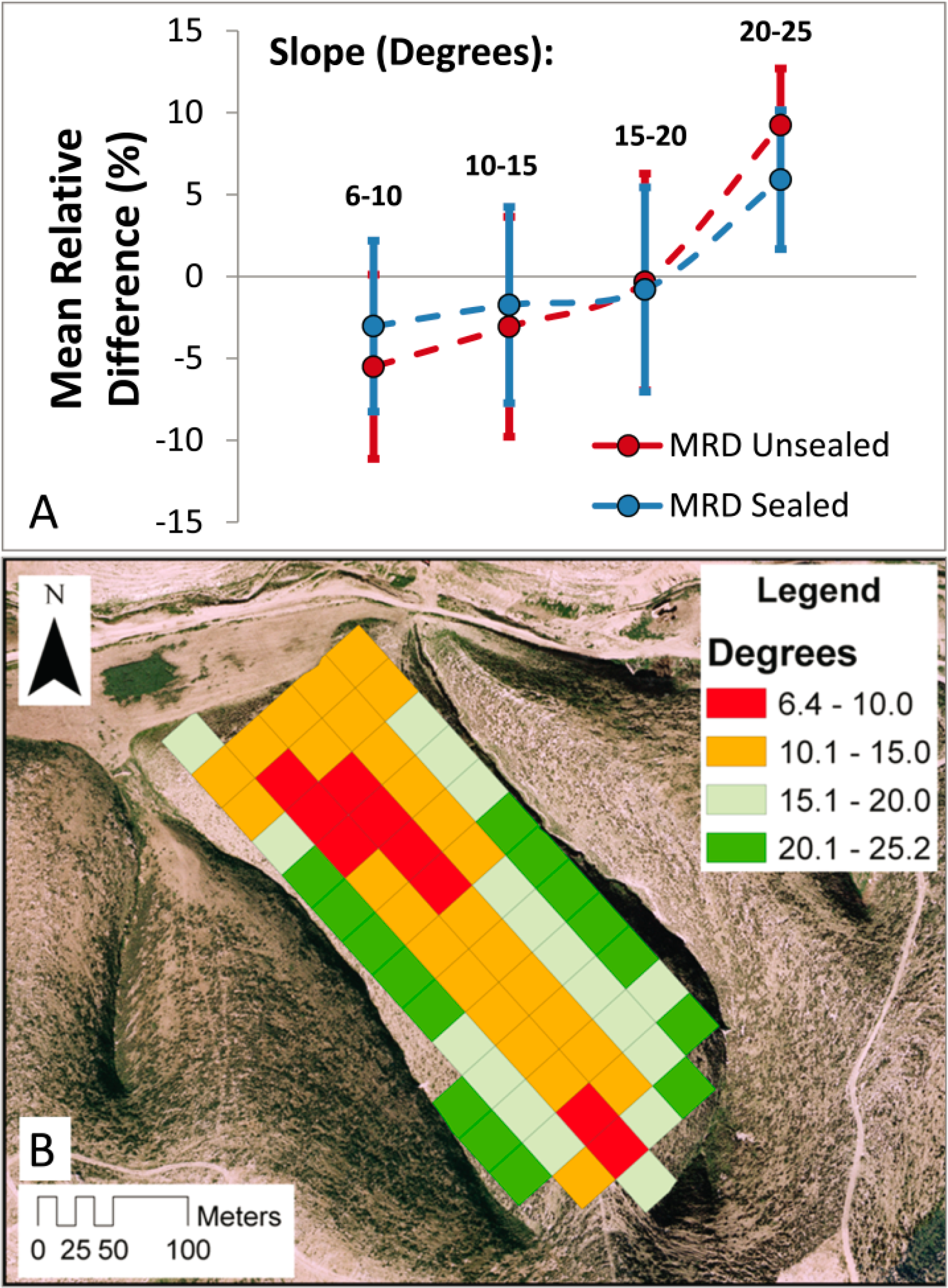
Following the methodology presented in Jacobs et al. [43] and Joshi et al. [1], to further study whether topographic and soil hydraulic variables could be good predictors of the MRD values in a quantitative manner, the results of the ANOVA analysis are presented in Table 2. The results indicate that for both the sealed and unsealed systems, the difference in MRD between the groups is most significant for the saturated water content value and the slope inclination. Figure 7A depicts the mean MRD in each of the four slope inclination groups, together with the spatial distribution of each zone along the hillslope (Figure 7B). For the sealed system, both the higher and lower backslope (10–15 and 15–20 degrees) emerge as optimal locations for sampling, estimating the hillslope mean soil moisture within ±2%. For the unsealed system, only sampling from the lower backslope (15–20°) allowed the estimation of the hillslope mean soil moisture within ±2%. However, for both the sealed and unsealed systems, all four slope-inclination zones had highly variable MRD levels (e.g., relatively large standard deviations), indicating that slope inclination alone may not be a good predictor of optimal locations for sampling soil moisture. Figure 8 depicts the relation between MRD and the slope inclination and the saturated water content value. While the relation between the MRD and the slope inclination is scattered across the entire range of MRD values, a strong linear relation was found between the saturated water content and the MRD (R2 values of 0.97 and 0.93 for the sealed and unsealed systems, respectively). This indicates that temporally stable hillslope locations (e.g., MRD of ±2%) could only be found within a narrow range of saturated water content (or porosity) values (θs = 0.482 − 0.486), closely representing the hillslope mean value (θs = 0.484).
4. Conclusions
The effect of soil surface sealing on soil moisture dynamics of the upper few centimeters of the soil profile, and its implications on remote sensing (RS) soil moisture estimates, was investigated here for the first time using a physically-based hydrological model. Model-based soil moisture realizations were used instead of real RS data, allowing increased flexibility in studying near-surface soil moisture dynamics at different temporal and spatial scales. Simulations were used to represent soil moisture at the typical soil layers corresponding to both the RS sensor readings (0–2 cm) and the ground measurements used to validate those readings (0–10 cm).
The bias in the validation of soil moisture using point measurements, as reflected in the soil moisture simulations for the two soil layers under interest, was found to vary both spatially and temporally. When averaged over seasonal time scales, the difference between the simulated soil moisture at the radar penetration depth and the simulated soil moisture at the ground validation depth was found to be minor. However, when intra-seasonal soil moisture dynamics where considered, a cyclic pattern was detected where during rainfall events, soil moisture values at the 0–10-cm layer are consistently lower than the soil moisture values at 0–2-cm layer. This trend is reversed during drying periods. The seal layer was found to intensify the simulated difference in soil moisture between these layers during rainfall events, in general, and during low-intensity rainfall events, in particular. However, the seal layer compensates for this intensification during the drying periods, reducing substantially the difference in soil moisture between the two soil layers, as compared with an unsealed system. Analysis of this cyclic pattern in the sealed and unsealed systems suggests that considering climatic conditions alone, the optimal time for sampling when the bias between the two soil layers is minimal is a few hours following a rainfall event for an unsealed system, and one or two days after rainfall for the sealed one. Since, in practice, the timing of validation is determined by the satellite overpass and not according to local climatic conditions, our results can assist in indicating the type of bias (e.g., overestimation or underestimation of the RS sensor) that could expected in the field during the satellite overpass.
Soil surface sealing was found to improve soil moisture temporal stability (SMTS), affecting the locations that best represent the hillslope mean soil-moisture value. Considering a mean relative difference (MRD) of ±2% of the mean soil moisture as a threshold for optimal sampling locations, the entire range of 10–20 degrees of slope inclination was found suitable under sealed conditions. In comparison, for the unsealed system, only the 15–20-degree range fit the threshold criteria. The saturated water content value, θs, which corresponds to soil porosity, was found to be the best predictor of the MRD value in both the sealed and unsealed systems, with optimal sampling locations found at sites characterized by a porosity similar to the mean porosity of the hillslope. The fact that porosity appears to be the main factor affecting hillslope-scale SMTS suggests that prior knowledge regarding the soil texture distribution in the field is crucial for the preparation and application of RS soil-moisture validation schemes. Further studies are needed to relate the mechanistic model estimations with soil moisture estimates from remotely sensed data under surface sealing conditions.
Acknowledgments
We thank three anonymous reviewers for their constructive comments, which helped to improve the manuscript. This research was supported by the Israel Science Foundation (ISF) (Grant No. 1184/11) and by the International Arid Lands Consortium (Grant No. 10R—09).
Author Contributions
This work was carried out in the framework of the PhD research of the first author Shai Sela, who was responsible for preparing the climatic data, writing the programming codes, analyzing the results and writing the manuscript. Tal Svoray and Shmuel Assouline were the PhD supervisors, and contributed to all stages of the work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
To test the bias that might result from using a 1D modeling approach instead of a 2D approach, five points from the validation set were randomly chosen (Figure A1), representing different geomorphic units and field conditions. In each location, measured soil moisture data (2–15-cm soil layer) was compared with simulated data resulting from the application of a 1D and 2D approaches to a fully-sealed profile. Hydrus 1D [58] and Hydrus 2D [74] models were used for the simulations. The seal layer hydraulic properties were modeled following Mualem and Assouline [30], with the seal layer assumed to have a uniform thickness of 2 cm. The prescribed boundary conditions (BC) for the model during the simulations consisted of a flux type (Neumann). The top and bottom BC for both the 1D and 2D applications were similar: open to rainfall and evapotranspiration at the top and free drainage at the bottom. Through this lower BC, the discharge flux was calculated according to Equation (A1):


References
- Joshi, C.; Mohanty, B.P.; Jacobs, J.M.; Ines, A.V.M. Spatiotemporal analyses of soil moisture from point to footprint scale in two different hydroclimatic regions. Water Resour. Res 2011, 47, W01508. [Google Scholar]
- Mohanty, B.P.; Skaggs, T.H. Spatio-temporal evolution and time-stable characteristics of soil moisture within remote sensing footprints with varying soil, slope, and vegetation. Adv. Water Resour 2001, 24, 1051–1067. [Google Scholar]
- Choi, M.; Jacobs, J.M.; Cosh, M.H. Scaled spatial variability of soil moisture fields. Geophys. Res. Lett 2007, 34. [Google Scholar] [CrossRef]
- Cosh, M.H.; Jackson, T.J.; Moran, S.; Bindlish, R. Temporal persistence and stability of surface soil moisture in a semi-arid watershed. Remote Sens. Environ 2008, 112, 304–313. [Google Scholar]
- Famiglietti, J.S.; Ryu, D.R.; Berg, A.A.; Rodell, M.; Jackson, T.J. Field observations of soil moisture variability across scales. Water Resour. Res 2008, 44. [Google Scholar] [CrossRef]
- Grayson, R.; Western, A.; Chiew, F.; Bloschl, G. Preferred states in spatial soil moisture patterns: Local and nonlocal controls. Water Resour. Res 1997, 33, 2897–2908. [Google Scholar]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W.; Hasenauer, S.; Hahn, S. Assimilation of surface- and root-zone ASCAT soil moisture products into rainfall-runoff modeling. IEEE Trans. Geosci. Remote Sens 2012, 50, 2542–2555. [Google Scholar]
- Holah, N.; Baghdadi, N.; Zribi, M.; Bruand, A.; King, C. Potential of ASAR/ENVISAT for the characterization of soil surface parameters over bare agricultural fields. Remote Sens. Environ 2005, 96, 78–86. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens 2003, 41, 215–229. [Google Scholar]
- Svoray, T.; Shoshany, M. Herbaceous biomass retrieval in habitats of complex composition: A model merging SAR images with unmixed Landsat TM data. IEEE Trans. Geosci. Remote Sens 2003, 41, 1592–1601. [Google Scholar]
- Svoray, T.; Shoshany, M. Multi-scale analysis of intrinsic soil factors from SAR-based mapping of drying rates. Remote Sens. Environ 2004, 92, 233–246. [Google Scholar]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ 1999, 70, 191–207. [Google Scholar]
- Escorihuela, M.J.; Chanzy, A.; Wigneron, J.P.; Kerr, Y.H. Effective soil moisture sampling depth of L-band radiometry: A case study. Remote Sens. Environ 2010, 114, 995–1001. [Google Scholar]
- Wigneron, J.; Chanzy, A.; de Rosnay, P.; Ruediger, C.; Calvet, J. Estimating the effective soil temperature at L-band as a function of soil properties. IEEE Trans. Geosci. Remote Sens 2008, 46, 797–807. [Google Scholar]
- Bruckler, L.; Witono, H.; Stengel, P. Near-surface soil-moisture estimation from microwave measurements. Remote Sens. Environ 1988, 26, 101–121. [Google Scholar]
- Raju, S.; Chanzy, A.; Wigenron, J.; Calvet, J.; Kerr, Y.; Laguerre, L. Soil-moisture and temperature profile effects on microwave emission at low frequencies. Remote Sens. Environ 1995, 54, 85–97. [Google Scholar]
- Cosh, M.; Jackson, T.; Bindlish, R.; Prueger, J. Watershed scale temporal and spatial stability of soil moisture and its role in validating satellite estimates. Remote Sens. Environ 2004, 92, 427–435. [Google Scholar]
- Albergel, C.; de Rosnay, P.; Gruhier, C.; Munoz-Sabater, J.; Hasenauer, S.; Isaksen, L.; Kerr, Y.; Wagner, W. Evaluation of remotely sensed and modeled soil moisture products using global ground-based in situ observations. Remote Sens. Environ 2012, 118, 215–226. [Google Scholar]
- Mohanty, B.P.; Skaggs, T.H.; Famiglietti, J.S. Analysis and mapping of field-scale soil moisture variability using high-resolution, ground-based data during the Southern Great Plains 1997 (SGP97) Hydrology Experiment. Water Resour. Res 2000, 36, 1023–1031. [Google Scholar]
- Albergel, C.; Ruediger, C.; Carrer, D.; Calvet, J.C.; Fritz, N.; Naeimi, V.; Bartalis, Z.; Hasenauer, S. An evaluation of ASCAT surface soil moisture products with in-situ observations in southwestern France. Hydrol. Earth Syst. Sci 2009, 13, 115–124. [Google Scholar]
- Choi, M.; Hur, Y. A microwave-optical/infrared disaggregation for improving spatial representation of soil moisture using AMSR-E and MODIS products. Remote Sens. Environ 2012, 124, 259–269. [Google Scholar]
- De Rosnay, P.; Calvet, J.; Kerr, Y.; Wigneron, J.; Lemaître, F.; Escorihuela, M.J.; Sabater, J.M.; Saleh, K.; Barrié, J.; Bouhours, G. SMOSREX: A long term field campaign experiment for soil moisture and land surface processes remote sensing. Remote Sens. Environ 2006, 102, 377–389. [Google Scholar]
- Parinussa, R.M.; Holmes, T.R.H.; de Jeu, R.A.M. Soil moisture retrievals from the WindSat spaceborne polarimetric microwave radiometer. IEEE Trans. Geosci. Remote Sens 2012, 50, 2683–2694. [Google Scholar]
- Le Morvan, A.; Zribi, M.; Baghdadi, N.; Chanzy, A. Soil moisture profile effect on radar signal measurement. Sensors 2008, 8, 256–270. [Google Scholar]
- Assouline, S. Rainfall-induced soil surface sealing: A critical review of observations, conceptual models, and solutions. Vadose. Zone J 2004, 3, 570–591. [Google Scholar]
- Augeard, B.; Assouline, S.; Fonty, A.; Kao, C.; Vauclin, M. Estimating hydraulic properties of rainfall-induced soil surface seals from infiltration experiments and X-ray bulk density measurements. J. Hydrol 2007, 341, 12–26. [Google Scholar]
- Bresson, L.; Moran, C.; Assouline, S. Use of bulk density profiles from X-radiography to examine structural crust models. Soil Sci. Soc. Am. J 2004, 68, 1169–1176. [Google Scholar]
- Tackett, J.; Pearson, R. Some characteristics of soil crusts formed by simulated rainfall. Soil Sci 1965, 99, 407. [Google Scholar]
- Mualem, Y.; Assouline, S. Modeling soil seal as a nonuniform layer. Water Resour. Res 1989, 25, 2101–2108. [Google Scholar]
- Assouline, S.; Mualem, Y. Modeling the dynamics of seal formation and its effect on infiltration as related to soil and rainfall characteristics. Water Resour. Res 1997, 33, 1527–1536. [Google Scholar]
- Assouline, S.; Mualem, Y. Runoff from heterogeneous small bare catchments during soil surface sealing. Water Resour. Res 2006, 42, W12405. [Google Scholar]
- Assouline, S.; Mualem, Y. Effect of rainfall-induced soil seals on the soil water regime: Drying interval and subsequent wetting. Transp. Porous Media 2003, 53, 75–94. [Google Scholar]
- Aubert, M.; Baghdadi, N.; Zribi, M.; Douaoui, A.; Loumagne, C.; Baup, F.; El Hajj, M.; Garrigues, S. Analysis of TerraSAR-X data sensitivity to bare soil moisture, roughness, composition and soil crust. Remote Sens. Environ 2011, 115, 1801–1810. [Google Scholar]
- Bresler, E.; Kemper, W.D. Soil water evaporation as affected by wetting methods and crust formation. Soil Sci. Soc. Am. Proc 1970, 34, 3–8. [Google Scholar]
- Schwartz, R.C.; Baumhardt, R.L.; Evett, S.R. Tillage effects on soil water redistribution and bare soil evaporation throughout a season. Soil Tillage Res 2010, 110, 221–229. [Google Scholar]
- Assouline, S.; Selker, J.S.; Parlange, J.Y. A simple accurate method to predict time of ponding under variable intensity rainfall. Water Resour. Res 2007, 43, W03426. [Google Scholar]
- Chen, L.; Sela, S.; Svoray, T.; Assouline, S. The roles of soil-surface sealing, microtopography and vegetation patches in rainfall-runoff processes in semiarid areas. Water Resour. Res 2013, 49, 1–15. [Google Scholar]
- Brocca, L.; Melone, F.; Moramarco, T.; Morbidelli, R. Soil moisture temporal stability over experimental areas in central Italy. Geoderma 2009, 148, 364–374. [Google Scholar]
- Hu, W.; Tallon, L.K.; Si, B.C. Evaluation of time stability indices for soil water storage upscaling. J. Hydrol 2012, 475, 229–241. [Google Scholar]
- Grayson, R.B.; Western, A.W. Towards a real estimation of soil water content from point measurements: Time and space stability of mean response. J. Hydrol 1998, 207, 68–82. [Google Scholar]
- Hu, W.; Shao, M.; Han, F.; Reichardt, K.; Tan, J. Watershed scale temporal stability of soil water content. Geoderma 2010, 158, 181–198. [Google Scholar]
- Jacobs, J.M.; Mohanty, B.P.; Hsu, E.C.; Miller, D. SMEX02: Field scale variability, time stability and similarity of soil moisture. Remote Sens. Environ 2004, 92, 436–446. [Google Scholar]
- Vachaud, G.; Desilans, A.P.; Balabanis, P.; Vauclin, M. Temporal stability of spatially measured soil-water probability density-function. Soil Sci. Soc. Am. J 1985, 49, 822–828. [Google Scholar]
- Vanderlinden, K.; Vereecken, H.; Hardelauf, H.; Herbst, M.; Martinez, G.; Cosh, M.H.; Pachepsky, Y.A. Temporal stability of soil water contents: A review of data and analyses. Vadose. Zone J 2012, 11. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Gebremichael, M.; Watts, C.J.; Bindlish, R.; Jackson, T.J. Comparison of ground-based and remotely-sensed surface soil moisture estimates over complex terrain during SMEX04. Remote Sens. Environ 2008, 112, 314–325. [Google Scholar]
- Gomez-Plaza, A.; Alvarez-Rogel, J.; Albaladejo, J.; Castillo, V. Spatial patterns and temporal stability of soil moisture across a range of scales in a semi-arid environment. Hydrol. Process 2000, 14, 1261–1277. [Google Scholar]
- Martinez, G.; Pachepsky, Y.A.; Vereecken, H.; Hardelauf, H.; Herbst, M.; Vanderlinden, K. Modeling local control effects on the temporal stability of soil water content. J. Hydrol 2013, 481, 106–118. [Google Scholar]
- Cassel, D.; Wendroth, O.; Nielsen, D. Assessing spatial variability in an agricultural experiment station field: Opportunities arising from spatial dependence. Agron. J 2000, 92, 706–714. [Google Scholar]
- Choi, M.; Jacobs, J.M. Soil moisture variability of root zone profiles within SMEX02 remote sensing footprints. Adv. Water Resour 2007, 30, 883–896. [Google Scholar]
- Heathman, G.C.; Larose, M.; Cosh, M.H.; Bindlish, R. Surface and profile soil moisture spatio-temporal analysis during an excessive rainfall period in the southern Great Plains, USA. Catena 2009, 78, 159–169. [Google Scholar]
- Choi, M.; Jacobs, J.M. Spatial soil moisture scaling structure during Soil Moisture Experiment 2005. Hydrol. Process 2011, 25, 926–932. [Google Scholar]
- Martinez, G.; Vanderlinden, K.; Vicente Giraldez, J.; Espejo, A.J.; Luis Muriel, J. Field-scale soil moisture pattern mapping using electromagnetic induction. Vadose. Zone J 2010, 9, 871–881. [Google Scholar]
- Penna, D.; Brocca, L.; Borga, M.; Dalla Fontana, G. Soil moisture temporal stability at different depths on two alpine hillslopes during wet and dry periods. J. Hydrol 2012, 477, 55–71. [Google Scholar]
- Martinez-Fernandez, J.; Ceballos, A. Temporal stability of soil moisture in a large-field experiment in Spain. Soil Sci. Soc. Am. J 2003, 67, 1647–1656. [Google Scholar]
- Pachepsky, Y.A.; Guber, A.K.; Jacques, D. Temporal persistence in vertical distributions of soil moisture contents. Soil Sci. Soc. Am. J 2005, 69, 347–352. [Google Scholar]
- Svoray, T.; Karnieli, A. Rainfall, topography and primary production relationships in a semiarid ecosystem. Ecohydrology 2011, 4, 56–66. [Google Scholar]
- Simunek, J.; M. Saito, S.H.; Sakai, M.; van Genuchten, M.T. The Hydrus-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2013; p. 340. [Google Scholar]
- Sela, S.; Svoray, T.; Assouline, S. Soil water content variability at the hillslope scale: Impact of surface sealing. Water Resour. Res 2012, 48, W03522. [Google Scholar]
- Saxton, K.; Rawls, W.; Romberger, J.; Papendick, R. Estimating generalized soil-water characteristics from texture. Soil Sci. Soc. Am. J 1986, 50, 1031–1036. [Google Scholar]
- Gala, T.S.; Aldred, D.A.; Carlyle, S.; Creed, I.F. Topographically based spatially averaging of SAR data improves performance of soil moisture models. Remote Sens. Environ 2011, 115, 3507–3516. [Google Scholar]
- Howard, C.; Bahat, D. Increased disintegration of subsoil layer of Eocene chalk near Beer-Sheva. Neues. Jahrb. Geol. Palaontol. Monatsh 2005, 6, 347–358. [Google Scholar]
- Boiffin, J. Structural Degradation of the Soil Surface by the Action of Rainfall (in French). Ph.D. Dissertation, Inst. Natl. d’Agronomie Paris-Grignon, Paris, France. 1984. [Google Scholar]
- Hadas, A.; Frenkel, H. Infiltration as affected by long-term use of sodic-saline water for irrigation. Soil Sci. Soc. Am. J 1982, 46, 524–530. [Google Scholar]
- Henkin, Z.; Seligman, N.; Kafkafi, U.; Prinz, D. End-of-season soil water depletion in relation to growth of herbaceous vegetation in a sub-humid Mediterranean dwarf-shrub community on two contrasting soils. Plant. Soil 1998, 202, 317–326. [Google Scholar]
- Kossovsky, A. Overland Flow in a Semi Arid Region, Lahav Hills Israel (in Hebrew). Master’s Thesis, Hebrew University of Jerusalem, Jerusalem, Israel. July 1994. [Google Scholar]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol 1970, 10, 282–290. [Google Scholar]
- Monteith, J. Evaporation and surface temperature. Q. J. R. Meteorol. Soc 1981, 107, 1–27. [Google Scholar]
- Montgomery, D.; Peck, E.; Vining, G. Introduction to Linear Regression Analysis; Wiley-Interscience: New York, NJ, USA, 2006. [Google Scholar]
- Mickey, R.M.; Dunn, O.J.; Clark, V.A. Applied Statistics: Analysis of Variance and Regression; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar]
- Martinez-Fernandez, J.; Ceballos, A. Mean soil moisture estimation using temporal stability analysis. J. Hydrol 2005, 312, 28–38. [Google Scholar]
- Gao, L.; Shao, M. Temporal stability of shallow soil water content for three adjacent transects on a hillslope. Agric. Water Manag 2012, 110, 41–54. [Google Scholar]
- Simunek, J.; van Genuchten, M.T.; Sejna, M. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose. Zone J 2008, 7, 587–600. [Google Scholar]
- Simunek, J.; van Genuchten, M.T.; Sejna, M. The HYDRUS Software Package for Simulating the Two-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, Technical Manual, Version 2.0, 2012. Available online: http://www.pc-progress.com/en/..%5Cdownloads%5CPgm_Hydrus3D2%5CHYDRUS3D%20Technical%20Manual.pdf (accessed on 31 July 2014).







| Parameter | Sealed | Unsealed |
|---|---|---|
| Depth | 0.604 | 0.162 |
| θs | −0.709 | −0.858 |
| Slope | - | - |
| Ei | - | 0.512 |
| Rock (%) | - | −0.481 |
| Total R2 | 0.912 | 0.922 |
| Sealed MRD | Unsealed MRD | ||||
|---|---|---|---|---|---|
| Parameter | F-Value | p-Value | Parameter | F-Value | p-Value |
| Depth | 0.847 | 0.473 | Depth | 1.019 | 0.390 |
| θs | 160.242 | 5.6E−30 | θs | 140.409 | 2.4E−28 |
| Slope | 6.953 | 0.0004 | Slope | 15.885 | 7.46E−8 |
| Ei | 5.075 | 0.0032 | Ei | 2.497 | 0.067 |
| Rock (%) | 1.446 | 0.237 | Rock (%) | 0.138 | 0.937 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sela, S.; Svoray, T.; Assouline, S. Soil Surface Sealing Effect on Soil Moisture at a Semiarid Hillslope: Implications for Remote Sensing Estimation. Remote Sens. 2014, 6, 7469-7490. https://doi.org/10.3390/rs6087469
Sela S, Svoray T, Assouline S. Soil Surface Sealing Effect on Soil Moisture at a Semiarid Hillslope: Implications for Remote Sensing Estimation. Remote Sensing. 2014; 6(8):7469-7490. https://doi.org/10.3390/rs6087469
Chicago/Turabian StyleSela, Shai, Tal Svoray, and Shmuel Assouline. 2014. "Soil Surface Sealing Effect on Soil Moisture at a Semiarid Hillslope: Implications for Remote Sensing Estimation" Remote Sensing 6, no. 8: 7469-7490. https://doi.org/10.3390/rs6087469
APA StyleSela, S., Svoray, T., & Assouline, S. (2014). Soil Surface Sealing Effect on Soil Moisture at a Semiarid Hillslope: Implications for Remote Sensing Estimation. Remote Sensing, 6(8), 7469-7490. https://doi.org/10.3390/rs6087469




