A New Method for Modifying Thresholds in the Classification of Tree Models for Mapping Aquatic Vegetation in Taihu Lake with Satellite Images
Abstract
: Aquatic vegetation plays an important role in maintaining the balance of lake ecosystems. Thus, classifying and mapping aquatic vegetation is a priority for lake management. Classification tree (CT) approaches have been used successfully to map aquatic vegetation from spectral indices obtained from remotely sensed images. However, due to the effects of extrinsic and intrinsic factors, applying a CT model developed for imagery from one date to imagery from another date or a different dataset likely would reduce the classification accuracy. In this study, three spectral features (SFs) were selected to develop a CT model for identifying aquatic vegetation in Taihu Lake. Three traditional CT models with three SFs were developed using CT analysis based on satellite images acquired on 11 July, 16 August and 26 September 2013, and corresponding ground-truth samples, from the Huangjing-1A/B Charge-Coupled Device (HJ-CCD) images, environment and disaster reduction small satellites that were launched by China Center for Resources Satellite Data and Application (CRESDA). The overall accuracies of traditional CT models were 82%, 80% and 84%. We then tested two methods to modify CT model thresholds to adjust the traditional CT models based on image date to determine if the results would enable us to map and classify aquatic vegetation for periods when no ground-based data were available. We assessed the results with ground-truth samples and area agreement with traditional CT models. Results showed that CT models modified from a linear adjustment based on the relationship between ranked values of SFs between two image dates produced map accuracies comparable with those obtained from the traditional CT models and suggest that the method we proposed is feasible for mapping aquatic vegetation types in lakes when ground data are not available.1. Introduction
Aquatic macrophytes play an important role in maintaining the balance of lake ecosystems and supporting socioeconomic functions [1]. For example, macrophytes stabilize sediments, regulate the nutrient cycle [2], slow water currents and maintain fishery production [3]. Studies have indicated that aquatic vegetation has a significant and positive effect on pollutant removal and thereby purifies water, which makes aquatic ecosystems shift from a turbid algal-dominated state to a clear-water, plant-dominated state [4,5]. In the eutrophic Taihu Lake of China (30°55′40″–31°32′58″N, 119°52′32″–120°36′10″E), it therefore is important to accurately map the distribution of and detect changes in aquatic vegetation for lake management.
At a large scale or across the whole lake, it is laborious and difficult to survey types and distribution of aquatic vegetation by traditional and conventional methods. Developing efficient, large-scale monitoring strategies is helpful for effectively tracking and mitigating harmful changes in the lake. Remote sensing has proven to be an effective tool for mapping the distribution of aquatic vegetation over such a large area. Aerial photographs commonly were used in the past to map aquatic vegetation [6,7]. With the rapid development of satellite sensors, multispectral and hyperspectral remote sensing have become more feasible for mapping and monitoring aquatic vegetation. For example, researchers have used high spatial resolution satellite images (e.g., IKONOS and QuickBird images) to illustrate fine-level habitat discrimination [8,9] and to identify submerged vegetation [10]. High resolution imagery also has been used to identify and detect plant communities in wetland settings [11]. Considering availability and accessibility, moderate spatial resolution multispectral satellite data, such as from the Landsat Multispectral Scanner (MSS), Thematic Mapper (TM) and Enhanced Thematic Mapper (ETM+) [12,13], and Satellite Pour l’Observation de la Terre (SPOT) imagery [14], have been widely used for mapping distribution of aquatic macrophytes and assessing spatial and temporal dynamics of aquatic vegetation [15,16]. Meanwhile, a variety of methods and algorithms based on remote sensing data have been applied to automatically identify aquatic vegetation, such as unsupervised isoclustering, supervised maximum likelihood classifiers [17], and tasseled-cap classification [18]. Supervised classification and classification trees have been the most widely and successfully used for classifying aquatic vegetation. For example, Ma et al. [19] developed a transparency-assisted classification tree to classify the aquatic vegetation in Taihu Lake and Zhao et al. [20] developed a CT model for mapping aquatic vegetation in Taihu Lake based on spectral indices. These studies have demonstrated that an accurate CT model for mapping aquatic vegetation could probably be developed using remote sensing imagery for a specific time, given enough ground-truth samples [21,22]. Ground-based data are expensive and often difficult to acquire. Thus, an important question is if aquatic vegetation can be mapped well without ground-truth samples, such as for mapping past conditions in lakes using historical archived satellite data for which corresponding ground-truth samples are unavailable.
It has been shown that the classification trees developed for one time period or image might not be adequate when applied to other periods or dates due to influences of various intrinsic and extrinsic factors [23]. To investigate this, we developed traditional CT models for mapping aquatic vegetation using ground-truth samples and corresponding HJ-CCD images from China’s HJ-1A/1B of the Environment and Disasters Monitoring Microsatellite Constellation Charge-Coupled Device (CCD) camera. We then tested a new approach to modify thresholds of spectral features in the traditional CT model to generate model that could be effectively applied to HJ-CCD images for different dates.
2. Materials and Methods
2.1. Study Area
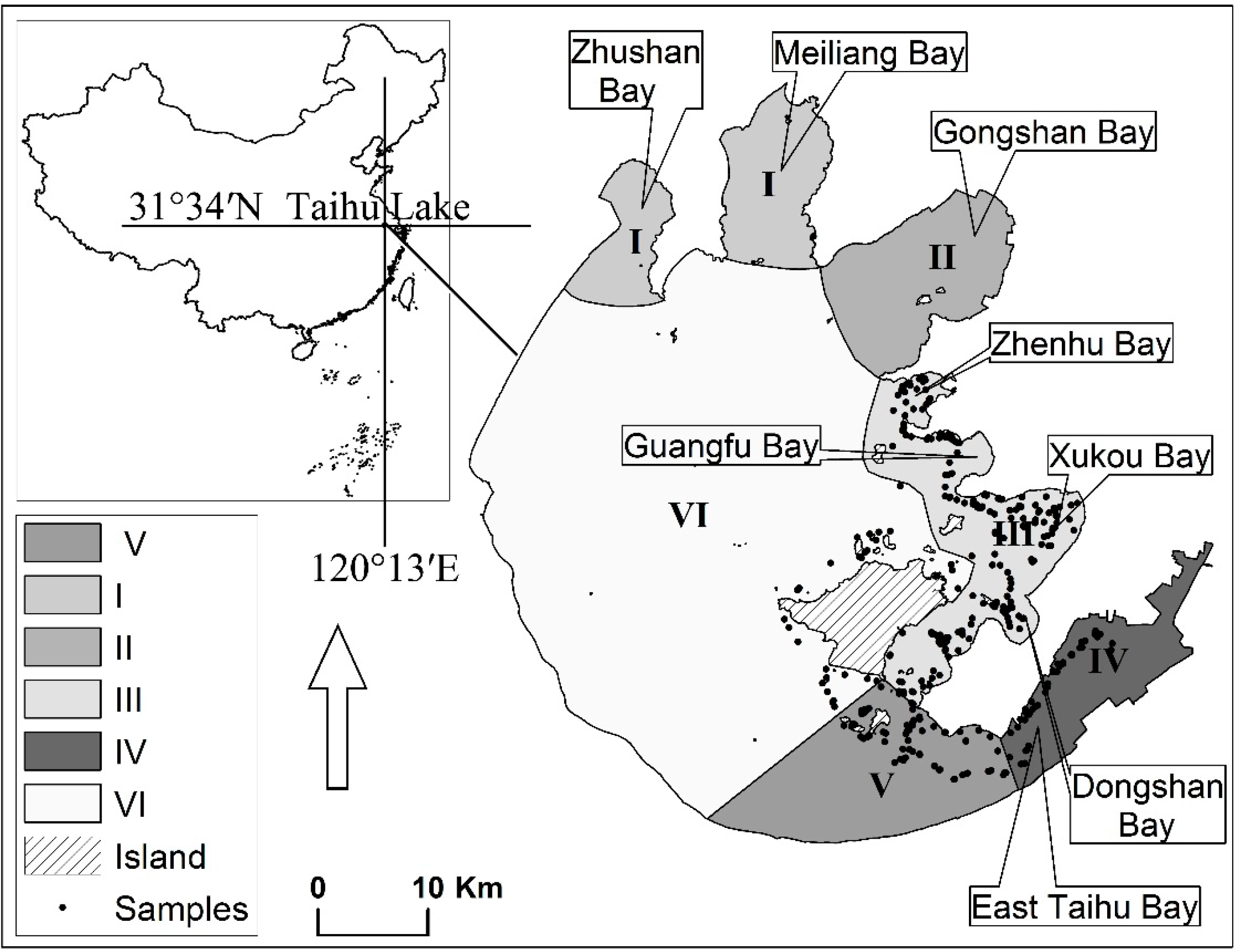
Taihu Lake (30°55′40″–31°32′58″N, 119°52′32″–120°36′10″E) is one of the five largest freshwater lakes in China, located in Jiangsu province (Figure 1). It is a typical large, shallow lake, with a maximal depth of less than 3 m and an average depth of 1.9 m, and covers an area of about 2338 km2. Across Taihu Lake, there are large difference in water parameter values, with Secchi depths ranging from 0 to 2.5 m, pH from 6.81 to 9.58, total nitrogen from 0.37 to 86.30 mg/L and total phosphorus from 0.01 to 6.48 mg/L.
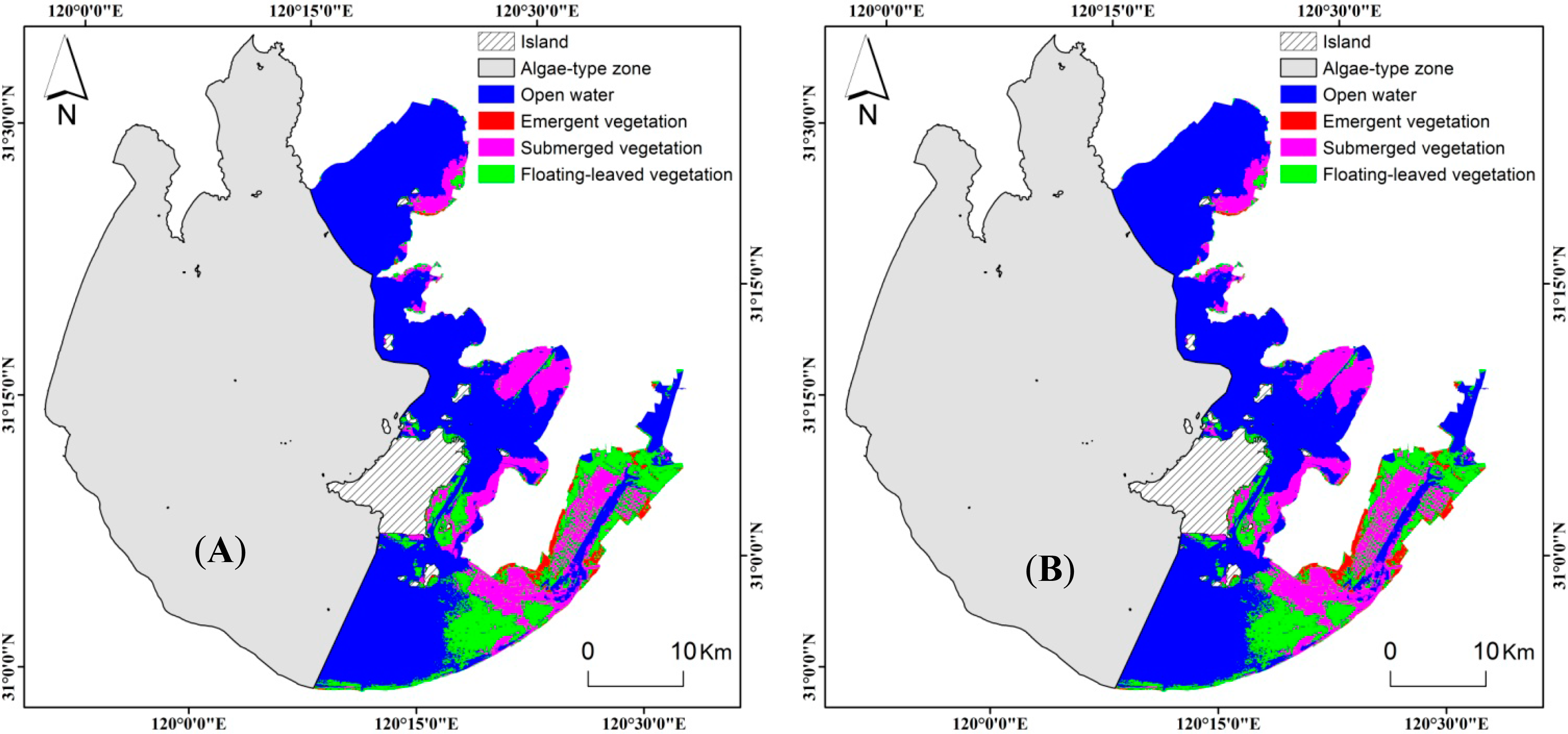
Taihu lake can be divided into six sections according to spatial variability in the relative influence of human activities and environmental factors [15] (Figure 1). Section I consists of Meiliang Bay and Zhushan Bay, where algae blooms occur frequently because of high concentrations of nitrogen and phosphorus. Section II is mainly situated in Gongshan Bay, where a large number of tributaries of the Yangtze River have been flowing into the lake since 2001. Section III consists of Zhenhu Bay, Guangfu Bay, Xukou Bay and Dongshan Bay, which are the main and traditional distribution areas of aquatic vegetation in Taihu. Section IV is the East Bay, which is covered with submerged vegetation, characteristic of good water quality and rich fishery production. Section V is located in the southeast area, which is the traditional distribution area of floating-leaved vegetation. Section VI is located in the central area and the western shores, making up more than 50% of the Lake and belonging to the algae-type zone. Lu et al. [24] divided the Taihu Lake into an algae-type zone (algal-dominated zone) and a grass-type zone (grass-dominated zone). Sections I and VI belong to the algae-type zone, and the other sections belong to the grass-type zone. According to field surveys, water quality in grass-type zone is significantly higher than in algae-type zone. We conducted the current study in the grass-type zone, in which exists three types of aquatic vegetation (Table 1).
2.2. Field Data Collection
Field surveys were carried out on 10–13 July (sample group I), 17–22 August (sample group II) and 23–26 September in 2013 (sample group III). A total of 434 ground-truth samples (112 samples in July, 143 samples in August and 179 samples in September) were collected for open water and aquatic vegetation in the grass-type Zone of Taihu Lake (Figure 1). Sampling plots for aquatic vegetation were limited to areas measuring at least 60 × 60 m (i.e., four pixels of a HJ-CCD image) with a relatively uniform distribution of vegetation. We used a portable GPS receiver with an accuracy of 3 m to record the center coordinates for each sample, along with recording the type and percent coverage of aquatic vegetation. We also used the GPS to record the boundary extent of the representative sample regions for emergent, floating-leaved and submerged vegetation to generate a polygon vector file.
2.3. Remote Sensing Data Pre-Processing
HJ-1A and HJ-1B satellites were launched by the China Center for Resources Satellite Data and Application (CRESDA) on 6 September 2008. They are sun-synchronous circular orbit satellites with an orbital altitude of 649 km. Charge-coupled device (CCD) sensors onboard the two satellites have similar spectral range and spatial resolution to the first four bands of Landsat TM/ETM+ (Table 2). However, the HJ-1A and HJ-1B satellite constellation provides a more frequent revisit time (2 days), and a wider swath width (360 km), which are considered of great importance for vegetation monitoring and observation, especially for wet summers (i.e., between June and September) in southern China. We used three cloudless HJ-CCD images acquired on 11 July, 18 August, and 26 September 2013.
All processing of remote sensing images were conducted with ENVI 4.5 software. Radiometric calibrations were made using coefficients provided with the image (e.g., gains and offsets). The FLAASH module in ENVI software was applied for atmospheric correction [25]. The input parameters were set based on the location, sensor type and ground weather conditions observed on the day the image was acquired. The atmospherically corrected images were geometrically corrected against a historical LandsatTM image with geometric accuracy of <0.5 pixel. Considering no aquatic macrophyte vegetation occurs in the algae-type zone except for emergent vegetation (mostly reeds) near the shore, the algae-type zone, including sections I and VI, was masked.
2.4. Methods
2.4.1. Classification Tree (CT) Model
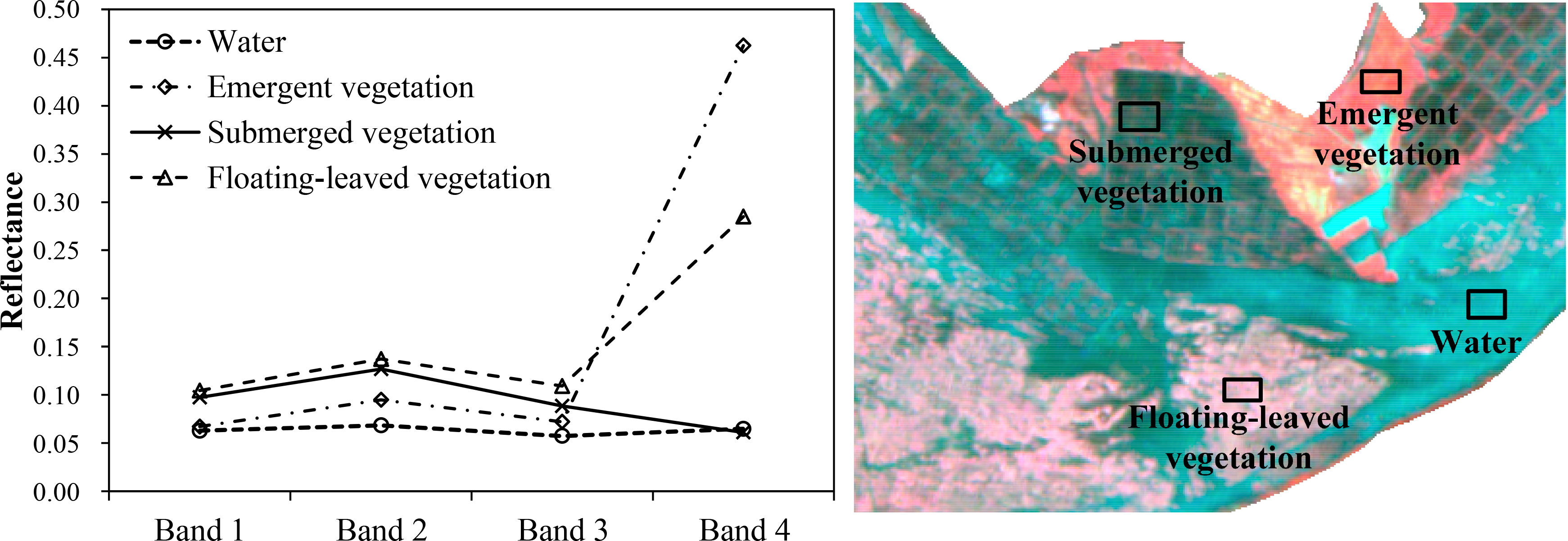
Classification tree (CT) analysis is based on dichotomous partitioning of data at certain thresholds of the value of explanatory variables, which determine the branch a particular sample will follow [26], and is considered robust with limited samples of remotely-sensed data [27]. The steps in our analysis for developing a CT model for mapping aquatic vegetation include: (1) selecting appropriate spectral variables according to spectral characteristics of aquatic vegetation; (2) determining the structure of the CT model and correct thresholds of the variables by unsupervised classification; and (3) assessing the classification accuracy of the resulting CT model. It can be difficult to identify water and types of aquatic vegetation with only a single reflectance band as shown in Figure 2. Spectral indices from band combination have been determined to be more suitable for vegetation classification than a single band for vegetation classification. In addition, studies have indicated that some image transform methods, such as principal components (PC) and tasseled cap (TC), can extract and strengthen some image information [28,29], and can be used to map wetlands [18]. Therefore, we used four PC bands and four TC bands, along with PC and TC transforms which were generated with the transform module of ENVI software, and additional spectral features (SFs) obtained from HJ-CCD images, and their potential for identifying emergent vegetation, floating-leaved vegetation and submerged vegetation. We conducted preliminary exploratory analyses to select a set of variables (Table 3) as input to develop a CT model.
2.4.2. Developing a Modified CT Model
The feature values from remotely sensed data can vary for different aquatic vegetation types as a growing season progresses, but it remains true that the between-class differences are far greater than within-class differences. Therefore, the hierarchic, structure and spectral features of a classification tree should be the same across different image dates, but with fluctuating value of spectral features [15,19].
CT model thresholds developed for one image might be inappropriate for an image acquired at a different time due to intrinsic and extrinsic factors. We developed a traditional classification CT model for each image date with the respective ground-based training samples corresponding to that date. We then developed modified CT modes based on two hypotheses:
Hypothesis I: The effects of intrinsic and extrinsic factors were the same for every pixel or changed in a linear fashion over time. With this hypothesis we assumed there was a good linear relationship between SFs from the two image dates and could develop a modified CT model for one image based on a linear adjustment of thresholds from a traditional CT model developed for the other date image [30]. We defined modified model as:
where is the threshold of spectral feature i in the modified CT model based on hypothesis I for date m, calculated using the linearly adjusted traditional CT model for date n; SFi is spectral feature i (i = 1, 2, or 3) (see Table 3); k is the slope of a linearly fitted line between the SFs of a given aquatic cover type on images for dates m and n; TCTn-SFi is the threshold of spectral feature i from the traditional CT developed for image date n; and h is the intercept of a linearly fitted line between the values of SFs for a given aquatic cover type on images for dates m and n.Hypothesis II: the ranked value for spectral feature i in one date image would be linearly related to the ranked values for that feature in a different date image [31]. With this hypothesis we assumed we could developed modified CT thresholds based on a linear model developed from the ranked SF values for the two image dates. We define this modified model as:
where is the threshold of spectral feature i in the modified CT model based on hypothesis II for date m, calculated using the linearly adjusted traditional model for date n; p is the slope of a linearly fitted line between the SFs of a given aquatic cover type on images for dates m and n; TCTn-SFi is the threshold of spectral feature i from the traditional CT model developed for image date n; q is the intercept of a linearly fitted line between the values of SFs for a given aquatic cover type on images for dates m and n.
To develop the methods for modifying the models under hypotheses I and II, we created three regions of interest as representative sample regions for different aquatic vegetation types (Table 4).
2.5. Model Validation
We evaluated three traditional CT models with the corresponding three groups of ground-truth samples. We used two methods to assess the modified CT models: (1) we quantified accuracy relative to the actual ground-truth samples and (2) we looked at area agreement between the classified maps created using modified and traditional CT models. For the former method, we applied a confusion matrix to compare agreement between ground-truth samples and classification results. We calculated producer’s, user’s and overall accuracy, and assumed the modified CT model having the highest accuracy was the best model. For the latter method, the distribution areas of three vegetation types in sections II, III, IV and V from classification maps obtained with modified CT models were compared with the result obtained with traditional CT models. The best modified CT model would be the one yielding area results most similar to the traditional CT model in the four sections of the classification map.
3. Results
3.1. Traditional CT Models Based on Measured Samples and Validation
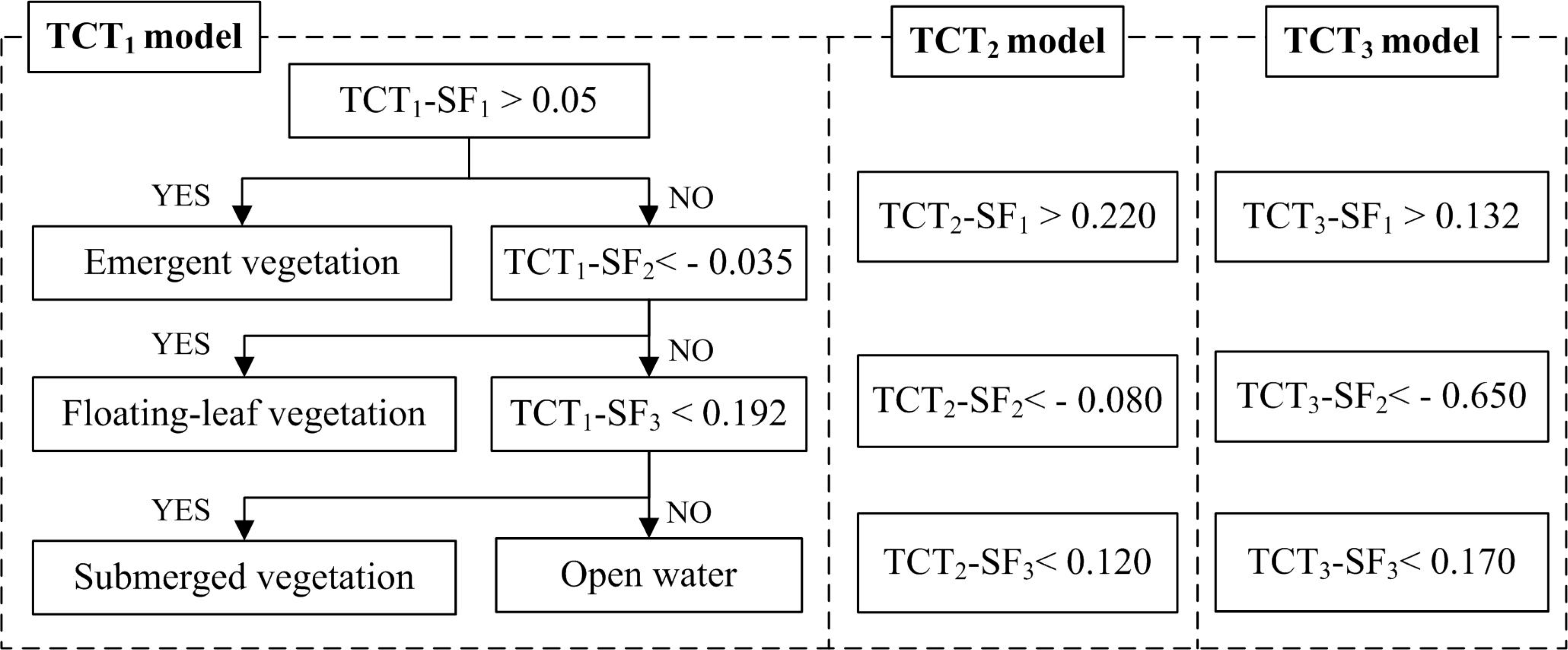
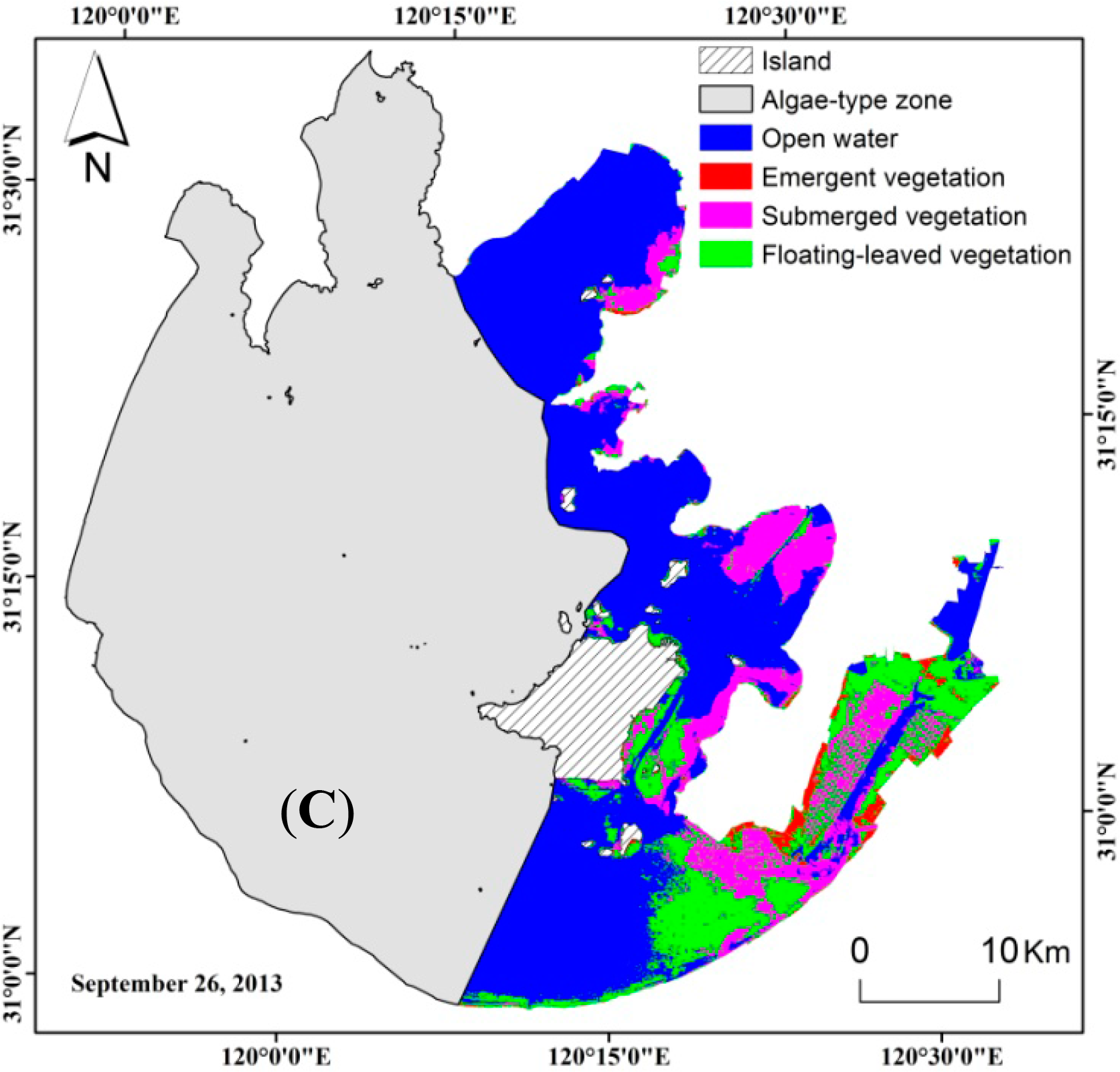
Classification trees constructed for the three image dates all based the first split on SF1 to identify emergent vegetation, the second split on SF2 to identify floating-leaved vegetation, and the third split on SF3 to identify submerged vegetation and water (Figure 3). The thresholds of SFs in the traditional CT models for July, August, and September were determined based on field data from these months, respectively.
Classification accuracies for the three models are shown in Table 5. Overall accuracies for traditional CT models for July, August and September were 82.1%, 79.7% and 84.4%, respectively. Among the misclassified samples, 83% were floating-leaved and submerged vegetation, the areal coverage of which was less than 20% in areas of occurrence and resulted in them being interpreted as water. These results suggest that it might be difficult to identify areas with low density of submerged and floating-leaved vegetation with moderate resolution images, such as from HJ-CCD and Landsat sensor data.
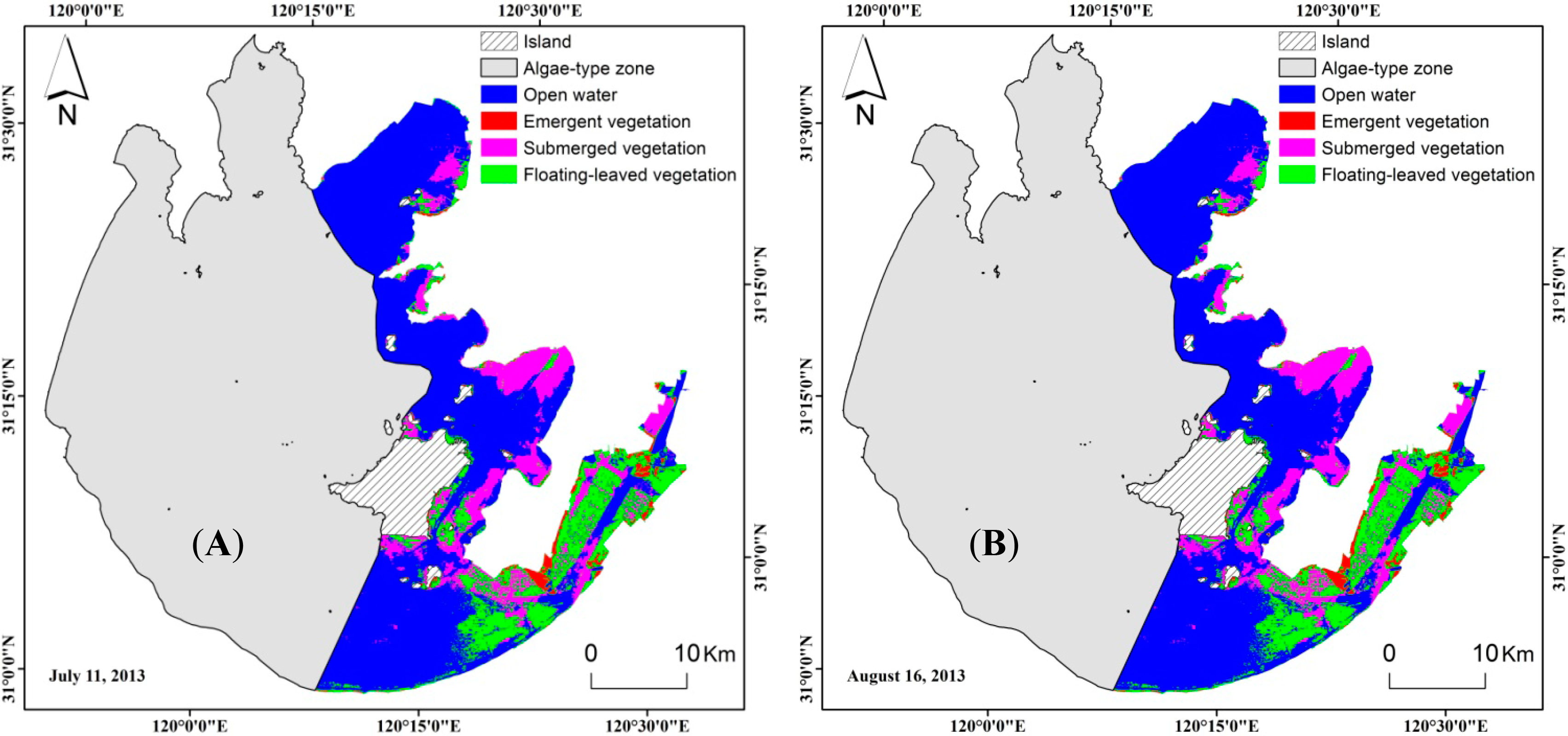
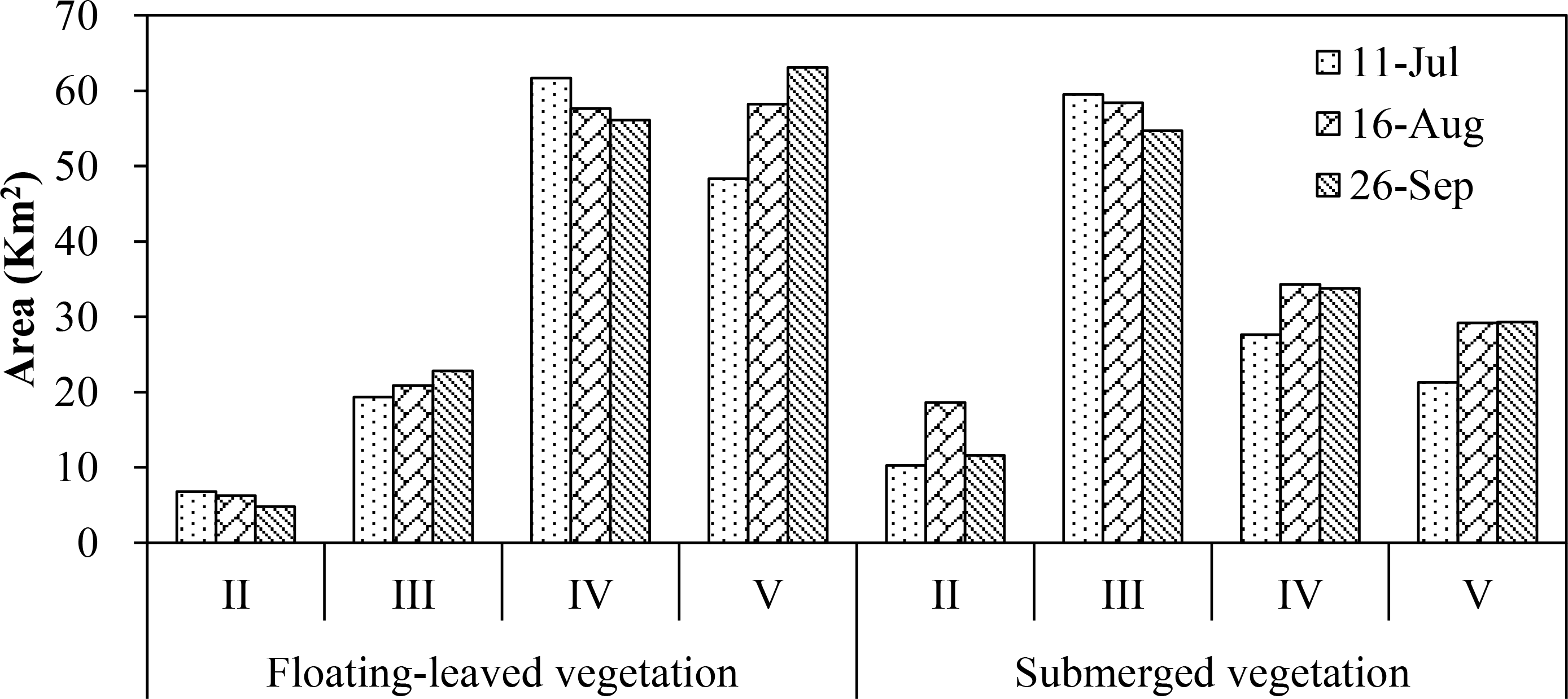
Figure 4 shows the classified maps resulting from models for the three images dates. The maps show little emergent vegetation, primarily distributed along the eastern shore of Taihu Lake. Floating-leaved was mainly distributed in sections IV and V and submerged vegetation was most prevalent in sections II and III (Figure 5). From 11 July to 16 August to 26 September, the area of floating-leaved vegetation was stable. Submerged vegetation in section II increased in extent from 11 July to 16 August and decreased in extent from 16 August to 26 September. In section III, the extent of floating-leaved vegetation increased while extent of submerged vegetation decreased over time. Floating-leaved vegetation in section IV increased from 11 July to 16 August, then decreased from 16 August to 26 September; Floating-leaved vegetation in section V decreased in extent over time while area of submerged vegetation increased from 11 July to 16 August, then stabilized (Figure 5). These results were consistent with information from the field survey.
3.2. Performance and Test of Methods Applied for Hypotheses I and II
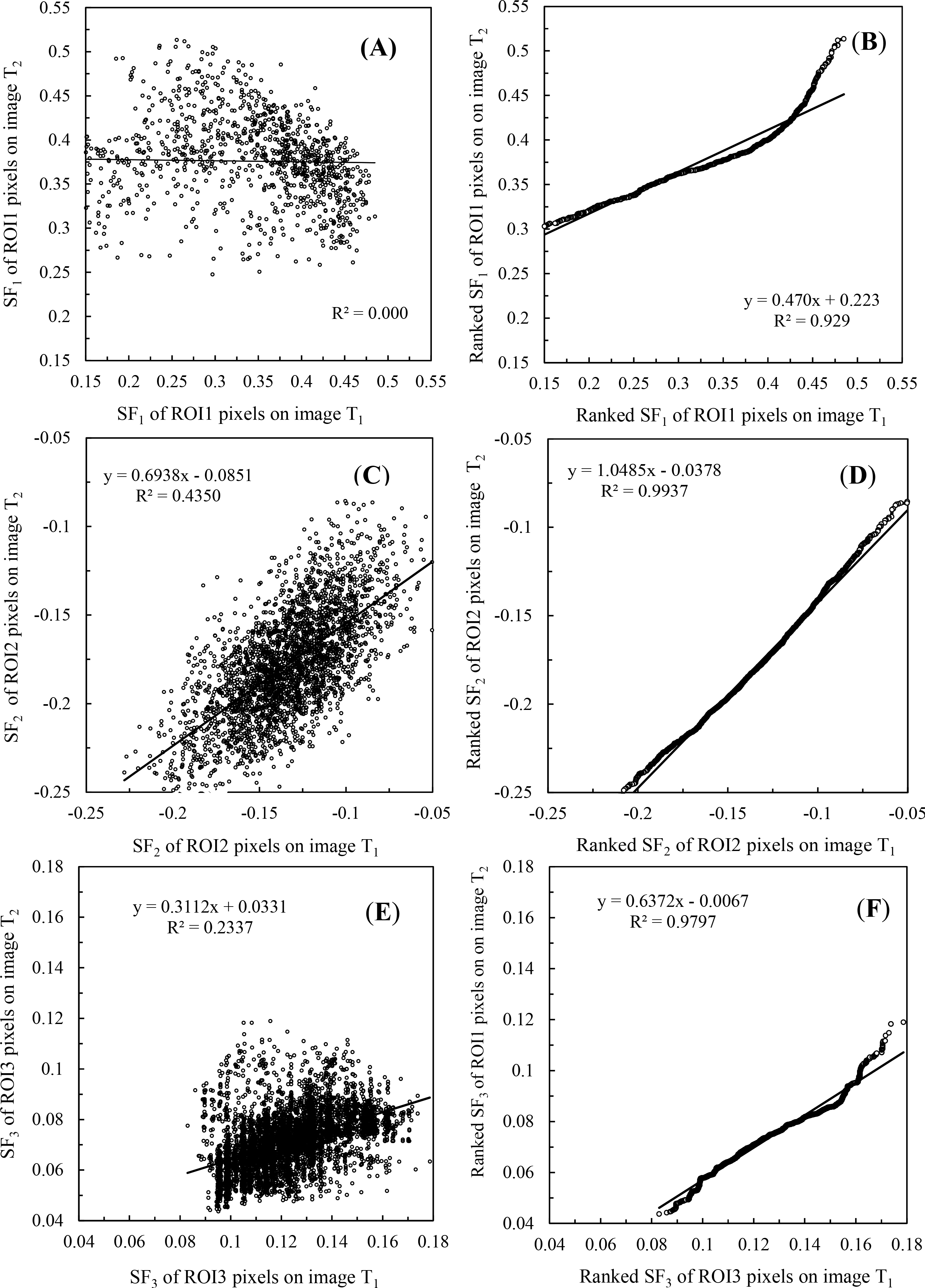
Scatterplots for SFs for the two regions of interest with different types from the image acquired on 11 July and 16 August under hypothesis I (Figure 6A,C,E) show little support for a linear correlation for either emergent or submerged vegetation types, but moderate support for floating-leaved vegetation. Scatterplots for the ranked SF values for the two regions under hypothesis II (Figure 6B,D,F) show strong support for a linear relation for all types, though a linear model seems less appropriate for emergent and submerged vegetation types in the tails of their SF distributions. Ranked SF values for all three vegetation types had overall R2 > 0.90. Equations for calculating modified threshold for SFs under the hypotheses I and II are shown in Tables 6 and 7.
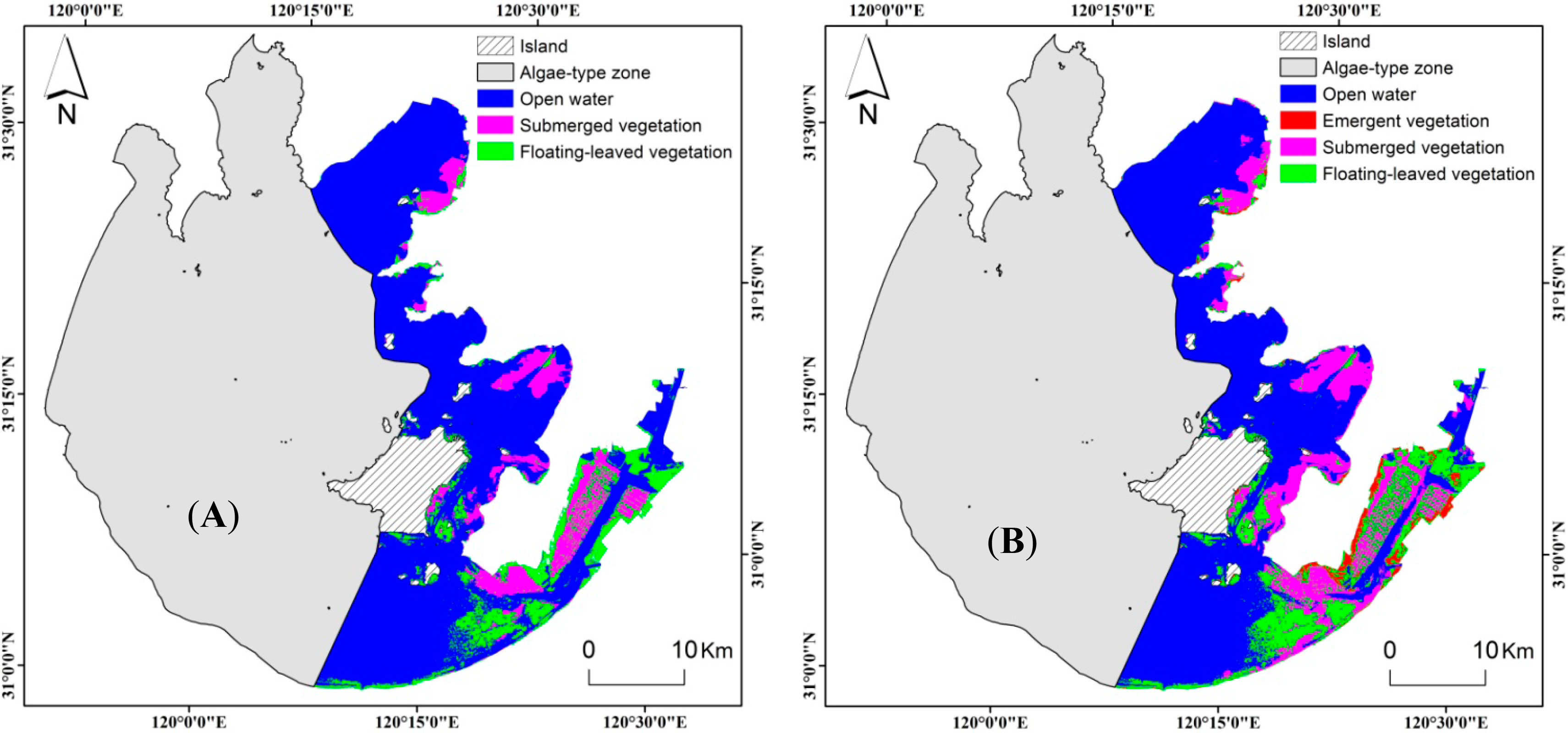
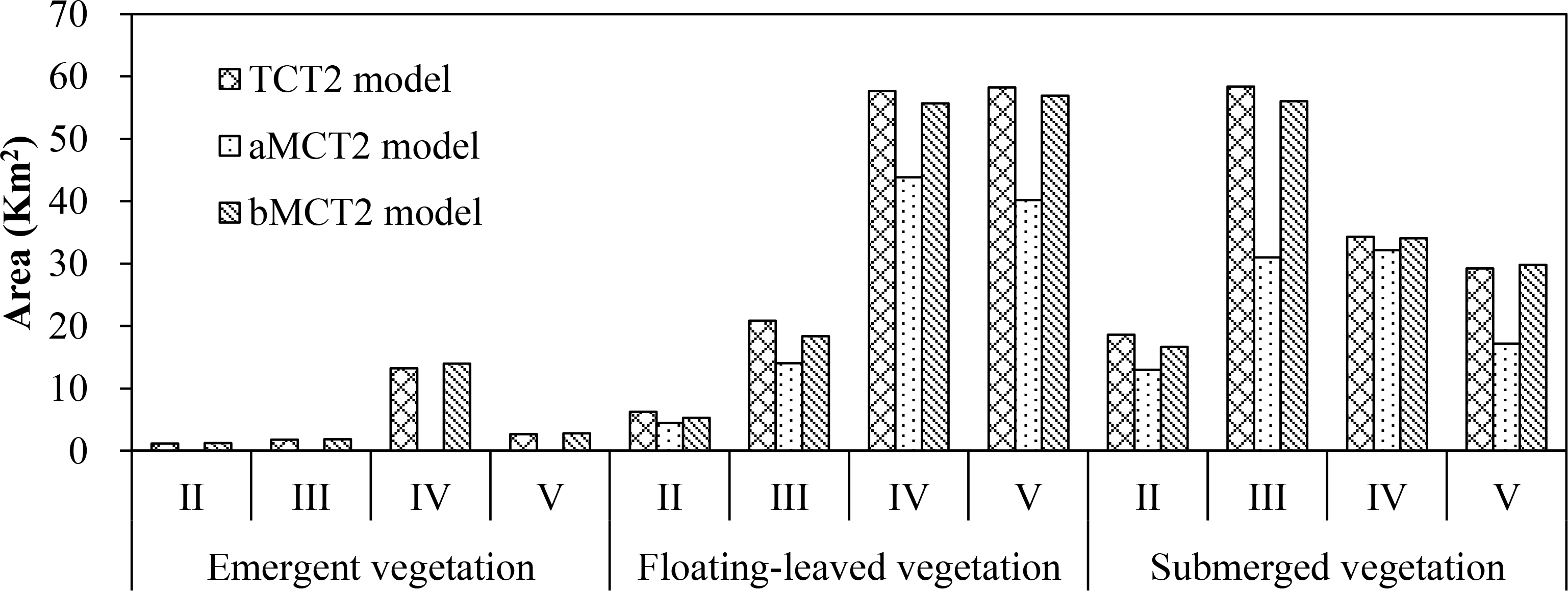
We applied the traditional and modified classification tree models developed under each hypothesis to generate maps for 16 August 2013 (Figure 7). There was little similarity in the distributions of aquatic vegetation types mapped with modified models developed under hypothesis I with the results from the traditional CT model (Figure 4B) developed with the image acquired for 16 August and corresponding field samples (sample group II). The spatial distributions of aquatic vegetation types based on hypothesis II, however, were consistent with the results from the traditional CT model (Figure 4B). Areal extents of aquatic vegetation types in the four sections mapped with the modified CT model under hypothesis I were substantially larger than the areas of aquatic vegetation types mapped with the traditional CT model, confirming that this approach was not appropriate for adjusting a CT model to map aquatic vegetation types for a point in time. Spatial extents of vegetation types mapped with CT thresholds modified under hypothesis II were fairly consistent with the areas mapped with the traditional CT model (Figure 8).
We assessed the accuracy of the three classification maps with the ground-truth samples from sample group II (Table 8). Results were highest for the traditional CT model generated for August, and the overall accuracy of modified CT model based on hypothesis II is higher than that based on hypothesis I.
3.3. Further Validation of Method II
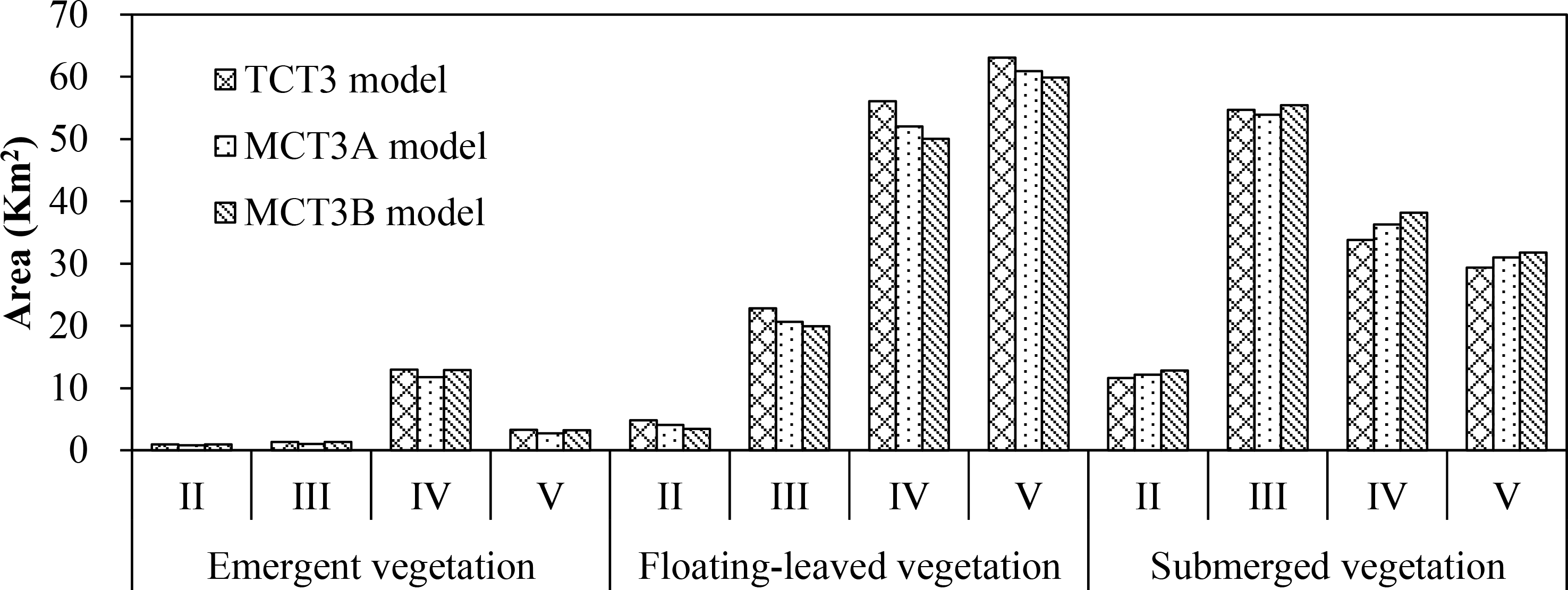
We verified that our approach under hypothesis II also would work for other combinations of image dates by developing modified thresholds for the 26 September image based on SF relationships with the 11 July image (Table 9) and 16 August image (Table 10). Resulting modified thresholds had small differences with those of the traditional CT model for 26 September (Figure 4C) and resulted in similar maps, as well (Figure 9, and see Figure 5C for area estimates).
We calculated areal extents of aquatic vegetation types in the four sections based on the maps developed for 26 September (Figure 10). Results show close agreement among three maps in total area calculated by vegetation type and sections. The greatest difference in area measurements was less than five square kilometers. We used ground-truth samples from September (sample group III) to assess user’s, producer’s, and overall accuracies for the maps generated for 26 September (Table 11). Overall accuracies ranged from 80% to 84%, corroborating earlier indication that the approach used for hypothesis II was effective and feasible for modifying a traditional CT model to accommodate other image dates.
4. Discussion
4.1. Intrinsic and Extrinsic Influences on Model Performance
Past research indicated that traditional CT models developed for one time period or image date could be inadequate when applied directly to other dates [20,22]. This is because the classification accuracy of CT models can be influenced substantially by intrinsic factors, such as aquatic vegetation conditions, and extrinsic factors, such as environmental or physical conditions. The intrinsic factors affecting the performance of a CT model can be related to changes in plant structural characteristics and foliar pigment content associated with phenological development. The extrinsic factors affecting the performance of a CT model are related to atmospheric conditions, water transparency, sun-view angle and other factors that vary with time and influence the remote sensing signal in ways independent of the condition of the aquatic vegetation [32,33]. Atmospheric conditions, which have a direct impact on remotely sensed reflectance, exhibits significant differences over time, especially in the wet season when atmospheric water vapor remains high [34]. The study by Zhao et al. [20] indicated also that 71.1% and 28.9% of the instability of traditional CT models originated from extrinsic and intrinsic factors, respectively, when applied to different time periods. Overall, there are many uncertainties and errors involved in applying the same CT model to identify aquatic vegetation types for different time periods.
We were unable to find any previous research studying whether each pixel is affected by the same intrinsic and extrinsic factors from one image date to another. If the effects of intrinsic and extrinsic factors on each pixel were the same or similar, there would be a good linear relationship between the SFs of two images dates, and the thresholds of SFs in a CT model generated from one image date could be linearly adjusted to fit another date (hypothesis I). However, our analysis showed that this assumption could not always be established (see Figure 6A,C,E) and we conclude: (1) that such an approach should be considered only when there is strong correlation between the SFs of two date images for a vegetation class of interest and (2) there are differences in the effects of intrinsic and extrinsic factors on each pixel over time that challenge the use of a modified model with an approach based on hypothesis I.
4.2. Influence of Vegetation Type on the Performance of CT Model Modified under Hypothesis II
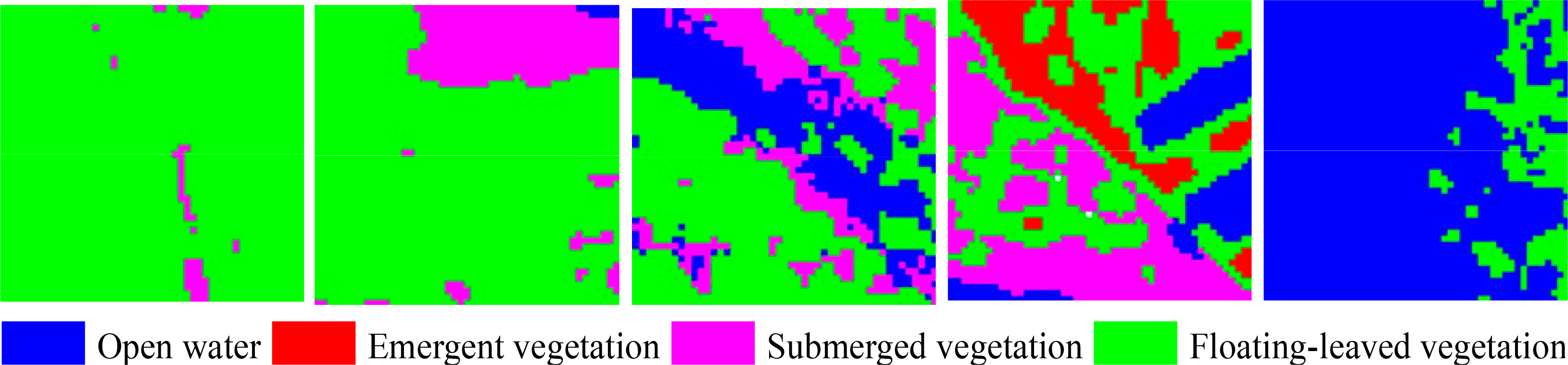
Our study indicated the approach developed under hypothesis II was effective for modifying model thresholds of SFs for mapping aquatic vegetation types in Taihu Lake with HJ-CCD imagery for all tested date combinations. With the approach it is crucial to select good representative sample regions for each vegetation type to modify model thresholds. For example, we selected five regions of interest for floating-leaved vegetation from the map classified for 11 July to test effects on a modified model for 16 August. The regions were equivalent in size, but had different percent cover by floating-leaved vegetation (Figure 11 and Table 12). SF2 values for pixels in the five regions of interest for images for 11 July and 16 August were extracted and sorted in descending order and five linear models were established to adjust SF2 values for modeling August aquatic vegetation classes. We also calculated differences between SF2 values for pixels from the traditional and modified models (Table 12).
The results suggested that regions of interest covered by larger proportions of floating-leaved vegetation would lead to smaller difference between SF2 values in the modified and traditional CT models. Therefore, we should select sample regions with pure pixels of the target vegetation type to the extent possible to develop a better modified CT model with the approach under hypothesis II.
4.3. Lake Management and Application
Eutrophication is one of the most serious problems in inland lakes, especially in Taihu [35]. Studies have reported in the literature that aquatic vegetation can purify water and transform aquatic ecosystems from a turbid algal-dominated state to a clear-water, plant-dominated state. However, an excessive amount of macrophytes, especially floating-leaved vegetation, can cause silting through the addition of large amounts of plant material to the lake bottom and the release of pollutants into the lake water when the plants die and decay, even resulting in grass-type lakes shifting to algae-type Lakes [36]. Therefore, it is important to monitor in real time the types and distribution areas of aquatic vegetation in Taihu Lake and to provide helpful information for effective management of aquatic vegetation, such as through harvesting and restoration, especially in the growth stage of aquatic vegetation (from June to October). Past research has also suggested that aquatic vegetation harvesting can be a very cost-effective method for removing excessive nutrients and protecting lakes from this adverse shift. Through such efforts, nutrients contained in the plant tissues are removed from lake ecosystem [36–38]. Combined with enough ground-truth samples, a CT model can be developed based on remote sensing images to monitor the distribution of aquatic vegetation. In most cases there are adequate remote sensing images available to monitor lakes through time, but a lack of corresponding ground-truth samples. It can therefore be difficult to develop a corresponding CT model to accurately map the distribution of aquatic vegetation. In this study, results showed an approach based on a linear relation of ranked values of spectral features for two image dates offered a feasible approach for mapping aquatic vegetation form remote imagery when corresponding ground-truth samples were not available. This provides the means to monitor the composition and distribution of aquatic vegetation types in shallow lake in near-real time to inform lakes management decisions.
5. Conclusions
In this paper, three traditional classification tree models of 11 July, 16 August and 26 September were developed based on three spectral features and corresponding group-truth samples for mapping aquatic vegetation types in Taihu Lake. Overall accuracies of three models were 82%, 79% and 84%, respectively.
Based on traditional classification tree model, we presented two approaches for modifying the CT thresholds to generate maps of aquatic vegetation types for image dates when no ground-truth samples would be available. By test and verification, we found that we could modify CT thresholds successfully with linear models derived from the ranked values of spectral features from two image dates to produce maps. In comparison, an approach based on an assumed directed linear relationship between spectral feature values calculated for pixels from two image dates did not provide a good foundation for modifying CT thresholds.
Acknowledgments
The research was supported by the State Key Program of the National Natural Science Foundation of China (41230853), National Natural Science Foundation of China (41301375) and the National High Technology Research and Development Program of China (2014AA06A509). We also acknowledge the Lake and Watershed Data Center, Scientific Data Sharing Platform and Watershed.
Author Contributions
Juhua Luo had the original idea for the study and implemented the methodology. Ronghua Ma was responsible for recruitment and contributed to manuscript organization Hongtao Duan and Weiping Hu supervised the research and provided valuable suggestions for the revision. Wenjiang Huang had significant contribution in data analysis and language polishing of our manuscript. Jinge Zhu offered measured samples to validate our models developed in this paper. Chen Lin offered background data about Taihu Lake. All authors contributed extensively to data collection and writing of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zimmer, K.D.; Hanson, M.A.; Herwig, B.R.; Konsti, M.L. Thresholds and stability of alternative regimes in shallow prairie–parkland lakes of Central North America. Ecosystems 2009, 12, 843–852. [Google Scholar]
- Brisson, J.; Chazarenc, F. Maximizing pollutant removal in constructed wetlands: Should we pay more attention to macrophyte species selection? Sci. Total Environ 2009, 407, 3923–3930. [Google Scholar]
- Tanner, C. Plants as ecosystem engineers in subsurface-flow treatment wetlands. Water Sci. Technol 2001, 44, 9–17. [Google Scholar]
- Marion, L.C.; Paillisson, J.-M. A mass balance assessment of the contribution of floating-leaved macrophytes in nutrient stocks in an eutrophic macrophyte-dominated lake. Aquat. Bot 2003, 75, 249–260. [Google Scholar]
- Van der Heide, T.; van Nes, E.H.; van Katwijk, M.M.; Olff, H.; Smolders, A.J. Positive feedbacks in seagrass ecosystems—Evidence from large-scale empirical data. PLoS One 2011. [Google Scholar] [CrossRef]
- Marshall, T.R.; Lee, P. Mapping aquatic macrophytes through digital image analysis of aerial photographs: An assessment. J. Aquat. Plant Manag 1994, 32, 61–66. [Google Scholar]
- Malthus, T.; George, D. Airborne remote sensing of macrophytes in Cefni Reservoir, Anglesey, UK. Aquat. Bot 1997, 58, 317–332. [Google Scholar]
- Fornes, A.; Basterretxea, G.; Orfila, A.; Jordi, A.; Alvarez, A.; Tintore, J. Mapping Posidonia oceanic from IKONOS. Isprs. J. Photogramm 2006, 60, 315–322. [Google Scholar]
- Laba, M.; Blair, B.; Downs, R.; Monger, B.; Philpot, W.; Smith, S.; Sullivan, P.; Baveye, P.C. Use of textural measurements to map invasive wetland plants in the Hudson River National Estuarine Research Reserve with IKONOS satellite imagery. Remote Sens. Environ 2010, 114, 876–886. [Google Scholar]
- Dogan, O.K.; Akyurek, Z.; Beklioglu, M. Identification and mapping of submerged plants in a shallow lake using quickbird satellite data. J. Environ. Manag 2009, 90, 2138–2143. [Google Scholar]
- Szantoi, Z.; Escobedo, F.; Abd-Elrahman, A.; Smith, S.; Pearlstine, L. Analyzing fine-scale wetland composition using high resolution imagery and texture features. Int. J. Appl. Earth Obs 2013, 23, 204–212. [Google Scholar]
- MacAlister, C.; Mahaxay, M. Mapping wetlands in the Lower Mekong Basin for wetland resource and conservation management using Landsat ETM images and field survey data. J. Environ. Manag 2009, 90, 2130–2137. [Google Scholar]
- Gullström, M.; Lundén, B.; Bodin, M.; Kangwe, J.; Öhman, M.C.; Mtolera, M.S.; Björk, M. Assessment of changes in the seagrass-dominated submerged vegetation of tropical Chwaka Bay (Zanzibar) using satellite remote sensing. Estuar. Coast. Shelf Sci 2006, 67, 399–408. [Google Scholar]
- Davranche, A.; Lefebvre, G.; Poulin, B. Wetland monitoring using classification trees and SPOT-5 seasonal time series. Remote Sens. Environ 2010, 114, 552–562. [Google Scholar]
- Zhao, D.; Lv, M.; Jiang, H.; Cai, Y.; Xu, D.; An, S. Spatio-Temporal variability of aquatic vegetation in Taihu lake over the past 30 years. PLoS One 2013. [Google Scholar] [CrossRef]
- Zhao, D.; Jiang, H.; Cai, Y.; An, S. Artificial regulation of water level and its effect on aquatic macrophyte distribution in Taihu Lake. PLoS One 2012. [Google Scholar] [CrossRef]
- Chauvaud, S.; Bouchon, C.; Maniere, R. Remote sensing techniques adapted to high resolution mapping of tropical coastal marine ecosystems (coral reefs, seagrass beds and mangrove). Int. J. Remote Sens 1998, 19, 3625–3639. [Google Scholar]
- Baker, C.; Lawrence, R.; Montagne, C.; Patten, D. Mapping wetlands and riparian areas using Landsat ETM+ imagery and decision-tree-based models. Wetlands 2006, 26, 465–474. [Google Scholar]
- Ma, R.; Duan, H.; Gu, X.; Zhang, S. Detecting aquatic vegetation changes in Taihu Lake, China using multi-temporal satellite imagery. Sensors 2008, 8, 3988–4005. [Google Scholar]
- Zhao, D.; Jiang, H.; Yang, T.; Cai, Y.; Xu, D.; An, S. Remote sensing of aquatic vegetation distribution in Taihu Lake using an improved classification tree with modified thresholds. J. Environ. Manag 2012, 95, 98–107. [Google Scholar]
- Noh, H.G.; Song, M.S.; Park, S.H. An unbiased method for constructing multilabel classification trees. Comput.Stat. Data Anal 2004, 47, 149–164. [Google Scholar]
- Jiang, H.; Zhao, D.; Cai, Y.; An, S. A method for application of classification tree models to map aquatic vegetation using remotely sensed images from different sensors and dates. Sensors 2012, 12, 12437–12454. [Google Scholar]
- Graetz, R. Satellite remote sensing of Australian rangelands. Remote Sens. Environ 1987, 23, 313–331. [Google Scholar]
- Lu, N.; Hu, W.; Deng, J.; Zhai, S.; Chen, X.; Zhou, X. Spatial distribution characteristics and ecological significance of alkaline phosphatase in water column of Taihu Lake. Environ. Sci 2009, 30, 2898–2903. [Google Scholar]
- Berk, A.; Adler-Golden, S.; Ratkowski, A.; Felde, G.; Anderson, G.; Hoke, M.; Cooley, T.; Chetwynd, J.; Gardner, J.; Matthew, M. Exploiting MODTRAN radiation transport for atmospheric correction: The FLAASH algorithm. Proceedings of the Fifth International Conference on Information Fusion, Annapolis, MA, USA, 8–11 July 2002; pp. 798–803.
- Olshen, L.B.J.F.R.; Stone, C.J. Classification and Regression Trees; Wadsworth International Group: Belmont, Canada, 1984. [Google Scholar]
- Tadjudin, S.; Landgrebe, D.A. A decision tree classifier design for high-dimensional data with limited training samples. Proceedings of the International Geoscience and Remote Sensing Symposium 1996, Remote Sensing for a Sustainable Future (IGARSS ’96), Lincoln, NE, USA, 27–31 May 1996; pp. 790–792.
- Dymond, C.C.; Mladenoff, D.J.; Radeloff, V.C. Phenological differences in Tasseled Cap indices improve deciduous forest classification. Remote Sens. Environ 2002, 80, 460–472. [Google Scholar]
- Jin, S.; Sader, S.A. Comparison of time series tasseled cap wetness and the normalized difference moisture index in detecting forest disturbances. Remote Sens. Environ 2005, 94, 364–372. [Google Scholar]
- Pu, R.; Gong, P.; Tian, Y.; Miao, X.; Carruthers, R.I.; Anderson, G.L. Using classification and NDVI differencing methods for monitoring sparse vegetation coverage: A case study of saltcedar in Nevada, USA. Int. J. Remote Sens 2008, 29, 3987–4011. [Google Scholar]
- Chapman McGrew, J.; Monroe, C.B. An Introduction to Statistical Problem Solving in Geography; Wm. C. Brown Publishers: Dubuque, IA, USA, 1993. [Google Scholar]
- Nelson, S.A.C.; Cheruvelil, K.S.; Soranno, P.A. Satellite remote sensing of freshwater macrophytes and the influence of water clarity. Aquat. Bot 2006, 85, 289–298. [Google Scholar]
- Silva, T.S.; Costa, M.P.; Melack, J.M.; Novo, E.M. Remote sensing of aquatic vegetation: Theory and applications. Environ. Monit. Assess 2008, 140, 131–145. [Google Scholar]
- Martínez-López, J.; Carreño, M.F.; Palazón-Ferrando, J.A.; Martínez-Fernández, J.; Esteve, M.A. Remote sensing of plant communities as a tool for assessing the condition of semiarid Mediterranean saline wetlands in agricultural catchments. Int. J. Appl. Earth Obs. Geoinf 2014, 26, 193–204. [Google Scholar]
- Duan, H.; Ma, R.; Hu, C. Evaluation of remote sensing algorithms for cyanobacterial pigment retrievals during spring bloom formation in several lakes of East China. Remote Sens. Environ 2012, 126, 126–135. [Google Scholar]
- Vereecken, H.; Baetens, J.; Viaene, P.; Mostaert, F.; Meire, P. Ecological management of aquatic plants: Effects in lowland streams. In Macrophytes in Aquatic Ecosystems: From Biology to Management; Springer: Berlin/Heidelberg, Germany, 2006; pp. 205–210. [Google Scholar]
- Reisinger, D.L.; Brabham, M.; Schmidt, M.F.; Victor, P.R.; Schwartz, L. Methodology, evaluation, and feasibility study of total phosphorus removal management measures in Lake George and nearby lakes. Fla. Water Resour. J 2008, 60, 42–50. [Google Scholar]
- Vymazal, J.; Kröpfelová, L.; Švehla, J.; Štíchová, J. Can multiple harvest of aboveground biomass enhance removal of trace elements in constructed wetlands receiving municipal sewage? Ecol. Eng 2010, 36, 939–945. [Google Scholar]
| Type | Dominant Species |
|---|---|
| Emergent vegetation | Phragmites communis, Zizania latifolia |
| Submerged vegetation | Vallisneria spiralis, Ceratophyllum demersum, Potamogeton malaianus, P. maackianus, Hydrilla varticillata, Potamogeton maackianus |
| Floating-leaved vegetation | Eichhornia crassipes, Lemna minor, Nymphoides peltata, Trapa bicornis |
| Sensor Type | Blue Band (Band 1) | Green Band (Band 2) | Red Band (Band 3) | Near-Infrared Band (Band 4) |
|---|---|---|---|---|
| HJ-1A/1B CCD | 430–520 | 520–600 | 630–690 | 760–900 |
| TM/ETM+ | 430–520 | 520–600 | 630–690 | 760–900 |
| Spectral Features (SFs) | Description |
|---|---|
| B1–4 are the four reflectance bands (j = 1, 2, …, 4). | |
| SF2: PC2 | PC2 is the second principal component of the principal component transform. |
| SF3: TC1–TC2 | TC1 and TC2 are the greenness index and brightness index of the tasseled-cap transform. |
| Region of Interest (ROI) | Number of Pixels | Class |
|---|---|---|
| ROI 1 | 1090 | Emergent vegetation |
| ROI 2 | 2813 | Floating-leaved vegetation |
| ROI 3 | 4228 | Submerged vegetation |
| Models | Predicted | |||||||
|---|---|---|---|---|---|---|---|---|
| OW | EV | SV | FV | CA (%) | OA (%) | |||
| Traditional CT model for July | Measured | OW | 17 | 0 | 0 | 0 | 100.00 | 82.14 |
| EV | 0 | 10 | 0 | 1 | 90.91 | |||
| SV | 6 | 0 | 38 | 5 | 77.55 | |||
| FV | 3 | 0 | 5 | 27 | 77.14 | |||
| Traditional CT model for August | Measured | OW | 30 | 0 | 0 | 3 | 90.91 | 79.72 |
| EV | 0 | 9 | 0 | 2 | 81.82 | |||
| SV | 21 | 0 | 46 | 0 | 68.66 | |||
| FV | 2 | 0 | 1 | 29 | 90.63 | |||
| Traditional CT model for September | Measured | OW | 40 | 0 | 0 | 0 | 100.00 | 84.36 |
| EV | 0 | 9 | 0 | 2 | 81.82 | |||
| SV | 21 | 0 | 75 | 2 | 76.53 | |||
| FV | 3 | 0 | 0 | 27 | 90.00 | |||
Note: OW = open water; EV = emergent vegetation; SV = submerged vegetation; FV = floating-leaved vegetation; CA = classification accuracy; OA = overall accuracy.
| Region of Interest (ROI) | R2 | Equation | Thresholds of | |
|---|---|---|---|---|
| ROI 2 | 0.4350 | −0.0608 | ||
| ROI 3 | 0.2337 | 0.7044 | ||
| Region of Interest (ROI) | R2 | Equation | Threshold of | |
|---|---|---|---|---|
| ROI 1 | 0.9290 | 0.2467 | ||
| ROI 2 | 0.9937 | −0.0745 | ||
| ROI 3 | 0.9797 | 0.1290 | ||
| Class | TCT2 | |||||
|---|---|---|---|---|---|---|
| UA (%) | PA (%) | UA (%) | PA (%) | UA (%) | PA (%) | |
| OW | 56.60 | 90.91 | 33.33 | 84.85 | 43.08 | 84.85 |
| FL | 97.87 | 68.66 | 86.36 | 28.36 | 87.80 | 53.73 |
| SV | 85.29 | 90.63 | 60.00 | 65.63 | 75.00 | 65.63 |
| OA (%) | 79.72 | 48.95 | 65.73 | |||
| Region of Interest (ROI) | R2 | Equation | Modified Threshold | |
|---|---|---|---|---|
| ROI 1 | 0.9738 | 0.1581 | ||
| ROI 2 | 0.985 | −0.0630 | ||
| ROI 3 | 0.9649 | 0.1743 | ||
| Region of Interest (ROI) | R2 | Equation | Modified Threshold | |
|---|---|---|---|---|
| ROI 1 | 0.9444 | 0.1310 | ||
| ROI 2 | 0.9612 | −0.0677 | ||
| ROI 3 | 0.9796 | 0.1786 | ||
| Class | Traditional CT Model for 26 September | Modified Model from 11 July Thresholds | Modified Model from 16 August Thresholds | |||
|---|---|---|---|---|---|---|
| UA (%) | PA (%) | UA (%) | PA (%) | UA (%) | PA (%) | |
| OW | 62.50 | 100.00 | 58.82 | 100.00 | 58.82 | 100.00 |
| EV | 100.00 | 81.82 | 100.00 | 81.82 | 100.00 | 81.82 |
| SV | 100.00 | 76.53 | 97.30 | 73.47 | 95.95 | 72.45 |
| LV | 87.10 | 90.00 | 85.71 | 80.00 | 85.71 | 80.00 |
| OA (%) | 84.35 | 81.01 | 80.45 | |||
| Training Regions | % of Training | Threshold of | Difference |
|---|---|---|---|
| A | 97.83 | −0.0836 | 0.0036 |
| B | 81.34 | −0.0701 | 0.0099 |
| C | 52.51 | −0.0674 | 0.0126 |
| D | 38.06 | −0.0382 | 0.0418 |
| E | 15.80 | −0.1486 | 0.0686 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Luo, J.; Ma, R.; Duan, H.; Hu, W.; Zhu, J.; Huang, W.; Lin, C. A New Method for Modifying Thresholds in the Classification of Tree Models for Mapping Aquatic Vegetation in Taihu Lake with Satellite Images. Remote Sens. 2014, 6, 7442-7462. https://doi.org/10.3390/rs6087442
Luo J, Ma R, Duan H, Hu W, Zhu J, Huang W, Lin C. A New Method for Modifying Thresholds in the Classification of Tree Models for Mapping Aquatic Vegetation in Taihu Lake with Satellite Images. Remote Sensing. 2014; 6(8):7442-7462. https://doi.org/10.3390/rs6087442
Chicago/Turabian StyleLuo, Juhua, Ronghua Ma, Hongtao Duan, Weiping Hu, Jinge Zhu, Wenjiang Huang, and Chen Lin. 2014. "A New Method for Modifying Thresholds in the Classification of Tree Models for Mapping Aquatic Vegetation in Taihu Lake with Satellite Images" Remote Sensing 6, no. 8: 7442-7462. https://doi.org/10.3390/rs6087442
APA StyleLuo, J., Ma, R., Duan, H., Hu, W., Zhu, J., Huang, W., & Lin, C. (2014). A New Method for Modifying Thresholds in the Classification of Tree Models for Mapping Aquatic Vegetation in Taihu Lake with Satellite Images. Remote Sensing, 6(8), 7442-7462. https://doi.org/10.3390/rs6087442










