Predictive Mapping of Dwarf Shrub Vegetation in an Arid High Mountain Ecosystem Using Remote Sensing and Random Forests
Abstract
:1. Introduction
2. Material and Methods
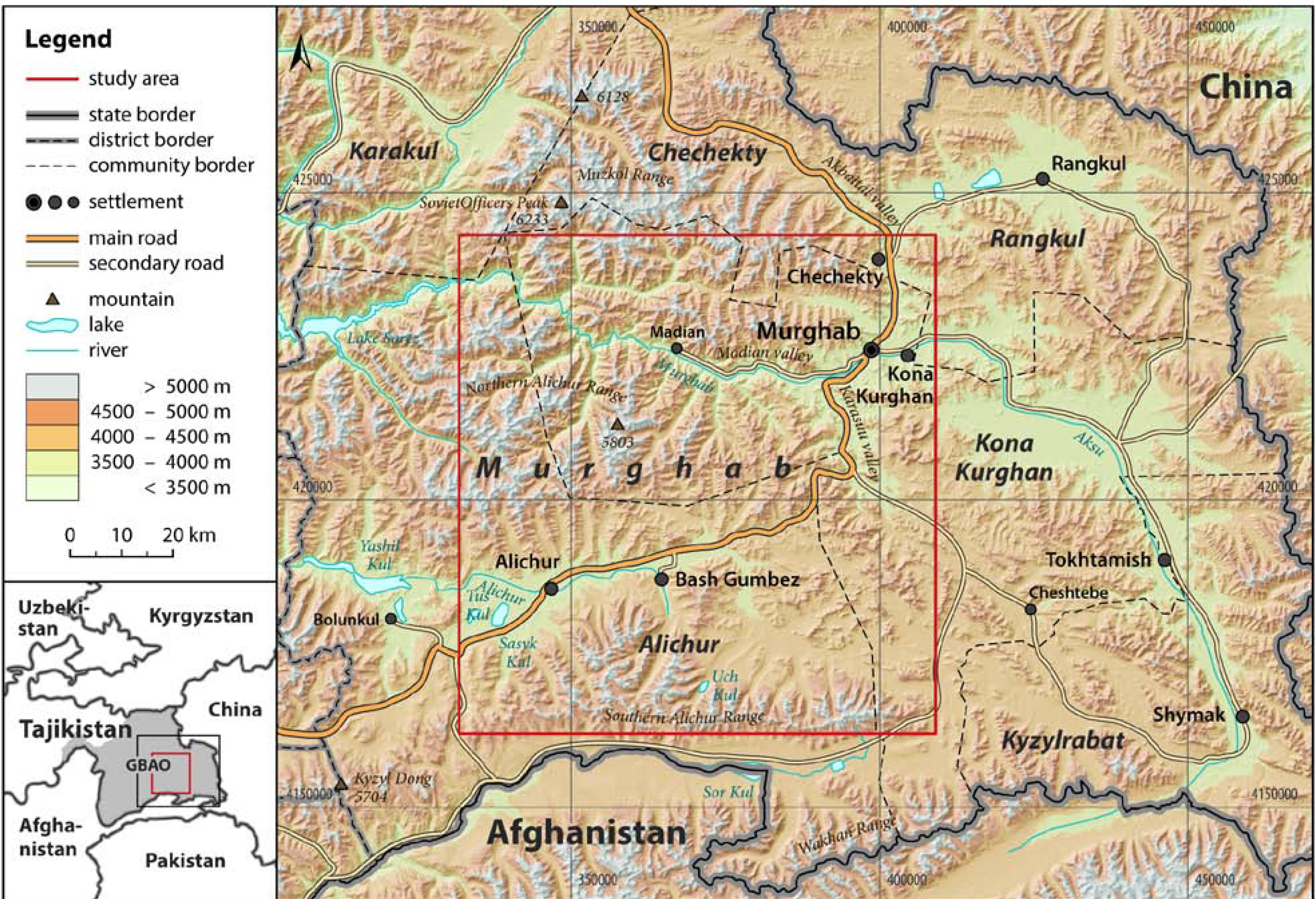
2.1. Study Area and Species
2.2. Explanatory Variable Data
2.3. Sample Data and Statistical Analysis
3. Results and Discussion
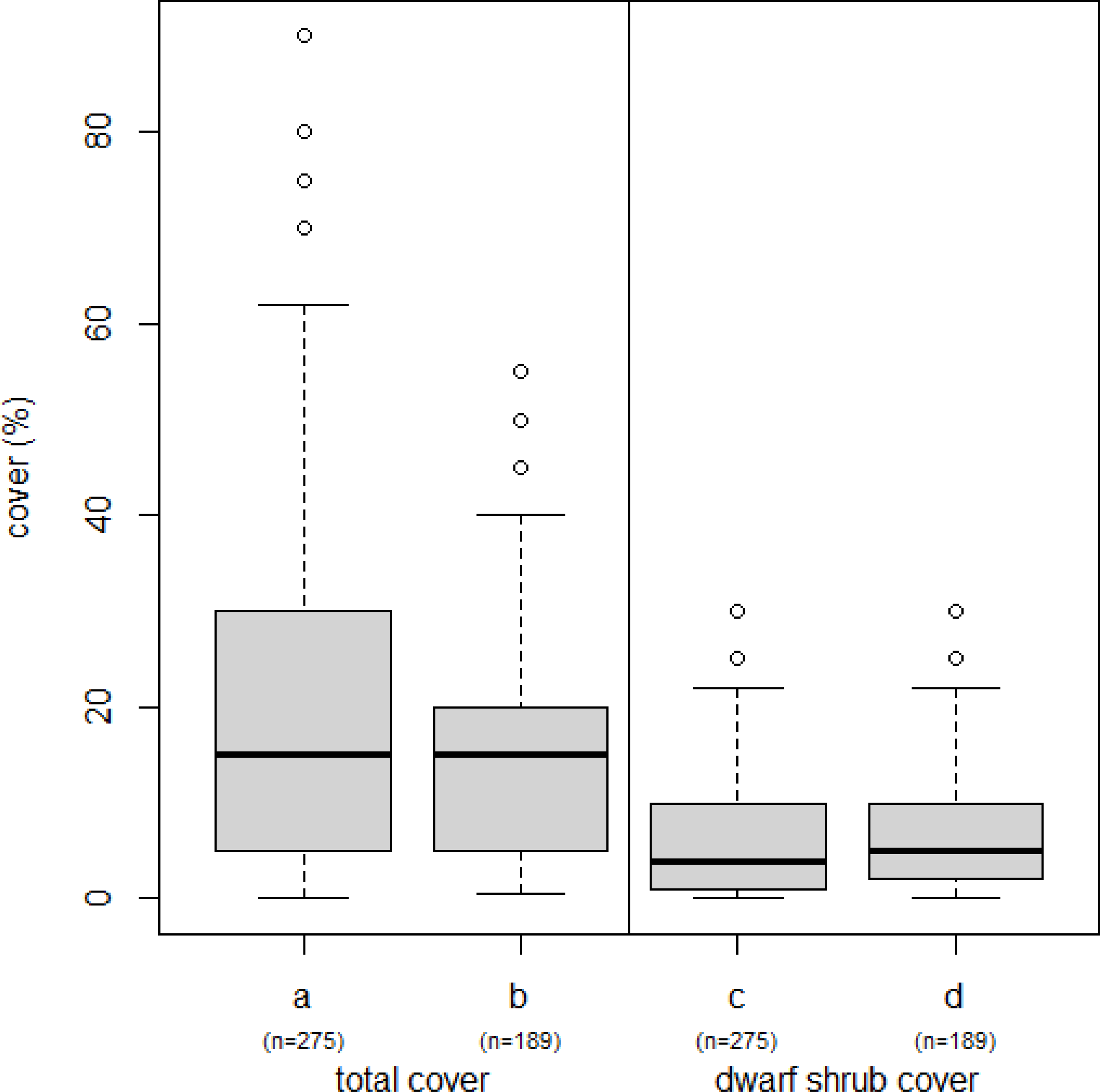
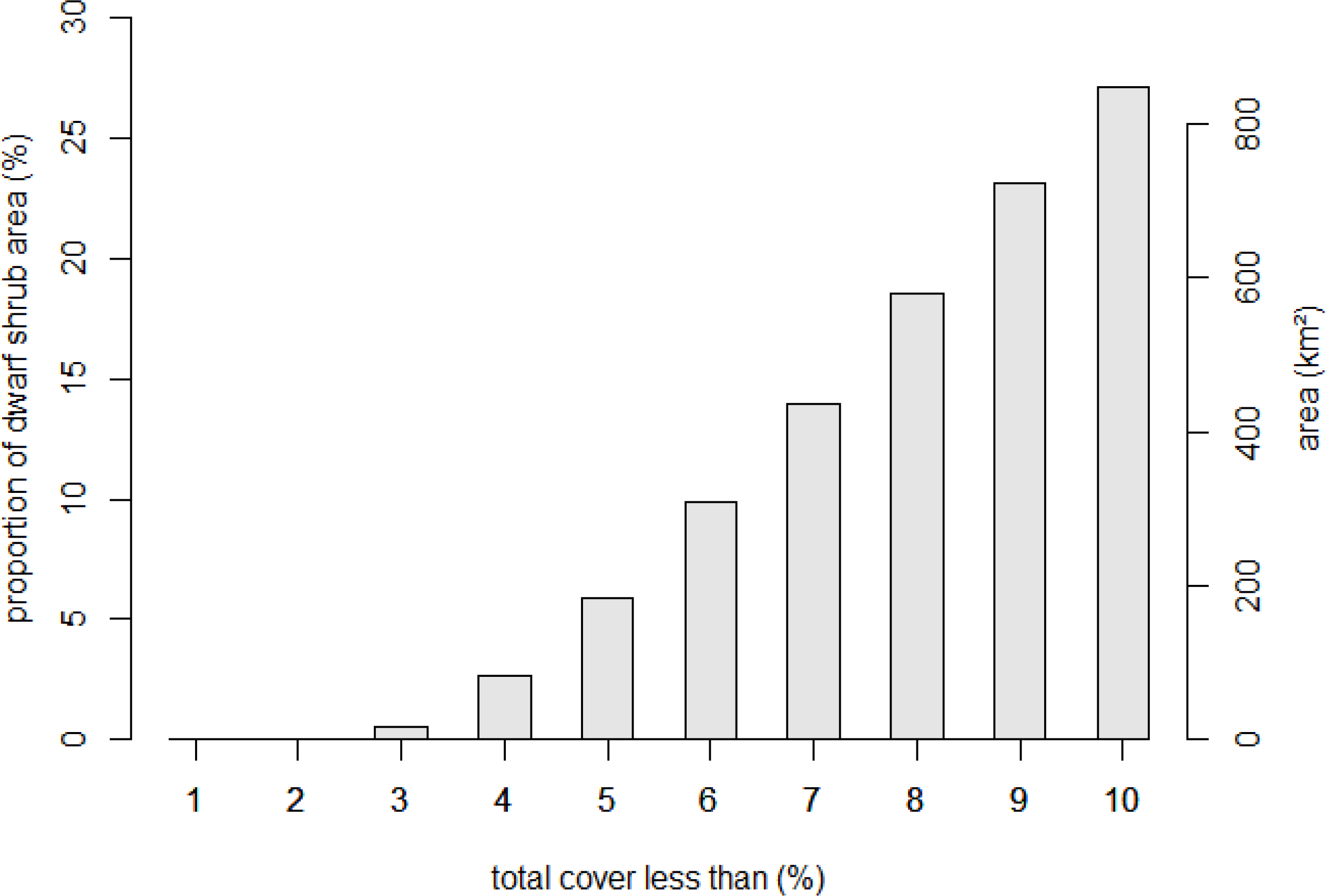
3.1. Descriptive Statistics
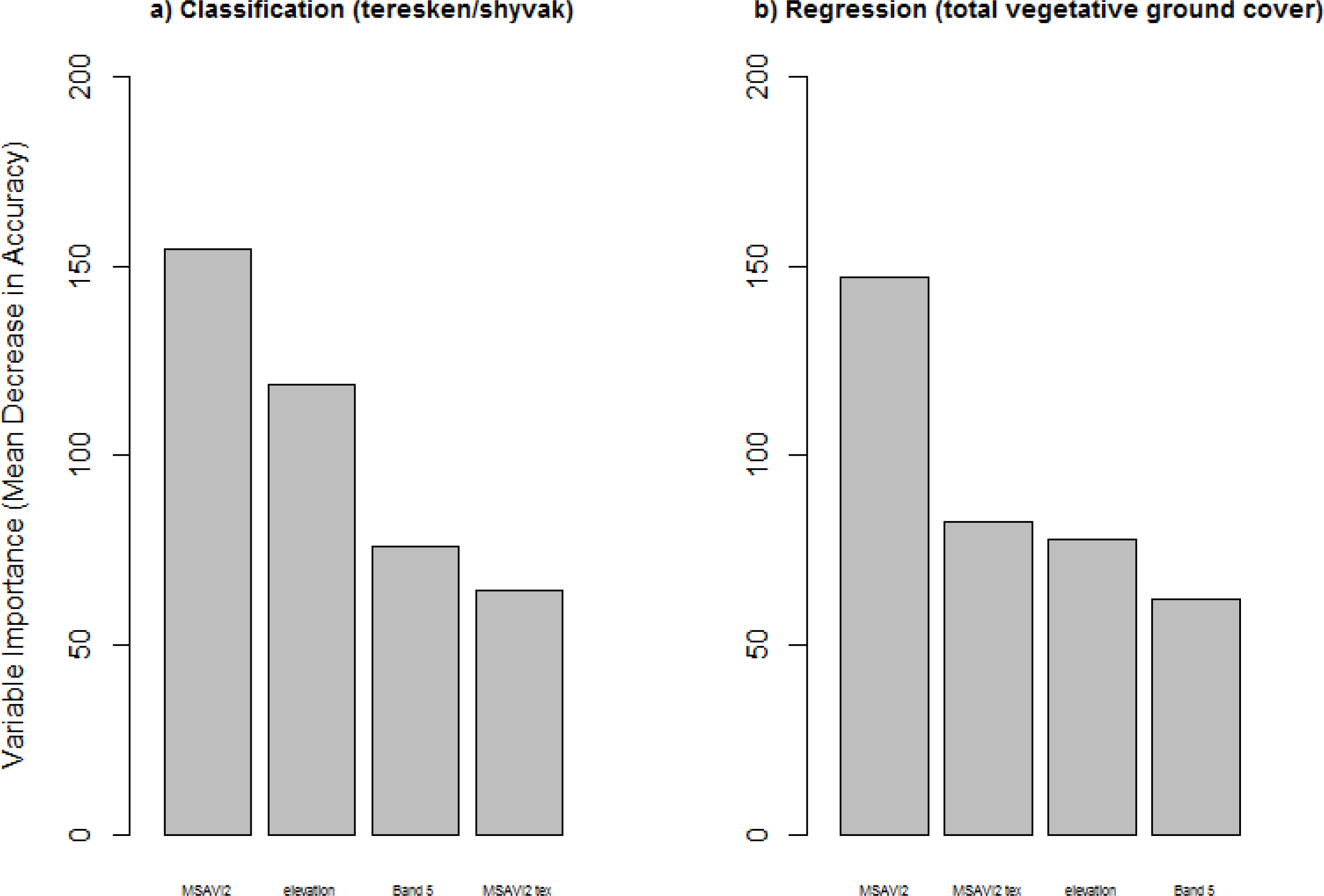
3.2. Species Distribution Model
3.3. Vegetation Cover Model
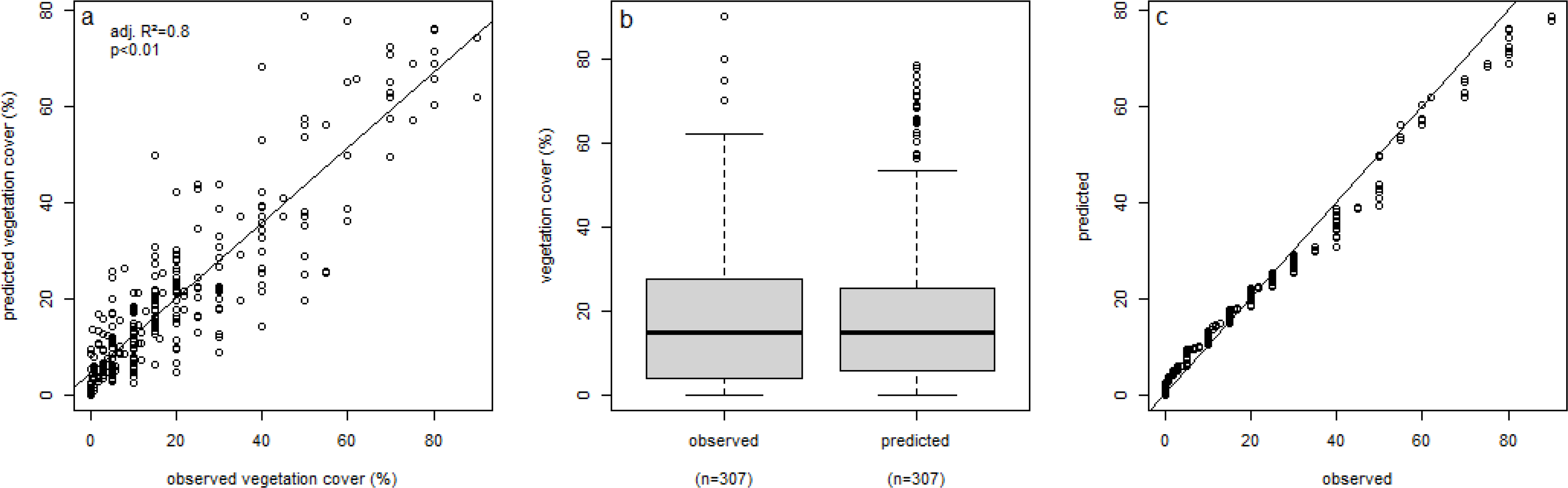
3.4. Model Evaluation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- UNEP. Global Environment Outlook 3—Past, Present and Future Perspectives; Earthscan Publications: London, UK; Sterling, VA, USA, 2002. [Google Scholar]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. J. Plant Ecol 2008, 1, 9–23. [Google Scholar]
- Kerr, J.T.; Ostrovsky, M. From space to species: Ecological applications for remote sensing. Trends Ecol. Evolut 2003, 18, 299–305. [Google Scholar]
- Brinkmann, K.; Patzelt, A.; Schlecht, E.; Buerkert, A. Use of environmental predictors for vegetation mapping in semi-arid mountain rangelands and the determination of conservation hotspots. Appl. Veg. Sci 2011, 14, 17–30. [Google Scholar]
- Dobrowski, S.Z.; Safford, H.D.; Cheng, Y.B.; Ustin, S.L. Mapping mountain vegetation using species distribution modeling, image-based texture analysis, and object-based classification. Appl. Veg. Sci 2008, 11, 499–508. [Google Scholar]
- Münchow, J.; Bräuning, A.; Rodríguez, E.F.; von Wehrden, H. Predictive mapping of species richness and plant species’ distributions of a peruvian fog oasis along an altitudinal gradient. Biotropica 2013, 45, 557–566. [Google Scholar]
- Van Etten, E.J.B. Mapping vegetation in an arid, mountainous region of western Australia. Appl. Veg. Sci 1998, 1, 189–200. [Google Scholar]
- Von Wehrden, H.; Zimmermann, H.; Hanspach, J.; Ronnenberg, K.; Wesche, K. Predictive mapping of plant species and communities using GIS and Landsat data in a southern Mongolian mountain range. Folia Geobot 2009, 44, 211–225. [Google Scholar]
- Irisarri, J.G.N.; Oesterheld, M.; Verón, S.R.; Paruelo, J.M. Grass species differentiation through canopy hyperspectral reflectance. Int. J. Remote Sens 2009, 30, 5959–5975. [Google Scholar]
- Dirnböck, T.; Dullinger, S.; Gottfried, M.; Ginzier, C.; Grabherr, G. Mapping alpine vegetation based on image analysis, topographic variables and canonical correspondence analysis. Appl. Veg. Sci 2003, 6, 85–96. [Google Scholar]
- Mansour, K.; Mutanga, O.; Everson, T. Remote sensing based indicators of vegetation species for assessing rangeland degradation: Opportunities and challenges. Afr. J. Agric. Res 2012, 7, 3261–3270. [Google Scholar]
- Leprieur, C.; Kerr, Y.H.; Mastorchio, S.; Meunier, J.C. Monitoring vegetation cover across semi-arid regions: Comparison of remote observations from various scales. Int. J. Remote Sens 2000, 21, 281–300. [Google Scholar]
- Escadafal, R.; Huete, A.R. Soil Optical Properties and Environmental Applications of Remote Sensing. Available online: http://www.isprs.org/proceedings/xxix/congress/part7/709_XXIX-part7.pdf (accessed on 22 July 2014).
- Franklin, J.; Miller, J.A. Mapping Species Distributions. Spatial Inference and Prediction; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Rapideye Homepage. Available online: http://www.rapideye.com (accessed on 19 March 2013).
- Fujisada, H.; Bailey, G.B.; Kelly, G.G.; Hara, S.; Abrams, M.J. ASTER DEM performance. IEEE Trans. Geosci. Remote Sens 2005, 43, 2707–2713. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn 2001, 45, 5–32. [Google Scholar]
- Walter, H.; Breckle, S. Ökologie der Erde Bd3. Spezielle Ökologie der gemäßigten und arktischen Zonen Euro-Nordasiens. Zonobiom VI–IX; Fischer: Stuttgart, Germany, 1991; Volume 3. [Google Scholar]
- Agakhanjanz, O.E. Besonderheiten in der natur der ariden gebirge der udssr. Petermanns Geogr. Mitt 1979, 123, 73–77. [Google Scholar]
- Miehe, G.; Winiger, M.; Böhner, J.; Yili, Z. The climatic diagram map of high Asia. Purpose and concepts. Erdkunde 2001, 55, 94–97. [Google Scholar]
- Vanselow, K.A. The High-Mountain Pastures of the Eastern Pamirs (Tajikistan)—An Evaluation of the Ecological Basis and the Pasture Potential. University of Erlangen-Nuremberg, Erlangen, Germany, 2011. [Google Scholar]
- Kraudzun, T. Livelihoods of the “new livestock breeders” in the eastern pamirs of tajikistan. In Pastoral Practices in High Asia—Agency of “Development” Effected by Modernisation, Resettlement and Transformation; Kreutzmann, H., Ed.; Springer: Dordrecht, The Netherlands, 2012; pp. 89–107. [Google Scholar]
- Breckle, S.; Wucherer, W. Vegetation of the Pamir (Tajikistan): Land use and desertification problems. In Land-Use Change and Mountain Biodiversity; Spehn, E., Liberman, M., Körner, C., Eds.; CRC/Taylor & Francis: Boca Raton, FL, USA, 2006; pp. 225–237. [Google Scholar]
- Vanselow, K.A.; Kraudzun, T.; Samimi, C. Grazing practices and pasture tenure in the eastern Pamirs: The nexus of pasture use, pasture potential and property rights. Mt. Res. Dev 2012, 32, 324–336. [Google Scholar]
- Akhmadov, K.; Breckle, S.; Breckle, U. Effects of grazing on biodiversity, productivity, and soil erosion of alpine pastures in Tajik Mountains. In Land Use Change and Mountain Biodiversity; Spehn, E., Liberman, M., Körner, C., Eds.; CRC/Taylor & Francis: Boca Raton, FL, USA, 2006; pp. 239–247. [Google Scholar]
- Kraudzun, T.; Vanselow, K.A.; Samimi, C. Realities and myths of the teresken syndrome—An evaluation of the exploitation of dwarf Shrub resources in the eastern Pamirs of Tajikistan. J. Environ. Manag 2014, 132, 49–59. [Google Scholar]
- Jusufbekov, C.J.; Kasach, A.E. Teresken na Pamire; Izd. Donish: Dushanbe, Tajikistan, 1972. [Google Scholar]
- Agachanianc, O.E. Osnovnie Problemy Fizicheskoy Geografii Pamira; Izd. Akademija Nauk Tadshikskoj SSR: Dushanbe, Tajikistan, 1966. [Google Scholar]
- Ladygina, G.M.; Litvinova, N.P. Produktivnost Nadsemnoj i Podsemnoj Fitomassy Nekotorych Ractitel’nych Soobshchestv Vycokogorij Pamira. In Biological Productivity and Mineral Cycling; Rodin, L.E., Smirnof, N.N., Eds.; Akademija Nauk CCCP: Leningrad, Russian, 1971; pp. 150–156. [Google Scholar]
- Litvinova, N.P. Biologicheskaja Produktivnost’ Pustynych Soobshchestv Vostochnogo Pamira; Akademija Nauk CCCP: Leningrad, Russian, 1969. [Google Scholar]
- Song, C.; Woodcock, C.E.; Seto, K.C.; Lenney, M.P.; Macomber, S.A. Classification and change detection using Landsat TM data: When and how to correct atmospheric effects? Remote Sens. Environ 2001, 75, 230–244. [Google Scholar]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ 1994, 48, 119–126. [Google Scholar]
- Smith, R.B. Filtering Images with Tntmips; MicroImages: Lincoln, NE, USA, 2006. [Google Scholar]
- Böhner, J.; Conrad, O.; Köthe, R.; Ringeler, A. Saga—System for Automated Geoscientific Analyses, 2.0.4; Göttingen: Hamburg, Germany, 2009. [Google Scholar]
- Hijmans, R.J.; van Etten, J. Raster: Geographic Analysis and Modeling 2, 1–16. Available online: http://cran.at.r-project.org/web/packages/raster/raster.pdf (accessed on 22 July 2014).
- Leyer, I.; Wesche, K. Multivariate Statistik in der Ökologie. Eine Einführung; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- McCune, B.; Keon, D. Equations for potential annual direct incident radiation and heat load. J. Veg. Sci 2002, 13, 603–606. [Google Scholar]
- Zuur, A.F.; Ieno, E.N.; Elphick, C.S. A protocol for data exploration to avoid common statistical problems. Methods Ecol. Evolut 2010, 1, 3–14. [Google Scholar]
- Justice, C.O.; Townshend, J.G. Integrating ground data with remote sensing. In Terrain Analysis and Remote Sensing; Townshend, J.G., Ed.; Allen and Unwin: London, UK, 1981; pp. 38–58. [Google Scholar]
- Ferrier, S.; Watson, G.; Pearce, J.; Drielsma, M. Extended statistical approaches to modelling spatial pattern in biodiversity in northeast New South Wales. I. Species-level modelling. Biodivers. Conserv 2002, 11, 2275–2307. [Google Scholar]
- Horning, N. Random forests: An algorithm for image classification and generation of continuous fields data sets. In Proceedings of the International Conference on Geoinformatics for Spatial Infrastructure Development in Earth and Allied Sciences, Osaka, Japan, 9–11 December 2010.
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall: New York, NY, USA, 1993. [Google Scholar]
- Prasad, A.; Iverson, L.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar]
- Brenning, A. Benchmarking classifiers to optimally integrate terrain analysis and multispectral remote sensing in automatic rock glacier detection. Remote Sens. Environ 2009, 113, 239–247. [Google Scholar]
- Liaw, A.; Wiener, M. Randomforest: Breiman and Cutler’s Random Forests for Classification and Regression 2012, 4, 6–7. Available online: online: http://cran.r-project.org/web/packages/randomForest/randomForest.pdf (accessed on 22 July 2014).
- Gaitán, J.J.; Bran, D.; Oliva, G.; Ciari, G.; Nakamatsu, V.; Salomone, J.; Ferrante, D.; Buono, G.; Massara, V.; Humano, G.; et al. Evaluating the performance of multiple remote sensing indices to predict the spatial variability of ecosystem structure and functioning in patagonian steppes. Ecol. Indic 2013, 34, 181–191. [Google Scholar]
- Vanselow, K.A.; Kraudzun, T.; Samimi, C. Land stewardship in practice: An example from the eastern Pamirs of Tajikistan. In Rangeland Stewardship in Central Asia; Squires, V., Ed.; Springer: Berlin, Germany, 2012; pp. 71–90. [Google Scholar]
- Kreutzmann, H. The tragedy of responsibility in high Asia: Modernizing traditional pastoral practices and preserving modernist worldviews. Pastor.: Res. Policy Pract 2013, 3. [Google Scholar] [CrossRef]
- Baccini, A.; Friedl, M.A.; Woodcock, C.E.; Warbington, R. Forest biomass estimation over regional scales using multisource data. Geophys. Res. Lett 2004, 31, L10501. [Google Scholar]
- Horning, N. Training Guide for Creating Percent Cover Images. Available online: http://biodiversityinformatics.amnh.org (accessed on 8 April 2013).
- Caires, S.; Sterl, A. A new nonparametric method to correct model data: Application to significant wave height from the ERA-40 re-analysis. J. Atmos. Ocean. Technol 2005, 22, 443–459. [Google Scholar]
| No. | Explanatory Variable | Derived From | |
|---|---|---|---|
| 1 | Band 1 | Reflectance of RapidEye Band 1 (blue; 440–510 nm) | |
| 2 | Band 2 | Reflectance of RapidEye Band 2 (green; 520–590 nm) | |
| 3 | Band 3 | Reflectance of RapidEye Band 3 (red; 630–690 nm) | |
| 4 | Band 4 | Reflectance of RapidEye Band 4 (red edge; 690–730 nm) | |
| 5 | Band 5 | Reflectance of RapidEye Band 5 (near-infrared; 760–880 nm) | |
| 6 | NDVI | ||
| 7 | MSAVI2 | (Qi et al. [32]) | |
| 8 | Band 1 texture | Standard deviation of a 3 × 3 pixel neighborhood calculated from Band 1 | |
| 9 | Band 2 texture | Standard deviation of a 3 × 3 pixel neighborhood calculated from Band 2 | |
| 10 | Band 3 texture | Standard deviation of a 3 × 3 pixel neighborhood calculated from Band 3 | |
| 11 | Band 4 texture | Standard deviation of a 3 × 3 pixel neighborhood calculated from Band 4 | |
| 12 | Band 5 texture | Standard deviation of a 3 × 3 pixel neighborhood calculated from Band 5 | |
| 13 | NDVI texture | Standard deviation of a 3 × 3 pixel neighborhood calculated from NDVI | |
| 14 | MSAVI2 texture | Standard deviation of a 3 × 3 pixel neighborhood calculated from MSAVI2 | |
| 15 | Elevation | derived from ASTER GDEM | |
| 16 | Slope | derived from ASTER GDEM using the terrain function | (Hijmans and van Etten [35]) |
| 17 | North exposedness | cos(aspect); aspect derived from ASTER GDEM using the terrain function | (Leyer and Wesche [36]) |
| 18 | East exposedness | sin(aspect); aspect derived from ASTER GDEM using the terrain function | (Leyer and Wesche [36) |
| 19 | Heat load | =–1.467 + 1.582 × cos(latitude) × cos(slope) − 1 × cos(foldedaspect) × sin(slope) × sin(latitude) − 0.262 × sind(latitude) × sin(slope) + 0.607 × sin(foldedaspect) × sin(slope) | (McCune and Keon [37]) |
| a | b | c | d | e | f | g | |
|---|---|---|---|---|---|---|---|
| Type | Classification | Class. | Class. | Class. | Class. | Regression | reg. |
| Response variable | pres./abs. A. leucotricha | pres./abs. K. ceratoides | pres./abs. K. ceratoides A. leucotricha | pres./abs. water | pres./abs. snow/ice | Total vegetative ground cover | dwarf shrub cover |
| n explanatory variables | 2 | 4 | 4 | 1 | 2 | 4 | 5 |
| Explanatory variables (in order of importance) | Heat load MSAVI2 | MSAVI2 Elevation MSAVI2 tex. B5 refl. | MSAVI2 Elevation MSAVI2 tex. B5 refl. | NDWI | Elevation B5 refl. | MSAVI2 MSAVI2 tex. Elevation B5 refl. | MSAVI2 Elevation Slope MSAVI2 tex. heat load |
| mtry | 2 | 2 | 2 | 1 | 1 | 2 | 3 |
| ntrees | 5000 | 5000 | 5000 | 5000 | 5000 | 5000 | 5000 |
| n observations | 278 | 278 | 278 | 307 | 307 | 307 | 307 |
| n presence | 52 | 179 | 189 | 15 | 17 | ||
| n absence | 226 | 99 | 89 | 292 | 290 | ||
| correctly vs. wrongly classified (presence) | 30:22 | 170:9 | 181:8 | 15:0 | 17:0 | ||
| correctly vs. wrongly classified (absence) | 207:19 | 71:28 | 71:18 | 292:0 | 290:0 | ||
| OOB class. accuracy (%) (presence) | 57.7 | 95.0 | 95.8 | 100 | 100 | ||
| OOB class. accuracy (%) (absence) | 91.6 | 71.8 | 80.0 | 100 | 100 | ||
| OOB class. accuracy (%) (total) | 85.2 | 86.7 | 90.6 | 100 | 100 | ||
| OOB accuracy (%) var. expl. | 80.2 | 47.5 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vanselow, K.A.; Samimi, C. Predictive Mapping of Dwarf Shrub Vegetation in an Arid High Mountain Ecosystem Using Remote Sensing and Random Forests. Remote Sens. 2014, 6, 6709-6726. https://doi.org/10.3390/rs6076709
Vanselow KA, Samimi C. Predictive Mapping of Dwarf Shrub Vegetation in an Arid High Mountain Ecosystem Using Remote Sensing and Random Forests. Remote Sensing. 2014; 6(7):6709-6726. https://doi.org/10.3390/rs6076709
Chicago/Turabian StyleVanselow, Kim André, and Cyrus Samimi. 2014. "Predictive Mapping of Dwarf Shrub Vegetation in an Arid High Mountain Ecosystem Using Remote Sensing and Random Forests" Remote Sensing 6, no. 7: 6709-6726. https://doi.org/10.3390/rs6076709
APA StyleVanselow, K. A., & Samimi, C. (2014). Predictive Mapping of Dwarf Shrub Vegetation in an Arid High Mountain Ecosystem Using Remote Sensing and Random Forests. Remote Sensing, 6(7), 6709-6726. https://doi.org/10.3390/rs6076709





