Abstract
Results of numerous evaluation studies indicated that satellite-rainfall products are contaminated with significant systematic and random errors. Therefore, such products may require refinement and correction before being used for hydrologic applications. In the present study, we explore a rainfall-runoff modeling application using the Climate Prediction Center-MORPHing (CMORPH) satellite rainfall product. The study area is the Gilgel Abbay catchment situated at the source basin of the Upper Blue Nile basin in Ethiopia, Eastern Africa. Rain gauge networks in such area are typically sparse. We examine different bias correction schemes applied locally to the CMORPH product. These schemes vary in the degree to which spatial and temporal variability in the CMORPH bias fields are accounted for. Three schemes are tested: space and time-invariant, time-variant and spatially invariant, and space and time variant. Bias-corrected CMORPH products were used to calibrate and drive the Hydrologiska Byråns Vattenbalansavdelning (HBV) rainfall-runoff model. Applying the space and time-fixed bias correction scheme resulted in slight improvement of the CMORPH-driven runoff simulations, but in some instances caused deterioration. Accounting for temporal variation in the bias reduced the rainfall bias by up to 50%. Additional improvements were observed when both the spatial and temporal variability in the bias was accounted for. The rainfall bias was found to have a pronounced effect on model calibration. The calibrated model parameters changed significantly when using rainfall input from gauges alone, uncorrected, and bias-corrected CMORPH estimates. Changes of up to 81% were obtained for model parameters controlling the stream flow volume.
1. Introduction
Any rainfall-runoff modeling requires accurate rainfall data as model input. However, accurate rainfall information in many world regions is hampered by limitations of ground-based observational networks. Rain gauge networks often have inadequate coverage and density, represent only point scale estimates and suffer from problems relating to data quality and inconsistency [1,2]. Alternative to in situ network data are satellite rainfall estimates (SREs), which potentially can be a viable alternative. However, SREs are known to suffer from sampling and estimation inaccuracies, which are manifested in the form of systematic (bias) and random errors [3–7]. Though a number of studies report on usage of SREs for runoff and soil moisture simulations [6,8,9], aspects of accuracy and representativeness of SREs for hydrologic modeling are not well investigated.
In the present study, we focus on bias correction of a particular SRE—the Climate Prediction Center (CPC) Morphing technique (CMORPH; [10]), and the effect of bias correction on hydrologic simulations for the Gilgel Abbay catchment, Lake Tana basin, Ethiopia. CMORPH is considered in this study owing to its relatively high space-time resolutions (30 min, 8 km). In this study CMORPH estimates are accumulated to a daily resolution, which matches the rain gauge sampling interval and the time step of the rainfall-runoff model used herein. A number of studies investigated the accuracy of CMORPH products across a range of space-time scales. Examples include seasonal or daily estimates at 0.25° × 0.25° spatial resolution [11–13], three-hourly estimates at 0.25° × 0.25° [14,15], and one-hourly estimates at 8 km × 8 km [1,5]. Results from these studies suggest that CMORPH estimates have significant systematic biases but also that estimates have random errors. Smith et al. [16] stated that CMORPH biases might be due to a diurnal sampling bias, tuning of the instrument or the rainfall algorithm, or unusual surface or atmospheric properties, which the algorithm does not correctly interpret. A Kalman filter approach has been recently adopted by the CMORPH developers to optimally integrate satellite-based estimates with rain gauge observations [17,18]. In the scientific literature, some evidence is presented that CMORPH bias exhibits spatio-temporal variation. For instance, Haile et al. [1] show that the total bias and its different components exhibit spatial variation in the Gilgel Abbay catchment, which is also selected for the present study. The authors concluded that over mountain areas CMORPH bias mostly is affected by missed rainfall detection. Particularly for lower elevated areas bias is affected by missed rainfall, false rainfall and differences in hit-rainfall estimates. For the Nile basin area, Habib et al. [11] showed that CMORPH bias (and other SREs) is largely affected by topography and latitude. The same study showed that CMORPH bias in the wet and dry seasons can be quite different.
The aforementioned studies indicate that it is crucial to reduce the systematic and random errors in SREs before products can be used in hydrologic and water resources applications. Methodologies for bias correction are developed in multi-sensor, radar-gauge approaches [19–21] and triggered applications in satellite remote sensing. Examples are on monthly-based bias correction [22], disaggregation of bias at daily scale to hourly scale [23], and merging satellite and gauge data by means of a non-parametric kernel smoother [24]. Vila et al. [25] compared five merging schemes: additive bias correction, ratio bias correction, gauge-to-satellite monthly correction factors, and a combined scheme. The authors concluded that the combined scheme, which considers both additive and multiplicative bias, outperformed the others. Other studies of bias-correction to satellite rainfall products are reported in Hong et al. [26], Chiang et al. [27], Tobin and Bennett [28], and Tian et al. [29]. These studies suggest that selection of bias correction scheme should depend on the desired level of accuracy and assumptions to represent spatial and temporal rainfall characteristics. However, selection also depends on the data requirements, computational expenses, and, more importantly, the hydrologic application the bias-adjusted product is used for. Overall, bias-corrected satellite rainfall products are expected to better match station records compared to satellite only products even in complex terrain [30] and as such correction should improve hydrological applications by improved rainfall representation. However, results by hydrological applications are not consistent and require further assessment.
Artan et al. [31] showed that negative bias of a satellite rainfall product in rainfall-runoff modeling could result in deterioration of modeling results. They also showed that a hydrologic model requires recalibration when satellite rainfall data is used to replace use of in-situ rainfall data. Zeweldi et al. [32] reported increased performance of a rainfall-runoff model when the model was calibrated using satellite data than when it was calibrated using rain gauge data. However, calibration could result in parameter values that are unrealistic and beyond limits as the model attempts to compensate for the large errors in rainfall input. Behrangi et al. [33] found that bias-adjustment of satellite-based precipitation products is critical and can yield substantial improvement in capturing both the streamflow pattern and magnitude at six-hourly and monthly time scales. Yong et al. [34] showed an improvement in the performance of a rainfall-runoff model after applying gauge-based bias correction to satellite-only rainfall products. However, Bitew and Gebremichael [8] reported improved model performance when using a satellite-only product (TRMM 3B42RT) as compared to a satellite-gauge bias corrected product (TRMM 3B42). Such results could be partly attributed to the fairly poor quality and/or lack of spatial representativeness of the sparse gauges that were used for the bias correction.
In the present study, the focus is mainly on analysis of the spatial and temporal variability of bias in CMORPH 30-min, 8 km × 8 km satellite-based rainfall product and on identifying the critical aspects of such variability from a hydrologic perspective in rainfall-runoff modeling. Results of such analyses are of relevance to product users to guide efforts for product adjustment before being used in further applications [35,36] and also for product developers to identify future needs for algorithmic enhancements. The specific objectives of this study are (i) to assess three bias correction schemes to the CMORPH 30-min, 8 km × 8 km product to adjust for spatial and temporal biases; and (ii) to assess how rainfall-runoff model calibration results are affected when bias-corrected CMORPH data is used instead of uncorrected and in situ rainfall data. The area of study is the Gilgel Abbay catchment in Ethiopia. The paper is structured as follows. Section 2 describes the data sets, the bias correction schemes, the hydrologic model, and the calibration approach. Section 3 presents results and discusses the findings and Section 4 concludes on the study.
2. Data and Methods
2.1. Study Setting
The study area is Gilgel Abbay catchment, which is the largest contributor to Lake Tana [37], the source of Upper Blue Nile River in Ethiopia. In the present study, the focus is on the gauged part of Gilgel Abbay for which daily time series of streamflow have been available since the 1970s (Figure 1). This part of the watershed is situated between latitudes of 10°56′N–11°22′N and longitudes of 36°49′E–37°24′E. It covers an area of about 1655 km2 with predominantly agricultural land cover and with clay to clay-loam as the prevailing soil type. The seasonal rainfall distribution of Gilgel Abbay is affected mainly by the location of the Intertropical Convergence Zone (ITCZ) with a rainy season, which coincides with the summer in the northern hemisphere (June–August). At short time scales (daily and sub-daily), rainfall distribution in this watershed is affected by orographic factors and the presence of Lake Tana [38,39]. The lowlands of Gigel Abbay receive more intense and short lasted rainfall as compared to its highlands [40].
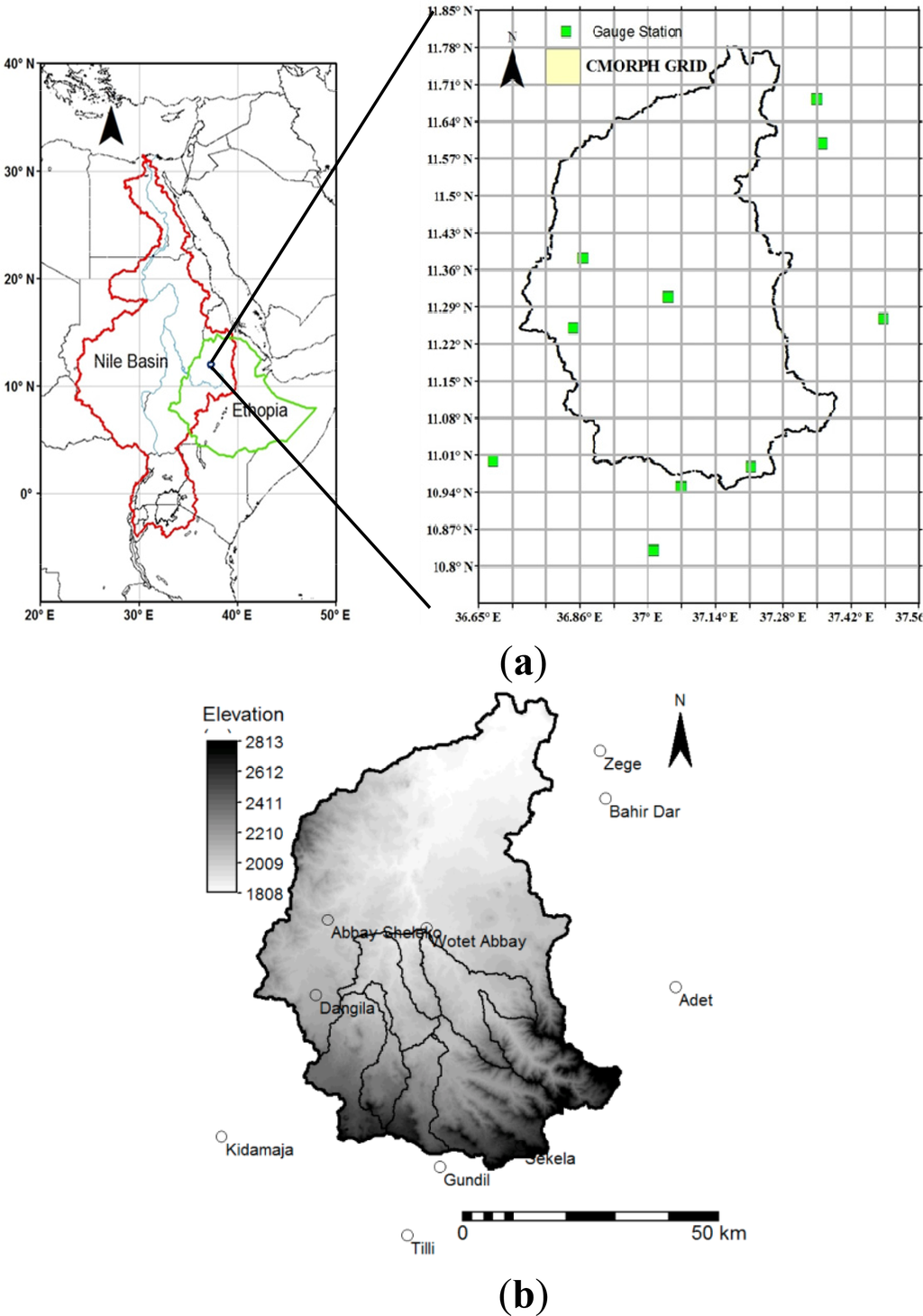
Figure 1.
Study site showing the location of the Gilgel Abbay catchment and its eight sub-catchments within the Nile Basin. The locations of the ten (10) rain gauge stations and the streamflow gauge are indicated. Note that the unit of terrain elevation is meters. (a) Geographic location of study area; (b) Terrain elevation and rain gauge stations.
2.2. CMORPH and Local Gauge Data
The satellite-rainfall product used in this study is the National Oceanic and Atmospheric Administration’s (NOAA) Climate Prediction Center (CPC) morphing technique (CMORPH) [10]. CMORPH combines rainfall estimates from multiple passive microwave (PMW) sensors, which include the Advanced Microwave Sounding Unit (AMSU-B), the Special Sensor Microwave Imager (SSM/I), the TRMM Microwave Imager (TMI), and the Advanced Microwave Scanning Radiometer—Earth Observing System (AMSR-E), respectively. To fill the time and space gap in the combined PMW based rainfall estimates, the algorithm used cloud motion vectors derived from spatial lag correlation of successive geostationary satellite IR images. These vectors are used to propagate the PMW based rainfall features for time periods between two successive PMW overpasses. The shape and intensity of the rainfall patterns is then morphed through linear interpolation using weights that are obtained from forward advection (previous to most current PMW overpass) and backward advection (most current to previous overpass) of rainfall features. The main advantage of CMORPH is its near real-time global coverage at relatively fine temporal and spatial scales (as fine as 30-min and 8 km × 8 km), which makes it a desirable candidate for hydrologic applications. In the current analysis, the 30-min, 8 km × 8 km CMORPH estimates are aggregated to daily time step to be consistent with rain gauge observation interval. In addition, streamflow time series are at daily time interval so aggregation results in optimal use of available satellite data to represent and to correct rainfall in respective time and space domains for stream flow modeling. Based on availability of rain gauge and streamflow data in the watershed, the current analysis period covers two years from January 2003 to December 2004.
Data is obtained from 10 rain gauges in the watershed (Figure 1) which are operated by the Ethiopian Meteorological Agency (EMA). Daily rainfall from these gauges has been evaluated and used in [37,41–43] and serve as reference to evaluate satellite rainfall estimates. For the study period, the average annual rainfall over Gilgel Abbay was about 1700 mm. The average daily rainfall rate exceeded 10 mm/day for 20% of the time and reached as high as 35 mm/day. The gauge network (Figure 1) is sparse and stations are unevenly distributed over the watershed. As a result, the “true” or real world rainfall distribution may not be well represented by the network, as rainfall varies over the area following topographic variation [1,38,39].
Meteorological observations at three stations in the watershed (Dangila, Adet, and Bahir Dar; Figure 1) were used to estimate monthly potential evapotranspiration (PET) using the Penman-Montheith method [44], which were then used as input to the hydrologic model.
Streamflow daily data is available for the upper part of Gilgel Abbay, which is gauged at Wotet Abbay, a small town near Bahir Dar. Consistency of streamflow daily time series was checked by visual inspection of concurrent rainfall and streamflow plots. We noticed that the baseflow record showed an abrupt increase in late 2005. Local people near the gauging site stated that the gauging station was moved by hundreds of meters downstream of the original site towards the end of 2005 due to road construction. However, this was not confirmed by officials in the Ministry of Water Energy. As a result we limited our analysis period to 2003 and 2004 for which CMORPH data is available and for which we have confidence in the quality of stream flow data.
2.3. Bias Formulation and Estimation
Satellite-based rainfall estimates exhibit large systematic and random errors. The systematic errors (i.e., bias) persist when the estimates are aggregated over time and, hence, may cause large uncertainties in hydrologic modeling. In addition, models could augment or suppress rainfall biases to larger or smaller streamflow based on the response mode of the model. Therefore, bias in rainfall products should be assessed and corrected before satellite rainfall products can be used in hydrologic applications.
In the current study, we estimate and correct the bias in CMORPH estimates as follows. For a selected day (d) and gauge (i), the multiplicative daily bias factor (BF) at a certain CMORPH pixel with a collocated gauge can be formulated as follows Equation (1):
where G and S represent daily gauge and CMORPH rainfall estimates, respectively, i refers to gauge location, t refers to a Julian day number; and l is length of a time window for bias calculation. The subscript “TSV” stands for “Time-Space Variable” since the bias in this formulation is estimated for a particular location and a particular day. Based on some preliminary analysis by the authors on rainfall distributions in the study area, a fixed time window of l = 7 days was selected to allow for adequate rainfall accumulation for bias calculation while still accounting for temporal variability in BF. The BF factor was calculated for a certain day only when a minimum of five rainy days were recorded within the preceding seven-day window with a minimum rainfall accumulation depth of 5 mm, otherwise no bias is estimated (i.e., assigned a value of 1). We chose five rainy days with minimum accumulation depth of 5 mm to ensure stability of the bias factors and avoid exaggerated values as a result of dividing large satellite estimates by small gauge values. We evaluated sensitivity of BF to different window lengths of 3, 7, and 10 days. We noticed that BF shows relatively lower sensitive during the wet season compared to the dry season. In the wet season, BF shows high variation and becomes highly erratic when the window length is reduced to three days as a result of small accumulation period. In the wet season, BF exceeds 2.0 for a three-day window length but is mostly well below 2.0 for a seven- and 10-day window length.
It is noted that Equation (1) ignores errors introduced by using a single gauge to represent rainfall amounts at the scale of the CMORPH pixel. Haile et al. [1] showed that the error variance of the gauge representativeness error in Gilgel Abbay could contribute as much as 30%–52% to the total variance of CMORPH-gauge rainfall hourly differences. Using the current dataset, we found that the spatial correlation of rainfall in the study area, at 8 km separation distance, increases from 0.55 at a daily scale to 0.91 for a seven-day accumulation scale. Therefore, it is reasonable to assume that the gauge representativeness error will be much smaller at a seven-day time window than that of the hourly base, and, thus, we proceed with using single-gauge observations as a reference for the bias estimation using Equation (1).
2.4. Schemes for Bias Correction
In the current analysis we test three schemes for bias correction:
- (i)
- The first one allows for correcting the bias at a pixel based (i.e., space variable) and at a daily scale (i.e., time varying), and is based on the using the BFTSV factor estimated from Equation (1). To apply a correction that accounts for spatial and temporal variability in the CMORPH bias, the pixel-based daily BFTSV factors were spatially interpolated using the inverse distance weight (IDW) method to yield a spatial and temporally varying field of BFs that cover the entire study area. We followed the approach of Haile et al. (2009) [38] in the same study area who showed good interpolation results by IWD. The CMOPRH daily rainfall fields were then multiplied by the BFTSV bias fields for the respective time windows to result in a new set of CMORPH estimates that as such are bias-corrected in a temporally and spatially varying scheme. This procedure is similar to the local-bias correction algorithm developed by Seo and Breidenbach [19], which is adopted in the operational version of the National Weather System-Multisensor Precipitation Estimation (NWS-MPE) system. The use of Equation (1) applies a bias correction factor that varies in space and time domains. We refer to this formulation as time and space variant (TSV) bias correction. To assess the implications for ignoring or for accounting of variability of bias, two more bias estimation and correction schemes were tested:
- (ii)
- Time and space fixed (TSF) bias correction: in this formulation the bias is obtained by using gauge and CMORPH estimates over the entire domain and over the total duration of the sample Equation (2):where n is the total number of gauges within the entire domain of the study and T is the full duration of the study period. The bias correction in this case is applied by multiplying the CMORPH estimates by the bias factor, BFTSF, to result in a new set of CMORPH estimates that are bias-corrected in a spatially and temporally-lumped scheme.
- (iii)
- Time variable (TV) bias correction: in this formulation the BF is spatially lumped over the entire domain but is still estimated for each daily time step Equation (3):
The bias correction in this case is applied by multiplying each daily CMORPH field by the daily bias factor, BFTV, to result in a new set of CMORPH estimates that are bias-corrected in a spatially-lumped but temporally-varying scheme.
2.5. Hydrologiska Byråns Vattenbalansavdelning (HBV-96) Hydrologic Model
In the present study, the Hydrologiska Byråns Vattenbalansavdelning (HBV-96) rainfall-runoff model [45] is used to perform the rainfall-runoff analysis using rainfall estimates by the three correction schemes. The HBV-96 model has been extensively evaluated for different regions on the globe [46–50] including Gilgel Abbay catchment [37,41,43]. HBV-96 can be classified as a conceptual model that relies on water balance equations to simulate runoff and mass exchanges across a set of surface and subsurface zones. Inputs to the model include rainfall, temperature, potential evapotranspiration, and percentage of forested and non-forested catchment areas.
The storage based HBV-96 has four routines that include (i) a precipitation accounting routine; (ii) a soil moisture routine; (iii) a quick runoff routine; and (iv) a base flow routine. The approach is characterised by three stores, which are the soil moisture reservoir, the upper zone store and the lower zone store. From the upper zone store quick runoff is simulated from the lower zone store base flow runoff is simulated. Routing of streamflow is optional and can be de-activated in model simulations. The precipitation accounting routine partitions precipitation into rainfall and snow based on a threshold value (TT). Precipitation is in the form of snow in case the actual temperature (T) is lower than TT. In the Gilgel Abbay area, the temperature is much higher than common values for TT and, as such, precipitation only is in the form of rainfall.
The soil moisture routine controls the formation of direct and indirect runoff. Direct runoff occurs when the simulated soil moisture (SM) in the soil moisture reservoir exceeds the maximum storage capacity as represented by field capacity (FC). Otherwise, rainfall infiltrates (IN) the soil moisture reservoir to add to the actual storage and to add to the flow of water to the upper zone store (indirect runoff).
Indirect runoff (R) is defined as follows:
This equation indicates that indirect runoff increases with increasing soil moisture storage (SM) but it reduces to zero when infiltration ceases. BETA is a parameter accounting for the non-linearity of indirect runoff from the soil layer.
Evapotranspiration losses are calculated from the soil moisture reservoir. Actual evapotranspiration (Ea) is highest (i.e., reaches its potential value (Ep)) when SM reaches or exceeds a certain ratio of FC. The ratio, denoted as LP, is used as a calibration parameter. Otherwise, Ea declines linearly as a function of soil moisture deficit represented by SM/FC:
Percolation (PERC) to the lower zone store occurs when water is available in the upper zone store. PERC is treated as a time-invariant process with a fixed value throughout the simulation period. Capillary transport is estimated as a function of soil moisture deficit (FC-SM) and a maximum value for capillary flow (CFLUX):
Quick runoff (Qq) and slow (base) flow (Qs) are defined as follows:
where UZ is the actual storage in the upper zone store, ALFA is a measure for the non-linearity of flow, Kq is a recession coefficient for quick runoff, LZ is the actual storage in the lower zone store and Ks is a recession coefficient for base flow. According to this formulation, the model has 8 parameters that can be used for model optimization and calibration, namely: FC, BETA, LP, ALPHA, Kq, Ks, PERC, and CFLUX.
Considering the large catchment area and significant topographic variation, and to make use of the spatially distributed data from CMORPH, the catchment has been partitioned in eight sub-catchments (Figure 1). The eight sub-catchments have size of 76, 121, 150, 165, 240, 242, 245, and 414 km2.
2.6. Model Calibration and Evaluation
The model was calibrated using four sets of rainfall data based on gauge observations, and three variants of bias corrected CMORPH estimates. In both cases, rainfall data were aggregated from their original spatial resolutions (gauge-point, or CMORPH pixel) to the scale of each sub-catchment.
The following two metrics were used to assess performance of the HBV-96 rainfall-runoff model: Nash-Sutcliffe (NS) efficiency, which provides a measure of random differences between simulated and observed streamflows, and QBias, which measures systematic differences (bias) in the simulated streamflow volumes:
where Qsim and Qobs represent simulated and observed daily flows, respectively, at a certain day i, and n represents the number of days in the sample. The over-bar symbol denotes the mean statistical operation. The values of NS, which is dimensionless, can range between −∞ and 1, where a value of 1 indicates a perfect fit. Similarly, a QBias value of 1 reflects bias-free streamflow simulations whereas streamflow overestimation and underestimation are reflected by bias values that are larger or smaller than 1, respectively.
A Monte-Carlo procedure was used to calibrate the HBV-96 model. In this procedure, prior ranges of the eight calibration parameters are selected based on the parameter value ranges specified by Rientjes et al. [37] who applied the HBV-96 model in a regionalization study in the (entire) Lake Tana basin area. In that particular study 60,000 parameters sets are generated randomly assuming a uniform distribution of parameter values within the specified, posterior, value ranges. The HBV-96 model was run for each parameters set and the corresponding objective function values (NS and QBias) are calculated. Following Rientjes et al. [37], the optimum parameters set is selected as the average value of the 25 parameter sets that are ranked highest in terms of the NS values. It is noted that a similar approach is followed in this study when calibrating the model in case CMORPH rainfall data is used as model input.
3. Results
3.1. Evaluation of CMORPH Estimates
Before presenting the results of the different bias correction schemes, we first examine the temporal and spatial variability in the CMORPH bias field, as reflected by BFTSV (Figure 2). The lowest, highest and mean values of BFTSV for a seven-day moving window are shown in the figure. These values are summarized based on BFTSV values calculated at the ten rain gauge stations within the study area. For each calendar day the minimum, maximum and mean are shown for the ensemble of network stations. The difference between the lowest and highest values shows the extent of the variation of the bias across the 10 stations in the study area. The mean values show pronounced seasonal variations and have different patterns throughout the two years. In general, CMORPH reports smaller rainfall amounts than gauge observations from mid-June to mid-August 2003, but reports larger rainfall amounts towards the end of the rainy season of 2003. This pattern is not shown in 2004, where positive and negative biases in CMORPH show lower variation in time. Overall, these results indicate that the bias in the CMORPH product exhibits pronounced variability in space and time over the study area. Possibly, this could be related to variations in rain generation mechanisms [11] but further investigations are needed for confirmation.
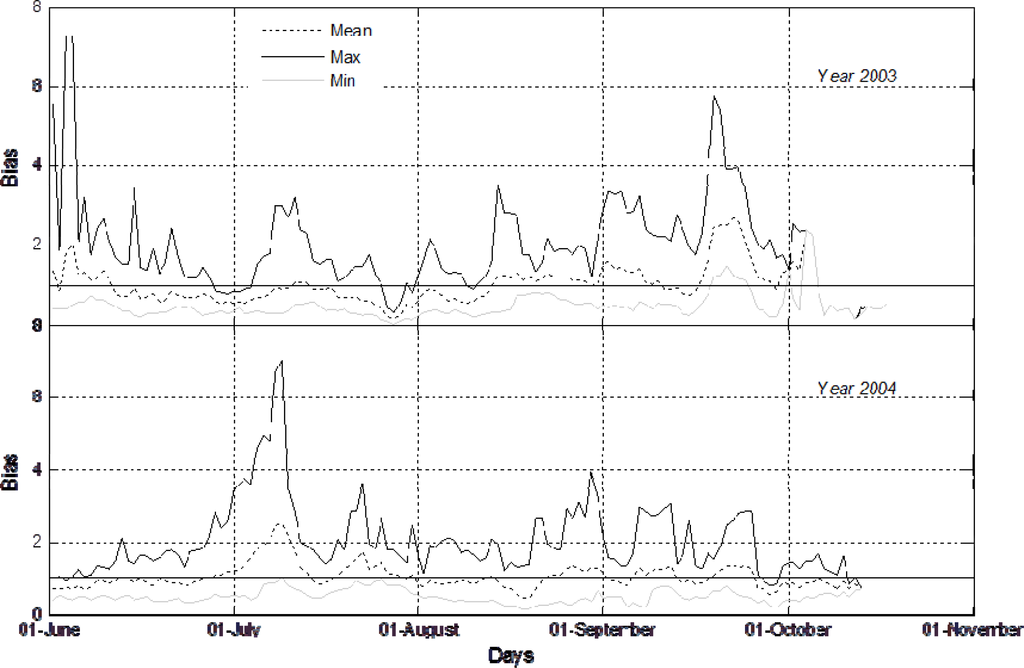
Figure 2.
Mean, minimum and maximum of CMORPH daily bias factors (BFTSV, Equation (1)) evaluated for the ensemble of ten network stations.
3.2. Results on Rainfall Bias Correction
To examine the implications of space and time variability presented above (Figure 2), we applied the three bias correction schemes described above (Equation (1)), time-space fixed (TSF), time variable (TV), and time-space variable (TSV), to the CMORPH product. We first assess how the different bias correction schemes impact the catchment-average rainfall at a monthly scale. Table 1 shows a summary of the ratios of CMORPH monthly catchment-average rainfall amounts (before and after correction) to the corresponding gauge amounts. Without bias correction, CMORPH mostly underestimated monthly rainfall by up to 37%. In 2003, the deviation of CMORPH during the wettest months (June–August) is reduced when TSF, TV, or TSV corrections are used. TSV correction shows noticeable change (up to 0.19) than TSF correction (only 0.01) in July 2003. In 2004, TSF correction leads to deterioration of the monthly agreement probably since their temporal variation is too pronounced to be ignored. The importance of accounting for temporal variation in CMORPH bias is illustrated again by the fact that TV and TSV corrections reduced the bias in 2004 by up to 0.07 and 0.07–0.14, respectively.

Table 1.
Ratios of monthly rainfall amounts of Climate Prediction Center-MORPHing (CMORPH) (without and with three bias correction schemes) to the corresponding gauge amounts.
3.3. Model Parameter Optimization Using Different Rainfall Inputs
We calibrated the HBV-96 model using gauge and CMORPH rainfall inputs for the year 2003–2004 (Table 2). Calibration based on the rain gauge network data serves as a reference for further assessments on effectiveness of bias-correction to the CMORPH estimates. The model was recalibrated using the satellite rainfall fields to examine how the model parameters are affected by bias in the rainfall input. In theory, each rainfall input represents a different model forcing and may result in different parameter values and model performance level as measured by NS and Qbias. Independent calibration of the HBV-96 model for different rainfall inputs resulted in satisfactory model performance (NS = ∼0.8 and QBias = ∼0.9). All optimum parameter values obtained using the correction schemes are within the allowable value ranges. The values of the optimized model parameters are inter-compared and percent change of each parameter value is shown with respect to the reference case. To allow comparison of parameter values over a common scale, changes are calculated after normalizing the parameter values using their allowable minimum and maximum values, which are set equal for all simulations. We note that the results of parameter optimization are affected by the rainfall input as shown by the percentage errors in Table 2. In particular, parameters (FC, Beta and LP) which control the volume of the simulated hydrograph showed large changes of up to 81% compared to the parameters using the reference gauge data sets. There is also a significant change in the quick recession coefficient (Kq), whereas those that control groundwater contributions (Ks, PERC and CFLUX) are less affected.

Table 2.
Calibrated values of the Hydrologiska Byråns Vattenbalansavdelning (HBV) model parameters using gauge and bias corrected CMORPH. Numbers in brackets represent percent changes in each parameter value (after normalizing with the allowable minimum and maximum range) with respect to the gauge-driven reference case. The last two rows show the NS and QBias values.
3.4. Effects of Rainfall Bias Corrections on Streamflow Simulations
Next, we applied the calibrated parameter set of the reference case to simulate streamflow using the uncorrected and bias-corrected CMORPH rainfall estimates. We chose to use the reference set of parameters to in all model simulations (gauge and CMORPH) to isolate the effect of rainfall bias from other sources of model uncertainty (e.g., parameter uncertainty). Figure 3 shows streamflow hydrographs for the reference case and for uncorrected CMORPH estimates. At the beginning and middle of the 2003 wet season, differences between CMORPH gauge rainfall amounts are negative for most of the time. For this reason, lower streamflow discharges are simulated. Towards the end of the rainy season of 2003, positive rainfall differences start to appear but this did not cause higher streamflow discharges than observed. It appears that the excess rainfall was stored in the different model stores instead of generating runoff. Relatively large positive differences in rainfall dominate towards the beginning of the wet season of 2004. This rainfall difference resulted in higher streamflow simulations than observed. The rainfall difference becomes negative throughout August 2004, but it did not produce negative streamflow biases, as the model stores had the excess rainwater from previous time steps stored. Overall, these results indicate that CMORPH bias propagates into model simulations. The bias correction affects moisture conditions which yielded lower (excess) runoff than observed.
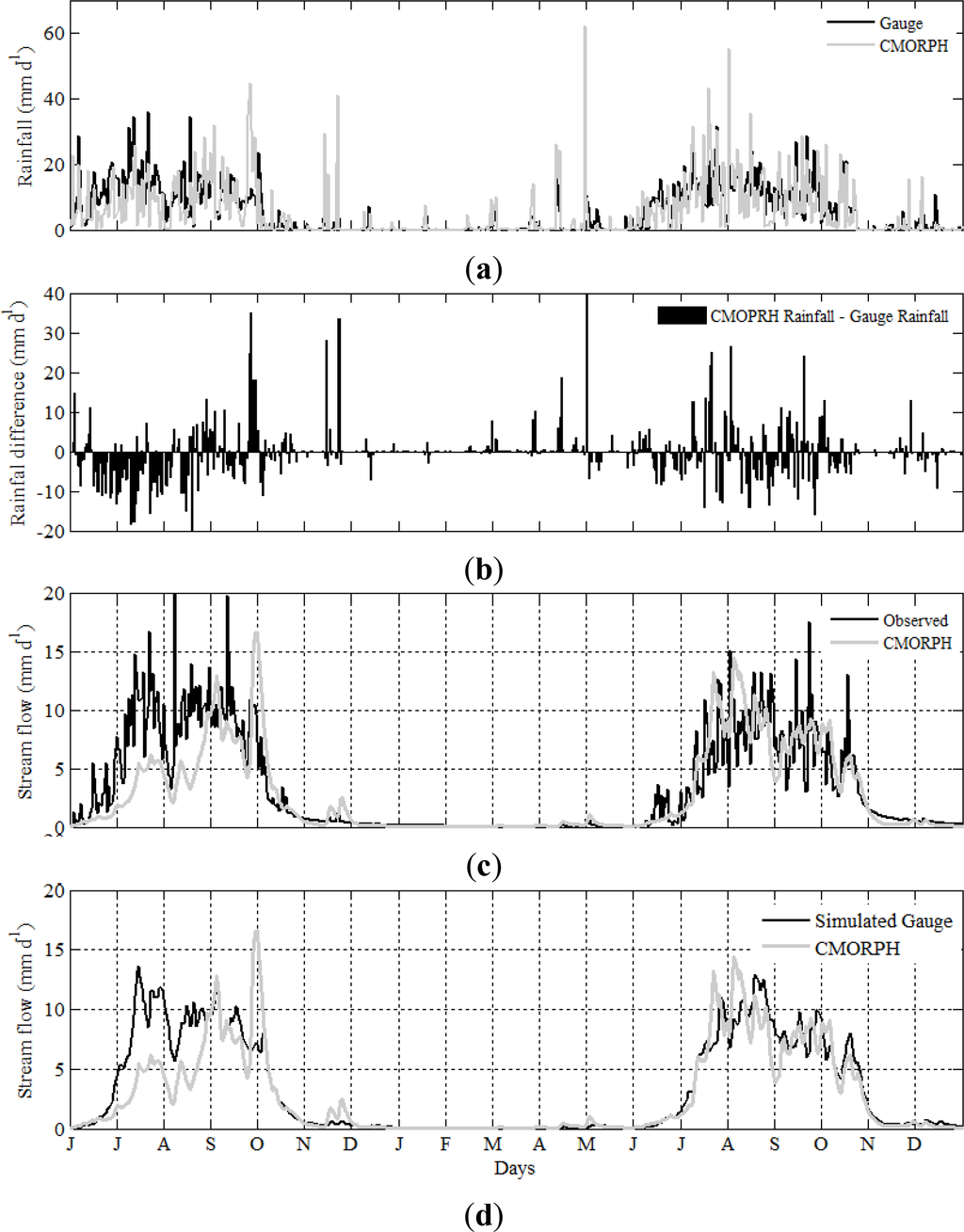
Figure 3.
(a) Comparison of daily catchment-average gauge and uncorrected CMORPH rainfall. (b) differences in daily rainfall estimates between gauge and CMORPH. (c) and (d) observed and simulated stream flow hydrographs for the year June 2003–December 2004 based on rainfall inputs from gauges and uncorrected CMORPH.
Next, we evaluated the effect of bias correction in CMORPH on HBV-96 model simulations (Figure 4). Here we show the streamflow hydrograph that is simulated using TSV bias-corrected CMORPH data, which produced the best result. Despite the applied bias correction, there are large differences (>10 mm·d−1) between catchment-average daily rainfall estimates obtained from TSV and gauges. However, it is apparent that the large CMORPH bias in 2003 was substantially reduced. As a result, the patterns and volumes of the observed hydrographs were better captured when using the bias-corrected CMORPH estimates than the uncorrected ones. Some observed peak flows were better captured as a result of correcting for the rainfall bias. The improvements are particularly substantial for the 2003 hydrographs where the uncorrected CMORPH had large negative bias. We note that use of bias corrected rainfall data has some advantages over gauge only data; however, some aspects of observed hydrograph were better captured by using gauge only data (e.g., the second half of July 2003). The simulated hydrographs based on both rainfall inputs show smaller fluctuation than the observed hydrograph. Such mismatches could be caused by deficiencies in the HBV-96 model structure, poor rainfall representation by the low density of the rain gauge network, or errors in streamflow observations, among others.
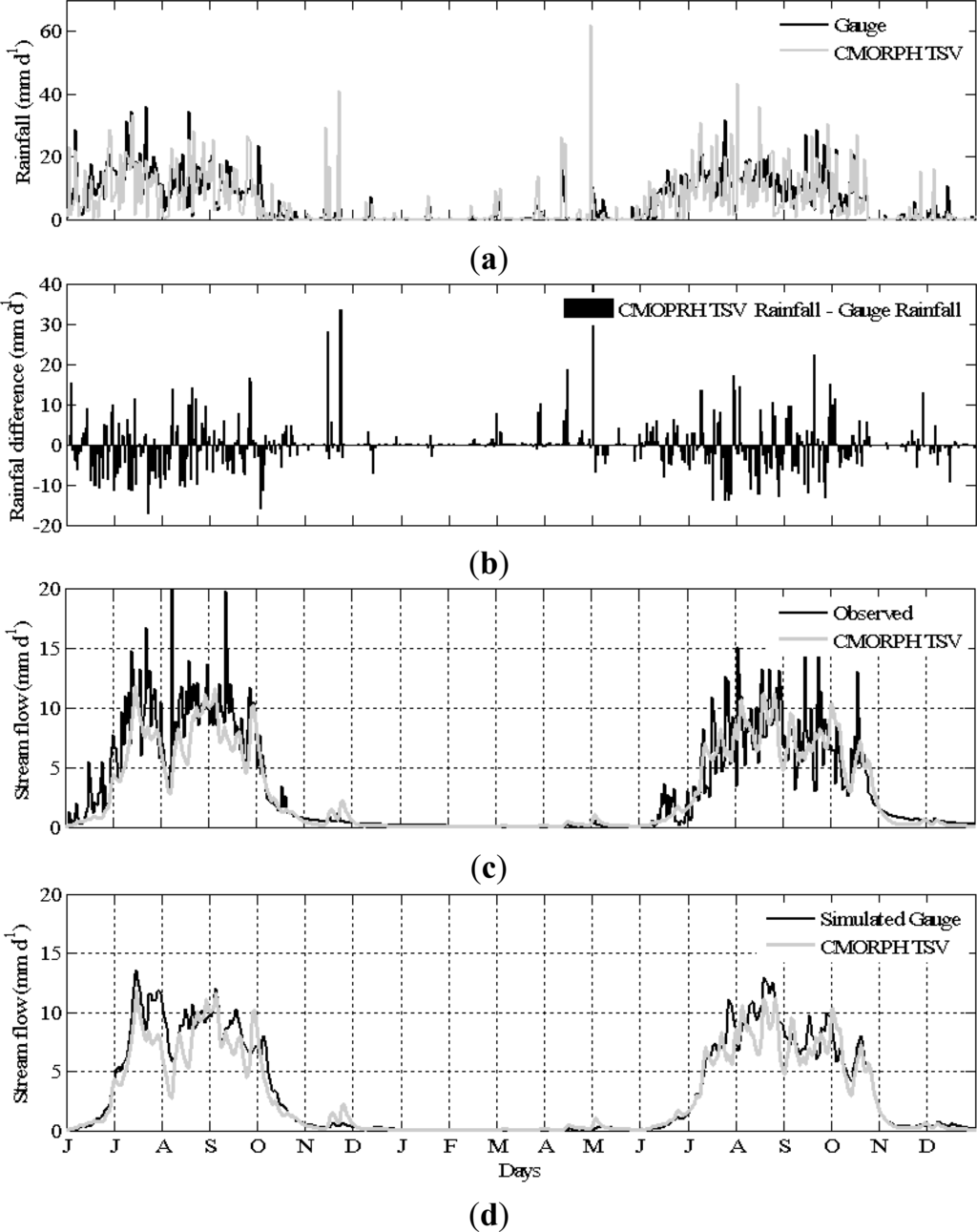
Figure 4.
(a) Comparison of daily catchment-average gauge rainfall and the corresponding TSV bias-corrected CMORPH. (b) differences in rainfall estimates between gauge and TSV bias-corrected CMORPH. (c) and (d) observed and simulated stream flow hydrographs for the year June 2003–December 2004 based on rainfall inputs from gauges and TSV bias-corrected CMORPH.
Next, we quantify the propagation of CMORPH rainfall biases in model simulations (Table 3). To separate the effect of rainfall errors from effects of model parameter uncertainty on model performance, gauge-based model simulations served as reference to compare the model performance objective functions. In June–August 2003, CMORPH rainfall amounts are smaller than those from gauges by −18% (CMORPH bias ratio = 0.82), which causes difference in streamflow volume of −27% (streamflow bias = 0.73) and increased for the same period of 2004 (from −5% to −27%). This rainfall-to-streamflow bias amplification persists for all of the CMORPH rainfall inputs but its extent became smaller when the temporal variability of the bias is considered (i.e., when using time-varying bias correction, BFTSV). For example, for CMORPH TSV rainfall input, the bias increased from −13% to only −17% in 2003 while it increased from −8% to 20% in 2004. The observed changes of rainfall-to-streamflow biases are probably due to the non-linearity in the rainfall-runoff relation and subsequent runoff generation in the HBV-96 model. For instance, small bias in rainfall input can propagate to result in larger streamflow bias when the catchment is wet than when it is dry.

Table 3.
Ratios of catchment-average seasonal rainfall amounts of CMORPH (without and with three bias correction schemes) to the corresponding gauge amounts. The corresponding values for streamflow biases (QBias) are also presented. The NS efficiency values for the streamflow simulations are shown between brackets.
Streamflow bias, QBias (Equation (9)), obtained using the uncorrected as well as the bias-corrected CMORPH rainfall inputs are shown in Figure 5 (see also Table 3). As compared to gauge-based simulations, the uncorrected and bias-corrected CMORPH data resulted in consistently smaller streamflow in the rainy season (June–August) of 2003 but larger streamflow towards the end of the rainy season. Note that this pattern has some resemblance to that of the rainfall biases (Figure 2). However, the temporal pattern of the streamflow biases in both 2003 and 2004 are smoother than those of the rainfall inputs. This possibly is a result of the filtering effect of the runoff model as it converts highly variable rainfall input to streamflow. The significantly large rainfall bias in October of 2004 is translated to a smaller streamflow bias probably as the model became relatively dry and therefore did not convert the excess rainfall input into surface runoff. CMORPH-based streamflow in 2003 is mostly 0.25 to 0.5 times the gauge observations showing underestimation though this streamflow differences became much smaller in 2004. Overall, these differences were reduced when the bias-corrected CMORPH rainfall amounts served as model inputs. An exception is that TSF, which is obtained using a space-time constant correction factor, only slightly altered the streamflow bias. For most parts of the wet season, the streamflow bias significantly decreased when time variable bias correction is applied. Accounting for both spatial and temporal variation of the CMORPH bias factor further reduced the streamflow bias.
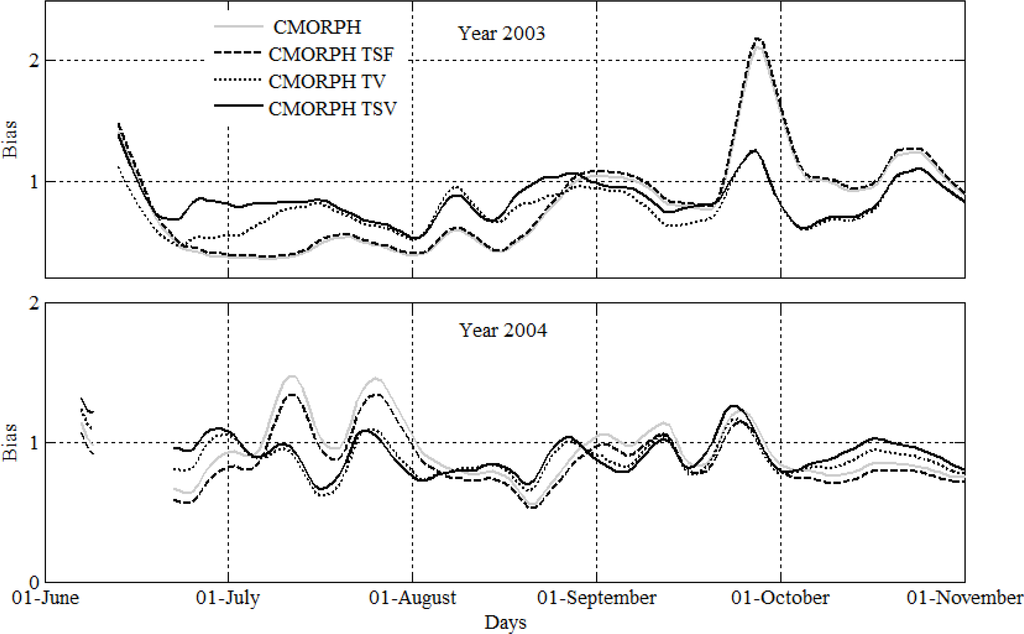
Figure 5.
Streamflow bias (QBias, Equation (9)) of streamflow simulations driven by different CMORPH rainfall inputs. QBias was calculated using a moving window of past 7 days. Streamflow simulations driven by gauge observations served as the reference.
4. Conclusions
Various studies have indicated that satellite rainfall products are contaminated with systematic and random errors. However, not much has been done to illustrate how these products can be made applicable for various purposes by reducing their errors. In this study, the effect of rainfall bias correction in a high-resolution satellite-based product (CMORPH) on the performance of a rainfall-runoff model was assessed. The study is unique as we assess the importance of space and time aspects of CMORPH bias for rainfall-runoff modeling in a data scarce catchment. Our findings contribute to efforts that aim towards enhancing the real-world applicability of satellite rainfall products. The study site is the Gilgel Abbay catchment at the source of the Blue Nile in Eastern Africa—an example of many world regions that can benefit from satellite-based rainfall products for resource assessments and monitoring. Results and conclusions of the present study are summarized below.
CMORPH has large rainfall biases (−2.3 mm·d−1 on average and by up to ±30 mm·d−1) with spatial as well as inter-annual and intra-annual variations in Gilgel Abbay catchment. Such biases could be related not only to rain generation mechanisms but also to the sampling and retrieval errors of satellite products [51]. We have showed through cross validation that it is not always the case that gauge-only, or satellite-only estimates, outperform one another. This suggests rainfall estimation can benefit from combined use of satellite and rain gauge data.
We applied three bias correction schemes to correct the bias CMORPH estimates. Space-time fixed, time variable and space-time variable bias factors were estimated to correct CMORPH estimates. One of the significant achievement of analysis indicated that the most important aspect of the CMORPH bias is its temporal variation as accounting for it substantially reduced the rainfall bias. In some instances, it was not possible to noticeably reduce the catchment-average bias. Particularly, absence of gauges in the middle and south-east parts of the catchment is presumed to have contributed to the observed mismatches between bias-corrected CMORPH and gauge rainfall amounts.
An application of the HBV hydrologic model indicated that the model should be calibrated independently for satellite-only or satellite-gauge rainfall data in order to achieve high model performance. However, we observed that the calibration procedure compensated for rainfall input errors by changing the optimum values of model parameters as rainfall input changes. In particular, parameters that control the volume of the simulated hydrograph showed largest sensitivity to the different rainfall inputs. However, it was noted that the optimal parameter values stayed within the physically allowable ranges.
HBV better captured observed hydrograph patterns and volume when bias-corrected CMORPH estimates were used instead of the uncorrected estimates. We observed that the runoff model translates small rainfall errors to larger streamflow errors. The magnitudes of such error amplifications became smaller for bias-corrected satellite data than those for the satellite-only data. In the present study, −18% bias of CMORPH rainfall inputs is translated to −27% streamflow bias. The bias amplification was reduced (from −13% rainfall bias to only −17% streamflow bias) when space and time varying bias corrections were applied to the CMORPH rainfall input. Accounting for the temporal variability of CMORPH bias has the largest influence on model simulations and should be taken into account. The error propagation is found to depend, not only on errors in rainfall inputs, but also on the accumulated rainfall which affect the actual moisture and water storage in the model stores. Future studies should assess comparative advantages of various bias correction algorithms that account for the temporal aspects of bias and that received applications in climate change and radar rainfall studies. There is also a need to devote efforts towards operationalizing the bias correction algorithms.
Acknowledgments
Support for this study was provided by the National Science Foundation (NSF) through Award Number OISE-0914618 to the University of Louisiana at Lafayette, and by the the NASA EPSCoR/BoR DART2 program and the NASA Grant to Louisiana Space (LaSPACE) Consortium. Support provided by the University of Louisiana at Lafayette Computational and Visualization Enterprise (CAVE) Consortium is acknowledged. Support is also received from the CGIAR Research Program on Water, Land and Ecosystems (WLE), which is led by International Water Management Institute (IWMI)
Author Contributions
Emad Habib and Alemseged Tamiru Haile had the original idea for the study with all co-authors carried out the design. Alemseged Tamiru Habib was responsible for mentoring and follow-up of study participants. Alemseged Tamiru Haile and Nazmus Sazib were responsible for data preparation and all authors carried out the analyses. Alemseged Tamiru Haile, and Emad Habib drafted the manuscript, which was revised by Tom Rientjes, Yu Zhang, and the other authors. Tom Rientjes provided the modeling tools. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haile, A.T.; Habib, E.; Rientjes, T.H.M. Evaluation of the Climate Prediction Center (CPC) morphing technique (CMORPH) rainfall product on hourly time scales over the source of the Blue Nile River. Hydrol. Process 2013, 27, 1829–1839. [Google Scholar]
- Kondragunta, C.; Shrestha, K. Automated real-time operational rain gauge quality controls in NWS hydrologic operations. In Proceedings of the 20th AMS Conference on Hydrology, Atlanta, GA, USA, 29 January–2 February 2006.
- AghaKouchak, A.; Mehran, A.; Norouzi, H.; Behrangi, A. Systematic and random error components in satellite precipitation data sets. Geophys. Res. Lett 2012, 39. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Grover-Kopec, E.; Lemma, M.; Connor, S.J.; Ropelewski, C.F. Validation of satellite rainfall products over East Africa’s complex topography. Int. J. Remote Sens 2007, 28, 1503–1526. [Google Scholar]
- Habib, E.; Haile, A.T.; Tian, Y.; Joyce, R. Evaluation of the high-resolution CMORPH satellite-rainfall product using dense rain gauge observations and radar-based estimates. J. Hydrometeorol 2012, 13, 1784–1798. [Google Scholar]
- Yilmaz, K.K.; Hogue, T.S.; Hsu, K.; Sorooshian, S.; Gupta, H.V.; Wagener, T. Intercomparison of rain gauge, radar, and satellite-based precipitation estimates with emphasis on hydrologic forecasting. J. Hydrometeorol 2005, 6, 497–517. [Google Scholar]
- Zhang, Y.; Seo, D-J.; Kitzmiller, D.; Lee, H.; Kuligowski, R.J.; Kim, D.; Kondragunta, C.R. Comparative strengths of SCaMPR satellite QPEs with and without TRMM ingest vs. gridded gauge-only analyses. J. Hydrometeorol 2013, 14, 153–170. [Google Scholar]
- Bitew, M.M.; Gebremichael, M. Assessment of satellite rainfall products for streamflow simulation in medium watersheds of the Ethiopian highlands. Hydrol. Earth Syst. Sci 2011, 15, 1147–1155. [Google Scholar]
- Bitew, M.M.; Gebremichael, M. Evaluation of satellite rainfall products through hydrologic simulation in a fully distributed hydrologic model. Water Resour. Res 2011, 47. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P.P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol 2004, 5, 487–503. [Google Scholar]
- Habib, E.; ElSaadani, M.; Haile, A.T. Climatology-focused evaluation of CMORPH and TMPA satellite rainfall products over the Nile Basin. J. Appl. Meteorol. Climatol 2012, 51, 2105–2121. [Google Scholar]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time rainfall estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc 2007, 88, 47–64. [Google Scholar]
- Pereira, F.A.J.; Carbone, R.E.; Janowiak, J.E.; Arkin, P.; Joyce, R.; Hallak, R.; Ramos, C.G.M. Satellite rainfall estimates over South America—Possible applicability to the water management of large watersheds. J. Am. Water Resour. Assoc 2010, 46, 344–360. [Google Scholar]
- Anagnostou, E.N.; Maggioni, V.; Nikolopoulos, E.I.; Meskele, T.; Hossain, F.; Papadopoulos, A. Benchmarking high-resolution global satellite rainfall products to radar and rain-gauge rainfall estimates. IEEE Trans. Geosci. Remote. Sens 2010, 48, 1667–1683. [Google Scholar]
- Sapiano, M.R.P.; Arkin, P.A. An Intercomparison and validation of high-resolution satellite precipitation estimates with 3-hourly gauge data. J. Hydrometeorol 2009, 10, 149–166. [Google Scholar]
- Smith, T.M.; Arkin, P.A.; Bates, J.J.; Huffman, G.J. Estimating bias of satellite-based precipitation estimates. J. Hydrometeorol 2006, 7, 841–856. [Google Scholar]
- CMORPH Improvements: A Kalman Filter Approach to Blend Various Satellite Rainfall Estimate Inputs and Rain Gauge Data Integration. Available online: http://adsabs.harvard.edu/abs/2009EGUGA..11.9810J (accessed on 25 September 2013).
- Joyce, R.J.; Xie, P.; Janowiak, J.E. Kalman filter based CMORPH. J. Hydrometeorol 2011, 12, 1547–1563. [Google Scholar]
- Seo, D.-J.; Breidenbach, J. Real-time correction of spatially nonuniform bias in radar rainfall data using rain gauge measurements. J. Hydrometeorol 2002, 3, 93–111. [Google Scholar]
- Seo, D.-J.; Briedenbach, J.P.; Johnson, E.R. Real-time estimation of mean field bias in radar rainfall data. J. Hydrol 1999, 223, 131–147. [Google Scholar]
- Zhang, J.; NOAA/NSSL; Norman, O.K.; Howard, K.; Vasiloff, S.; Langston, C.; Kaney, B.; Arthur, A.; van Cooten, S.; Kelleher, K.; et al. National Mosaic and QPE (NMQ) system—Description, results and future plan. In Proceedings of the 34th Conference on Radar Meteor, Williamsburg, VA, USA, 6 October 2009.
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.J.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM multisatellite precipitation analysis (TMPA).Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol 2007, 8, 38–55. [Google Scholar]
- Boushaki, F.I.; Hsu, K.-L.; Sorooshian, S.; Park, G.-H.; Mahani, S.; Shi, W. Bias adjustment of satellite precipitation estimation using ground-based measurement: A case study evaluation over the southwestern United States. J. Hydrometeorol 2009, 10, 1231–1242. [Google Scholar]
- Li, M.; Shao, Q. An improved statistical approach to merge satellite rainfall estimates and raingauge data. J. Hydrol 2010, 385, 51–64. [Google Scholar]
- Vila, D.A.; de Goncalves, L.G.G.; Toll, D.L.; Rozante, J. Statistical evaluation of combined daily gauge observations and rainfall satellite estimates over continental South America. J. Hydrometeorol 2009, 10, 533–543. [Google Scholar]
- Hong, Y.; Hsu, K.; Moradkhani, H.; Sorooshian, S. Uncertainty quantification of satellite precipitation estimation and Monte Carlo assessment of the error propagation into hydrologic response. Water Resour. Res 2006, 42. [Google Scholar] [CrossRef]
- Chiang, Y.-M.; Hsu, K.-L.; Chang, F.-J.; Hong, Y.; Sorooshian, S. Merging multiple precipitation sources for flash flood forecasting. J. Hydrol 2007, 340, 183–196. [Google Scholar]
- Tobin, K.J.; Bennett, M.E. Adjusting satellite precipitation data to facilitate hydrologic modeling. J. Hydrometeorol 2010, 11, 966–978. [Google Scholar]
- Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B. Real-time bias reduction for satellite-based precipitation estimates. J. Hydrometeorol 2010, 11, 1275–1285. [Google Scholar]
- Krakauer, N.Y.; Pradhanang, S.M.; Lakhankar, T.; Jha, A.K. Evaluating satellite products for precipitation estimation in mountain regions: A case study for Nepal. Remote Sens 2013, 5, 4107–4123. [Google Scholar]
- Artan, G.; Gadain, H.; Smith, J.L.; Asante, K.; Bandaragoda, C.J.; Verdin, J.P. Adequacy of satellite derived rainfall data for stream flow modeling. Nat. Hazards 2007, 43, 167–185. [Google Scholar]
- Zeweldi, D.A.; Gebremichael, M.; Downer, C.W. On CMORPH rainfall for stream flow simulation in a small, Hortonian watershed. J. Hydrometeorol 2011, 12, 456–466. [Google Scholar]
- Behrangi, A.; Khakbaz, B.; Jaw, T.C.; AghaKouchak, A.; Hsu, K.; Sorooshian, S. Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrol 2011, 397, 225–237. [Google Scholar]
- Yong, B.; Ren, L.-L.; Hong, Y.; Wang, J.-H.; Gourley, J.J.; Jiang, S.-H.; Chen, X.; Wang, W. Hydrologic evaluation of Multisatellite Precipitation Analysis standard precipitation products in basins beyond its inclined latitude band: A case study in Laohahe basin, China. Water Resour. Res 2010, 46. [Google Scholar] [CrossRef]
- Sorooshian, S.; AghaKouchak, A.; Arkin, P.; Eylander, J.; Foufoula-Georgiou, E.; Harmon, R.; Hendrickx, J.; Imam, B.; Kuligowski, R.; Skahill, B.; et al. Advanced concepts of remote sensing of precipitation at multiple scales. Bull. Am. Meteorol. Soc 2011, 92, 1353–1357. [Google Scholar]
- Gebremichael, M.; Anagnostou, E.N.; Bitew, M. Critical steps for continuing advancement of satellite rainfall applications for surface hydrology in the Nile River basin. J. Am. Water Resour. Assoc 2010, 46, 361–366. [Google Scholar]
- Rientjes, T.H.M.; Perera, B.U.J.; Haile, A.T.; Reggiani, P.; Muthuwatta, L.P. Regionalisation for lake level simulation—The case of Lake Tana in the Upper Blue Nile, Ethiopia. Hydrol. Earth Syst. Sci 2011, 15, 1167–1183. [Google Scholar]
- Haile, A.T.; Rientjes, T.H.M.; Gieske, A.S.M.; Gebremichael, M. Rainfall variability over mountainous and adjacent lake areas: The case of Lake Tana basin at the source of the Blue Nile River. J. Appl. Meteorol. Climatol 2009, 48, 1696–1717. [Google Scholar]
- Rientjes, T.H.M.; Haile, A.T.; Ayele, A.F. Diurnal rainfall variability over the Upper Blue Nile: A remote sensing based approach. Int. J. Appl. Earth Obs. Geoinf 2013, 21, 311–325. [Google Scholar]
- Haile, A.T.; Rientjes, T.H.M.; Habib, E.; Jetten, V.; Gebremichael, M. Rain event properties at the source of the Blue Nile River. Hydrol. Earth Syst. Sci 2011, 15, 1023–1034. [Google Scholar]
- Abdo, K.S.; Fiseha, B.M.; Rientjes, T.H.M.; Gieske, A.S.M.; Haile, A.T. Assessment of climate change impacts on the hydrology of Gilgel Abbay catchment in Lake Tana basin, Ethiopia. Hydrol. Process 2009, 23, 3661–3669. [Google Scholar]
- Rientjes, T.H.M.; Haile, A.T.; Mannaerts, C.M.M.; Kebede, E.; Habib, E. Changes in land cover and stream flows in Gilgel Abbay catchment, Upper Blue Nile basin—Ethiopia. Hydrol. Earth Syst. Sci. Discuss 2011, 7, 9567–9598. [Google Scholar]
- Wale, A.; Rientjes, T.H.M.; Gieske, A.S.M.; Getachew, H.A. Ungauged catchment contributions to Lake Tana’s water balance. Hydrol. Process 2009, 23, 3682–3693. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper; United Nations Food and Agriculture Organization: Rome, Italy, 1998; p. 300. [Google Scholar]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol 1997, 201, 272–288. [Google Scholar]
- Booij, M.J. Impact of climate change on river flooding assessed with different spatial model resolutions. J. Hydrol 2005, 303, 176–198. [Google Scholar]
- Deckers, D.L.E.H.; Booij, M.J.; Rientjes, T.H.M.; Krol, M.S. Catchment variability and parameter estimation in multi-objective regionalisation of a rainfall-runoff model. Water Resour. Manag 2010, 24, 3961–3985. [Google Scholar]
- Merz, R.; Blöschl, G. Regionalisation of catchment model parameters. J. Hydrol 2004, 287, 95–123. [Google Scholar]
- Rientjes, T.H.M.; Muthuwatta, L.P.; Bos, M.G.; Booij, M.J.; Bhatti, H.A. Multi-variable calibration of a semi-distributed hydrological model using streamflow data and satellite based evapotranspiration. J. Hydrol 2013, 505, 276–290. [Google Scholar]
- Seibert, J. Estimation of parameter uncertainty in the HBV model. Nord. Hydrol 1997, 28, 4–5. [Google Scholar]
- Gebremichael, M.; Krajewski, W.F. Characterization of the temporal sampling error inspace-time-averaged rainfall estimates from satellites. J. Geophys. Res 2004, 109. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).