An Approach to Persistent Scatterer Interferometry
Abstract
:1. Introduction
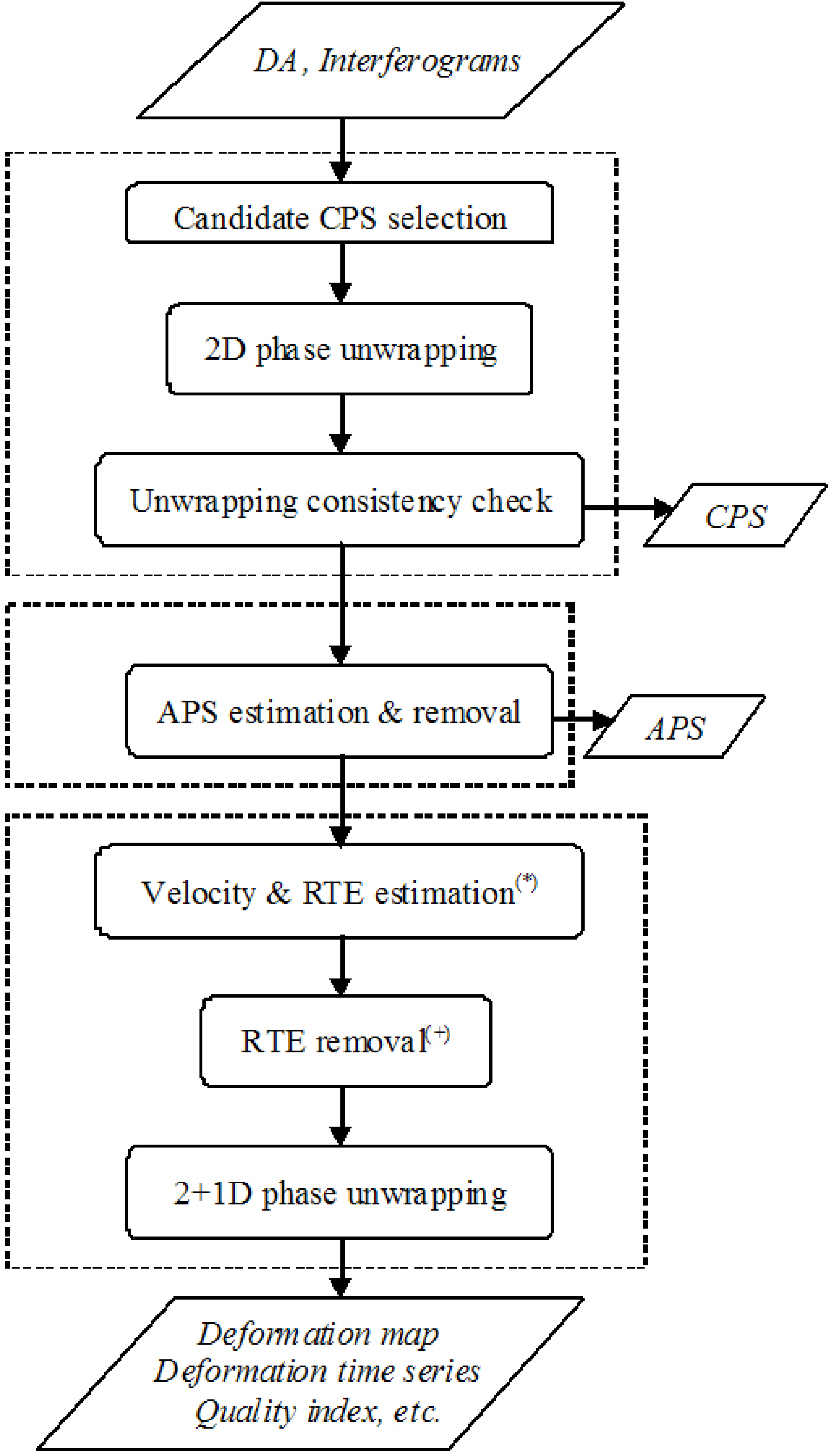
2. The PSIG Procedure
- Candidate Cousin PS (CPS) selection. In this step, a set of PSs with phases characterized by a moderate spatial variation is sought. This is accomplished by using at least a seed PS and searching for its “cousins”, i.e., PSs with similar characteristics (the details are described in the next section). An iterative process is used to ensure an appropriate CPS coverage and density;
- Phase unwrapping consistency check. This check is based on a LS estimation, followed by the analysis of the so-called residuals (the details are described in the next section). The final set of CPSs is selected at this stage;
- Estimation of deformation velocity and RTE. The deformation velocity and RTE are computed over a dense set of PSs (much denser than the selected CPSs), from the M wrapped APS-free interferograms, using the method of the periodogram [1]. Optionally, an extension of the two-parameter model can be used to account for the thermal expansion [24];
- RTE removal. The RTE phase component is removed from the wrapped APS-free interferograms. The linear deformation component can optionally be removed and then, in a later stage, added back to the deformation time series. The same procedure can be done with the thermal expansion component;
- 2+1D phase unwrapping. A 2+1D phase unwrapping is executed on the set of M APS- and RTE-free interferograms to obtain the final deformation phase time series, a quality index for each time series and other parameters related to the detection and correction of unwrapping errors (detailed information is provided in Section 4.2).
3. First Processing Block
- Candidate CPS selection;
- 2D phase unwrapping on the selected CPSs;
- Phase unwrapping consistency check.
3.1. Candidate CPS Selection
- (1)
- At least one seed PS is chosen with the following characteristics: φDefo_SEED = 0, φTher_SEED = 0, φRTE_SEED = 0 and φNoise_SEED = 0 small. In other words, a PS located on the ground, with no deformation or thermal expansion and characterized by small noise is sought.
- (2)
- The candidate CPSs are those PSs that satisfy the following condition:where is the 90th percentile of , where k runs over the minimum set of N − 1 independent interferograms, where N is the number of images, and Thr is a phase threshold. Before computing their absolute value and ordering them, the values are unwrapped using this simple rule: if then , if then and if then . The use of the 90th percentile confers robustness to the filter: it can cope with up to 10% of outliers. The threshold is discussed in the following section. This operation is repeated for all the PSs that fall within a given window, which is centred on the seed. The window size (Win) is set to have relatively small values of ΔφAtmo_i,j. It is worth noting that the above condition is more restrictive than the ones based on the classical two-parameter model (mean deformation velocity and RTE), see [32,33]. However, the proposed procedure is computationally lighter than the one based on the two-parameter model.
- (3)
- This operation is repeated recursively, using a given candidate CPS as seed, until the area of interest is sufficiently covered by CPSs. Additional seeds might be required to cover isolated areas or to increase the CPS density in a given area.
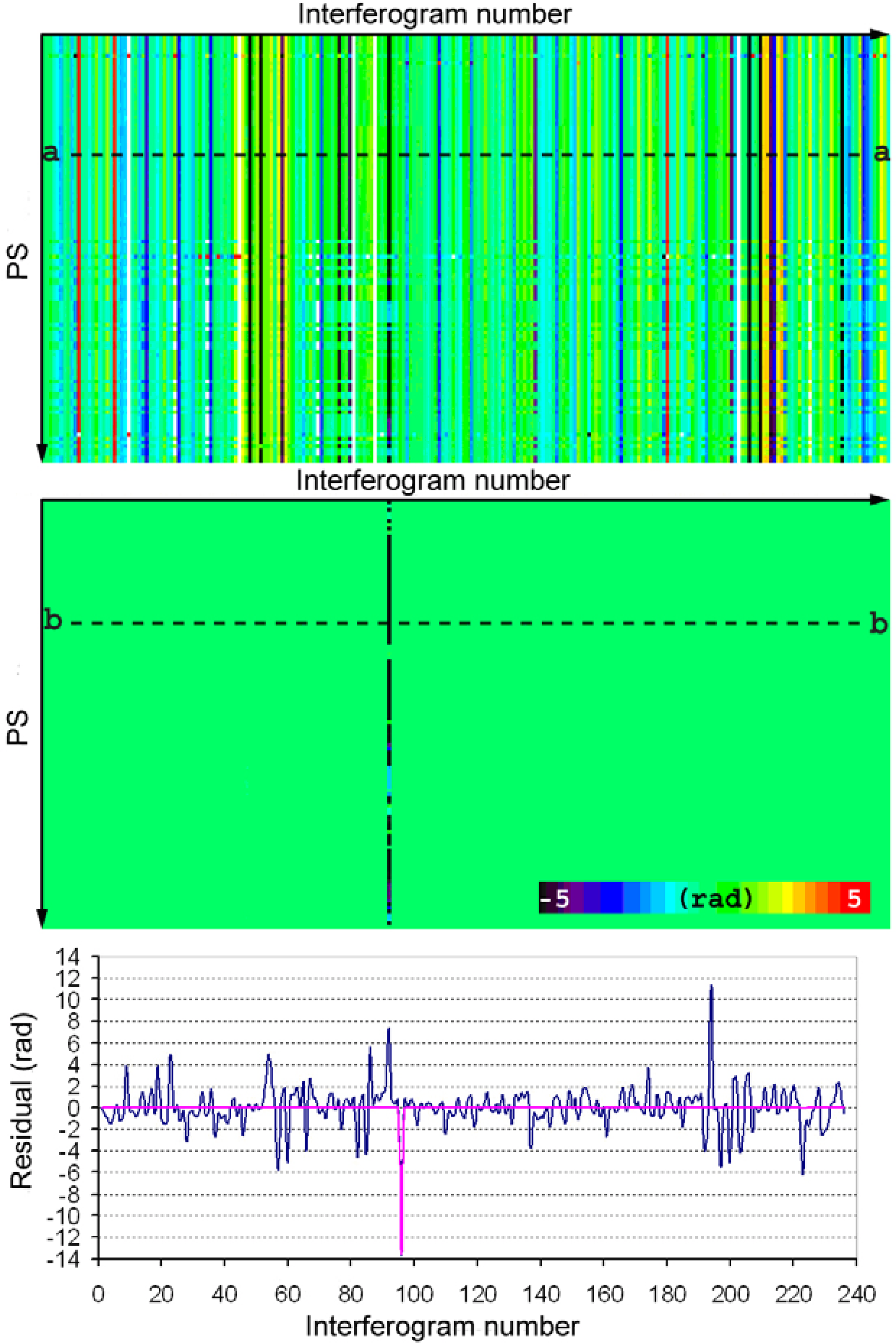
3.2. Phase Unwrapping Consistency Check
3.3. Candidate CPS Selection: Main Parameters
4. Third Processing Block
- Estimating the deformation velocity and RTE and, optionally, the thermal expansion;
- Removing the RTE component from the APS-free interferograms. The deformation velocity and the thermal expansion components are optionally removed;
- Performing the 2+1D phase unwrapping.
4.1. 2+1D Phase Unwrapping
- (1)
- Performing the first LS estimation, computing the residuals (Equation (6));
- (2)
- Temporally removing the highest absolute residual (outlier candidate) from the network, and performing a new LS estimation;
- (3)
- Checking the residual of the outlier candidate: if it is a multiple of 2π (within a given tolerance), the observation is corrected and reaccepted. In this way, it is possible to correct the unwrapping errors. Otherwise, the decision of re-entering or rejecting the outlier candidate is based on the comparison of its old and new residuals;
- (4)
- Performing a new LS estimation, computing the residuals and restarting the procedure from point (2). The procedure is executed iteratively from points (2)–(4) until there are no remaining outlier candidates, i.e., there is no residual above a given threshold. Then, the correction of the unwrapping-related errors is extended to all the residuals that, within a given tolerance, are multiples of 2π.
4.2. 2+1D Phase Unwrapping: Description of the Outputs
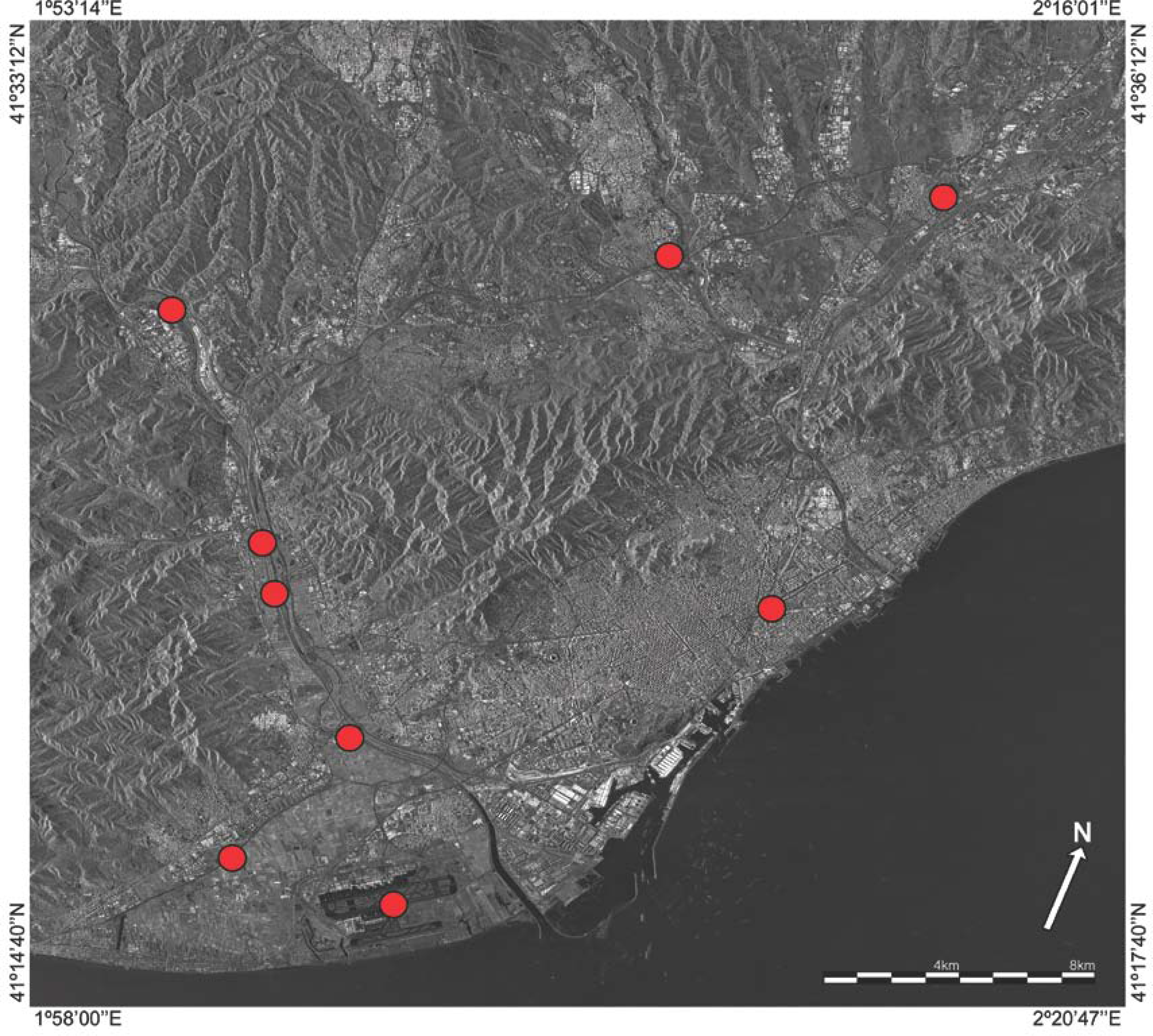
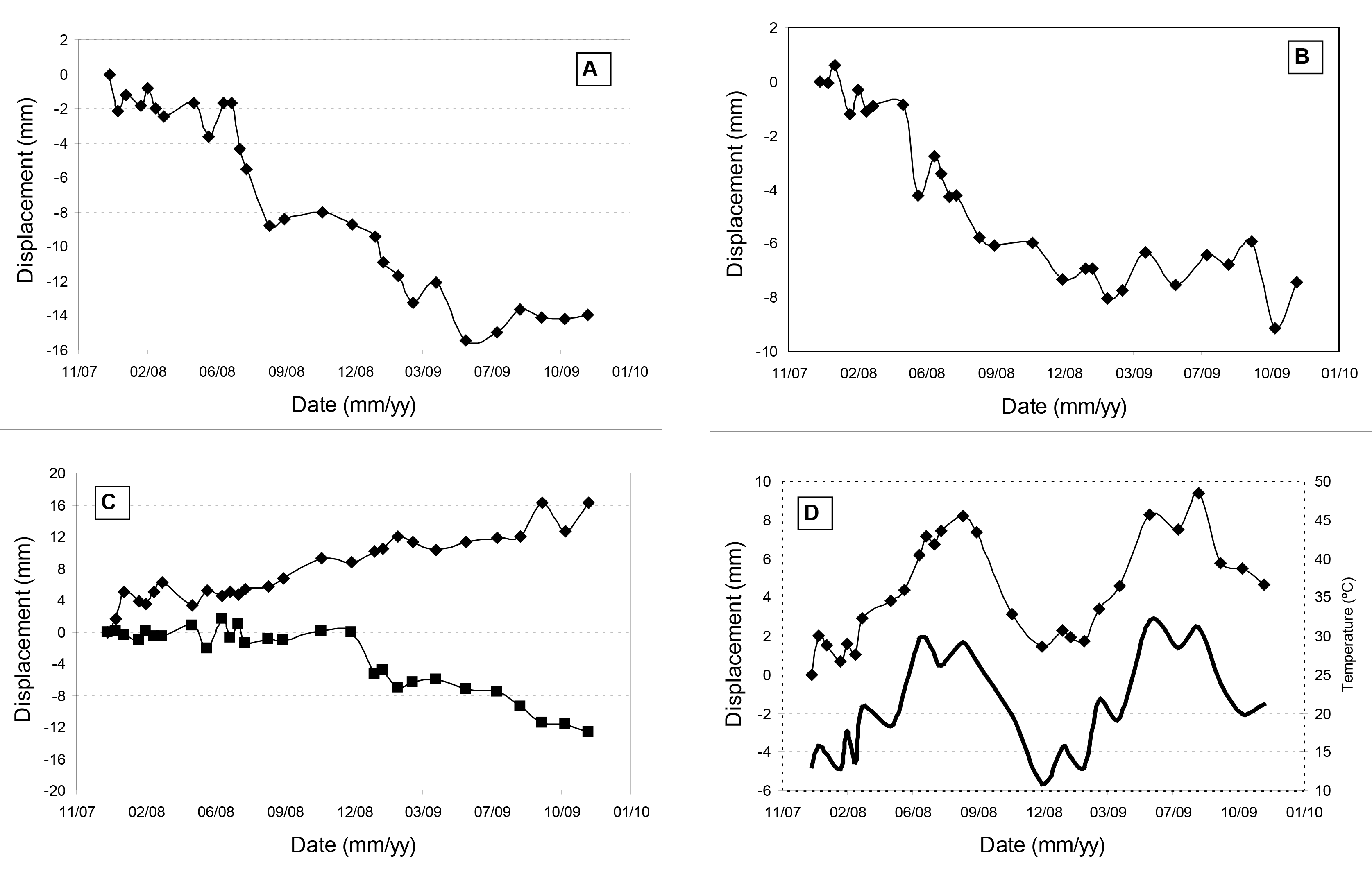
5. Analysis of the Barcelona Dataset
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens 2000, 38, 2202–2212. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens 2001, 39, 8–20. [Google Scholar]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens 2002, 40, 2375–2383. [Google Scholar]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens 2004, 42, 1377–1386. [Google Scholar]
- Pepe, A.; Sansosti, E.; Berardino, P.; Lanari, R. On the generation of ERS/ENVISAT DInSAR time-series via the SBAS technique. IEEE Geosci. Remote Sens. Lett 2005, 2, 265–269. [Google Scholar]
- Pepe, A.; Manunta, M.; Mazzarella, G.; Lanari, R. A space-time minimum cost flow phase unwrapping algorithm for the generation of persistent scatterers deformation time-series. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2007), Barcelona, Spain, 23–28 July 2007.
- Pepe, A.; Berardino, P.; Bonano, M.; Euillades, L.D.; Lanari, R.; Sansosti, E. SBAS-based satellite orbit correction for the generation of DInSAR time-series: Application to RADARSAT-1 data. IEEE Trans. Geosci. Remote Sens 2011, 49, 5150–5165. [Google Scholar]
- Mora, O.; Mallorquí, J.J.; Broquetas, A. Linear and nonlinear terrain deformation maps from a reduced set of interferometric SAR images. IEEE Trans. Geosci. Remote Sens 2003, 41, 2243–2253. [Google Scholar]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett 2004, 31. [Google Scholar] [CrossRef]
- Crosetto, M.; Crippa, B.; Biescas, E. Early detection and in-depth analysis of deformation phenomena by radar interferometry. Eng. Geol 2005, 79, 81–91. [Google Scholar]
- Crosetto, M.; Biescas, E.; Duro, J.; Closa, J.; Arnaud, A. Generation of advanced ERS and Envisat interferometric SAR products using the stable point network technique. Photogram metric Eng. Remote Sens. 2008, 74, 443–450. [Google Scholar]
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. Interferometric point target analysis for deformation mapping. In Proceedings of the 2003 Geoscience and Remote Sensing Symposium (IGARSS 2003), Toulouse, France, 21–25 July 2003.
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens 2011, 49, 3460–3470. [Google Scholar]
- Navarro-Sanchez, V.D.; Lopez-Sanchez, J.M. Spatial adaptive speckle filtering driven by temporal polarimetric statistics and its application to PSI. IEEE Trans. Geosci. Remote Sens 2013, 99, 1–10. [Google Scholar]
- Adam, N.; Rodriguez-Gonzalez, F.; Parizzi, A.; Liebhart, W. Wide area persistent scatterer interferometry. In Proceedings of the 2011 Geoscience and Remote Sensing Symposium (IGARSS 2011), Vancouver, BC, Canada, 24–29 July 2011.
- Kampes, B.M.; Hanssen, R.F. Ambiguity resolution for permanent scatterer interferometry. IEEE Trans. Geosci. Remote Sens 2004, 42, 2446–2453. [Google Scholar]
- Van Leijen, F.J.; Hanssen, R.F. Persistent scatterer density improvement using adaptive deformation models. In Proceedings of the 2007 Geoscience and Remote Sensing Symposium (IGARSS 2007), Barcelona, Spain, 23–28 July 2007.
- Perissin, P.; Ferretti, A. Urban-target recognition by means of repeated spaceborne SAR images. IEEE Trans. Geosci. Remote Sens 2007, 45, 4043–4058. [Google Scholar]
- Lombardini, F. Differential tomography: A new framework for SAR interferometry. IEEE Trans. Geosci. Remote Sens 2005, 43, 37–44. [Google Scholar]
- Fornaro, G.; Serafino, F.; Reale, D. 4D SAR imaging for height estimation and monitoring of single and double scatterers. IEEE Trans. Geosci. Remote Sens 2009, 47, 224–237. [Google Scholar]
- Crosetto, M.; Monserrat, O.; Iglesias, R.; Crippa, B. Persistent scatterer interferometry: Potential, limits and initial C- and X-band comparison. Photogramm. Eng. Remote Sens 2010, 76, 1061–1069. [Google Scholar]
- Gernhardt, S.; Adam, N.; Eineder, M.; Bamler, R. Potential of very high resolution SAR for persistent scatterer interferometry in urban areas. Ann. GIS 2010, 16, 103–111. [Google Scholar]
- Duro, J.; Mora, O.; Agudo, M.; Arnaud, A. First results of Stable Point Network software using TerraSAR-X data. In Proceedings of the 2010 8th European Conference on Synthetic Aperture Radar (EUSAR), Aachen, Germany, 7–10 June 2010.
- Monserrat, O.; Crosetto, M.; Cuevas, M.; Crippa, B. The thermal expansion component of Persistent Scatterer Interferometry observations. IEEE Geosci. Remote Sens. Lett 2011, 8, 864–868. [Google Scholar]
- Fornaro, G.; Reale, D.; Verde, S. Bridge thermal dilation monitoring with millimeter sensitivity via multidimensional SAR imaging. IEEE Geosci. Remote Sens. Lett 2013, 10, 677–681. [Google Scholar]
- Wegmüller, U.; Walter, D.; Spreckels, V.; Werner, C.L. Nonuniform ground motion monitoring with TerraSAR-X persistent scatterer interferometry. IEEE Trans. Geosci. Remote Sens 2010, 48, 895–904. [Google Scholar]
- Liu, G.; Jia, H.; Zhang, R.; Zhang, H.; Jia, H.; Yu, B.; Sang, M. Exploration of subsidence estimation by persistent scatterer InSAR on time series of high resolution TerraSAR-X images. IEEE J. Sel. Top. Appl. Earth Obs. 2011, 4, 159–170. [Google Scholar]
- Bonano, M.; Manunta, M.; Pepe, A.; Paglia, L.; Lanari, R. From previous C-band to new X-band SAR systems: Assessment of the DInSAR mapping improvement for deformation time-series retrieval in urban areas. IEEE Trans. Geosci. Remote Sens 2013, 51, 1973–1984. [Google Scholar]
- Reale, D.; Fornaro, G.; Pauciullo, A. Extension of 4-D SAR imaging to the monitoring of thermally dilating scatterers. IEEE Trans. Geosci. Remote Sens 2013, 51, 5296–5306. [Google Scholar]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens 1998, 36, 813–821. [Google Scholar]
- Costantini, M.; Farina, A.; Zirilli, F. A fast phase unwrapping algorithm for SAR interferometry. IEEE Trans. Geosci. Remote Sens 1999, 37, 452–460. [Google Scholar]
- Fornaro, G.; Pauciullo, A.; Serafino, F. Deformation monitoring over large areas with multipass differential SAR interferometry: A new approach based on the use of spatial differences. Int. J. Remote Sens 2009, 30, 1455–1478. [Google Scholar]
- Costantini, M.; Falco, S.; Malvarosa, F.; Minati, F. A new method for identification and analysis of persistent scatterers in series of SAR images. In Proceedings of the 2008 Geoscience and Remote Sensing Symposium (IGARSS 2008), Boston, MA, USA, 7–11 July 2008.
- Baarda, W. A Testing Procedure for Use in Geodetic Networks, Delft, The Netherlands; Kanaalweg 4, Rijkscommissie voor Geodesie, 1968.
- Förstner, W. Reliability, gross error detection and self-calibration. ISPRS Int. Arch. Photogramm 1986, 26, 1–34. [Google Scholar]
- Björck, Å. Numerical Methods for Least Square Problems; Siam: Philadelphia, PA, USA, 1996. [Google Scholar]



| Dataset | # Images | # Seed PSs | Area (km2) | Candidate CPSs | Candidate CPS Density (PS/km2) | Selected CPSs (%) |
|---|---|---|---|---|---|---|
| Barcelona | 28 | 9 | 1019 | 611,813 | 600 | 87 |
| Burgos | 11 | 1 | 113 | 82,841 | 733 | 74 |
| Seattle | 30 | 5 | 365 | 34,594 | 95 | 82 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Devanthéry, N.; Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Crippa, B. An Approach to Persistent Scatterer Interferometry. Remote Sens. 2014, 6, 6662-6679. https://doi.org/10.3390/rs6076662
Devanthéry N, Crosetto M, Monserrat O, Cuevas-González M, Crippa B. An Approach to Persistent Scatterer Interferometry. Remote Sensing. 2014; 6(7):6662-6679. https://doi.org/10.3390/rs6076662
Chicago/Turabian StyleDevanthéry, Núria, Michele Crosetto, Oriol Monserrat, María Cuevas-González, and Bruno Crippa. 2014. "An Approach to Persistent Scatterer Interferometry" Remote Sensing 6, no. 7: 6662-6679. https://doi.org/10.3390/rs6076662
APA StyleDevanthéry, N., Crosetto, M., Monserrat, O., Cuevas-González, M., & Crippa, B. (2014). An Approach to Persistent Scatterer Interferometry. Remote Sensing, 6(7), 6662-6679. https://doi.org/10.3390/rs6076662







