A Photogrammetric and Computer Vision-Based Approach for Automated 3D Architectural Modeling and Its Typological Analysis
Abstract
:1. Introduction
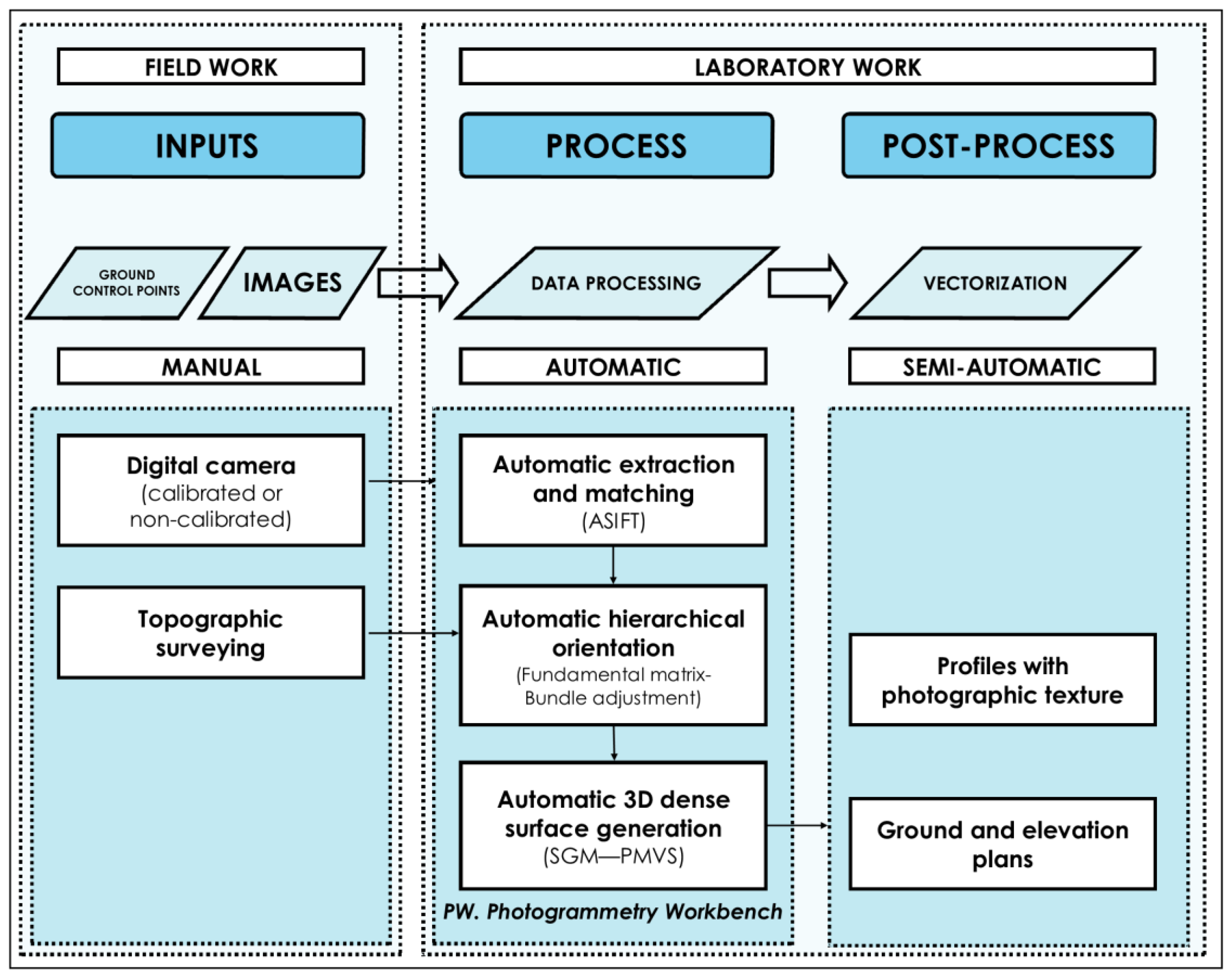
2. Methodology
2.1. Data Collection Protocol
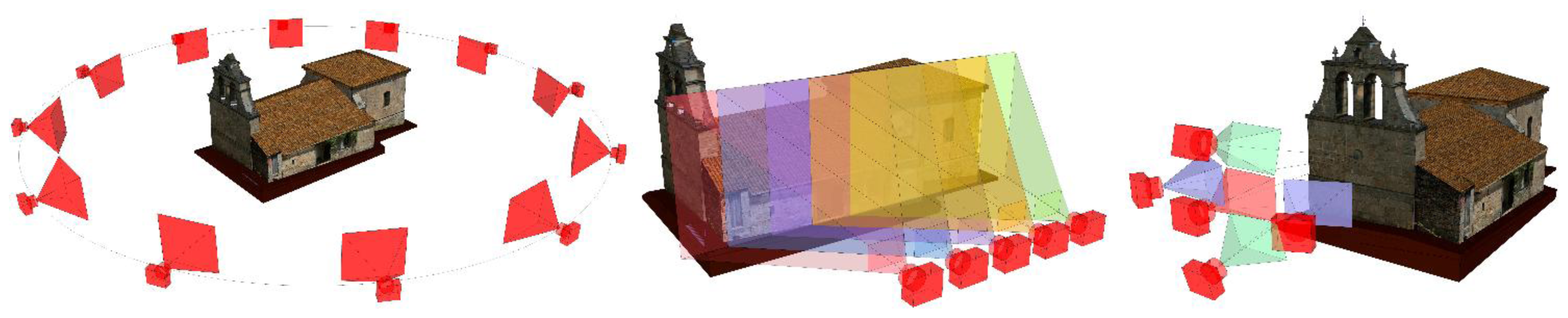
- Circular or “ring” network: used to obtain a 3D model of the whole building, which will then allow establishing the sections necessary to sketch the ground plan. The images axis must converge at the center of the object, and the minimum overlap between adjacent images must be about 80%. Moreover, the number of images in the corners should be higher, so that the user can “tie” the different façades of the object. The network of the shooting process should maintain an appropriate proportion between the base (distance between shots) and the distance to the object. As a general rule, in order to ensure image correspondence in the orientation process, the distance between two adjacent camera stations must be so that the camera axis forms an angle of intersection of approximately 15° with the object. The number of images necessary to obtain all of the measurements depends on the size, shape, morphology and location of the object (in relation to adjacent buildings) and the focal length (Figure 2, left).
- Planar or mosaic network: particularly recommended to document the façade of a building. It requires taking some frontal images of the façade, with an overlap higher than 80% between adjacent shots (Figure 2, center).
- Independent basic network: When documenting a small and accessible façade or any isolated architectonic element, the shooting network may consist of five images forming a cross with an overlap between adjacent shots higher than 90%. The main shot is a frontal image of the façade, which is then combined with four more images of the left, right, upper and lower part of the main shot, to conform a global, slight converging perspective (Figure 2, right).
2.2. Extraction and Matching of Features
2.3. Hierarchical Orientation of Images
2.4. Dense Model Generation
3. Results and Discussion
3.1. Context
3.2. Fieldwork
3.3. Laboratory Work
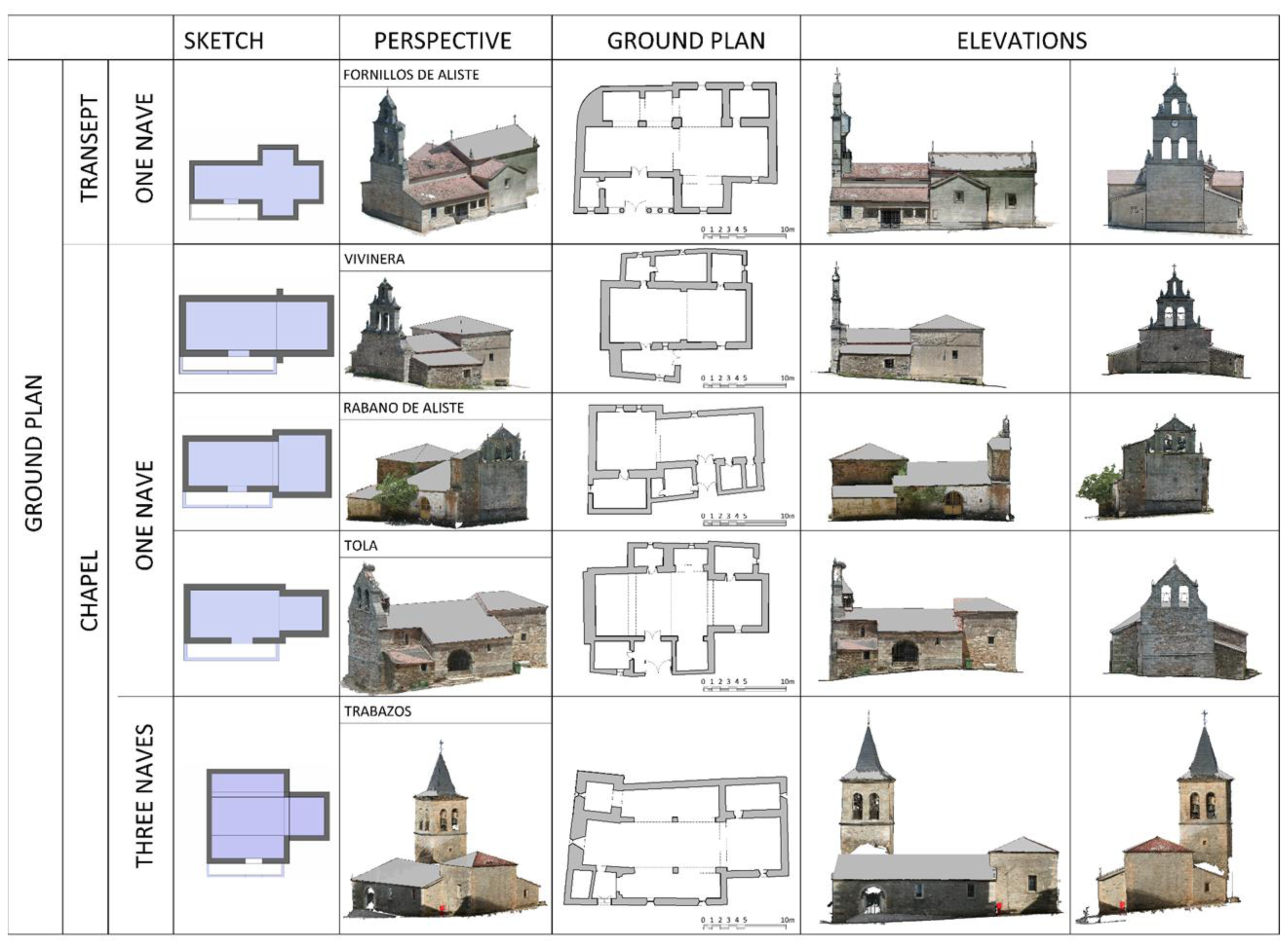
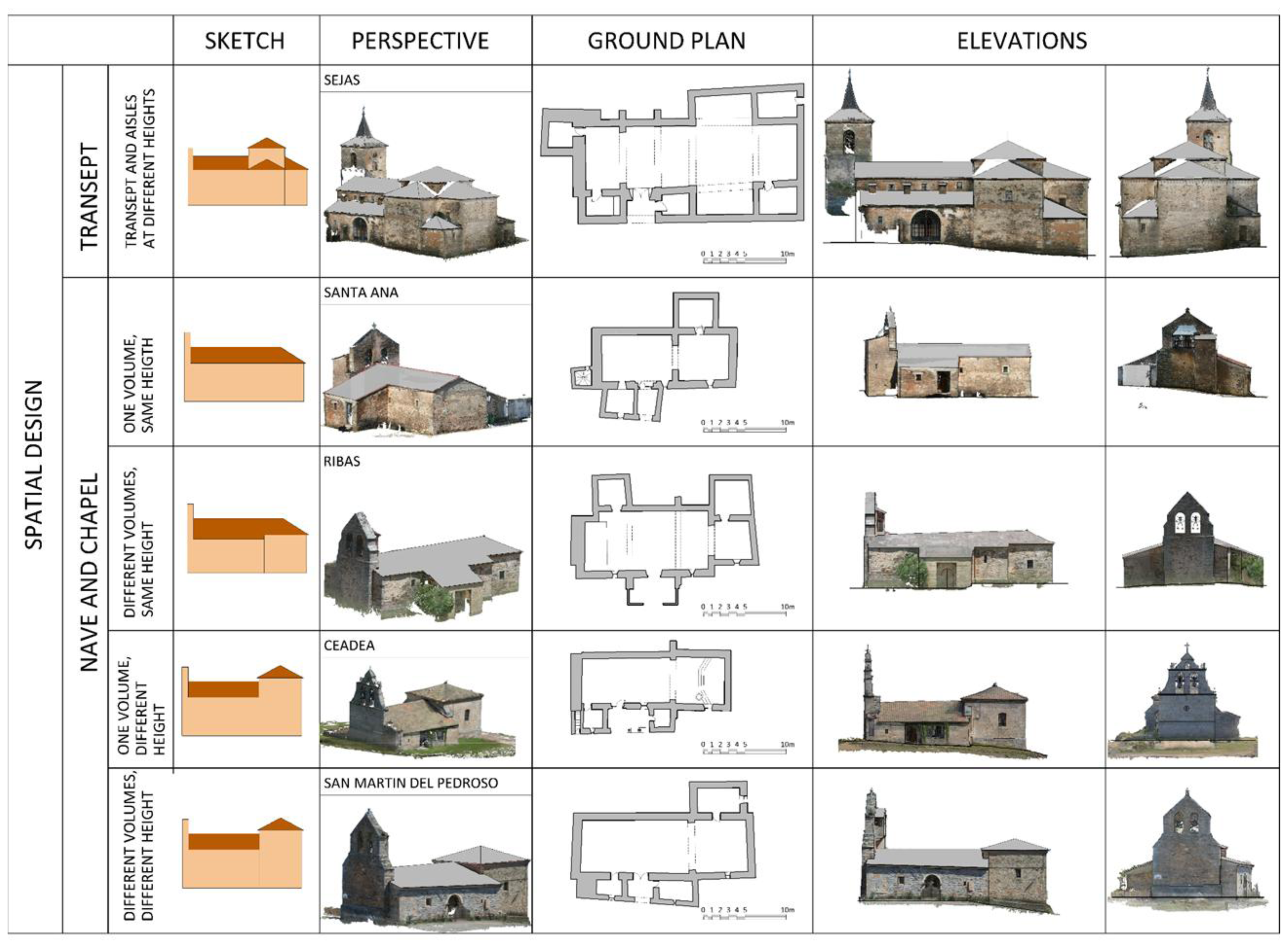
3.4. Typological Analysis
4. Conclusions
- (a)
- The graphic quality of the models is supported basically by the point quantity, between 20 and 50 million points, which usually equals or surpasses the resolution provided by terrestrial laser systems (TLS).
- (b)
- Even though the data volume may seem high, the working times must be taken into account: between 30 and 60 min of fieldwork and from 6 to 16 h of laboratory work, which, once again, can be compared with laser scanner performance. The image capture times are lower than those of a laser scanner (between 1/2 and 1/3 depending on the TLS performance), whereas the laboratory work times are similar. Therefore, compared to laser scanner technology in terms of devices availability and the difficulty of processes, photogrammetry stands out as a more advantageous solution.
- (c)
- The high degree of accuracy (root mean square deviation of block adjustment; the results range from 1/4 to 1/3 of a pixel) is mainly due to the high level of redundancies (high number of tie points), which allows the user to adjust the images accurately
- (d)
- The high level of redundancies (tie points), between 80,000 and 650,000 with an average of about 300,000, is due to the high number of images, between 28 and 177 with an average of about 90. Although the number of images may seem excessive, this issue must be contrasted to the time spent in the process.
- (e)
- The results are highly consistent with each other: RMS are always between 0.18 and 0.33 pixels or between 0.0011 and 0.0037 mm, which guarantee the quality and reliability of the methodology chosen for the study.
- (f)
- The different number of images needed for each church, which ranges from 28 to 177, as stated before, depends on the surroundings of the religious building, as well as on the possibility of fitting the whole object into the image. The size of the building is also important, although all the different aspects do not result in relevant differences, either in time or accuracy.
- (g)
- With regard to the typological analysis, the approach developed improves the current techniques for the recording of architectural cultural heritage. Moreover, the method is suitable to carry out a typological classification study, where the reduction of image capture times (between 1/2 and 1/3, as stated above) allows the researcher to document a great number of buildings/architectural heritage in little time and by non-specialist staff, due to the simplicity of the process. Besides, the high resolution of the models, with GSDs between 0.006 and 0.008 mm, indicates that the method could be used for projects that require larger scales.
- (h)
- These methods are appealing to architects due to their simplicity and speed. Better quality and more robust surveys are obtained, as not only the shape of the building was accessed, but also the information about its color and texture. The fieldwork hours are reduced with no negative effect on accuracy, and it is easier to systematize the process, by following the protocol set out in the present study.
Conflicts of Interest
- Author ContributionsAll authors contributed extensively to the work presented in this paper.
References
- Haala, N.; Peter, M.; Kremer, J.; Hunter, G. Mobile lidar mapping for 3D point cloud collection in urban areas—A performance test. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2008, 37, 1119–1127. [Google Scholar]
- Schindler, K. An overview and comparison of smooth labeling methods for land-cover classification. IEEE Trans. Geosci. Remote Sensi 2012, 50, 4534–4545. [Google Scholar]
- Liu, G.-H.; Liu, X.-Y.; Feng, Q.-Y. High-accuracy three-dimensional shape acquisition of a large-scale object from multiple uncalibrated camera views. Appl. Opt 2011, 50, 3691–3702. [Google Scholar]
- Gruen, A.; Akca, D. Mobile Photogrammetry. In Dreiländertagung SGPBF, DGPF und OVG, Proceedings of 2007 Wissenschaftlich-Technische Jahrestagung der DGPF, Muttenz, Basel, 19–21 June 2007; 16, pp. 441–451.
- Kraus, K. Photogrammetry. Fundamentals and Standard Processes; Dummlers Verlag: Bonn, Germany, 1993; Volume 1. [Google Scholar]
- Arias, P.; Caamano, J.C.; Lorenzo, H.; Armesto, J. 3D modeling and section properties of ancient irregular timber structures by means of digital photogrammetry. MICE Comput.-Aided Civ. Infrastruct. Eng 2007, 22, 597–611. [Google Scholar]
- Lorenzo, H.; Arias, P. A methodology for rapid archaeological site documentation using ground-penetrating radar and terrestrial photogrammetry. Geoarchaeology 2005, 20, 521–535. [Google Scholar]
- Arias, P.; Armesto, J.; Vallejo, J.; Lorenzo, H. Close range digital photogrammetry and software application development for planar patterns computation. Dyna 2009, 76, 7–15. [Google Scholar]
- Robertson, D.P.; Cipolla, R. Structure from Motion. In Practical Image Processing and Computer Vision; John Wiley: Hoboken, NJ, USA, 2009; p. 49. [Google Scholar]
- Quan, L. Image-Based Modeling; Springer: New York, NY, USA, 2010. [Google Scholar]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer: New York, NY, USA, 2011; p. 824. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Hirschmüller, H. Accurate and Efficient Stereo Processing by Semi-Global Matching and Mutual Information. Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005.
- Deseilligny, M.P.; Clery, I. Apero, an Open Source Bundle Adjusment Software for Automatic Calibration and Orientation of Set of Images. Proceedings of the 2011 ISPRS Commission V Symposium, Image Engineering and Vision Metrology, Trento, Italy, 2–4 March 2011; XXXVIII-5/W16, pp. 269–276.
- Habbecke, M.; Kobbelt, L. Iterative Multi-View Plane Fitting. Proceedings of the 2006 International Fall Work-Shop Vision, Modeling, and Visualization, Aachen, Germany, 22–24 November 2006; pp. 73–80.
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 17–22 June 2006; 1, pp. 519–528.
- Furukawa, Y.; Ponce, J. Accurate, dense, and robust multiview stereopsis. IEEE Trans. Pattern Anal. Mach. Intell 2010, 32, 1362–1376. [Google Scholar]
- Waldhäusl, P.; Ogleby, C. 3 × 3 rules for simple photogrammetric documentation of architecture. Int. Arch. Photogramm. Remote Sens 1994, 30, 426–429. [Google Scholar]
- Patias, P.; Santana Quintero, M. Introduction to Heritage Documentation. In CIPA Heritage Documentation Best Practices and Applications; Stylianidis, E., Patias, P., Santana Quintero, M., Eds.; The ICOMOS & ISPRS Committee for Documentation of Cultural Heritage: Athens, Greece, 2011; Volume XXXVIII-5/C19, pp. 9–13. [Google Scholar]
- Joglekar, J.; Gedam, S.S. Area based image matching methods—A survey. Int. J. Emerg. Technol. Adv. Eng 2012, 2, 130–136. [Google Scholar]
- Gruen, A. Adaptive least squares correlation: A powerful image matching technique. S. Afr. J. Photogramm. Remote Sens. Cartogr 1985, 14, 175–187. [Google Scholar]
- Smith, S.M.; Brady, J.M. Susan—A new approach to low level image processing. Int. J. Comput. Vis 1997, 23, 45–78. [Google Scholar]
- Lowe, D.G. Object Recognition from Local Scale-Invariant Features. Proceedings of the 1999 IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; 2, pp. 1150–1157.
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust Wide Baseline Stereo from Maximally Stable Extremal Regions. Procceding of the 2002 British Machine Vision Conference, Citeseer, Cardiff, UK, 2–5 September 2002; pp. 384–393.
- Bay, H.; Ess, A.; Tuytelaars, T.; van Gool, L. Speeded-up robust features (surf). Comput. Vis. Image Underst 2008, 110, 346–359. [Google Scholar]
- Morel, J.-M.; Yu, G. Asift: A new framework for fully affine invariant image comparison. SIAM J. Imaging Sci 2009, 2, 438–469. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis 2004, 60, 91–110. [Google Scholar]
- Moisan, L.; Stival, B. A probabilistic criterion to detect rigid point matches between two images and estimate the fundamental matrix. Int. J. Comput. Vis 2004, 57, 201–218. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar]
- Longuet-Higgins, H.C. A computer algorithm for reconstructing a scene from two projections. Nature 1981, 293, 133–135. [Google Scholar]
- Horn, B.K.P. Recovering baseline and orientation from essential matrix. J. Opt. Soc. Am 1990, 1–10. [Google Scholar]
- Fraser, C.S.; Shortis, M.R.; Ganci, G. Sensor and System Calibration. In Multisensor System Self-Calibration; Society of Photo-Optical Instrumentation Engineers (SPIE): Philadelphia, PA, USA, 1995; pp. 2–18. [Google Scholar]
- Brown, D. Close-range camera calibration. Photogramm. Eng 1971, 37, 855–866. [Google Scholar]
- Luhmann, T.; Robson, S.; Kyle, S.; Harley, I. Close Range Photogrammetry: Principles, Methods and Applications; Whittles: Dunbeath, UK, 2007; p. 528. [Google Scholar]
- Harris, C.; Stephens, M. A Combined Corner and Edge Detector. In The Fourth Alvey Vision Conference; University of Sheffield Printing Office: Manchester, UK, 1988; pp. 147–151. [Google Scholar]
- González, R.C.; Woods, R.E. Digital Image Processing, 3rd ed; Addison-Wesley: Massachusetts, MA, USA, 1992. [Google Scholar]
- Almagro Gorbea, A. Levantamiento Arquitectónico; Universidad de Granada: Granada, Spain, 2004. [Google Scholar]
- Letellier, R.; Schmid, W.; LeBlanc, F.; Eppich, R.; Chabbi, A. Recording, Documentation, and Information Management for the Conservation of Heritage Places: Guiding Principles; Getty Conservation Institute: Los Angeles, CA, USA, 2007. [Google Scholar]
- San José Alonso, J.I. Arquitectura Religiosa en Sanabria: Sus Espacios, Organizaciones y Tipologías; Instituto de Estudios Zamoranos Florián de Ocampo: Zamora, Spain, 1994. [Google Scholar]




| Municipality | Town | Municipality | Town | Municipality | Town |
|---|---|---|---|---|---|
| ALCAÑICES | Alcañices | FONFRIA | Fonfría | RABANO | Rábano de Aliste |
| Alcorcillo | Arcillera | San Mamed | |||
| Santa Ana | Bermillo de Alba | Sejas de Aliste | |||
| Vivinera | Brandilanes | Tola | |||
| FIGUERUELA | Figueruela de Arriba | Castro de Alcañices | TRABAZOS | Trabazos | |
| Figueruela de Abajo | Ceadea | Latedo | |||
| Gallegos del Campo | Fornillos | Nuez de Aliste | |||
| Moldones | Moveros | San Martín del Pedroso | |||
| Riomanzanas | Salto de Castro | Villarino tras la Sierra | |||
| Villarino de Manzanas | VINAS | Viñas de Aliste | |||
| Flechas | Ribas | ||||
| San Blas | |||||
| Vega de Nuez | |||||
| Fornillos | Vivinera | Rabano | Tola | Trabazos | Sejas | Santa Ana | Ribas | Ceadea | S. Martin Pedroso | |
|---|---|---|---|---|---|---|---|---|---|---|
| FIELDWORK | ||||||||||
| Measurements (m) | 25 × 16 × 20 | 18 × 16 × 12 | 21 × 13 × 12 | 22 × 16 × 14 | 27 × 16 × 23 | 32 × 17 × 22 | 20 × 15 × 10 | 23 × 16 × 11 | 19 × 10 × 11 | 22 × 15 × 13 |
| No. of images | 86 | 72 | 127 | 152 | 177 | 78 | 38 | 91 | 28 | 79 |
| Distance max/min (m) | 22.40/10.30 | 16.20/4.50 | 30.80/3.50 | 25.30/2.90 | 25.30/2.60 | 16.50/2.80 | 15.10/4.50 | 19.30/9.70 | 30.15/5.20 | 31.10/5.70 |
| Fieldwork (minutes) | 45 | 40 | 50 | 60 | 70 | 45 | 35 | 40 | 30 | 45 |
| LABORATORY WORK | ||||||||||
| Tie points | 227,666 | 252,895 | 407,975 | 651,467 | 429,726 | 353,976 | 188,221 | 249,567 | 82,149 | 224,492 |
| No. of 3D points | 22,319,921 | 20,913,054 | 39,624,832 | 53,447,764 | 44,416,441 | 25,141,761 | 11,138,274 | 17,894,546 | 4,854,354 | 17,302,829 |
| GSD (m) | 0.008 | 0.007 | 0.006 | 0.006 | 0.006 | 0.006 | 0.006 | 0.008 | 0.007 | 0.008 |
| RMSE (m/pix) | 0.0022/0.28 | 0.0014/0.26 | 0.0018/0.31 | 0.0037/0.33 | 0.0011/0.18 | 0.0017/0.28 | 0.0015/0.26 | 0.0023/0.30 | 0.0015/0.22 | 0.0022/0.29 |
| Laboratory work (hours) | 14 | 10 | 15 | 15 | 17 | 16 | 7 | 12 | 6 | 12 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
García-Gago, J.; González-Aguilera, D.; Gómez-Lahoz, J.; San José-Alonso, J.I. A Photogrammetric and Computer Vision-Based Approach for Automated 3D Architectural Modeling and Its Typological Analysis. Remote Sens. 2014, 6, 5671-5691. https://doi.org/10.3390/rs6065671
García-Gago J, González-Aguilera D, Gómez-Lahoz J, San José-Alonso JI. A Photogrammetric and Computer Vision-Based Approach for Automated 3D Architectural Modeling and Its Typological Analysis. Remote Sensing. 2014; 6(6):5671-5691. https://doi.org/10.3390/rs6065671
Chicago/Turabian StyleGarcía-Gago, Jesús, Diego González-Aguilera, Javier Gómez-Lahoz, and Jesús Ignacio San José-Alonso. 2014. "A Photogrammetric and Computer Vision-Based Approach for Automated 3D Architectural Modeling and Its Typological Analysis" Remote Sensing 6, no. 6: 5671-5691. https://doi.org/10.3390/rs6065671
APA StyleGarcía-Gago, J., González-Aguilera, D., Gómez-Lahoz, J., & San José-Alonso, J. I. (2014). A Photogrammetric and Computer Vision-Based Approach for Automated 3D Architectural Modeling and Its Typological Analysis. Remote Sensing, 6(6), 5671-5691. https://doi.org/10.3390/rs6065671






