Applicability of Multi-Frequency Passive Microwave Observations and Data Assimilation Methods for Improving NumericalWeather Forecasting in Niger, Africa
Abstract
:Nomenclature
| AMSR | Advanced Microwave Scanning Radiometer |
| AMSR-E | AMSR on Earth Observing System |
| AMSR-2 | AMSR-2nd generation on GCOM-W1 satellite |
| NCEP | National Centers for Environmental Prediction |
| LPRM | NASA Land Parameter Retrieval Model |
| ARPS | The Advanced Regional Prediction System |
| CALDAS | Coupled Atmosphere and Land Data Assimilation System |
| EnKF | Ensemble Kalman Filter |
| CMDAS | Cloud Microphysics Data Assimilation System |
| LDAS | Land Data Assimilation Sysatem |
| LDAS-A | LDAS coupled with an Atmospheric model |
| NWP | Numerical Weather Prediction |
| IR data | InfraRed data |
| SiB2 | Simple Biosphere model version-2 |
| TRMM | Tropical Rainfall Measuring Mission |
1. Introduction
2. Dataset, Models and Method
2.1. Dataset
2.1.1. Initial and Boundary Conditions
2.1.2. AMSR-E Brightness Temperature Data
2.1.3. In Situ Data
2.1.4. Satellite-Derived Soil Moisture Products
2.1.5. Satellite Cloud and Rainfall Products
2.2. Models
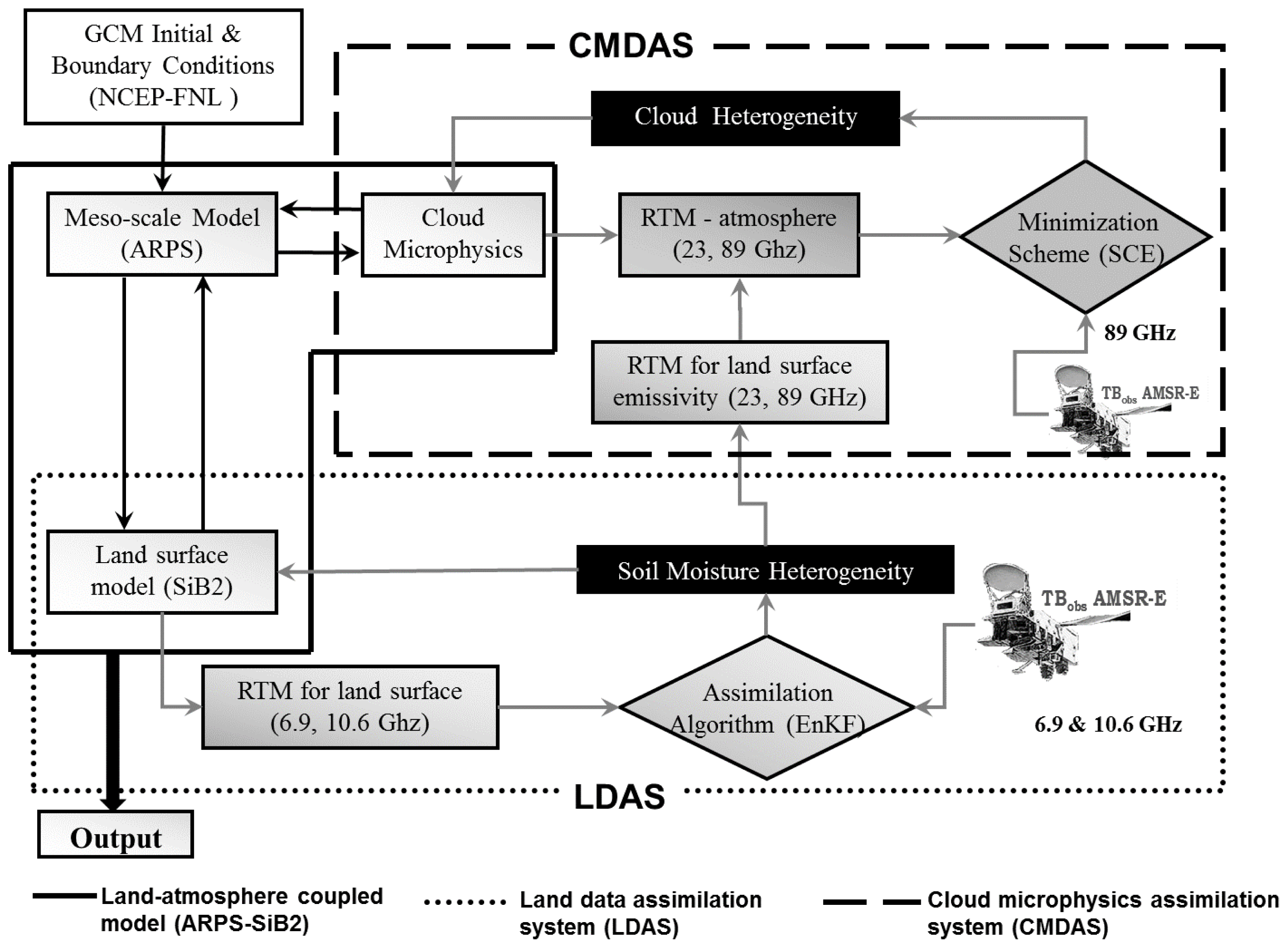
2.3. Method
- As shown in Figure 1, the land-atmosphere mesoscale model (ARPS-SiB2) was established using initial and boundary conditions from NCEP-FNL data.
- The ARPS model was integrated for a predefined period (10 min) and the calculated atmospheric forcing data transferred to the SiB2 model.
- At the beginning of the SiB2 integration, the ensemble (50 members) of soil moisture profiles was generated. SiB2 was executed independently for each ensemble member of the soil moisture profile, retaining the same model parameters and atmospheric forcing. At the end of the SiB2 calculation, the mean values of the updated soil state and fluxes were computed and fed back to the ARPS model as the lower boundary conditions of the atmospheric model. Then, the ARPS-SiB2 model was integrated forward in time.
- At times, when AMSR-E observations were available, the brightness temperatures at 6.9 and 10.65 GHz were perturbed to produce an ensemble of observations with prescribed statistics. The SiB2-driven ensemble of soil moisture profiles, surface temperature, and canopy temperature were used to obtain the simulated brightness temperatures using the forward microwave radiative transfer model. The EnKF calculated the assimilated soil moisture profiles using simulated and observed brightness temperatures, as shown in Equation (4). In the case of soil moisture assimilation (no cloud assimilation), the updated soil state and fluxes were fed back to the ARPS model and the ARPS-SiB2 model was integrated forward in time.
- In the case of cloud data assimilation, CMDAS was activated as soon as the LDAS completed the soil moisture assimilations. The control variables (profiles of temperature, specific humidity, pressure, air density, mixing ratio of cloud water, rain water, hail, snow, and cloud ice) were obtained from ARPS as an initial state to run the model operator (Lin’s ice microphysics [24]). The 4-stream fast model calculated the modeled brightness temperatures for 89 GHz at the satellite level by considering the land surface as the lowest boundary. Land surface emissivity was calculated using assimilated soil moisture content. The Shuffle Complex Evolution scheme was used to estimate the assimilated cloud parameters (i.e., cloud liquid water, snow, and rain) by minimizing the cost function calculated between the modeled and observed brightness temperatures. Then, the updated soil state and fluxes were fed back to the ARPS-SiB2 model.
- Finally, with the reinitialized land surface and atmospheric conditions, the ARPS-SiB2 model was integrated forward in time to predict the land and atmospheric evolution until the next AMSR-E observations were available. The results from the ARPS-Sib2 model were recorded at 30-min intervals.
3. Experiment Descriptions
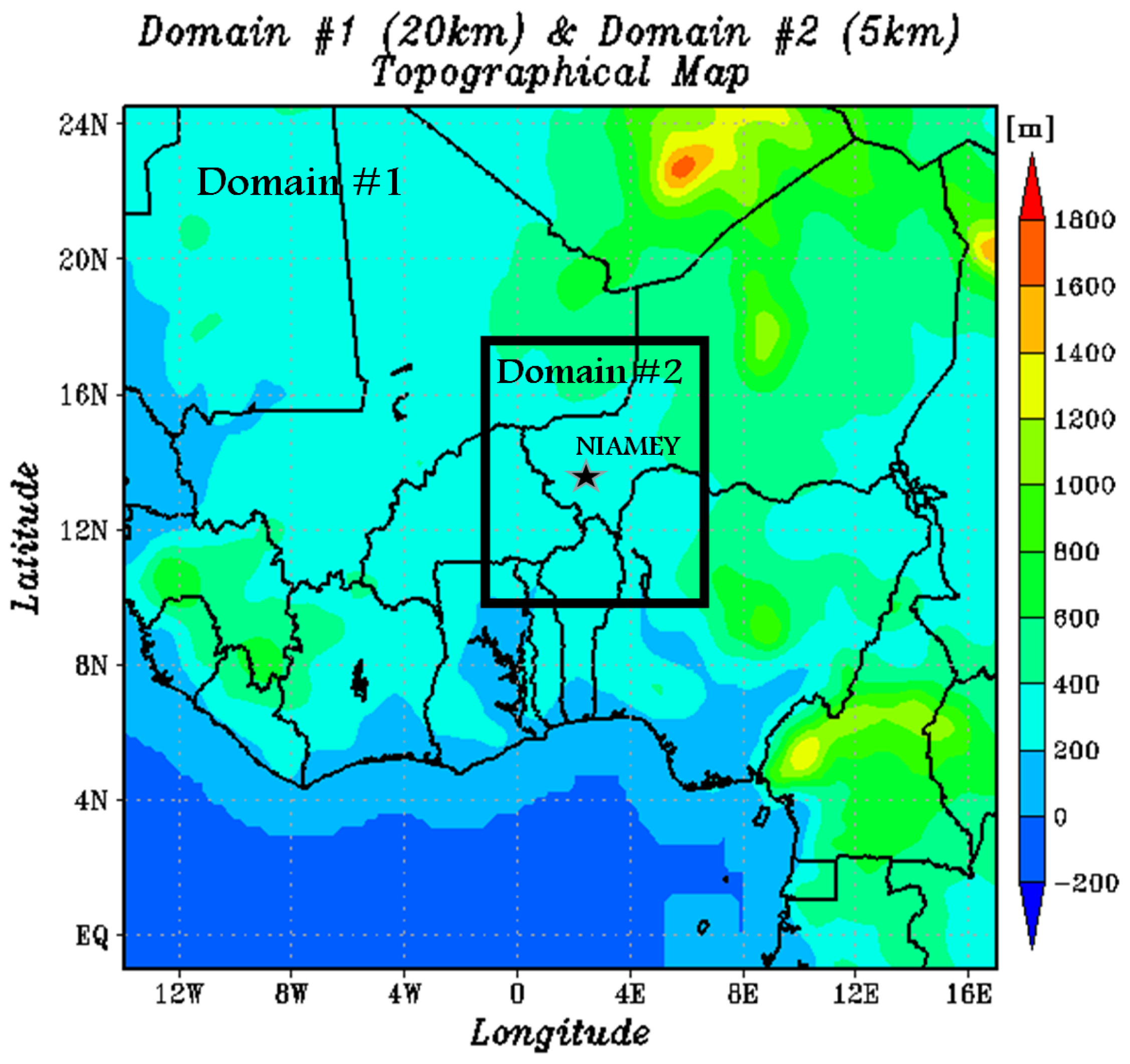
Study Domain and Model Configuration
4. Results and Discussions
4.1. Distribution of Surface Soil Moisture
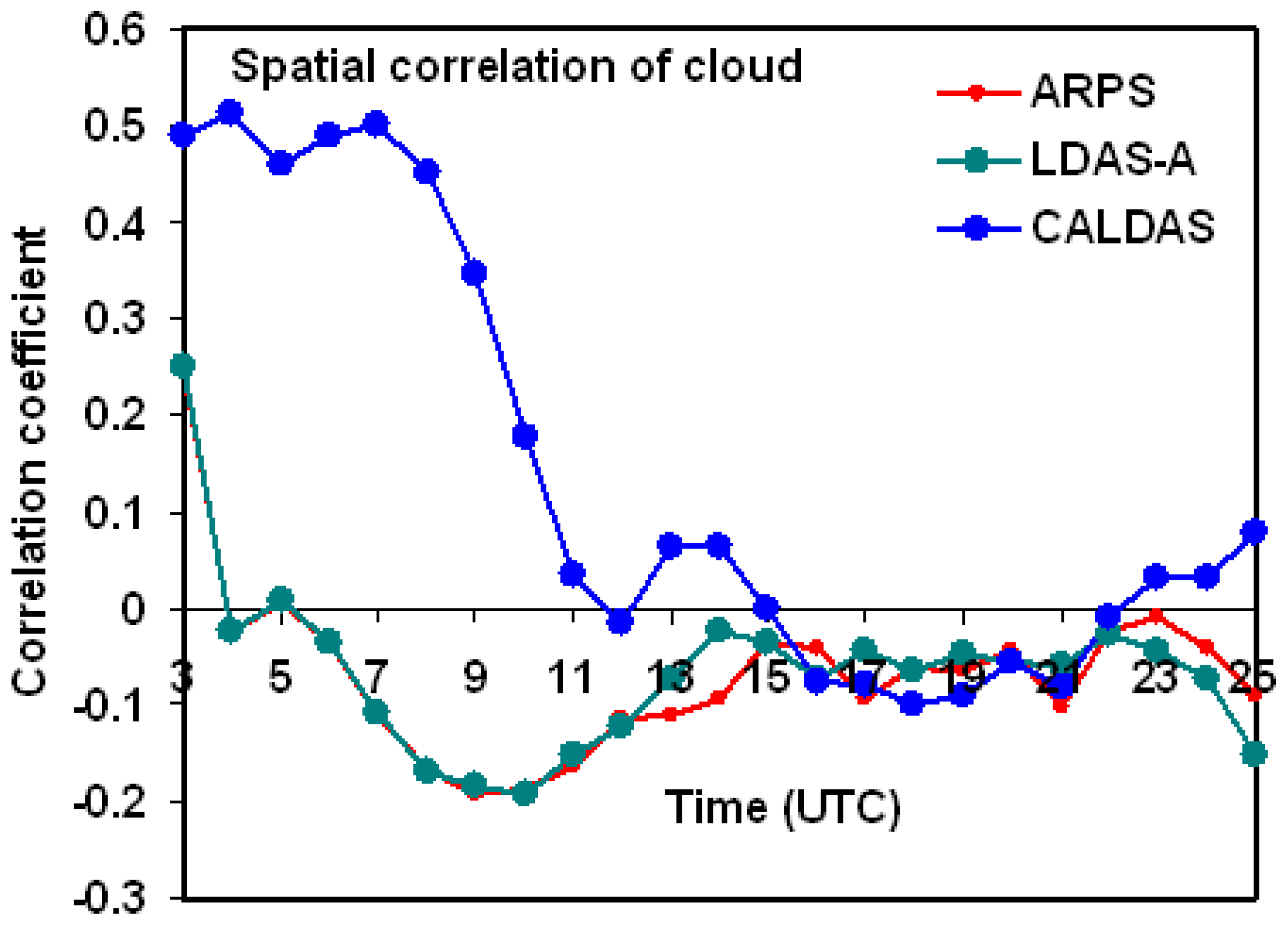
4.2. Comparisons of Cloud Condensate With Satellite IR Observations
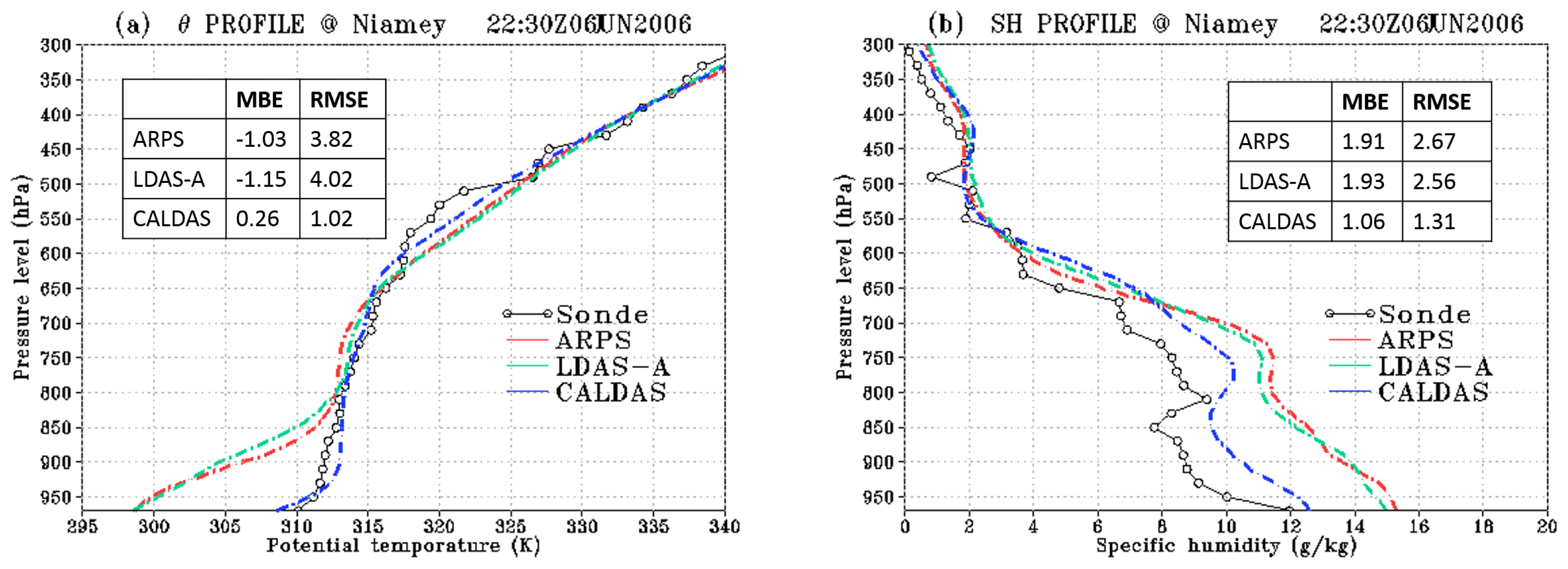
4.3. Evaluation of Land–Atmosphere Interactions
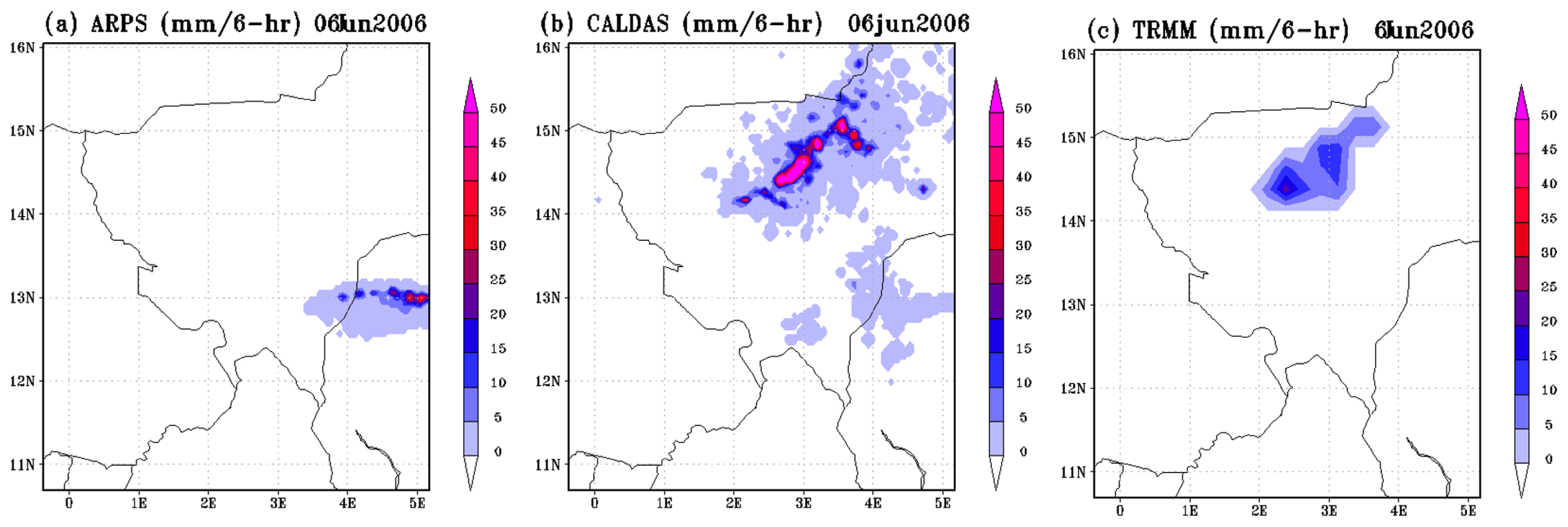
4.4. Evaluation oF Rainfall Forecast
5. Conclusions
Acknowledgments
Conflicts of Interest
- Author ContributionsMohamed Rasmy coupled the satellite data assimilation systems within a mesoscale model, performed numerical simulations, analyzed satellite retrievals and model results, and wrote the manuscript. Xin Li contributed significantly for developing the data assimilation components and provided constructive comments and suggestions for coupling the components within a mesoscale model. Toshio Koike supervised the research work, outlined the design of data assimilation systems, and assisted with the system developments as well as the manuscript writing.
References
- Intergovernmental Panel on Climate Change, Fourth Assessment Report: Climate Change 2007: The AR4 Synthesis Report; Intergovernmental Panel on Climate Change: Geneva, Switherland, 2007.
- Sohne, N.; Chaboureau, J.; Guichard, F. Verification of cloud cover forecast with satellite observation over West Africa. Mon. Weath. Rev 2008, 136, 4421–4434. [Google Scholar]
- Jackson, T.J.; Schmugge, T. Vegetation effects on the microwave emission of soils. Remote Sens. Environ 1991, 36, 203–212. [Google Scholar]
- Jackson, T.; le Vine, D.M.; Hsu, A.Y.; Oldak, A.; Starks, P.J.; Swift, C.T.; Isham, J.D.; Haken, M. Soil moisture mapping at regional scales using microwave radiometry: The Southern Great Plains Hydrology Experiment. IEEE Trans. Geosci. Remote Sens 1997, 37, 2136–2151. [Google Scholar]
- Paloscia, S.; Pampaloni, P. Microwave polarization index for monitoring vegetation growth. IEEE Trans. Geosci. Remote Sens 1988, 26, 617–621. [Google Scholar]
- Wentz, F.J.; Meissner, T. Supplement 1 Algorithm Theoretical Basis Document: AMSR-E Ocean Algorithms; NASA: Santa Rosa, CA, USA, 2007. [Google Scholar]
- Koster, R.; Suarez, M.; Higgins, R.; van de Dool, H. Observational evidence that soil moisture variations affect precipitation. Geophys. Res. Lett 2003, 30. [Google Scholar] [CrossRef]
- Koster, R.; Suarez, M.; Liu, P.; Jambor, U.; Berg, A.; Kistler, M.; Reichle, R.; Rodell, M.; Famiglietti, J. Realistic initialization of land surface states: impacts on subseasonal forecast skill. J. Hydrometeor 2004, 5, 1049–1063. [Google Scholar]
- Scipal, K.; Drusch, M.; Wagner, W. Assimilation of a ERS scatterometer derived soil moisture index in the ECMWF numerical weather prediction system. Adv. Water Resour 2008, 31, 1101–1112. [Google Scholar]
- Draper, C.S.; Mahfouf, J.-F.; Walker, J. P. An EKF assimilation of AMSR-E soil moisture into the ISBA land surface scheme. J. Geophys. Res 2009, 114. [Google Scholar] [CrossRef]
- Rasmy, M.; Koike, T.; Boussetta, S.; Lu, H.; Li, X. Development of a satellite land data assimilation system coupled with a mesoscale model in the Tibetan Plateau. IEEE Trans. Geosci. Remote Sensing 2011, 49, 2847–2862. [Google Scholar]
- Rasmy, M.; Koike, T.; Kuria, D.; Mirza, C.; Li, X.; Yang, K. Development of the coupled atmosphere and land data assimilation system (CALDAS) and its application over the Tibetan Plateau. IEEE Trans. Geosci. Remote Sens 2012, 50, 4227–4242. [Google Scholar]
- Fujii, H.; Koike, T.; Imaoka, K. Improvement of the AMSR-E Algorithm for soil moisture estimation by introducing a fractional vegetation coverage dataset derived from MODIS data. J. Remote Sens. Soc. Jpn 2009, 29, 282–292. [Google Scholar]
- Jeu, R.; Wagner, W.; Holmes, T.; Dolman, A.; Giesen, N.; Friesen, J. Global soil moisture patterns observed by space borne microwave radiometers and scatterometers. Surv. Geophys 2008, 29, 399–420. [Google Scholar]
- Xue, M.; Droegemeier, K.K.; Wong, V.; Shapiro, A.; Brewster, K.; Carr, F.; Weber, D.; Liu, Y.; Wang, D. The Advanced Regional Prediction System (ARPS)— A multi-scale nonhydrostatic atmospheric simulation and prediction tool. Part II: Model physics and applications. Meteorol. Atmos. Phys 2001, 76, 143–166. [Google Scholar]
- Sellers, P.J.; Los, S.; Tucker, C.; Justice, C.; Dazlich, D.; Collatz, G. A revised land surface parameterization (SiB2) for atmospheric GCMs, Part II: The generation of global fields of terrestrial biophysical parameters from satellite data. J. Clim 1996, 9, 706–737. [Google Scholar]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn 2003, 53, 343–367. [Google Scholar]
- Fujii, H.; Koike, T. Development of a TRMM/TMI algorithm for precipitation in the Tibetan Plateau by considering effects of land surface emissivity. J. Meteorol. Soc. Jpn 2001, 79, 475–483. [Google Scholar]
- Reichle, R.H.; McLaughlin, D.B. Hydrologic data assimilation with the ensemble Kalman filter. Mon. Weath. Rev 2002, 130, 103–114. [Google Scholar]
- Huang, C.; Li, X.; Lu, L. Experiments of one-dimensional soil moisture assimilation system based on ensemble Kalman filter. Remote Sens. Environ 2008, 112, 889–900. [Google Scholar]
- Mirza, C.R.; Koike, T.; Yang, K.; Graf, T. Retrieval of Atmospheric integrated water vapor and cloud liquid water content over the ocean from satellite data using the 1-D-Var ice cloud microphysics data assimilation system (IMDAS). IEEE Trans. Geosci. Remote Sens 2008, 46, 119–129. [Google Scholar]
- Liu, G. A fast and accurate model for microwave radiance calculations. J. Meteorol. Soc. Jpn 1998, 76, 335–343. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res 1992, 28, 1015–1031. [Google Scholar]
- Lin, Y.; Farley, R.; Orville, H. Bulk parameterization of the snow field in a cloud model. J. Clim. Appl. Meteorol 1983, 22, 1065–1089. [Google Scholar]
- Kain, J.; Fritsch, J. Convective Parameterization for mesoscale models: The kain-fritsch scheme. Meteoro. Monogr. Amer. Meteor. Soc 1993, 24, 165–170. [Google Scholar]
- Jackson, T.J.; Cosh, M.H.; Bindlish, R.; Starks, P.J.; Bosch, D.D.; Seyfried, M.; Goodrich, D.C.; Moran, M.S.; Du, J. Validation of advanced microwave scanning radiometer soil moisture products. IEEE Tran. Geosci. Remote Sens 2010, 48, 4256–4272. [Google Scholar]



© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rasmy, M.; Koike, T.; Li, X. Applicability of Multi-Frequency Passive Microwave Observations and Data Assimilation Methods for Improving NumericalWeather Forecasting in Niger, Africa. Remote Sens. 2014, 6, 5306-5324. https://doi.org/10.3390/rs6065306
Rasmy M, Koike T, Li X. Applicability of Multi-Frequency Passive Microwave Observations and Data Assimilation Methods for Improving NumericalWeather Forecasting in Niger, Africa. Remote Sensing. 2014; 6(6):5306-5324. https://doi.org/10.3390/rs6065306
Chicago/Turabian StyleRasmy, Mohamed, Toshio Koike, and Xin Li. 2014. "Applicability of Multi-Frequency Passive Microwave Observations and Data Assimilation Methods for Improving NumericalWeather Forecasting in Niger, Africa" Remote Sensing 6, no. 6: 5306-5324. https://doi.org/10.3390/rs6065306
APA StyleRasmy, M., Koike, T., & Li, X. (2014). Applicability of Multi-Frequency Passive Microwave Observations and Data Assimilation Methods for Improving NumericalWeather Forecasting in Niger, Africa. Remote Sensing, 6(6), 5306-5324. https://doi.org/10.3390/rs6065306




