Abstract
The characterization of canopy structure is crucial for modeling eco-physiological processes. Two commonly used metrics for characterizing canopy structure are the gap fraction and the effective Plant Area Index (PAIe). Both have been successfully retrieved with terrestrial laser scanning. However, a systematic assessment of the influence of the laser scan properties on the retrieval of these metrics is still lacking. This study investigated the effects of resolution, measurement speed, and noise compression on the retrieval of gap fraction and PAIe from phase-shift FARO Photon 120 laser scans. We demonstrate that FARO’s noise compression yields gap fractions and PAIe that deviate significantly from those based on scans without noise compression and strongly overestimate Leaf Area Index (LAI) estimates based on litter trap measurements. Scan resolution and measurement speed were also shown to impact gap fraction and PAIe, but this depended on leaf development phase, stand structure, and LAI calculation method. Nevertheless, PAIe estimates based on various scan parameter combinations without noise compression proved to be quite stable.
1. Introduction
Information about forest canopy structure is crucial for understanding the significant role forest canopies play in global processes such as water and carbon cycling. Parker [1] gives a general definition of canopy structure as “the organization in space and time, including the position, extent, quantity, type and connectivity, of the above-ground components of vegetation”. In addition to simple forest stand-based descriptors, such as stem density or mean tree height, descriptors related to the amount, distribution, and orientation of foliage within the canopy are vitally important for understanding plant physiology and growth [1]. These foliage metrics include the Leaf Area Index (LAI), commonly defined for flat leaves as half the total leaf area per unit ground surface area [2], and the foliage area volume density (FAVD), defined as the volume density function of foliage area [3].
Ground-based methods for the estimation of LAI are usually grouped into two categories; direct and indirect methods [4]. The direct methods include destructive sampling and litterfall collection [4]. The indirect methods include methods based on leaf contact, such as the inclined point quadrat [5], and passive optical methods, such as hemispherical photography or LI-COR’s Plant Canopy Analyzer (PCA) [4]. As the direct methods are costly, labor intensive and time-consuming [4,6], indirect LAI methods are more commonly applied.
Indirect optical estimates of LAI are all based on a common theoretical framework that uses the probability of non-interception of light passing through the forest canopy to infer structural characteristics. They also rely on a number of theoretical assumptions about the canopy structure, specifically that the foliage elements are planar and distributed randomly within the canopy volume (according to a Poisson point process) [4,7]. In reality, the structure of forest canopies deviates from these assumptions. Forest canopies are a collection of foliage, twigs, and branches that are often clumped around branches and into discrete crown. Various researchers have proposed modifications of the Monsi and Saeki equations relating gap probability to LAI using correction factors that account for leaf and needle clumping or the contribution of woody vegetation components (see [8] for a detailed review). As these correction factors are difficult to measure directly, they are usually inferred from the indirect passive optical measurements. Additionally, passive optical methods are susceptible to specific hemispherical sky illumination conditions, in particular direct sunlight, that can impact apparent gap probability for a given canopy structure (e.g., [9–12]).
Light Detection and Ranging (LiDAR), sometimes referred to as laser scanning, has received increased attention in forestry in recent years as a means of overcoming the limitations of conventional indirect structural measurements. Depending on the platform that the scanner operates from, laser scanning is commonly categorized into airborne laser scanning (ALS), and terrestrial laser scanning (TLS) or terrestrial LiDAR (TLiDAR). LiDAR is based on the emission of a highly collimated laser pulse and registering its reflected signal from objects. This yields not only explicit 3-D information (range and location relative to the scanner position) but also information about the magnitude of the reflected signal in relation to the magnitude of the emitted pulse (i.e., its apparent reflectance [3]).
Two common range measurement methods are used in commercial TLS instruments, phase-shift and time-of-flight [13]. Phase-shift scanners use the difference in phase between the emitted and received continuous laser beam with its power modulated at a series of frequencies. Time-of-flight scanners are based on a measurement of the time difference between the emission of a laser pulse and the registering of a reflected return pulse. While phase-shift scanners record only a single range per measurement direction, time-of-flight scanners may record more than one range or even continuously record the return intensities as a waveform [14]. Range measurement methods can influence the resulting data properties (e.g., maximum range, ranging error and noise, measurement speed). In turn, these may influence the retrieval of vegetation structural metrics.
While phase-shift scanners are characterized by extremely high measurement speeds, their maximum range tends to be more restrictive than time-of-flight scanners [15]. Both, phase-shift and time-of-flight scanners, have been successfully used for the retrieval of structural and biophysical forest metrics. These include tree positions (e.g., [16,17]), tree height (e.g., [18,19]), diameter at breast height (e.g., [20,21]), stem volume (e.g., [22,23]), biomass (e.g., [24–26]).
Terrestrial laser scanning has been shown to be particularly useful in the retrieval of gap fraction and LAI. This is due to the low sensitivity to variable sky illumination conditions, and the enhanced information content captured within the 3-D data [27]. In particular the possibility of explicitly characterizing three-dimensional canopy structure is widely acknowledged as the major benefit of TLS (e.g., [3,7,28,29]). This is fundamental in the characterization of the orientation and 3-D distribution of vegetative elements (leaves, branches, stems) within the forest canopy (as defined by [1]), but also allows detailed analysis of the size and 3-D distribution of canopy gaps, leading to increased understanding of radiative transfer through the canopy [30,31]. The ability to measure the 3-D distributions of canopy gaps and vegetative elements also allows explicit analysis of clumping, which can only be indirectly inferred from passive-optical measurements, such as hemispherical photography [3,7,32].
Another advantage of the 3-D data provided by TLS is the possibility to more accurately measure leaf area [28,33,34]. Two general methods of estimating LAI using TLS have been identified [11]: gap fraction and voxel based methods. The voxel approach [27,29–31,35,36] divides the 3-D scanner environment into cubic volume elements (voxels), which are populated by canopy elements based upon ray-tracing of the scan data. Leaf area can then be estimated based on the number and location of voxels, which are shown to contain vegetation. More sophisticated 3-D approaches have also been demonstrated, such as the tree reconstruction by Côté et al. [37], or the geometrical crown depth method of Huang and Pretzsch [38].
By comparison, the gap fraction approach uses the numbers of laser returns in given zenith angle ranges to an estimate of gap probability. These gap probability measurements are subsequently used to determine LAI, in a similar manner to methods well known in hemispherical photography [6,10,11,39–42]. However, the 3-D information from the scanner can be further utilized to determine the vertical distribution of this LAI in the form of vertical foliage profiles [3,9,12,32].
The gap fraction methods that solely rely on the angular gap fraction information (2D methods) have two main disadvantages: (1) they lose the 3-D information [10] and (2) they are limited in their application to single scans. This is in contrast to the 3-D methods, which are mostly based upon merged scan point clouds from multiple scans acquired at different locations. Although the merging of scans from different viewpoints is associated with higher computational demands, as well as a time-consuming scan data acquisition and registration, it is, thus far, the most effective method for reducing the effect of occlusion.
Both 3-D and 2-D based LAI estimation methods are influenced by the so-called edge effect [28], where partial interception of the beam occurs at the edge of objects, and the remaining pulse travels further to hit other objects or travel through canopy gaps. While the intensity information recorded by full waveform scanners allows an accurate assessment of the proportion of the beam intercepted, and thus the true within beam gap fraction [12], complete interception or gap must be assumed with the discrete return time-of-flight and phase-shift scanners. Partial interceptions in phase-shift scanner data may also produce artifacts caused by range averaging which can confuse gap filtering and result in the total disregard of partial interceptions in gap probability calculations [39].
Of significant concern in vegetation structure assessment is also the inability of phase-shift scanners to unambiguously record non-interception of the beam. This results in randomly distributed points within canopy gaps that need to be addressed through firmware filtering or post processing. Both the artifacts caused by range averaging and the beam non-interceptions need to be filtered. Traditionally in TLS, filtering is applied to reduce noise, which usually refers to the ranging noise defined as the standard deviation of the distances about the best-fit plane of the points on a planar target [43]. This type of noise depends on a number of factors including the targets’ reflectivity and can be minimized by noise compression (i.e., increase the signal-to-noise ratio usually achieved by averaging of multiple returns within a pulse window) [43]. In vegetation structure assessment noise is important as it contains information about the size and distribution of gaps within the canopy. In many cases, filtering is based on both the inferred location and intensity of laser returns. As return intensities are the result of complex interactions of a number of factors including scanner properties such as beam divergence, beam spot size, range, return response threshold [29], and target properties such as orientation, surface texture, and bidirectional reflectance characteristics [27,37,40], the estimation of gap fraction and LAI from phase-shift scanner data is heavily influenced by the filtering methods applied.
This paper investigates the effects of scanner and scan properties on the retrieval of gap fraction and PAIe derived from phase-shift scanner data. The application of phase-shift scanners for the retrieval of gap fraction and related metrics has not been investigated when compared to discrete return time-of-flight scanners (e.g., [10,11,28,29–31,33,37–42]) and time-of-flight full waveform scanners (e.g., [3,9,12,33,34,44]). This study tries to bridge this gap by investigating the effects of the main phase-shift scan properties of scan resolution (angular step size) and measurement speed (pulses per second), as well as a scanner-specific noise compression and firmware based data filtering using a phase-shift FARO Photon 120 terrestrial laser scans.
2. Materials and Methods
2.1. Study Site
The study site (49°16′N, 7°48′E) is located in the Pfälzerwald forest near Kaiserslautern, Germany. The study was carried out at two test plots within stands where permanent forest monitoring is carried out. This monitoring has produced a large pool of in situ biophysical and structural measurements including litterfall. One test plot was established at a pure beech (Fagus sylvatica) stand, which is characterized by a distinct overstorey of dominant trees around 50 years old and a layer of emerging trees younger than 50 years. The other test plot was established at a mixed stand of 200-year-old oak (Quercus petraea) trees in the overstorey and young beech (Fagus sylvatica) trees in the understorey. Mean diameter at breast height (DBH) and mean tree height for the beech stand were 16.4 cm (σ = 7.3) and 18.5 m (σ = 5.7). The stem density of the beech stand was 1032 trees per ha. Mean DBH and mean tree height for the oak-beech stand were 34 cm (σ = 17.1) and 30.7 m (too few height measurements available for reliable standard deviation for tree height). The stem density of the oak-beech stand was 283 trees per ha. Both stands were characterized by consistent slopes (∼3°) and mean elevations of around 522 m.
2.2. Data Acquisition and Scanner Characteristics
Terrestrial Laser Scanning was carried out with a FARO Photon 120 phase shift instrument [43]. This scanner operates at a wavelength of 785 nm, with measurement speeds of up to 976,000 points per second, and with variable angular step sizes. The beam diameter (at exit) is 3.3 mm and beam divergence is 0.16 mrad [43]. The height above ground of the instruments beam emission point was set to 1.75 m and scans were performed at single locations with a field-of-view of 360° horizontal and 310° vertical, providing an almost complete spherical capture of the scanner’s surroundings.
To assess the effects on gap fraction and PAIe retrieval, scans were performed with different angular step size, measurement speed, and noise compression (Table 1). Scan parameters were chosen to provide comparable datasets at each plot while not exceeding scanning times of 15 min. Each scan setting was tested at the centre points of the two test plots and on four different dates (24 April 2013, 2 May 2013, 10 May 2013, 7 June 2013). Dates were chosen to cover the phenology of leaf development. Leaf development took place predominantly between the second and third measurement dates. As such, the first two dates can be characterized as leaf-off, while the latter two dates can be characterized as leaf-on.

Table 1.
FARO Photon 120 scanner parameter sets used at each of the two study plots (modified from table in [43]). Resolution refers to the ratio of the maximum resolution of 40,000 pts/360° for each rotation of the scan head. Noise compression factors 2× and 4× refer to the averaging of ranges within two by two and four by four laser pulse windows respectively. Durations of the hardware filtering are approximate.
All scans were performed with the FARO Photon 120 hardware filters, “clear sky” and “clear contour”, activated. The “clear sky” filter removes scan points with low intensity, which result from intercepting no object, i.e., mainly when the scanner views open sky. The “clear contour” filter removes scan points with large separation to surrounding points, which can be the result of intercepting multiple objects, mainly at the edges of foreground objects [43]. In addition to these hardware filters, three different levels of noise compression can be set prior to scanning with the FARO Photon 120: no compression, noise compression by averaging neighboring scan points in a two by two window, and noise compression by averaging scan points in a four by four window [43].
LAI measurements obtained by collection of leaf litter were used as reference. As litterfall LAI for the year laser scans were recorded (2013) were not yet available, long-term averages for the test sites [45] were used in this study. As the beech stand was thinned shortly before the last scan date, the long-term average for the beech stand was not included.
2.3. Scan Data Pre-Processing
The scan data was collected in the proprietary FARO format and exported to PTX, an ASCII-based format that orders the scan points (Cartesian coordinates relative to the instrument optical center and laser return intensities) according to measurement time while recording non-returns as zero for all Cartesian axes. Spherical coordinates (zenith, azimuth, and range) are then computed from the Cartesian coordinates. In cases where a zero range was recorded (i.e., sky points) zenith and azimuth angles were interpolated from valid (non-zero) neighboring returns. The coordinate system conversion allows projecting the scan data as 2D raster images with azimuth and zenith representing x and y. The original Cartesian coordinates, as well as the range and intensity information, were stored as separate image bands. Figure 1 shows a subset of range images for the different scan parameter sets applied in this study. The difference in the visual appearance of these subsets demonstrates the influence of the scan parameters, particularly apparent in the level of noise within the canopy gaps.

Figure 1.
Scan range images based on the different scan parameter sets applied in this study. Legend: Scan resolution is displayed as the fraction of the full resolution (40,000 points per 360°). Scan speed is displayed in kilo-points per second. The single asterisk denotes scans performed with 2× noise compression and the double asterisk denotes scans performed with 4× noise compression.
2.4. Scan Data Filtering
Phase shift scanners, such as the FARO Photon 120 are known to suffer from noise (see Section 1). While for traditional applications of terrestrial laser scanning noise is mostly treated as unwanted data and simply removed from the point cloud, noise is important in vegetation structural analysis as it contains information about the size and distribution of gaps within the canopy.
To develop a data processing scheme for a consistent and accurate detection of canopy gaps, the effects of FARO’s hardware filtering were studied in detail based on two sets of test scans: The first set included scans performed with and without the “clear sky” filter and with “clear contour” activated in both cases. The second set includes scans performed with and without the “clear contour” filter and with “clear sky” activated in both cases. Constant intensity thresholds were used to separate sky returns from the “clear sky” and “clear contour” filtered scan returns. In addition, the sensitivity of the gap fraction and PAIe estimates to threshold changes was assessed by varying the threshold by ±5%.
To deal with the noise that results from beam non-interceptions (see Section 1 and Figure 1), we applied a kernel-based majority filter (kernel of 3 × 3 pixels) to the 2D scan images, i.e., each image pixel which is not classified as sky is checked for its 8 surrounding pixels. If the majority of these are classified as sky, the centre pixel is assumed to be noise and consequently reclassified as sky. To assess the effect of this type of noise on the retrieval of gap fraction and PAIe, the scan data was analyzed both with and without applying the majority filtering.
2.5. Gap Fraction and PAIe Calculation
The indirect optical methods of estimating gap fraction and Leaf Area Index are mainly based on modeling the radiation transmission through the canopy (see [46]). Assuming a random azimuthal foliage distribution and using Beer’s Law, this gap probability is modeled as a function of foliage projection function G toward a zenith angle θ, LAI, and path length through the canopy (the cosine of θ) such that:
The clumping of canopy elements, particularly into individual tree crows can lead to an increase in the gap probability for a given LAI. In this case, the term effective LAI is often used in the above equation [47]. In addition, since the distinction between foliage and woody material can often not be made with the passive-optical instruments, the estimated leaf area is truly a Plant Area Index (PAI). Hence in this study the term effective Plant Area Index (PAIe) is used. For active-optical instruments such as TLS, various approaches to the estimation of gap fraction and LAI exist (see Section 1). In this study the gap fraction based approach was followed. In this approach gap fraction is inferred from the number of laser pulses with no returns from the canopy within some zenith angle range dθ (Ngap) as a proportion of the total number of pulses emitted by the instrument within dθ (Npulses). Note that this is the complement to fractional cover based on canopy hits Ncanopy:
Based on gap fractions averaged over zenith angle ranges dθi, e.g., LI-COR PCA measurements [49], Equation (3) can be integrated numerically by summing the weighted logarithms of the individual zenith angle ranges’ gap fractions (Equation (4)).
With the LI-COR PCA, five zenith angle ranges (0–13°, 16–28°, 32–43°, 47–58°, 61–74°) are used. The weights sinθidθi are based on the centre angles of these ranges. The weights are then normalized to sum to one [49]. Sometimes only ranges 1–4 with a stronger weighting of the fourth range are used in the calculation of LAI to reduce the effects of multiple scattering which is strongest in the higher zenith angles resulting in a frequent underestimation of LAI [50]. Leblanc and Chen [51] also showed that while the fifth range is least sensitive to changes in canopy LAI, the third and fourth ranges are most stable in case of variable sky radiation. The strong weighting of the fourth range is based on the theory that for an idealized random foliage distribution and a view angle of 57.5°, the projection coefficient G (∼0.5) is independent of the mean leaf angle [52]. This is used to determine LAI directly from gap fraction measurements at this angle [3]:
In this study, in order to assess the effects of resolution, measurement speed, and noise compression on the retrieval of gap fraction, and hence their influence on the calculation of PAIe, the numerical integration of Equation (4) based on ranges 1–4 and based on ranges 1–5 was used. These are, hereafter, referred to as PAIe (0–58°) and PAIe (0–74°). In addition, the gap fraction retrieved from a small zenith range (±2.5°) centered on 57.5° was used in accordance with Equation (5) to calculate PAIe, hereafter referred to as the PAIe (57.5°).
3. Results and Discussion
3.1. Data Filtering
One of the key challenges in the use of phase-shift laser scanners for vegetation structural assessment is the correct and unambiguous identification of canopy gaps. This requires different filtering methods to those employed for application in built structures such as engineering and mining. Figure 2 depicts the intensity and range images of the set of test scans filtered (hereafter referred to as the filtered scan) and unfiltered (hereafter referred to as the raw scan) with the FARO “clear sky” filter. To analyze the range and intensity distribution of sky points, scan regions visually identified as sky were subset and statistics calculated. The corresponding histograms are depicted in Figure 3. While the range values of the sky points from the raw scan show a uniform random distribution, the intensity distribution shows a distinct bimodal pattern which spans almost the full value range. From these observations it is obvious that for raw scans, sky points cannot be separated from non-sky points based on the range and intensity distributions alone (i.e., a simple thresholding is not applicable).

Figure 2.
Range and intensity images of the test scans without “clear sky” filtering (Left) and with “clear sky” filtering (Right). Intensity images are displayed above their respective range image. The images’ grayscales were stretched to maximize the contrast between sky and canopy, with black and white corresponding to minimum and maximum values respectively.
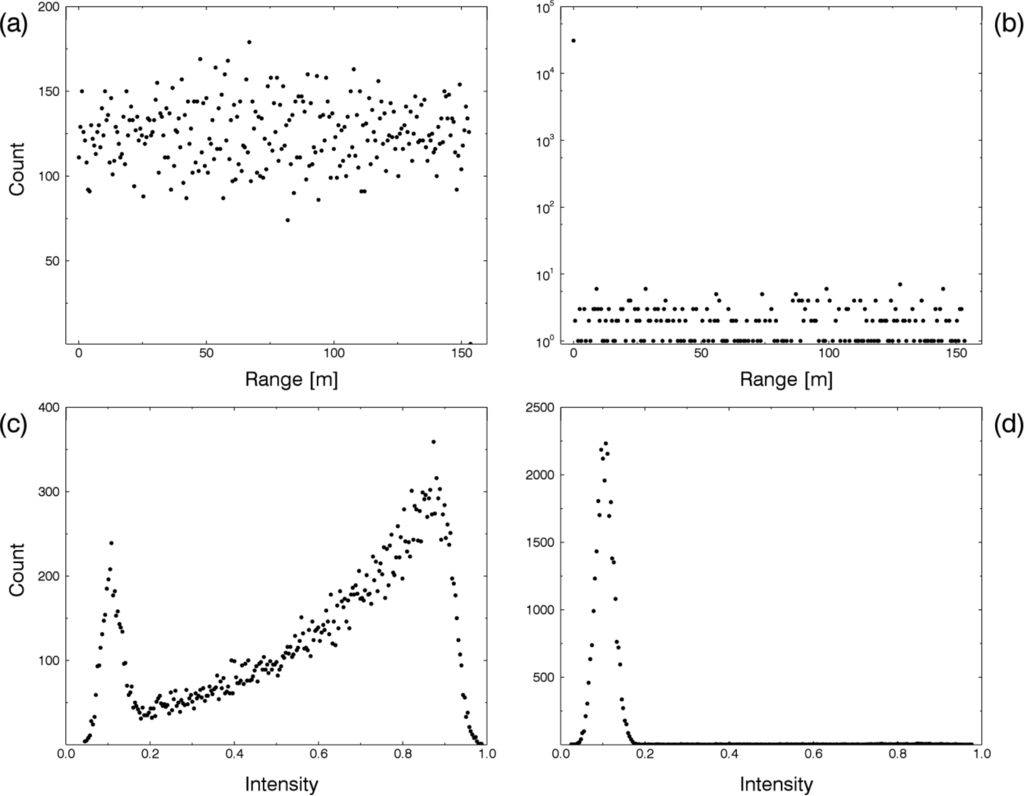
Figure 3.
Range and intensity histograms of sky points retrieved from the images’ canopy gaps displayed in Figure 2. (a) Range histogram of the unfiltered scan, (b) Range histogram of the filtered scan, (c) Intensity histogram of the unfiltered scan, (d) Intensity histogram of the filtered scan.
As mentioned, scan points identified by the “clear sky” filter are assigned zero range (Figure 3b). The presence of a number of non-zero values in Figure 3b reveals that the “clear sky” filter does not detect all sky points. These also show in Figure 3d as the small number of high intensities protruding from an otherwise normal distribution. As the histograms are based on sky points retrieved from the same image regions of the raw and the filtered scan, another interesting observation to note is that the “clear sky” algorithm obviously rescales the intensity values of sky points to achieve this normal distribution (see Figure 3b,d).
To further analyze hardware filter interactions, the second test set was used to plot the intensity distribution of all scan points which were assigned zero range by the hardware filters (Figure 4). As higher intensity values are assumed to be not sky, the bimodal shape of the histogram from the scan without the “clear contour” filter reveals that the “clear sky” algorithm erroneously filters non-sky points (Figure 4a). Their occurrence increases strongly in case of additionally applying the “clear contour” filter (Figure 4b). These erroneously filtered non-sky points can also be visually identified in the range images as the random black pixels spreading over the foliage (Figure 2).
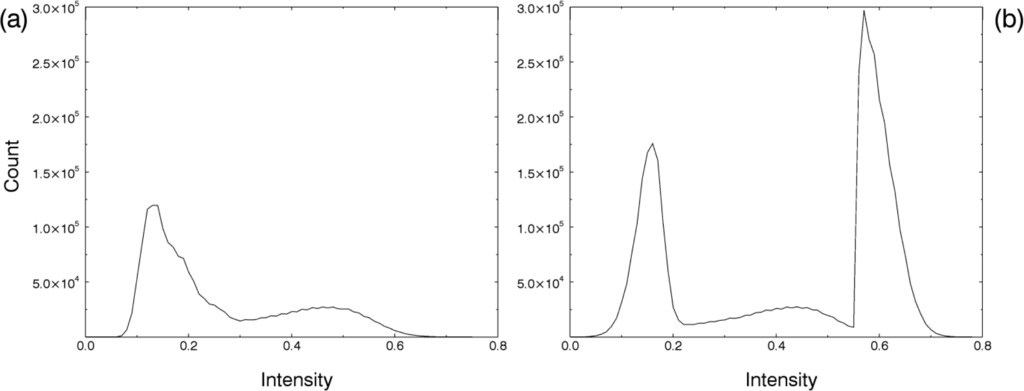
Figure 4.
Intensity histograms of all filtered scan points retrieved from the second set of test scans. (a) Scan filtered only with “clear sky”. (b) Scan filtered with “clear sky” and “clear contour”.
While the peak centered on the intensity value of 0.6 in Figure 4b can be explained by beam interceptions of multiple targets with high intensities such as stems or branches, the increase in the peak centered at 0.15 may be explained by partial interceptions of the beam. Clearly, the removal of these non-sky points by the hardware filtering will result in an overestimation of gap fraction.
To deal with errors of omission in the detection of sky points we applied a three by three pulse window kernel-based majority filter. This was run and resulted in complete removal of unfiltered points from the sky region of the test scan. To deal with errors of commission, where true and partial vegetation returns were considered sky, a simple intensity threshold was applied, such that all points with an intensity value greater than a threshold were considered true vegetation returns. However, since histograms represent scene-dependent statistics, the histogram-based intensity thresholding is not straightforward. This is obvious from Figure 5 which shows the intensity histograms of sky points for scans of different scan resolution and measurement speed. Based on these observations from the test scan regions we applied a constant intensity threshold of 0.3.
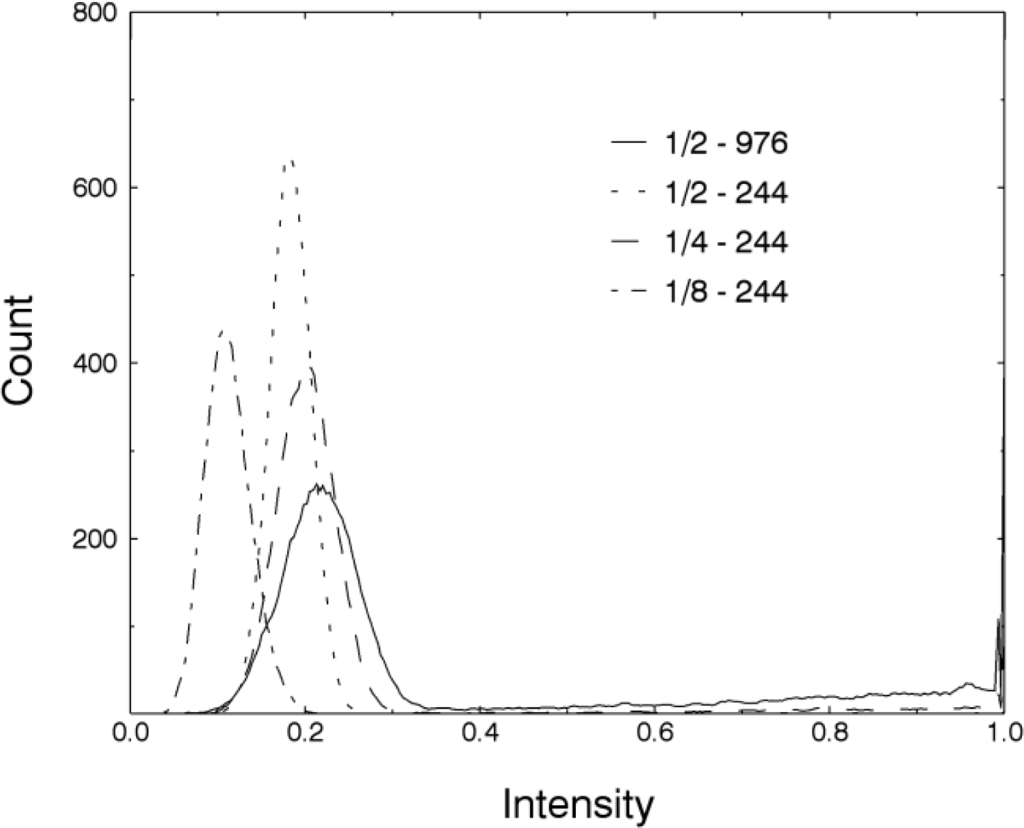
Figure 5.
Intensity histograms of sky points retrieved from test scan regions with different scan parameters (scan resolution and measurement speed).
3.2. Gap Fraction
To investigate whether the effects of the scan parameters on the retrieval of gap fraction exhibit a dependency on zenith angle, leaf development phase, and stand structure, the retrieved gap fractions were plotted separately for zenith rings of 10° width, for leaf-off and leaf-on development phases, and for the two test plots of different stand structure (Figures 6 and 7). The most striking feature of Figures 6 and 7 are the strong differences in the gap fractions retrieved from scans, with and without noise compression. Gap fractions from noise-compressed scans are much lower than those from non-compressed scans. This effect is independent of zenith, leaf development phase, stand structure, and the other parameters (i.e., scan resolution and measurement speed) investigated. The differences are less pronounced for high to medium zenith angles (0–55°) than low zenith angles (>55°), in particular for leaf-on scans (Figures 6 and 7).
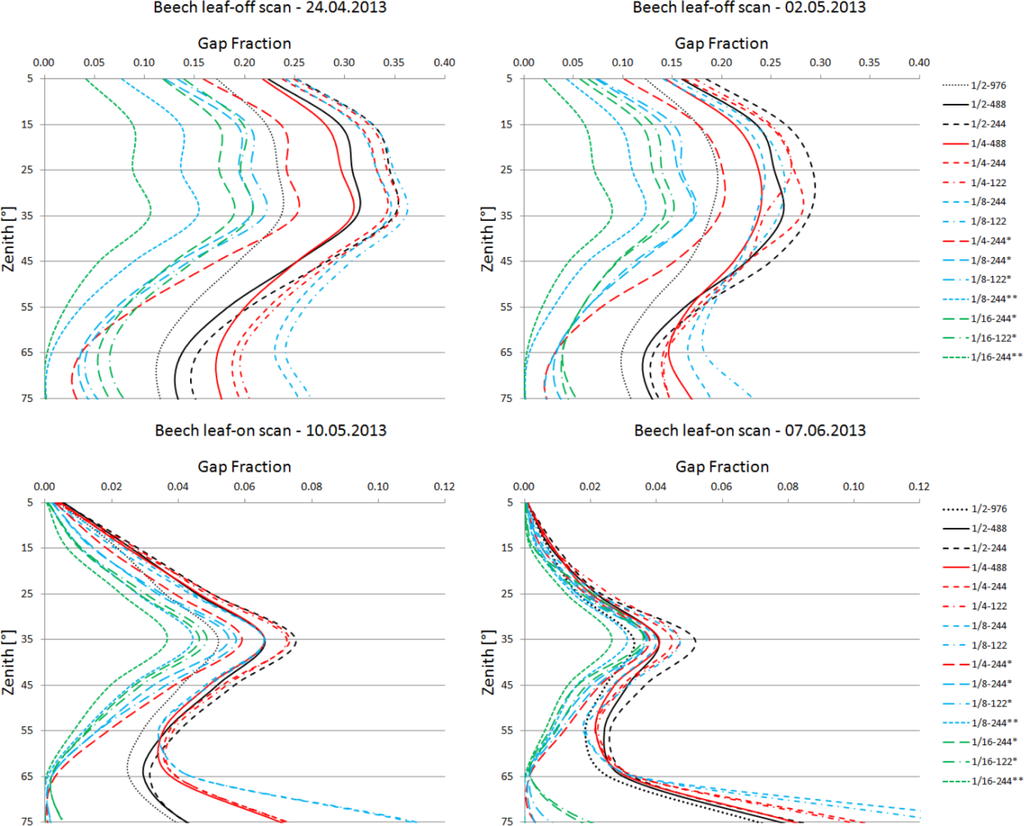
Figure 6.
Average gap fractions of the scans collected at the Beech plot with different scan parameters. Legend (scan parameters): Scan resolution is displayed as the fraction of the maximum scan resolution. Scan speed is displayed in kpts/s. The single and double asterisks denote scans performed with the 2-factor and 4-factor noise compression.
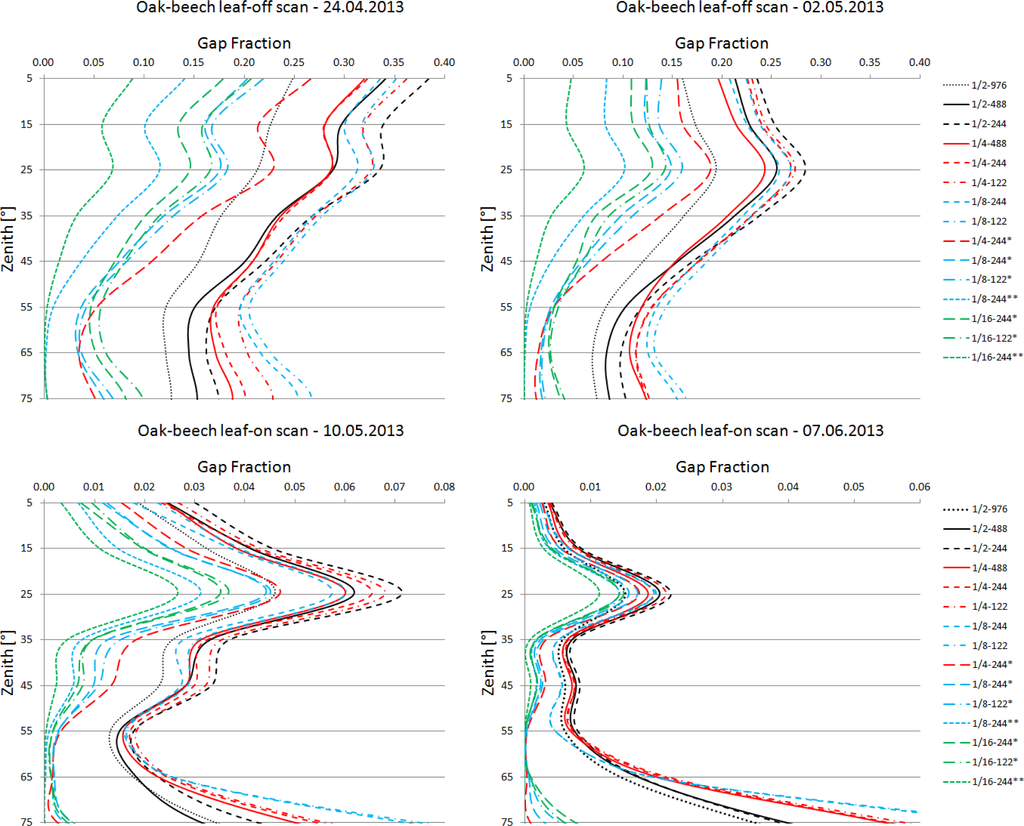
Figure 7.
Average gap fractions of the scans collected at the Oak-beech plot with different scan parameters. Legend (scan parameters): Scan resolution is displayed as the fraction of the maximum scan resolution. Scan speed is displayed in kpts/s. The single and double asterisks denote scans performed with the 2-factor and 4-factor noise compression.
This can be explained by the combined effects of stand structure, laser beam divergence, scan resolution (point density), range, and the noise compression algorithm (see Section 2.2). Due to the increasing laser beam spot size and point spacing with range (spot sizes of 0.45 cm, 0.97 cm, and 1.85 cm for ranges of 10 m, 30 m, and 60 m; for a list of point densities achieved see Table 1), and the larger canopy path lengths for low zenith angles, the probability of hitting only gaps is reduced strongly for low zenith angles and in case of a general decrease of gaps with canopy closing.
With regard to the level of noise compression, the 4-factor noise compression results in smaller gap fractions compared to the 2-factor noise compression, due to the stronger spatial averaging. However, absolute gap fraction differences between the two noise compression factors are smaller for leaf-on scans and for low zenith angles (Figures 6 and 7). While for leaf-on scans this is caused by the general decrease of large gaps with canopy closing, the smaller differences for low zenith angles is the result of stand structure, laser beam divergence, scan resolution, and range. Based on these results it is clear that stand structure is a key factor in determining the magnitude of the noise compression effect. For low-density stands with a large proportion of between-canopy gaps, the spatial averaging of scan points should influence the gap fraction estimation a lot less compared to dense stands with a large proportion of smaller within-canopy gaps.
With regard to the effects of the scan resolutions and measurement speeds applied in combination with the noise compression, the different measurement speeds result in marginal differences, which however seem to be larger for high zenith angles and for leaf-off scans. This is observed for both test plots and both the 1/8 and 1/16 scan resolutions (Figures 6 and 7). By contrast, the scan resolutions have a stronger effect on the gap fraction estimates, yielding larger gap fractions for high zenith angles with increasing scan resolution. This effect is less pronounced for leaf-on scans. For low zenith angles (>55°) this pattern is reversed, i.e., gap fraction increase with decreasing resolution. This can be observed for the different leaf development phases and for both plots (Figures 6 and 7). Given the decreasing probability of hitting only gap within the low zenith angle range for scans with decreasing resolution due the spatial averaging of larger scan point spacing, this reversal is difficult to explain. A possible explanation might be that with decreasing resolution an increasing proportion of low zenith scan points is erroneously filtered and removed by the hardware filters.
With regard to the effect of the scan parameters on the gap fractions derived from the scans without noise compression, a similar dependency on zenith angle can be observed for the scan resolution. For angles greater than 55°, gap fractions increase with decreasing resolution, an effect which is independent of leaf development phase and stand structure (Figures 6 and 7). Again, this might be attributed to the fact that scan points are disproportionally filtered out from lower resolution scans. Gap fractions retrieved from zenith angles smaller than 55° exhibit no systematic pattern as a function of scan resolution. Scans performed with the resolutions 1/4 and 1/8 also show gap fraction differences between the two measurement speeds 244 and 122 kpts/s which appear to be random, rather than systematic. By contrast, a distinct effect of measurement speed can be observed for the scans with resolution 1/2, i.e., an increase in gap fraction with decreasing scan speed. This effect is independent of leaf development phase and stand structure, and it is more pronounced for high to medium zenith angles (0–55°) and for leaf-off scans (Figures 6 and 7). The reason for this effect is the higher noise level (i.e., larger number of undetected sky points) present within canopy gaps with increasing measurement speed (see Figure 1). Since there is, (a) a larger number of gaps within the high to medium zenith canopy regions compared to the low zenith angles; and (b) a general larger number of gaps during the leaf-off phase, the magnitude of this noise is more pronounced for high to medium zenith angles and for leaf-off scans.
3.3. PAIe
To investigate how the differences in the retrieved gap fractions resulting from the different scan parameters translate into differences in PAIe, in particular accounting for the effects of using different LAI calculation methods, PAIe was calculated with three methods (see Section 2.5) for the two plots and the four different acquisition dates (Figures 8 and 9). As was to be expected from the gap fraction results, the strong effect of the noise compression is clearly reflected in the PAIe results. For the scans with parameter combinations 1/4-244, 1/8-244, and 1/8-122, which allow a direct comparison of the magnitude of this effect (see Table 1), PAIe increases by 54%, 73%, and 76% (mean of the three LAI methods and in the order of the above-mentioned parameter combinations) for the leaf-off beech scans, by 27%, 30%, and 28% for the leaf-on beech scans, by 64%, 84%, and 83% for the leaf-off oak-beech scans, and by 44%, 42%, and 41% for the leaf-on oak-beech scans.
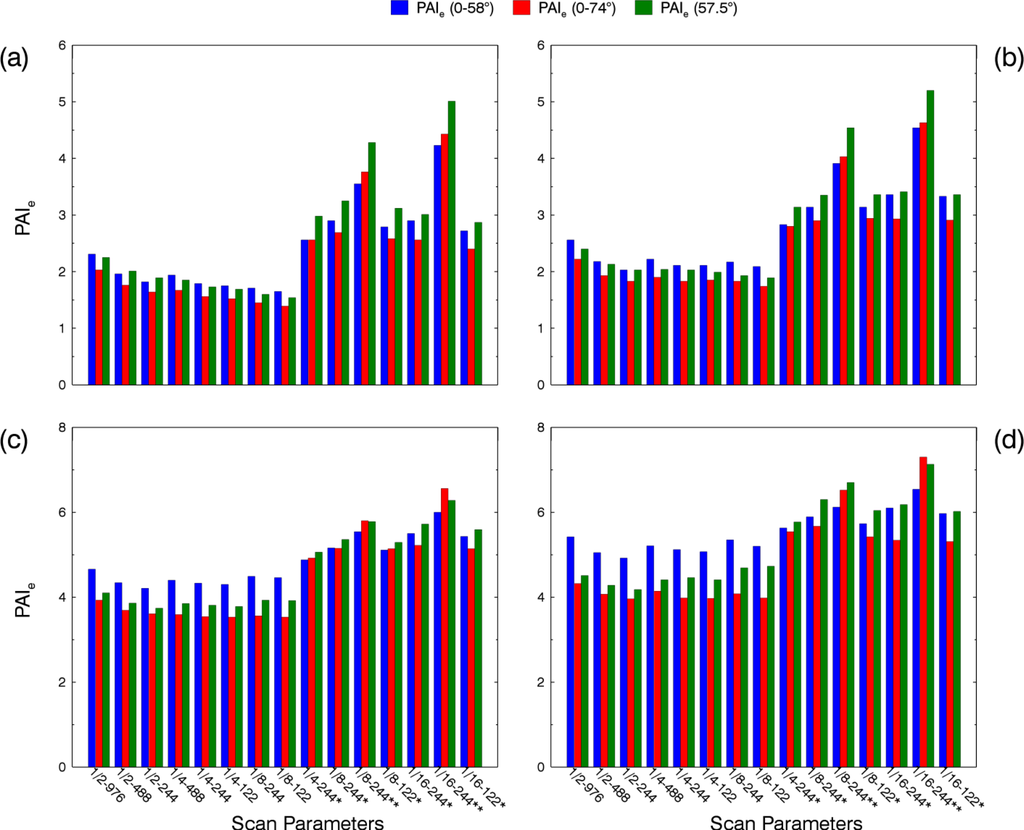
Figure 8.
Effective PAI based on the scans collected at the Beech plot with different scan parameters. Leaf-off dates: (a) 24 April 2013. (b) 2 May 2013. Leaf-on dates: (c) 10 May 2013. (d) 7 June 2013. Scan parameters: Scan resolution is displayed as the fraction of the maximum scan resolution. Scan speed is displayed in kpts/s. The single and double asterisks denote scans performed with the 2-factor and 4-factor noise compression.
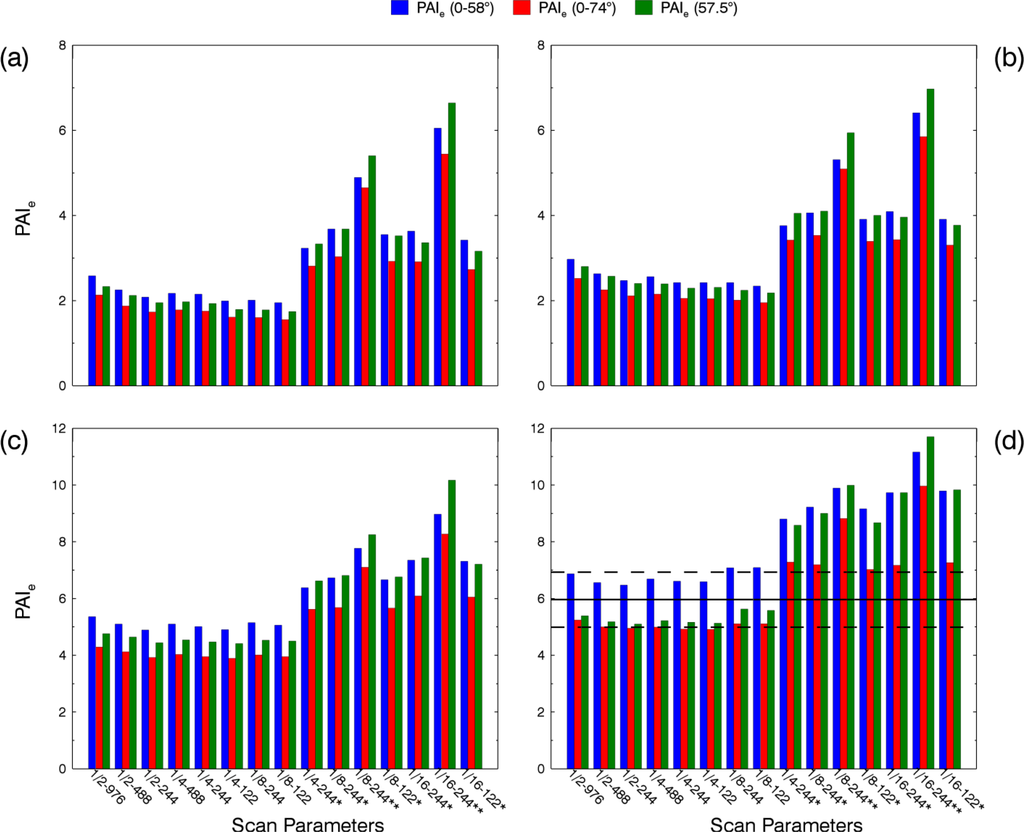
Figure 9.
Effective PAI based on the scans collected at the Oak-Beech plot with different scan parameters. Leaf-off dates: (a) 24 April 2013. (b) 2 May 2013. Leaf-on dates: (c) 10 May 2013. (d) 7 June 2013. Scan parameters: Scan resolution is displayed as the fraction of the maximum scan resolution. Scan speed is displayed in kpts/s. The single and double asterisks denote scans performed with the 2-factor and 4-factor noise compression. The lines in 9 (d) depict the mean (solid line) and standard deviations (dashed lines) of the litterfall LAI for the period 2004–2008.
The effect of the noise compression level itself can be observed from the scans with parameter combinations 1/8-244 and 1/16-244 (see Table 1). Compared to the 2-factor compression, applying the 4-factor noise compression increases the PAIe by 32% and 55% (mean of the three LAI methods and in the order of the above-mentioned parameter combinations) for the leaf-off beech scans, by 9% and 17% for the leaf-on beech scans, by 42% and 76% for the leaf-off oak-beech scans, and by 17% and 28% for the leaf-on oak-beech scans.
The stronger effect for the leaf-off scans can be attributed to the larger number of gaps with noise (i.e., undetected sky points) present. Since noise compression particularly affects the gap fraction retrieved from low zenith angles (see Section 3.2), the LAI calculation methods with a stronger weighting of gap fractions from these zenith regions, PAIe (0–58°) and PAIe (57.5°), are affected by noise compression more strongly than the PAIe (0–74°): PAIe increase by 69% and 81% compared to 52% (leaf-off beech), by 76% and 88% compared to 68% (leaf-off oak-beech), by 41% and 33% compared to 12% (leaf-on beech), and by 42% and 55% compared to 30% (leaf-on oak-beech). These averages are based on the percentage deviations in PAIe of all scan pairs with comparable parameter combinations and the 2-factor noise compression. The 4-factor noise compressed scans confirm this trend. By contrast, the resolutions and measurement speeds applied in combination with the noise compression only have a marginal influence on the PAIe (Figures 8 and 9).
With regard to the effect of the scan parameters applied without noise compression, a pattern of decreasing PAIe with decreasing measurement speed and with decreasing scan resolution can be observed, in particular for the leaf-off scans. This effect is also more pronounced for the 1/2 resolution than resolutions 1/4 and 1/8, as a consequence of the observed gap fraction pattern (see Section 3.2). Concerning the different LAI calculation methods applied, the PAIe derived from the uncompressed scans decrease in the order of methods, PAIe (0–58°), PAIe (57.5°), and PAIe (0–74°). This effect is enhanced with gradual canopy closing (Figures 8 and 9). In spite of the various scan resolutions and measurement speeds applied, the PAIe estimates based on the scan parameter combinations without noise compression are quite stable, in particular taking into account the variability induced by the use of different LAI calculation methods: The mean PAIe standard deviations (standard deviations of the PAIe values from all parameter combinations without noise compression averaged for the three LAI methods) are 0.22, 0.15, 0.13, 0.16 for the beech scans, and 0.20, 0.19., 0.13, 0.19 for the oak-beech scans (in ascending order of dates). By comparison, the mean PAIe range of the LAI methods (range of the PAIe calculated with the three LAI methods averaged for all parameter combinations without noise compression) are 0.24, 0.29, 0.77, and 1.11 for the beech scans, and 0.39, 0.39, 1.05, and 1.72 for the oak-beech scans (again in ascending order of dates).
To assess whether the PAIe based on the scans with our without noise compression are closer to the “true” LAI, the mean and standard deviations of litterfall LAI for the oak-beech plot was included in the analysis (Figure 9d). As actual 2013 litterfall LAI are not yet available, and litterfall can vary considerably from year to year, the comparison with litterfall LAI is supposed to allow for an indication of trend rather than a rigorous validation. In addition, whereas litterfall actually yields a measure of foliage mass and area, the LAI derived from terrestrial laser scanning in this study represents an effective Plant Area Index (i.e., not accounting for clumping and the proportion of woody components). Based on a study of estimating LAI, clumping, and woody area index from digital hemispherical photography [45], which was carried out at a number of permanent forest monitoring sites including the two where the present study was carried out, we used an average clumping index of 0.84 along with an average woody area index of 0.2 to derive an approximate multiplication factor of 0.95 for the conversion from PAIe to LAI. Hence, LAI derived from TLS in this study are only slightly smaller than their corresponding PAIe. Despite the approximate nature of this comparison, the litterfall LAI indicate that the “true” LAI is overestimated strongly by applying noise compression, in particular considering the unrealistically high PAIe for the scans acquired during the leaf-off period (see Figures 8 and 9).
3.4. Majority Filtering
To assess the magnitude of the error of omission caused by the “clear sky” filter, an image-based majority kernel filtering was applied to all scans (see Sections 2.4 and 3.1). PAIe derived from this filtering were then compared to PAIe derived without applying the majority filtering (Table 2).

Table 2.
Percentage deviation in Plant Area Index (PAIe) caused by the majority filtering (“filtered”) in relation to the PAIe derived from the unfiltered scans (“raw”). Percentage deviation = (PAIe (filtered)—PAIe (raw))/PAIe (raw).
The results reflect the visual impression of the different scans’ range images in Figure 1 with respect to the major trend: The higher the measurement speed the greater the amount of undetected sky points. Hence, PAIe differences increase with increasing speed. This can be observed for the scans performed without noise compression during both the leaf-off and the leaf-on phase. Differences are, however, more pronounced during leaf-off due to the higher amount of gaps and therefore a higher amount of undetected sky points. The fact that the uncompressed scans with scan resolution 1/8 yield the highest PAIe differences are noteworthy, in particular considering their visual appearance (Figure 1). This might be explained by a potential erroneous removal of valid scan points at the border regions of branches and sky by the applied majority filter. This effect might be particularly enhanced for leaf-off scans with low scan resolution where a large number of coarsely depicted border regions are present.
Another trend, which can be observed in the results, is that PAIe differences are smaller for the scans with FARO’s noise compression compared to those without noise compression (Table 2). This is an indication of the efficiency of the noise compression to reduce the error of omission. With regard to the different LAI methods used, PAIe differences based on the PAIe (0–58°) and PAIe (0–74°) methods were shown to be larger than those based on the PAIe (57.5°) method (Table 2). This is easily explained by the fact that the former also include gap fractions from high zenith angles in their calculation. As these have a larger proportion of gaps compared to the zenith range around 57.5°, the PAIe (0–58°) and PAIe (0–74°) are affected more strongly by the “clear sky” filter’s error of omission.
Overall, PAIe differences between the majority filtered and unfiltered scans are relatively small (on average less than 5%), which hints at a rather marginal effect of the omission error on the PAIe estimates. However, the small differences may very well be partly due to an inefficient removal of the undetected sky points by the applied majority filter, in particular considering the dense occurrence of these points within canopy gaps of scans with very high measurement speeds (see Figure 1). An iterative filtering might help to solve this problem, however, this may also increase the potential erroneous removal of valid scan points at the border regions of branches and sky by the majority filter. Alternative approaches to deal with the “clear sky” filter’s error of omission might be devised, e.g., based on the additional color information from a simultaneous acquisition of canopy photos.
3.5. Threshold Variation
To assess the sensitivity of the PAIe estimates to changes in the intensity threshold used to separate correctly filtered sky points from falsely filtered scan points (see Sections 2.4 and 3.1), the default threshold used in this study was varied by ±5%. Results are presented separately for the leaf-off and leaf-on scans (Table 3a,b). In general, decreasing the threshold has a stronger effect on PAIe than increasing the threshold, regardless of scan parameters, LAI method, and stand structure (Table 3a,b). This is due to the characteristic low intensity distribution of sky points (see Figures 4b and 5). However, this effect seems to be dependent on the leaf development phase with much larger PAIe differences for leaf-off scans than for leaf-on scans, which indicates that for open canopies with higher ambient noise the intensity distribution of sky points tends to shift to a higher value range.

Table 3.
(a) The effect of threshold variation on the PAIe calculated from the leaf-off scans and with different LAI calculation methods. (b) The effect of threshold variation on the PAIe calculated from the leaf-on scans and with different LAI calculation methods.
Furthermore noise compressed scans tend to be less sensitive to threshold changes than uncompressed scans. This is most likely due to the strong general reduction in “clear contour” filtered scan points and erroneously “clear sky” filtered scan points as a result of the noise compression algorithm, and which results in unimodal rather than bimodal intensity histograms that are typical for the uncompressed scans (see Figure 4a,b in Section 3.1).
Another trend, which can be observed is that for the leaf-off scans the applied resolutions influence the sensitivity to threshold changes, i.e., PAIe differences increase with decreasing resolution. For the leaf-on scans this trend is less pronounced and influenced by stand structure, too. This observation hints at a combined effect of scan resolution and ambient noise on the intensity distribution of filtered scan points and therefore a different sensitivity to threshold changes. By contrast, the measurement speed exhibited no systematic sensitivity to threshold changes.
With regard to the different LAI calculation methods applied, the PAIe estimates based on the PAIe (57.5°) method and the leaf-on scans without noise compression are more sensitive to threshold variations compared to PAIe (0–58°) and PAIe (0–74°) methods (Table 3a,b). This pattern, however, could not be observed for the compressed leaf-on scans and the leaf-off scans in general. This might be explained by the fact that during the leaf-off phase, gap fractions of the lower zenith angles are generally larger compared to the leaf-on phase, and therefore less influenced by threshold changes. In addition, applying noise compression might disproportionately reduce “clear sky” and “clear contour” filtered scan points for low zenith angles, resulting in such small gap fractions that relatively small threshold variations have little effect.
Including the gap fractions of higher zenith angles into the LAI calculation seems to have a stabilizing effect with regard to the sensitivity of the PAIe estimates to threshold changes: On average (mean of the different scan parameter combinations), PAIe based on the PAIe (0–58°) and PAIe (0–74°) methods vary from −4.8% to 6.5% for the leaf-on beech scans, and from −6.1% to 7.7% for the leaf-on oak-beech scans (Table 3b). By comparison, PAIe based on the PAIe (57.5°) method vary from −11.1% to 11.2% for the leaf-on beech scans, and from −8.9% to 11.5% for the leaf-on oak-beech scans (Table 3b). This variability in the PAIe estimation induced by threshold changes shows that the threshold selection is a critical part of the proposed approach of extracting gap fraction and PAIe from phase shift FARO laser scans.
The results indicate that applying a constant threshold value for scans with different scan parameters and collected for stands with different structure and leaf development phase is not the optimal solution, as histograms represent scene-dependent scan statistics. The implementation of an automated threshold selection based on the intensity distribution of filtered scan points retrieved for each scan separately might be a potential solution. However, due to the lack of true reference data this approach cannot be validated in the present study. Besides such a validation would have to be based on the retrieved gap fraction instead of PAIe, and reference data for the size and distribution of gaps in the canopy is generally hard to obtain [3,37].
Approaches for the identification of scan pulses from canopy gaps based on the variance of neighboring scan points (with regard to range, intensity, and color information) from phase shift scans without the use of hardware filtering could be an alternative [53]. Yet again, the rigorous assessment of any such approach is hardly possible without the availability of true gap fraction reference data. When comparing the above-mentioned PAIe variability induced by changing the threshold to the variability induced by using different LAI calculation methods (see Section 3.3), threshold changes have a smaller effect than the LAI calculation itself. If, in addition the low variability induced by the different scan parameters applied without noise compression is considered, PAIe estimates based on using a constant intensity threshold of 0.3 yield reasonable values when compared to the mean long-term litterfall LAI (see Section 3.3).
4. Conclusions
This study investigated the effects of scan resolution, measurement speed, and noise compression on the retrieval of gap fraction and effective Plant Area Index from phase-shift FARO Photon 120 terrestrial laser scans. It could be demonstrated that FARO’s noise compression algorithm yields gap fractions and PAIe which deviate significantly from those based on scans without noise compression. Mean litterfall LAI were also strongly overestimated by the scans performed with noise compression.
We, therefore, conclude that while noise compression might generally help to reduce the noise in phase-shift terrestrial laser scans without affecting the retrieval of structural forest metrics such as stem diameter [54], FARO’s noise compression should not be applied for retrieving gap fraction and related structural metrics such as the PAIe. The parameters, scan resolution and measurement speed, were shown to influence the retrieval of these metrics, too. However, the magnitudes of these effects proved to be smaller than the effect of noise compression, and proved to depend on zenith, leaf development phase, stand structure, and LAI calculation method.
Nevertheless, the overall PAIe estimates based on the scan parameter combinations without noise compression exhibited a relative stability, in spite of the various scan parameter combinations applied. This conclusion was drawn from the fact that the variation in the PAIe estimation induced by the scan resolutions and measurement speeds applied without noise compression was significantly lower than the variation induced by applying different LAI calculation methods. This gives confidence in using phase-shift TLS for a reliable and consistent retrieval of gap fraction as the base for estimating PAIe.
It could also be demonstrated that scans performed with high measurement speeds (978 and 488 kpt/s) are especially prone to noise when FARO’s “clear sky” and “clear contour” filters are applied. The post-processing filtering approach applied in this study could reduce this noise to some effect, but, due to the lack of a true gap fraction reference, it could not be properly assessed. Unless any such post-processing approach is proven to be effective and working, we suggest performing phase-shift FARO scans with lower measurement speeds (244 and 122 kpt/s) to reduce this type of noise.
While the proposed approach of identifying sky points from hardware filtered FARO scans by using a constant intensity threshold yielded reasonable PAIe when compared to the mean long-term litterfall LAI, the implementation of a variable threshold selection based on each scan’s specific intensity distribution might be a better solution. Considering that the hardware filters are mostly company secret and were not developed for specialized applications, such as vegetation structural analysis, developing specialized filters for raw scan data would probably be most appropriate. However, the availability of gap fraction reference data is crucial for the rigorous assessment of any such approach, including 3-D based approaches.
Above all, more research is required to investigate the effects of scan parameters for different phase-shift laser scanners as well as the effects of different scanner properties, most notably the ranging principle, on the retrieval of gap fraction and LAI. Compared to the passive-optical instruments such as the LI-COR PCA or digital hemispherical photography, TLS offers a number of advantages, e.g., the improved characterization of clumping due to the 3D information, or the lower sensitivity to variable sky illumination.
Due to the technical progress in the field of terrestrial and mobile laser scanning, the information content provided by the laser scanners is steadily increasing (e.g., multi-spectral lasers, UAV-based applications), which will greatly enhance the retrieval of structural forest metrics, such as the separation of woody from non-woody vegetation components. With decreasing costs, increasing scanner operability (reduction in size and weight, longer battery lives, etc.), and with increasing research corroborating the reliable and consistent retrieval of structural forest metrics, there is a good chance that TLS will be routinely applied in forest inventory and as a tool for collecting reference data to, e.g., validate airborne and satellite based remote sensing data.
Acknowledgments
The authors would like to thank T. Udelhoven for providing the FARO Photon 120 and A. Lewien and family for support with the logistics of the field campaign. The authors would also like to thank the anonymous reviewers whose valuable comments helped to improve the quality of the manuscript.
Author Contributions
Pyare Pueschel is the principal author of this manuscript responsible for the research concept, the collection, analysis and interpretation of the data, and for writing major portions of the manuscript. Glenn Newnham provided IDL code for the processing of raw scan data, contributed to the discussion and interpretation of results, and contributed some portions of the written manuscript. Joachim Hill contributed to the research concept and to the discussion of results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Parker, G.G. Structure and Microclimate of Forest Canopies. In Forest Canopies: A Review of Research on a Biological Frontier; Lowman, M., Nadkarni, N., Eds.; Academic Press: San Diego, CA, USA, 1995; pp. 73–106. [Google Scholar]
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ 1992, 15, 421–429. [Google Scholar]
- Jupp, D.L.B.; Culvenor, D.S.; Lovell, J.L.; Newnham, G.J.; Strahler, A.H.; Woodcock, C.E. Estimating forest LAI profiles and structural parameters using a ground-based laser called Echidna®. Tree Physiol 2008, 29, 171–181. [Google Scholar]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination: Part I. Theories, sensors and hemispherical photography. Agric. For. Meteorol 2004, 121, 19–35. [Google Scholar]
- Warren Wilson, J. Inclined point quadrats. New Phytol 1960, 59, 1–8. [Google Scholar]
- Seidel, D. Terrestrial Laser Scanning: Applications in Forest Ecological Research. PhD Thesis, Georg-August Universität, Göttingen, Germany. 2011. [Google Scholar]
- Zheng, G.; Moskal, L.M. Retrieving leaf area index (LAI) using remote sensing: Theories, methods and sensors. Sensors 2009, 9, 2719–2745. [Google Scholar]
- Weiss, M.; Baret, F.; Smith, G.J.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination: Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol 2004, 121, 37–53. [Google Scholar]
- Strahler, A.H.; Jupp, D.L.B.; Woodcock, C.E.; Schaaf, C.B.; Yao, T.; Zhao, F.; Yang, X.; Lovell, J.; Culvenor, D.; Newnham, G. Retrieval of forest structural parameters using a ground-based lidar instrument (Echidna®). Can. J. Remote Sens 2008, 34, S426–S440. [Google Scholar]
- Guang, Z.; Moskal, L.M.; Soo-Hyung, K. Retrieval of effective leaf area index in heterogeneous forests with terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens 2013, 51, 777–786. [Google Scholar]
- Ramirez, F.; Armitage, R.; Danson, F. Testing the application of terrestrial laser scanning to measure forest canopy gap fraction. Remote Sens 2013, 5, 3037–3056. [Google Scholar]
- Zhao, F.; Yang, X.; Schull, M.A.; Román-Colón, M.O.; Yao, T.; Wang, Z.; Zhang, Q.; Jupp, D.L.B.; Lovell, J.L.; Culvenor, D.S. Measuring effective leaf area index, foliage profile, and stand height in New England forest stands using a full-waveform ground-based lidar. Remote Sens. Environ 2011, 115, 2954–2964. [Google Scholar]
- Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial lidar technology in forest science: Application fields, benefits and challenges. Ann. For. Sci 2011, 68, 959–974. [Google Scholar]
- Newnham, G.; Armston, J.; Muir, J.; Goodwin, N.; Tindall, D.; Culvenor, D.; Püschel, P.; Nyström, M.; Johansen, K. Evaluation of Terrestrial Laser Scanners for Measuring Vegetation Structure: A Comparison of the Faro Focus 3D 120, Leica C10, Leica HDS7000 and Riegl VZ100a; CSIRO: Melbourne, Australia, 2012. [Google Scholar]
- Van Genechten, B. Theory and Practice on Terrestrial Laser Scanning: Training Material Based on Practical Applications; Santana Quintero, M., Lerma, J.L., Heine, E., van Genechten, B., Eds.; Universidad Politecnica de Valencia Editorial: Valencia, Spain, 2008. [Google Scholar]
- Simonse, M.; Aschoff, T.; Spiecker, H.; Thies, M. Automatic Determination of Forest Inventory Parameters Using Terrestrial Laserscanning. Proceedings of the ScandLaser Scientific Workshop on Airborne Laser Scanning of Forests, Umea, Sweden, 3–4 September 2003.
- Aschoff, T.; Spiecker, H. Algorithms for the automatic detection of trees in laser scanner data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 66–70.
- Maas, H.G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens 2008, 29, 1579–1593. [Google Scholar]
- Antonarakis, A.S. Evaluating forest biometrics obtained from ground lidar in complex riparian forests. Remote Sens. Lett 2011, 2, 61–70. [Google Scholar]
- Bienert, A.; Scheller, S.; Keane, E.; Mullooly, G.; Mohan, F. Application of Terrestrial Laser Scanners for the Determination of Forest Inventory Parameters. Proceedings of the ISPRS Commission V Symposium “Image Engineering and Vision Metrology”, Dresden, Germany, 25–27 September 2006.
- Lovell, J.L.; Jupp, D.L.B.; Newnham, G.J.; Culvenor, D.S. Measuring tree stem diameters using intensity profiles from ground-based scanning lidar from a fixed viewpoint. ISPRS J. Photogramm. Remote Sens 2011, 66, 46–55. [Google Scholar]
- Tansey, K.; Selmes, N.; Anstee, A.; Tate, N.J.; Denniss, A. Estimating tree and stand variables in a Corsican pine woodland from terrestrial laser scanner data. Int. J. Remote Sens 2009, 30, 5195–5209. [Google Scholar]
- Pueschel, P.; Newnham, G.; Rock, G.; Udelhoven, T.; Werner, W.; Hill, J. The influence of scan mode and circle fitting on tree stem detection, stem diameter and volume extraction from terrestrial laser scans. ISPRS J. Photogramm. Remote Sens 2013, 77, 44–56. [Google Scholar]
- Yao, T.; Yang, X.; Zhao, F.; Wang, Z.; Zhang, Q.; Jupp, D.; Lovell, J.; Culvenor, D.; Newnham, G.; Ni-Meister, W. Measuring forest structure and biomass in New England forest stands using Echidna ground-based lidar. Remote Sens. Environ 2011, 115, 2965–2974. [Google Scholar]
- Holopainen, M.; Vastaranta, M.; Kankare, V.; Räty, M.; Vaaja, M.; Liang, X.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Viitala, R. Biomass Estimation of Individual Trees Using Stem and Crown Diameter TLS Measurements. Proceedings of the 2011 ISPRS Workshop Laser Scanning, Calgary, AB, Canada, 29–31 August 2011; XXXVIII-5/W12.
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens 2013, 75, 64–75. [Google Scholar]
- Béland, M.; Baldocchi, D.D.; Widlowski, J.-L.; Fournier, R.A.; Verstraete, M.M. On seeing the wood from the leaves and the role of voxel size in determining leaf area distribution of forests with terrestrial lidar. Agric. For. Meteorol 2014, 184, 82–97. [Google Scholar]
- Eitel, J.U.H.; Vierling, L.A.; Long, D.S. Simultaneous measurements of plant structure and chlorophyll content in broadleaf saplings with a terrestrial laser scanner. Remote Sens. Environ 2010, 114, 2229–2237. [Google Scholar]
- Henning, J.G.; Radtke, P.J. Ground-based laser imaging for assessing three-dimensional forest canopy structure. Photogramm. Eng. Remote Sens 2006, 72, 1349–1358. [Google Scholar]
- Van der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Muys, B.; Coppin, P. Assessment of light environment variability in broadleaved forest canopies using terrestrial laser scanning. Remote Sens 2010, 2, 1564–1574. [Google Scholar]
- Bittner, S.; Gayler, S.; Biernath, C.; Winkler, J.B.; Seifert, S.; Pretzsch, H.; Priesack, E. Evaluation of a ray-tracing canopy light model based on terrestrial laser scans. Can. J. Remote Sens 2012, 38, 619–628. [Google Scholar]
- Zhao, F.; Strahler, A.H.; Schaaf, C.L.; Yao, T.; Yang, X.; Wang, Z.; Schull, M.A.; Román, M.O.; Woodcock, C.E.; Olofsson, P. Measuring gap fraction, element clumping index and LAI in Sierra forest stands using a full-waveform ground-based lidar. Remote Sens. Environ 2012, 125, 73–79. [Google Scholar]
- Clawges, R.; Vierling, L.; Calhoon, M.; Toomey, M. Use of a ground-based scanning lidar for estimation of biophysical properties of western larch (larix occidentalis). Int. J. Remote Sens 2007, 28, 4331–4344. [Google Scholar]
- Yang, X.; Strahler, A.H.; Schaaf, C.B.; Jupp, D.L.B.; Yao, T.; Zhao, F.; Wang, Z.; Culvenor, D.S.; Newnham, G.J.; Lovell, J.L. Three-dimensional forest reconstruction and structural parameter retrievals using a terrestrial full-waveform lidar instrument (Echidna®). Remote Sens. Environ 2013, 135, 36–51. [Google Scholar]
- Moskal, L.M.; Zheng, G. Retrieving forest inventory variables with terrestrial laser scanning (TLS) in urban heterogeneous forest. Remote Sens 2011, 4, 1–20. [Google Scholar]
- Hosoi, F.; Omasa, K. Voxel-based 3-D modeling of individual trees for estimating leaf area density using high-resolution portable scanning lidar. IEEE Trans. Geosci. Remote Sens 2006, 44, 3610–3618. [Google Scholar]
- Côté, J.-F.; Widlowski, J.-L.; Fournier, R.A.; Verstraete, M.M. The structural and radiative consistency of three-dimensional tree reconstructions from terrestrial lidar. Remote Sens. Environ 2009, 113, 1067–1081. [Google Scholar]
- Huang, P.; Pretzsch, H. Using terrestrial laser scanner for estimating leaf areas of individual trees in a conifer forest. Trees 2010, 24, 609–619. [Google Scholar]
- Danson, F.; Armitage, R.; Bandugula, V.; Ramirez, F.; Tate, N.; Tansey, K.; Tegzes, T. Terrestrial Laser Scanners to Measure Forest Canopy Gap Fraction. Proceedings of the 8th SilviLaser, Edinburgh, Scotland, 17–19 September 2008.
- Danson, F.M.; Hetherington, D.; Morsdorf, F.; Koetz, B.; Allgower, B. Forest canopy gap fraction from terrestrial laser scanning. IEEE Geosci. Remote Sens. Lett 2007, 4, 157–160. [Google Scholar]
- Zheng, G.; Moskal, L.M. Spatial variability of terrestrial laser scanning based leaf area index. Int. J. Appl. Earth Obs. Geoinf 2012, 19, 226–237. [Google Scholar]
- Calders, K.; Verbesselt, J.; Bartholomeus, H.; Herold, M. Applying Terrestrial Lidar to Derive Gap Fraction Distribution Time Series During Bud Break. Proceedings of the SilviLaser 2011, 11th International LiDAR Forest Applications Conference, Hobart, Australia, 16–20 October 2011.
- FARO, Faro Laser Scanner Photon 20/120 User’s Manual; FARO: Korntal-Münchingen, Germany, 2010.
- Hilker, T.; Leeuwen, M.; Coops, N.; Wulder, M.; Newnham, G.; Jupp, D.B.; Culvenor, D. Comparing canopy metrics derived from terrestrial and airborne laser scanning in a Douglas-fir dominated forest stand. Trees 2010, 24, 819–832. [Google Scholar]
- Greve, M. Vergleich von Methoden zur Erhebung des Blattflächenindex in Wäldern (In German)/Comparison of Methods for the Estimation of Leaf Area Index in Forests. M.Sc. Thesis, University of Trier, Trier, Germany. 2010. [Google Scholar]
- Ross, J.K. The Radiation Regime and Architecture of Plant Stands; Junk Publishers: The Hague, The Netherlands, 1981; p. 391. [Google Scholar]
- Black, T.A.; Chen, J.-M.; Lee, X.; Sagar, R.M. Characteristics of shortwave and longwave irradiances under a Douglas-fir forest stand. Can. J. For. Res 1991, 21, 1020–1028. [Google Scholar]
- Miller, J.B. A formula for average foliage density. Aust. J. Bot 1967, 15, 141–144. [Google Scholar]
- LI-COR Inc, LAI-2000 Plant Canopy Analyzer. Instruction Manual; LICOR Inc: Lincoln, NE, USA, 1992.
- Chen, J.M.; Govind, A.; Sonnentag, O.; Zhang, Y.; Barr, A.; Amiro, B. Leaf area index measurements at Fluxnet-Canada forest sites. Agric. For. Meteorol 2006, 140, 257–268. [Google Scholar]
- Leblanc, S.G.; Chen, J.M. A practical scheme for correcting multiple scattering effects on optical LAI measurements. Agric. For. Meteorol 2001, 110, 125–139. [Google Scholar]
- Wilson, J.W. Analysis of the spatial distribution of foliage by two-dimensional point quadrats. New Phytol 1959, 58, 92–101. [Google Scholar]
- Newnham, G.; Mashford, J.; Püschel, P.; Armston, J.; Culvenor, D.; Siggins, A.; Nyström, M.; Goodwin, N.; Muir, J. Non-Parametric Point Classification for Phase-Shift Laser Scanning. Proceedings of the SilviLaser 2012, Vancouver, BC, Canada, 16–19 September 2012.
- Pueschel, P. The influence of scanner parameters on the extraction of tree metrics from faro photon 120 terrestrial laser scans. ISPRS J. Photogramm. Remote Sens 2013, 78, 58–68. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).