Abstract
In this paper, we aim to detect crop injury from glyphosate, a herbicide, by both traditionally used spectral indices and newly extracted features with leaf hyperspectral reflectance data for non-Glyphosate-Resistant (non-GR) soybean and non-GR cotton. The new features were extracted by canonical analysis technique, which could provide the largest separability to distinguish the injured leaves from the healthy ones. Spectral bands used for constructing these new features were selected based on the sensitivity analysis results of a physically-based leaf radiation transfer model (leaf optical PROperty SPECTra model, PROSPECT), which could help extend the effectiveness of these features to a wide range of leaf structures and growing conditions. This approach has been validated with greenhouse measured data acquired in glyphosate treatment experiments. Results indicated that glyphosate injury could be detected by NDVI (Normalized Difference Vegetation Index), RVI (Ratio Vegetation Index), SAVI (Soil Adjusted Vegetation Index), and DVI (Difference Vegetation Index) in 48 h After the Treatment (HAT) for soybean and in 72 HAT for cotton, but the other spectral indices either showed little use for separation, or did not show consistent separation for healthy and injured soybean and cotton. Compared with the traditional spectral indices, the new features were more feasible for the early detection of glyphosate injury, with leaves sprayed with a higher rate of glyphosate solution having larger feature values. This trend became more and more pronounced with time. Leaves sprayed with different glyphosate rates showed some separability 24 HAT using the new features and could be totally distinguished at and beyond 48 HAT for both soybean and cotton. These findings demonstrated the feasibility of applying leaf hyperspectral reflectance measurements for the early detection of glyphosate injury using these newly proposed features.
1. Introduction
With the increased use of glyphosate as an herbicide in Glyphosate-Resistant (GR) cropping systems, glyphosate drift has been of particular concern in recent years [1]. When glyphosate is applied to GR crops, its drift onto off-target sensitive crops such as non-Glyphosate-Resistant (non-GR) soybean and non-GR cotton, may cause injury, significant reduction in yield or quality, or even mortality [2]. About 30 cases of herbicide drift onto non-target crops are reported in Mississippi each year, with more than 70% of these caused by glyphosate [3].
Many studies have indicated that foliar biochemistry would change as a result of glyphosate treatment. Reddy et al. [4] found that glyphosate application on non-GR soybean could induce reduction of leaf chlorophyll content and decrease nodule biomass and leghemoglobin content. Koger et al. [5] found that visual injury and plant height reduction could be observed for rice within seven days after glyphosate treatment. More recently, Reddy et al. [6] reported that, in an aerial glyphosate drift experiment, chlorophyll reduction is about 80% for non-GR soybean leaves sprayed with 0.866 kg·ae/ha glyphosate solution, and higher than 40% for non-GR cotton leaves within one week after treatment. These changes could be attributed to the biochemical effects of glyphosate. When glyphosate is applied to non-GR crops, it will be metabolized by plants via pathways similar to those in certain microorganisms [7]. Aminomethylphosphonic acid, the main metabolite of glyphosate, will be found in the leaves of these glyphosate treated plants [8]. It exhibits a half-life of 25–75 days and is known to cause chlorosis of leaves, which would cause a continuing injury to non-GR plants [9]. Therefore, foliar biochemistry is a potential indicator of glyphosate injury for non-GR crops, and the leaf injuries from glyphosate are always accompanied by reduction of chlorophyll content.
For the early detection of crop injury from off-target drift of glyphosate, reflectance spectra are ideal indicators because subtle changes of leaves’ interior structure and growth status caused by stress factors could induce the abnormalities in the spectrum [2,10]. For many years hyperspectral reflectance measurements have been widely and successfully applied to monitor the vitality and stresses of crops [11–13]. Based on hyperspectral data, many spectral indices have been proposed and used for crop health assessment and stress detection, including vegetation indices, derivative analysis features and continuous removal transformed features [14–17]. In a study aiming to develop a narrow waveband spectral index for assessing the physiological state of sunflowers, Gamon et al. [18] proposed a hyperspectral index (PRI, Physiological Reflectance Index) which was well correlated with the epoxidation state of the xanthophyll cycle pigments in order to study the diurnal changes of nitrogen- and water-stressed sunflower leaves. Based on Gamon’s work, Peñuelas et al. [19] further investigated the association between nitrogen- and water-stressed sunflower leaves and a larger group of spectral indices including a priori physiological indices (PRI, for example), multivariate indices (PC1, first Principal Component), and derivative analysis indices (dG, maximum of the first derivative of reflectance in the Green). It was found that these indices were well associated with leaf diurnal physiological status and each spectral index had its own advantages in plant stress monitoring. More recently, as an emerging method for spectral and time series analysis, wavelet analysis was used by Blackburn and Ferwerda [20] and Cheng et al. [21] to relate extracted wavelet features with leaf chlorophyll concentration and water content, respectively, for monitoring the general physiological status of plant leaves, and achieved encouraging results.
For glyphosate-induced crop injury detection, similar methods were introduced in recent years. For example, an airborne glyphosate drift experiment was conducted in 2009 to identify the effects of aerially applied glyphosate on cotton plants, and NDVI images were mapped for damage assessment [22]. In a glyphosate injury detection experiment at the leaf scale carried out in the greenhouse, Huang et al. [2] used hyperspectral reflectance data to distinguish glyphosate injured soybean and cotton from the healthy ones by calculating vegetation indices including NDVI (Normalized Difference Vegetation Index), RVI (Ratio Vegetation Index), SAVI (Soil Adjusted Vegetation Index), and DVI (Difference Vegetation Index) for each leaf. Also for the soybean planted in a greenhouse environment, Yao et al. [23] verified that hyperspectral imaging of plant canopy reflectance could be a useful tool for early detection of soybean crop injury due to glyphosate application, and that spectral derivative analysis proved to be better than the vegetation indices. From these studies we can see that the detection of glyphosate injury by spectral analysis is still in the phase of feasibility study, and most experiments were performed in a controllable greenhouse to alleviate other stress factors, e.g., water, temperature and pest. However, since the vegetation indices and derivative indices used in these studies were not specifically designed for glyphosate-induced leaf stress detection and may not be suitable for this problem, a more thorough investigation is needed.
In this study, we study the early detection of glyphosate-induced crop injury with leaf hyperspectral reflectance data. The changes in leaf spectral response after the spray of glyphosate are quantitatively assessed by examining the temporal trends of several hyperspectral and derivative indices and proposing a new spectral analytical approach for glyphosate injury detection. Five spectral bands, which are potentially more informative of leaf living status, are selected based on the sensitivity analysis result of a physically-based leaf Radiation Transfer (RT) model (leaf optical PROperty SPECTra model, PROSPECT) [24]. A spectral transformation technique named canonical analysis is introduced as a feature extraction procedure for generating new spectral features from the selected spectral bands. The traditionally used spectral indices and the newly extracted features are then tested by greenhouse datasets containing simultaneous biochemical and reflectance measurements from glyphosate treatment experiments. Finally, the results and effectiveness of the methods are compared and analyzed.
2. Methodology
2.1. Experiment Design and Data Measurement
The experiment was conducted in a greenhouse located at the USDA-ARS Crop Production Systems Research Unit, Stoneville, Mississippi on 17–20 December 2012, and repeated 4–7 February 2013. The growth conditions for the plants were under control with temperature maintained at 23.9 °C during the daytime and 21.1 °C during the nighttime. Four weeks after being planted, the plants were treated and measured for spectral reflectance. The four week schedule was determined by weed scientists to simulate the situation in field to effectively control weeds. Complete Randomized Design (CRD) was used in the experiments to analyze the effect of glyphosate with minimum confounding factors arising from other uncertainties.
In each experiment, 36 pots of non-GR cottons (cultivar FM955LL) and 36 pots of non-GR soybeans (cultivar SO80120LL) were used to obtain leaf reflectance spectra and foliar biochemical properties. For each crop, the pots were randomly divided into 3 treatment groups: 12 pots were sprayed with 0.433 kg·ae/ha solution of glyphosate (0.5X group; X = 0.866 kg·ae/ha, which is the label rate of the commercial glyphosate we used); another 12 pots were sprayed with half of the 0.5X dose (0.25X group); the remaining 12 pots were used as controls with no glyphosate treatment (CTRL group). Glyphosate solutions were prepared using a commercial formulation of the potassium salt of glyphosate (Roundup WeatherMax, Monsanto Agricultural Co., St. Louis, MO), and applied using a CO2-pressurized backpack sprayer that delivered 140 L/ha of spray solution at 193 kPa. After the glyphosate spray, leaf reflectance and biochemical parameters (detailed explanations in Section 2.3): Chlorophyll content (Chl), Equivalent Water Thickness (EWT) and Leaf Mass per Area (LMA) of three plants for each group were measured at 6, 24, 48, 72 h After the Treatment (HAT) to study plant response to glyphosate.
Leaf reflectance measurements were acquired by using an ASD integrating sphere apparatus (as shown in Figure 1) coupled with the ASD FieldSpec 3 Hi-Res spectroradiometer (ASD Inc., Boulder, CO, USA), yielding a 1 nm spectral sampling interval in the visible to near-infrared spectral range (400–2,500 nm). Connected with the integrating sphere, Spare Lamps (Qty 2, Osram #64225, 6 V, 10 W) provided a collimated beam as the light source, which illuminated the sample or the Reference Standard.
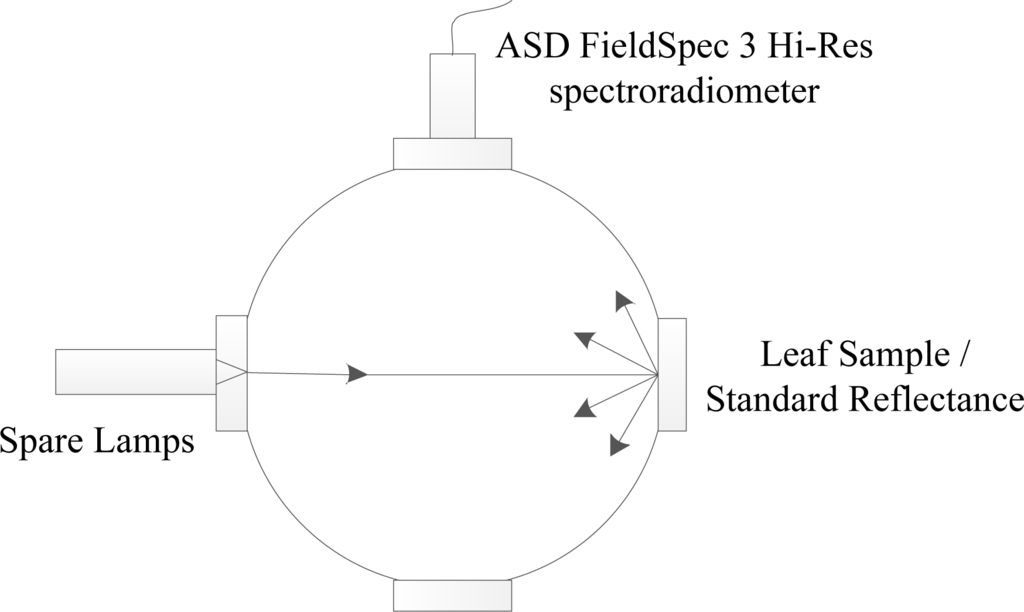
Figure 1.
Sketch of the ASD integrating sphere apparatus.
The reflectance of leaf sample was measured following the procedure described in the manual of ASD integrating sphere [25] in which three measurements are required: sample measurement (Is), stray light measurement (Id), and Reference Standard measurement (Ir). These spectra were collected in raw DN (Digital Number) mode. An integration time of 544 ms was used for all the measurements. With the known reflectance of the Reference Standard, Rr, the reflectance of the sample for a given center wavelength and spectral bandpass, Rs, is calculated as follows:
One of the lowermost trifoliate leaves for soybean and twin leaves for cotton were selected for the measurements of the reflectance. These leaves were identified before the glyphosate treatment to make sure leaves at the same position of each plant were used for all four days. The leaves were large enough to cover the port of the integrating sphere. The location of the leaf sample changed three times during the measurement (avoiding main veins of the leaf in the port) to acquire the mean spectrum of the leaf.
After the leaf reflectance measurement, the leaf sample’s area was immediately measured using a LI-COR 3100 Area Meter (LI-COR, Inc., Lincoln, NE, USA). Then it was dropped into the vial with DiMethyl SulfOxide (DMSO) and covered with aluminum foil. After 24 h in the dark environment, the solution was used for Chl analysis using a Shimadzu UV160U Spectrophotometer (Shimadzu Corp., Kyoto, Japan). In order to calculate EWT and LMA, the remaining leaves of the plants were scanned to determine the Leaf Area (LA) and weighed to measure their Fresh Weight (FW). Then they were oven-dried at 45–50 °C for 48 h, and reweighed to determine the Dry Weight (DW). The EWT and LMA were calculated as follows:
Leaf biochemical measurements of soybean and cotton leaves acquired in the first and second experiments were summarized in Tables 1 and 2, respectively. In each experiment, the mean values and standard deviations of the biochemical parameters were derived from 3 leaves in the same group. The separation analysis of the mean values was conducted using Duncan’s multiple range test (please refer to Section 3.1 for details). These two experiments are identical in experimental design and growing conditions. The datasets acquired in the first and second experiment were denoted as Dataset I and Dataset II, respectively.

Table 1.
Leaf biochemical measurements of soybean and cotton leaves acquired in the first experiment conducted on 17–20 December 2012. The mean values and standard deviations of the biochemical parameters (Chlorophyll content, Chl; Equivalent Water Thickness, EWT; Leaf Mass per Area, LMA) measured for each treatment group (CTRL group with no glyphosate treatment; 0.25X group treated with 0.217 kg·ae/ha solution of glyphosate; 0.5X group treated with 0.433 kg·ae/ha solution of glyphosate) at each time period after treatment (6, 24, 48, and 72 h After Treatment (HAT)) are shown in the table. The separation analysis of the mean values was conducted using Duncan’s multiple range test.*

Table 2.
Leaf biochemical measurements of soybean and cotton leaves acquired in the second experiment conducted on 4–7 February 2013. The mean values and standard deviations of the biochemical parameters (Chlorophyll content, Chl; Equivalent Water Thickness, EWT; Leaf Mass per Area, LMA) measured for each treatment group (CTRL group with no glyphosate treatment; 0.25X group treated with 0.217 kg·ae/ha solution of glyphosate; 0.5X group treated with 0.433 kg·ae/ha solution of glyphosate) at each time period after treatment (6, 24, 48, and 72 h After Treatment (HAT)) are shown in the table. The separation analysis of the mean values was conducted using Duncan’s multiple range test.*
2.2. Spectral Indices for Glyphosate Injury Detection
A total of fourteen spectral indices (as listed and explained in Table 3) were used in the study to test their usefulness in detecting crop stress caused by glyphosate application. These indices were calculated based on their proposed formulas, which were successfully used for detecting different crop stresses [19,26–28]. Some of the indices, such as NDVI, RVI, SAVI, and DVI have already been introduced as indicators of glyphosate-induced leaf injury in recent years [2,22,23].

Table 3.
Spectral indices used for crop injury detection.
2.3. Spectral Band Selection Based on Sensitivity Analysis of PROSPECT Model
The traditional method for spectral band selection is to perform correlation analysis between leaf biochemical constituents and spectral features and then select the most statistically significant spectral bands [21] or to directly choose the maximum absorption wavelengths [29]. However, this process strongly relies on characteristics of the experimental datasets, which were commonly composed of spectra from a limited number of samples, and thus would not be applicable to a wide range of species and leaf structure. Moreover, as noted by Le Maire et al. [29], these wavelengths did not always capture the most meaningful spectral information, and wavelengths in their neighborhood were usually preferred. Consequently, in the study, we selected spectral bands based on the sensitivity analysis of a leaf RT model instead of the experimental datasets, aiming to achieve a more generalized result.
Chlorophyll, water, and dry matters like cellulose and lignin that compose cell wall are fundamental biochemical constituents of plants. Their abundance in leaves is closely tied to leaf vigor, phylogenic traits such as leaf structure and photosynthetic efficiency. They are potential indicators for environmentally induced stress detection. The PROSPECT model [24,30–34] is a physically based leaf RT model that considers the leaf as a succession of absorbing layers. This model could accurately simulate leaf hemispherical reflectance and transmittance spectra in the spectral band of 400–2,500 nm as a function of leaf structure parameter (N, number of compact layers specifying the average number of air/cell wall interfaces within the mesophyll), Chl (Ca+b, chlorophyll a+b content, in unit of μg/cm2), EWT (Cw, mass of water per leaf area, in unit of g/cm2) and LMA (Cm, mass of dry matter per leaf area, in unit of g/cm2). The model has been widely used to investigate the relationship between leaf biochemical parameters and reflectance spectrum for a wide range of species during the last two decades [35]. Therefore, PROSPECT was employed in the study to investigate the sensitive spectral domains for the biochemical sensitivity test.
Sensitivity analysis investigates the response of a model to variations of its input parameters by statistically calculating a limited, but representative number of simulations [36]. Since the uncertainty in the output Y of a model can be apportioned to different sources of uncertainty in the model input Xi, the total variance Vt of the model output Y can be decomposed as
To calculate Vi, one should first estimate the Expectation (E) of Y for a fixed value of Xi (i.e., to calculate E(Y|Xi)), and then estimate the Variance (V) of E(Y|Xi) for different values of Xi, which could be expressed as
Similarly, Vi,j, Vi,j,m, … could be calculated as
and so on. For a given input variable Xi, its first order sensitivity index (SXi) and total sensitivity index (STXi) are defined as
where k refers to the total number of inputs. The first order sensitivity index gives the independent effect of the corresponding parameters, while the total sensitivity index contains both independent effect of each parameter and the interaction effects with the others.
An estimation procedure for the first order sensitivity index is the classical FAST (Fourier Amplitude Sensitivity Test), developed by Cukier et al. [37] and then systematized by Cukier et al. [38] and Koda et al. [39]. An extension to FAST was proposed by Saltelli et al. [40] for the estimation of the total sensitivity index. The advantage of the Extended FAST (EFAST) is that it allows the simultaneous computation of the first order and the total sensitivity indices for a given input variable Xi. Thus the EFAST method was employed for the following sensitivity analysis of leaf biochemical parameters. The calculations were programmed using Visual C++.
2.4. Feature Extraction Procedure
In this study, an improved spectral transformation procedure called canonical analysis [41] was used for the generation of transformed spectral features, in which the group separation is optimized. Using this procedure, a new axis can be constructed for which
(σA is the standard deviation among groups and σB is the standard deviations within the groups) is as large as possible, and thus the largest possibility will be generated to discriminate injured leaves from healthy ones.
Given one particular transformation vector d, which defines the first canonical axis (FCA), and the groups that will be optimally separated, the corresponding within-group and among-group variances can be defined as
where A is among-group covariance matrix and B is within-group covariance matrix.
In order to determine the transformation vector d, λ should be maximized, which is defined as
which is equivalent to solving the following equation
This equation is a generalized eigenvalue equation and could be solved for the unknown eigenvalue λ and eigenvector d. The FCA will be in the direction of d and λ will give the associated ratio of among-group to within-group variance along that axis.
The canonical analysis can provide good separability with reduced dimensionality. When choosing the FCA corresponding to the largest λ, as the extracted feature for glyphosate injury detection, the groups will have maximum separation. In this study, the canonical analysis was programmed using Visual C++.
2.5. Statistical Analysis
The mean values of the leaf biochemical contents, spectral indices and FCA features of CTRL, 0.25X, and 0.5X groups at 6, 24, 48, and 72 HAT respectively were calculated. Each mean value was averaged from six leaves in the same group across the two experiments. A one-way Analysis Of Variance (ANOVA) with Duncan’s multiple range test with a p-value of 0.05 was applied to differentiate these mean values. SPSS 19 Statistics (SPSS Inc., Chicago, IL, USA) was used for the analysis. Moreover, linear discriminant analysis was implemented for each time period after treatment with MATLAB 7.12.0 (R2011a) (Mathworks Inc., Natick, MA, USA).
To test the effectiveness of the newly extracted FCA features, a two-fold cross validation scheme was used in this analysis, with all data in Dataset I and II of the same group and HAT being randomly divided into two parts (denoted as Part I and Part II). One part was used as calibration dataset for FCA feature extraction, and the other used as validation dataset for Duncan’s multiple range test and linear discriminant analysis. This process was performed twice with Part I for calibration and Part II for validation (Round I) firstly, followed by Part II for calibration and Part I for validation (Round II).
3. Results and Discussion
3.1. Variations in Leaf Biochemical Contents after Treatment
From the leaf biochemical parameters of soybean and cotton presented in Tables 1 and 2, it can be seen that Chl of the three groups indicated different trends after the treatment, with leaves treated with higher dose showing a more rapid decrease in Chl. The EWT and LMA were relatively stable. Mean values of the leaf biochemical contents were calculated across the two experiments (Tables 1 and 2). Duncan’s multiple range tests were applied to differentiate these mean values. Results showed that means of Chl were significantly different between each group at and beyond 48 HAT for both soybean and cotton, whereas the EWT and LMA showed no significant difference during 6–72 HAT. This indicated that, compared with EWT and LMA, Chl was more responsive to the glyphosate-induced crop injury.
3.2. Variations in Spectral Indices after Treatment
The mean values of spectral indices calculated for soybean and cotton leaves are presented in Tables 4 and 5, respectively. Duncan’s multiple range tests (p = 0.05) were performed to examine the separability of these values. By contrasting the three groups with different treatments at 6, 24, 48, 72 HAT, it was found that for soybean, the NDVI, RVI, SAVI, and DVI of 0.25X and 0.5X groups were significantly different from that of the CTRL group at 48 HAT, but there was no significant difference between the 0.25X group and 0.5X group. At 72 HAT for soybean, the three groups could be totally distinguished from each other at the 0.05 level by NDVI and RVI. For cotton, the NDVI, RVI, SAVI, and DVI of 0.25X and 0.5X groups were significantly different from those of CTRL group only at 72 HAT. PRI values showed a distinguishable difference among the three soybean groups at 48 and 72 HAT. But for cotton, PRI failed to show a significant difference among different groups, except at 48 HAT. NPCI showed a similar result as PRI for both soybean and cotton. The WRE of CTRL group also showed significant difference from the 0.25X and 0.5X group at 72 HAT for soybean, but there was no similar result for cotton. Besides NDVI, RVI, SAVI, DVI, PRI, NPCI, and WRE, the other spectral indices did not indicate useful information for distinguishing injured leaves from healthy ones for both soybean and cotton leaves.

Table 4.
Calculated spectral indices of the three groups of soybean leaves at 6, 24, 48, 72 HAT. Each value is a mean of six leaves. The separation results are based on the Duncan’s multiple range test.*

Table 5.
Calculated spectral indices of the three groups of cotton leaves at 6, 24, 48, 72 HAT. Each value is a mean of six leaves. The separation results are based on the Duncan’s multiple range test.*
3.3. FCA Feature Extraction
In the sensitivity analysis test of PROSPECT model, ranges of Ca+b, Cw, and Cm were defined as 2.8086–19.106 μg/cm2, 0.0098–0.0267 g/cm2 and 0.0018–0.0045 g/cm2, respectively, since the ranges could cover all greenhouse measured values in Dataset I and Dataset II. N was assigned a reasonable range of 1–4, which could describe a wide range of mesophyll structures of different leaf species. A thousand combinations of the parameters were randomly selected from their ranges as the inputs and 1,000 reflectance spectra were produced from model simulation. All the simulated spectral reflectance combined with the corresponding selected values of input parameters were used as input data for the test. The results of the PROSPECT sensitivity analysis of leaf biochemical parameters are shown in Figure 2. It was found that N was the most sensitive parameter within the entire spectral region from 400 nm to 2,500 nm, and was relatively more sensitive in the near-infrared range (670–1,300 nm). Ca+b was the most sensitive parameter in the visible bands (400–670 nm), with low sensitivity in other bands. Cw was comparatively more sensitive in the shortwave-infrared band (1,300–2,500 nm), especially at the wavelengths corresponding to the water absorption peaks. Cm was a relatively insensitive parameter with sensitivities lower than 0.2 at most wavelengths. These results are consistent with the former studies [24,42].
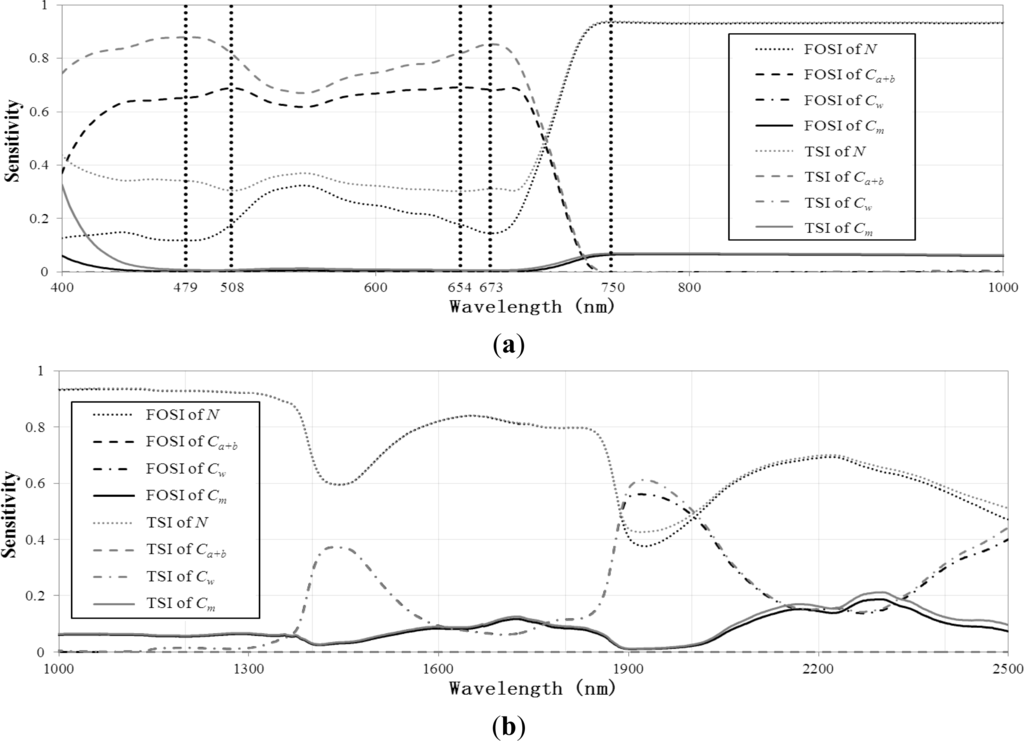
Figure 2.
Sensitivity indices of PROSPECT input parameters simulated by EFAST (Extended Fourier Amplitude Sensitivity Test) method. (a) 400–1,000 nm, (b) 1,000–2,500 nm. FOSI: First Order Sensitivity Index, TSI: Total Sensitivity Index. The spectral positions of these selected bands (479, 508, 654, 673, 750 nm) are marked with vertical dotted lines.
Then five potentially informative bands were selected based on the sensitivity analysis of the leaf biochemical parameters for extracting new spectral features. From the statistical analysis of leaf biochemical contents presented in Section 3.1, we could conclude that Chl was a potential indicator of glyphosate injury. Therefore, two bands, 479 nm and 508 nm, located in the blue domain corresponding to peaks of first order and total sensitivity index curves of Ca+b respectively were selected (Figure 2a). Similarly, two other bands, 654 nm and 673 nm, located at the peaks in the red domain were selected. In the near-infrared domains, leaf structural parameter N, Cw and Cm are more sensitive (Figure 2). Since EWT and LMA of the three groups showed no significant difference 6–72 HAT, only the band for N was considered in this domain. Corresponding to the peaks of the first order and total sensitivity index of N positioned at the same band, the fifth band (750 nm) was selected where the chlorophyll sensitivity was close to zero. This band could potentially provide the information of leaf structure instead of chlorophyll content [43]. The locations of these selected spectral bands are shown in Figure 2a.
The reflectance values of these five selected bands were then used to construct the among-group covariance matrix (A, a 5 × 5 matrix) and the within-group covariance matrix (B, a 5 × 5 matrix). All data acquired in the two experiments (Dataset I and Dataset II) were used to construct these matrices. Then by solving Equation (13), five eigenvalues (λ) and corresponding five eigenvectors (d) were obtained. As noted before, the eigenvector with the largest eigenvalue contains the largest separability. Therefore, largest λ and the corresponding eigenvector d were used to construct the FCA features. For soybean, the largest λ was 0.22, and the corresponding eigenvector d was (0.18, 0.55, 0.76, 0.30, 0.02)T. For cotton, the largest λ was 0.18, and the corresponding eigenvector d was (0.26, 0.65, 0.64, 0.33, 0.03)T. Therefore, the FCA features (FCAs for soybean and FCAc for cotton) could be expressed by the following linear combinations of the selected five spectral bands:
where R1, R2, R3, R4, and R5 Rλ5 are the reflectance values at 479 nm, 508 nm, 652 nm, 673 nm, and 750 nm, respectively.
3.4. Leaf Stress Detection by FCA Feature
Figure 3a presents the temporal variation of FCAs for soybean leaves of all three groups. It could be seen that at 6 HAT, there were no noticeable differences among the FCAs values of the three groups, which is reasonable considering damage would not be detectable. At and beyond 24 HAT, differences appear more and more pronounced, with a consistent trend of higher spray rate exhibiting larger FCAs values. A similar trend was observed for cotton in Figure 3b, with larger differences among these three groups from 24 HAT to 72 HAT, compared with the result of soybeans.
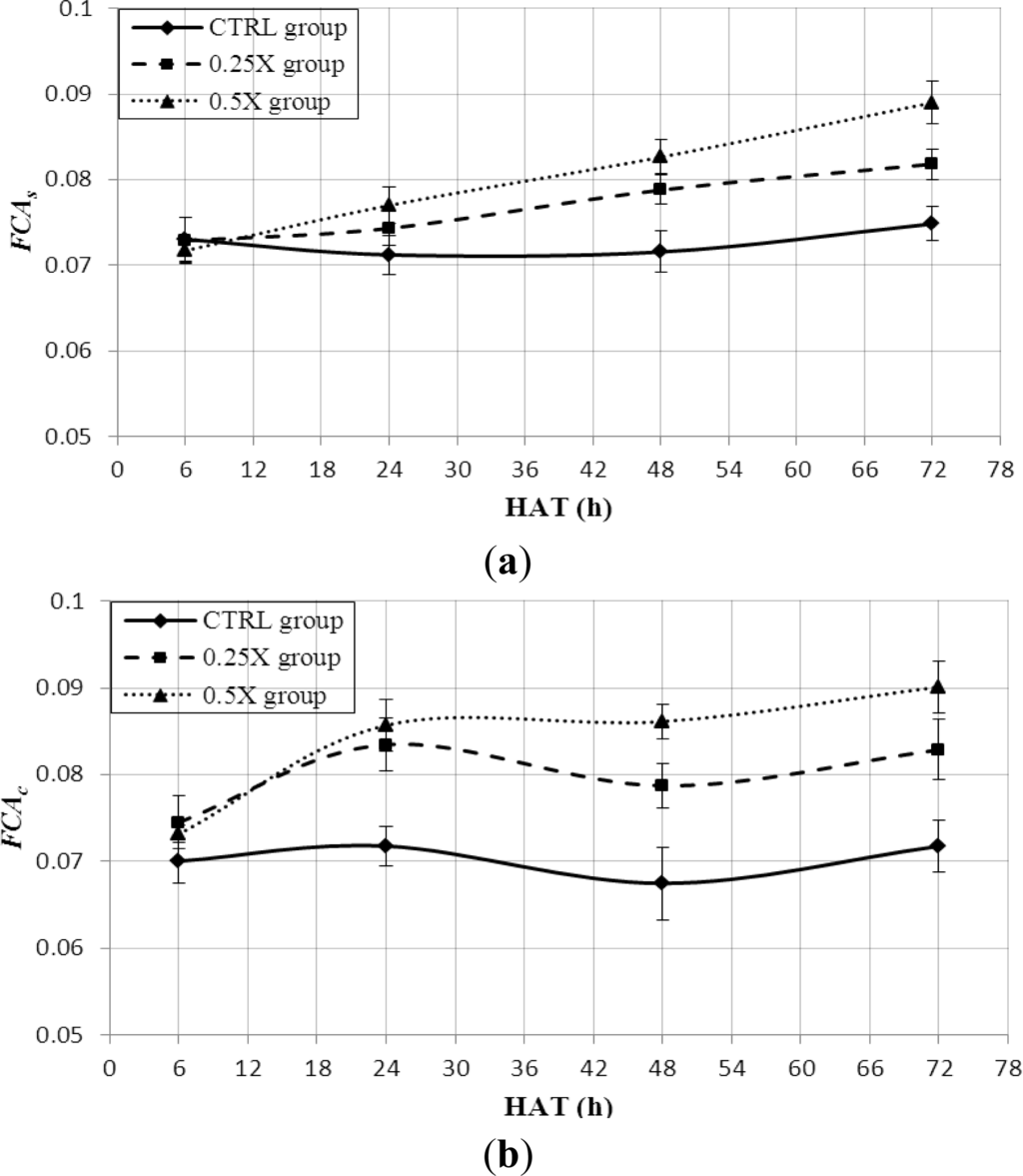
Figure 3.
(a) FCAs variation of soybean leaves of the three groups at 6, 24, 48, 72 HAT. (b) FCAc variation of cotton leaves of the three groups at 6, 24, 48, 72 HAT. Each point is a mean value of six leaves for the same treatment. Error bar presents the standard deviation of each point.
Duncan’s multiple range test (p = 0.05) results for soybean are shown in Table 6. It can be seen that the FCAs of the 0.5X group was significantly different from that of the CTRL group at 24 HAT, but the FCAs of the 0.25X group was neither significantly different from that of the CTRL group nor that of the 0.5X group. At and beyond 48 HAT, the three groups could be totally distinguished by FCAs, with significant differences. For cotton (Table 7), FCAc of 0.25X and 0.5X groups were significantly different from that of the CTRL group but not significantly different from each other. Similar to soybean, the three groups of cotton could be distinguished by FCAc at and beyond 48 HAT.

Table 6.
FCAs calculated for experimental soybean leaves of the three groups at 6, 24, 48, 72 HAT. Each value is a mean of six leaves for the same group. The statistics are analyzed by Duncan’s multiple range tests.*

Table 7.
FCAc calculated for experimental cotton leaves of the three groups at 6, 24, 48, 72 HAT. Each value is a mean of six leaves for the same group. The statistics are analyzed by Duncan’s multiple range tests*.
3.5. Cross Validation for FCA Feature
The two-fold cross validation scheme was performed by splitting the entire data set randomly into Part I and Part II as described in Section 2.5. Part I was used for FCA feature extraction and Part II was used for the validation (Round I). This process was repeated by replacing Part I with Part II (Round II).
Results of the Duncan’s multiple range tests by these processes for soybean and cotton are separately shown in Tables 8 and 9. It can be seen that, in both Round I and Round II, the three groups could be totally distinguished from each other by the FCA features for both soybean and cotton at and beyond 48 HAT, which verified the results acquired in Tables 6 and 7.

Table 8.
Cross validation results for FCAs based on Duncan’s multiple range tests*. Each value is a mean of three soybean leaves for the same group in the validation dataset.

Table 9.
Cross validation results for FCAc based on Duncan’s multiple range tests *. Each value is a mean of three cotton leaves for the same group in the validation dataset.
Then, linear discriminant analysis was implemented for each time period after treatment. The results for soybean and cotton are summarized in Tables 10 and 11, respectively. In general, classification accuracy for each treatment group increased gradually with the time (HAT). For FCAs values of soybean leaves shown in Table 10 (from 6 HAT to 48 HAT), the accuracy for each group increased from below 50% to 100%. At and beyond 48 HAT, all leaf samples could be accurately classified into the correct group. For FCAc values for cotton leaves shown in Table 11, a similar result was obtained that tended to exhibit less false classification probability with time. At 6 HAT it was difficult to differentiate the treatment groups with the FCA features. Starting from 24 HAT, accuracies of classification increased with time and reached 100% for all groups 48 HAT. These results are consistent with cross validation results of the Duncan’s multiple range tests, which illustrate that the three groups could be totally distinguished from each other by FCA features at and beyond 48 HAT.

Table 10.
Linear discriminant analysis with a two-fold cross validation schema for FCAs values of soybean leaves.

Table 11.
Linear discriminant analysis with a two-fold cross validation schema for FCAc values of cotton leaves.
3.6. Injury Detection Success by FCA Features
The relationships between the extracted FCA features (FCAs for soybean and FCAc for cotton) and the leaf chlorophyll content (in unit of μg/cm2) measured were analyzed (Figure 4). Results showed that FCA features and leaf chlorophyll content were well correlated. The correlation coefficients were 0.69 for soybean and 0.66 for cotton, and the RMSE (Root Mean Square Error) values were 1.21 μg/cm2 for soybean and 2.04 μg/cm2 for cotton. This indicated that FCA features were capable of reflecting chlorophyll reduction caused by glyphosate treatment. This could be one of the major reasons why glyphosate injury could be successfully detected by FCA features. The second main reason may be attributed to the good separability provided by canonical analysis process, since the first canonical axis, which corresponds to the largest eigenvalue, contained the maximum separation among the three groups. Consequently, these newly extracted spectral features were capable of detecting the onset of glyphosate injury. Compared with FCA features, the traditionally used spectral indices were poorly related to leaf chlorophyll content in our study. The highest correlation coefficients were acquired between NDVI and Chl, with 0.55 for soybean and 0.51 for cotton. In a study aiming to determine the glyphosate-induced stress level of soybean and cotton leaves, Huang et al. [2] attempted to construct the relationships between leaf stress and spectral indices such as NDVI, RVI, SAVI and DVI to separate the high-dose (0.433 kg·ae/ha) and low-dose (0.217 kg·ae/ha) glyphosate-treated leaves from the untreated ones. However, these indices did not always indicate good divisibility, and separation results were not consistent with time. Our results lead to a similar conclusion with a larger group of spectral indices, which confirms the difficulty in relating spectral indices to glyphosate-induced leaf stress level. These results indicate that spectral indices are less effective for detecting the onset of glyphosate injury. Since glyphosate is phytotoxic to crops by an unknown mechanism, further studies are needed to fully explore the biochemical basis of the relationship between glyphosate injury and leaf reflectance spectrum.
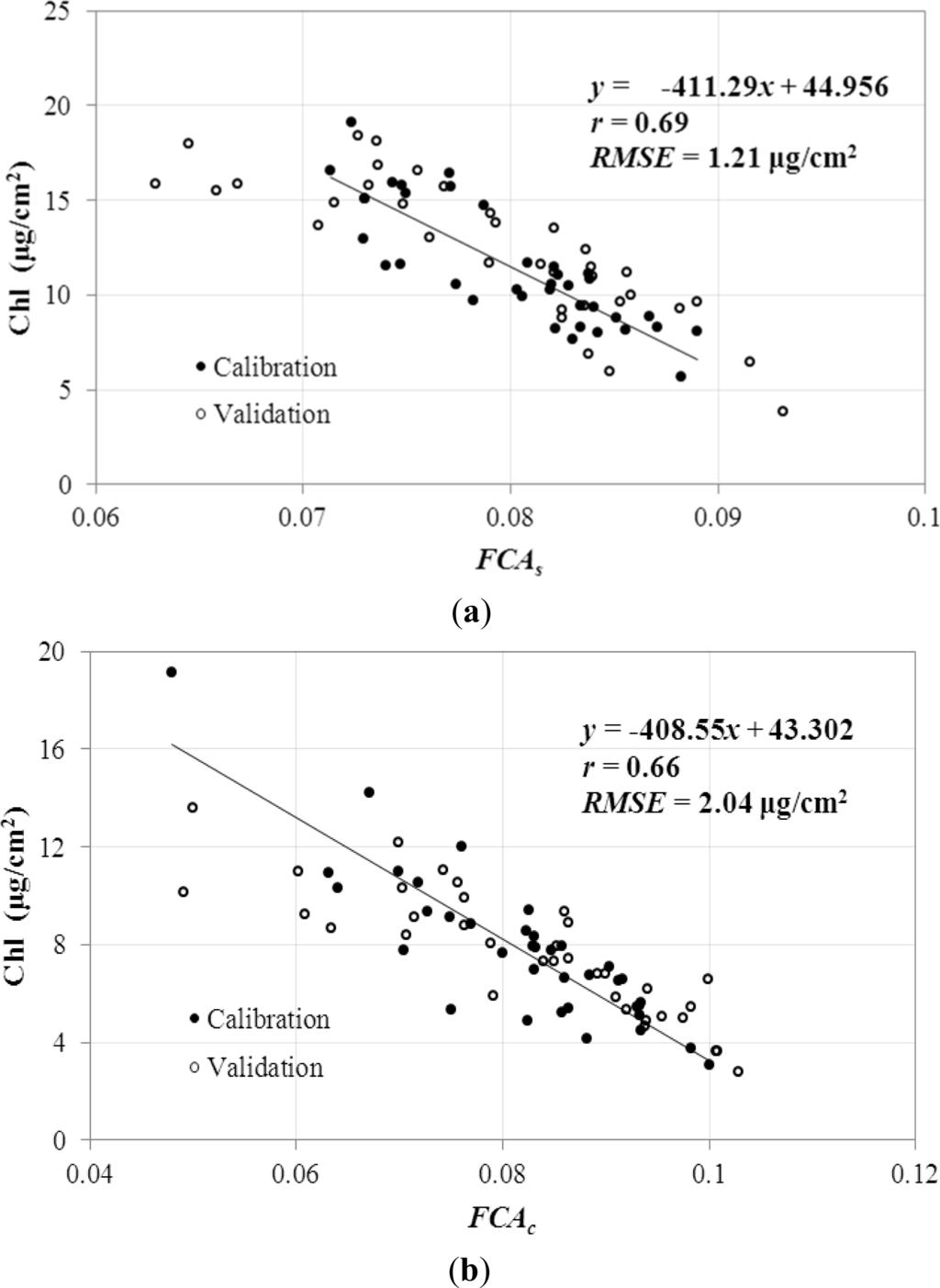
Figure 4.
Relationships between FCA and leaf chlorophyll content (Chl): (a) soybean; (b) cotton.
3.7. Advantages and Potential of the FCA Features
In this study, we demonstrated that by employing FCA features, leaf hyperspectral reflectance measurements are useful for early detection of glyphosate injury for non-GR soybean and non-GR cotton leaves. Sensitivity analysis enables the selection of optimal spectral bands most indicative of leaf chlorophyll and structural variations. The spectral bands used for canonical analysis were selected based on the sensitivity result of the PROSPECT model, which ensures that their effectiveness would not be limited to certain calibration datasets. Canonical analysis technique used for FCA feature extraction process gives a novel view to the selections of the most discriminating features, which provides more robust separation for the CTRL, 0.25X, and 0.5X groups. The FCA features exhibited the largest separation among groups for distinguishing injured leaves from healthy ones.
This study was conducted in a greenhouse under controlled growing conditions to focus on the stress induced by herbicide glyphosate. This experiment has demonstrated the potential for these techniques for applicability in the field. Under field conditions, other stress factors, such as stress caused by water deficit, temperature and pests may induce similar abnormalities in leaf reflectance spectra. Therefore, a priori knowledge (e.g., farm management data) that the stress is largely caused by glyphosate should be helpful to effectively use the method proposed here. This study indicated that glyphosate injured plants can be distinguished from the healthy ones by spectral features extracted from hyperspectral data in a timely manner. More datasets containing a wider range of crop species and growing status are needed to further test the effectiveness of the FCA features. As the new features are extracted for glyphosate injury detection at the leaf scale, there are some questions as to whether FCA features are still effective at the canopy scale by airborne or space-borne observation. Different from the spectra of leaves, canopy spectral features are strongly affected by crop architecture, sun and viewing geometry, and the contribution of soil background [44], which may present difficulties in the quantitative assessment of damage to crops caused by glyphosate injury. Our future research studies would focus on addressing these problems and further improving the technique for practical use.
4. Conclusions
Accurate and timely evaluation of stress exhibited by glyphosate treated plants using foliar hyperspectral reflectance data has important implications for precision agriculture. This study demonstrated that by using traditional spectral indices and newly extracted FCA features (FCAs for soybean and FCAc for cotton), non-GR crop injury caused by glyphosate could be detected shortly after the spray by plant leaf reflectance spectra. The results indicate that the glyphosate injury could be detected by NDVI, RVI, SAVI, and DVI 48 HAT for soybean and 72 HAT for cotton, and the other spectral indices either showed little useful information for separation (dg, dG, dRE, CGFN, EGFN, NPQI, and SFDR), or did not show consistent results for soybean and cotton (WRE, PRI and NPCI). We have also demonstrated that, compared against those traditionally used spectral indices, the FCA features extracted by the canonical analysis technique were superior at early detection of glyphosate injury for non-GR soybean and non-GR cotton leaves, with a consistent trend of higher spraying rate corresponding to higher injury. This trend was more pronounced with time. The three groups with different spray rates showed some separability at 24 HAT by the FCA features and could be distinguished at, and beyond, 48 HAT for both soybean and cotton. Moreover, the spectral bands used in the FCA features were selected based on the sensitivity analysis results of a leaf RT model (leaf optical PROperty SPECTra model, PROSPECT), which can extend the effectiveness of these features to a wide range of leaf structures and growing conditions. These results demonstrate the feasibility of using leaf hyperspectral reflectance measurements for the early detection of glyphosate injury through these newly proposed FCA features.
Acknowledgments
This work is jointly supported by the Chinese Natural Science Foundation under Project 41371325 and 40901156, the State Key Laboratory of Remote Sensing Science (Grant No. 2009kfjj022), and the Civil Aerospace Technology Pre-research Project of China (Grant No. D040201-03). This work also contributes to Integrated Sustainable Crop Production Systems for the United States Department of Agriculture, Agricultural Research Service, National Program 305, Crop Production. Thanks go to Efren Ford and Paige Goodlett for their technical assistance. The authors are thankful to the anonymous reviewers who provided constructive comments to improve this manuscript.
Author Contributions
Feng Zhao proposed the research method, designed, and conducted the experiments, and contributed extensively in manuscript writing and revision. Yanbo Huang conceived the research, organized the experiments, and made significant contributions in research design, data acquisition and manuscript preparation and revision. Yiqing Guo conducted the data analysis and prepared the manuscript. Krishna N. Reddy provided suggestions for experiment design and operation and personnel support for plant leaf biological parameter measurement. Matthew A. Lee, Reginald S. Fletcher, and Steven J. Thomson all made considerable efforts in editing the manuscript.
Disclaimer
Mention of trade names or commercial products in this publication is solely for the purpose of providing specific information and does not imply recommendation or endorsement by the US Department of Agriculture.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bellaloui, N.; Reddy, K.N.; Zablotowicz, R.M.; Mengistu, A. Simulated glyphosate drift influences nitrate assimilation and nitrogen fixation in non-glyphosate-resistant soybean. J. Agric. Food Chem 2006, 54, 3357–3364. [Google Scholar]
- Huang, Y.; Thomson, S.J.; Molin, W.T.; Reddy, K.N.; Yao, H. Early detection of soybean plant injury from glyphosate by measuring chlorophyll reflectance and fluorescence. J. Agric. Sci 2012, 4, 117–124. [Google Scholar]
- Ding, W.; Reddy, K.N.; Krutz, L.J.; Thomson, S.J.; Huang, Y.; Zablotowicz, R.M. Biological response of soybean and cotton to aerial glyphosate drift. J. Crop Improv 2011, 25, 291–302. [Google Scholar]
- Reddy, K.N.; Hoagland, R.E.; Zablotowicz, R.M. Effect of glyphosate on growth, chlorophyll, and nodulation in glyphosate-resistant and susceptible soybean (Glycine max) varieties. J. New Seeds 2000, 2, 37–52. [Google Scholar]
- Koger, C.H.; Shaner, D.L.; Krutz, L.J.; Walker, T.W.; Buehring, N.; Henry, W.B.; Thomas, W.E.; Wilcut, J.W. Rice (Oryza sativa) response to drift rates of glyphosate. Pest Manag. Sci 2005, 61, 1161–1167. [Google Scholar]
- Reddy, K.N.; Ding, W.; Zablotowicz, R.M.; Thomson, S.J.; Huang, Y.; Krutz, L.J. Biological responses to glyphosate drift from aerial application in non-glyphosate-resistant corn. Pest Manag. Sci 2010, 66, 1148–1154. [Google Scholar]
- Ding, W.; Reddy, K.N.; Zablotowicz, R.M.; Bellaloui, N.; Arnold Bruns, H. Physiological responses of glyphosate-resistant and glyphosate-sensitive soybean to aminomethylphosphonic acid, a metabolite of glyphosate. Chemosphere 2011, 83, 593–598. [Google Scholar]
- Sammons, D.R.; Tran, M. Examining yellow flash in Roundup ready soybean. North Cent. Weed Sci. Soc. Proc 2008, 63, 120. [Google Scholar]
- Mamy, L.; Barriuso, E.; Gabrielle, B. Environmental fate of herbicides trifluralin, metazachlor, metamitron and sulcotrione compared with that of glyphosate, a substitute broad spectrum herbicide for different glyphosate-resistant crops. Pest Manag. Sci 2005, 61, 905–916. [Google Scholar]
- Krezhova, D.D.; Yanev, T.K.; Ivanov, S.V.; Alexieva, V.S. Remote Sensing of the Effect of the Herbicide Glyphosate on the Leaf Spectral Reflectance of Pea Plants (Pisum Sativum l.). In New Developments and Challenges in Remote Sensing; Millpress: Rotterdam, The Netherlands, 2007; pp. 45–52. [Google Scholar]
- Moshou, D.; Bravo, C.; West, J.; Wahlen, S.; McCartney, A.; Ramon, H. Automatic detection of “yellow rust” in wheat using reflectance measurements and neural networks. Comput. Electron. Agric 2004, 44, 173–188. [Google Scholar]
- Oppelt, N.; Mauser, W. Hyperspectral monitoring of physiological parameters of wheat during a vegetation period using AVIS data. Int. J. Remote Sens 2004, 25, 145–159. [Google Scholar]
- Duveiller, G.; Weiss, M.; Baret, F.; Defourny, P. Retrieving wheat green area index during the growing season from optical time series measurements based on neural network radiative transfer inversion. Remote Sens. Environ 2011, 115, 887–896. [Google Scholar]
- Carter, G.A. Ratios of leaf reflectances in narrow wavebands as indicators of plant stress. Int. J. Remote Sens 1994, 15, 697–703. [Google Scholar]
- Riaño, D.; Vaughan, P.; Chuvieco, E.; Zarco-Tejada, P.J.; Ustin, S.L. Estimation of fuel moisture content by inversion of radiative transfer models to simulate equivalent water thickness and dry matter content: Analysis at leaf and canopy level. IEEE Trans. Geosci. Remote Sens 2005, 43, 819–826. [Google Scholar]
- Blackburn, G.A. Wavelet decomposition of hyperspectral data: A novel approach to quantifying pigment concentrations in vegetation. Int. J. Remote Sens 2007, 28, 2831–2855. [Google Scholar]
- Colombo, R.; Meroni, M.; Marchesi, A.; Busetto, L.; Rossini, M.; Giardino, C.; Panigada, C. Estimation of leaf and canopy water content in poplar plantations by means of hyperspectral indices and inverse modeling. Remote Sens. Environ 2008, 112, 1820–1834. [Google Scholar]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ 1992, 41, 35–44. [Google Scholar]
- Peñuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves. Remote Sens. Environ 1994, 48, 135–146. [Google Scholar]
- Blackburn, G.A.; Ferwerda, J.G. Retrieval of chlorophyll concentration from leaf reflectance spectra using wavelet analysis. Remote Sens. Environ 2008, 112, 1614–1632. [Google Scholar]
- Cheng, T.; Rivard, B.; Sanchez-Azofeifa, A. Spectroscopic determination of leaf water content using continuous wavelet analysis. Remote Sens. Environ 2011, 115, 659–670. [Google Scholar]
- Huang, Y.; Thomson, S.J.; Ortiz, B.V.; Reddy, K.N.; Ding, W.; Zablotowicz, R.M.; Bright, J.R. Airborne remote sensing assessment of the damage to cotton caused by spray drift from aerially applied glyphosate through spray deposition measurements. Biosyst. Eng 2010, 107, 212–220. [Google Scholar]
- Yao, H.; Huang, Y.; Hruska, Z.; Tomson, S.J.; Reddy, K.N. Using vegetation index and modified derivative for early detection of soybean plant injury from glyphosate. Comput. Electron. Agric 2012, 89, 145–157. [Google Scholar]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ 1990, 34, 75–91. [Google Scholar]
- Integrating Sphere User Manual ASD; Document 600660 Rev. B; ASD Inc: Boulder, CO, USA, 2008.
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ 1974, 351, 309–317. [Google Scholar]
- Barnes, J.D.; Balaguer, L.; Manrique, E.; Elvira, S.; Davison, A.W. A reappraisal of the use of DMSO for the extraction and determination of chlorophylls a and b in lichens and higher plants. Environ. Exp. Bot 1992, 32, 85–100. [Google Scholar]
- Filella, I.; Peñuelas, J. The red edge position and shape as indicators of plant chlorophyll content, biomass and hydric status. Int. J. Remote Sens 1994, 15, 1459–1470. [Google Scholar]
- Le Maire, G.; François, C.; Dufrene, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ 2004, 89, 1–28. [Google Scholar]
- Fourty, T.; Baret, F.; Jacquemoud, S.; Schmuck, G.; Verdebout, J. Leaf optical properties with explicit description of its biochemical composition: Direct and inverse problems. Remote Sens. Environ 1996, 56, 104–117. [Google Scholar]
- Baret, F.; Fourty, T. Estimation of leaf water content and specific leaf weight from reflectance and transmittance measurements. Agronomie 1997, 17, 455–464. [Google Scholar]
- Jacquemoud, S.; Ustin, S.L.; Verdebout, J.; Schmuck, G.; Andreoli, G.; Hosgood, B. Estimating leaf biochemistry using the PROSPECT leaf optical properties model. Remote Sens. Environ 1996, 56, 194–202. [Google Scholar]
- Jacquemoud, S.; Bacour, C.; Poilve, H.; Frangi, J.P. Comparison of four radiative transfer models to simulate plant canopies reflectance: Direct and inverse mode. Remote Sens. Environ 2000, 74, 471–481. [Google Scholar]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ 2008, 112, 3030–3043. [Google Scholar]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ 2009, 113, S56–S66. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis, The Primer; John Wiley & Sons Ltd: West Sussex, UK, 2008. [Google Scholar]
- Cukier, R.I.; Fortuin, C.M.; Schuler, K.E.; Petschek, A.G.; Schaibly, J.H. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys 1973, 59, 3873–3878. [Google Scholar]
- Cukier, R.I.; Levine, H.B.; Shuler, K.E. Nonlinear sensitivity analysis of multiparameter model systems. J. Comput. Phys 1978, 26, 1–42. [Google Scholar]
- Koda, M.; Mcrae, G.J.; Seinfeld, J.H. Automatic sensitivity analysis of kinetic mechanisms. Int. J. Chem. Kinet 1979, 11, 427–444. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Chan, K. A quantitative, model independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar]
- Lejeune, M.; Caliński, T. Canonical analysis applied to multivariate analysis of variance. J. Multivar. Anal 2000, 72, 100–119. [Google Scholar]
- Li, P.; Wang, Q. Retrieval of leaf biochemical parameters using PROSPECT inversion: A new approach for alleviating ill-posed problems. IEEE Trans. Geosci. Remote Sens 2011, 49, 2499–2506. [Google Scholar]
- Knipling, E.B. Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sens. Environ 1970, 1, 155–159. [Google Scholar]
- Zhao, F.; Gu, X.; Verhoef, W.; Wang, Q.; Yu, T.; Liu, Q.; Huang, H.; Qin, W.; Chen, L.; Zhao, H. A spectral directional reflectance model of row crops. Remote Sens. Environ 2010, 114, 265–285. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).