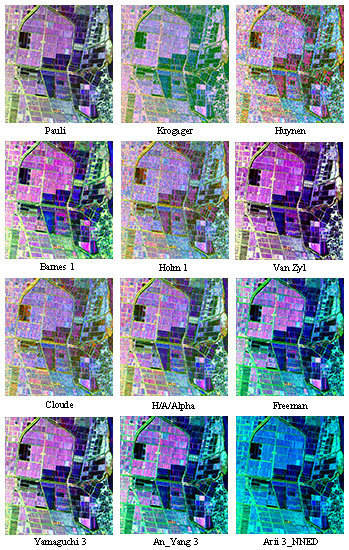
The Influence of Polarimetric Parameters and an Object-Based Approach on Land Cover Classification in Coastal Wetlands
Abstract
:1. Introduction
2. Study Area and Datasets
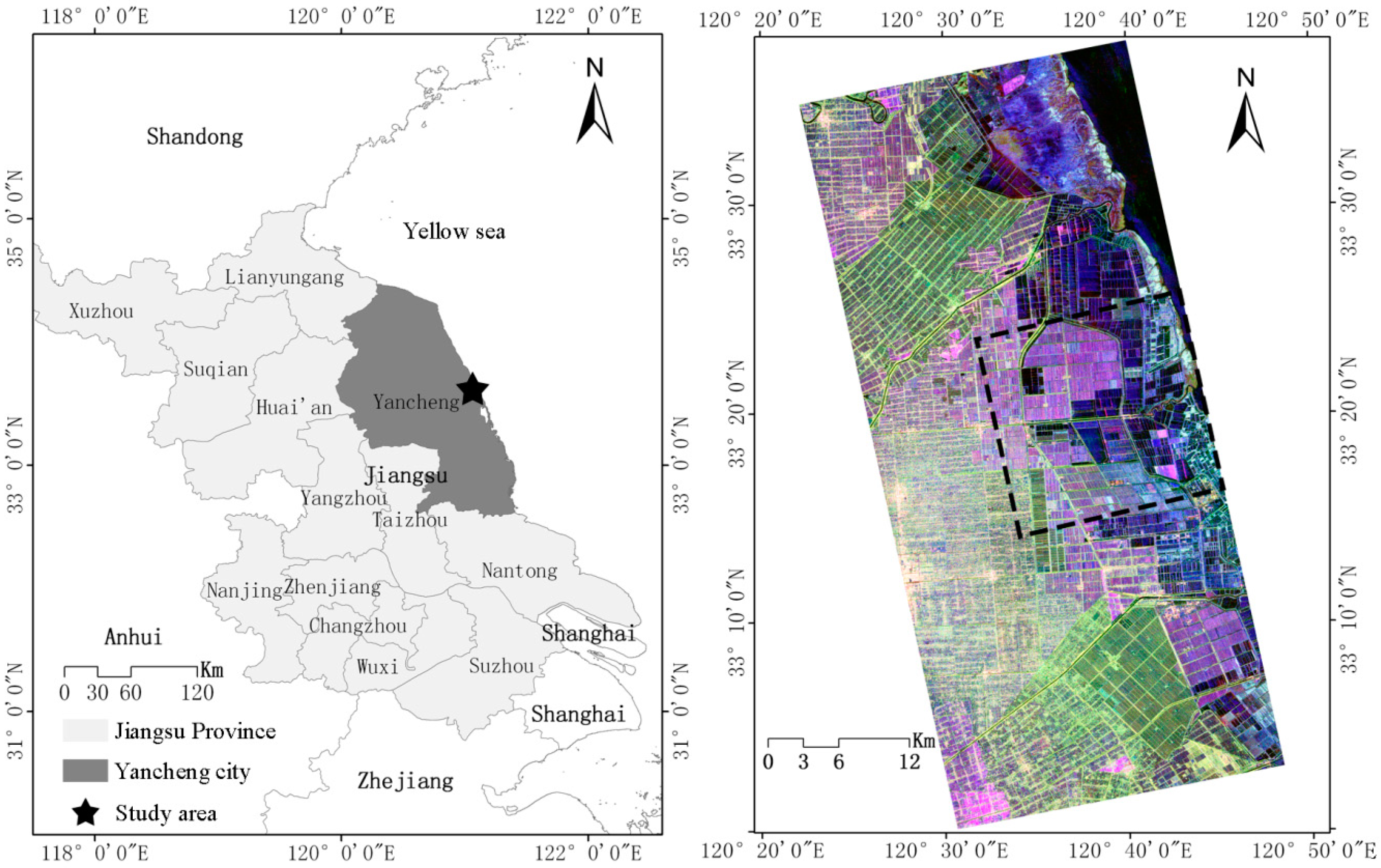

3. Methodology
3.1. Polarimetric Decomposition and Parameter Extraction
| Decomposition Method | Polarimetric Parameters | ||
|---|---|---|---|
| Pauli [22] | Pauli_a | Pauli_b | Pauli_c |
| Krogager [24] | Krogager_KS | Krogager_KD | Krogager_KH |
| Huynen [25] | Huynen_T11 | Huynen_T22 | Huynen_T33 |
| Barnes1 [26] | Barnes1_T11 | Barnes1_T22 | Barnes1_T33 |
| Barnes2 [26] | Barnes2_T11 | Barnes2_T22 | Barnes2_T33 |
| Holm1 [27] | Holm1_T11 | Holm1_T22 | Holm1_T33 |
| Holm2 [27] | Holm2_T11 | Holm2_T22 | Holm2_T33 |
| VanZyl3 [28] | VanZyl3_Vol | VanZyl3_Odd | VanZyl3_Dbl |
| Cloude [22] | Cloude_T11 | Cloude_T22 | Cloude_T33 |
| H/A/Alpha [29] | H/A/A_T11 | H/A/A_T22 | H/A/A_T33 |
| Freeman2 [30] | Freeman2_Vol | Freeman2_Ground | |
| Freeman3 [31] | Freeman_Vol | Freeman_Odd | Freeman_Dbl |
| Yamaguchi3 [32] | Yamaguchi3_Vol | Yamaguchi3_Odd | Yamaguchi3_Dbl |
| Yamaguchi4 [33] | Yamaguchi4_Vol | Yamaguchi4_Odd | Yamaguchi4_Dbl |
| Neumann [34] | Neumann_delta_mod | Neumann_delta_pha | Neumann_tau |
| Touzi [35] | TSVM_alpha_s | TSVM_alpha_s1 | TSVM_alpha_s2 |
| An_Yang3 [36] | An_Yang3_Vol | An_Yang3_Odd | An_Yang3_Dbl |
| An_Yang4 [37] | An_Yang4_Vol | An_Yang4_Odd | An_Yang4_Dbl |
| Arii3_NNED [38] | Arii3_NNED_Vol | Arii3_NNED_Odd | Arii3_NNED_Dbl |
| Arii3_ANNED [39] | Arii3_ANNED_Vol | Arii3_ANNED_Odd | Arii3_ANNED_Odd |
3.2. Object-Based Image Analysis and Feature Calculation

3.3. Decision Tree Algorithm
3.4. Methods for Comparison
4. Results and Discussion
4.1. Constructed Decision Tree and Selected Polarimetric Parameters
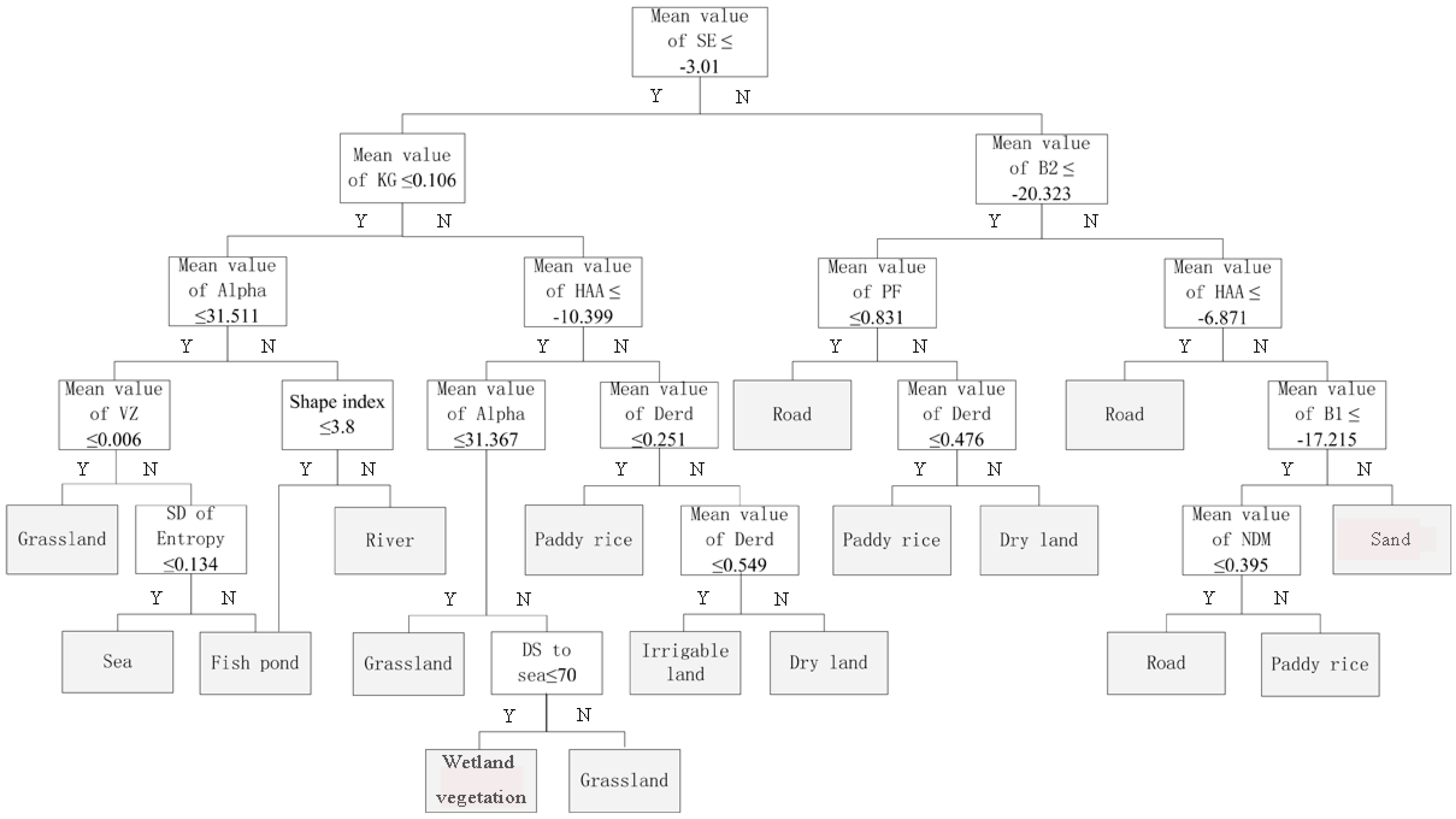

4.2. LULC Classification Results
| Method | Accuracy | Class | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SA | DL | FP | GL | IL | PR | RI | RO | S | W | ||
| Proposed method | PA (%) | 83.2 | 88.8 | 86.0 | 84.6 | 80.3 | 84.9 | 95.3 | 92.0 | 88.8 | 93.5 |
| UA (%) | 89.2 | 87.1 | 89.5 | 86.4 | 87.4 | 90.9 | 85.5 | 85.2 | 90.0 | 80.7 | |
| OA (%) | 87.3 | ||||||||||
| WSC | PA (%) | 84.3 | 77.9 | 42.8 | 75.4 | 76.1 | 74.1 | 30.3 | 89.3 | 52.3 | 94.6 |
| UA (%) | 83.4 | 87.2 | 6.6 | 78.8 | 87.4 | 71.6 | 80.7 | 87.9 | 17.3 | 72.5 | |
| OA (%) | 66.6 | ||||||||||
| PWPP | PA (%) | 88.6 | 79.4 | 73.6 | 74.4 | 67.9 | 75.7 | 73.4 | 91.1 | 49.2 | 89.3 |
| UA (%) | 83.0 | 84.3 | 24.6 | 67.6 | 90.6 | 71.6 | 80.7 | 92.1 | 79.6 | 72.5 | |
| OA (%) | 74.0 | ||||||||||
| PWOS | PA (%) | 90.6 | 78.8 | 92.6 | 72.8 | 69.4 | 82.4 | 51.6 | 90.7 | 55.6 | 92.1 |
| UA (%) | 79.6 | 84.8 | 82.5 | 67.6 | 90.6 | 78.8 | 23.4 | 93.2 | 89.0 | 77.6 | |
| OA (%) | 77.1 | ||||||||||
| PWTG | PA (%) | 87.8 | 79.9 | 61.6 | 71.8 | 71.2 | 75.7 | 75.6 | 90.1 | 47.6 | 84.5 |
| UA (%) | 84.4 | 87.1 | 14.0 | 65.6 | 87.4 | 71.7 | 80.8 | 92.1 | 84.1 | 72.5 | |
| OA (%) | 73.2 | ||||||||||
| PNNC | PA (%) | 87.6 | 80.5 | 94.6 | 70.7 | 65.5 | 89.5 | 65.7 | 90.3 | 82.6 | 94.4 |
| UA (%) | 79.5 | 83.8 | 69.7 | 67.1 | 91.7 | 81.2 | 81.8 | 88.4 | 84.6 | 77.8 | |
| OA (%) | 80.5 | ||||||||||
5. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mitsch, W.J.; Gosselink, J.G. The value of wetlands: Importance of scale and landscape setting. Ecol. Econ. 2000, 35, 25–33. [Google Scholar] [CrossRef]
- Awange, J.L.; Kiema, J.B.K. Marine and coastal resources. In Environmental Geoinformatics; Springer-Verlag: Berlin Heidelberg, Germany, 2013; pp. 397–413. [Google Scholar]
- Ozesmi, S.; Bauer, M. Satellite remote sensing of wetlands. Wetl. Ecol. Manag. 2002, 10, 381–402. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Study on characteristics of land cover change using MODIS NDVI time series. J. Zhejiang Univ. Sci. A 2009, 35, 105–110. [Google Scholar]
- Byrd, K.B.; O’Connell, J.L.; di Tommaso, S.; Kelly, M. Evaluation of sensor types and environmental controls on mapping biomass of coastal marsh emergent vegetation. Remote Sens. Environ. 2014, 149, 166–180. [Google Scholar] [CrossRef]
- Dabrowska-Zielinska, K.; Budzynska, M.; Tomaszewska, M.; Bartold, M.; Gatkowska, M.; Malek, I.; Turlej, K.; Napiorkowska, M. Monitoring wetlands ecosystems using ALOS PALSAR (L-Band, HV) supplemented by optical data: A case study of Biebrza Wetlands in northeast Poland. Remote Sens. 2014, 6, 1605–1633. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Lin, H. A comparison study of impervious surfaces estimation using optical and SAR remote sensing images. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 148–156. [Google Scholar] [CrossRef]
- Gosselin, G.; Touzi, R.; Cavayas, F. Polarimetric Radarsat-2 wetland classification using the Touzi decomposition: Case of the Lac Saint-Pierre Ramsar wetland. Can. J. Remote Sens. 2014, 39, 491–506. [Google Scholar] [CrossRef]
- Touzi, R.; Deschamps, A.; Rother, G. Wetland characterization using polarimetric RADARSAT-2 capability. Can. J. Remote Sens. 2007, 33, S56–S67. [Google Scholar] [CrossRef]
- Yajima, Y.; Yamaguchi, Y.; Sato, R.; Yamada, H.; Boerner, W.M. POLSAR image analysis of wetlands using a modified four-component scattering power decomposition. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1667–1673. [Google Scholar] [CrossRef]
- Cable, J.; Kovacs, J.; Shang, J.; Jiao, X. Multi-temporal polarimetric RADARSAT-2 for land cover monitoring in northeastern Ontario. Canada. Remote Sens. 2014, 6, 2372–2392. [Google Scholar] [CrossRef]
- Van Beijma, S.; Comber, A.; Lamb, A. Random forest classification of salt marsh vegetation habitats using quad-polarimetric airborne SAR, elevation and optical RS data. Remote Sens. Environ. 2014, 149, 118–129. [Google Scholar] [CrossRef]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Peña, J.M.; Gutiérrez, P.A.; Hervás-Martínez, C.; Six, J.; Plant, R.E.; López-Granados, F. Object-based image classification of summer crops with machine learning methods. Remote Sens. 2014, 6, 5019–5041. [Google Scholar] [CrossRef]
- Ban, Y.; Hu, H.; Rangel, I.M. Fusion of Quickbird MS and RADARSAT SAR data for urban land-cover mapping: Object-based and knowledge-based approach. Int. J. Remote Sens. 2010, 31, 1391–1410. [Google Scholar] [CrossRef]
- Shi, W.; Yang, B.; Li, Q. An object-oriented data model for complex objects in three-dimensional geographical information systems. Int. J. Geogr. Inf. Sci. 2003, 17, 411–430. [Google Scholar] [CrossRef]
- Benz, U.; Pottier, E. Object based analysis of polarimetric SAR data in alpha-entropy-anisotropy decomposition using fuzzy classification by eCognition. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Sydney, Australia, 9–13 July 2001; pp. 1427–1429.
- Niu, X.; Ban, Y. Multi-temporal RADARSAT-2 polarimetric SAR data for urban land-cover classification using an object-based support vector machine and a rule-based approach. Int. J. Remote Sens. 2012, 34, 1–26. [Google Scholar] [CrossRef]
- Qi, Z.; Yeh, A.G.O.; Li, X.; Lin, Z. A novel algorithm for land use and land cover classification using RADARSAT-2 polarimetric SAR data. Remote Sens. Environ. 2012, 118, 21–39. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric SAR speckle filtering. In Polarimetric Radar Imaging: From Basics to Applications, 1st ed.; CRC Press: London, UK, 2009; pp. 161–165. [Google Scholar]
- Sartori, L.R.; Imai, N.N.; Mura, J.C.; Novo, E.M.L.M.; Silva, T.S.F. Mapping macrophyte species in the Amazon Floodplain wetlands using fully polarimetric ALOS/PALSAR data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4717–4728. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Krogager, E. New decomposition of the radar target scattering matrix. Electron. Lett. 1990, 26, 1525–1527. [Google Scholar] [CrossRef]
- Huynen, J.R. The Stokes matrix parameters and their interpretation in terms of physical target properties. In Proceedings of the Journées Internationales de la Polarimétrie Radar, Nantes, France, 20–22 March 1990.
- Barnes, R.M. Roll-invariant decomposition for the polarization covariance matrix. In Proceedings of the Polarimetry Technology Workshop, Redstone Arsenal, AL, USA, 16–18 August 1988.
- Holm, W.A.; Barnes, R.M. On radar polarization mixed target state decomposition techniques. In Proceedings of the 1988 USA National Radar Conference, Ann Arbor, MI, USA, 20–21 April 1988; pp. 20–21.
- Van Zyl, J.J. Application of cloude target decomposition theorem to polarimetric imaging radar data. Radar Polarim. 1993, 1748, 184–191. [Google Scholar]
- Pottier, E.; Lee, J.S. Application of the «H/A/alpha» polarimetric decomposition theorem for unsupervised classification of fully polarimetric SAR data based on the wishart distribution. In Proceedings of the CEOS SAR Workshop, Toulouse, France, 26–29 October 1999; pp. 335–340.
- Freeman, A. Fitting a two-component scattering model to polarimetric SAR data from forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Singh, G.; Cui, Y.; Sang Eun, P.; Yamada, H.; Sato, R. Comparison of model-based four-component scattering power decompositions. In Proceedings of the 2013 Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Tsukuba, Japan, 23–27 September 2013.
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Pottier, E. A general model-based polarimetric decomposition scheme for vegetated areas. In Proceedings of the 4th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry-PolInSAR, Frascati, Italy, 26–30 January 2009.
- Touzi, R. Target scattering decomposition in terms of roll-invariant target parameters. IEEE Trans. Geosci. Remote Sens. 2007, 45, 73–84. [Google Scholar] [CrossRef]
- An, W.; Cui, Y.; Yang, J. Three-component model-based decomposition for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2732–2739. [Google Scholar] [CrossRef]
- An, W.; Xie, C.; Yuan, X.; Cui, Y.; Yang, J. Four-component decomposition of polarimetric SAR images with deorientation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1090–1094. [Google Scholar] [CrossRef]
- Arii, M.; Van Zyl, J.J.; Kim, Y. Adaptive model-based decomposition of polarimetric SAR covariance matrices. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1104–1113. [Google Scholar] [CrossRef]
- Arii, M.; Van Zyl, J.; Kim, Y. Improvement of adaptive-model based decomposition with polarization orientation compensation. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 95–98.
- Wang, L.; Sousa, W.P.; Gong, P. Integration of object-based and pixel-based classification for mapping mangroves with IKONOS imagery. Int. J. Remote Sens. 2004, 25, 5655–5668. [Google Scholar] [CrossRef]
- Baatz, M.; Benz, U.; Dehghani, S.; Heynen, M.; Holtje, A.; Hofmann, P.; Lingenfelder, I.; Mimler, M.; Sohlbach, M.; Weber, M. ECognition Professional User Guide 4; Definiens Imaging: Munich, Germany, 2004. [Google Scholar]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Loh, W.Y.; Shih, Y.S. Split selection methods for classification trees. Stat. Sin. 1997, 7, 815–840. [Google Scholar]
- Lee, J.S.; Grunes, M.R.; Ainsworth, T.L.; Du, L.J.; Schuler, D.L.; Cloude, S.R. Unsupervised classification using polarimetric decomposition and the complex Wishart classifier. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2249–2258.45. [Google Scholar] [CrossRef]
- Refregier, P.; Morio, J. Shannon entropy of partially polarized and partially coherent light with Gaussian fluctuations. J. Opt. Soc. A 2006, 23, 3036–3044. [Google Scholar] [CrossRef]
- Allain, S.; Ferro-Famil, L.; Pottier, E. A polarimetric classification from PolSAR data using SERD/DERD parameters. In Proceedings of the 6th European Conference on Synthetic Aperture Radar, Dresden, Germany, 16–18 May 2006.
- Ainsworth, T.L.; Cloude, S.R.; Lee, J.S. Eigenvector analysis of polarimetric SAR data. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Toronto, ON, Canada, 24–28 June 2002; pp. 626–628.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; He, X.; Wang, J.; Xiao, R. The Influence of Polarimetric Parameters and an Object-Based Approach on Land Cover Classification in Coastal Wetlands. Remote Sens. 2014, 6, 12575-12592. https://doi.org/10.3390/rs61212575
Chen Y, He X, Wang J, Xiao R. The Influence of Polarimetric Parameters and an Object-Based Approach on Land Cover Classification in Coastal Wetlands. Remote Sensing. 2014; 6(12):12575-12592. https://doi.org/10.3390/rs61212575
Chicago/Turabian StyleChen, Yuanyuan, Xiufeng He, Jing Wang, and Ruya Xiao. 2014. "The Influence of Polarimetric Parameters and an Object-Based Approach on Land Cover Classification in Coastal Wetlands" Remote Sensing 6, no. 12: 12575-12592. https://doi.org/10.3390/rs61212575
APA StyleChen, Y., He, X., Wang, J., & Xiao, R. (2014). The Influence of Polarimetric Parameters and an Object-Based Approach on Land Cover Classification in Coastal Wetlands. Remote Sensing, 6(12), 12575-12592. https://doi.org/10.3390/rs61212575