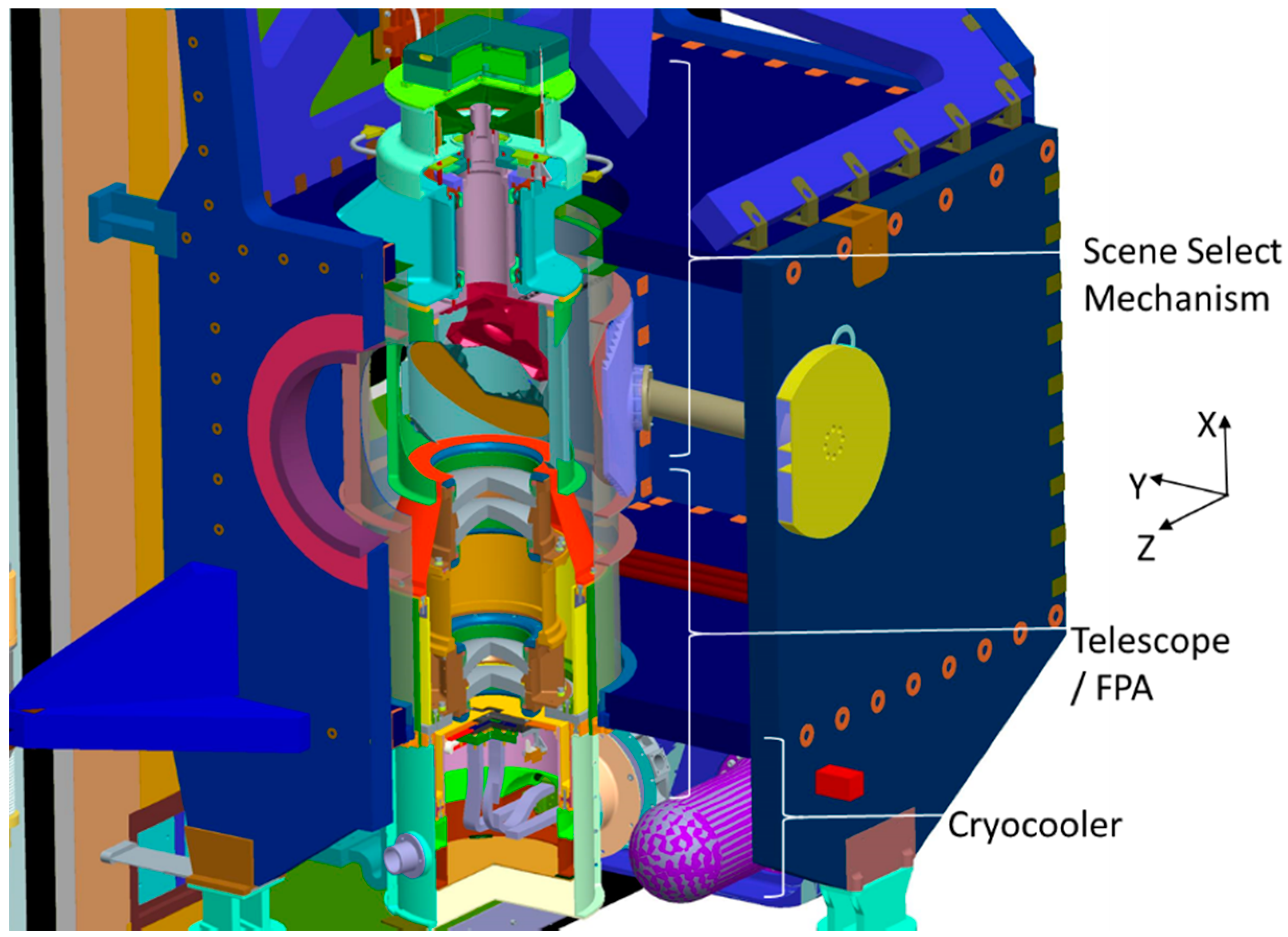
The first TIRS Earth image was acquired on 7 March 2013, more than a week before the initial OLI Earth imaging operations. This provided an opportunity to verify the TIRS alignment to the spacecraft as well as the TIRS internal alignment prior to the availability of corresponding OLI imagery. A TIRS acquisition from 8 March 2013 over Landsat world-wide reference system (WRS) path 142, row 048 was examined to provide an early check on TIRS pointing. Tie points between the TIRS image and a Landsat 5 Thematic Mapper reference image from the Global Land Survey (GLS) 2010 data set, were measured manually to provide a coarse estimate of TIRS-to-spacecraft alignment. These measurements confirmed that the TIRS geometric model was performing as expected with a pointing bias of approximately 1.5 kilometers in each direction. They also identified a significant (approximately 5-pixel) misalignment of SCA-A. Coarse updates based upon these initial measurements were applied to the TIRS-to-spacecraft alignment and to the SCA-A Legendre coefficient model to facilitate subsequent precise corrections.
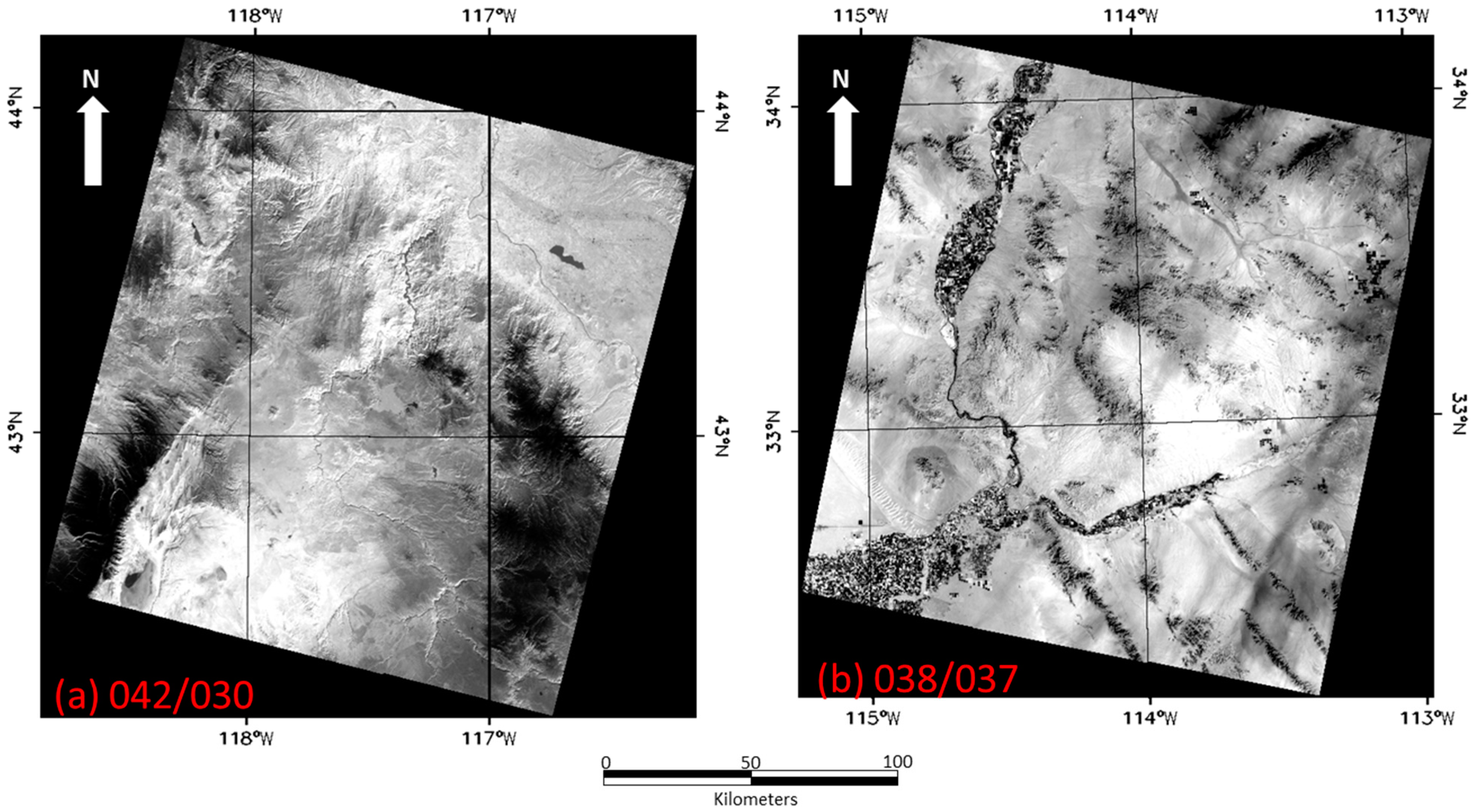
Cloud-free TIRS images over geometric calibration sites were then used to perform an initial quantitative update to the TIRS-to-spacecraft alignment. TIRS images over WRS path 042, row 030 from 9 March shown on the left side of
Figure 8, and over WRS path 038, row 037 from 11 March shown on the right side of
Figure 8, were used with Landsat 5 SWIR band reference images in the initial calibration. The coarse alignment updates made it possible to register the TIRS and GLS reference images sufficiently for the automated TIRS alignment calibration to operate. The TIRS alignment calibration procedure calculates corrections to both the TIRS-to-spacecraft and TIRS SCA-to-SCA alignments, and is described in the next section.
3.1. TIRS Alignment Calibration
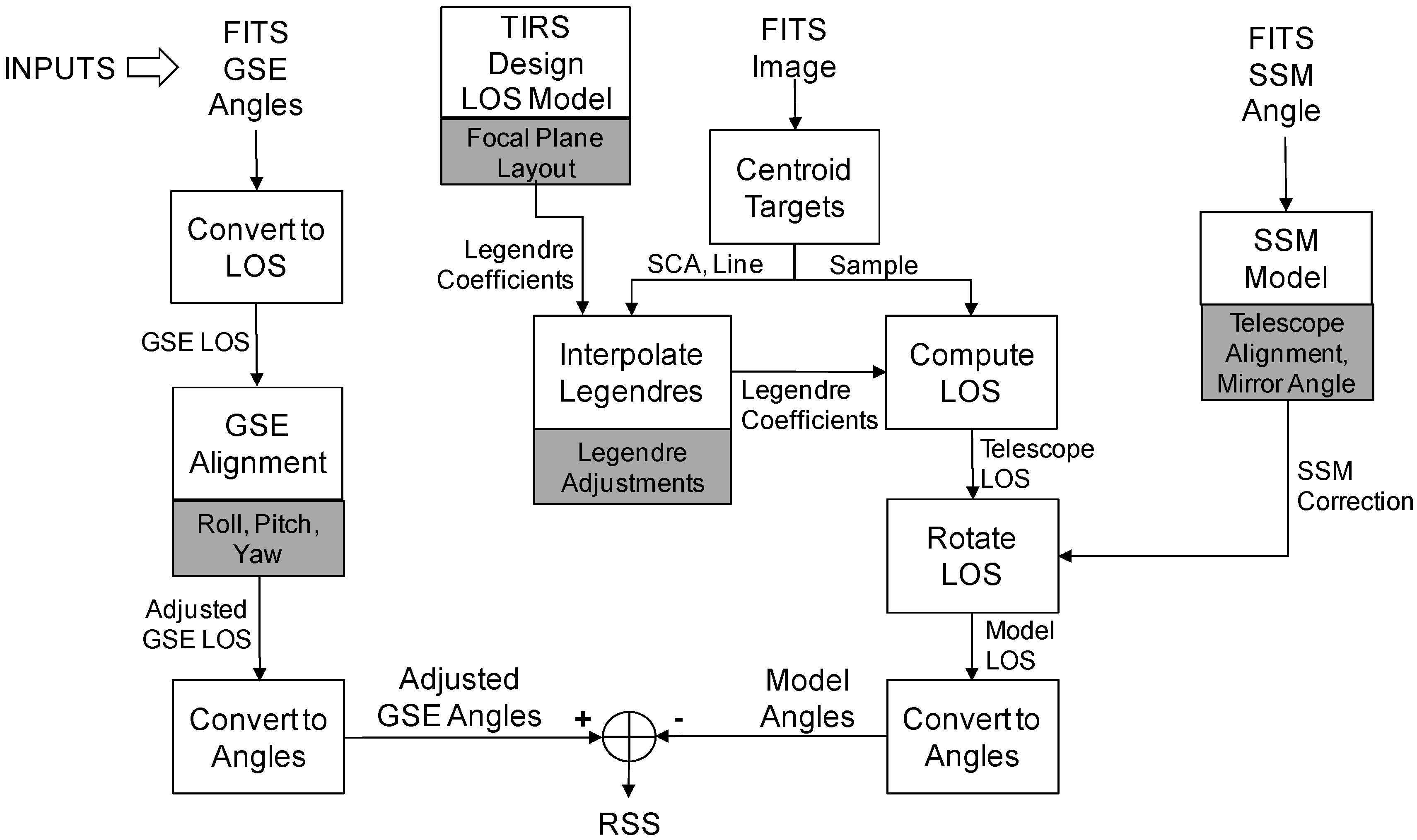
The on-orbit TIRS alignment calibration algorithm [
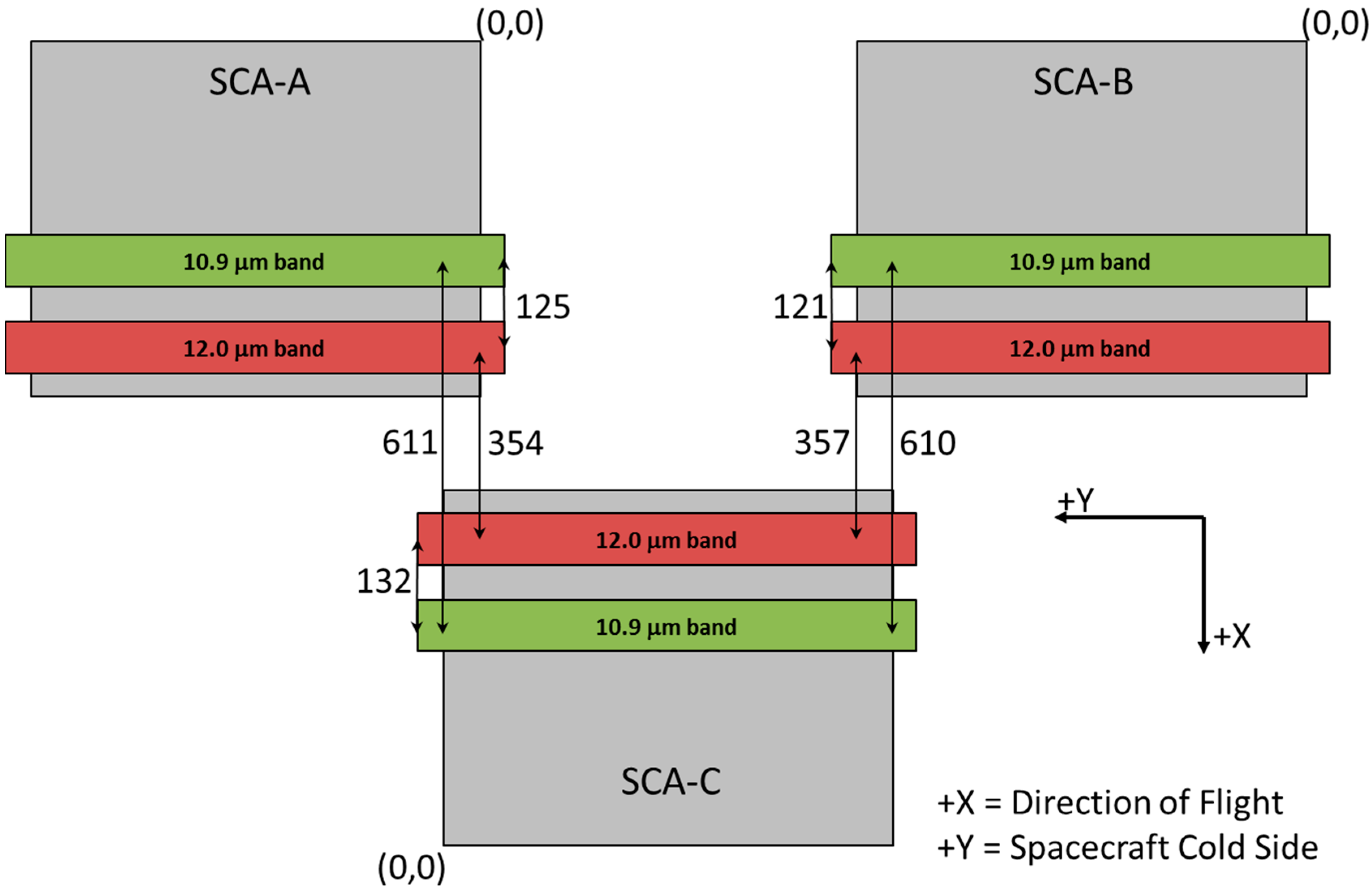
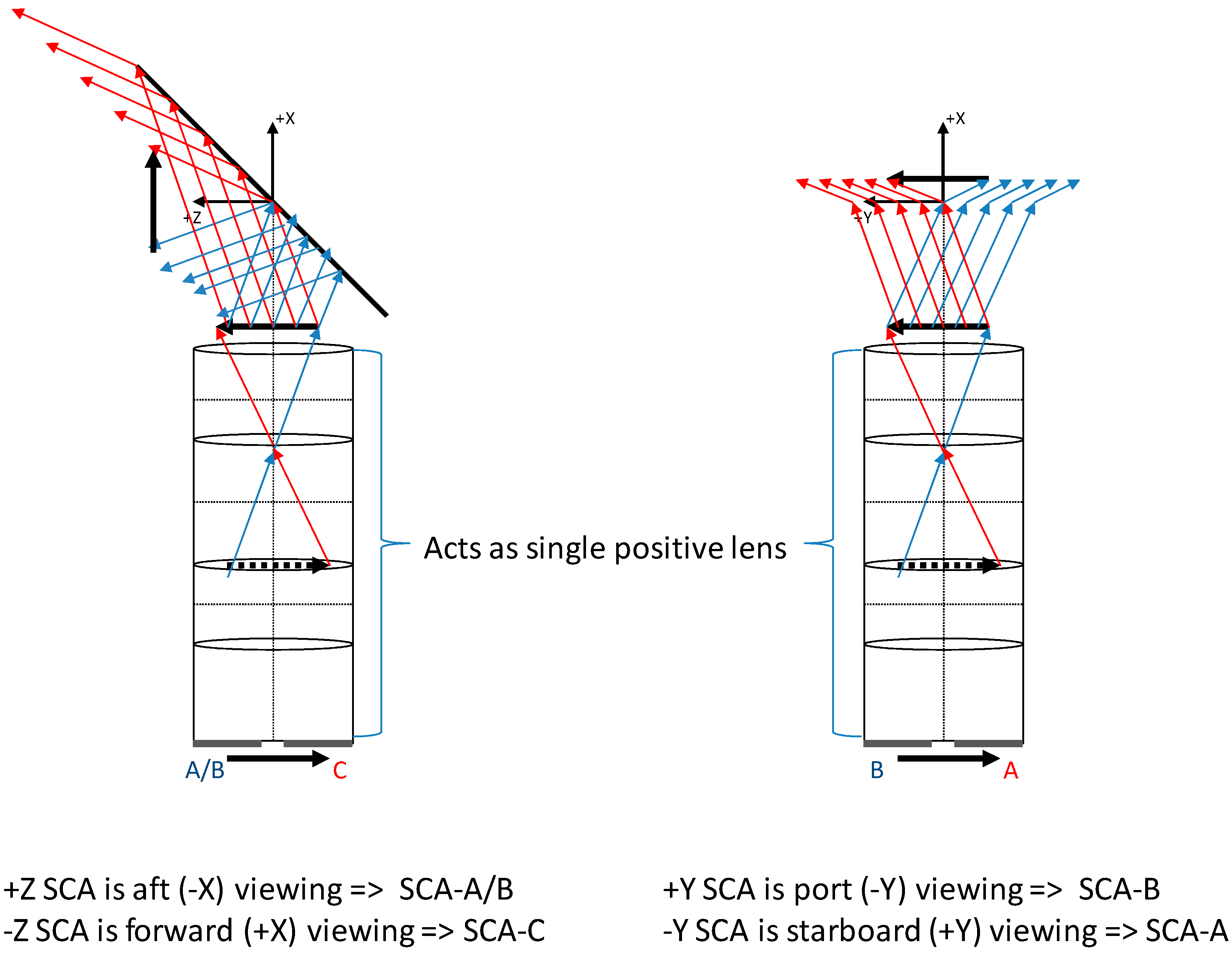
7] was developed to simultaneously accomplish two objectives: (1) to measure TIRS-to-OLI instrument alignment, and (2) to detect and correct TIRS SCA-to-SCA misalignment. This is accomplished by generating Level 1T terrain and ground control point corrected TIRS images of the 10.9-micrometer band (band 10) in which each TIRS SCA is stored in its own output file. These SCA-separated images are then correlated with a Level 1T reference image created using the OLI SWIR1 (1610-nanometer) band (band 6). The measured image displacements from each SCA are used to estimate the overall alignment relationship between the TIRS and OLI instruments and to simultaneously correct any SCA-specific misalignments by adjusting the 8 Legendre coefficients that constitute each SCA’s line-of-sight model for the 10.9 micrometer band. The ultimate objective of this calibration is to ensure accurate registration between the TIRS and OLI spectral bands
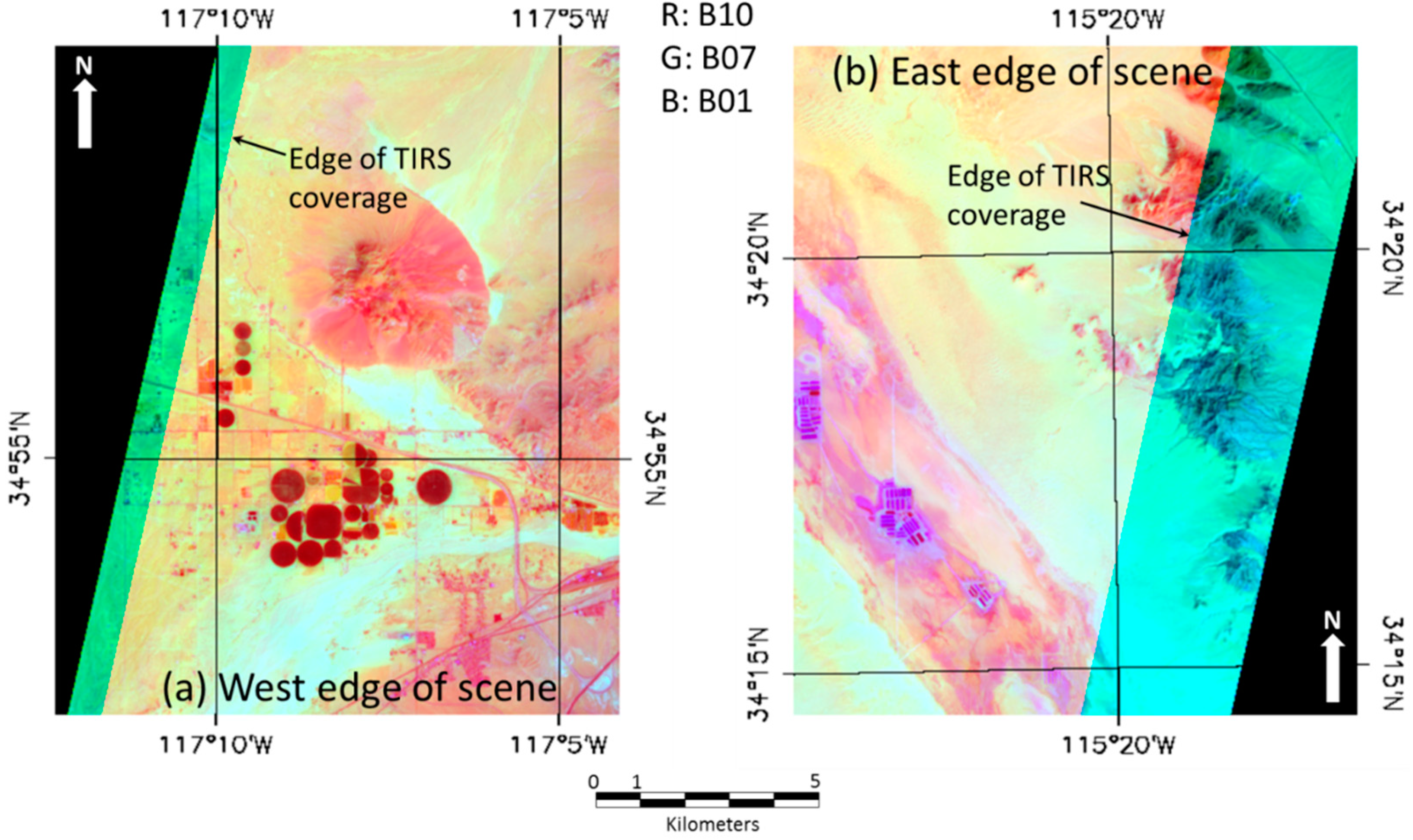
Figure 8.
Initial TIRS alignment calibration images, acquired prior to the first Operational Land Imager (OLI) imaging. (a) The interval on the left from WRS 042/030 acquired 9 March 2013 and (b) the interval on the right from WRS 038/037 acquired on 11 March 2013, provided the first complete TIRS on-orbit alignment calibration update, using Landsat 5 Thematic Mapper data as a reference.
Figure 8.
Initial TIRS alignment calibration images, acquired prior to the first Operational Land Imager (OLI) imaging. (a) The interval on the left from WRS 042/030 acquired 9 March 2013 and (b) the interval on the right from WRS 038/037 acquired on 11 March 2013, provided the first complete TIRS on-orbit alignment calibration update, using Landsat 5 Thematic Mapper data as a reference.
Reliably matching data acquired by emissive (thermal) spectral bands with data from reflective spectral bands can be challenging due to the substantial differences in spectral response that are observed for many Earth targets. The ASTER mission was successful in operationally matching thermal bands to VNIR bands [
10,
11]. The approach used for TIRS relies on experience derived from Landsat 7 ETM+ data where it was found that the thermal and SWIR bands yielded the most consistent correlation performance [
12].
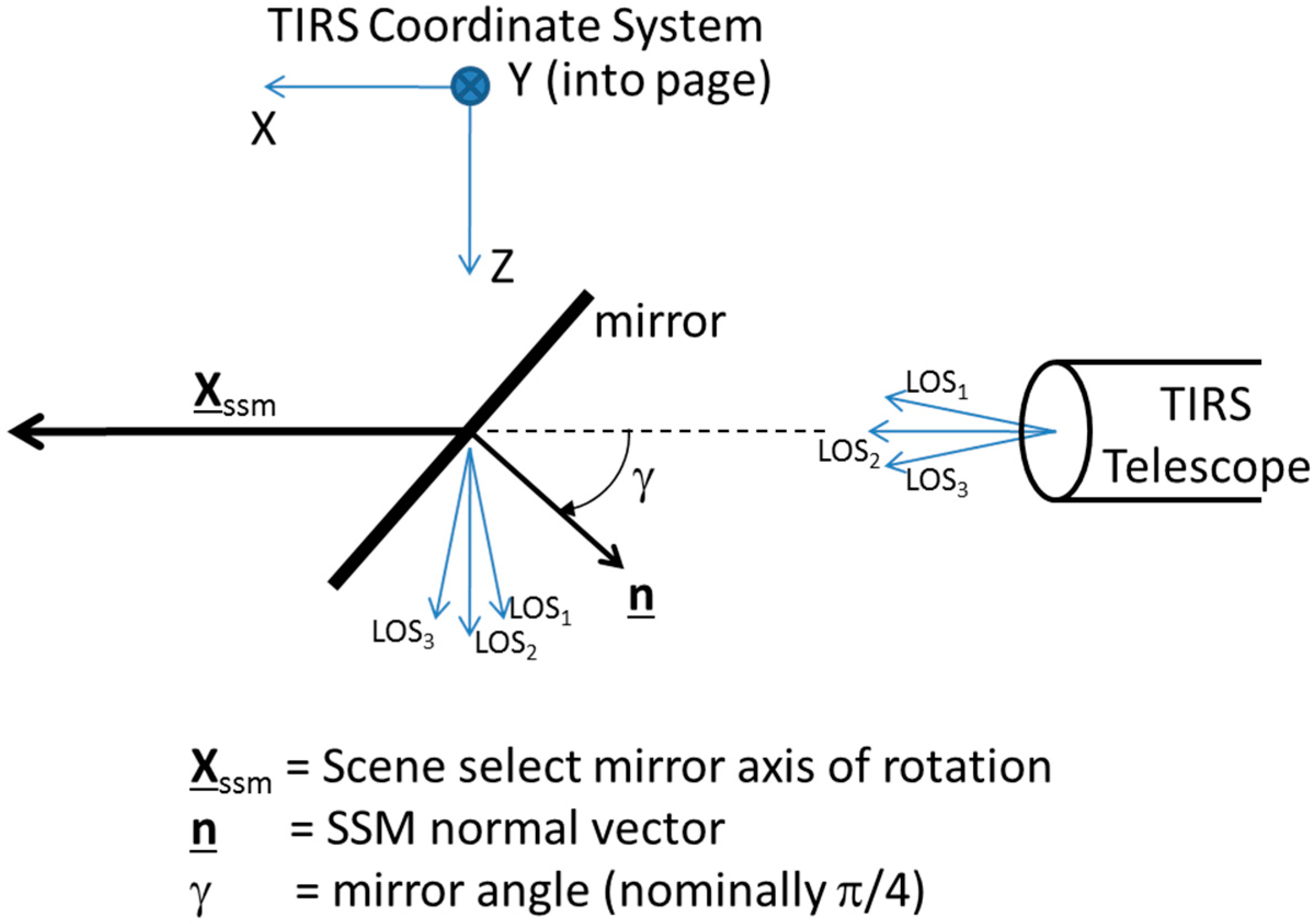
The fundamental measurements used to perform the TIRS alignment calibration are TIRS-to-OLI image displacements measured at tie points in geometrically corrected Level 1T image space, using automated image correlation techniques. All of the TIRS geometric characterization and calibration algorithms utilize normalized gray scale correlation with a surface fitting polynomial to locate the peak of the correlation function to sub-pixel accuracy. This approach is similar to that used by ASTER [
11] and ETM+ [
12]. When using well-defined image targets this method has been found to yield accuracy of 0.1 pixel or better [
13]. The Level 1T row/column pixel coordinates of the original “search” TIRS tie point and of the corresponding “reference” location from the OLI image are both projected back into geometrically uncorrected TIRS line/detector image space using the TIRS geometric model. The detector coordinate is then used to compute a line-of-sight vector using the current Legendre coefficient model, per Equations (9) and (10). The search and reference line-of-sight vector coordinates and the search and reference line coordinates are differenced to compute apparent pointing offsets in the coordinate system used by the Legendre coefficient line-of-sight model:
where:
and
are the reference and search line-of-sight vectors, respectively.
Observations of this type for all three TIRS SCAs are used to simultaneously solve for 27 calibration parameter corrections: 3 TIRS-to-OLI alignment angles (roll-pitch-yaw) + (4 along-track 10.9 micrometer band Legendre coefficients + 4 cross-track 10.9 micrometer band Legendre coefficients) × 3 SCAs. Each X/Y observation pair contributes information to the three alignment angle corrections and to the 8 Legendre coefficient corrections for the SCA in which it was measured.
The alignment angle and Legendre coefficient corrections are highly correlated, so additional constraints are imposed on the fitting procedure to ensure that angular alignment adjustments are not absorbed by the Legendre polynomial model. These constraints are applied to the Legendre coefficient corrections to ensure that: (1) the sum of the cross-track corrections at the mid-points of the three SCAs is zero (suppressing roll effects); (2) the sum of the along-track corrections at the mid-points of the three SCAs is zero (suppressing pitch effects); and (3) the along-track corrections at the mid-points of the outboard SCAs are the same (suppressing yaw effects). Substituting a normalized detector coordinate of zero into equation (10) above shows that the adjustment to the X and Y line-of-sight coordinates for the center of an SCA can be constructed from the Legendre coefficient corrections as:
where:
Δcoef_x0k and Δcoef_x2k are the first and third x Legendre corrections for SCA k,
Δcoef_y0k and Δcoef_y2k are the first and third y Legendre corrections for SCA k.
The constraint equations can thus be formulated as follows:
The collection of tie point measurements plus the three constraints are used in a least squares procedure to simultaneously estimate values for all 27 corrections. This solution procedure is iterated with a T-distribution outlier detection test that identifies and eliminates invalid tie point measurements. The final computed corrections are added to the current calibration parameters to create updated versions of the TIRS-to-OLI alignment and the Legendre coefficient line-of-sight model. The updated TIRS-to-OLI alignment matrix is then pre-multiplied by the OLI-to-spacecraft alignment matrix to construct the TIRS-to-spacecraft alignment matrix that is stored in the calibration parameter file (CPF) for operational use.
3.2. TIRS On-Orbit Alignment Calibration Operations
During the Landsat 8 commissioning period the first priority for geometric calibration was to refine the OLI geometric model [
3]. Since the TIRS alignment calibration procedure uses OLI SWIR band imagery for its reference, a well calibrated OLI is a prerequisite for TIRS on-orbit calibration. Once well-calibrated OLI data were available, a series of 16 cloud-free scenes of geometric calibration sites, acquired between 21 March 2013, and 13 April 2013, were used to refine the TIRS alignment calibration. These calibration sites are arid regions, selected to provide a broad latitude distribution in both the northern and southern hemispheres, where Landsat 7 experience has shown that good SWIR band to thermal band correlation can be expected. It is important that clouds be avoided as the slight difference in along-track pointing direction of the TIRS and OLI detectors will introduce differences in the apparent locations of clouds that depend upon the cloud altitude. Clouds provide an extreme example of the parallax sensitivity that makes it necessary to terrain correct Landsat 8 image products to ensure proper instrument-to-instrument, SCA-to-SCA, and band-to-band alignment.
The measurements collected in the OLI/TIRS calibration scenes refined the initial TIRS alignment calibration derived from TIRS-only data to yield the first operational on-orbit calibration of the TIRS-to-OLI (and TIRS-to-spacecraft) alignment and the 10.9 micrometer band line-of-sight model.
Table 5 shows the magnitude of the total TIRS instrument alignment and SCA placement adjustments applied to the prelaunch TIRS geometric model. Note that these adjustments include the effects of both the initial coarse corrections and the subsequent results from the TIRS alignment calibration procedure.
Table 5.
On-orbit estimate of TIRS-to-spacecraft alignment, changes from the prelaunch alignment, and SCA placement updates resulting from Legendre coefficient model refinement. The alignment results show that the prelaunch TIRS alignment measurement met the TIRS alignment knowledge requirement of 2 milliradians (3 σ) [
9]. Note the large adjustment to the cross-track position of SCA-A.
Table 5.
On-orbit estimate of TIRS-to-spacecraft alignment, changes from the prelaunch alignment, and SCA placement updates resulting from Legendre coefficient model refinement. The alignment results show that the prelaunch TIRS alignment measurement met the TIRS alignment knowledge requirement of 2 milliradians (3 σ) [9]. Note the large adjustment to the cross-track position of SCA-A.
| Parameter | Roll (Milliradians) | Pitch (Milliradians) | Yaw (Milliradians) |
| On-Orbit TIRS-to-Spacecraft Alignment | 0.197 | 2.148 | 2.265 |
| Change from Prelaunch Alignment | −1.576 | 1.447 | 0.521 |
| SCA | Along-Track Offset (Microradians) | Cross-Track Offset (Microradians) |
| A | −49 | −753 |
| B | −77 | −102 |
| C | 156 | 77 |
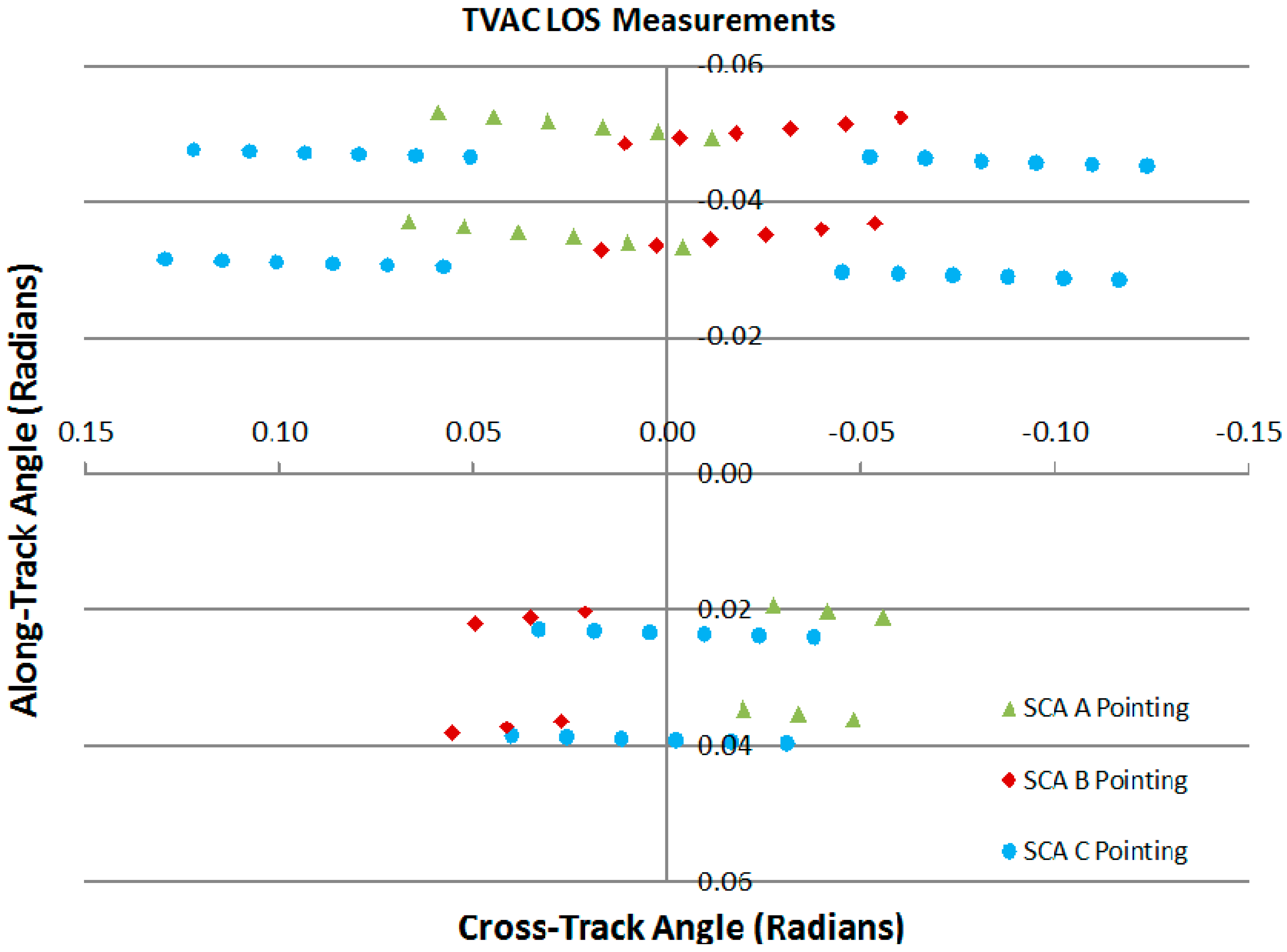
Noting that the TIRS pixel dimension is 142 microradians, the magnitude of the SCA-A cross-track adjustment can be seen to be more than 5 pixels. The sign of this adjustment is such that it counteracts the approximately 3.5-pixel adjustment applied as a result of the prelaunch TVAC measurements. The other SCA placement adjustments are on the order of one TIRS pixel or less, but they are larger than expected based upon the prelaunch calibration results. A loss of index in the steering mirror position telemetry during TVAC testing is suspected as the source of the anomalous cross-track error in prelaunch position for SCA-A.
Figure 9.
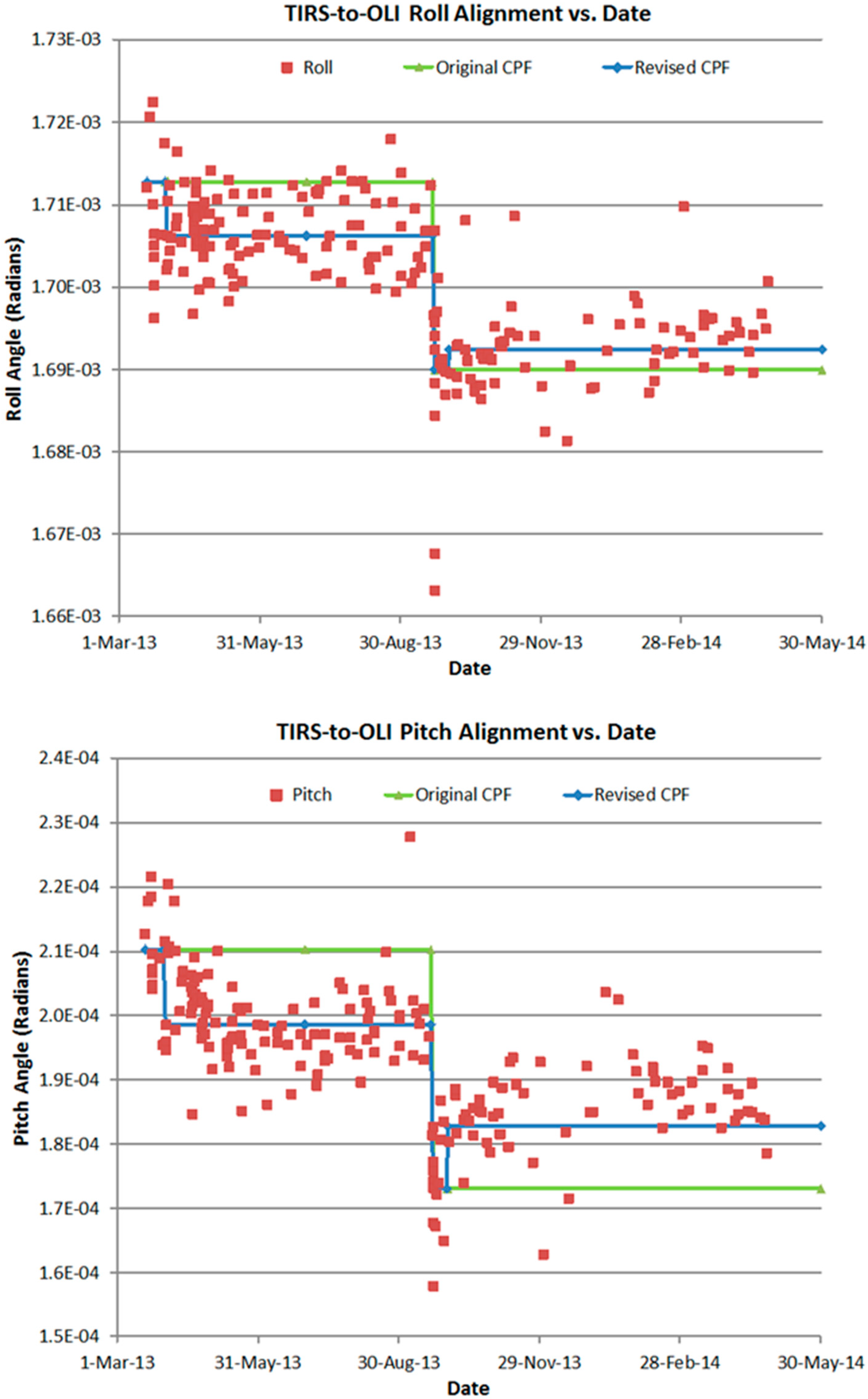
TIRS-to-OLI (a) roll (top) and (b) pitch (bottom) alignment measurements over time show a step discontinuity at the spacecraft safe-hold anomaly that occurred in late-September 2013. An update to the alignment calibration was issued shortly after imaging operations resumed (green lines). The entire calibration time history was subsequently refined (blue lines) in preparation for the February 2014 data reprocessing campaign.
Figure 9.
TIRS-to-OLI (a) roll (top) and (b) pitch (bottom) alignment measurements over time show a step discontinuity at the spacecraft safe-hold anomaly that occurred in late-September 2013. An update to the alignment calibration was issued shortly after imaging operations resumed (green lines). The entire calibration time history was subsequently refined (blue lines) in preparation for the February 2014 data reprocessing campaign.
TIRS alignment calibration operations continue to be performed routinely to ensure that TIRS/OLI registration accuracy is maintained. These measurements have captured several changes in TIRS alignment behavior that have led to additional on-orbit adjustments to the TIRS-to-spacecraft alignment calibration. No significant changes to TIRS Legendre coefficient line-of-sight model have been observed.
Figure 9 shows the time history of TIRS-to-OLI roll and pitch alignment measurements through the first quarter of 2014. Changes in this relationship, as distinct from common changes in the alignment of the two instruments to the spacecraft, can lead to errors in emissive-to-reflective band registration.
Figure 9 shows an abrupt change in apparent alignment in September 2013. This change was associated with an attitude control anomaly and resulting spacecraft safe-hold event that led to significant changes in the temperature environment around the instrument deck. Once imaging operations resumed following this event the TIRS alignment was checked and found to be more than 30 microradians different than the then-current calibrated value in the pitch axis. A smaller roll axis change was observed. The anomalous data points in this area are a result of using less-than-ideal scenes to make alignment measurements in the immediate aftermath of the anomaly.
An immediate update to the TIRS alignment calibration was issued to compensate for the observed change. The green lines on
Figure 9 show the calibrated values. The TIRS alignment appeared to partially recover towards its previous condition in the weeks following the anomaly. This motivated an additional calibration update effective on 1 October 2013. When the decision was made to reprocess the entire Landsat 8 data set, in order to implement a significant improvement to the radiometric calibration knowledge, an additional refinement to the TIRS alignment calibration time history was implemented to better capture the changes in behavior that occurred during the commissioning period as the spacecraft was being maneuvered into its operational orbit. This change is most easily seen in the pitch axis where there is a declining trend in the early data. An additional source of variation affecting the early commissioning data that were acquired prior to achieving the operational WRS-2 orbit was a series of adjustments to the control temperatures for the TIRS telescope. The TIRS instrument team made these adjustments as part of the process of achieving best focus for the TIRS instrument.
The revised calibration, shown by the blue lines in
Figure 9, was used during the data reprocessing campaign conducted in February 2014, and is the basis for the performance results reported below.
Table 6 shows the current best estimates of the TIRS-to-OLI alignment angles and the magnitudes of the adjustments that have been made over time.
Table 6.
TIRS-to-OLI alignment calibration angles over time are shown along with the magnitude of the adjustments that have been applied.
Table 6.
TIRS-to-OLI alignment calibration angles over time are shown along with the magnitude of the adjustments that have been applied.
| Time Period | Roll Angle (Micro-radians) | Roll Change (Micro-radians) | Pitch Angle (Micro-radians) | Pitch Change (Micro-radians) | Yaw Angle (Micro-radians) | Yaw Change (Micro-radians) |
|---|
| Launch–31MAR2013 | 1713 | - | 210 | - | 2753 | - |
| 01APR2013–20SEP2013 | 1706 | −6 | 199 | −12 | 2770 | 16 |
| 21SEP2013–30SEP2013 | 1690 | −16 | 173 | −25 | 2775 | 5 |
| 01OCT2013–30SEP2014 | 1692 | 2 | 183 | 10 | 2761 | −14 |
The largest alignment adjustments shown in
Table 6 are associated with the late-September 2013 spacecraft safe-hold event described above. A more recent spacecraft safe-hold did not lead to a similar alignment disruption due to more careful management of the on-board heaters, and resulting temperatures, during the event. This was a lesson learned from the first anomaly. The apparent sensitivity of TIRS alignment to the temperature environment was not unexpected as prelaunch thermal/mechanical analysis had predicted that measureable within-orbit thermally induced changes in TIRS pointing might be expected [
8]. Though some evidence of a latitude-dependent alignment effect has been observed, it is within the allowable instrument alignment stability thresholds so a position-in-orbit based alignment model has not been attempted and is not currently contemplated. The within-orbit effect as well as the potential for seasonal thermal effects motivates continued careful monitoring. Additional alignment updates will continue to be issued as events dictate.
3.3. TIRS Band Alignment Calibration
As described above, the TIRS alignment calibration procedure is used to refine both the overall TIRS-to-OLI alignment knowledge and the Legendre polynomial operational line-of-sight model coefficients for the 10.9-micrometer band (band 10) on each individual TIRS SCA. Having updated the pointing model for band 10, the alignment of the TIRS 12.0-micrometer band (band 11) to band 10 must be updated to restore TIRS internal band-to-band consistency. The TIRS band alignment calibration process uses SCA-separated images containing both TIRS spectral bands to measure band-to-band tie points with band 10 serving as the reference for band 11. The spectral similarity of the two bands makes this a relatively straightforward process with little sensitivity to scene content, other than the necessity of avoiding clouds. A set of ten cloud-free calibration scenes over desert sites, a subset of those used for TIRS alignment calibration, was used for on-orbit TIRS band alignment calibration. As was the case for TIRS alignment, tie point offsets measured in Level 1T image space are converted to the corresponding uncorrected detector/line coordinates and then to along-track and cross-track angular displacements using Equations (11) and (12). The preprocessed tie point measurements from each SCA are then used in a least squares solution to compute updates to the eight band 11 Legendre coefficients for that SCA. The Legendre coefficient updates for the calibration scenes were averaged to generate the final on-orbit update to the band 11 line-of-sight model.
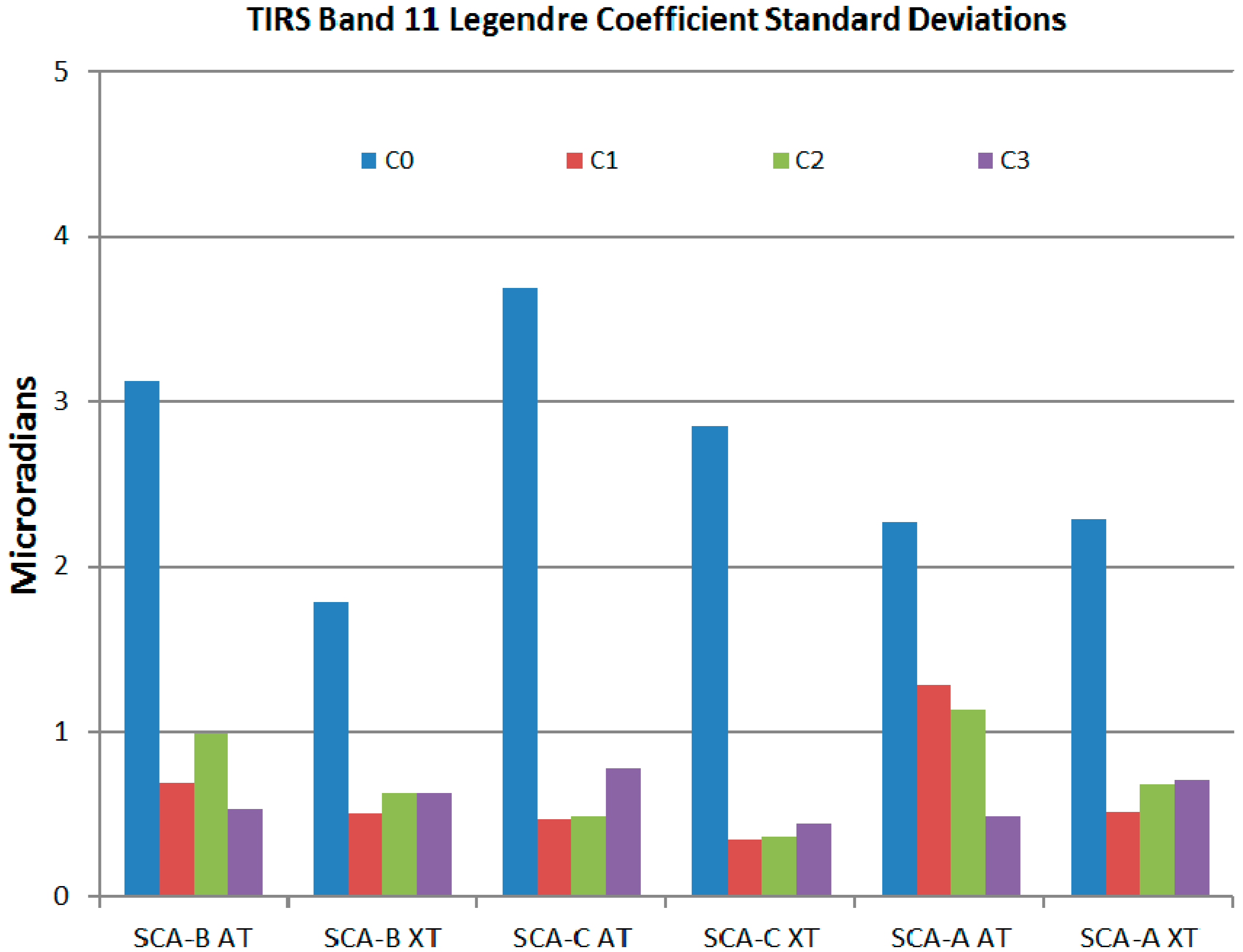
The standard deviations of the calculated Legendre coefficient updates are shown in
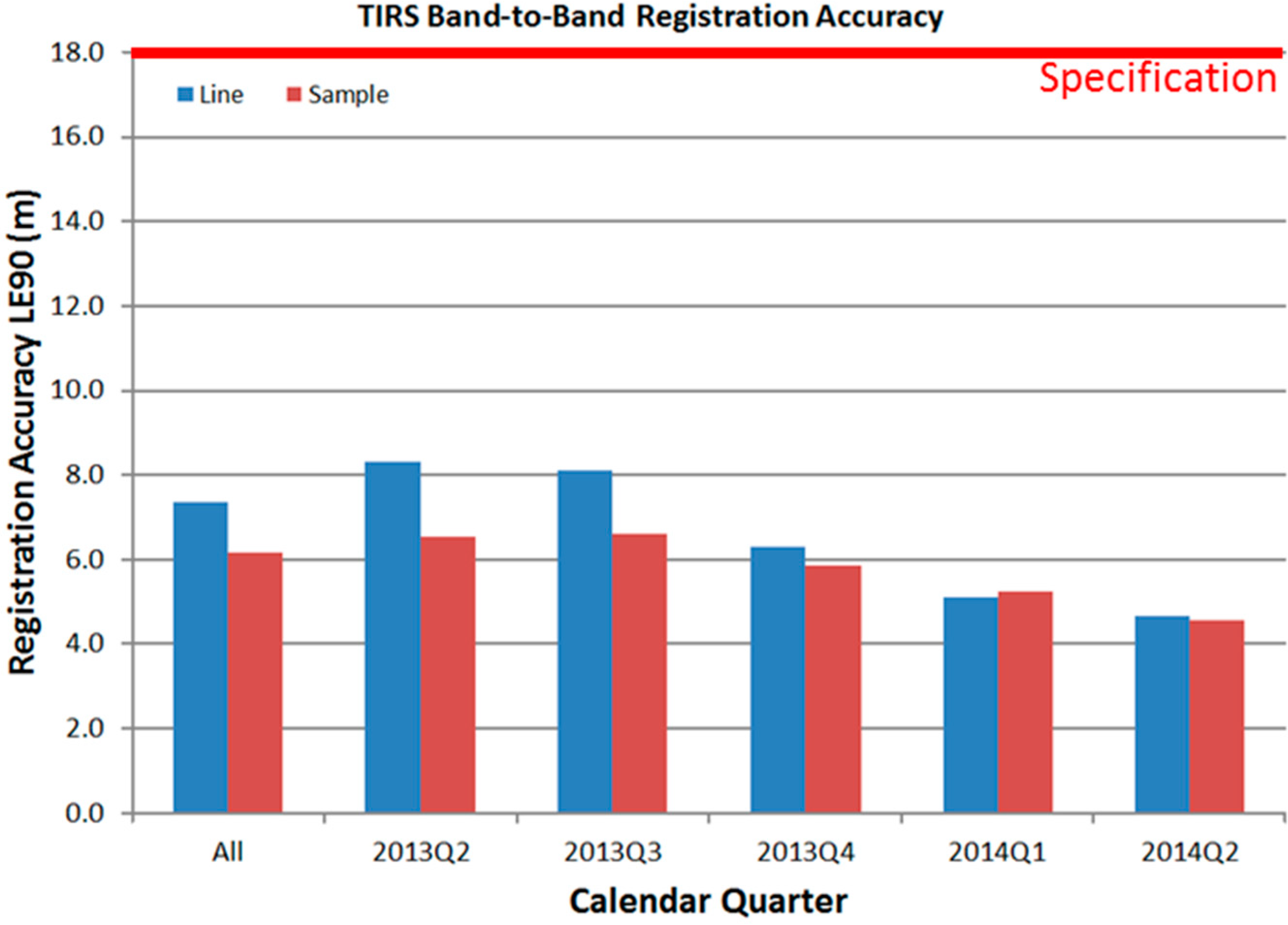
Figure 10. Converting the standard deviations to 90% linear error (LE90) and summing the contributions from the four coefficients for each direction and SCA yields a maximum uncertainty less than 6.4 meters in the along-track direction and less than 4.9 meters in the cross-track direction. Calibration error should thus contribute only a small amount to the 18-meter (LE90) TIRS band registration performance requirement.