An EOF-Based Algorithm to Estimate Chlorophyll a Concentrations in Taihu Lake from MODIS Land-Band Measurements: Implications for Near Real-Time Applications and Forecasting Models
Abstract
:1. Introduction
2. Data and Method
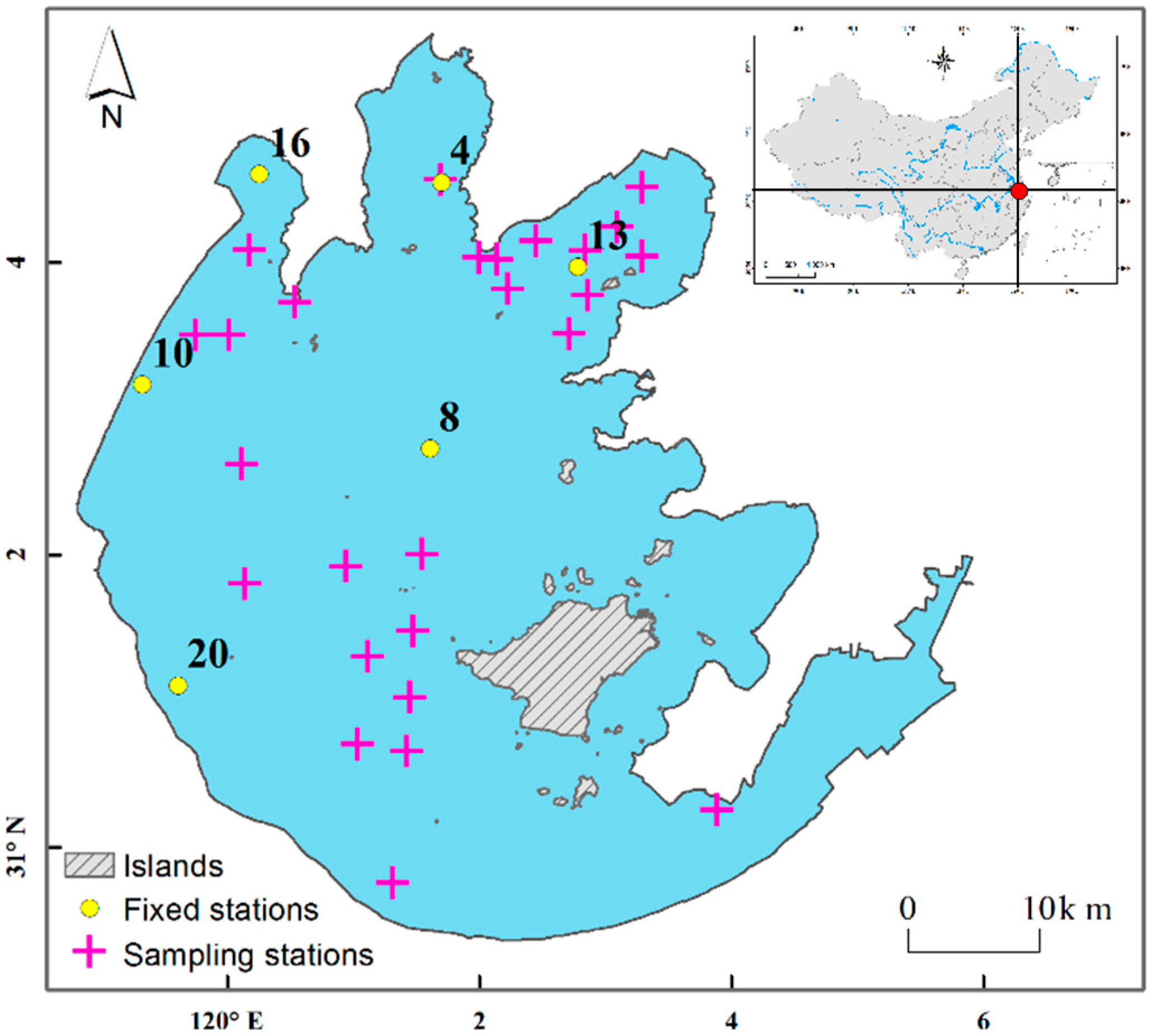
2.1. Study Area
2.2. Field Data
2.3. MODIS Satellite Data
| Season (Months) | # Of Images |
|---|---|
| Spring (April, May, June) | 211 |
| Summer (July, August, September) | 192 |
| Autumn (October, November, December) | 203 |
| Winter (January, February, March) | 247 |
| Total # of Images | 853 |
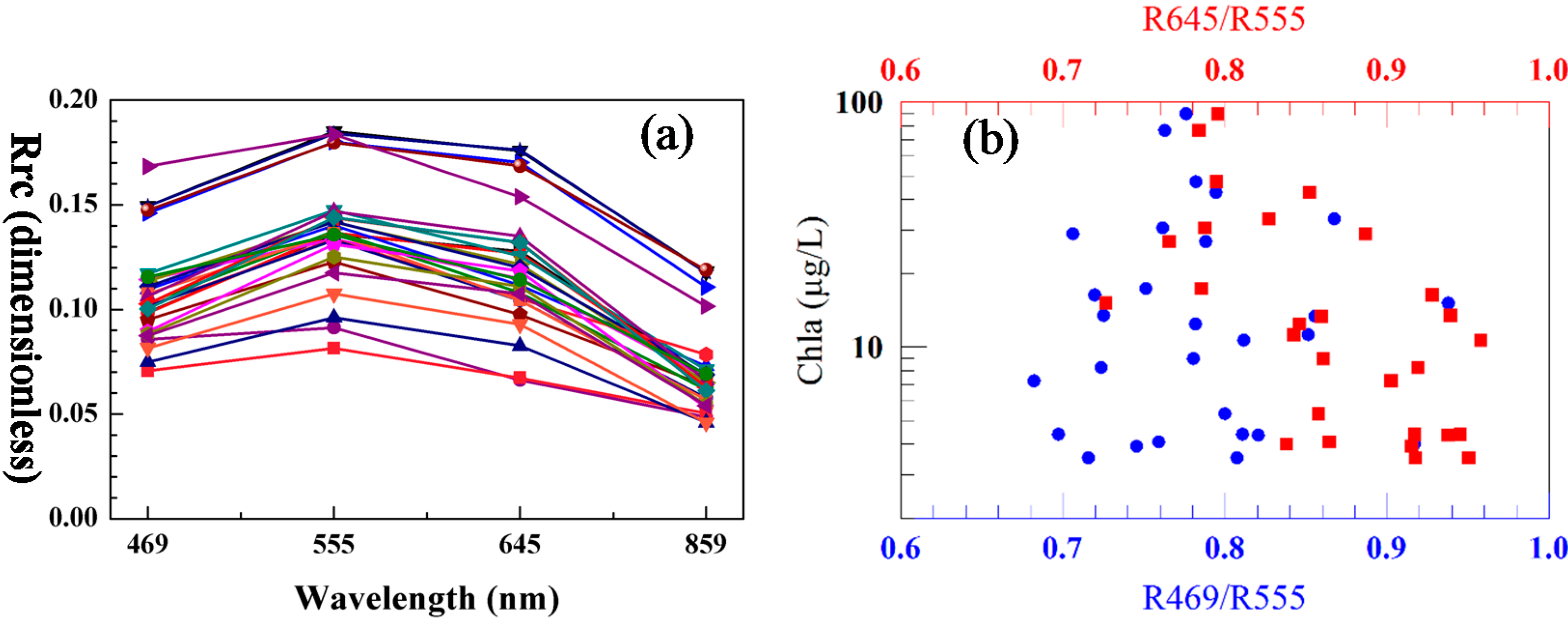
2.4. Algorithm Development
2.5. Algorithm Evaluation
3. Results
3.1. Algorithm Development
3.2. Algorithm Validation
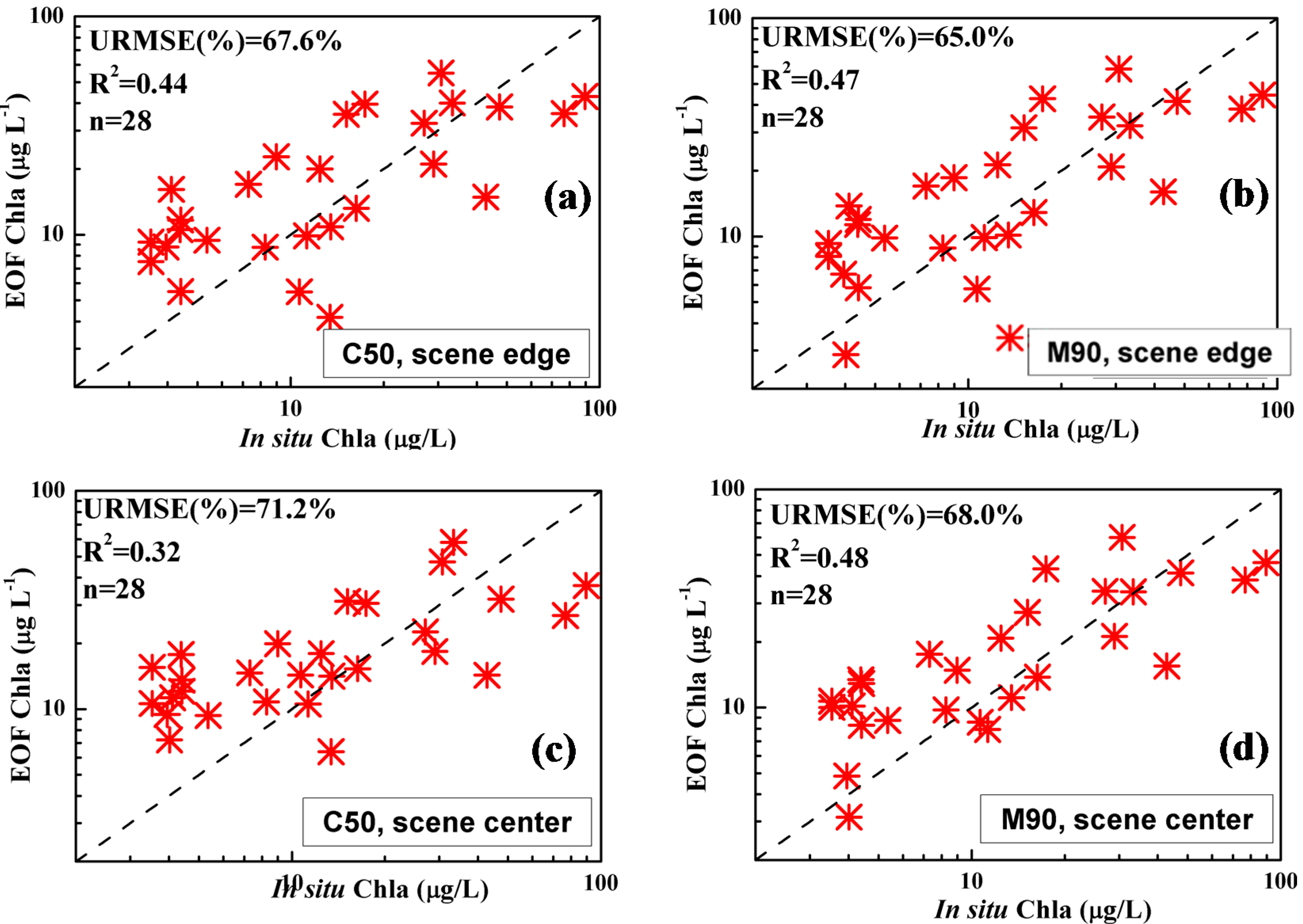
3.2.1. Validation Using MODIS Data and Field Data
3.2.2. Validation Using MODIS Data Alone
3.2.3. Sensitivity Test Using Radiative Transfer Simulations
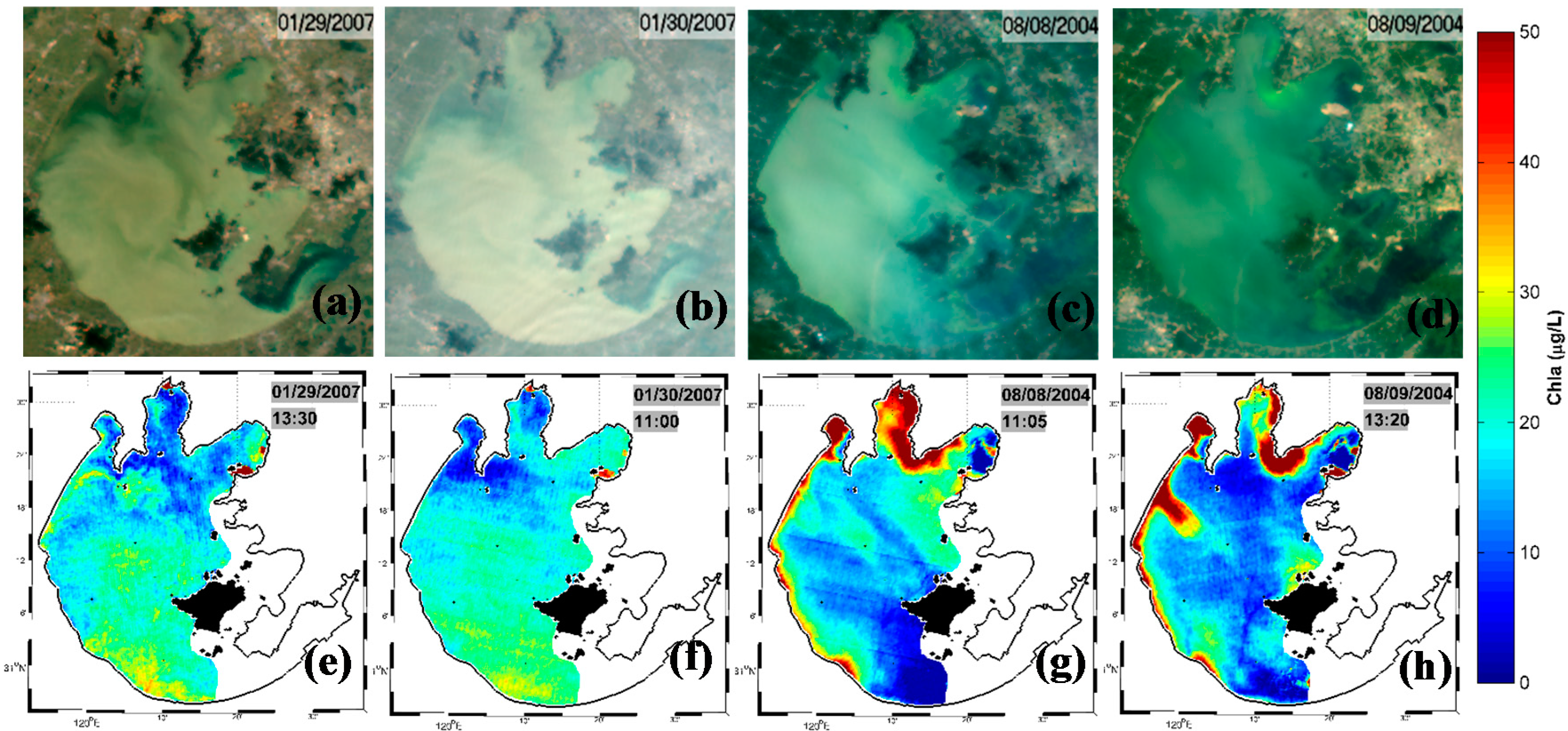
3.3. Application to Long-Term MODIS Data

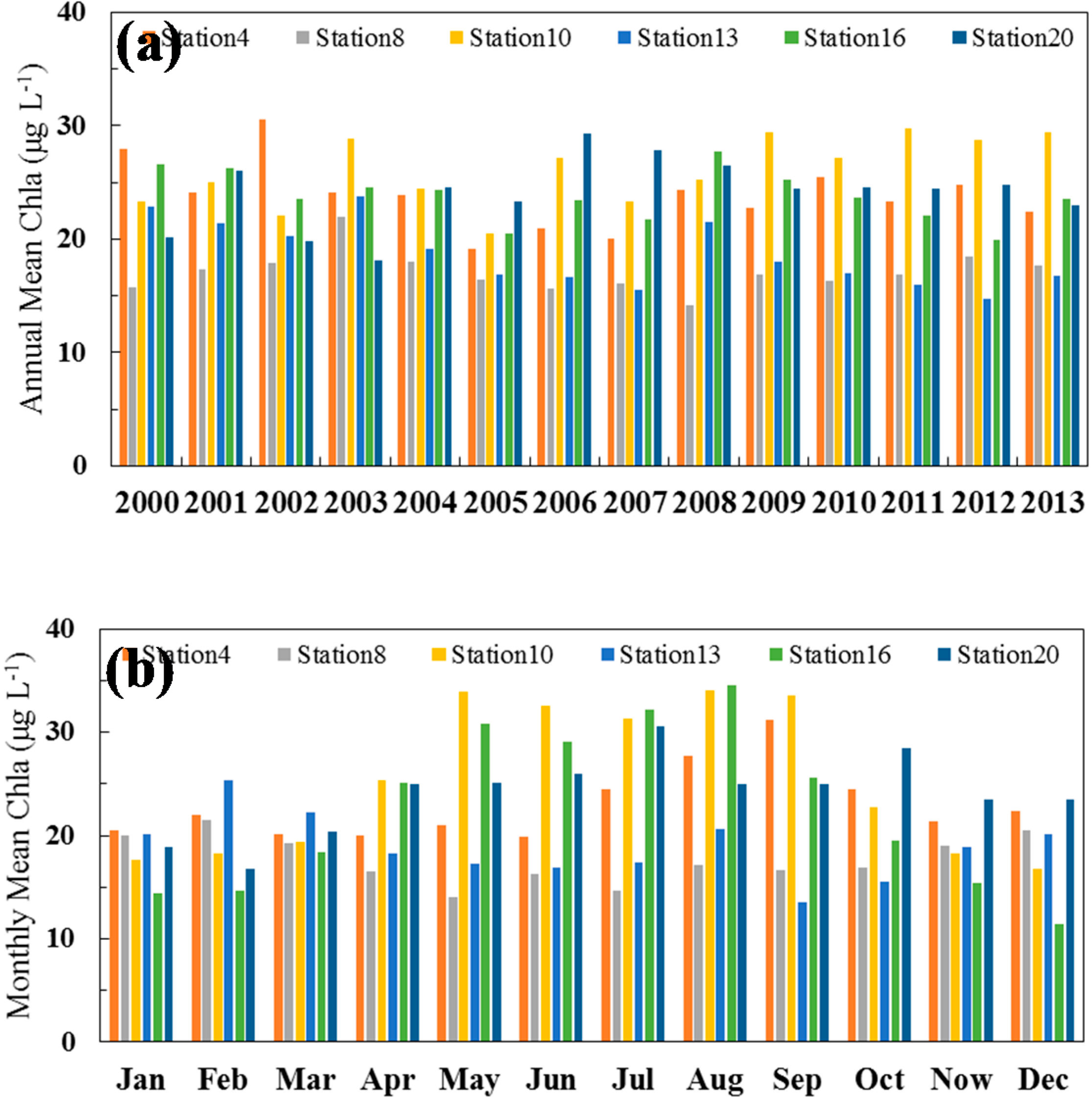
3.4. Data Assimilation Results Using Default Chla and New Chla: A Comparison
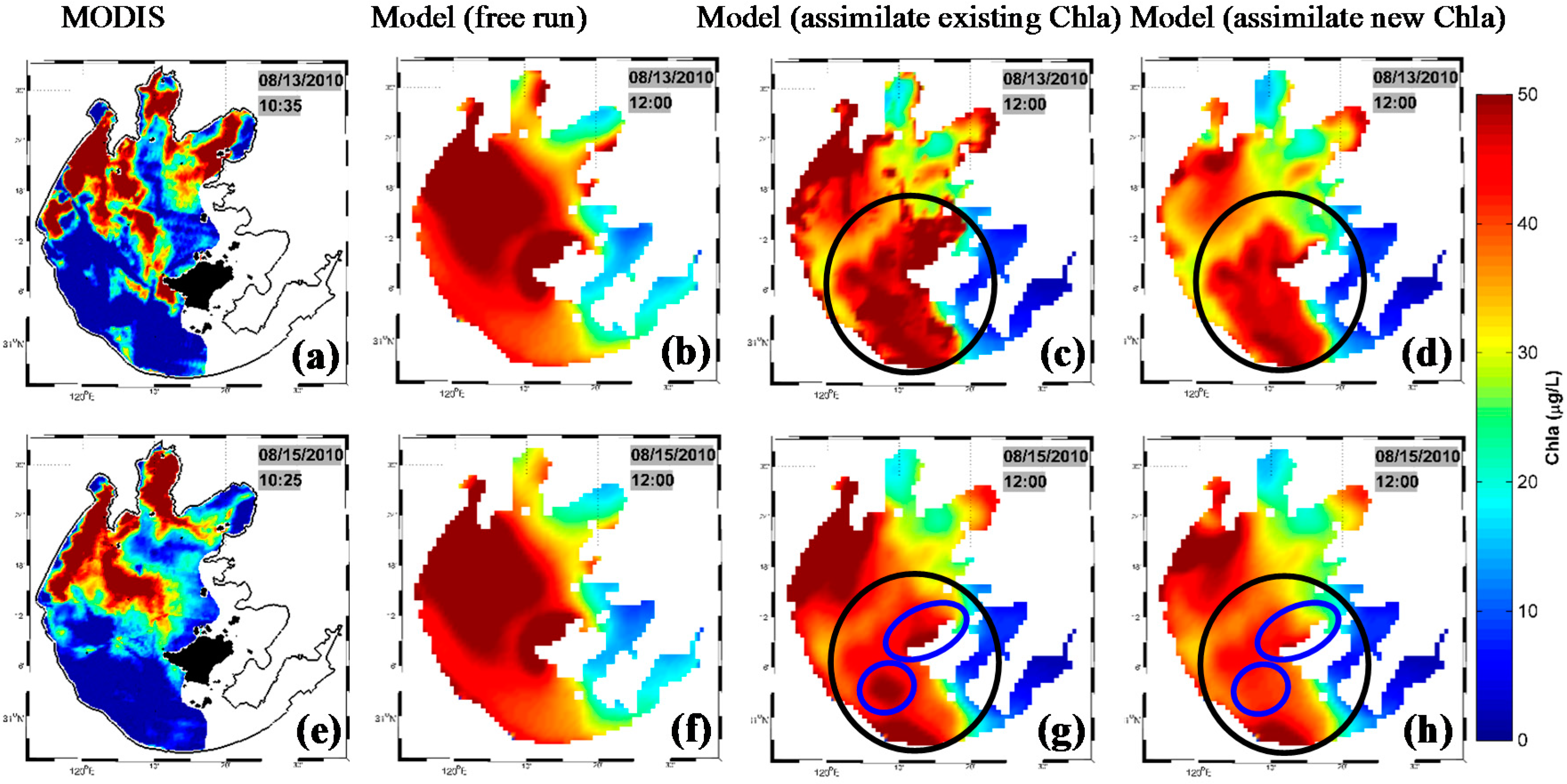
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kahru, M.; Mitchell, B.G. Ocean color reveals increased blooms in various parts of the world. Eos Trans. Am. Geophys. Union 2008. [Google Scholar] [CrossRef]
- Lapointe, B.E.; Langton, R.; Bedford, B.J.; Potts, A.C.; Day, O.; Hu, C. Land-based nutrient enrichment of the Buccoo Reef Complex and fringing coral reefs of Tobago, West Indies. Mar. Pollut. Bull. 2010, 60, 334–343. [Google Scholar] [CrossRef] [PubMed]
- Beman, J.M.; Arrigo, K.R.; Matson, P.A. Agricultural runoff fuels large phytoplankton blooms in vulnerable areas of the ocean. Nature 2005, 434, 211–214. [Google Scholar] [CrossRef] [PubMed]
- Brand, L.E.; Compton, A. Long-term increase in Karenia brevis abundance along the Southwest Florida Coast. Harmful Algae 2007, 6, 232–252. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Zhou, M. Progress of the project ecology and oceanography of harmful algal blooms in China. Adv. Earth Sci. 2006, 21, 673–679. (In Chinese) [Google Scholar]
- Liu, D.; Keesing, J.K.; Xing, Q.; Shi, P. World’s largest macroalgal bloom caused by expansion of seaweed aquaculture in China. Mar. Pollut. Bull. 2009, 58, 888–895. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Li, D.; Chen, C.; Ge, J.; Muller-Karger, F.E.; Liu, J.; Yu, F.; He, M.X. On the recurrent Ulva prolifera blooms in the Yellow Sea and East China Sea. J. Geophys. Res.: Oceans (1978–2012) 2010, 115. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Ma, R.; Yu, K.; Li, D.; Shang, S. Moderate resolution imaging spectroradiometer (MODIS) observations of cyanobacteria blooms in Taihu Lake, China. J. Geophys. Res. Oceans (1978–2012) 2010, 115. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Xu, X.; Kong, F.; Zhang, S.; Kong, W.; Hao, J.; Shang, L. Two-decade reconstruction of algal blooms in China’s Lake Taihu. Environ. Sci. Technol. 2009, 43, 3522–3528. [Google Scholar] [CrossRef] [PubMed]
- Schaeffer, B.A.; Hagy, J.D.; Conmy, R.N.; Lehrter, J.C.; Stumpf, R.P. An approach to developing numeric water quality criteria for coastal waters using the SeaWiFS satellite data record. Environ. Sci. Technol. 2012, 46, 916–922. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.M. Approaches to monitoring, control and management of harmful algal blooms (HABs). Ocean Coast. Manag. 2009, 52, 342–347. [Google Scholar] [CrossRef] [PubMed]
- Kudela, R.; Seeyave, S.; Cochlan, W. The role of nutrients in regulation and promotion of harmful algal blooms in upwelling systems. Prog. Oceanogr. 2010, 85, 122–135. [Google Scholar] [CrossRef]
- Bouma, J.; Van der Woerd, H.; Kuik, O. Assessing the value of information for water quality management in the North Sea. J. Environ. Manag. 2009, 90, 1280–1288. [Google Scholar] [CrossRef]
- Kong, F.; Ma, R.; Gao, J.; Wu, X. The theory and practice of prevention, forecast and warning on cyanobacteria bloom in Lake Taihu. J. Lake Sci. 2009, 3, 314–328. [Google Scholar]
- Sellner, K.G.; Doucette, G.J.; Kirkpatrick, G.J. Harmful algal blooms: Causes, impacts and detection. J. Ind. Microbiol. Biotechnol. 2003, 30, 383–406. [Google Scholar] [CrossRef] [PubMed]
- Pierson, D.C.; Strömbeck, N. A modelling approach to evaluate preliminary remote sensing algorithms: Use of water quality data from Swedish Great Lakes. Geophysica 2000, 36, 177–202. [Google Scholar]
- Thiemann, S.; Kaufmann, H. Determination of chlorophyll content and trophic state of lakes using field spectrometer and IRS-1C satellite data in the Mecklenburg Lake District, Germany. Remote Sens. Environ. 2000, 73, 227–235. [Google Scholar] [CrossRef]
- Ruddick, K.G.; Gons, H.J.; Rijkeboer, M.; Tilstone, G. Optical remote sensing of chlorophyll a in case 2 waters by use of an adaptive two-band algorithm with optimal error properties. Appl. Opt. 2001, 40, 3575–3585. [Google Scholar] [CrossRef]
- Tassan, S.; Ferrari, G.M. Variability of light absorption by aquatic particles in the near-infrared spectral region. Appl. Opt. 2003, 42, 4802–4810. [Google Scholar] [CrossRef]
- Dal’Olmo, G.; Gitelson, A.A.; Rundquist, D.C.; Leavitt, B.; Barrow, T.; Holz, J.C. Assessing the potential of SeaWiFS and MODIS for estimating chlorophyll concentration in turbid productive waters using red and near-infrared bands. Remote Sens. Environ. 2005, 96, 176–187. [Google Scholar] [CrossRef]
- Jiao, H.; Zha, Y.; Gao, J.; Li, Y.; Wei, Y.; Huang, J. Estimation of chlorophyll a concentration in Lake Tai, China using in situ hyperspectral data. Int. J. Remote Sens. 2006, 27, 4267–4276. [Google Scholar] [CrossRef]
- Tzortziou, M.; Herman, J.R.; Gallegos, C.L.; Neale, P.J.; Subramaniam, A.; Harding, L.W., Jr.; Ahmad, Z. Bio-optics of the Chesapeake Bay from measurements and radiative transfer closure. Estuar. Coast. Shelf Sci. 2006, 68, 348–362. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.C.; Barrow, T.; Fisher, T.R.; Gurlin, D.; Holz, J. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Lu, H. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes: The case of Taihu Lake, China. Remote Sens. Environ. 2009, 113, 1175–1182. [Google Scholar] [CrossRef]
- Le, C.; Hu, C.; English, D.; Cannizzaro, J.; Kovach, C. Climate-driven chlorophyll-a changes in a turbid estuary: Observations from satellites and implications for management. Remote Sens. Environ. 2013, 130, 11–24. [Google Scholar] [CrossRef]
- Keiner, L. Estimating oceanic chlorophyll concentrations with neural networks. Int. J. Remote Sens. 1999, 20, 189–194. [Google Scholar]
- Craig, S.E.; Jones, C.T.; Li, W.K.; Lazin, G.; Horne, E.; Caverhill, C.; Cullen, J.J. Deriving optical metrics of coastal phytoplankton biomass from ocean colour. Remote Sens. Environ. 2012, 119, 72–83. [Google Scholar] [CrossRef]
- Hu, C.; Barnes, B.B.; Murch, B.; Carlson, P. Satellite-based virtual buoy system to monitor coastal water quality. Opt. Eng. 2014, 53, 051402–051402. [Google Scholar] [CrossRef]
- Hu, C.; Feng, L.; Lee, Z.; Davis, C.O.; Mannino, A.; McClain, C.R.; Franz, B.A. Dynamic range and sensitivity requirements of satellite ocean color sensors: Learning from the past. Appl. Opt. 2012, 51, 6045–6062. [Google Scholar] [CrossRef] [PubMed]
- Le, C.; Hu, C.; Cannizzaro, J.; Duan, H. Long-term distribution patterns of remotely sensed water quality parameters in Chesapeake Bay. Estuar. Coast. Shelf Sci. 2013, 128, 93–103. [Google Scholar] [CrossRef]
- Millie, D.F.; Weckman, G.R.; Young, W.A., II; Ivey, J.E.; Fries, D.P.; Ardjmand, E.; Fahnenstiel, G.L. Coastal “Big Data” and nature-inspired computation: Prediction potentials, uncertainties, and knowledge derivation of neural networks for an algal metric. Estuar. Coast. Shelf Sci. 2013, 125, 57–67. [Google Scholar]
- Popova, E.; Lozano, C.; Srokosz, M.; Fasham, M.; Haley, P.; Robinson, A. Coupled 3D physical and biological modelling of the mesoscale variability observed in North-East Atlantic in spring 1997: Biological processes. Deep Sea Res. Part I: Oceanogr. Res. Pap. 2002, 49, 1741–1768. [Google Scholar] [CrossRef]
- Hu, W.; Jørgensen, S.E.; Zhang, F. A vertical-compressed three-dimensional ecological model in Lake Taihu, China. Ecol. Model. 2006, 190, 367–398. [Google Scholar] [CrossRef]
- Anderson, L.A.; Robinson, A.R.; Lozano, C.J. Physical and biological modeling in the Gulf Stream region: I Data assimilation methodology. Deep Sea Res. Part I: Oceanogr. Res. Pap. 2000, 47, 1787–1827. [Google Scholar] [CrossRef]
- Natvik, L.-J.; Evensen, G. Assimilation of ocean colour data into a biochemical model of the North Atlantic: Part 1. Data assimilation experiments. J. Mar. Syst. 2003, 40, 127–153. [Google Scholar] [CrossRef]
- Nerger, L.; Gregg, W.W. Assimilation of SeaWiFS data into a global ocean-biogeochemical model using a local SEIK filter. J. Mar. Syst. 2007, 68, 237–254. [Google Scholar] [CrossRef]
- Tjiputra, J.F.; Polzin, D.; Winguth, A.M. Assimilation of seasonal chlorophyll and nutrient data into an adjoint three-dimensional ocean carbon cycle model: Sensitivity analysis and ecosystem parameter optimization. Glob. Biogeochem. Cycles 2007, 21. [Google Scholar] [CrossRef]
- Mao, J.; Lee, J.H.; Choi, K. The extended Kalman filter for forecast of algal bloom dynamics. Water Res. 2009, 43, 4214–4224. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Fennel, K.; Mattern, J.P.; Wilkin, J. Data assimilation with a local Ensemble Kalman Filter applied to a three-dimensional biological model of the Middle Atlantic Bight. J. Mar. Syst. 2012, 94, 145–156. [Google Scholar] [CrossRef]
- Huang, J.; Gao, J.; Liu, J.; Zhang, Y. State and parameter update of a hydrodynamic-phytoplankton model using ensemble Kalman filter. Ecol. Model. 2013, 263, 81–91. [Google Scholar] [CrossRef]
- Ishizaka, J. Coupling of coastal zone color scanner data to a physical-biological model of the southeastern US continental shelf ecosystem: 2. An Eulerian model. J. Geophys. Res.: Oceans (1978–2012) 1990, 95, 20183–20199. [Google Scholar] [CrossRef]
- Qi, L.; Ma, R.; Hu, W.; Loiselle, S.A. Assimilation of MODIS chlorophyll a data into a coupled hydrodynamic-biological model of Taihu Lake. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1623–1631. [Google Scholar]
- Kong, W.; Ma, R.; Duan, H. The neural network model for estimation of chlorophyll-a with water temperature in Lake Taihu. J. Lake Sci. 2009, 21, 193–198. [Google Scholar]
- Gons, H.J. Optical teledetection of chlorophyll a in turbid inland waters. Environ. Sci. Technol. 1999, 33, 1127–1132. [Google Scholar] [CrossRef]
- Han, L.; Rundquist, D.C. Comparison of NIR/RED ratio and first derivative of reflectance in estimating algal-chlorophyll concentration: A case study in a turbid reservoir. Remote Sens. Environ. 1997, 62, 253–261. [Google Scholar] [CrossRef]
- Ma, R.; Dai, J. Investigation of chlorophyll a and total suspended matter concentrations using Landsat ETM and field spectral measurement in Taihu Lake, China. Int. J. Remote Sens. 2005, 26, 2779–2795. [Google Scholar] [CrossRef]
- Yacobi, Y.Z.; Moses, W.J.; Kaganovsky, S.; Sulimani, B.; Leavitt, B.C.; Gitelson, A.A. NIR-red reflectance-based algorithms for chlorophyll-a estimation in mesotrophic inland and coastal waters: Lake Kinneret case study. Water Res. 2011, 45, 2428–2436. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, M.; Qin, B.; Van der Woerd, H.J.; Li, J.; Li, Y. Modeling remote-sensing reflectance and retrieving chlorophyll-a concentration in extremely turbid Case-2 waters (Lake Taihu, China). IEEE Trans. Geosci. Remote Sens. 2009, 47, 1937–1948. [Google Scholar] [CrossRef]
- Kahru, M.; Kudela, R.M.; Anderson, C.R.; Manzano-Sarabia, M.; Mitchell, B.G. Evaluation of satellite retrievals of ocean chlorophyll-a in the California Current. Remote Sens. 2014, 6, 8524–8540. [Google Scholar] [CrossRef]
- Blondeau-Patissier, D.; Gower, J.F.R.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Qin, B.; Xu, P.; Wu, Q.; Luo, L.; Zhang, Y. Environmental issues of lake Taihu, China. Hydrobiologia 2007, 581, 3–14. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, W.; Gu, K.; Li, Q.; Zheng, D.; Zhai, S. An improved ecological model and software for short-term algal bloom forecasting. Environ. Model. Softw. 2013, 48, 152–162. [Google Scholar] [CrossRef]
- Guo, L. Doing battle with the green monster of Taihu Lake. Science 2007, 317, 1166–1166. [Google Scholar] [CrossRef] [PubMed]
- Ma, R.; Tang, J.; Dai, J.; Zhang, Y.; Song, Q. Absorption and scattering properties of water body in Taihu Lake, China: Absorption. Int. J. Remote Sens. 2006, 27, 4277–4304. [Google Scholar] [CrossRef]
- Ma, R.; Tang, J.; Dai, J. Bio-optical model with optimal parameter suitable for Taihu Lake in water colour remote sensing. Int. J. Remote Sens. 2006, 27, 4305–4328. [Google Scholar]
- Pinckney, J.; Papa, R.; Zingmark, R. Comparison of high-performance liquid chromatographic, spectrophotometric, and fluorometric methods for determining chlorophyll a concentrations in estaurine sediments. J. Microbiol. Methods 1994, 19, 59–66. [Google Scholar] [CrossRef]
- NASA Ocean Biology Processing Group. OceanColor Web. Available online: http://oceancolor.gsfc.nasa.gov (accessed on 15 February 2014).
- Hu, C.; Chen, Z.; Clayton, T.D.; Swarzenski, P.; Brock, J.C.; Muller-Karger, F.E. Assessment of estuarine water-quality indicators using MODIS medium-resolution bands: Initial results from Tampa Bay, FL. Remote Sens. Environ. 2004, 93, 423–441. [Google Scholar] [CrossRef]
- O’Reilly, J.; Maritorena, S.; Siegel, D.; Siegel, D.A.; Margaret, C.; Dierdre, T.; Greg, M.; Mati, K.; Francisco, P.C.; Strutton, P.; et al. Ocean color chlorophyll a algorithms for SeaWiFS, OC2, and OC4: Version 4. In SeaWiFS Postlaunch Technical Report Series, Volume 11, SeaWiFS Postlaunch Calibration and Validation Analyses, Part 3; Hooker, S.B., Firestone, E.R., Eds.; NASA, Goddard Space Flight Center: Greenbelt, MD, USA, 2000; pp. 8–23. [Google Scholar]
- Barnes, B.B.; Hu, C.; Cannizzaro, J.P.; Craig, S.E.; Hallock, P.; Jones, D.L.; Lehrter, J.C.; Melo, N.; Schaeffer, B.A.; Zepp, R.; et al. Estimation of diffuse attenuation of ultraviolet light in optically shallow Florida Keys waters from MODIS measurements. Remote Sens. Environ. 2014, 140, 519–532. [Google Scholar] [CrossRef]
- Song, K.; Li, L.; Tedesco, L.P.; Li, S.; Clercin, N.A.; Hall, B.E.; Li, Z.; Shi, K. Hyperspectral determination of eutrophication for a water supply source via genetic algorithm-partial least squares (GA-PLS) modeling. Sci. Total Environ. 2012, 426, 220–232. [Google Scholar] [PubMed]
- Campbell, J.W. The lognormal distribution as a model for bio-optical variability in the sea. J. Geophys. Res.: Oceans (1978–2012) 1995, 100, 13237–13254. [Google Scholar] [CrossRef]
- Hooker, S.B.; Lazin, G.; Zibordi, G.; McLean, S. An evaluation of above- and in-water methods for determining water-leaving radiances. J. Atmos. Ocean. Technol. 2002, 19, 486–515. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res.: Oceans (1978–2012) 2012, 117. [Google Scholar] [CrossRef]
- Gregg, W.W.; Casey, N.W. Global and regional evaluation of the SeaWiFS chlorophyll data set. Remote Sens. Environ. 2004, 93, 463–479. [Google Scholar]
- Hu, W.; Zhai, S.; Zhu, Z.; Han, H. Impacts of the Yangtze River water transfer on the restoration of Lake Taihu. Ecol. Eng. 2008, 34, 30–49. [Google Scholar]
- Duan, H.; Ma, R.; Zhang, Y.; Loiselle, S.A.; Xu, J.; Zhao, C.; Zhou, L.; Shang, L. A new three-band algorithm for estimating chlorophyll concentrations in turbid inland lakes. Environ. Res. Lett. 2010, 5. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W.; Tang, J. Water property monitoring and assessment for China’s inland Lake Taihu from MODIS-Aqua measurements. Remote Sens. Environ. 2011, 115, 841–854. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, R.; Li, J.; Zhang, B.; Duan, H. A validation study of an improved SWIR iterative atmospheric correction algorithm for MODIS-Aqua measurements in Lake Taihu, China. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4686–4695. [Google Scholar] [CrossRef]
- Le, C.; Hu, C.; English, D.; Cannizzaro, J.; Chen, Z.; Feng, L.; Boler, R.; Kovach, C. Towards a long-term chlorophyll a data record in a turbid estuary using MODIS observations. Prog. Oceanogr. 2013, 109, 90–103. [Google Scholar] [CrossRef]
- Chen, Y.; Qin, B.; Gao, X. Prediction of blue-green algae bloom using stepwise multiple regression between algae & related environmental factors in Meiliang Bay, Lake Taihu. J. Lake Sci. 2001, 1, 63–71. [Google Scholar]
- Lee, J.H.; Huang, Y.; Dickman, M.; Jayawardena, A. Neural network modelling of coastal algal blooms. Ecol. Model. 2003, 159, 179–201. [Google Scholar] [CrossRef]
- Muttil, N.; Chau, K.-W. Neural network and genetic programming for modelling coastal algal blooms. Int. J. Environ. Pollut. 2006, 28, 223–238. [Google Scholar]
- Laanemets, J.; Lilover, M.-J.; Raudsepp, U.; Autio, R.; Vahtera, E.; Lips, I.; Lips, U. A fuzzy logic model to describe the cyanobacteria Nodularia spumigena blooms in the Gulf of Finland, Baltic Sea. Hydrobiologia 2006, 554, 31–45. [Google Scholar] [CrossRef]
- Hamilton, D.P.; Schladow, S.G. Prediction of water quality in lakes and reservoirs Part I—Model description. Ecol. Model. 1997, 96, 91–110. [Google Scholar] [CrossRef]
- Schladow, S.G.; Hamilton, D.P. Prediction of water quality in lakes and reservoirs: Part II—Model calibration, sensitivity analysis and application. Ecol. Model. 1997, 96, 111–123. [Google Scholar] [CrossRef]
- Sacau-Cuadrado, M.; Conde-Pardo, P.; Otero-Tranchero, P. Forecast of red tides off the Galician coast. Acta Astronaut. 2003, 53, 439–443. [Google Scholar] [CrossRef]
- Allen, J.; Smyth, T.J.; Siddorn, J.R.; Holt, M. How well can we forecast high biomass algal bloom events in a eutrophic coastal sea? Harmful Algae 2008, 8, 70–76. [Google Scholar] [CrossRef]
- Los, F.; Villars, M.; Van der Tol, M. A 3-dimensional primary production model (BLOOM/GEM) and its applications to the (southern) North Sea (coupled physical-chemical-ecological model). J. Mar. Syst. 2008, 74, 259–294. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Bendoricchio, G. Fundamentals of Ecological Modelling; Elsevier: Oxford, UK, 2001. [Google Scholar]
- Li, W.; Qin, B.; Zhu, G. Forecasting short-term cyanobacterial blooms in Lake Taihu, China, using a coupled hydrodynamic-algal biomass model. Ecohydrology 2013, 7, 794–802. [Google Scholar]
- Huang, J.; Gao, J.; Hörmann, G. Hydrodynamic-phytoplankton model for short-term forecasts of phytoplankton in Lake Taihu, China. Limnol. Ecol. Manag. Inland Waters 2012, 42, 7–18. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, L.; Hu, C.; Duan, H.; Barnes, B.B.; Ma, R. An EOF-Based Algorithm to Estimate Chlorophyll a Concentrations in Taihu Lake from MODIS Land-Band Measurements: Implications for Near Real-Time Applications and Forecasting Models. Remote Sens. 2014, 6, 10694-10715. https://doi.org/10.3390/rs61110694
Qi L, Hu C, Duan H, Barnes BB, Ma R. An EOF-Based Algorithm to Estimate Chlorophyll a Concentrations in Taihu Lake from MODIS Land-Band Measurements: Implications for Near Real-Time Applications and Forecasting Models. Remote Sensing. 2014; 6(11):10694-10715. https://doi.org/10.3390/rs61110694
Chicago/Turabian StyleQi, Lin, Chuanmin Hu, Hongtao Duan, Brian B. Barnes, and Ronghua Ma. 2014. "An EOF-Based Algorithm to Estimate Chlorophyll a Concentrations in Taihu Lake from MODIS Land-Band Measurements: Implications for Near Real-Time Applications and Forecasting Models" Remote Sensing 6, no. 11: 10694-10715. https://doi.org/10.3390/rs61110694
APA StyleQi, L., Hu, C., Duan, H., Barnes, B. B., & Ma, R. (2014). An EOF-Based Algorithm to Estimate Chlorophyll a Concentrations in Taihu Lake from MODIS Land-Band Measurements: Implications for Near Real-Time Applications and Forecasting Models. Remote Sensing, 6(11), 10694-10715. https://doi.org/10.3390/rs61110694








