Evaluating Saturation Correction Methods for DMSP/OLS Nighttime Light Data: A Case Study from China’s Cities
Abstract
: Remotely sensed nighttime lights (NTL) datasets derived from the Defense Meteorological Satellite Program’s Operational Linescan System (DMSP/OLS) have been identified as a good indicator of the urbanization process and have been widely used to study such demographic and economic variables as population distribution and density, electricity consumption, and carbon emission. However, one issue must be considered in the application of NTL data, i.e., saturation in the bright cores of urban centers. In this study, we evaluate four correction methods in China’s cities: the linear regression model and the cubic regression model at the regional level, and the Human Settlement Index (HSI) and the Vegetation Adjusted NTL Urban Index (VANUI) at a pixel level. The results suggest that both correction methods at the regional level improve the correlation between NTL data and socioeconomic variables. However, since the methods can only be used on saturated pixels, the correction effects are limited, as the saturated area in Chinese cities is rather small. HSI and VANUI increase the inter-urban variability within certain cities, especially when their vegetation health and abundance is negatively correlated with NTL. However, the indices may induce bias when applied in a large region with a diverse natural environment and vegetation, and the application of HSI with a relatively high sensitivity of HSI to NDVI may be limited as NTL approaches maximum. Proper methods for reducing saturation effects should thus vary with different study areas and research purposes.1. Introduction
Urbanization is associated with a booming population, socio-economic growth, and land use change [1,2]. The monitoring and measurement of urban dynamics are essential to understand global urbanization. For more than a decade, nighttime light (NTL) data collected by the Defense Meteorological Satellite Program/Operational Linescan System (DMSP/OLS) have been widely used to study urbanization [3–7]. The OLS has a unique capacity for global mapping of artificial lighting present at the Earth’s surface, such as that generated by human settlements, gas flares, fires, and fishing boats [8]. Although NTL does not directly measure human settlements or urban land cover, it is identified as a good indicator of human activity [9–12]. NTL data have been archived since 1992 and are comprised of all available DMSP/OLS data for calendar years; each grid of the image has a digital number (DN), ranging from 0–63, that indicates annual average NTL intensity [13]. In recent years, numerous studies have been conducted on the relationship between NTL data and key socioeconomic variables, such as electricity consumption [14–17], gross domestic product (GDP) [18–23], carbon emission [24–26], economic activity [27–30], and population distribution and density [31–34]. Since statistical data or sufficiently accurate data on these variables is lacking in certain countries and regions, NTL data offer a unique way to study the social economy. Furthermore, with archival data from a period of more than 20 years, since 1992, and with the sensors continuing to record data, NTL data would benefit from time series studies of the urbanization process.
Although DMSP/OLS NTL data consistently demonstrate a strong capacity to evaluate economic distribution over both global and regional scales, the data’s weakness is obvious. As the satellite data were initially used to produce nighttime cloud imagery, the sensor was typically operated in a high gain setting to enable the detection of moonlit clouds. However, with six bit quantization and a limited dynamic range, the recorded data are saturated in the bright cores of urban centers, in which the nighttime light may be brighter, but the DN values are all 63 [35]. The loss of inner-urban variation caused by saturation effects reduces the correlation between the detected nighttime light and economic activities and therefore limits the application of NTL data [36,37]. The saturation issue poses a significant challenge in the application of DMSP/OLS data in the assessment of urbanization processes. The utility of these data for urban applications could be greatly improved if the saturation of NTL data values were corrected or reduced [38]. In an attempt to solve the problem, several global nighttime light products with no saturation have been released (more information on the product can be found on the National Oceanic and Atmospheric Administration website [39]). However, the data are only available for a very limited number of years, which makes it difficult to use NTL data to study a specific year or a long time series. Furthermore, several methods have been developed to correct or reduce NTL saturation, which can be regarded as a remedy for the released non-saturated data. The correction methods can be divided into two categories: those that can only be applied at the regional scale and those that can be used at a pixel scale.
(1) Regional Scale
Hara et al. [40] proposed a linear correction method for the saturated light. With the total number of pixels arranged in increasing order of DN values in an arbitrary area, a linear regression model is determined by the first pixel with DN = 63. Based on the assumption that the tendency of DN change in the saturated area is similar to that of the non-saturated area, Letu et al. [41] obtained a cubic regression equation from the DN of the non-saturated part of stable light and applied it to correct the saturated part.
(2) Pixel Scale
In 1996–1997, Letu et al. [42] developed a saturated light correction method at a pixel scale using a radiance calibration image. They assumed the NTL intensity to be constant in the saturated areas during 1996–1999 and derived a linear regression model from a comparison between the non-saturated part of the stable light image in 1999 and the radiance calibration image in 1996–1997 and used the model to correct saturation for the 1999 image. In order to apply the method, NTL must not change during the observation time. Thus, the method has limited applicability for correcting NTL saturation in numerous developing countries, such as India and China, since their NTL may change due to rapid urban expansion [38]. In addition, the application of this method depends on the availability of a radiance calibration image. By setting the gain of the detector significantly lower than its typical operational setting, it would be possible to observe brightness variations within urban centers. Therefore, Ziskin et al. [35] produced an NTL product in 2006 with no saturation by combining a limited set of NTL data obtained in a lower setting with the operational data acquired at high gain settings. The calibrated data of Ziskin’s method are accurate and of high quality. However, the approach is very labor- and cost-intensive. As the data acquired in low gain settings are sparse and only available for a very limited number of years, the method is unlikely to be used to correct the entire historical NTL archive [38,43]. Previous research has shown that vegetation indices or vegetation abundance are closely correlated in a negative manner with key urban features. Based on this rationale, Lu et al. [44] proposed the Human Settlement Index (HSI), combining DMSP/OLS and Terra MODIS Normalized Difference Vegetation Index (NDVI) data to enhance urban features in saturated areas, and Zhang et al. [38] developed the Vegetation Adjusted NTL Urban Index (VANUI), which also uses MODIS NDVI and NTL.
In summary, the two correction models at the regional scale are based on the change in DN values of NTL data. The saturation effects are corrected by applying the feature of DN change in the non-saturated area. In contrast, the four methods at a pixel scale all utilize NTL images and other satellite data. In terms of data viability, HSI and VANUI can be used for a long-term series; however, the methods of Letu and Ziskin, in which radiance calibration images are combined with NTL data acquired in low gain settings, are only applicable for a limited number of years.
Similar to the DMSP/OLS NTL data, a new generation of nighttime light images without saturation effects was acquired by the Visible Infrared Imaging Radiometer Suite (VIIRS) carried on the Suomi National Polar-Orbiting Partnership (NPP) satellite [45]. The NPP-VIIRS is configured to collect visible and infrared imagery and radiometric measurements of land, atmosphere, cryosphere, and oceans [46,47]. In the current study, the available NPP-VIIRS global nighttime light images were generated using the VIIRS day/night band data collected on nights with zero moonlight during the following periods: 18–26 April 2012, 11–23 October 2012, and January 2013 [48]. Although the NPP-VIIRS data have not been filtered to remove light detections associated with fires, gas flares, volcanoes, or auroras, and while the background noise has not been subtracted, this data has an obvious advantage over DMSP/OLS: saturation is not an issue with the NPP-VIIRS data since a wider radiometric detection range has been used [49]. The VIIRS day/night band on Suomi NPP has a specified dynamic range of approximately seven orders of magnitude from 3×10−9 W·cm−2·sr−1 to 0.02 W·cm−2·sr−1 [50]. Furthermore, the NPP-VIIRS data employ onboard calibration, which is not available for the DMSP-OLS data [51]. A more detailed introduction to NPP-VIIRS is provided on the National Aeronautics and Space Administration website [52].
In this paper, we focused on the problem of NTL saturation. Although several kinds of correction methods have been proposed, no assessment has been made of where and under what conditions a particular method should be applied. The purpose of this paper is to determine the best fitting model for reducing saturation effects. A series of statistical correlation analyses was conducted to evaluate the correction methods from current studies. In light of data availability, we applied four feasible methods in mainland China: the linear regression model and the cubic regression model available at the regional level, and HSI and VANUI at a pixel level. The NPP-VIIRS data were used as a means to evaluate the correction results.
2. Study Area and Data
2.1. Study Area
In 2012, saturation occurred in 135 cities in mainland China (excluding Hong Kong, Macao, and Taiwan), sixty-four of which were defined as severely saturated cities in this study, whose saturated area was more than 30 km2, or the saturated area was equal to more than 1% of the total lit area. To highlight the difference between the original data and the corrected data, 62 severely saturated cities were included in the case study area, as shown in Table 1 (Shanghai and Xiamen were excluded; an explanation for this decision is presented later in this paper).
2.2. Data Collection
The linear model and the cubic regression model act on the regions with DN = 63 and leave the other regions unchanged. To increase the difference between the original data and the corrected data, the NTL image from 2012 was used since the amount of light in China has increased rapidly in recent years [20], and the image from 2012 has a larger saturated area than those from other years. Statistical data on population, GDP, built-up area, and electric power consumption in the selected 62 cities were collected to evaluate the correction results.
HSI and VANUI correction methods can be used at a pixel level. In order to evaluate their correction results, we derived grid maps from various sources: population and GDP distribution in 2003, global radiance calibrated NTL data (with no sensor saturation) in 2003 and 2006, and the NPP-VIIRS image in 2012. Thus, NTL images from 2003, 2006, and 2012 were all used. All data sets used and their detailed descriptions are listed in Table 2.
3. Methods
3.1. Data Processing
As mentioned above, the NPP-VIIRS image is a preliminary product with background noise unassociated with economic activities, such as fires and volcanoes. Shi et al. [49] used DMSP/OLS data to remove data noise and to improve the accuracy and reliability of NPP-VIIRS data. First, the pixels with DN > 0 in the DMSP/OLS image from 2012 were taken as a mask to extract NPP-VIIRS data; two thresholds were then used to correct the outliers in the extracted NPP-VIIRS data, i.e., the pixels with negative DN values were assigned a 0, and pixels greater than 235.13 were smoothed by their eight neighbors. The upper threshold of 235.13 was set as the highest DN value of the three most developed cities in China: Beijing, Shanghai, and Guangzhou. Unlike Shi et al. [49], we took the mean value of the maximum DN in each of the three cities as the upper threshold since we thought that their development should be similar and mean DN could better reduce data bias. All the grid maps were reprojected to a Lambert azimuthal equal area projection with a spatial resolution of 1000 m.
3.2. Implementing Correction Methods
Ziskin’s method [35] and Letu’s method [42], combining radiance calibration images and NTL data acquired in low gain settings, were not considered in this study because of their limited applicability in correcting NTL saturation. The other four methods discussed above were implemented and evaluated in this article. The regression models available only at the regional scale were applied for data from 2012 within administrative units. Additionally, the pixel-based correction methods were applied for data from 2003, 2006, and 2012.
(1) Regional Scale
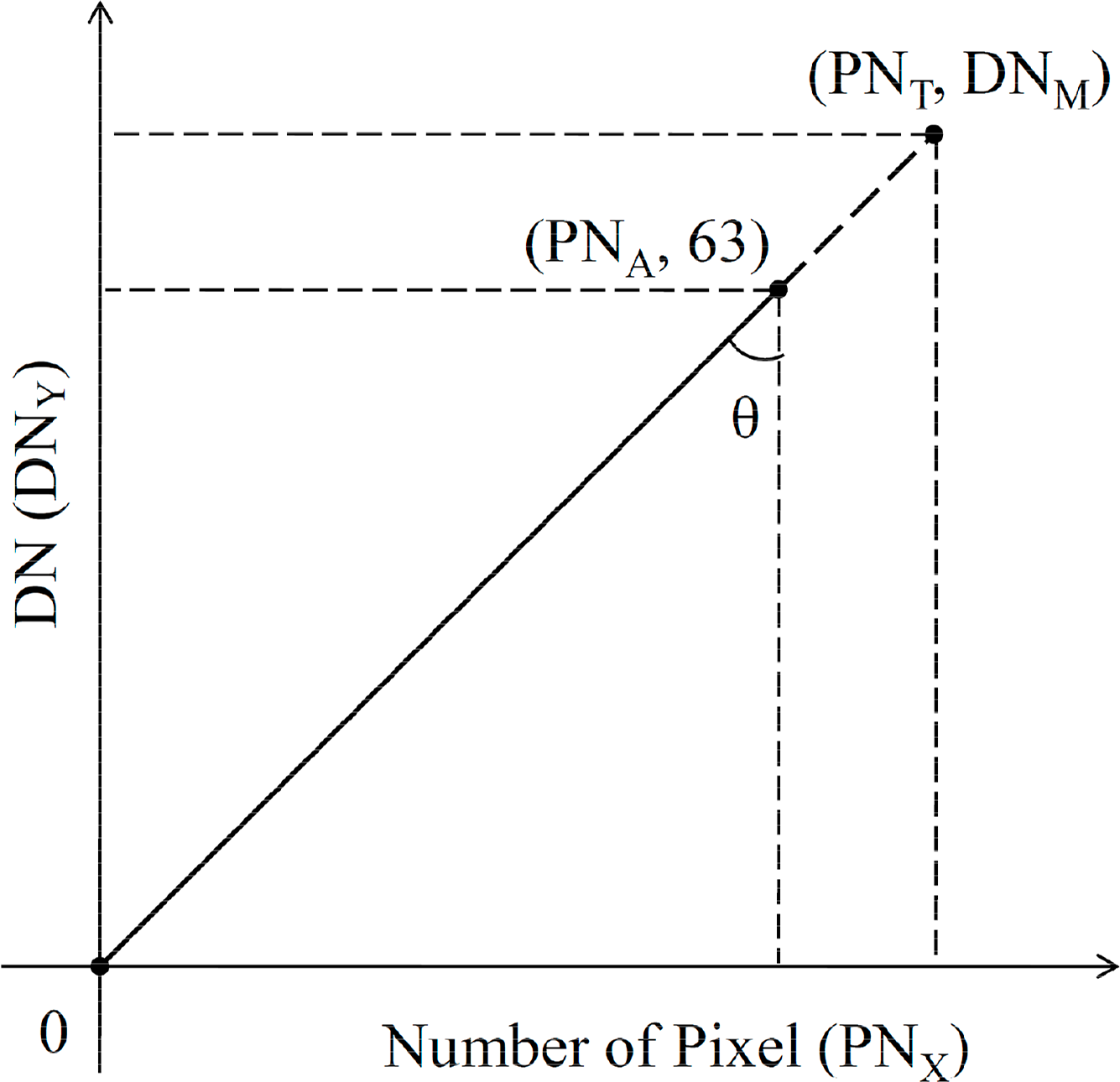
The general idea of Hara’s linear regression model for correcting saturation is presented in Figure 1 [40]. The X-axis shows the accumulated number of pixels (PNX), while the Y-axis shows the arbitrary DN value (DNY).
The angle θ of the right triangle is calculated using Equation (1), Equation (2) is used to calculate the corrected DN from the accumulated number of pixels, and Equation (3) is used to determine the total value of calibrated DN.
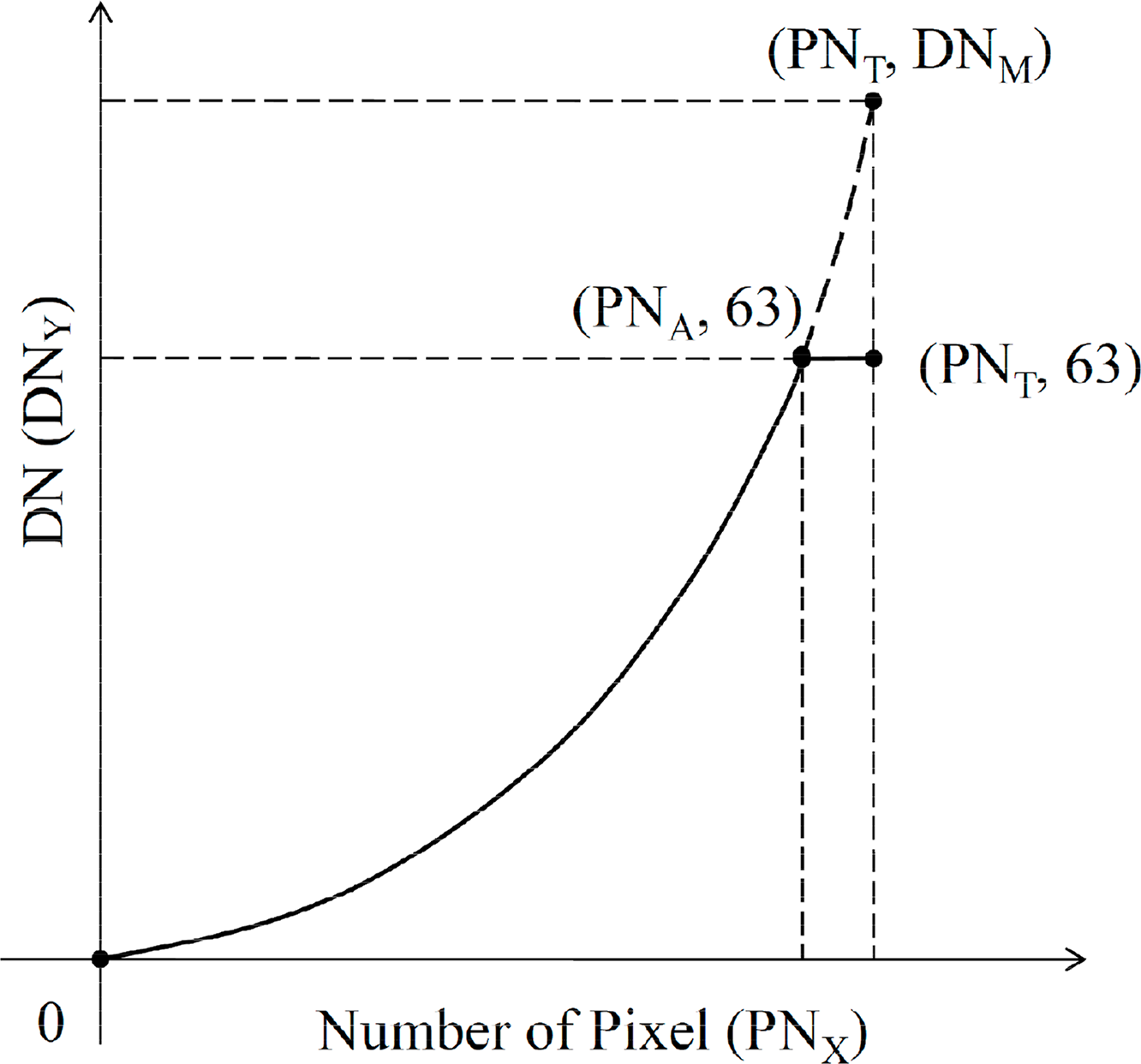
Similar to Hara’s method, the cubic regression model (Figure 2) is also based on the tendency of DN change in non-saturated areas to correct saturation effects.
The two correction methods were applied in the 62 cities, and the accuracy was verified by using statistical data pertaining to population, GDP, built-up area, and electric power consumption.
(2) Pixel Scale
The HSI method and the VANUI method both use contemporaneous NDVI to correct DN saturation based on the principle that key urban features are inversely correlated with vegetation health and abundance.
The methods were performed in 2003, 2006, and 2012. To reduce the effects of dim lighting in NTL images, pixels with DN < 12 were not considered in the analysis [53]. Further, pixels with negative values were removed from NDVIMAX and NDVIMEAN images to exclude water bodies. In general, a higher level of urbanization should result in a lower NDVI and a higher NTL, thus generating higher values in HSI and VANUI. However, the coarse spatial resolution of NTL and NDVI, as well as data bias, could cause outliers in the HSI and VANUI images. Therefore, a threshold method was used to remove noise, which is similar to that used to correct the VIIRS-NPP image; i.e., the average of the highest HSI and VANUI in Beijing, Shanghai, and Guangzhou was used as the upper limit, so each pixel with larger values than the upper limit would be given a new value from their eight neighbors.
4. Results
4.1. Saturation Correction at Regional Scale
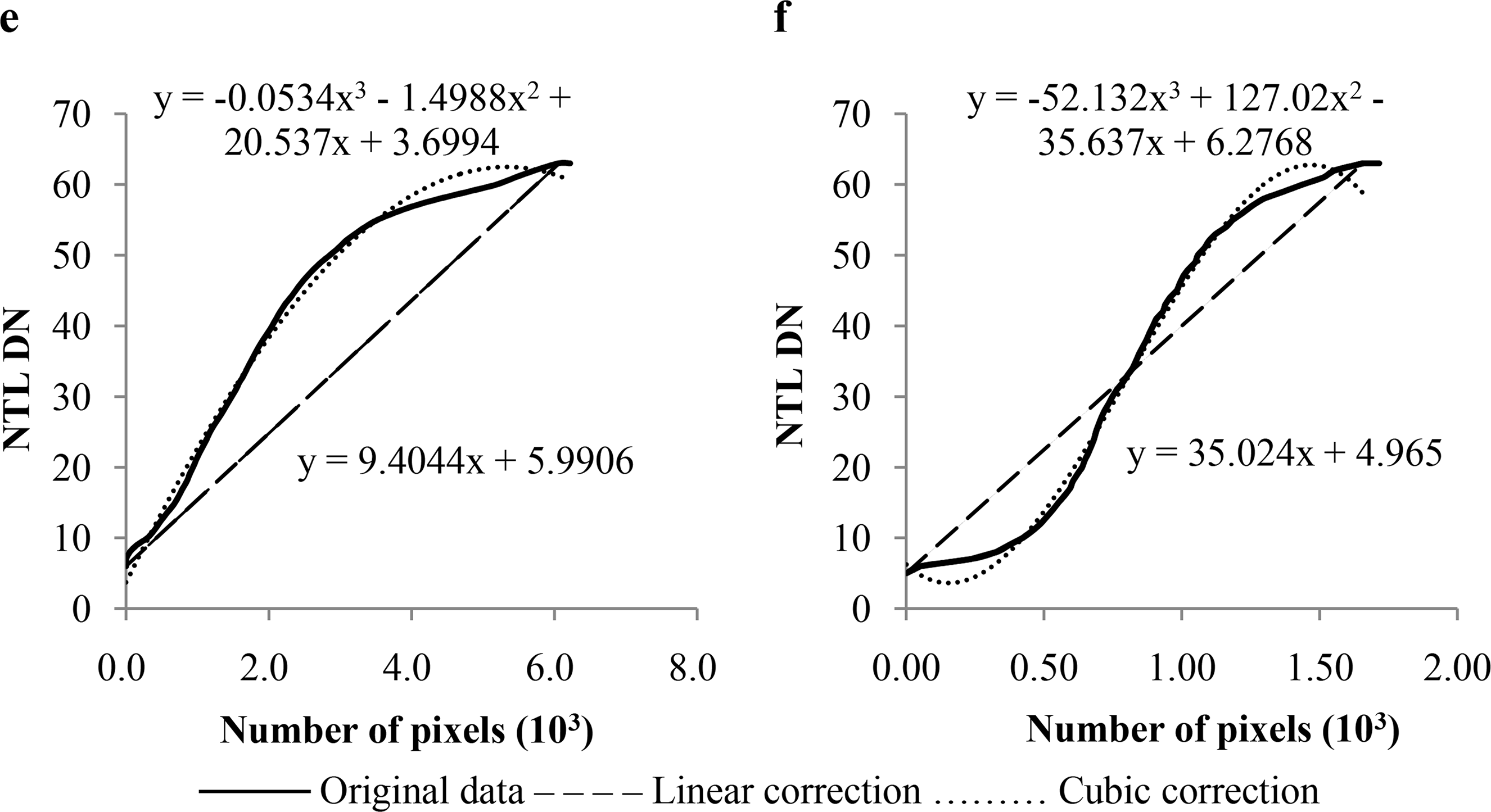
The curves of NTL DN change in most cities present a concave shape, such as those of Beijing (Figure 3a) and Xian (Figure 3b), whereas cities like Suzhou (Figure 3c) and Zhuhai (Figure 3d) have convex shaped curves. These two types of curves fit the linear regression model and the cubic regression model. However, the cubic regression models in Shanghai (Figure 3e) and Xiamen (Figure 3f) imply an incorrect decrease in the curves of NTL DN change. Therefore, the cubic regression model cannot be applied in Shanghai or Xiamen, and these two cities were excluded from analysis.
4.2. Saturation Correction at a Pixel Scale
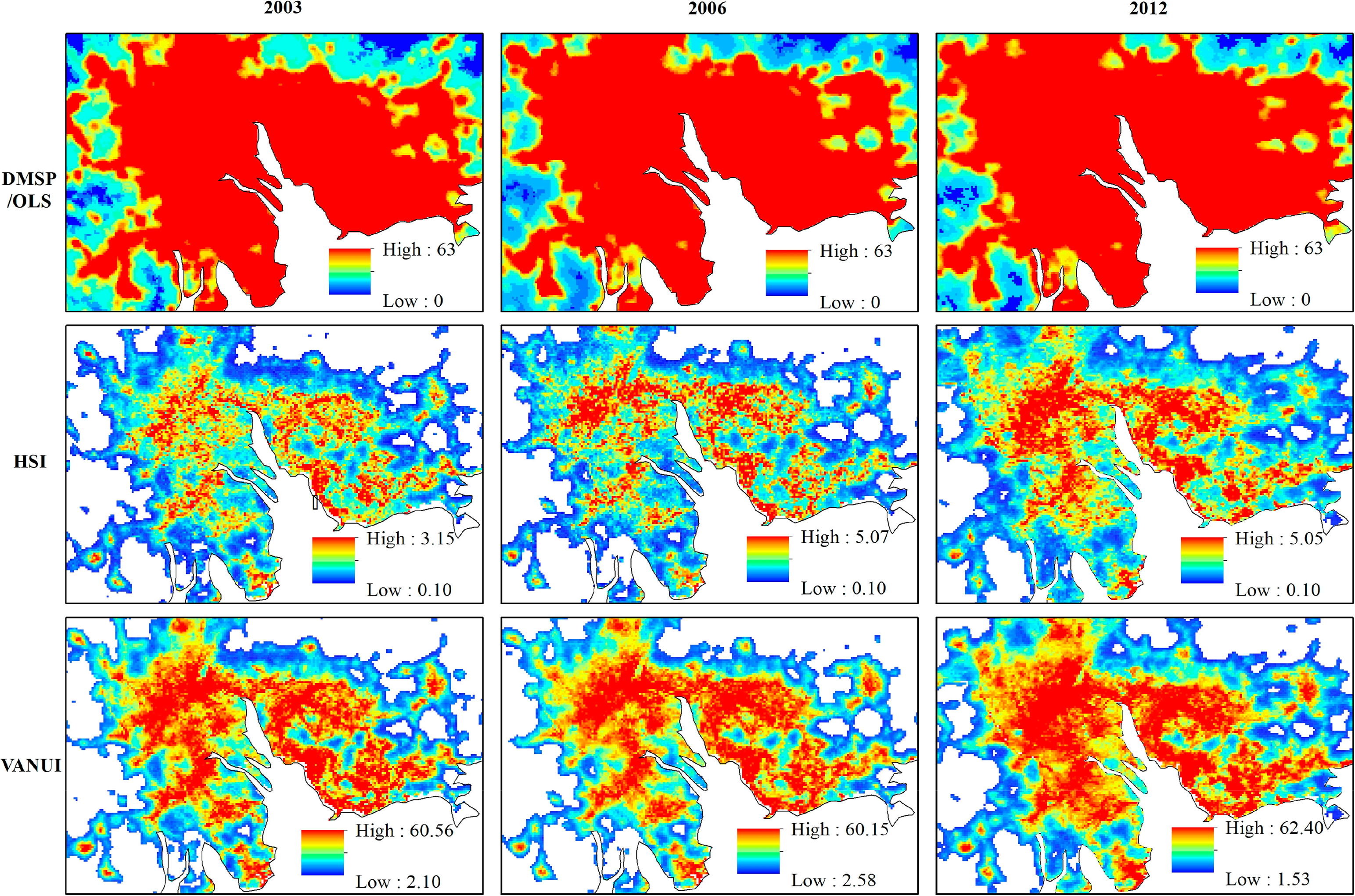
The correction methods of HSI and VANUI were performed in the regions with DMSP/OLS DN ≥ 12 and NDVI ≥ 0 in 2003, 2006, and 2012. Figure 4 shows the correction results in part of the Pearl River Delta. It is obvious that both HSI and VANUI captured finer details in the bright urban centers.
4.3. The Comparison between the Linear Correction Model and the Cubic Correction Model
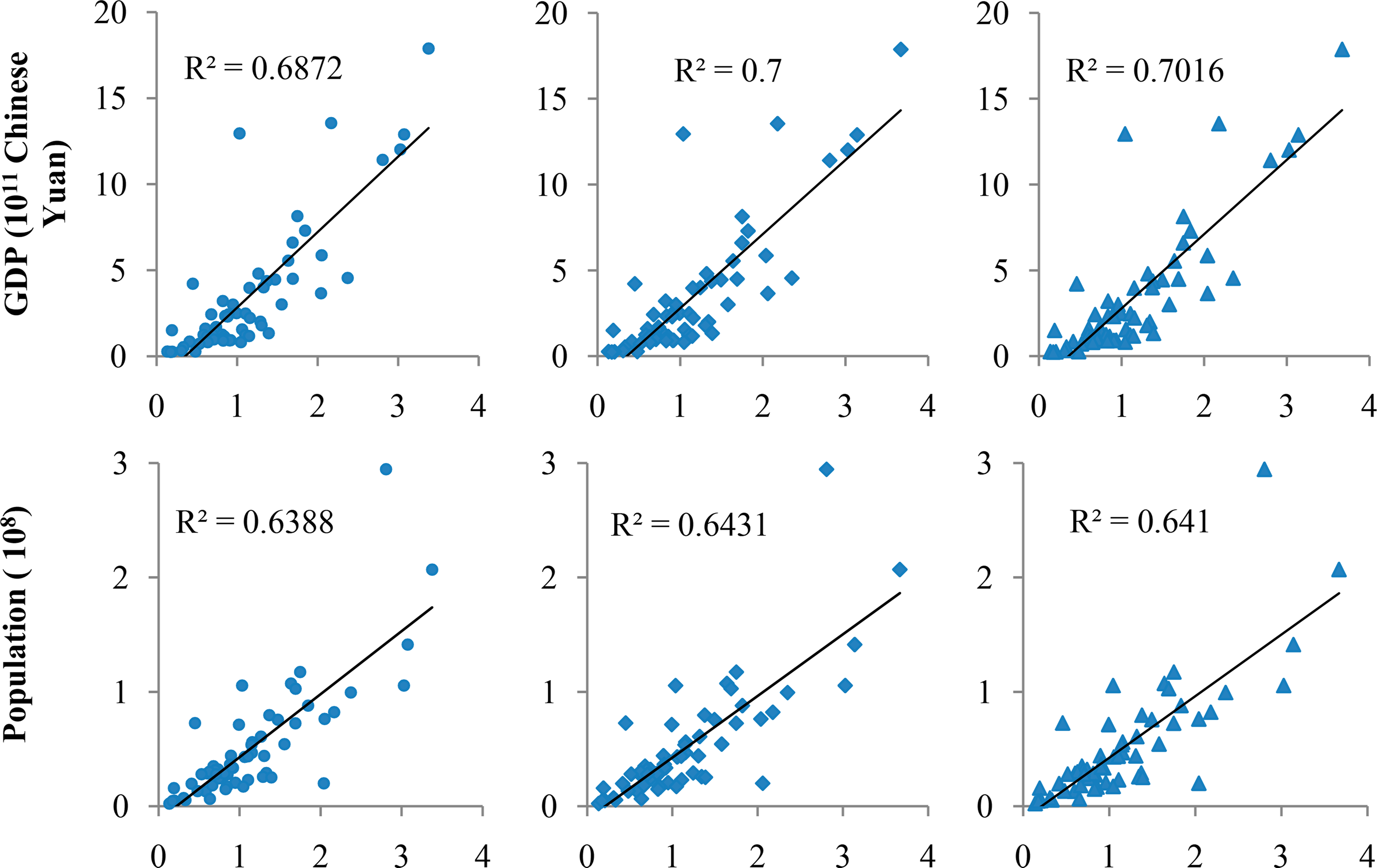
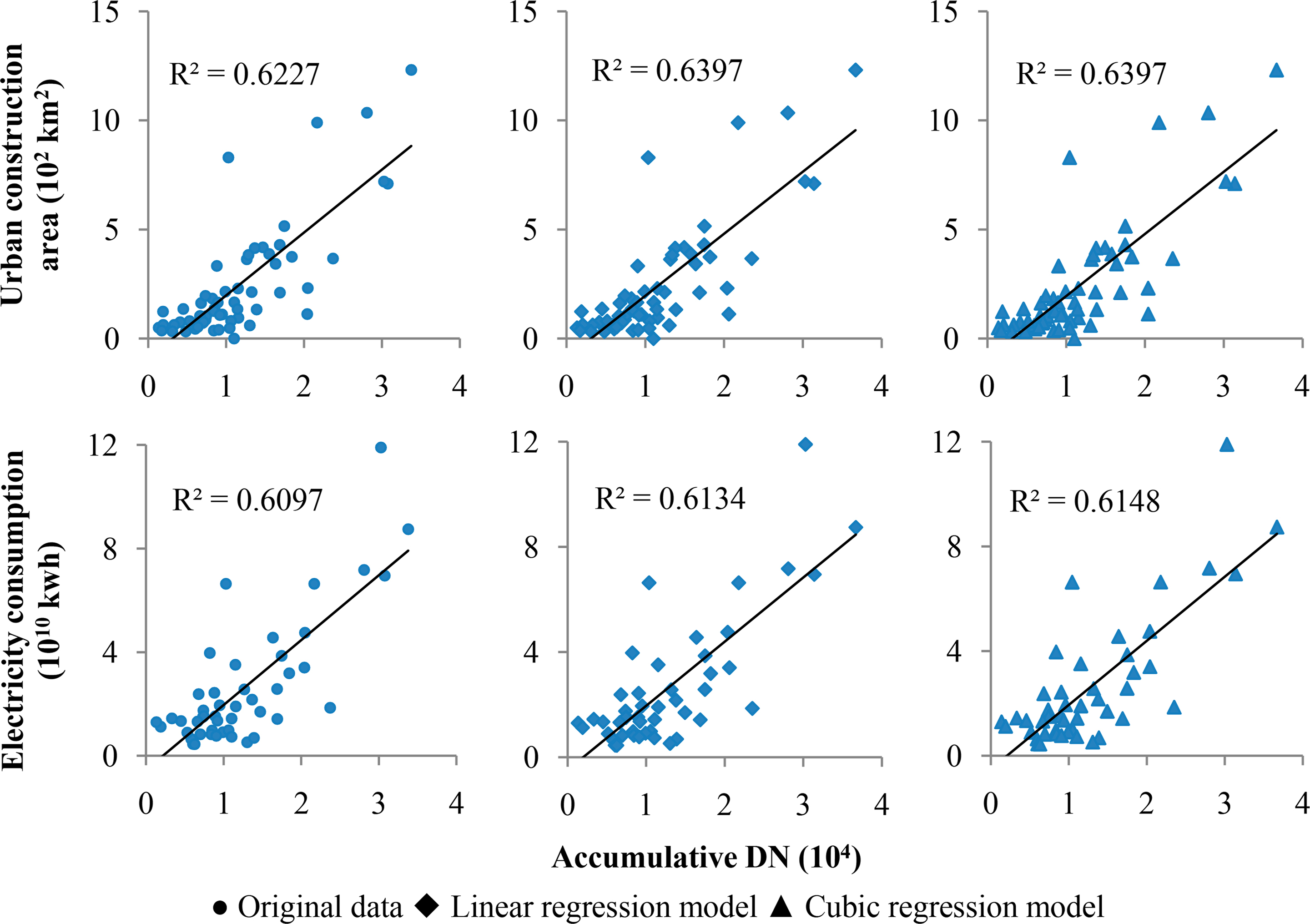
To evaluate the correction results of the linear correction model and the cubic correction model, the cumulative DN of the original NTL data and the corrected data were calculated in the 62 cities and then taken into the Pearson correlation with four socioeconomic variables: urban construction area (km2), GDP (109 RMB), population (107), and electricity consumption (1011 kilowatt hour) (because of the lack of data, only 47 cities were taken into the Pearson correlation with regards to electricity consumption).
As shown in Table 3, both the original cumulative DN and the corrected cumulative DN are correlated with the socioeconomic variables (significant at 0.01 level). Linear regression was then applied between cumulative DN and the socioeconomic variables, as shown in Figure 5. The results of the Pearson correlation and the linear regression both imply that the NTL data are good indicators for socioeconomic activity.
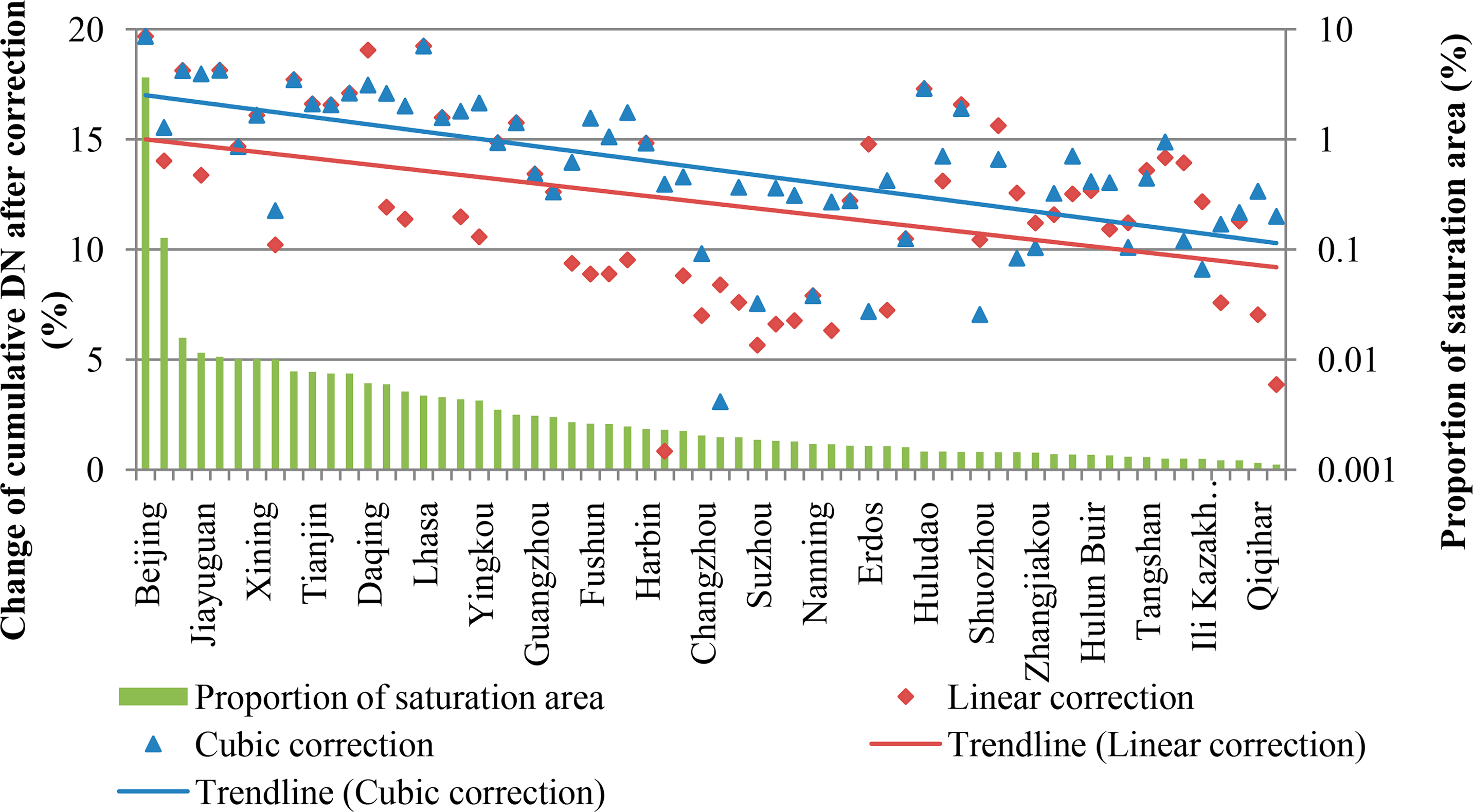
On the other hand, the results of the Pearson correlation and linear regression indicate that the two correction methods did not obviously improve the correlation between NTL and economic activities. This may be because the correction methods were only performed on the pixels with original DN = 63, while China is a developing country with a small saturated area. To test this hypothesis, we further analyzed the relationship between the change of NTL data after correction and the area of saturation in the 62 cities. Figure 6 shows that the correction effects tend to decrease with decreasing saturated area.
4.4. The Comparison between HSI and VANUI
Two assessments were used to evaluate the ability of HSI and VANUI to reduce saturation. First, the original NTL data and corrected data of HSI and VANUI were taken into the Pearson correlation at a pixel level in the regions with DMSP/OLS DN ≥ 12 and NDVI ≥ 0 in mainland China with grid maps of population and GDP in 2003, radiance calibrated NTL data in 2003 and 2006, and VIIRS-NPP data in 2012. The results (significant at the 0.01 level) in Table 4 demonstrate that the correlation coefficients of the original NTL data are larger than those of HSI and smaller than those of VANUI, which indicates that VANUI enhances the correlation in the national area and HSI reduces the application of NTL.
Second, the Pearson correlation coefficients in each of the 62 cities were calculated to analyze the correction results at the city level. To represent how well the correction methods reduced NTL saturation, the average (AVG) and standard deviation (STDEV) of the Pearson correlation coefficients of the original data, HSI, and VANUI in 62 cities were calculated. Table 5 shows that except for the average of HSI with radiance calibrated data in 2003 and 2006, most average values of HSI and VANUI are higher than those of the original data. Additionally, the correction results of VANUI are more stable than those of HSI, since the standard deviations of VANUI are smaller.
To evaluate the methods used with the former linear regression model and cubic regression model, the cumulative DN of HSI and VANUI were calculated in 62 cities. The correlation results in Table 6 (significant at the 0.01 level) show that HSI and VANUI do not have higher coefficients than the original data in some variables. HSI only improves the correlation coefficients of electricity consumption, and the coefficients of VANUI are higher than those of the original NTL data, with the exception of population.
5. Discussion
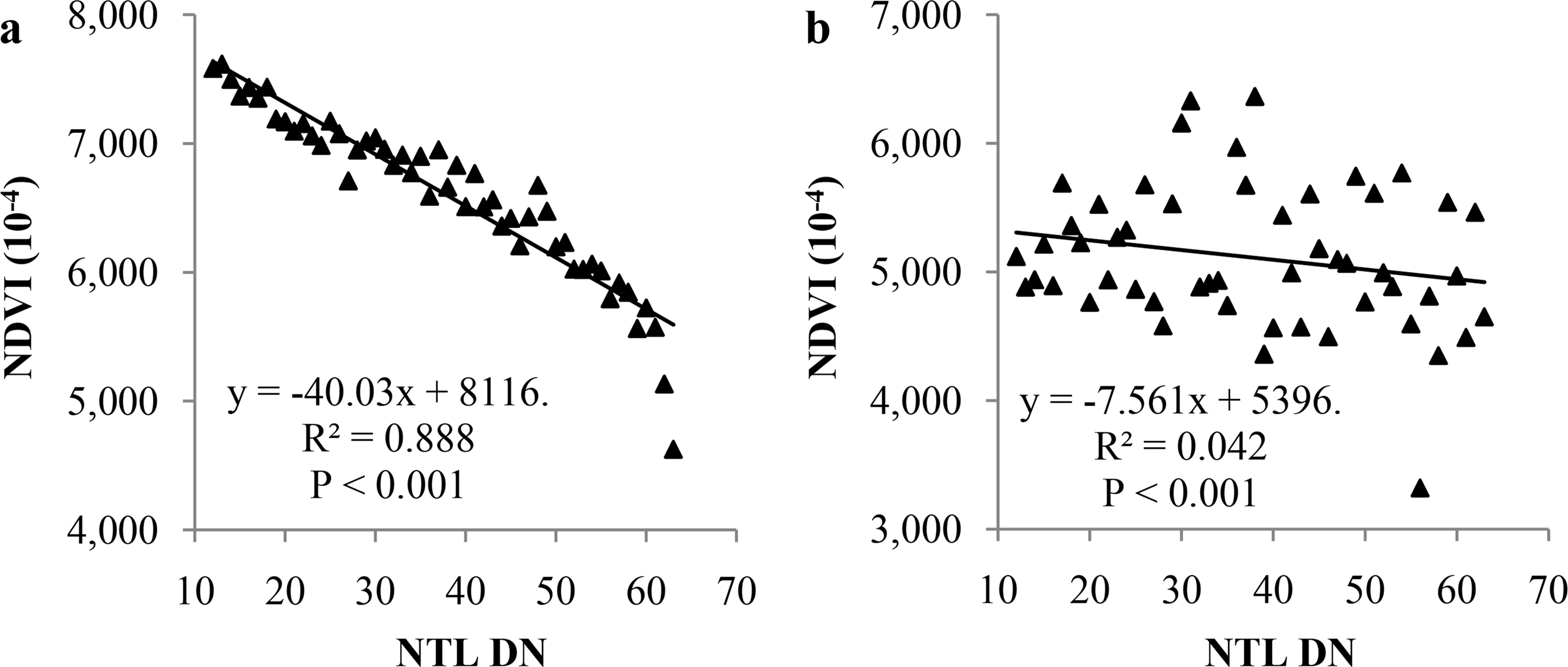
Since the HSI and VANUI did not perform well in some cases, we further analyzed the factors that might contribute to errors. First, we examined the major assumption of the two indices that key urban features and vegetation are inversely correlated. In a city where vegetation health and abundance can be considered constant, the indices may be helpful in capturing details in bright urban cores. However, in a city of diverse natural environments and vegetation, the inconstant environmental background could influence the accuracy of HSI and VANUI. To analyze the relationship between NTL data and NDVI, we calculated the mean of the annual maximum NDVI of each NTL DN in the 62 cities (we consider the annual maximum NDVI and the annual average NDVI are the same in this analysis, since the correlation coefficient between them is larger than 0.9 at a significant level of 0.01). The results show that the assumption is valid in most eastern and central cities, such as Tianjin in 2012 (Figure 7a), but invalid in some western cities, like Wuzhong in 2012 (Figure 7b). A further comparison between these two kinds of cities reveals that most eastern and central cities are located on the vegetated region, where the change of NDVI in urban areas is very different from non-urbanized areas; however, the western cities have some desert land, which makes the change of NDVI caused by urbanization difficult to recognize.
Next, we explored if the correlation between NTL DN and NDVI would influence the correction results of HSI and VANUI. The form of a ratio ( and ) was used to measure correction results.
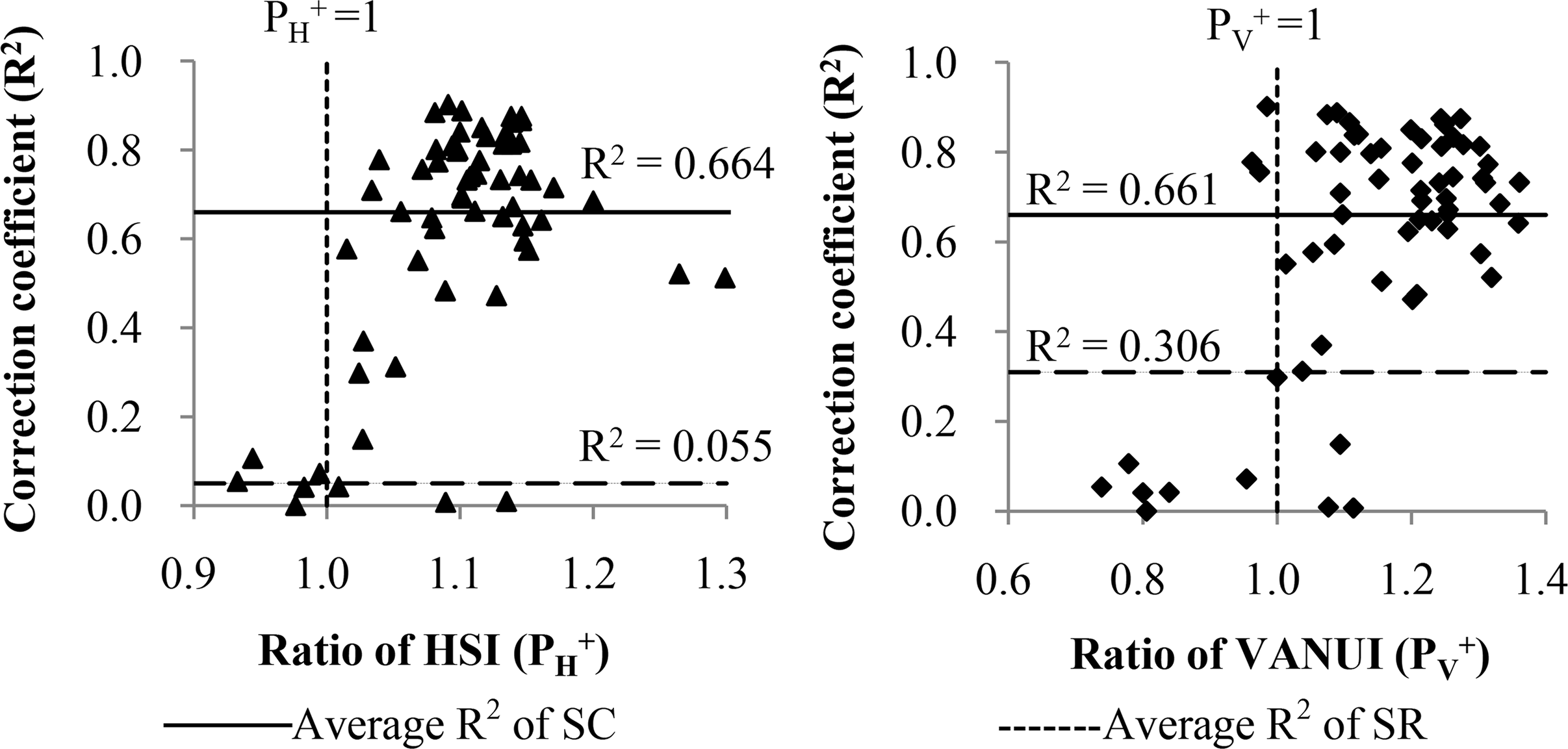
It is obvious that a ratio higher than 1.0 indicates that saturation was reduced. Therefore, the 62 cities were divided into two groups: the saturation-corrected (SC) with ratio>1.0 and the saturation-remaining (SR) with ratio ≤ 1.0. Table 7 shows the average of the correlation coefficients of each group and implies that cities whose saturation is corrected by HSI and VANUI tend to have higher correlation coefficients. Figure 8 shows an example from 2012. The number of cities in Group SC (on the right side of PH+ = 1 and PV+ = 1 lines) is larger than that of Group SR (on the left side of PH+ = 1 and PV+ = 1 lines). Additionally, most cities in Group SR have smaller correlation coefficients (R2) than Group SC.
Combining NTL DN and NDVI, HSI and VANUI are also affected by these two factors. We calculated HSI and VANUI with an interval of 10 DN (e.g., 13, 23, 33, etc.) and 0.1 NDVI (e.g., 0, 0.1, 0.2, etc.) to show the variation trend. As illustrated in Figure 9, NDVI has a larger impact on HSI and VANUI when NTL DN is higher. When NTL DN is constant, HSI decreases sharply with NDVI, and VANUI decreases steadily. Therefore, in urban areas, which have relatively high NTL DN and low NDVI, HSI is more sensitive to NDVI or NTL DN than VANUI. Also, HSI is unavailable when NTL is 63 and NDVI is 0.
6. Conclusion
The correction methods at the regional level, i.e., the linear regression model and the cubic regression model, are established based on the tendency of DN change in unsaturated areas; therefore, the methods can be used to correct historical NTL without additional data. We applied the two methods in 62 cities in China. The results demonstrate that both methods reduce saturation effects and improve the correlation between NTL data and socioeconomic variables. However, since the methods only perform in saturated areas, which are small in China, the correction effects are limited. The methods may perform better in developed countries, where more pixels are DN = 63.
Based on the principle that vegetation and urban features are inversely correlated, the correction methods at a pixel level, HSI and VANUI, combine NTL with contemporaneous NDVI to correct saturation effects in bright urban cores. Our analysis shows that the correction results vary with study scale and study area. At the country level, VANUI is useful in reducing saturation. In contrast, HSI reduces the correlation between NTL data and economic variables. At the city level, the correction results of HSI are much improved, and the correction effects of VANUI are more stable than that of HSI. Then, we analyzed two factors that may impact the correction results of HSI and VANUI. First, NDVI is helpful in increasing inter-urban variability within certain cities, where the vegetation health and abundance can be considered constant. However, in a large region with diverse natural environments and vegetation, the HSI and VANUI may result in errors. Second, HSI is sensitive to changes in NDVI when NTL DN is high, which is usually found in urban areas, so this may limit the application of HSI. Therefore, the correction method needs to be selected according to the study area and the purpose of research.
Acknowledgments
This research was supported by the National Natural Science Foundation of China (No. 41322004). We thank five anonymous reviewers for their constructive remarks.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Seto, K.C.; Sanchez-Rodriguez, R.; Fragkias, M. The new geography of contemporary urbanization and the environment. Annu. Rev. Environ. Resour 2010, 35, 167–194. [Google Scholar]
- Ji, W.; Ma, J.; Twibell, R.W.; Underhill, K. Characterizing urban sprawl using multi-stage remote sensing images and landscape metrics. Comput. Environ. Urban Syst 2006, 30, 861–879. [Google Scholar]
- Imhoff, M.L.; Tucker, C.J.; Lawrence, W.T.; Stutzer, D.C. The use of multisource satellite and geospatial data to study the effect of urbanization on primary productivity in the United States. IEEE Trans. Geosci. Remote Sens 2000, 38, 2549–2556. [Google Scholar]
- Imhoff, M.L.; Lawrence, W.T.; Stutzer, D.C.; Elvidge, C.D. A technique for using composite DMSP/OLS “ city lights” satellite data to map urban area. Remote Sens. Environ 1997, 61, 361–370. [Google Scholar]
- Lawrence, W.T.; Imhoff, M.L.; Kerle, N.; Stutzer, D. Quantifying urban land use and impact on soils in Egypt using diurnal satellite imagery of the Earth surface. Int. J. Remote Sens 2002, 23, 3921–3937. [Google Scholar]
- Imhoff, M.L.; Lawrence, W.T.; Elvidge, C.D.; Paul, T.; Levine, E.; Privalsky, M.V. Using nighttime DMSP/OLS images of city lights to estimate the impact of urban land use on soil resources in the United States. Remote Sens. Environ 1997, 59, 105–117. [Google Scholar]
- Hansen, J.; Ruedy, R.; Sato, M.; Imhoff, M.; Lawrence, W.; Easterling, D.; Peterson, T.; Karl, T. A closer look at United States and global surface temperature change. J. Geophys. Res.-Atmos 2001, 106, 23947–23963. [Google Scholar]
- Elvidge, C.D.; Imhoff, M.L.; Baugh, K.E.; Hobson, V.R.; Nelson, I.; Safran, J.; Dietz, J.B.; Tuttle, B.T. Night-time lights of the world: 1994–1995. ISPRS J. Photogramm 2001, 56, 81–99. [Google Scholar]
- Croft, T.A. Nighttime images of the earth from space. Sci. Am 1978, 239, 86–98. [Google Scholar]
- Witmer, F.D.W.; O’Loughlin, J. Detecting the effects of wars in the Caucasus regions of Russia and Georgia using radiometrically normalized DMSP-OLS nighttime lights imagery. Giscience Remote Sens 2011, 48, 478–500. [Google Scholar]
- Bharti, N.; Tatem, A.J.; Ferrari, M.J.; Grais, R.F.; Djibo, A.; Grenfell, B.T. Explaining seasonal fluctuations of measles in Niger using nighttime lights imagery. Science 2011, 334, 1424–1427. [Google Scholar]
- Li, X.; Chen, F.R.; Chen, X.L. Satellite-observed nighttime light variation as evidence for global armed conflicts. J-STARS 2013, 6, 2302–2315. [Google Scholar]
- Baugh, K.; Elvidge, C.D.; Ghosh, T.; Ziskin, D. Development of a 2009 stable lights product using DMSP-OLS data. APAN 2010, 30, 114–130. [Google Scholar]
- Townsend, A.C.; Bruce, D.A. The use of night-time lights satellite imagery as a measure of Australia’s regional electricity consumption and population distribution. Int. J. Remote Sens 2010, 31, 4459–4480. [Google Scholar]
- Chand, T.R.K.; Badarinath, K.V.S.; Elvidge, C.D.; Tuttle, B.T. Spatial characterization of electrical power consumption patterns over India using temporal DMSP-OLS night-time satellite data. Int. J. Remote Sens 2009, 30, 647–661. [Google Scholar]
- Lo, C.P. Urban indicators of China from radiance-calibrated digital DMSP-OLS nighttime images. Ann. Assn. Amer. Geogr 2002, 92, 225–240. [Google Scholar]
- Zhao, N.; Ghosh, T.; Samson, E.L. Mapping spatio-temporal changes of Chinese electric power consumption using night-time imagery. Int. J. Remote Sens 2012, 33, 6304–6320. [Google Scholar]
- Wu, J.; Wang, Z.; Li, W.; Peng, J. Exploring factors affecting the relationship between light consumption and GDP based on DMSP/OLS nighttime satellite imagery. Remote Sens. Environ 2013, 134, 111–119. [Google Scholar]
- Sutton, P.C.; Elvidge, C.D.; Ghosh, T. Estimation of gross domestic product at sub-national scales using nighttime satellite imagery. Int. J. Ecol. Econ. Stat 2007, 8, 5–21. [Google Scholar]
- Elvidge, C.D.; Hsu, F.C.; Baugh, K.E.; Ghosh, T. National trends in satellite observed lighting: 1992–2012. In Global Urban Monitoring and Assessment through Earth Observation; CRC Press: Boca Raton, FL, USA, 2014; pp. 97–118. [Google Scholar]
- Li, X.; Ge, L.; Chen, X. Detecting Zimbabwe’s decadal economic decline using nighttime light imagery. Remote Sens 2013, 5, 4551–4570. [Google Scholar]
- Chen, X.; Nordhaus, W.D. Using luminosity data as a proxy for economic statistics. Proc. Nat. Acad. Sci. USA 2011, 108, 8589–8594. [Google Scholar]
- Zhao, N.; Currit, N.; Samson, E. Net primary production and gross domestic product in China derived from satellite imagery. Ecol. Econ 2011, 70, 921–928. [Google Scholar]
- Doll, C.N.H.; Muller, J.P.; Elvidge, C.D. Night-time imagery as a tool for global mapping of socioeconomic parameters and greenhouse gas emissions. Ambio 2000, 29, 157–162. [Google Scholar]
- Raupach, M.R.; Rayner, P.J.; Paget, M. Regional variations in spatial structure of nightlights, population density and fossil-fuel CO2 emissions. Energ. Policy 2010, 38, 4756–4764. [Google Scholar]
- Ghosh, T.; Elvidge, C.D.; Sutton, P.C.; Baugh, K.E.; Ziskin, D.; Tuttle, B.T. Creating a global grid of distributed fossil fuel CO2 emissions from nighttime satellite imagery. Energies 2010, 3, 1895–1913. [Google Scholar]
- Doll, C.N.H.; Muller, J.P.; Morley, J.G. Mapping regional economic activity from night-time light satellite imagery. Ecol. Econ 2006, 57, 75–92. [Google Scholar]
- Henderson, J.V.; Storeygard, A.; Weil, D.N. Measuring economic growth from outer space. Am. Econ. Rev 2012, 102, 994–1028. [Google Scholar]
- Ghosh, T.; Powell, R.L.; Elvidge, C.D.; Baugh, K.E.; Sutton, P.C.; Anderson, S. Shedding light on the global distribution of economic activity. Open Geogr. J. 2010, 3, 148–161. [Google Scholar]
- Wu, J.; Liu, H.; Peng, J.; Ma, L. Hierarchical structure and spatial pattern of China’s urban system: Evidence from DMSP/OLS nightlight data (In Chinese). J. Geogr. Sci 2014, 69, 759–770. [Google Scholar]
- Amaral, S.; Monteiro, A.M.V.; Camara, G.; Quintanilha, J.A. DMSP/OLS night-time light imagery for urban population estimates in the Brazilian Amazon. Int. J. Remote Sens 2006, 27, 855–870. [Google Scholar]
- Chowdhury, P.K.R.; Maithani, S.; Dadhwal, V.K. Estimation of urban population in Indo-Gangetic plains using night-time OLS data. Int. J. Remote Sens 2012, 33, 2498–2515. [Google Scholar]
- Sutton, P. Modeling population density with night-time satellite imagery and GIS. Comput. Environ. Urban Syst 1997, 21, 227–244. [Google Scholar]
- Sutton, P.; Roberts, D.; Elvidge, C.; Baugh, K. Census from heaven: An estimate of the global human population using night-time satellite imagery. Int. J. Remote Sens 2001, 22, 3061–3076. [Google Scholar]
- Ziskin, D.; Baugh, K.; Hsu, F.C.; Ghosh, T.; Elvidge, C. Methods used for the 2006 radiance lights. APAN 2010, 30, 131–142. [Google Scholar]
- Li, X.; Xu, H.; Chen, X.; Li, C. Potential of NPP-VIIRS nighttime light imagery for modeling the regional economy of China. Remote Sens 2013, 5, 3057–3081. [Google Scholar]
- Elvidge, C.D.; Cinzano, P.; Pettit, D.R.; Arvesen, J.; Sutton, P.; Small, C.; Nemani, R.; Longcore, T.; Rich, C.; Safran, J.; et al. The nightsat mission concept. Int. J. Remote Sens 2007, 28, 2645–2670. [Google Scholar]
- Zhang, Q.; Schaaf, C.; Seto, K.C. The Vegetation Adjusted NTL Urban Index: A new approach to reduce saturation and increase variation in nighttime luminosity. Remote Sens. Environ 2013, 129, 32–41. [Google Scholar]
- National Oceanic and Atmospheric Administration. Global Radiance Calibrated Nighttime Lights. Available online: http://ngdc.noaa.gov/eog/dmsp/download_radcal.html (accessed on 15 June 2014).
- Hara, M.; Okada, S.; Yagi, H.; Moriyama, T.; Shigehara, K.; Sugimori, Y. Progress for stable artificial lights distribution extraction accuracy and estimation of electric power consumption by means of DMSP/OLS nighttime imagery. Int. J. Remote Sens. Earth Sci 2004, 1, 31–42. [Google Scholar]
- Letu, H.; Hara, M.; Yagi, H.; Naoki, K.; Tana, G.; Nishio, F.; Shuhei, O. Estimating energy consumption from night-time DMSP/OLS imagery after correcting for saturation effects. Int. J. Remote Sens 2010, 31, 4443–4458. [Google Scholar]
- Letu, H.; Hara, M.; Tana, G.; Nishio, F. A saturated light correction method for DMSP/OLS nighttime satellite imagery. IEEE Trans. Geosci. Remote Sens 2012, 50, 389–396. [Google Scholar]
- Elvidge, C.D.; Baugh, K.E.; Dietz, J.B.; Bland, T.; Sutton, P.C.; Kroehl, H.W. Radiance calibration of DMSP-OLS low-light imaging data of human settlements. Remote Sens. Environ 1999, 68, 77–88. [Google Scholar]
- Lu, D.S.; Tian, H.Q.; Zhou, G.M.; Ge, H.L. Regional mapping of human settlements in southeastern China with multisensor remotely sensed data. Remote Sens. Environ 2008, 112, 3668–3679. [Google Scholar]
- Elvidge, C.D.; Zhizhin, M.; Hsu, F.-C.; Baugh, K.E. VIIRS nightfire: Satellite pyrometry at night. Remote Sens 2013, 5, 4423–4449. [Google Scholar]
- Xiong, X.; Butler, J.; Chiang, K.; Efremova, B.; Fulbright, J.; Lei, N.; McIntire, J.; Oudrari, H.; Sun, J.; Wang, Z. VIIRS on-orbit calibration methodology and performance. J. Geophys. Res. Atmos 2013. [Google Scholar] [CrossRef]
- Cao, C.Y.; Xiong, J.; Blonski, S.; Liu, Q.H.; Uprety, S.; Shao, X.; Bai, Y.; Weng, F.Z. Suomi NPP VIIRS sensor data record verification, validation, and long-term performance monitoring. J. Geophys. Res.-Atmos 2013, 118, 11664–11678. [Google Scholar]
- National Oceanic and Atmospheric Administration. VIIRS DNB Cloud Free Composites. Available online: http://ngdc.noaa.gov/eog/viirs/download_monthly.html (accessed on 15 June 2014).
- Shi, K.; Yu, B.; Huang, Y.; Hu, Y.; Yin, B.; Chen, Z.; Chen, L.; Wu, J. Evaluating the ability of NPP-VIIRS nighttime light data to estimate the gross domestic product and the electric power consumption of China at multiple scales: A comparison with DMSP-OLS data. Remote Sens 2014, 6, 1705–1724. [Google Scholar]
- Liao, L.B.; Weiss, S.; Mills, S.; Hauss, B. Suomi NPP VIIRS day-night band on-orbit performance. J. Geophys. Res.-Atmos 2013, 118, 12705–12718. [Google Scholar]
- Elvidge, C.D.; Baugh, K.E.; Zhizhin, M.; Hsu, F.-C. Why VIIRS data are superior to DMSP for mapping nighttime lights. APAN 2013, 35, 62–69. [Google Scholar]
- National Aeronautics and Space Administration. Polar-Orbiting Missions. Available online: http://npp.gsfc.nasa.gov/index.html (accessed on 15 June 2014).
- Ma, T.; Zhou, C.H.; Pei, T.; Haynie, S.; Fan, J.F. Quantitative estimation of urbanization dynamics using time series of DMSP/OLS nighttime light data: A comparative case study from China’s cities. Remote Sens. Environ 2012, 124, 99–107. [Google Scholar]


| No. | City | Saturated Area (Saturated Pixels) (km2) | Ratio of Saturation (%) | No. | City | Saturated Area (Saturated Pixels) (km2) | Ratio of Saturation (%) |
|---|---|---|---|---|---|---|---|
| 1 | Anshan | 90 | 1.812 | 32 | Lanzhou | 123 | 2.735 |
| 2 | Baotou | 173 | 3.201 | 33 | Lhasa | 45 | 3.373 |
| 3 | Bayingolin * | 56 | 0.798 | 34 | Liaoyang | 54 | 1.478 |
| 4 | Beijing | 1754 | 17.807 | 35 | Mudanjiang | 56 | 0.825 |
| 5 | Changchun | 200 | 2.498 | 36 | Nanning | 94 | 1.169 |
| 6 | Changji** | 37 | 0.435 | 37 | Panjin | 104 | 3.552 |
| 7 | Changzhou | 67 | 1.555 | 38 | Qingdao | 85 | 0.804 |
| 8 | Chaoyang | 48 | 0.506 | 39 | Qinhuangdao | 76 | 2.159 |
| 9 | Chengdu | 90 | 1.022 | 40 | Qiqihar | 40 | 0.318 |
| 10 | Chifeng | 54 | 0.513 | 41 | Sanya | 18 | 1.287 |
| 11 | Chongqing | 50 | 0.235 | 42 | Shenyang | 420 | 4.466 |
| 12 | Daqing | 338 | 3.932 | 43 | Shenzhen | 203 | 10.524 |
| 13 | Datong | 127 | 1.966 | 44 | Shijiazhuang | 59 | 0.598 |
| 14 | Dezhou | 40 | 0.435 | 45 | Shuozhou | 49 | 0.812 |
| 15 | Dongying | 97 | 2.086 | 46 | Songyuan | 57 | 1.070 |
| 16 | Ordos | 162 | 1.081 | 47 | Suzhou | 101 | 1.366 |
| 17 | Fushun | 47 | 2.094 | 48 | Taiyuan | 162 | 3.893 |
| 18 | Guangzhou | 163 | 2.450 | 49 | Tangshan | 61 | 0.582 |
| 19 | Harbin | 377 | 1.854 | 50 | Tianjin | 487 | 4.453 |
| 20 | Hohhot | 195 | 2.399 | 51 | Tongliao | 48 | 0.712 |
| 21 | Huludao | 37 | 0.831 | 52 | Urumchi | 360 | 6.002 |
| 22 | Hulun Buir | 68 | 0.683 | 53 | Weihai | 42 | 0.813 |
| 23 | Ili *** | 37 | 0.500 | 54 | Wuhai | 20 | 1.316 |
| 24 | Jiayuguan | 39 | 5.313 | 55 | Wuzhong | 53 | 1.485 |
| 25 | Jilin | 37 | 0.656 | 56 | Xining | 85 | 5.024 |
| 26 | Jinan | 337 | 5.129 | 57 | Xian | 104 | 1.881 |
| 27 | Jinchang | 20 | 1.768 | 58 | Yinchuan | 199 | 4.367 |
| 28 | Jinzhou | 43 | 0.697 | 59 | Yingkou | 107 | 3.145 |
| 29 | Karamay | 134 | 3.889 | 60 | Zhangjiakou | 62 | 0.783 |
| 30 | Kunming | 279 | 3.302 | 61 | Zhengzhou | 78 | 1.087 |
| 31 | Langfang | 73 | 1.164 | 62 | Zhuhai | 19 | 5.013 |
*Bayingolin Mongol Autonomous Prefecture;**Changji Hui Autonomous Prefecture;***Ili Kazakh Autonomous Prefecture.
| Data Set | Period | Data Source | Description |
|---|---|---|---|
| Population and GDP grid maps | 2003 | China Data Sharing Infrastructure of Earth System Science | Spatial resolution of 1000 m, produced from land use data and statistical data |
| DMSP/OLS NTL (radiance calibrated) | 2003, 2006 | NOAA-National Geophysical Data Center | Spatial resolution of 1000 m |
| DMSP/OLS NTL (stable light) | 2003, 2006, 2012 | NOAA-National Geophysical Data Center | Spatial resolution of 1000 m |
| MODIS NDVI | 2003, 2006, 2012 | NASA-LAADS Web | Spatial resolution of 1000 m, 8-day composite |
| Statistical data | 2012 | China Economic and Social Development Statistical Database | Population, GDP, Built-up area, Electric power consumption |
| Administrative boundary | 2012 | China National Fundamental Geographic Information System | City level |
| NPP-VIIRS NTL | 2012 | NOAA-National Geophysical Data Center | Spatial resolution of 500 m |
| Variables | GDP | Population | Urban Construction Area | Electricity Consumption |
|---|---|---|---|---|
| Number of cities | 62 | 62 | 62 | 47 |
| Original data | 0.829 ** | 0.799 ** | 0.794 ** | 0.781 ** |
| Linear correction | 0.837 ** | 0.802 ** | 0.804 ** | 0.783 ** |
| Cubic correction | 0.838 ** | 0.801 ** | 0.804 ** | 0.784 ** |
**Correlation is significant at the 0.01 level (2-tailed).
| Variables | Population (2003) | GDP (2003) | Radiance Calibrated Data | VIIRS-NPP (2012) | |
|---|---|---|---|---|---|
| (2003) | (2006) | ||||
| Original data | 0.395 ** | 0.476 ** | 0.600 ** | 0.691 ** | 0.598 ** |
| HSI | 0.364 ** | 0.393 ** | 0.511 ** | 0.598 ** | 0.574 ** |
| VANUI | 0.438 ** | 0.485 ** | 0.617 ** | 0.710 ** | 0.635 ** |
**Correlation is significant at the 0.01 level (2-tailed).
| Variables | Population (2003) | GDP (2003) | Radiance Calibrated Data | VIIRS-NPP (2012) | ||
|---|---|---|---|---|---|---|
| (2003) | (2006) | |||||
| AVG | Original data | 0.522 | 0.547 | 0.729 | 0.779 | 0.572 |
| HSI | 0.591 | 0.608 | 0.710 | 0.758 | 0.653 | |
| VANUI | 0.577 | 0.597 | 0.752 | 0.806 | 0.629 | |
| STDEV | Original data | 0.121 | 0.136 | 0.094 | 0.075 | 0.092 |
| HSI | 0.189 | 0.142 | 0.136 | 0.158 | 0.148 | |
| VANUI | 0.188 | 0.063 | 0.048 | 0.060 | 0.065 | |
| Variables | GDP | Population | Urban Construction Area | Electricity Consumption |
|---|---|---|---|---|
| Number of cities | 62 | 62 | 62 | 47 |
| Original data | 0.829 ** | 0.799 ** | 0.794 ** | 0.781 ** |
| HSI | 0.748 ** | 0.563 ** | 0.788 ** | 0.788 ** |
| VANUI | 0.845 ** | 0.678 ** | 0.830 ** | 0.830 ** |
**Correlation is significant at the 0.01 level (2-tailed).
| Variables | Population | GDP | Radiance Calibrated Data | VIIRS-NPP | ||
|---|---|---|---|---|---|---|
| (2003) | (2003) | (2003) | (2006) | (2012) | ||
| HSI | SC | 0.605 | 0.611 | 0.646 | 0.646 | 0.664 |
| SR | 0.314 | 0.291 | 0.451 | 0.433 | 0.055 | |
| VANUI | SC | 0.602 | 0.584 | 0.608 | 0.592 | 0.661 |
| SR | 0.114 | 0.026 | 0.383 | 0.286 | 0.306 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Wu, J.; Li, W.; Peng, J.; Liu, H. Evaluating Saturation Correction Methods for DMSP/OLS Nighttime Light Data: A Case Study from China’s Cities. Remote Sens. 2014, 6, 9853-9872. https://doi.org/10.3390/rs6109853
Ma L, Wu J, Li W, Peng J, Liu H. Evaluating Saturation Correction Methods for DMSP/OLS Nighttime Light Data: A Case Study from China’s Cities. Remote Sensing. 2014; 6(10):9853-9872. https://doi.org/10.3390/rs6109853
Chicago/Turabian StyleMa, Lin, Jiansheng Wu, Weifeng Li, Jian Peng, and Hao Liu. 2014. "Evaluating Saturation Correction Methods for DMSP/OLS Nighttime Light Data: A Case Study from China’s Cities" Remote Sensing 6, no. 10: 9853-9872. https://doi.org/10.3390/rs6109853
APA StyleMa, L., Wu, J., Li, W., Peng, J., & Liu, H. (2014). Evaluating Saturation Correction Methods for DMSP/OLS Nighttime Light Data: A Case Study from China’s Cities. Remote Sensing, 6(10), 9853-9872. https://doi.org/10.3390/rs6109853




