Abstract
Accurate inversion of land surface geo/biophysical variables from remote sensing data for earth observation applications is an essential and challenging topic for the global change research. Land surface temperature (LST) is one of the key parameters in the physics of earth surface processes from local to global scales. The importance of LST is being increasingly recognized and there is a strong interest in developing methodologies to measure LST from the space. Landsat 8 Thermal Infrared Sensor (TIRS) is the newest thermal infrared sensor for the Landsat project, providing two adjacent thermal bands, which has a great benefit for the LST inversion. In this paper, we compared three different approaches for LST inversion from TIRS, including the radiative transfer equation-based method, the split-window algorithm and the single channel method. Four selected energy balance monitoring sites from the Surface Radiation Budget Network (SURFRAD) were used for validation, combining with the MODIS 8 day emissivity product. For the investigated sites and scenes, results show that the LST inverted from the radiative transfer equation-based method using band 10 has the highest accuracy with RMSE lower than 1 K, while the SW algorithm has moderate accuracy and the SC method has the lowest accuracy.1. Introduction
Land surface temperature (LST) is a key parameter in the physics of the earth surface through the process of energy and water exchange with the atmosphere, which plays an important role in a wide variety of scientific studies, such as ecology, hydrology, and global change studies [1,2]. Thermal infrared (TIR) remote sensing provides a unique method for obtaining LST information at the regional and global scales since most of the energy detected by the sensor in this spectral region is directly emitted by the land surface [3]. Many efforts have been devoted to establish methods for retrieving the LST from remote sensing data, and significant progresses have been made over the past decade [4].
The Landsat project provides a particular opportunity for the LST retrieval [5–7], as it has a relatively long data record period, with the launch of Landsat 3 in 1978 [8]. From the Multispectral Scanner (MSS) of Landsat 3 to the Thematic Mapper (TM) of Landsat 4 and 5, and following by the Enhanced Thematic Mapper Plus (ETM+) of Landsat 7, there was only one thermal infrared channel available [8,9] (Figure 1). Therefore, a single-channel (SC) algorithm was developed to derive LST from this band. Influential researches were conducted mainly by Jimenez-Munoz et al. [10–12] and Qin et al. [13]. Accurate determination of the LST using the SC method requires high-quality atmospheric transmittance/radiance code to estimate the atmospheric features involved in the radiative transfer equation [14]. Previous TM and ETM+ sensors (Figure 1) have only one thermal band, while the Landsat 8 TIRS has two spectrally adjacent thermal bands. That is suitable for the split-window (SW) algorithm. The SW algorithm uses two thermal bands typically located in the atmospheric window between 10 and 12 μm [15]. The basis of the SW algorithm is that the radiance attenuation for atmospheric absorption is proportional to the radiance difference of simultaneous measurements at two different wavelengths, each subject to different amounts of atmospheric absorption [3]. It is the most widely used algorithm for LST retrieval due to the simplicity and robustness.
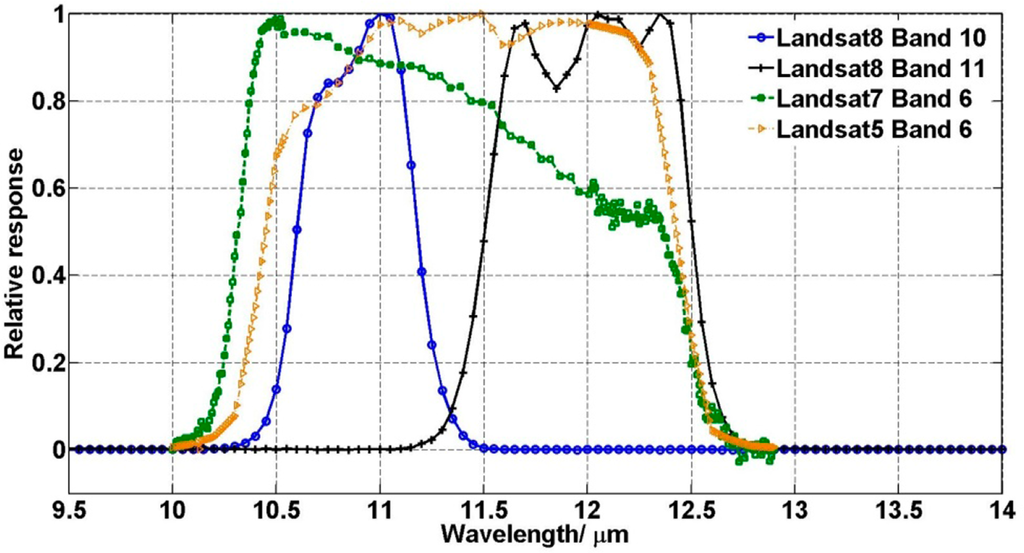
Many operational LST products have been generated using different SW algorithms from various sensors, including the Advanced Very High Resolution Radiometer (AVHRR) [16], Advanced Along-Track Scanning Radiometer (AATSR) [17], Moderate Resolution Imaging Spectroradiometer (MODIS) [18], Spinning Enhanced Visible and Infrared Imager (SEVIRI) [19] and Geostationary Operational Environmental Satellites (GOES) [20]. A review of the SW algorithm and different published researches can be found in [14,21].
Most recent studies for LST retrieval from Landsat 8 TIRS are by Rozenstein et al. [22] and Jimenez-Munoz et al. [23]. The former one derived a SW algorithm and studied the parameters’ (including water vapor content and land surface emissivity) sensitivity of the algorithm [22]. While the latter introduced the SC method and another general SW algorithm from forward-simulated atmospheric profile databases. In this paper, three different LST retrieval approaches were explored and compared for the TIRS, including the radiative equation-based method, the SW algorithm and the SC method. For the radiative transfer equation-based method, the atmospheric profile was extracted from the NCEP data set and used to simulate atmospheric transmittance, downwelling and upwelling radiance from the MODTRAN (MODerate resolution atmospheric TRANsmission) model. For the SW algorithm, we chose the algorithm developed by Mao et al. [24,25], which only depends on atmospheric transmittance and land surface emissivity. The theory was originally created to estimate LST from Landsat TIR images by a single mono-window algorithm [13], then adapted to a split-window algorithm for MODIS and ASTER images [24,26]. In this study, the coefficients of the SW algorithm were re-parameterized, corresponding to the TIRS’ spectral response curve. Meanwhile, the atmospheric transmittance was simulated from water vapor content with typical atmospheric profiles by the moderate resolution atmospheric transmission (MODTRAN) model. For the SC method, a novel algorithm from Jimenez-Munoz et al. [12] was used. The land surface emissivity was derived from a NDVI thresholds method [27]. Four SURFRAD sites were selected to conduct the validation and methods’ comparison. The aims of this study were: (1) testing the suitability of three presented methods for LST estimation from the Landsat 8 TIRS imagery, and (2) comparing and analyzing retrieval results of those methods. Therefore, it showed different procedures to the readers for retrieving LST from Landsat 8 TIRS data in order to contribute more employments of this sensor in the future.
2. Methods and Data
2.1. Radiative Transfer Equation and Radiative Transfer Theory Based Method
A simplified radiative transfer equation can express the apparent radiance received by a sensor [25]:
Bi(Ti) the radiance received by channel i of the sensor with brightness temperature Ti, the detail of the TIRS’ calibration can be found at USGS Landsat Project website.
Bi(Ts) the ground radiance
τi(θ) atmospheric transmittance for channel i when view zenith angle is θ. TIRS is treated as nadir viewing since the view angle is no more than 7.5° [28].
ɛi surface emissivity for channel i
downwelling path radiance
upwelling path radiance
According to Plank’s law, Bi(Ts) can be expressed as:
With the thermal radiance measured at sensor level, accompany with the atmospheric parameters obtained with radiosounding, which can be used to estimate , and τi from the radiative transfer model, the LST can be retrieved according to Equation (4). However, in this study, we only used the spatial and temporal closest atmospheric profile from the original 1° × 1° NCEP reanalysis data to simulate , , and τi from the MODTRAN model for TIRS, since radiosonde profiles are not usually available except in dedicated field campaigns or around meteorological radiosounding stations with launching times when satellites passes. The atmospheric profile used in this study was the NCEP final operational global analysis data. This product is from the Global Data Assimilation System (GDAS), which continuously collects observational data from the Global Telecommunications System (GTS) and other sources for numerous analyses. The data is on a longitude/latitude grid and generated globally every 6 h (0:00, 06:00, 12:00 and 18:00 UTC). The extracted atmospheric profiles have 26 mandatory levels from 1000 to 10 hPa [29,30]. Other vertical atmospheric parameters include the geopotential height, the air temperature and the relative humidity. We extracted the NCEP profiles from the on-line atmospheric correction tools [31]. A recent study proved that the NCEP has enough vertical resolution for the atmospheric profile which is effective for the τ simulation in the radiative transfer model [29]. However, there is an argument for the accuracy of NCEP data when it is applied to large and complex terrain areas due to spatial and temporal resolution [32]. Comparison between NCEP, AIRS, MOD07 L2 products and the radiosonde measurement for LST retrieval from the single window algorithm revealed that the interpolated NCEP data is fairly accurate for local simulation [33]. Consequently, we used the NCEP data to simulate , , and τi from the MODTRAN model. As for the land surface emissivity, we will discuss it in the following section.
2.2. Development of the Split Window Algorithm
Qin et al. figured that and can be expressed as [13,26]:
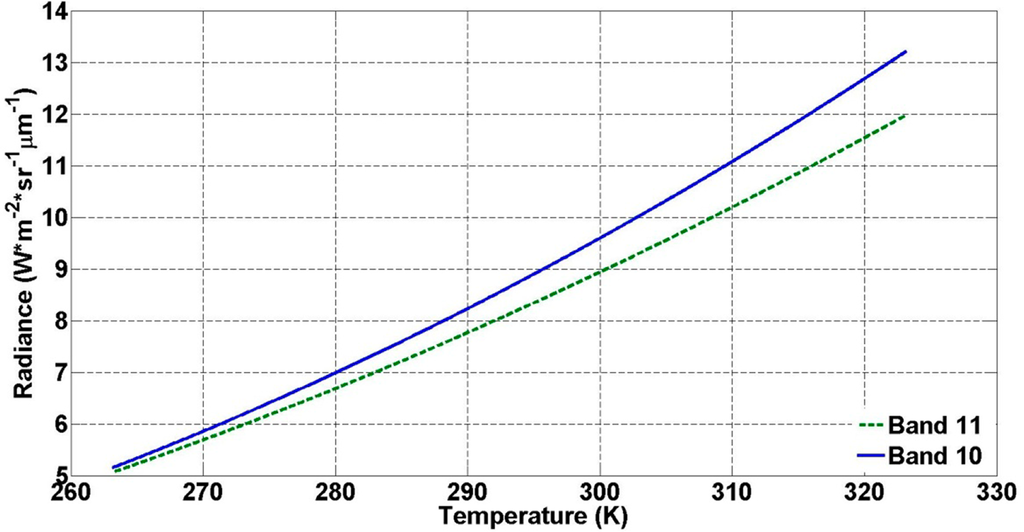
Based on Plank’s law, the spectral radiance emitted by an object is a nonlinear function. Thus, we linearized Planck’s radiance function through the application of Taylor’s expansion, since the simulated radiance received by two bands of the TIRS with spectral response curves (Figure 1) at the range of −10 °C to 50 °C (Figure 2) is close to a linear function.
In Equation (9)T is the brightness temperature, other parameters have the same meanings with previous equations.
The Taylor expansion of Planck’s function for band 10 and 11 (i) is presented as Equation (10), where Tj refers to the brightness temperature T10, T11 for respective bands, Ta and Ts as the atmospheric temperature and the land surface temperature. The parameter Li is defined in Equation (11). As mentioned before, we simulated the temperature range from −10 °C to 20 °C and 20 °C to 50 °C for calculating the piecewise linear relationship between Li and T. It has been suggested by Rozenstein et al. [22] and Qin et al. [26] and proved to have better performance for the linearization for Planck’s function. Results are shown in Table 1. The high coefficient of determination (r2) and low root mean square error (RMSE) indicate that the linearization for Li from T is reasonable in corresponding temperature range.

Overall, the Equations (7) and (8) can be overwritten as follows:
L10 and L11, can be calculated from Table 1 within a specific brightness temperature range for band 10 and 11 respectively. Ts is hereby calculated from Equations (12) and (13) with the elimination of ∂B10(T10)/∂T and ∂B11(T10)/∂T as following:
Therefore, the unknown variables needed to inverse TS in Equation (18) are τ10, τ11, which are atmospheric transmittances for band 10 and 11 of TIRS; and ɛ10, ɛ11, which are land surface emissivities for respective bands.
Because of many technical difficulties, the atmospheric transmittance is usually not available in situ when satellite passes. Generally, the most practical way to determine the atmospheric transmittance is through the simulation of local atmospheric conditions, especially with water vapor content [13,24,26]. In this study, we simulated the relationship between the atmospheric transmittance (τ) and the water vapor content (w) with two typical atmospheric profiles: the 1976 US standard and the Mid-latitude Summer atmospheric profile from MODTRAN. The range of water vapor content is from 0.2 g/cm2 to 6.0 g/cm2, with a 0.2 g/cm2 interval. Qin et al. [26] showed that it is better to divide the water vapor content range into several sections and evaluate each of them separately in order to achieve a better accuracy, when this relation is applied for a large range of values. Thus, we divided the water vapor range into two ranges: 0.2–3.0 g/cm2 and 3.0–6.0 g/cm2, and used the quadratic regression for each range to simulate the relationship between τ and w, showed in Table 2. The estimation equations listed in Table 2 have high r2 and low RMSE, which indicates that the estimation of transmittance with water vapor content by these equations has high accuracy.

2.3. Single Channel Method
Although the Landsat 8 TIRS has two spectrally adjacent channels which are suitable for the split window methods, the single channel (SC) method is still applicable for those bands. In this study, we used a general SW method proposed by Jimenez-Munoz et al. [12,34] for LST retrieval. The equation for this general SW method is as [11]:
All the symbols have the same meaning in former equations. For Ψ1, Ψ2, Ψ3, they are derived from the water vapor content [11,12]:
The parameters η, ξ, χ, φ are related to the effective band wavelength. According to the relative spectral response curves of TIRS (Figure 1), effective band wavelengths are 10.896 μm and 12.006 μm for band 10 and 11 respectively. Jimenez-Munoz et al. [12] suggested that those parameters can be parameterized as a third degree regression with the wavelength, at the wavelength range of 8–12 μm. Therefore, those parameters which we used to estimate Ψ1, Ψ2, Ψ3 from the water vapor content (w) are listed in Table 3.

The SC method has been applied to Landsat 5 TM, Landsat 7 ETM+, MODIS ASTER and ENVISAT AATSR sensors’ TIR bands for LST retrieval [10,12,33,35]. It has reasonable accuracy and only needs two parameters for LST inversion: the land surface emissivity (ɛ) and the water vapor content (w), which is very applicable for handling single channel TIR data. In this study, we used the SC method for LST inversion with Landsat 8 TIRS imagery.
2.4. Land Surface Emissivity Estimation
As mentioned in Sections 2.1–2.3, the land surface emissivity (ɛ) is indispensable for LST inversion. The emissivity of land, unlike that of oceans, can differ significantly from unity and vary with vegetation, surface moisture, roughness, and viewing angles [36]. Although a series of simultaneous LST and LSE retrieval methods have been proposed [14,37–39] and proved to be more accurate for satellite-derived LST. In this study, we still used the LST retrieval methods with prior known LSE, since the simultaneous methods need specific requirements and sophisticated algorithms [14,38,39], while the prior known LSE methods appear to be more practical with reasonable accuracy [27,40] for LST retrieval from Landsat imagery [11,41].
Three major methods were proposed for LSE estimation before LST inversion: classification-based emissivity method (CBEM) [42,43], NDVI-based emissivity method (NBEM) [44–46] and day/night temperature-independent spectral-indices (TISI) based method [47–49]. The CBEM obtains the LSE image from a classification image, in which an emissivity value for each class is assumed in advance. However, this is not very operative because we need a good knowledge of the study area and emissivity measurements on the surfaces representatives of different classes coincident with the satellites transiting time [11]. Meanwhile, several requirements may limit the usage of the TISI method. First of all, approximate atmospheric corrections and concurrence of both MIR and TIR data are required [50]. Then, the surfaces must be observed under similar observation conditions, e.g., viewing angle, during both day and night [51,52]. Additionally, accurate image co-registration must be performed [51]. Due to the orbit and revisiting cycle, the TISI method is not applicable for Landsat 8 TIRS. An alternative, operative procedure is the NBEM [11]. Because of its simplicity, this method has already been applied to various sensors with access to VNIR data [27,46,50,53,54]. In this study, a NDVI thresholds method was used for LSE estimation from Landsat 8 imagery as the following Equation:
The emissivities of vegetation (ɛv) and soil (ɛs) were calculated from the MODIS UCSB (University of California, Santa Barbara) emissivity library, using the following equation [55]:
The vegetation fraction (Pv) is derived from NDVI. For Landsat 8 imagery, it is calculated from red and near infrared bands (band 4 and 5) from the Operational Land Imager (OLI):
C in Equation (25) is a term which takes the cavity effect into account due to the surface roughness (C = 0 for flat surfaces). Sobrino et al. [50] suggested that Ci can be estimated as the following:
F' is the geometrical factor ranging between 0 and 1, depending on the geometrical distribution of the surface [27,40], which is typical 0.55 [56].
The pixel is considered as bare soil (Pv = 0), when NDVI < 0.2. For this circumstance, the emissivity is estimated from a empirical relationship with the red band reflectance ρ4, which is also derived from MODIS UCSB emissivity library [11,27,57]. The relationships for band 10 and 11 are: ɛ10 = 0.973−0.047ρ4, ɛ11 = 0.984−0.026ρ4 (Pv = 0).

2.5. Validation Sites and Landsat 8 Imagery Processing
Four Surface Radiation budget network (SURFRAD) sites operated by the National Oceanic and Atmospheric Administration (NOAA) were selected for algorithm validation, corresponding to 41 scenes of Landsat8 imagery (Table 5). SURFRAD is the first network to operate across the United States. It began in 1995 with four stations and expanded to six in 1998 [58]. The primary objective is to support climate research with accurate, continuous, long-term measurements of the surface radiation budget over the United States [59]. Primary measurements in each SURFRAD site are the downwelling and upwelling components of broadband solar and thermal infrared irradiance. Ancillary observations include direct, diffuse solar and photosynthetically active radiation, UVB, spectral solar, and meteorological parameters [59–61]. All the data are downloaded, quality controlled, and processed into daily files that are distributed freely to the public in near real time by anonymous FTP and the WWW server.

At four validation sites, high-quality in situ measurements of upwelling and downwelling long wave radiations are provided [59]. In this study, SURFRAD observations were used for the evaluation of LST retrieval. The surface skin temperature Ts can be estimated from the following equation [62]:
The F↑ and F↓ are upwelling and dowelling thermal infrared (3–50 μm) irradiance at the time when the Landsat 8 transits the sites. The ground measurement is 1-min interval, and the exact imaging time was accessed from the metadata for each scene. In the formula, σ is the Stefan-Boltzmann constant (σ = 5.6705×10−8 W·m−2·K−4), and ɛb is the broadband emissivity, which is converted from the two spectral (ɛ31, ɛ32) emissivities of the 8-day MODIS Land Surface Temperature and Emissivity product (MOD11A2). Emissivities were extracted from the nearest date corresponding to the imaging date in the product for each validation site. We applied 3 × 3 pixels quality mask (emissivity error flag: 00, indicating average emissivity error ≤0.01) with the center of site’s location. Pixels with good quality were averaged as the site’s emissivity.
The conversion from narrow bands emissivities to broad band emissivity is as following [63]:
The water vapor content which used in the SW algorithm and SC method is derived from site’s meteorology observations. The saturated water vapor pressure ( ) is calculated from dry air (T) temperature and air pressure (P) [64]:
Real water pressure is then derived from the relative humility (RH):
The unit of e is hectopascal and the unit of w is g/cm2, the convert factor is 0.098. T, P and RH are meteorology observations from the SURFRAD site.
Forty-one scenes of Landsat 8 imagery were downloaded from the USGS EarthExplorer Website. We ordered the reprocessed imagery after 3 February 2014 to ensure that the original data is accurate enough for the LST inversion, as it has been announced that the offsets are removed about 2.1 K from Band 10 and about 4.4 K from Band 11, relative to products processed prior to 3 February 2014. The conversion from digital number (DN) to radiance, reflectance and at-satellite brightness temperature followed the guideline at the USGS website. Calibration parameters were directly accessed from the metadata file.
All images were atmospherically corrected with the ACTOR module in PCI Geomatica 2013 SP3. A cloud mask was generated based on the cirrus band (Band 9) and quality assessment (QA) band to avoid the disturbance of cloud. The geometric correction was performed by the same software, using a 1″/3 national elevation dataset provided by USGS.
3. Results and Discussion
3.1. Results from the Radiative Transfer Equation Based Method
Ground based LST (LST_g) are shown in Table 6. LST inverted from Landsat 8 TIRS band 10 and 11 (LST_RT_b10 and LST_RT_b11), using the radiative transfer equation-based method are shown in Tables 7 and 8.



The bias (difference between estimated LST and ground LST), SD (standard deviation of the bias) and RMSE (root mean square error for estimated LST and ground LST) are also shown for each site. For both band 10 and 11 inverted LST, there is a general positive bias at selected sites, except for the Goodwin Greek site. For band 10 and 11, biases are 0.06 K and 0.05 K with all samples, indicating a slight overestimation.
For band 10, RMSE at four sites are 0.87 K, 1.01 K, 0.93 K and 0.57 K, while for band 11, RMSE are 1.17 K, 1.19 K, 1.12 K and 0.75 K. The accuracy for LST_RT_b10 is higher than LST_RT_b11. As it has been announced that the calibration variability of band 10 is 0.12 W/m2/sr/μm (∼0.8 K) and 0.2 W/m2/sr/μm (∼1.75 K) for band 11 by the USGS Landsat website. Although we used the reprocessed Landsat 8 data in this study, there is still large calibration uncertainty associated with band 11, which leads to the error for LST estimation. Meanwhile, this is expected, since band 11 is more affected by the water vapor continuum absorption and thus more sensitive to errors in atmospheric profiles [33].
Moreover, the accuracy of the radiative transfer equation-based method depends mostly on how well the atmospheric profiles are able to represent the actual atmosphere over the site when the sensor captures image. In this study, the NCEP reanalysis data was used as the atmospheric profile, since the lack of the real time radiosonde data for each scene of Landsat 8 image. Wan and Li [65] proposed a method to evaluate the quality of atmospheric profiles by analyzing the difference between the LSTs derived from instruments which have split window bands at 11 and 12μm, such as MODIS and AATSR. Coll et al. [33] compared different sources of atmospheric profiles for land surface temperature retrieval from single channel thermal infrared data, including radiosonde, NCEP, Aqua AIRS and MOD07L2, and suggested that NCEP reanalysis profiles provide an alternative to radiosonde data. In this study, we compared the LST estimated from TIRS band 10 and 11, the result is shown in Table 9. There is a general overestimation trend for LST_RT_b11 than LST_RT_b10 at Bondville and Sioux Falls, while underestimation at Fort Peck and Goodwin Greek. However, all the difference is less than 1 K. The RMSE are 0.53 K, 0.26 K, 0.34 K and 0.25 K for each site respectively, suggesting that the NCEP is fairly accurate enough for retrieving LST from Landsat 8 TIRS band 10 & 11 based on the radiative transfer equation.

3.2. Results from the SW Algorithm
Results for LST estimated from the Landsat 8 TIRS (LST_SW), using the SW algorithm are show in Table 10. There is a general underestimation for four sites except for the Sioux Falls site, as the bias is 0.07 K for this site. The bias for all sites is −0.15 K, suggesting an underestimation for all scenes. Meanwhile, the standard deviation of the bias for the Goodwin Greek site is 1.18 K, higher than other sites. Landscape around Goodwin Creek is rural pasture land with several ponds surrounded, which was checked from the high resolution image in Google Earth. Variations in the landscape leads to the emissivity estimation errors, since we only considered soil and vegetation for ɛ in this study. It may also note that the point scale ground measurement is largely incompetent to the pixel area retrieval from satellite [66].

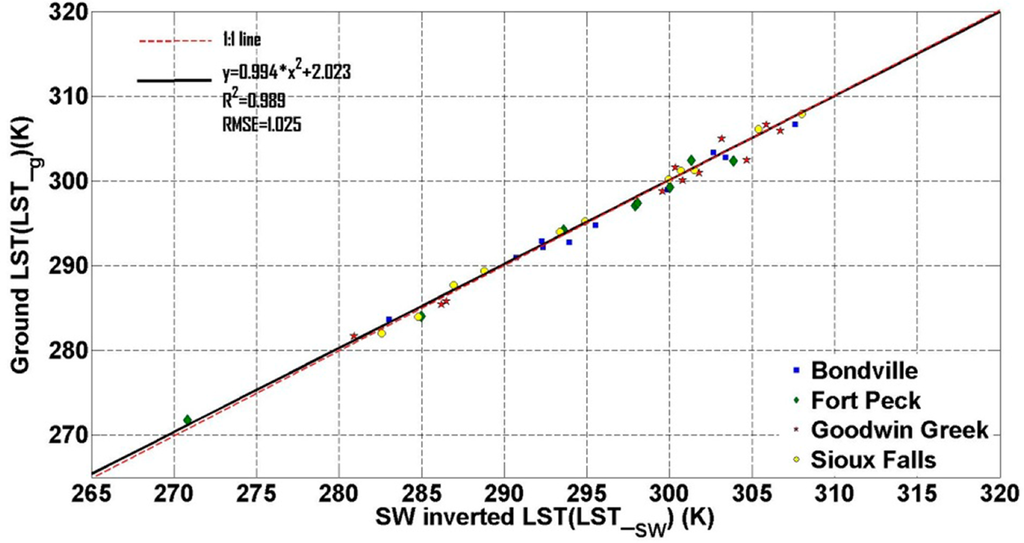
Figure 3 illustrates the comparison of LST_g and inverted LST (LST_SW). It shows that they have high correlation (R2 = 0.989). However, there is an underestimate trend for high LST condition, which can also be found from Table 3. Since the hypothesis behind Mao et al. [24] method is that the difference of Ta and is fairly insignificant, it should be tested for high water vapor content and high air temperature conditions. That may also introduce external error for LST inversion. RMSE for Bondville and Fort Pack sites are 0.72 K and 0.73 K, while 1.18 K and 1.15 K for Goodwin Greek and Sioux Falls sites for (Table 10), and 1.025 K for all sites (Figure 3), suggesting that the SW algorithm has the potential for accurate LST inversion from TIRS imagery.
3.3. Results from the SC Theory
LST estimated from the Landsat 8 TIRS band 10 and 11 (LST_SC_b10 and LST_SC_b11), using single channel method are showed in Tables 11 and 12. Overestimation happens for all sites using both bands (bias > 0). For all samples, biases are 0.44 K with band 10 and 0.73 K with band 11. RMSE for LST_SC_b11 are 1.78 K, 1.43 K, 1.71 K and 1.34 K for each site respectively, which are higher than RMSE of LST_SC_b10. It has the similar situation with radiative transfer equation based method, indicating that band 11 has larger calibration uncertainty. Moreover, we used the function proposed by Jimenez-Munoz and Sobrino [12] to calculate the parameters used for the SC method. However, it has to be noted that the general spectral response function with a full width half maximum (FWHM) of 1 μm applied to simulate the function may introduce extra errors [12,34]. Moreover, Jimenez-Munoz and Sobrino [34] figured out that the most important error source in SC method is due to atmospheric effects, which leads to an error on the LST between 0.2 K and 0.7 K, and the land surface emissivity uncertainty, which leads to an error on the LST between 0.2 K and 0.4 K.


The most recent study by Jimenez-Munoz et al. [23] indicates that higher water vapor content will introduce more error into the LST estimation, but can be partly solved by computing the atmospheric functions directly. In our study, this has been consolidated by comparing the result for radiative transfer equation based method and SC method for band 10 of TIRS, since LST estimated from the former has higher accuracy than the latter. As for band 11, the LST estimation accuracy is not acceptable for both methods. It has to be noted that we cannot ensure the effect of errors in LSE on LST inversion in this study, because of the lack of ground LSE measurement. It must be pointed out that, the uncertainty inside the MODIS product we used for the derivation of ground LST will introduce external error for result verification, although many other studies have used it for LST products’ validation [62,67,68].
3.4. Comparison of Three Methods
RMSE of LST estimated from the radiative transfer equation-based method using band 10 and 11 are 0.903 K and 1.153 K for all 41 samples, compared with 1.39 K and 1.67 K for the SC method. RMSE for SW algorithm is 1.025 K (Figure 3) for all samples. It shows that the LST retrieval from band 11 has more uncertainty than band 10 (Tables 7, 8, 11 and 12). The radiative transfer equation-based method using band 10 has the highest accuracy with RMSE less than 1 K, while the SW algorithm has moderate accuracy. However, the difference is not quite obvious (with RMSE difference of 0.122 K). Specifically, for Good Greek and Sioux Falls sites, the former (RMSE: 0.93 K and 0.57 K) outperforms the latter (RMSE: 1.25 K and 1.10 K) (Tables 7 and 10). For the Bondville site, the latter has lower RMSE of 0.73 K than the former of 1.17 K (Tables 7 and 10). For the Fort Peck site, the difference is not obvious. As mentioned in Section 2.5, the stray light issue introduces disturbance from nearby area to the scene of TIRS, leading to larger uncertainty for LST retrieval. The USGS Landsat website has recommended not using band 11 for SW algorithm. In this study, the highest accuracy for LST retrieval comes from the radiative transfer equation-based method, using band 10 along with NCEP atmospheric profile. The SW algorithm has medium accuracy compared with other two methods. While the SC method has the lowest accuracy. Results for LST retrieval from band 11 show larger uncertainty than band 10, which is consistent with the announced TIRS calibration issue.
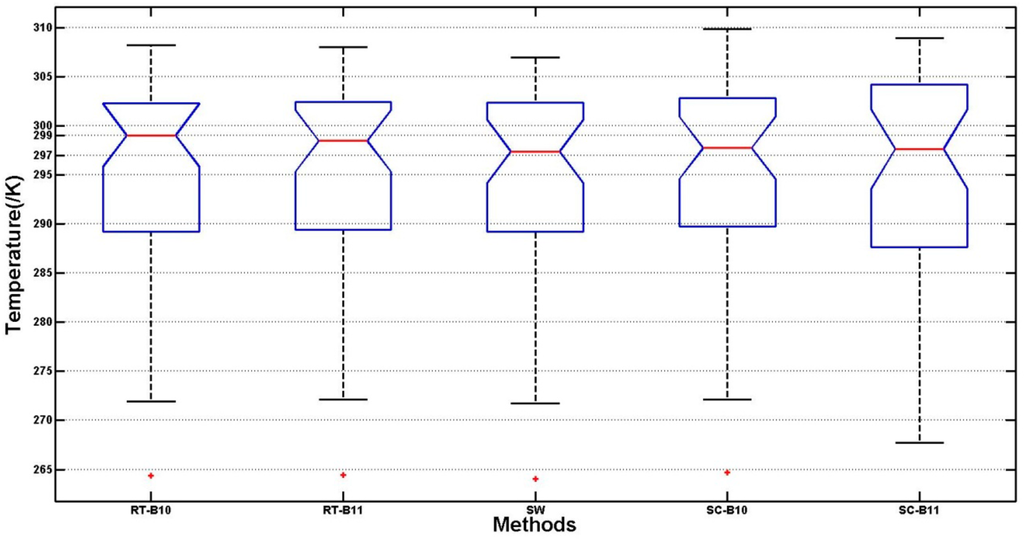
Furthermore, we applied the one side analysis of variance (ANOVA) [69] for these methods. The box plot of the estimated LST is shown in Figure 4. F-value and P-value for the ANOVA are 0.09 and 0.9865 respectively, which indicates that the differences between three presented methods are not significant. It consolidates the comparison of RMSE. Moreover, we used t test [70] for results from the radiative transfer equation-based method using band 10 and the SW algorithm. The p-value is 0.0972 (larger than 0.05, less than 0.1), which suggests that results from these two methods are moderately different.
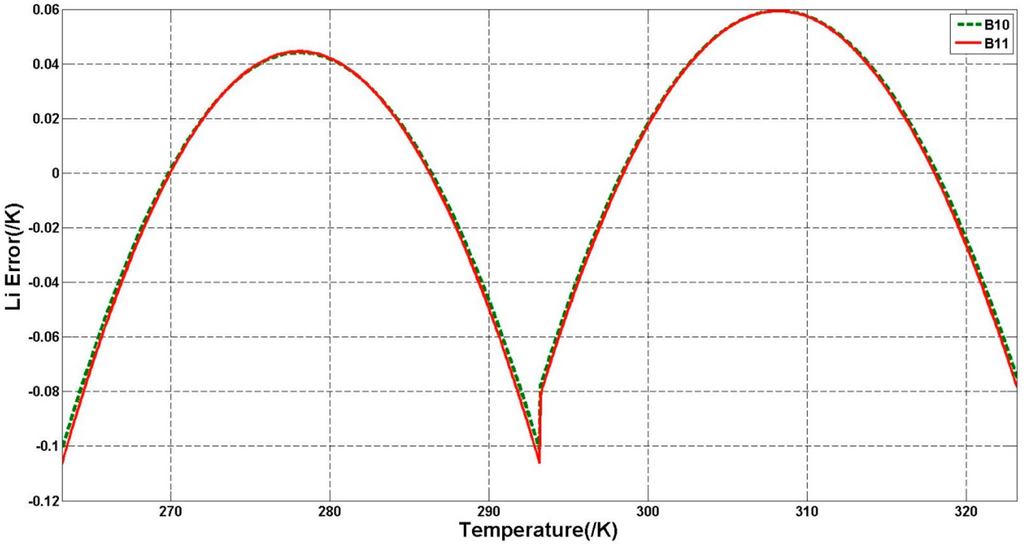
Meanwhile, it should be noted that we derived a more general SW algorithm in this study. The parameter Li was estimated by the piecewise linear fitting (−10–20 °C and 20–50 °C, Table 1), while the atmospheric transmittance was estimated by the piecewise quadratic regression (0.2–3.0 g/cm2 and 3.0–6.0 g/cm2 under two typical atmospheric profiles, Table 2). These division may not fall into the prevailing range of the validation sites’ condition. However, it does not reduce the validity of the algorithm. The errors for Li estimation are shown in Figure 5 and absolute errors are less than 0.1 K under most conditions. As for the atmospheric transmittance (τ), Qin et al. [26] revealed that the even the |T10-T11| is less than 0.5 K, the split window algorithm can still produce a very accurate LST estimation in spite of a big transmittance error, although Rozenstein et al. [22] suggested that the contribution of τ error to the LST estimation is complex and also depends on the emissivity in both channels.
4. Conclusions
We applied the radiative transfer equation based method, the split window algorithm and the single channel method to the Landsat 8 TIRS data. For the first method, the NECP data was used to simulate the parameters needed as inputs for MODTRAN model. For the SW algorithm, coefficients were adapted based on spectral response functions of two TIRS bands (band 10 and 11). Atmospheric transmittance was derived from the MODTRAN model, using standard atmospheric profile. For the SC method, parameters were derived from the regression of a general spectral function corresponding to simulated atmospheric absorption profiles. Land surface emissivity were estimated by the NDVI threshold method. Forty-one scenes of imagery were used for validation at four selected SURFRAD sites with high frequency irradiance measurement and MODIS LSE product. For the investigated sites and scenes, results show that LST retrieval from the radiative transfer equation-based method using band 10 has the highest accuracy with RMSE ≤1 K, while the SW algorithm has moderate accuracy and the SC method has the lowest accuracy with all scenes. For those methods using single band, LST estimated from band 10 has higher accuracy than band 11. Future work should focus on theoretical evaluations of the effect for input parameters’ (LSE, atmospheric transmittance) errors on estimated LST. Since the limitation of validation sites and scenes, the range of ground temperature in this study is mostly within 10°C to 30°C and the surrounding areas are relative homogeneous. More land surface types and different temporal scenes should be tested to verify the investigated three methods for LST estimation from Landsat 8 TIRS imagery.
Acknowledgments
We sincerely appreciate the help from the researchers affiliated with the SURFRAD network. We are grateful to the Earth System Research Laboratory, Global Monitoring Division from National Oceanic and Atmospheric Administration (NOAA) for providing the radiation data at four selected sites and the US Geological Survey (USGS) for providing Landsat-8 imagery and supplement data. Special thanks are given to the experts from USGS, who attended the Landsat Technical Working Group (LTWG) #23 Meeting (Saskatoon, SK Canada, 9–13 June 2014). We would also like to thank all anonymous reviewers for their dedicated working. It helps a lot for the revision of this paper. This study was funded by the Chinese Scholarship Council (CSC). The research was partially supported by the Western Heritage.
Author Contributions
Xiaolei Yu is the principal author of this paper. Xiaolei Yu and Xulin Guo worked on the methodology and the processing of the Landsat 8 TIRS data. Zhaocong Wu participated in the interpretation of the results and the final version of this contribution.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liang, S.; Li, X.; Wang, J. Advanced Remote Sensing: Terrestrial Information Extraction and Applications; Elsevier Science: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Zhang, Z.; He, G. Generation of Landsat surface temperature product for China, 2000–2010. Int. J. Remote Sens 2013, 34, 7369–7375. [Google Scholar]
- Jimenez-Munoz, J.C.; Sobrino, J.A. Split-window coefficients for land surface temperature retrieval from low-resolution thermal infrared sensors. IEEE Geosci. Remote Sens. Lett 2008, 5, 806–809. [Google Scholar]
- Li, H.; Sun, D.; Yu, Y.; Wang, H.; Liu, Y.; Liu, Q.; Du, Y.; Wang, H.; Cao, B. Evaluation of the VIIRS and MODIS LST products in an arid area of northwest China. Remote Sens. Environ 2014, 142, 111–121. [Google Scholar]
- Weng, Q.; Fu, P. Modeling annual parameters of clear-sky land surface temperature variations and evaluating the impact of cloud cover using time series of Landsat TIR data. Remote Sens. Environ 2014, 140, 267–278. [Google Scholar]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ 2014, 145, 55–67. [Google Scholar]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ 2014, 145, 154–172. [Google Scholar]
- Markham, B.L.; Storey, J.C.; Williams, D.L.; Irons, J.R. Landsat sensor performance: History and current status. IEEE Trans. Geosci. Remote Sens 2004, 42, 2691–2694. [Google Scholar]
- Huang, C.; Goward, S.N.; Masek, J.G.; Thomas, N.; Zhu, Z.; Vogelmann, J.E. An automated approach for reconstructing recent forest disturbance history using dense Landsat time series stacks. Remote Sens. Environ 2010, 114, 183–198. [Google Scholar]
- Jimenez-Munoz, J.C.; Cristobal, J.; Sobrino, J.A.; Soria, G.; Ninyerola, M.; Pons, X. Revision of the single-channel algorithm for land surface temperature retrieval from Landsat thermal-infrared data. IEEE Trans. Geosci. Remote Sens 2009, 47, 339–349. [Google Scholar]
- Sobrino, J.A.; Jimenez-Munoz, J.C.; Paolini, L. Land surface temperature retrieval from Landsat TM 5. Remote Sens. Environ 2004, 90, 434–440. [Google Scholar]
- Jimenez-Munoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res.: Atmos 2003. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens 2001, 22, 3719–3746. [Google Scholar]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ 2013, 131, 14–37. [Google Scholar]
- Sobrino, J.A.; Caselles, V.; Coll, C. Theoretical split-window algorithms for determining the actual surface temperature. Il Nuovo Cimento C 1993, 16, 219–236. [Google Scholar]
- Pedelty, J.; Devadiga, S.; Masuoka, E.; Brown, M.; Pinzon, J.; Tucker, C.; Roy, D.; Ju, J.; Vermote, E.; Prince, S. Generating a long-term land data record from the AVHRR and MODIS instruments. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, 2007 (IGARSS 2007), Barcelona, Spain, 23–28 July 2007; pp. 1021–1025.
- Coll, C.; Valor, E.; Galve, J.M.; Mira, M.; Bisquert, M.; García-Santos, V.; Caselles, E.; Caselles, V. Long-term accuracy assessment of land surface temperatures derived from the advanced along-track scanning radiometer. Remote Sens. Environ 2012, 116, 211–225. [Google Scholar]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens 1996, 34, 892–905. [Google Scholar]
- Niclòs, R.; Galve, J.M.; Valiente, J.A.; Estrela, M.J.; Coll, C. Accuracy assessment of land surface temperature retrievals from MSG2-SEVIRI data. Remote Sens. Environ 2011, 115, 2126–2140. [Google Scholar]
- Sun, D.; Pinker, R.T. Estimation of land surface temperature from a geostationary operational environmental satellite (GOES-8). J. Geophys. Res.: Atmos 2003. [Google Scholar] [CrossRef]
- Quattrochi, D.A.; Luvall, J.C. Thermal Remote Sensing in Land Surface Processing; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Rozenstein, O.; Qin, Z.; Derimian, Y.; Karnieli, A. Derivation of land surface temperature for Landsat-8 TIRS using a split window algorithm. Sensors 2014, 14, 5768–5780. [Google Scholar]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Skokovic, D.; Mattar, C.; Cristobal, J. Land surface temperature retrieval methods from Landsat-8 thermal infrared sensor data. IEEE Geosci. Remote Sens. Lett 2014, 11, 1840–1843. [Google Scholar]
- Mao, K.; Qin, Z.; Shi, J.; Gong, P. A practical split-window algorithm for retrieving land-surface temperature from MODIS data. Int. J. Remote Sens 2005, 26, 3181–3204. [Google Scholar]
- Mao, K.; Qin, Z.; Shi, J.; Gong, P. The research of split-window algorithm on the MODIS. Geomat. Inf. Sci. Wuhan Univers 2005, 30, 703–707. [Google Scholar]
- Qin, Z.; Dall’Olmo, G.; Karnieli, A.; Berliner, P. Derivation of split window algorithm and its sensitivity analysis for retrieving land surface temperature from NOAA-advanced very high resolution radiometer data. J. Geophys. Res.: Atmos 2001, 106, 22655–22670. [Google Scholar]
- Sobrino, J.A.; Jimenez-Muoz, J.C.; Soria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martinez, P. Land surface emissivity retrieval from different VNIR and TIR sensors. IEEE Trans. Geosci. Remote Sens 2008, 46, 316–327. [Google Scholar]
- Schott, J.; Gerace, A.; Brown, S.; Gartley, M.; Montanaro, M.; Reuter, D.C. Simulation of image performance characteristics of the Landsat data continuity mission (LDCM) thermal infrared sensor (TIRS). Remote Sens 2012, 4, 2477–2491. [Google Scholar]
- Li, H.; Liu, Q.; Du, Y.; Jiang, J.; Wang, H. Evaluation of the NCEP and MODIS atmospheric products for single channel land surface temperature retrieval with ground measurements: A case study of HJ-1B IRS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2013, 6, 1399–1408. [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc 1996, 77, 437–471. [Google Scholar]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An atmospheric correction parameter calculator for a single thermal band earth-sensing instrument. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, 2003 (IGARSS’03), Toulouse, France, 21–25 July 2003; pp. 3014–3016.
- Coe, M.T. Modeling terrestrial hydrological systems at the continental scale: Testing the accuracy of an atmospheric GCM. J. Clim 2000, 13, 686–704. [Google Scholar]
- Coll, C.; Caselles, V.; Valor, E.; Niclòs, R. Comparison between different sources of atmospheric profiles for land surface temperature retrieval from single channel thermal infrared data. Remote Sens. Environ 2012, 117, 199–210. [Google Scholar]
- Jimenez-Munoz, J.C.; Sobrino, J.A. Error sources on the land surface temperature retrieved from thermal infrared single channel remote sensing data. Int. J. Remote Sens 2006, 27, 999–1014. [Google Scholar]
- Jimenez-Munoz, J.C.; Sobrino, J.A. A single-channel algorithm for land-surface temperature retrieval from ASTER data. IEEE Geosci. Remote Sens. Lett 2010, 7, 176–179. [Google Scholar]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 8–14 μm atmospheric window. Remote Sens. Environ 1992, 42, 83–106. [Google Scholar]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.-H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens 2012, 34, 3084–3127. [Google Scholar]
- Masiello, G.; Serio, C. Simultaneous physical retrieval of surface emissivity spectrum and atmospheric parameters from infrared atmospheric sounder interferometer spectral radiances. Appl. Opt 2013, 52, 2428–2446. [Google Scholar]
- Masiello, G.; Serio, C.; de Feis, I.; Amoroso, M.; Venafra, S.; Trigo, I.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from geostationary infrared radiances. Atmos. Meas. Tech 2013, 6, 3613–3634. [Google Scholar]
- Sobrino, J.A.; Raissouni, N.; Li, Z.-L. A comparative study of land surface emissivity retrieval from NOAA data. Remote Sens. Environ 2001, 75, 256–266. [Google Scholar]
- Coll, C.; Galve, J.M.; Sanchez, J.M.; Caselles, V. Validation of Landsat-7/ETM+ thermal-band calibration and atmospheric correction with ground-based measurements. IEEE Trans. Geosci. Remote Sens 2010, 48, 547–555. [Google Scholar]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for advanced spaceborne thermal emission and reflection radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens 1998, 36, 1113–1126. [Google Scholar]
- Peres, L.F.; DaCamara, C.C. Emissivity maps to retrieve land-surface temperature from MSG/SEVIRI. IEEE Trans. Geosci. Remote Sens 2005, 43, 1834–1844. [Google Scholar]
- Van de Griend, A.; Owe, M. On the relationship between thermal emissivity and the normalized difference vegetation index for natural surfaces. Int. J. Remote Sens 1993, 14, 1119–1131. [Google Scholar]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ 1996, 57, 167–184. [Google Scholar]
- Momeni, M.; Saradjian, M. Evaluating NDVI-based emissivities of MODIS bands 31 and 32 using emissivities derived by day/night LST algorithm. Remote Sens. Environ 2007, 106, 190–198. [Google Scholar]
- Wan, Z.; Li, Z.-L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens 1997, 35, 980–996. [Google Scholar]
- Becker, F.; Li, Z.-L. Temperature-independent spectral indices in thermal infrared bands. Remote Sens. Environ 1990, 32, 17–33. [Google Scholar]
- Becker, F.; Li, Z.-L. Towards a local split window method over land surfaces. Int. J. Remote Sens 1990, 11, 369–393. [Google Scholar]
- Sobrino, J.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: Application to Morocco. Int. J. Remote Sens 2000, 21, 353–366. [Google Scholar]
- Dash, P.; Göttsche, F.-M.; Olesen, F.-S.; Fischer, H. Separating surface emissivity and temperature using two-channel spectral indices and emissivity composites and comparison with a vegetation fraction method. Remote Sens. Environ 2005, 96, 1–17. [Google Scholar]
- Dash, P.; Göttsche, F.-M.; Olesen, F.-S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice-current trends. Int. J. Remote Sens 2002, 23, 2563–2594. [Google Scholar]
- Sobrino, J.A.; Romaguera, M. Land surface temperature retrieval from MSG1-SEVIRI data. Remote Sens. Environ 2004, 92, 247–254. [Google Scholar]
- Sobrino, J.A.; Kharraz, J.E.; Li, Z.L. Surface temperature and water vapour retrieval from MODIS data. Int. J. Remote Sens 2003, 24, 5161–5182. [Google Scholar]
- Tang, B.-H.; Wu, H.; Li, C.; Li, Z.-L. Estimation of broadband surface emissivity from narrowband emissivities. Opt. Express 2011, 19, 185–192. [Google Scholar]
- Sánchez, J.; Scavone, G.; Caselles, V.; Valor, E.; Copertino, V.; Telesca, V. Monitoring daily evapotranspiration at a regional scale from Landsat-TM and ETM+ data: Application to the Basilicata region. J. Hydrol 2008, 351, 58–70. [Google Scholar]
- Baldridge, A.; Hook, S.; Grove, C.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ 2009, 113, 711–715. [Google Scholar]
- Augustine, J.A.; DeLuisi, J.J.; Long, C.N. SURFRAD—A national surface radiation budget network for atmospheric research. Bull. Am. Meteorol. Soc 2000, 81, 2341–2357. [Google Scholar]
- Augustine, J.A.; Hodges, G.B.; Cornwall, C.R.; Michalsky, J.J.; Medina, C.I. An update on SURFRAD—The GCOS surface radiation budget network for the continental United States. J. Atmos. Ocean. Technol 2005, 22, 1460–1472. [Google Scholar]
- DeLuisi, J.; Augustine, J.; Cornwall, C.; Hodges, G. Contrasting ARM’s SRB measurements with six SURFRAD stations. In Proceedings of the 9th ARM Science Team, San Antonio, TX, USA, 22–26 March 1999; pp. 1–6.
- Augustine, J.A.; Hodges, G.B.; Dutton, E.G.; Michalsky, J.J.; Cornwall, C.R. An aerosol optical depth climatology for NOAA’s national surface radiation budget network (SURFRAD). J. Geophys. Res.: Atmos 2008. [Google Scholar] [CrossRef]
- Yu, Y.; Tarpley, D.; Privette, J.L.; Flynn, L.E.; Xu, H.; Chen, M.; Vinnikov, K.Y.; Sun, D.; Tian, Y. Validation of GOES-R satellite land surface temperature algorithm using SURFRAD ground measurements and statistical estimates of error properties. IEEE Trans. Geosci. Remote Sens 2012, 50, 704–713. [Google Scholar]
- Wang, K.; Wan, Z.; Wang, P.; Sparrow, M.; Liu, J.; Zhou, X.; Haginoya, S. Estimation of surface long wave radiation and broadband emissivity using moderate resolution imaging spectroradiometer (MODIS) land surface temperature/emissivity products. J. Geophys. Res.: Atmos 2005. [Google Scholar] [CrossRef]
- Buck, A.L. New equations for computing vapor pressure and enhancement factor. J. Appl. Meteorol 1981, 20, 1527–1532. [Google Scholar]
- Wan, Z.; Li, Z.L. Radiance-based validation of the v5 MODIS land-surface temperature product. Int. J. Remote Sens 2008, 29, 5373–5395. [Google Scholar]
- Hale, R.C.; Gallo, K.P.; Tarpley, D.; Yu, Y. Characterization of variability at in situ locations for calibration/validation of satellite-derived land surface temperature data. Remote Sens. Lett 2010, 2, 41–50. [Google Scholar]
- Qian, Y.; Qiu, S.; Wang, N.; Kong, X.; Wu, H.; Ma, L. Land surface temperature and emissivity retrieval from time-series mid-infrared and thermal infrared data of SVISSR/FY-2C. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2013, 6, 1552–1563. [Google Scholar]
- Yu, Y.; Privette, J.L.; Pinheiro, A.C. Evaluation of split-window land surface temperature algorithms for generating climate data records. IEEE Trans. Geosci. Remote Sens 2008, 46, 179–192. [Google Scholar]
- Miller, R.G., Jr. Beyond Anova: Basics of Applied Statistics; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Lee, E.T.; Wang, J.W. Statistical Methods for Survival Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).