Remote Sensing Based Yield Estimation in a Stochastic Framework — Case Study of Durum Wheat in Tunisia
Abstract
: Multitemporal optical remote sensing constitutes a useful, cost efficient method for crop status monitoring over large areas. Modelers interested in yield monitoring can rely on past and recent observations of crop reflectance to estimate aboveground biomass and infer the likely yield. Therefore, in a framework constrained by information availability, remote sensing data to yield conversion parameters are to be estimated. Statistical models are suitable for this purpose, given their ability to deal with statistical errors. This paper explores the performance in yield estimation of various remote sensing indicators based on varying degrees of bio-physical insight, in interaction with statistical methods (linear regressions) that rely on different hypotheses. Performances in estimating the temporal and spatial variability of yield, and implications of data scarcity in both dimensions are investigated. Jackknifed results (leave one year out) are presented for the case of wheat yield regional estimation in Tunisia using the SPOT-VEGETATION instrument. Best performances, up to 0.8 of R2, are achieved using the most physiologically sound remote sensing indicator, in conjunction with statistical specifications allowing for parsimonious spatial adjustment of the parameters.1. Introduction
Satellite instruments providing frequent, coarse resolution observations, such as AVHRR (Advanced Very High Resolution Radiometer), SPOT-VGT (SPOT-VEGETATION), or MODIS (Moderate Resolution Imaging Spectroradiometer), have been used extensively for crop monitoring and yield estimation at the regional scale (for a review see [1, 2]). The rationale for using optical remote sensing (RS) observations to predict yield is based on the close relationship between crop biomass and yield, often formalized in the so-called harvest index (i.e., fraction of the total aboveground biomass allocated to the grains). Biomass is itself estimated from vegetation spectral properties derived from satellite observations. However, the definition of the transfer functions from satellite observations to biomass, and from biomass to yield, presents several challenges.
The derivation of biomass proxies (hereafter BP) from satellite observations usually proceeds in two steps. First, the top of canopy spectral reflectances of vegetation are retrieved from top of atmosphere satellite observations by taking atmospheric effects into account. This is typically achieved using atmospheric radiative transfer models (e.g., [3,4]). Second, the BP is derived from the estimated canopy reflectances. A pragmatic and widespread approach to extract the relevant information from the various spectral reflectances relies on the computation of vegetation indexes (e.g., NDVI, Normalized Difference Vegetation Index) that are thought to be proportional to the aboveground biomass. Vegetation indexes are subjected to intrinsic limitations (e.g., saturation of the signal) and contaminations from different sources (e.g., illumination and observation geometry, 3D structure of the vegetated medium, and background reflectance) [5]. More modern approaches make use of canopy radiative transfer models to derive key vegetation variables (e.g., LAI, leaf area index; FAPAR, Fraction of Absorbed Photosynthetically Active Radiation) from canopy reflectances [6–8]. The advantage of these methods is that they provide access to inherent vegetation properties largely decontaminated of external factors [9]. In particular, FAPAR acts as an integrated indicator of the status and health of vegetation, and plays a major role in driving gross primary productivity [10].
BPs can be estimated with either approach at different times during the growing season. The correlation between the BP and the final yield is expected to increase with later estimates since they are closer to harvest. However, the best timing cannot be known a priori and must be determined from the data. Alternatively, time series of RS indicators can be further manipulated to derive more physiologically sound BPs, for example, by retrieving their peak level or amplitude during the season (e.g., [11]), expressing the RS indicator as a function of thermal instead of calendar time [12], or cumulating their values during an appropriate time period (e.g., [13]).
The selected BP then needs to be translated into grain yield. Two groups of techniques are mainly used to accomplish this step: statistical modeling, both parametric and non-parametric, and crop growth modeling. Models of the first category rely on the availability of reference information (from actual ground measurements usually aggregated at some spatial level) for the empirical estimation of the conversion coefficients. Conversely, in the second group of techniques, RS data is assimilated [14] into more or less detailed models describing the physiological mechanisms of crop growth and development [15]. Both groups of techniques can explicitly deal with measurement uncertainties, systematic and random, typical of RS and yield data. Pros and cons are discussed in [1, 16].
This manuscript focuses on empirical regression modeling and aims to understand the implications, in terms of regional wheat yield estimation performance, of (i) the choice of BP and (ii) the differences in assumptions underlying a chosen set of regression models.
We investigate different RS approaches of increasing physical meaning by considering four BPs: the NDVI and the FAPAR value at a specific time of the year, and the integrated FAPAR and APAR (Absorbed Photosynthetically Active Radiation, the product of FAPAR and incident PAR) values during the period of plant activity. We also use six regression models, from a general country level to more region-specific ones, and the analysis is restricted to the linear framework for describing the relationships between the BP and yield. However, the models vary on their ability to locally adjust the relationship between the BP and actual yields, on their parsimony with respect to the number of parameters to be estimated, and on the implied assumptions concerning the error term they rely on.
The overall goal is to select the combination BP and statistical model that provides the best predictive capacity, avoiding over/under-parameterization given the dimension of the data set available for the calibration of the model. Overparameterization occurs when the amount of information contained in the calibration data is not enough to estimate the model parameters. The resulting model fits the calibration dataset, but produces large errors when used in prediction. Underparameterization refers to a situation in which the available information is not fully exploited by the restricted set of model parameters.
We address three additional important issues related to regional crop monitoring. First is the importance of distinguishing between the ability of a model to estimate the temporal and spatial variability of yield. In fact, in regional yield estimation studies, the model performance in predicting the interannual variability in yield is seldom decoupled from the overall performance in space and time together. However information regarding the temporal variability is of high practical importance for crop monitoring and yield forecasting, whilst information regarding the spatial variability may be of little practical use as the model may only be describing geographic variation in yield.
Second, the implications of data scarcity on model performance. Data availability can restricted by the limited length of RS time series used for crop monitoring (e.g., 14 years for SPOT-VGT). This issue is expected to be even more critical with new satellite missions (e.g., the future ESA-Sentinel 2) if a multi-sensor approach is not used to produce consistent long-term time series, integrating different sensors. Further data restrictions must also be faced in many regions of the world where only a shorter archive of ground yield measurements is available. Therefore, data constraints are investigated and discussed when choosing among statistical models, relying on different assumptions and with varying number of parameters to be estimated to avoid model over/under-parameterization.
Third, for specific applications such as crop monitoring in food-insecure regions, a qualitative yield assessment may be the only solution in the absence of ground calibration measurements. This is often achieved by comparing a BP, at a given time, with its “long-term” average or to a particular reference year (e.g., [17]). For this purpose, indications about the most robust RS-based yield indicator to be used in the absence of local calibration are proposed.
The investigation is performed on durum wheat yield data covering ten Tunisian governorates over the period of 1999–2011, using observations from the SPOT-VGT instrument.
2. Study Area and Data
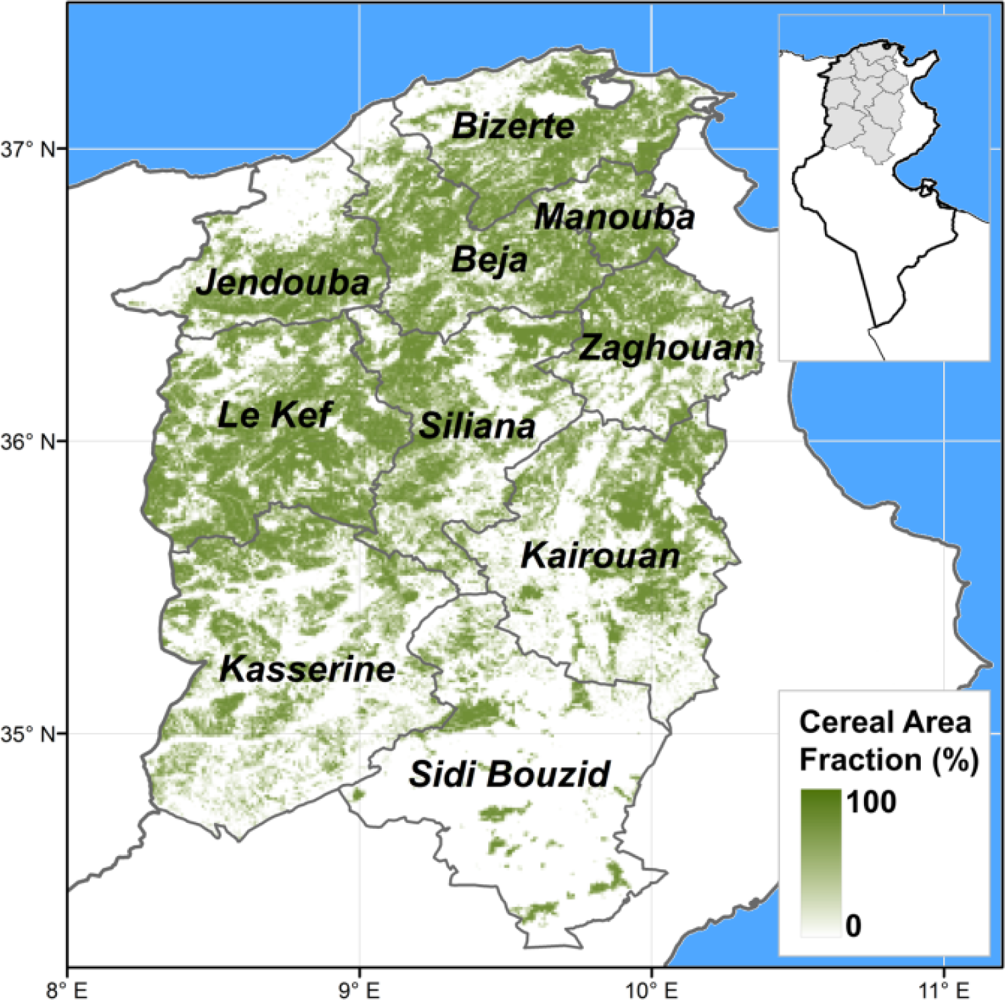
The study area encompasses ten governorates in North Tunisia (Beja, Bizerte, Jendouba, Kairouan, Kasserine, Le Kef, La Manouba, Sidi Bouzid, Siliana and Zaghouan; Figure 1) contributing to about 90% of the national production of wheat. Their climate ranges from semiarid in the South, to Mediterranean in the North. Average precipitations in the period of September to August ranges from 200 mm (Sidi Bouzid, in the South) to 610 mm (Jendouba, in the Northwest). Most cereals are winter crops, sowing takes place in autumn (between October and December depending on the temporal distribution of autumn rainfalls), and crops are harvested in summer (from June to July). Irrigated croplands represent a minor fraction of cereal areas (about 6% at the national level).
In the study area, durum wheat accounts for 60% of the total cereal production, and 51% of the cropped area. Agricultural practices and mineral fertilization are expected to play a role in determining wheat yield, whereas temperature is not considered a major limiting factor compared to the strong inter-annual variability of rainfalls [18].
2.1. Remote Sensing Data
This study is based on the analysis of maximum value composited dekadal (here defined as a 10-day period) NDVI and FAPAR products from the JRC-MARS archive (Joint Research Centre of the European Commission, Monitoring Agricultural Resources Unit) derived from calibrated, cloud-screened, and atmospherically corrected (SMAC algorithm, [3]) SPOT-VGT imagery at 1/112° (about 1 km) spatial resolution for the period of 1998–2011 [19]. FAPAR is estimated using the CYCLight algorithm [20].
2.2. Official Yield Statistics
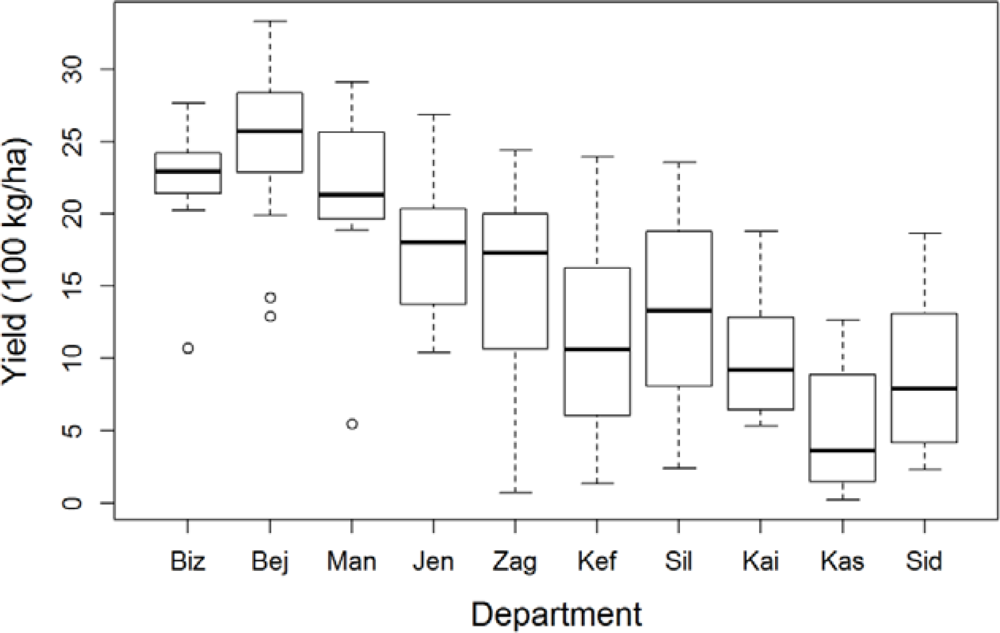
The statistical department of the Ministry of Agriculture provided the archive of durum wheat (Triticum durum desf.) grain yield, sowed, and harvested area. Yield statistics are obtained from ground sample surveys and are available as governorate level averages of grain weight per unit of sowed area from 1980 to 2011. Years overlapping with the RS time series were used for the purpose of this analysis (from 1999 to 2011, 13 years in total). The dataset includes 128 observations (13 yearly yield records for 10 governorates; yields for the La Manouba governorate are only available from 2001, consecutive to its creation). Yield is highly variable in both space and time (Figure 2) and no significant yield temporal trend, tested as the significance of the regression year vs. yield, is present in any of the governorates during this time period (all p-values greater than 0.16, mean and standard deviation equal to 0.47 and 0.20, respectively).
3. Methods
Wheat yield is estimated through empirical linear regression models relating RS-derived indicators of aboveground biomass to yield statistics at governorate level. Aboveground biomass is thus assumed to be the main predictor of yield in this study area, characterized by low to moderate productivity compared to other regions of the world (e.g., European Union mean yield is above 5,000 kg/ha, source: Eurostat). Limitations of this approach are represented by the marginal presence of high-yield irrigated crops for which grain productivity may not be linearly related to biomass and the possible occurrence of meteorological (e.g., dry conditions, and heavy rains) or biological disturbances (e.g., diseases) affecting the crop during its late development stages and leading to yield reduction not associated with green biomass reductions, and thus not easily detected by RS methods.
3.1. RS-Derived Biomass Proxies
Four candidate BPs of increasing biophysical meaning have been selected from the range of existing techniques proposed to estimate vegetation biomass (see [1, 2]). The first two are computed according to the simple and effective method used by the Centre National de la Cartographie et de la Télédétection (CNCT, Tunis) for the production of cereal production forecast bulletins. The method assumes that the “greenness” attained at a given time of the year is a predictor of the final grain yield. This specific timing is selected by finding the NDVI (or FAPAR) dekad that provides the highest correlation with yearly yield records (e.g., [21,22]). FAPAR is considered in the analysis in order to evaluate if it provides any improvement with respect to the vegetation index. The retrieval of the appropriate dekad was performed at both national and governorate level. The governorate-level retrieval attempts to take into account possible phenological differences among governorates. Hereafter, these proxies will be referred to as NDVIx and FAPARx (where x indicates the selected dekad), respectively.
The last two proxies belong to the group of techniques opting for the integration of the RS indicator over an appropriate time interval (automatically retrieved of fixed a priori) rather than selecting a single timing (e.g., [23, 24]). Such proxies are computed according to the phenologically-tuned method used by JRC-MARS to analyze the vegetation development in arid and semi-arid ecosystems in the absence of ground measurements [25]. They represent two variations of the light use efficiency approach [26], in which the biomass production proxy is linearly related to the integral of FAPAR and APAR, respectively. With FAPAR, the incident radiation is not considered a limiting factor. The integral is computed between the start of the growing period (start_dek), and the beginning of the descending phase of the seasonal FAPAR profile (end_dek), which are computed for each pixel and each crop-growing season. The latter corresponds to the beginning of the senescence phase, and roughly overlaps with anthesis. Hereafter, these proxies will be referred to as CUMFAPAR and CUMAPAR, respectively. Incident PAR needed to compute APAR is derived from ERA Interim and Operational models estimate of incident global radiation produced by ECMWF (European Centre for Medium-Range Weather Forecasts), downscaled at 0.25° spatial resolution and aggregated at dekadal temporal resolution [27]. No conversion factors (from global radiation to PAR, and from APAR to dry matter production) have been applied since the performance of linear regression models is insensitive to linear transformations in the data.
The cumulative value is calculated, as shown in the example of Figure 3. First, satellite FAPAR data of each growing season are fitted by a Parametric Double Hyperbolic Tangent (PDHT) mathematical model mimicking the seasonal trajectory [25]. Second, the integration limits are defined as follows: the growth phase (start_dek) starts when the value of the modeled time series exceeds the initial base value (asymptotic model value before the growth phase) plus 5% of the seasonal growth amplitude; the decay phase (end_dek) starts when the value of the modeled time series drops below the maximum fitted value minus 5% of the decay amplitude. Finally, such integration limits are used to compute CUMFAPAR (CUMAPAR) as the integral of the modeled values (modeled values times incident PAR) after the removal of the base FAPAR level.
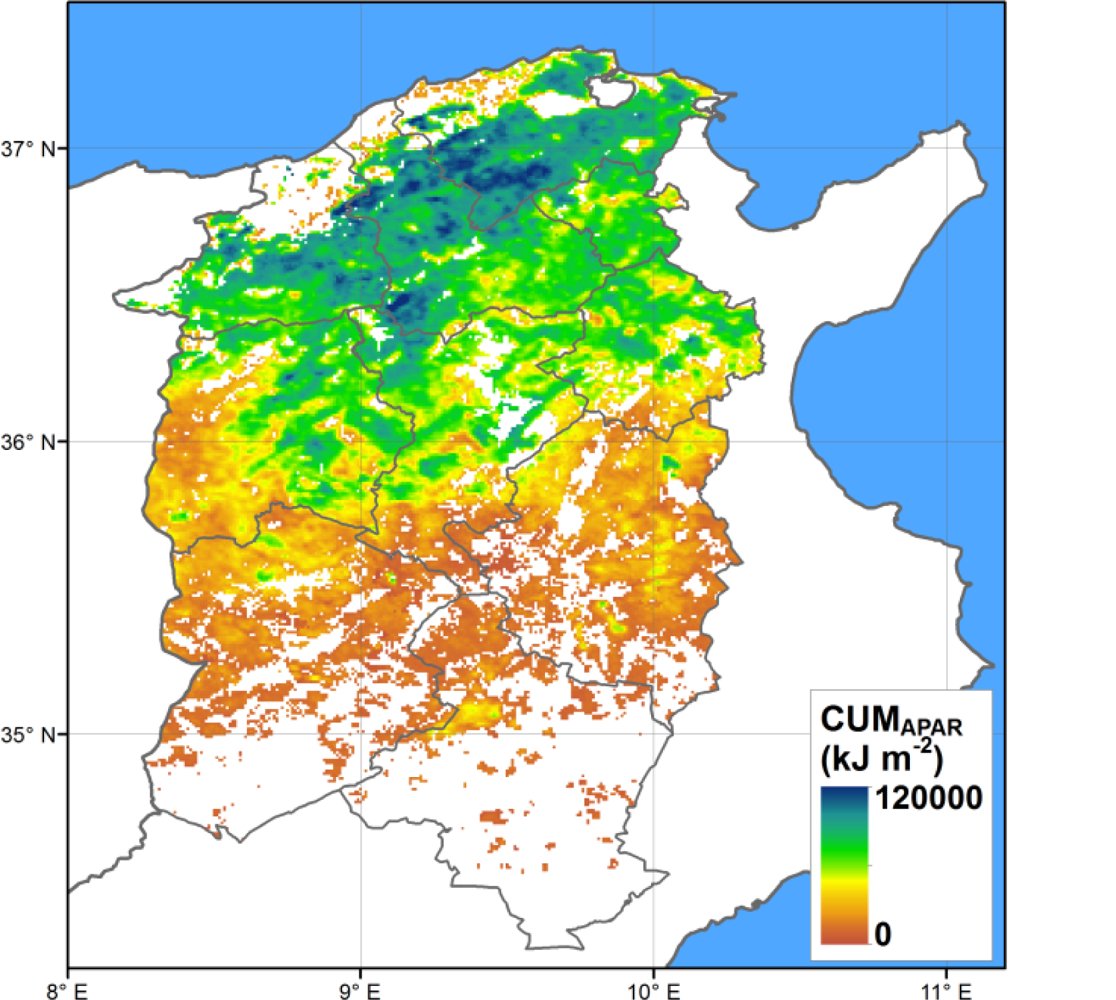
All the candidate proxies are computed for each year in which RS data is available, and for each pixel in the study area. As an example, the spatial distribution of the CUMAPAR is presented in Figure 4, showing the North-South gradient of decreasing productivity.
Pixel level biomass proxies are then aggregated at the governorate level as the weighted average according to each pixel’s area occupied by cereals [28]. The cereal cover within the VGT pixel (Figure 1) was derived from the land cover/land use produced by the INFOTEL project at a spatial scale of 1:25,000 [29].
3.2. Statistical Modeling
The conversion of biomass proxies into actual yields is not a straightforward task. First, the relationship between the two variables may vary, in functional form (e.g., from linear to logarithmic) and in magnitude (i.e., value of coefficients), between crops and varieties, locations, and possibly from year to year. Second, both biomass proxies and yield data are prone to measurement errors. Uncertainties in RS data result from a wide range of processes and are both systematic and random, while yield statistics may be affected by sampling and measurement biases and errors. Third, the spatial aggregation methods used to retrieve the regional figures of the two variables may not be fully coherent. Typically, the regional average of the RS indicator is computed on a static crop mask while the actual crop area may vary from year to year. Finally, data availability is a major concern since yield and RS time series “long enough” to allow for a reliable estimation of the conversion parameters are often not available.
The empirical estimation of this relationship is often made through regression techniques. Models and specifications differ in the hypothesized nature of the link between the variables and in the properties of the subsequent residuals. This is an important issue since wrong choices can lead to biased, inefficient, and inconsistent parameter estimates. The simplest and most widespread way of modeling the relationship between yield and biomass proxies is through Ordinary Least Squares regression (OLS):
Although it is recognized that such differences are present at different geographic scales, the spatial information needed for their detailed modeling is not available. Therefore, an alternative approach consists in estimating the yield at the governorate level (G-OLS) to account for these spatial heterogeneities:
Both models estimate G + 1, instead of 2 × G parameters. Equation (3) refers to a model where only the slope is adjusted at the governorate level and it is named Governorate-Slope OLS (GS-OLS). Equation (4) corresponds to a fixed effects (FE) panel model that can be expressed in the form of Equation (1), where the error term εi,d is not assumed to be iid, but to have a fixed governorate component [30]:
Although GS-OLS and FE models are more parsimonious than G-OLS, they can still suffer a significant loss of degrees of freedom from the estimation of governorate-specific parameters in datasets where the number of governorates is large. This can be avoided if ud is assumed (i) to be iid(0, σu2), (ii) independent from vi,d and, (iii) independent from BPi,d. In this case, the random effects model (RE) is suitable for a consistent, unbiased, and efficient estimation of the unobservable governorate-specific effects (see [30] for the details). The hypothesis underlying the RE model can be tested through the Hausman Test [31] in order to determine if, or not, the FE model should be preferred to it, while the Breusch-Pagan Lagrange multiplier test (LM-test) [30] allows the modeler to decide between the RE and the P-OLS. The use of this approach reduces the number of parameters to be estimated to 4, two for the slope and intercept, and two for the characterization of the variances of the unobservable effects (i.e., σu2 and σv2). The estimation of the RE model and the predictions of the model has been performed based on the maximum likelihood technique described in [30].
To take into account possible phenological differences among governorates when using NDVIx and FAPARx as BPs, we also considered a G-OLS model for which the most correlated dekad x is selected at the governorate level (named Dek-G-OLS). Note, that while this approach may be able to better adapt to the local phenology, it indirectly results in a further loss of degrees of freedom because the retrieval of appropriate dekad is performed using the calibration data set.
All the models are assessed using a jackknife technique, leaving one year out at a time (G observations). The following prediction performance indicators are computed for predictions for the year left out: root mean square error (RMSE), and . measures the fraction of yield variability that is explained by the model, in both the spatial and the temporal dimensions. aims to measure the performance of a model in reproducing the temporal variability of the data and not the spatial:
Finally, as data scarcity is a major concern when modeling yields based on RS data, an analysis is run in order to understand how model performance deteriorates with respect to decreasing data availability. We simulated increasing data scarcity in both the temporal and spatial dimensions. In the first case, jackknifed results are again reported but leaving n years out of the calibration and predicting for those years (n × G observations). In the second case, the number of governorates included in the analysis is progressively reduced while leaving n years out for computing the predictive performances. This analysis is of particular interest since the models used in the comparison estimate different number of parameters and are then expected to have different deterioration patterns.
To facilitate the analysis of the results, a table summarizing the acronyms used for the biomass proxies and statistical models is provided in Table A1 in Appendix.
4. Results and Discussion
We found that NDVI in the second dekad of April (i.e., NDVI11) and FAPAR in the third dekad of April (i.e., FAPAR12) provided the maximum correlation with yield and so we used them as the first two BPs in the following analysis. For the second two BPs, the phenologically-tuned CUMFAPAR and CUMAPAR, we did not perform any tuning for computing the integration limits.
Before comparing the performances of the different BP-statistical model combinations, it is worth presenting the results of the statistical tests that can be performed in order to guide the choice between regression specifications. F-tests show that models that have a governorate-specific adjustment (i.e., G-OLS, GS-OLS and FE) should be preferred to OLS (all p-values < 0.01). The same applies when testing the RE with respect to the OLS with the LM-test (all p-values < 0.01). These tests show that the increased number of model parameters, always producing a better fit of the data, gives a significant performance improvement. In doing that, they anticipate the jackknifed results presented in the following sections. However, other performed tests show that no significant improvements (at 10%) can be achieved once a simple spatial adjustment is adopted: neither the F-test, that compares G-OLS to GS-OLS, and to FE, neither the Hausman test, that compares the FE to the RE, allow the modeler to reject the null hypothesis that more parsimonious models perform as well as the ones producing a greater loss of degrees of freedom.
4.1. Overall Predictive Capabilities
In general, fairly good performances are observed in the Tunisian study case for all combinations of BP-statistical model we tested. Jackknifed values are reported in Table 1 and range from 0.66 (P-OLS model using NDVI11) to 0.80 (FE model using CUMAPAR). This latter combination explains 80% of the actual yield variability over the 13 years and 10 governorates included in the analysis. The jackknifed scatterplot of modeled vs. observed yield for this model is reported in Figure 5.
With respect to the choice of BP, the one with the higher physical relevance, i.e., CUMAPAR, consistently appears as the best yield predictor across models. However, the magnitude of the improvement is rather low, ranging from 6% to less than 1%. With respect to the choice of the statistical model, the FE appears as the best performing regardless of BP used. This confirms that the relationship between yield and BP is not necessarily spatially homogenous, and that governorate-specific errors are best accommodated using an FE model. Holding the BP constant and considering FAPAR12 and CUMAPAR, FE model performances are not substantially different from the other models allowing for some governorate tuning: G-OLS, GS-OLS, and RE. However, the implications of opting for FE, GS-OLS, or RE models instead of P-OLS or G-OLS are important since the P-OLS cannot take local errors into account, while G-OLS may suffer from over-parameterization.
Despite the small the sample size (128 observations), several statistically significant differences have been detected: the FE model using CUMAPAR outperforms all tested BPs when using the P-OLS model and, with the exception of the FE, all statistical models that make use of NDVI11 or CUMFAPAR as BP. However, once the FE model is adopted no conclusion can be reached with respect to what BP is to be used (no statistically significant differences between FE models).
4.2. Predicting Temporal Variability
The following step of the analysis is to assess to what extent the combinations of BP-models are able to mimic the temporal variability of the data. This is accomplished by analyzing the jackknifed , which measures the fraction of the temporal variance explained by the model, instead of the (Table 2).
As expected, a lower fraction of the yield variance is explained by the BPs when considering the temporal variability instead of the overall variability. ranges from 0.36 (P-OLS using NDVI11) to a maximum of 0.61 for the FE model using CUMAPAR. The range of , is greater than the range of the , and the differences in the performances of models are detected with a higher statistical significance because the tests the more challenging ability to predict the temporal variability of yield. Only four combinations of a statistical model and a BP cannot be said to perform less well than the FE-CUMAPAR with less than 10% chances of error. The first two also rely on CUMAPAR as BP and model the relationship with yield using GS-OLS or RE. Here, it is worth noting that results are robust to changes in growth and decay thresholds used for the computation of CUMAPAR and CUMFAPAR (all combinations having been tested using 1%, 5% and 10% thresholds). The second two make use of the FAPAR12 combined with either the FE or the RE model. Therefore, for operational application specific to the Tunisia case study, FAPAR12 may be selected since it more easily implemented and available earlier in the season (at dekad 12 in the present case) as opposed to CUMAPAR, which requires the whole season of observations. However, care must be taken in adopting the single-timing approach to more extended and/or heterogeneous geographical settings. In fact, the method is not robust to significant changes in crop phenology that may occur due to differences in climatological conditions or farming practices. Facing these conditions, prior knowledge about climate, soil, and cropping systems should be exploited to segment the study area into regions with similar characteristics. Then, the best correlated dekad should be selected for each region and its empirical predictive capability tested.
In other operational crop monitoring applications, where no reliable yield data is available for model calibration, the BP is the only available information. Typically, in such situations the BP values are compared at different spatial locations and different times to highlight anomalies. For this purpose one would requires the linear relation between the BP and yield to be spatially homogenous. In fact, without ground measurement, it is not possible to spatially adapt the relationship. An insight on the spatial homogeneity of the relationship between the various BPs and yield is obtained by analyzing their performance when the P-OLS is used (i.e., one single relationship for all governorates). Table 2 shows that the BPs based on the cumulated values of FAPAR and APAR are more suitable for this purpose than those using the optimal dekad value (0.45 and 0.46 against 0.36 and 0.4). Significance tests on the differences confirm these finding: P-OLS-CUMAPAR performs significantly better than P-OLS-NDVI11 and P-OLS-FAPAR12 at 1% and 5% confidence levels, respectively. The same applies for P-OLS-CUMFAPAR, suggesting that cumulated values over the actual season should be used in the absence of ground measurements.
Finally, the application of the Dek-G-OLS, did not improve the performances of yield estimation ( = 0.70 and = 0.39). The search for the most correlated dekad at each governorate separately increased the loss of degrees of freedom and resulted in a selection of heterogeneous and somehow erratic timing ranging from dekad 1 (first of January, early in the growing season), to 11 and 12 (last two of April, as selected at the national level), and 15 and 18 (June and July, corresponding to the harvest period). A possible explanation may refer to the fact that allowing for some simple governorate-specific phenology adjustment is not sufficient because crop phenology is a complex phenomenon driven by climate (i.e., rainfall temporal distribution) and management practices (i.e., sowing dates). The crop cycle may therefore change at a spatial scale finer than that of the administrative governorates, and exhibit inter-annual variability, two features that can only be tackled with a phenology-based approach such as that of the CUM BPs.
4.3. Effects of Data Scarcity
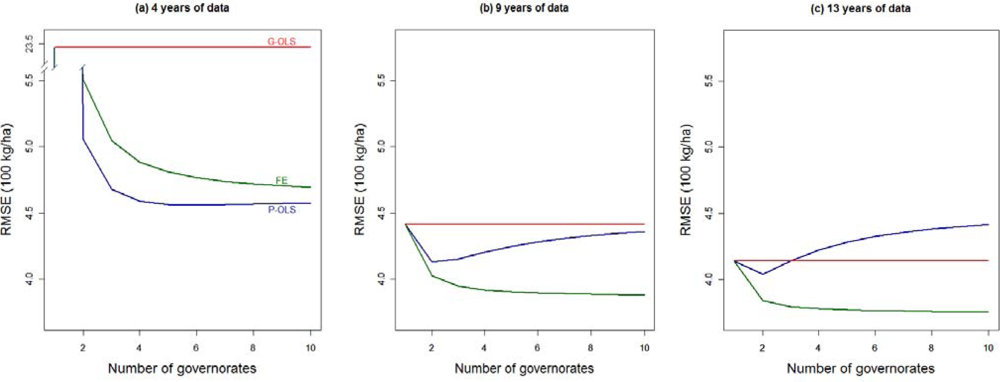
The effects of data scarcity in the temporal dimension on the different modeling solutions are investigated by reducing the number of years on which the models are fitted from the original 13 down to four. For this purpose, we only analyzed the best candidate BPs (FAPAR12 and CUMAPAR) and all statistical models but GS-OLS (Figure 6).
As expected, Figure 6 shows that a reduction of data availability has a negative impact on predictive performance, and that increases in RMSE are not evenly distributed across models. Models consuming more degrees of freedom suffer more from the reduction of the number of years used in the estimation process. The highest contrast is observed between P-OLS (two parameters) in which performance remains nearly stable and G-OLS (20 parameters), for which the RMSE increases rapidly and breaks down when less than six years of data are available. In this example G-OLS should only be considered when more than 10 years of data is available. However, better models are available for archives with at least four years of data: the FE (11 parameters) and RE (four parameters) models allowing governorate-specific tuning provide the best performances and are fairly robust to sample size reductions. Figure 6 also shows that, holding the BP constant, the RMSE rank between the FE and RE is inverted when the number of years is reduced to less than 10. This indicates that, below this threshold, parameter parsimony is effective and the RE model should be selected. Above this threshold, although the hypothesis on which the RE model relies on cannot be rejected, the FE model is less affected by overparameterization and becomes suitable as well. In this case, performance consideration may guide the choice toward the FE model. A similar rank inversion can be observed around nine years between G-OLS and P-OLS.
With respect to the BP used, it’s worth noting that the use of the more physiologically meaningful CUMAPAR improves the performances under two circumstances: when no governorate-specific tuning is performed (i.e., P-OLS) and when a FE or RE model is used with a reduced dataset (12 years or less).
Another source of data scarcity to be explored is the number of spatial entities (i.e., governorates) included in the analysis. Figure 7 shows how the jackknifed RMSE evolves when fewer governorates are available for the analysis of three levels of years of data available: four, nine, and the full Tunisian sample of 13 years. It is worth mentioning that the jackknifing process applied is again in terms of years, predictions only being performed for the considered governorates in each simulation. Moreover, for each number of governorates stated in the graphs, all possible combinations between the 10 available governorates have been taken into consideration. Note that the RMSE stated in Figure 6 corresponds to the ones in Figure 7 for 10 governorates.
By definition, the performance of G-OLS is insensitive to reductions of sample size in the spatial domain. Also by definition, the performance of the three models converges when a single governorate is used. The FE remains the best performing model regardless of the number of governorates, provided more than five years of data is available for the analysis. In fact, given the amount of available data, the estimation of the unobserved fixed effects guarantees the model to perform better than both the P-OLS (that assumes a unique relationship between BP and yield), and G-OLS, as fewer parameters need to be estimated. Consequently, the FE model’s RMSE is lower and robust to sever data restrictions both in the temporal and the spatial domains (Figures 6 and 7, respectively).
Figure 7 also contributes to a better understanding of the tradeoff between data availability and the capacity of the model to take spatial heterogeneity into account. When only a few years of data are available (in our case 4 years) overparameterization represents a major threat and the P-OLS appears the most suitable solution. When modeling is constrained by limited observations in the temporal domain, increased data availability through the inclusion of additional spatial entities is very valuable. However, the decrease of RMSE will depend on how spatially specific the model is. While the RMSE of the G-OLS remains at very high levels (2,350 kg/ha, Figure 7(a)), it decreases by 78% for the P-OLS as soon as two governorates are included in the analysis. In these conditions, parsimony is then advised, since the P-OLS also outperforms the FE. When more years are integrated into the analysis, the estimation of unobserved factors as fixed effects becomes the best strategy. The spatial homogeneity in the yield-BP relation, incorrectly assumed by the P-OLS generates an increase of the RMSE from the point where more than two governorates are considered. In cases where 13 years of observational data are available (Figure 7(c)), there is a point (i.e., three governorates) from which the number of governorates included in the analysis, and more specifically the heterogeneity between spatial entities, generates a deterioration on the performances of the P-OLS that eventually performs worse than the G-OLS. On the other hand, the performance increases obtained with the P-OLS model by reducing the number of pooled governorates suggests that a further modeling strategy involving the “wise” pooling of governorates into larger entities with similar characteristics (i.e., climate, soil properties, management practices, etc.) may be efficient as well.
5. Conclusions
In a case study of regional durum wheat yield estimation in Tunisia using 13 years of low-resolution SPOT-VGT observations, we have explored the interactions among four different remote sensing biomass proxies characterized by increasing physiological meaning, and six different statistical models relying on different hypotheses and using a varying number of degrees of freedom. The analysis aimed at assessing the improvements of the adoption of more sophisticated biomass proxies and the tradeoff between model complexity and data availability.
Results show that the high yield variability (spatial and temporal) in Tunisia can be predicted using Earth observation techniques with jackknifed up to 0.8. Best performances are achieved using the most physiologically sound remote sensing indicator (the phenologically-tuned cumulative value of the absorbed photosynthetically active radiation) in conjunction with statistical model allowing for parsimonious spatial adjustment of the parameters (the Fixed Effects model). Fair performances ( ≥ 0.75) are guaranteed, regardless the adopted biomass proxy, when the most appropriate statistical model is employed (i.e., Fixed or Random Effects). Among the proxies derived from a single observation, FAPAR always outperformed NDVI regardless of the statistical model used, empirically confirming its superior suitability for vegetation productivity studies.
When focusing on the ability of the models to describe the temporal yield variability, the ranking between biomass proxy-statistical model combinations remained stable, although the values were lower than the values. Differences among model performances could be detected with a higher significance, suggesting that the choice of the more appropriate combination between biomass proxy and statistical model specification is even more important if the modeler is mainly interested in temporal predictions.
The results also showed that for qualitative crop monitoring, where crop conditions are to be assessed in the complete absence of ground calibration measurements, phenologically-tuned biomass proxies should be preferred to single observation indicators. First, because yield ground measurements are needed for the selection of the optimal NDVI or FAPAR dekad while the phenological tuning is performed in absence of such information; and secondly, because phenologically-tuned biomass proxies have been shown to have a more robust linear relationship with yields.
Finally, we assessed the role played by data scarcity on the yield estimation accuracy. Results confirm that the selection of the model specification should take into account the number of observations available, and not merely the expected spatial heterogeneity of the yield-BP relationship.
Acknowledgments
We thank our colleagues Dominique Fasbender and Josh Hooker for the support in the statistical analysis and the revision of the manuscript. We thank Myriam Haffani, head of SCAT project (Suivi des Cultures Annuelles par Télédétection) at Centre National de Cartographie et de Télédétection (CNCT, Tunisia) for her precious collaboration.
References
- Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using low resolution satellite imagery for yield prediction and yield anomaly detection. Remote Sens. 2012. submitted.. [Google Scholar]
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens. 2012. submitted.. [Google Scholar]
- Rahman, H.; Dedieu, G. SMAC: A simplified method for the atmospheric correction of satellite measurements in the spectrum. Int. J. Remote Sens 1994, 15, 123–143. [Google Scholar]
- Vermote, E.F.; Kotchenova, S. Atmospheric correction for the monitoring of land surfaces. J. Geophys. Res.-Atmos. 2008. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Verstraete, M.M. Theoretical limits to the estimation of the leaf area index on the basis of visible and nearinfrared, remote sensing data. IEEE Trans. Geosci. Remote Sens 1997, 35, 1438–1445. [Google Scholar]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ 2002, 83, 214–231. [Google Scholar]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Nino, F.; Weiss, M.; Samain, O.; et al. LAI, FAPAR, and FCover CYCLOPES global products derived from Vegetation. Part 1: Principles of the algorithm. Remote Sens. Environ 2007, 110, 305–316. [Google Scholar]
- Gobron, N.; Pinty, B.; Taberner, M.; Mélin, F; Verstraete, M.; Widlowski, J.-L. Monitoring the photosynthetic activity of vegetation from remote sensing data. Adv. Space Res 2005, 38, 2196–2202. [Google Scholar]
- Pinty, B.; Lavergne, T.; Widlowsky, J.-L.; Gobron, N.; Verstraete, M.M. On the need to observe vegetation canopies in the near-infrared to estimate visible light absorption. Remote Sens. Environ 2009, 113, 10–23. [Google Scholar]
- Prince, S.D.; Goward, S.N. Global primary production: a remote sensing approach. J. Biogeogr 1995, 22, 815–835. [Google Scholar]
- Bernardes, T.; Moreira, M.A.; Adami, M.; Giarolla, A.; Rudorff, B.F.T. Monitoring biennial bearing effect on coffee yield using MODIS remote sensing imagery. Remote Sens 2012, 4, 2492–2509. [Google Scholar]
- Duveiller, G.; Lopez-Lozanom, R.; Baruth, N. Enhanced processing of low spatial resolution fAPAR time series for sugarcane yield forecasting and monitoring. Remote Sens. 2012. submitted.. [Google Scholar]
- Mulianga, B.; Bégué, A.; Simoes, M.; Todoroff, P. Forecasting regional sugarcane yield based on time integral and spatial aggregation of MODIS NDVI. Remote Sens. 2012. submitted.. [Google Scholar]
- Liang, S. Four Dimensional Data Assimilation. In Quantitative Remote Sensing of Land Surfaces; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2004; pp. 398–430. [Google Scholar]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modelling. Int. J. Appl. Earth Obs. Geoinf 2007, 9, 165–193. [Google Scholar]
- Delécolle, R.; Maas, S.J.; Guerif, M.; Baret, F. Remote sensing and crop production models: Present trends. ISPRS J. Photogramm 1992, 47, 145–161. [Google Scholar]
- Sannier, C.A.D.; Taylor, J.C.; Du Plessis, W. Real-time monitoring of vegetation biomass with NOAA-AVHRR in Etosha National Park, Namibia, for fire risk assessment. Int. J. Remote Sens 2002, 23, 71–89. [Google Scholar]
- Latiri, K.; Lhomme, J.P.; Annabi, M.; Setter, T.L. Wheat production in Tunisia: Progress, inter-annual variability and relation to rainfall. Eur. J. Agron 2010, 33, 33–42. [Google Scholar]
- Mars Web Viewer, Available online: http://www.marsop.info/marsop3 (accessed on 25 August 2012).
- Weiss, M.; Baret, F.; Eerens, H.; Swinnen, E. FAPAR Over Europe for the Past 29 Years: A Temporally Consistent Product Derived from AVHRR and VEGETATION Sensor. Proceedings of the Third RAQRS Workshop, Valencia, Spain, 27 September–1 October 2010; pp. 428–433.
- Mkhabela, M.S.; Bullock, P.; Raj, S.; Wang, S.; Yang, Y. Crop yield forecasting on the Canadian Prairies using MODIS NDVI data. Agric. Forest Meteorol 2011, 151, 385–393. [Google Scholar]
- Kogan, F.; Salazar, L.; Roytman, L. Forecasting crop production using satellite-based vegetation health indices in Kansa, USA. Int. J. Remote Sens 2012, 33, 2978–2814. [Google Scholar]
- Funk, C; Budde, M.E. Phenologically-tuned MODIS NDVI-based production anomaly estimates for Zimbabwe. Remote Sens. Environ 2009, 113, 115–125. [Google Scholar]
- Balaghi, R.; Tychon, B.; Eerens, H.; Jlibene, M. Empirical regression models using NDVI, rainfall and temperature data for early prediction of wheat grain yields in Morocco. Int. J. Appl. Earth Obs. Geoinf 2008, 10, 438–452. [Google Scholar]
- Meroni, M.; Verstraete, M.M.; Rembold, F.; Urbano, F.; Kayitakire, F. Analysis of Productivity Anomalies for Food Security Monitoring Based on Remote Sensing Derived Phenology-Indicators. Proceedings of First EARSeL Workshop on Temporal Analysis of Satellite Images, Mykonos, Greece, 23–25 May 2012.
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol 1972, 9, 747–766. [Google Scholar]
- Meteorological Data from ECMWF Models, Available online: http://marswiki.jrc.ec.europa.eu/agri4castwiki/index.php/Meteorological_data_from_ECMWF_models (accessed on 15 August 2012).
- Genovese, G.; Vignolles, C.; Negre, T.; Passera, G. A methodology for a combined use of Normalized Difference Vegetation Index and CORINE land cover data for crop yield monitoring and forecasting. A case study on Spain. Agronomie 2001, 21, 91–111. [Google Scholar]
- INFOTEL, Inventaire des Forêts par Télédétection. Résultats du Deuxième Inventaire Forestier et Pastoral National; CNCT (Ministère de la Défense Nationale, Tunisie), Direction Générale des Forêts (Ministère de l’Agriculture), Direction Générale de la Recherche Scientifique (Ministère de l’Enseignement Supérieure et de la Recherche Scientifique, Tunisie): Tunis, Tunisia, 2010.
- Baltagi, B.H. The One-Way Error Component Regression Model. In Econometric Analysis of Panel Data, 3rd ed.; John Wiley & Sons Ltd: West Sussex, UK, 2005; pp. 11–28. [Google Scholar]
- Hausman, J.A. Specification tests in econometrics. Econometrica 1978, 46, 1251–1271. [Google Scholar]
- Steiger, J.H. Tests for comparing elements of a correlation matrix. Psychol. Bull 1980, 87, 245–251. [Google Scholar]
Appendix
| Biomass proxies (in order of increasing bio-physical insight) | |
| NDVIx | NDVI value for the xth dekad from the beginning of the year |
| FAPARx | FAPAR value for the xth dekad from the beginning of the year |
| CUMFAPAR | Cumulative FAPAR value during the growing period (estimated for each pixel, each season) |
| CUMAPAR | Cumulative FAPAR*PAR value during the growing period (estimated for each pixel, each season) |
| Statistical models (in order of increasing parameterization) | |
| P-OLS | Pooled Ordinary Least Squares, 2 parameters |
| RE | Random Effects model, 4 parameters (slope, intercept, and variances of the unobservable effects) |
| GS-OLS | Governorate Slope OLS, slopes estimated for each governorate, single intercept, G + 1 parameters (G is the number of governorates) |
| FE | Fixed Effects model, intercepts estimated for each governorate, single slope, G + 1 parameters |
| G-OLS | Governorate specific OLS, intercepts and slopes estimated for each governorate, 2 × G parameters |
| Dek-G-OLS | G-OLS model for which the most correlated dekad is selected for each governorate, 2 × G parameters plus G dekad selections |



| P-OLS (Pooled OLS, n = 2) | G-OLS (Gov. OLS, n = 20) | GS-OLS (Gov. Slope OLS, n = 11) | FE (Fixed Effects, n = 11) | RE (Random Effects, n = 4) | |
|---|---|---|---|---|---|
| NDVI11 | 0.66<<< | 0.71<< | 0.74<<< | 0.75 | 0.75<<< |
| FAPAR12 | 0.68<<< | 0.75 | 0.77 | 0.79 | 0.78 |
| CUMFAPAR | 0.71<<< | 0.72<< | 0.75<< | 0.77 | 0.76< |
| CUMAPAR | 0.72<< | 0.75 | 0.78 | 0.80 | 0.79 |
| P-OLS (Pooled OLS, n = 2) | G-OLS (Gov. OLS, n = 20) | GS-OLS (Gov. Slope OLS, n = 11) | FE (Fixed Effects, n = 11) | RE (Random Effects, n = 4) | |
|---|---|---|---|---|---|
| NDVI11 | 0.36<<< | 0.43<<< | 0.50<<< | 0.53< | 0.52<<< |
| FAPAR12 | 0.40<<< | 0.51< | 0.57< | 0.60 | 0.59 |
| CUMFAPAR | 0.45<<< | 0.45<<< | 0.53<<< | 0.55< | 0.54<<< |
| CUMAPAR | 0.46<<< | 0.53< | 0.58 | 0.61 | 0.60 |
Share and Cite
Meroni, M.; Marinho, E.; Sghaier, N.; Verstrate, M.M.; Leo, O. Remote Sensing Based Yield Estimation in a Stochastic Framework — Case Study of Durum Wheat in Tunisia. Remote Sens. 2013, 5, 539-557. https://doi.org/10.3390/rs5020539
Meroni M, Marinho E, Sghaier N, Verstrate MM, Leo O. Remote Sensing Based Yield Estimation in a Stochastic Framework — Case Study of Durum Wheat in Tunisia. Remote Sensing. 2013; 5(2):539-557. https://doi.org/10.3390/rs5020539
Chicago/Turabian StyleMeroni, Michele, Eduardo Marinho, Nabil Sghaier, Michel M. Verstrate, and Olivier Leo. 2013. "Remote Sensing Based Yield Estimation in a Stochastic Framework — Case Study of Durum Wheat in Tunisia" Remote Sensing 5, no. 2: 539-557. https://doi.org/10.3390/rs5020539
APA StyleMeroni, M., Marinho, E., Sghaier, N., Verstrate, M. M., & Leo, O. (2013). Remote Sensing Based Yield Estimation in a Stochastic Framework — Case Study of Durum Wheat in Tunisia. Remote Sensing, 5(2), 539-557. https://doi.org/10.3390/rs5020539




