Abstract
Accurate terrain models are a crucial component of studies of river channel evolution. In this paper we describe a new methodology for creating high-resolution seamless digital terrain models (DTM) of river channels and their floodplains. We combine mobile laser scanning and low-altitude unmanned aerial vehicle (UAV) photography-based methods for creating both a digital bathymetric model of the inundated river channel and a DTM of a point bar of a meandering sub-arctic river. We evaluate mobile laser scanning and UAV-based photogrammetry point clouds against terrestrial laser scanning and combine these data with an optical bathymetric model to create a seamless DTM of two different measurement periods. Using this multi-temporal seamless data, we calculate a DTM of difference that allows a change detection of the meander bend over a one-year period.
Keywords:
UAV; mobile laser scanning; LiDAR; photogrammetry; optical bathymetry; seamless DTM; DTM; elevation; river; Finland 1. Introduction
Accurate terrain models are a crucial component of hydraulic modelling applications and fluvial geomorphology [1,2]. River dynamics studies, in particular, require high quality terrain models of both the river bed and the floodplain [3]. River studies generally focus on either the inundated river channel, or the dry floodplain, but in order to understand the processes at work, the whole channel needs to be considered at once. Due to the technological differences of various data acquisition methods on land and under water, seamless high-resolution digital terrain models (DTM) are still rarely produced. While aerial laser scanning based DTMs of relatively high resolution are becoming more widely available, in a fluvial context they only cover the river banks and floodplain; the river bed is often no more than a coarse approximation of reality based on relatively sparse sonar points or cross-sectional surveys. Hicks et al. [4] have combined aerial laser scanning with multispectral imaging to create a DTM of the inundated channel and river banks for 2D hydraulic modelling while others (e.g., [5]) have combined aerial laser scanning with interpolations of field-surveyed transects to create a contiguous DTM of a river channel. Williams et al. [6] have recently produced a continuous DTM of a braided river system by combining terrestrial laser scanning with optical bathymetry. Even though bathymetric or green LiDAR can be used for mapping underwater topography, its use in rivers is still fairly limited [7,8].
High discharges cause changes to the channel morphology that are not limited to the low flow channel or the floodplain alone. Subarctic rivers experience spring flooding on an annual basis that can cause considerable geomorphic changes, while summer low flows also drive erosion and deposition in an ongoing process [2]. Having an accurate, high-resolution, seamless DTM of the river channel and floodplain allows us to detect morphological changes of the whole river channel more accurately than using traditional methods. This makes a more comprehensive understanding of the evolution of the channel possible.
In this study we present a new methodology to create seamless topographic models in river environments that bridge the gap between the dry floodplain and the submerged river bed. To achieve this we combine advanced boat-based and terrestrial mobile laser scanning methods with high-resolution UAV-based photography to create optical bathymetric models of the river bed as well aerial photogrammetry-based topographic models of the floodplain. In this study UAV-photography is used for the first time to create very high resolution optical bathymetric models based on Lyzenga’s [9] linear transform model.
We first describe the novel methodology and then show an example of how the multitemporal seamless data we produce can be applied to conduct change detection on a meander bend of a sandy river. We present this case study to highlight some of the advantages and shortcomings of the topographic modelling methodology presented. Because a range of techniques is involved in creating the seamless models, we set out by giving a background on each of the techniques: mobile LiDAR, UAV photography and optical bathymetric modelling. In this study UAV photography is used for photogrammetric purposes as well as bathymetric modelling. We then explain the data collection and processing for each method, and evaluate the data produced by each method against independent reference data (TLS and RTK-GNSS data). Based on this assessment, we build the most accurate seamless model possible using this methodology for two time steps. We then demonstrate how these multitemporal seamless data can perform in a change detection study of a river bend. Based on this, we discuss the accuracies achievable using the different methods and their shortcomings, particularly in regards to change detection.
2. Background
2.1. Background on LiDAR in River Remote Sensing
High-quality topographical and bathymetrical data at different scales are required to study fluvial processes and river dynamics. These are particularly required for hydro- and morphodynamic modelling [10], which have been developed over the last two decades. Nowadays, airborne remote sensing and traditional field survey methods such as GPS and tachymetry surveys (e.g., [11]) are widely used in hydrological studies, but the use of more sophisticated terrestrial survey methods, such as close-range photogrammetry (e.g., [12]) or terrestrial laser scanning (TLS) (e.g., [13]) is still rather limited.
Numerous studies reported that the accuracy of DEMs is crucial for fluvial geomorphological mapping and hydrodynamic modelling [3,14,15]. Promising results in data acquisition for fluvial studies have been obtained using satellite remote sensing data or highly accurate LiDAR (Light Detection and Ranging/Laser scanning) DEMs instead of traditional ground surveys or national survey maps [15]. Improved simulation of flow characteristics and river dynamics can be achieved with accurate geometric and surface roughness data as input data to hydro- and morphodynamic models.
Ground surveys can be carried out using LiDAR (e.g., ALS (Airborne Laser Scanning), TLS (Terrestrial Laser Scanning) and MLS (Mobile Laser Scanning)) based on distance measurements and precise orientation of these measurements between a sensor and a reflecting object. This has been demonstrated to be usable for instance in high-quality 3D models of forested environments (e.g., [16]). In the case of hydrodynamic modelling, information describing the roughness of streams can be modelled with LiDAR [17]. For accurate measurements, TLS is ideal for accuracy verification and change detection. It could also be used in micro-scale fluvial geomorphological applications such as orientation mapping and volume calculations of dunes and ripples [18] or measuring grain sizes (from fine gravel to boulder size sediments) on the riverbed [19].
TLS suffers from the limitation that data collection is spatially limited due to its static nature. Modern mobile mapping systems (MMS) overcome this limitation by integrating a multi-sensor system consisting of data acquisition sensors (e.g., LiDAR) for determining the positions of objects remotely, and various navigation sensors (GPS, IMU) on a rigid, moving platform [20–23]. Typical requirements for MMS include that visible objects should be measured with an accuracy of a few decimetres with a maximum speed of 50–60 km/h and desired objects should be collected within a range of several tens of metres. One of the latest MMS applications is a boat-based, mobile mapping system (BoMMS) [24]. BoMMS-LiDAR for fluvial applications provides high-density point clouds allowing very effective sampling of detailed riverine topography. Hohenthal et al. [25] reviewed different kinds of laser scanning methods and their applications in fluvial research in detail.
2.2. Background on UAV Remote Sensing
UAV-based remote sensing offers a fast and accurate approach to acquire remote sensing data, mostly in the form of aerial photography, at a relatively low cost. Mini-UAVs are generally not regulated as strictly as larger UAVs, which allows for more flexible operation and shorter response times. Typically mini-UAVs are flown below 150 m above ground level and from these altitudes the achievable resolution and accuracy is typically in the range of a few centimetres [26]. Compared to traditional airborne remote sensing, UAVs enable rapid deployment as well as new possibilities through high frequency multi-temporal data.
During the last few years, as UAVs have become less expensive and easier to operate, their professional civilian use has increased. In the field of remote sensing, most of the systems used are mini-UAVs with a digital camera for aerial photography [27–30]. Images from the digital camera provide accurate data that can be processed with existing methods and algorithms into point clouds and surface models for further use. Recently, through the miniaturization of measurement instruments and the increasing payload capacity of mini-UAVs, other sensors have also been applied in remote sensing applications including thermal cameras, spectrometers and laser scanners [26,31].
In many regions, regulations restrict what kind of aircraft can be used and where it can be flown. Typical restrictions include 20 or 25 kg maximum take-off weight limit and flying within line-of-sight as well as a maximum altitude of 150 m. In aerial photography applications the weight limit does not cause serious difficulties for the measurements, but the other two restrictions often limit the target area to a few hundred metres in radius. In larger scale campaigns this often means that multiple flights have to be undertaken and even then, the areas that can be covered are limited to a few hectares, especially in the case of rivers with forested banks, where line-of-sight can be quite limited.
Other challenges may include flight time, payload capacity, reliability and weather conditions. The flight time and payload capacity of the UAV are not typically a serious problem in photogrammetric use, as digital cameras can be very light. However, if higher grade cameras, such as full-frame digital single-lens reflex cameras (DSLR) are to be used, the UAV also needs to be larger in order to be able to carry the camera and provide long enough a flight time. Reliability is often an issue, as the build quality and reliability is not on the same level with full-size aircraft. Often the airframes are based on hobby-grade parts and therefore reliability has not been the primary design concern. Weather conditions such as wind and cloudiness may cause severe problems for aerial photography as typically, mini-UAVs are not designed for wind exceeding 5 or 10 m · s−1. Cloudiness may cause problems with the image quality as the light conditions may vary between pictures and flights.
The most important challenge in river environments is the areal coverage, i.e., width and length of the river. On narrow rivers it may be possible to fly just one flight line over the middle of the river while the camera’s field of view covers the whole width. However, if the river is too wide to be covered with a single flight line, it will require flying back and forth, which significantly increases the flight time required. The possibility to fly along the river is limited by the line-of-sight requirement described above. With a single flight it may be possible to cover, for example, half a kilometre of the river, but if the target area is multiple kilometres long, it may require many flights.
2.3. Background on Optical Bathymetric Modelling in Rivers
The biggest challenge in mapping river environments lies in creating an accurate and continuous representation of the submerged river bed itself. While small reaches of shallow rivers can be surveyed using tachymetry [32] or a pole-mounted Real Time Kinematic Global Navigation Satellite System (RTK-GNSS), the limits of these methods are reached fairly quickly as the size of the area to be surveyed or the water depth increases. Furthermore, the accuracy of the terrain model that can be created based on points surveyed in this fashion depends largely on the density of the point pattern, which is directly proportional to time spent surveying. On the one hand, the positional accuracy of the points measured using tachymetry or RTK-GNSS can hardly be surpassed by other measuring techniques, but on the other hand, remote sensing methods can provide much wider and more homogeneous spatial coverage.
The most widely used method for mapping underwater topography is sonar (e.g., [33]). Both single-beam and multi-beam or swathe sonar can be used in rivers. While the coverage and density of single-beam sonar points has the same limitations as the above-mentioned direct measurement methods, the method is much faster to apply and not limited to shallow water only. On the contrary, sonar systems generally have minimum depth requirements of around 1 m in order for them to work [5]. Due to their side-oriented sensors, swathe-sonar such as the Kemijoki Aquatic Technology AquaticSonar system [34] is able to measure shallow water near the river banks and measures a vastly higher point density. Such a system measures a transect at a time and the gap between transects depends on the travel speed of the boat. However, even though shallow areas can be measured at a distance, the system is also dependent on the water being deep enough to deploy the boat, a limit which can be quickly reached in natural rivers and streams. Measurements may therefore be limited to flood periods. Furthermore, the field of view of side-scanning sonar systems increases with water depth, and conversely narrows to the point of being unable to cover the river bed in shallow rives. In order to cover the whole river bed and to avoid possible shadowing by islands, it is likely necessary to conduct multiple passes [35], and this need increases with decreasing water depth.
Airborne remote sensing methods allow us to map larger areas of rivers contiguously and without minimum depth requirements. Airborne bathymetric mapping methods derive depth either based on the return time of an actively emitted light beam, in the case of green LiDAR, or on the spectral properties of recorded solar light, in the case of aerial photography based bathymetry [36]. Because these methods rely on light penetration in the water column, they are dependent on reasonably low turbidity.
While green LiDAR is not yet used much for measuring river bathymetry [37], river bed topography has been mapped successfully using aerial photography using linear transform [38–41] or band ratio transform methods [42–45]. The most commonly used method is the deep-water correction algorithm developed by Lyzenga [9]. The method uses deep-water radiance in order to isolate the depth signal of the radiance recorded in an aerial or satellite image. Subtracting the radiance of an image pixel containing water deep enough for the river bed not to be visible from the image gives a value X, the natural logarithm of which is linearly related to depth, thus allowing a simple regression model to be established between these Lyzenga X values and measured reference depth points. Flener [46] has recently presented an algorithm for estimating this deep water radiance value in shallow rivers where it cannot be retrieved from the images otherwise, allowing the use of Lyzenga’s model in shallow rivers where it performs best. Optically based bathymetric models reach their limit at a depth level where the radiance of the image bands used for modelling gets saturated, and therefore no longer changes with depth [47]. This situation can occur at depths shallower than Secchi depth because most natural river beds are not pure white, so they reflect less light than a Secchi disc [46].
River researchers employing photography based bathymetry modelling have mostly focused on aerial photography, because the higher spatial resolution that can be achieved this way suits the scale of analysis better than coarser satellite data. However, high resolution satellite data has recently also been used to map gravel bed rivers in Wyoming, USA [48].
Aerial imagery based bathymetry models of rivers allow mapping river bed topography at scales wider than the reach scale. Unlike methods that are based on point measurements, these models are based on raster input data and therefore do not require interpolation of any kind to achieve a surface model. Each image pixel is converted directly into a depth value. This spatial contiguity offsets the possibly lower vertical accuracy that can be achieved with some of the other methods mentioned above.
Aerial imagery based bathymetric models rely on the river bed being visible, so that depth can be modelled (e.g., [44]). This means that the water has to be reasonably clear, the water surface has to be calm enough so as to avoid ripples that cause bi-directional reflectance problems, and the view of the river has to be unobstructed by overhanging trees, for instance.
In this study we employ the Lyzenga [9] algorithm combined with Flener’s [46] deep water estimation and apply it to high resolution photographs that were acquired using an unmanned aerial vehicle (UAV).
3. Study Area
The test area for all models is a meander bend of the river Pulmanki, located in northernmost Finnish Lapland (69°56’N, 28°2’E). The river Pulmanki flows in a valley of glaciofluvial deposits from the last glaciation, surrounded by fells. The river is about 20–30 m wide during summer low flow, depending on the water level, and the riverbed consists of sandy sediments. Kasvi et al. [18] and Alho and Mäkinen [49] describe the geomorphology of this study site in great detail. The typical discharges of the river Pulmanki vary between about 4 m3 · s−1 during summer low flow and 40 m3 · s−1 during the annual snow-melt induced spring flood. The water level can be two to four metres higher during flood time than during summer low flow, depending on the size of the flood. This flow regime combined with the unstable sediments make this a very dynamic river [50] that is ideal for change detection studies.
4. Data Collection
In this study we combine a range of measurement methods that allow us to create high resolution topographic data of the study area. We use the ROAMER mobile mapping system (MMS) developed by the Finnish Geodetic Institute (FGI), which can be applied both as a boat based mobile mapping system (BoMMMS) [24,51] and cart/backpack-based MMS (Akhka) [52]. To the best of our knowledge, this is the most advanced mobile laser scanning platform currently employed in fluvial studies. We combine these scanning methods with low-altitude aerial photography we gather using an unmanned aerial vehicle (UAV). We use these images to create both an image-based bathymetric model of the river bed and a photogrammetry-based point cloud of the study area. All methods were applied during two field campaigns, during the end of August and early September 2010 and 2011. During this time of the year, the water levels of the rivers in this area of the sub-arctic are usually at their lowest. This allowed us to scan a large part of the channel using LiDAR. Furthermore, this maximised the chances of the bathymetric modelling being successful due to low turbidity and low water levels, minimising the risk of the deeper parts of the channel exceeding attenuation depth. During our field campaigns, the water depth in the study area did not exceed 1.5 m. Turbidity outside of the spring flood is extremely low, meaning that the whole river bed was visible from the air.
4.1. LiDAR
Table 1 gives an overview of the laser scanners, IMU and GPS navigation equipment we used during the different field campaigns. We used a Leica HDS6100 scanner in stationary mode (TLS) and Faro Photon 120 scanner mounted on mobile scanning platforms for the mobile mapping system setups.

Table 1.
Laser scanning systems used. We used two different scanners, one deployed on a stationary platform and one deployed on three different mobile scanning platforms.
4.1.1. MLS Field Measurements (2010–2011)
The MLS systems we used consisted of a Faro Photon 120 laser scanner and NovAtel SPAN navigation system with NovAtel DL4plus GPS receiver, NovAtel 702 GPS antenna and Honeywell HG1700 AG58 inertial measurement unit. In the ROAMER system these instruments are integrated into a platform with an adjustable scanning angle, designed at FGI. In 2010 we operated the ROAMER MLS system on a boat to collect laser scanning data of the point bar shoreline and the steep banks. We collected data of other parts of the point bars using ROAMER installed on top of a cart. In 2011 ROAMER was again set up on a boat, but we mapped the point bars using the Akhka backpack MLS system. In Akhka the measurement instruments are installed on a compact and rigid platform, which is attached to the frame of a backpack. Figure 1 shows the different setups of the ROAMER system. In all cases the scanning frequency was set to 49 profiles per second and the point measurement frequency was 244,000 points per second. The profile spacing was 2–3 cm at an average speed of 4 km/h. The scanner field-of-view is 320 degrees, which means that, in case of the boat installation, no data was acquired below the scanner (boat) and in case of the cart and backpack installations, above the scanner (sky). The BoMMS and CartMMS measurements produced a 200 m trajectory that took three minutes to measure in each case. The Akhka trajectory was 350 m long and took 4.5 min to measure in the field. We used spherical reference targets for orienting the scans to the coordinate system. We used five targets in 2010 and four targets in 2011. The location of each reference target was measured using an RTK-GPS and can be seen in Figures 2 and 3.

Figure 1.
Different setups for the FGI ROAMER mobile mapping system: BoMMS (left); CartMMS (centre); Akhka (right).
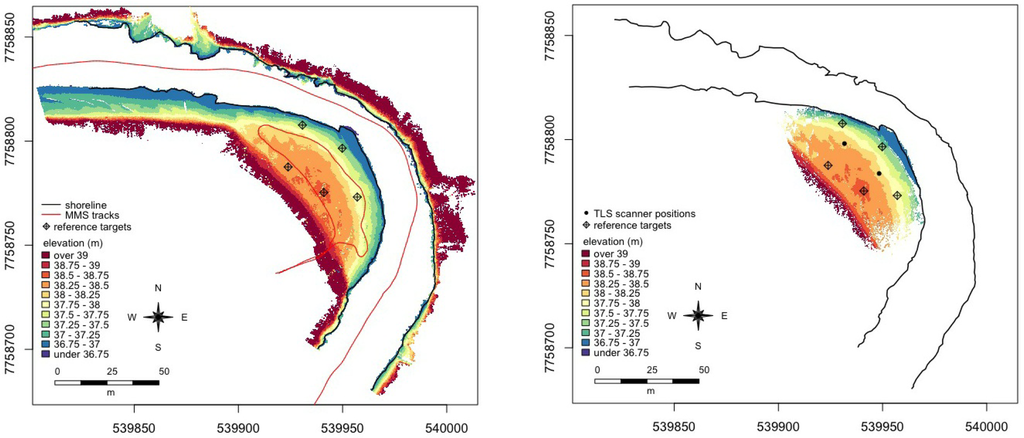
Figure 2.
Moble LiDAR point cloud of 2010 (left) and TLS reference point cloud 2010 (right) coloured by elevation.
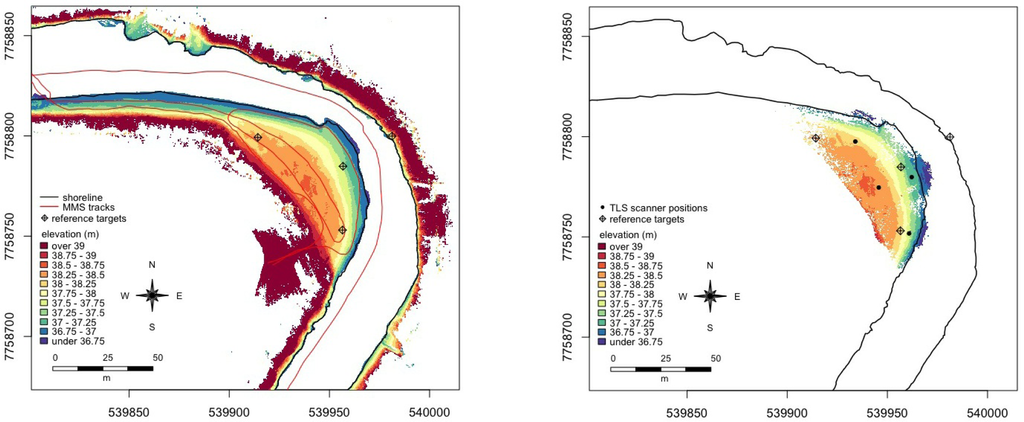
Figure 3.
Mobile LiDAR point cloud of 2011 (left) and TLS reference point cloud 2011 (right) coloured by elevation.
We enabled the Clear Contour and Clear Sky hardware filtering provided by the scanner unit in the MLS data collection on-the-fly to reduce measurement noise, especially from the sky. The Clear Contour filter removes incorrect measurements at the edges of objects by removing scan points resulting from hitting two objects with the laser spot, which mainly happens at the edges of objects. The Clear Sky hardware filter removes scan points resulting from hitting no objects at all, which mainly happens when scanning the sky.
4.1.2. MLS Data Processing
During preprocessing, dark points with an intensity value of less than 800 (the full range being 11 bit, 0–2,047) were removed to further reduce weak returns from objects. Then, below ground surface noise was partially removed manually to avoid problems with ground classification by removing all points with an elevation lower than the water surface elevation.
We classified the MLS point cloud datasets based on the principles of Axelsson [53]. The method takes three parameters: terrain angle, limiting the maximum slope of the surface to be created; iteration angle, the maximum angle between a point, its projection on the triangulated plane along the triangle normal, and the closest triangle vertex; and iteration distance, limiting vertical jumps that can occur with large triangles. The smaller the iteration angle, the less eager the routine is to follow changes in the point cloud (small undulations in terrain or hits on low vegetation). We used an 88 degree terrain angle, a 25 degree iteration angle and a 20 cm iteration distance for the classification of the ground points of the point bar in question. We processed all the MLS data from BoMMS for both years 2010 and 2011, CartMMS for 2010 and Akhka for 2011 using the same parameters with a few manually pointed ground points on each to start the ground classification iteration. The ground classification with the selected parameter values succeeded in removing vegetation from the edge of the point bar and the opposing bank.
In order to create a DTM suitable for analysis, it is necessary to reduce the vast amount of points measured by the MLS. In the first step, we combined the ground data from different MLS sources into two point sets, one for each year.
The next step differed slightly for the two datasets as the 2010 ground data was reduced directly using model keypoint thinning [54]. Due to the very large data size of the 2011 data set, it was first averaged to a 5 cm grid and reduction was carried out with a thinning method allowing a 1 cm elevation difference tolerance between local points, preserving the central points of a local group of points. As a result, we generated two MLS DTMs for the point bar to be combined with the UAV bathymetry DTMs. The 2010 DTM consisted of 2.1 million 3D points with an average density of 140 pts/m2. The 2011 DTM had 1.7 million points with an average density of 70 pts/m2. Regarding the performance of the two thinning methods applied, the result is expected to be equal for both data sets because the point density of the original data is stupendous combined with millimetre scale ranging precision, and due to the selected ground distance of 5 cm. Figures 2 and 3 show the MLS point clouds for 2010 and 2011 respectively next to the TLS point clouds used for their evaluation.
4.1.3. TLS Field Measurements (2010–2011)
We used a Leica HDS6100 laser scanner to acquire terrestrial laser scanning data to use as reference data of the study area during both field campaigns. The TLS measurements and the installation of reference targets of the study area took 30 min. The point bar area was scanned with a 360° horizontal field of view (FOV) and a resolution that produced a point spacing of 6 mm at a 10 m distance from the scanner. We conducted two scans in 2010 and four scans in 2011 using the same sphere reference targets as for MMS for orientation of the scans to the coordinate system. The location of each reference target was measured using an RTK-GPS. The achievable accuracy of the RTK-GPS measurements is 1 cm + 1–2 ppm horizontally and 1.5–2 cm + 2 ppm vertically (RMSE) [55]. The final accuracy of the TLS point cloud is on the same level as that of the RTK-GPS-measured target spheres.
The TLS data was classified using the same method as the MLS data using the method developed by Axelsson [53]: the maximum ground surface inclination was set to 88°, the maximum iteration angle was 25° to the triangular surface between these points and a maximum allowable difference of 20 cm to already triangulated surfaces. The parameters were chosen to suit the data set, taking into consideration terrain slope, roughness and point density. After the ground classification, every hundredth point was used for the comparison to the MLS data (cf. Figures 2 and 3).
4.2. UAV Photography
4.2.1. UAV Field Measurements (2010–2011)
We carried out two UAV measurement campaigns in 2010 and 2011. The UAVs used in these measurements were regular 700- or 800-class radio controlled helicopters. In 2010 we used a 12.3 megapixel Nikon D5000 camera with a 14 mm F/2.8 Samyang lens with a diagonal viewing angle of 94° mounted on-board a Minicopter Maxi-Joker 3DD and in 2011 a 16.2 megapixel Nikon D5100 with a 20/2.8 AF-D with a diagonal viewing angle of 71° on-board an Align T-Rex 700E. The cameras were set to automatically shoot one image every second. The flights were performed on 31 August 2010 and 11 September 2011. The camera settings for each flight were set according to the light conditions at the time of flight, ensuring sufficiently fast shutter speeds to eliminate the effects of airframe vibration. Focus was set to manual and locked at infinity. The weather conditions during 2010 were bright, slightly overcast and the camera was set to 1/4,000s, F/5.6, ISO 800. During the 2011 flight conditions were more overcast and the camera was set to 1/1,000s, F/5.6, ISO 800. In 2010, the flight duration was three min and the minimum, mean and maximum flight heights above ground were 58 m, 71.3 m and 86.8 m respectively. In 2011, the total flight time was six min and the minimum, mean and maximum flight heights above ground were 79.6 m, 127.5 m and 145.1 m. Ground control target points (GCP) made of 60 × 60 cm plywood with high contrast paint and a precise centre point were located along the river reaches under survey in fairly regular intervals. The points (3 in 2020, 5 in 2011) were surveyed using a RTK-GNSS.
The most challenging aspects of the UAV measurements were coverage and UAV reliability. Because the UAV was manually controlled and there was no real-time feedback on the location or image coverage of the UAV, some of the areas were not covered sufficiently to be reconstructed for later analysis. Also the reliability of the aerial vehicles caused problems; in 2010 one the UAVs had a malfunction and ended up falling into the river being measured. This is the reason why the UAV and the camera model were changed between the campaigns.
4.2.2. UAV Image Processing (2010–2011)
The images of all flights were evaluated for image quality. Quality issues relate mostly to reflection of the sky on the water surface and illumination changes during the time of the flights. There were no clouds reflecting on the water surface but there was some effect of sunlight illumination changing during flight time. Based on these quality considerations, a subset of suitable images was chosen to create the final image mosaics.
In 2010, 185 images were captured during the three-minute flight. Due to the camera shooting an image every second during the entire flight, most of these images were captured during take-off and landing, which is the slowest part of the flight. 41 images were used for further processing, selected for maximising areal coverage, image overlap and image quality. In 2011, 27 out of a total of 213 images captured were used for processing.
All the selected images were converted from RAW to TIFF with the white-balance set to flash mode and +0.5 exposure boost. Lens distortion was removed and the images were centred on the real optical centre of the lens using Matlab, based on a set of calibration images shot in the field prior to each flight. An initial estimate of exterior orientation was calculated by manually collecting common target points from overlapping images using the iWitness photogrammetry software. The orientation was then improved using the aerial triangulation functions in BAE Systems’ Socet Set software, which automatically finds similar features in the images, creating a denser common point network.
The mosaics were projected to the elevation of the water level of the river using the GNSS-measured ground control points and exported as GeoTIFF (Figure 4). Using GCP:s as a benchmark both images have under 10 cm positional errors in XYZ. The image resolution on the ground varies between a few mm up to 20 cm at its worst. The final image mosaics were sampled to a 5 cm GSD (ground sample distance) in Socet Set.
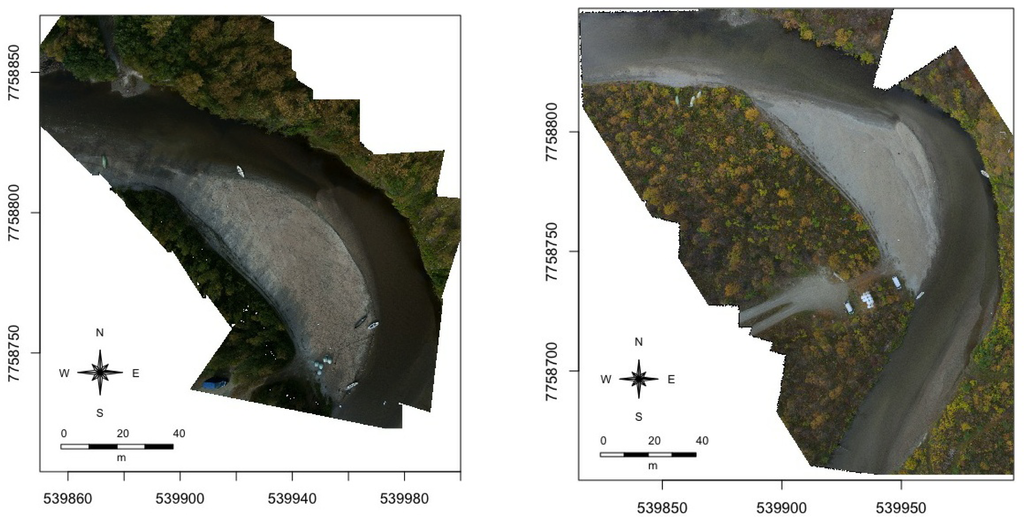
Figure 4.
UAV image mosaics of 2010 (left) and 2011 (right). Both images are RGB at 0.05 m ground sample distance. The distortion notable outside the river bed stems form the image distortion at the edges of the frames in combination with the planar rectification of the mosaic to the water level of the river.
The photogrammetry point clouds produced based on the distortion-corrected images using Autodesk 123D were georeferenced to the GCPs (Figure 5).
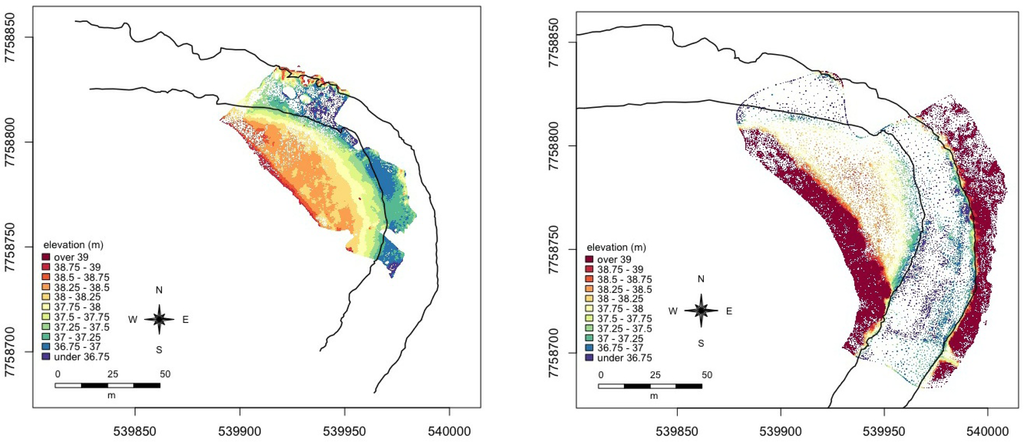
Figure 5.
UAV photogrammetry-derived point cloud of 2010 (left) and 2011 (right) coloured by elevation.
4.3. UAV-Bathymery Modelling
4.3.1. Ground Data Measurements (2010–2011)
In 2010, 197 river bed elevation points were measured using an RTK-GPS. These points were converted to depth data by subtracting the elevation from an interpolated water surface, also based on RTK-GPS points. This depth data is required for calibrating the optical bathymetric model.
In order to gather more points for analysis, in 2011 we used a remote controlled boat with a Sontek RiverSurveyor M9 ADCP on board to measure water depth points directly, as well as water surface points. An RTK-GPS was mounted on the boat in addition to the Sontek DGPS in order to get accurate location data for the depth measurements. The sonar of the Sontek M9 measures depths >0.18 m with an accuracy of 2.5% of the depth and saves measurements at 1 s intervals. The ADCP-measured depth points were merged with the RTK-GPS data by combining the time stamps of the two GPS devices.
4.3.2. Building the Bathymetry DSM
We built the bathymetric models as rasters based on the image mosaics produced from the UAV images. The models were calculated using Lyzenga’s [9] model. Since none of the area to be modelled exceeded Secchi depth we estimated deep water radiance values according to the method developed by Flener [46]. The depth models as well as their deep water radiance parameters were calibrated using 100-fold random sub-sampling cross-validation with a 70% training set and 30% test set. The means of the cross-validation output were used to determine the regression coefficients needed to build the depth model and the mean of the accuracy statistics of all cross-validation runs were used to determine model accuracy. The image-based model produces a bathymetry raster that has the same spatial properties as the image raster did, in this case a grid with a ground resolution of 0.05 m (Figure 6). The bathymetry raster was finally converted to elevation values by subtracting the depth values form an interpolated water surface. For the 2010 model, this surface was based on two water level points measured at the shoreline, while for the 2011 model, the water surface was based on an interpolation of the water level points measured by the ADCP–RTK-GPS setup. In order to facilitate combining the bathymetry data with the LiDAR data, the raster was converted to regularly spaced 3D point data.
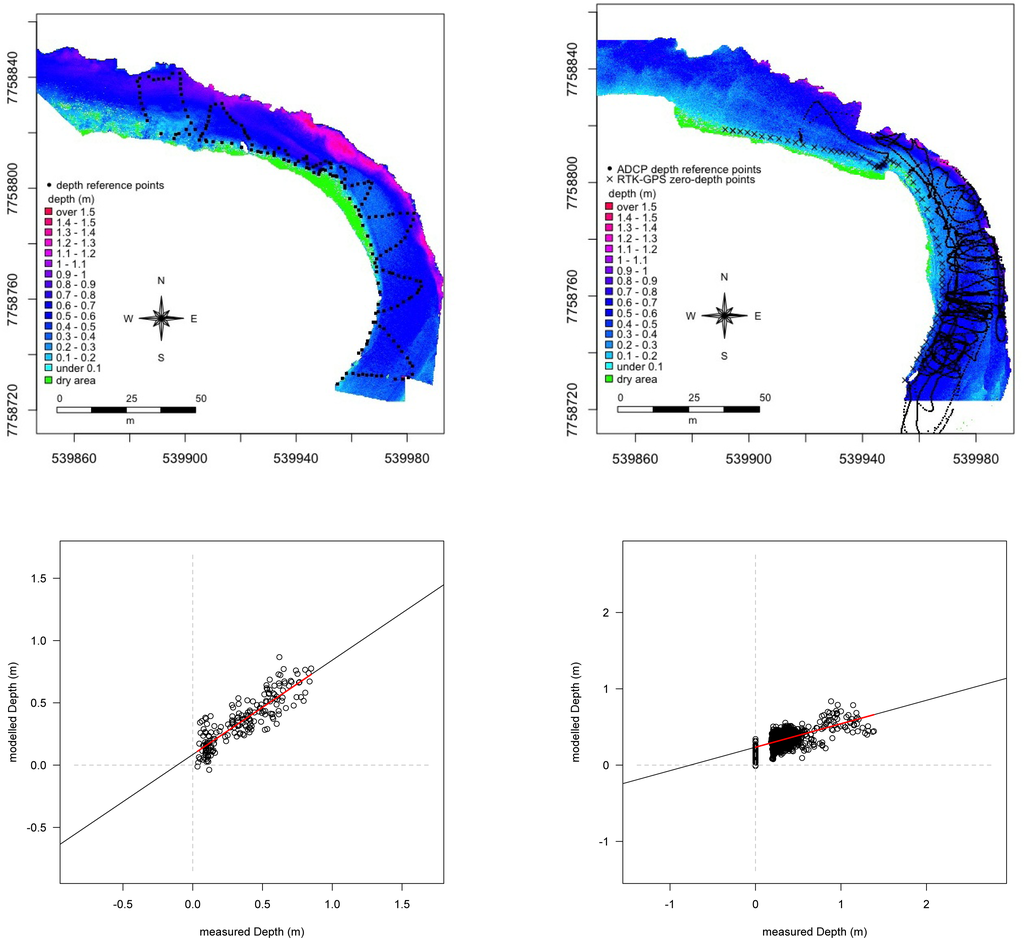
Figure 6.
Bathymetric models of 2010 (left) and 2011 (right) using the Lyzenga model with calibrated Lsi values. The plots show the modelled depths vs. the measured depths at the ground data reference points. Green areas were modelled as dry (i.e., negative depths).
5. Accuracy Assessment
We evaluated the different models against measured reference data in order to assess their accuracy: we used the TLS point cloud as reference data on the dry part of our study area and the GPS based river bed elevation points as the primary reference for the submerged riverbed. The TLS point cloud is the highest quality representation of the land surface that is available [56], being of the same level of accuracy as the RTK-GPS measured target points used for its georectification. Figures 2 and 3 show the mobile laser scanning point clouds and the TLS data used as reference for the 2010 and 2011 measurement campaigns respectively.
We used the TerraScan software package to evaluate the different point clouds against each other. This involves calculating locally triangulated surface models around each reference point using the closest measured points and calculating the elevation difference between the reference point to the same xy coordinate on the model surface. Table 2 summarises these accuracy assessments along with the accuracy assessment based on the cross-validation of the bathymetric model.

Table 2.
Accuracy assessment of the seamless model using TLS as reference data on the dry part of the point bar and measured depth points in the submerged part of the river channel. The bathymetry cross-validation accuracy data is included here for comparison to the final seamless model results, where depth has been converted to elevation. The average magnitude indicates the average absolute elevation difference and the dz values denote the minimum and maximum elevation differences between the compared data sets. All values are in metres.
Mobile laser scanning clearly delivers the most accurate data, with an RMS error of under 2 cm compared to the TLS data. Figure 7A shows that the mobile laser data is in very good agreement with the TLS reference data.
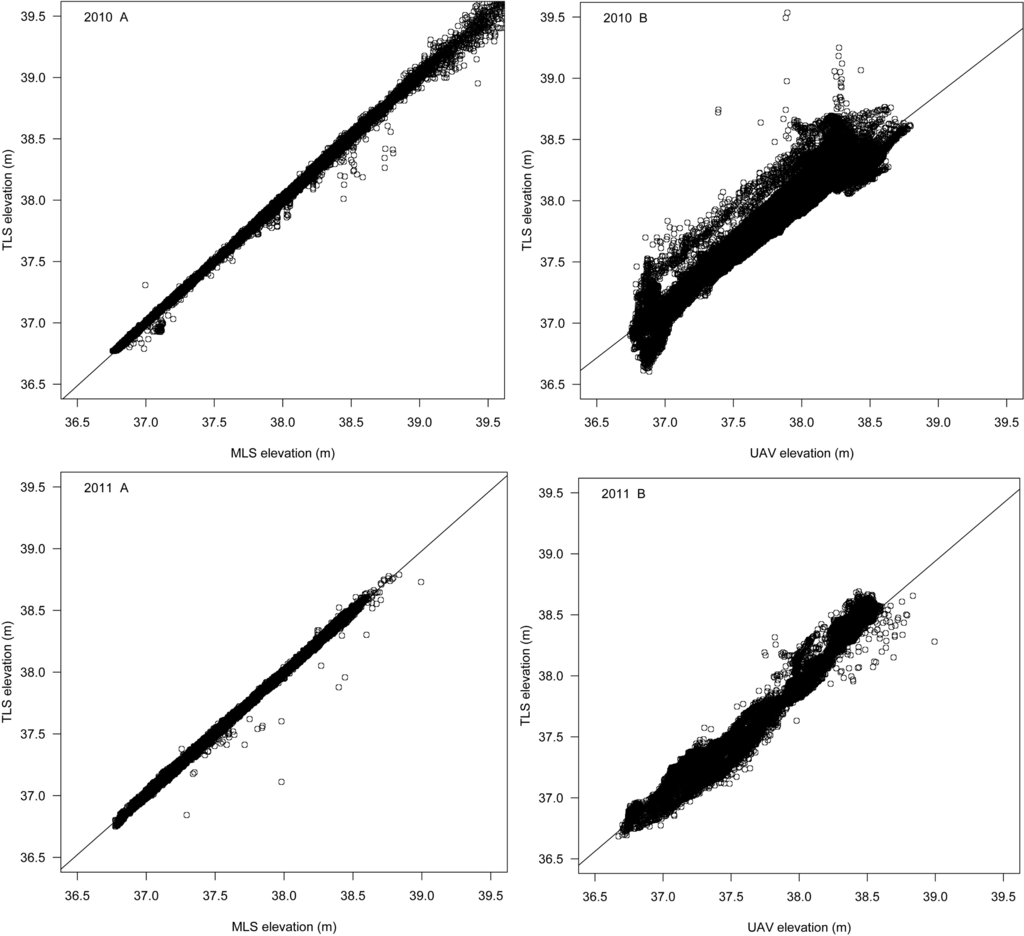
Figure 7.
Elevation points of MLS vs. TLS models (A) and UAV photogrammetry vs. TLS (B) of 2010 (left) and 2011 (right).
The bathymetric models deliver fairly accurate depth data with RMSE varying between 8 and 10 cm in cross-validation of modelled and measured depths. When looking at the elevation data of the river bed (rather than depth data) relative to RTK-GNSS-measured elevations, the error doubles.
The UAV photogrammetry data vary in accuracy between the two years. The 2011 point cloud, with an RMSE of 0.088, is about twice as accurate as the one produced form the 2010 images. The point cloud of 2010 covers a smaller area and includes some areas on the pointbar area that exhibit low point density due to low contrast, making it difficult for the algorithms to locate common points in different pictures, causing the overall error to be larger. The 2010 image network was less constant than that of 2011, causing limited image overlap in some areas, due to a more varying flight height and pattern. The 2011 flight was at a slightly higher and more constant altitude with a more consistent flight pattern, leading to a better photogrammetric result. Figure 7 (2010 B) shows that, while the spread of points is larger than that of the MLS data, the errors are concentrated at the higher elevations, which is where the artefacts are located on the sandbank.
6. Building the Seamless DTM
We produced the seamless terrain model of the meander bend by combining the MLS data (BoMMS + CartMMS in 2010; BoMMS + Akhka in 2011) for the dry area of the point bar with the bathymetry model created from the UAV pictures. Based on the results of the accuracy analysis of all data sets, this gives us the pest possible seamless DTM. The data sets contained some overlapping areas because the very clear water allowed the BoMMS data to also include some bathymetry points near the shoreline (the system used a 785 nm wavelength laser beam), while the bathymetric model also included some dry areas. Milan et al. [57] had also found that the signal of a red TLS can penetrate water, although they found the accuracy to decrease with increasing depth. Vaaja et al. [51] found a clear change in intensity values at the border of submerged and non-submerged terrain. This change in intensity is visualised in Figure 8. Vetter et al. [5] also delineated the water surface area of a river using the intensity of ALS returns. Based on this observation, we separated these areas by digitizing the shoreline according to the BoMMS intensity data. Because the positional accuracy of the underwater BOMMS points is unknown, due to light refraction at the water surface, especially at the relatively shallow scanning angle, we deleted these points from contiguous model using the extracted shoreline. The UAV-imagery-based bathymetry point data was used exclusively for the underwater part of the channel. Figure 9 shows the contiguous model created by combining the point cloud data of the MLS and the UAV-bathymetry. Figure 10 shows two transects for each year through the whole model, including the dry pointbar and the riverbed. The transect line locations are shown in Figure 9. Figure 11 illustrates the entire processing chain required to produce the contiguous DEM from mobile LiDAR data and bathymetry data created from UAV-photography.
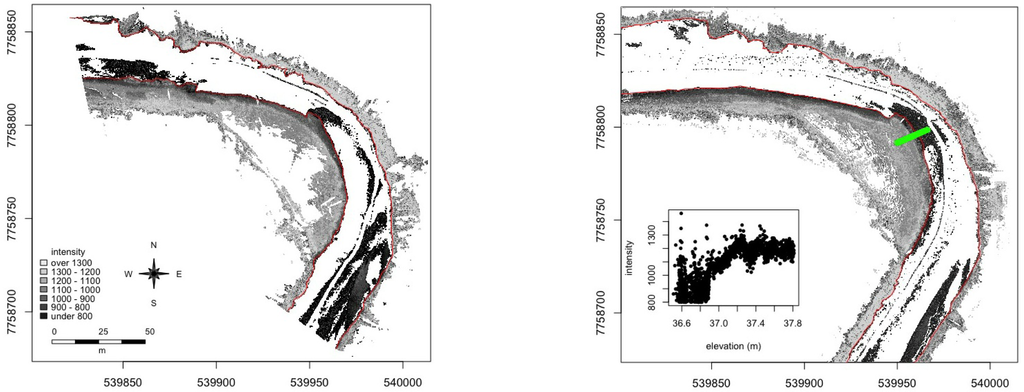
Figure 8.
Map of the BoMMS intensity data of 2010 (left) and 2011 (right) used to determine the shoreline (marked in red). The intensity change at the edge between inundated and non-inundated river bed that is used in the digitization of the shoreline is clearly visible in the scatterplot of the transect marked in green.
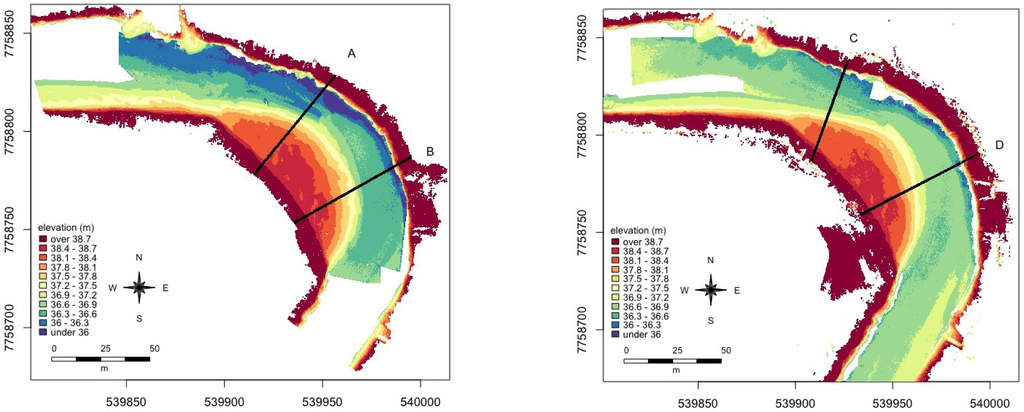
Figure 9.
Seamless digital elevation model of 2010 and 2011 combining mobile laser scanning data with the UAV-based bathymetry as a 3D point cloud coloured by elevation. The lines indicate the transects shown in Figure 10.
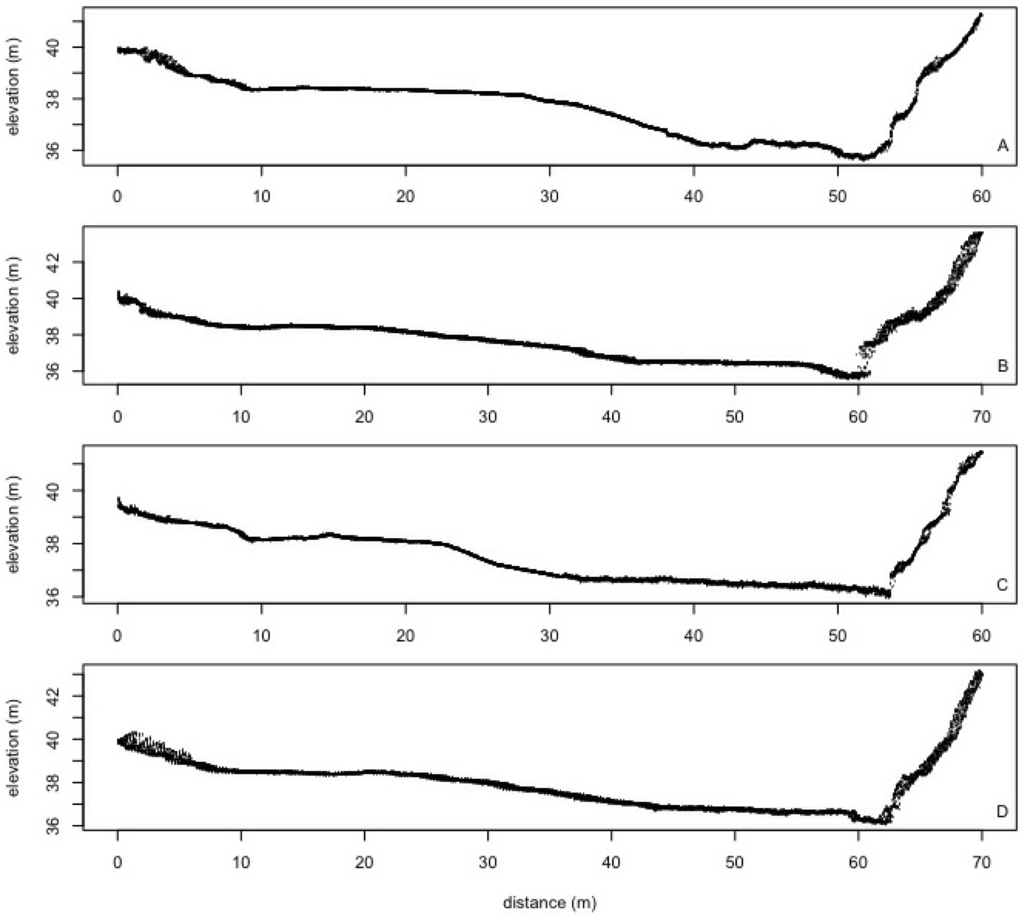
Figure 10.
Transects of elevation data indicating the seamless merging of the MLS data with the bathymetry data. The location of the transects is indicated in Figure 9.
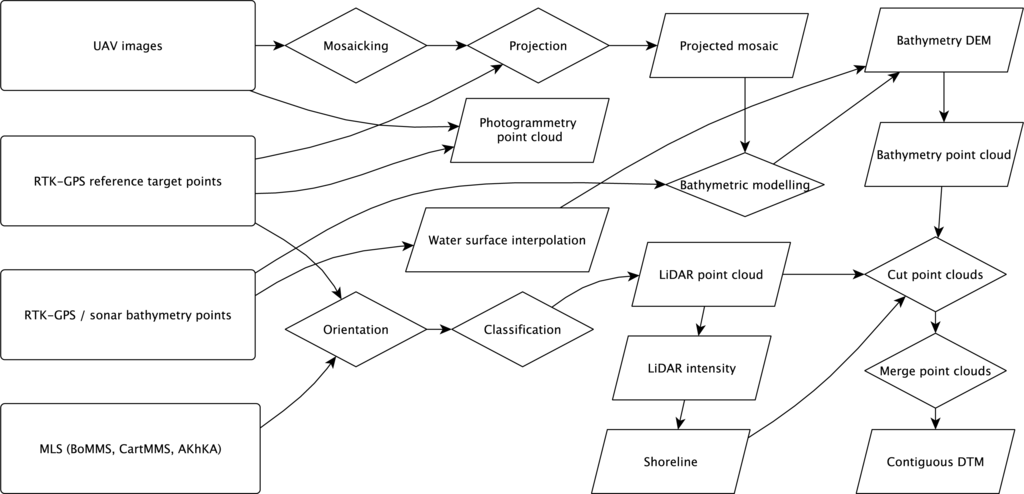
Figure 11.
Flowchart illustrating the process of creating a contiguous DTM from LiDAR and UAV-photography data.
7. Change Detection
In order to demonstrate the use of multitemporal seamless DTM data, we analyse the geomorphological changes that happened between the two measurement campaigns in the autumn of 2010 and 2011. To conduct the change detection, we computed a difference map between the seamless models created for each year (Figure 12).
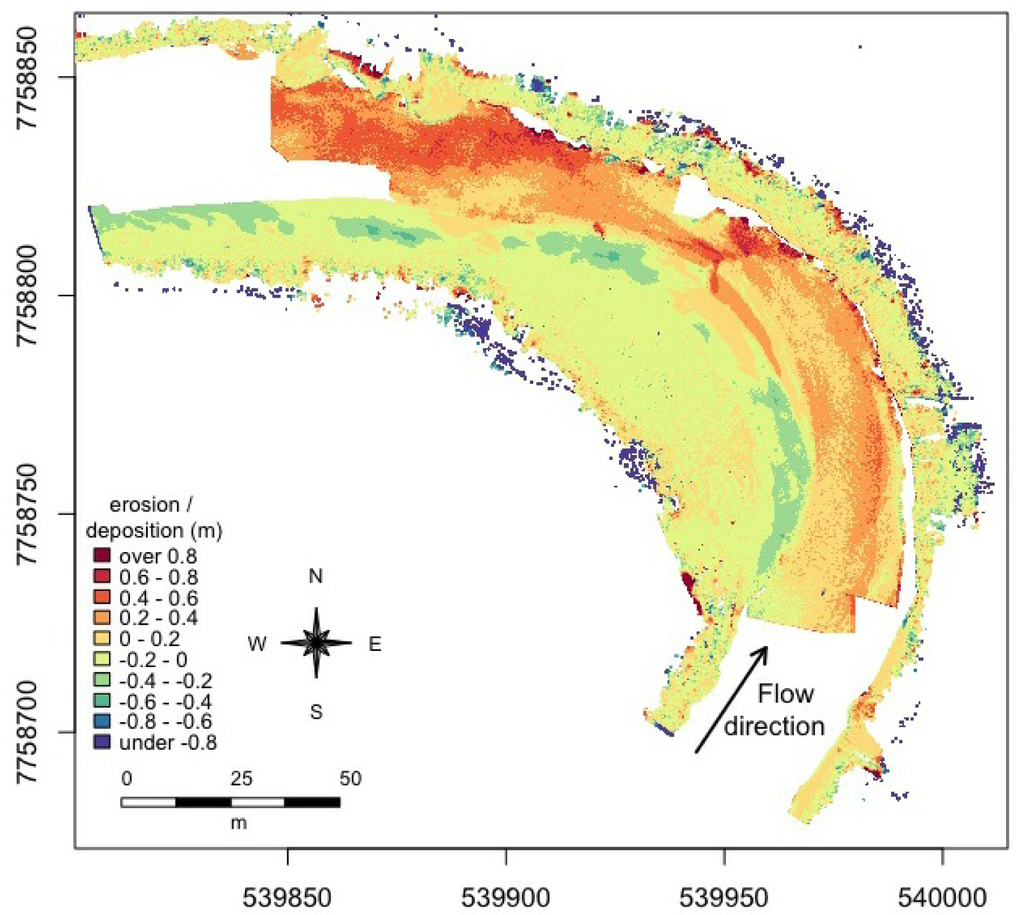
Figure 12.
Difference map between 2010 and 2011 based on the contiguous models we produced. Orange and red colours indicate areas deposition; green and blue colours indicate areas of erosion.
The range of accuracies delivered by the various techniques is reflected in the level of significant change detection (LoD) calculated according to Milan et al. [57]. The LoD is a measure to take account of the combined error of two DTMs when using them for detecting changes that is based on the standard deviation of the data sets to be compared and is expressed at different confidence levels. Due to the differences in the measuring techniques and the associated differences in DTM precision, we calculated separate LoD values for each measurement technique: at a 95% confidence limit, the MLS data has an LoD of 0.0453 m, the UAV-bathymetry data has a LoD of 0.4343 m and the UAV-photogrammetry data has a LoD of 0.4728 m.
The point bar of the studied bend was inundated only during the spring flood peak and thus, the change detection of the area is based on laser scanning data. 56.6 % of the area experienced changes that were larger than the smallest possible detectable change (LoD = 0.0453 m). Erosion dominated the point bar and was mostly less than 0.1 m. On the point bar platform, most of the area experienced almost no net erosion or deposition. Changes were more notable on the point bar margin: erosion up to 0.3 m was located on the point bar head and tail margins while up to 0.4 m of material had deposited on the apex of the point bar margin.
The part of the channel, which was continuously inundated, experienced mostly net deposition. The changes on this area were mapped with the UAV-based depth model. 15.4% of the area experienced changes that were detectable using our methodology (LoD = 0.4728 m). The magnitude of the deposition varied mainly between 0.1 m and 0.5 m but was up to 1 m in some places. Minor deposition (0.1–0.2 m) dominated the upper part of the bend; only at the thalweg was the deposition thicker, i.e., up to 0.5 m. The shape of the changes on the convex side of the thalweg resembles dunes, which indicates that dunes have been moving on the river bed on the upper part of the bend. On the downstream part of the bend, the deposition magnitudes were larger: up to 0.7 m of sediment had deposited on the thalweg, right beyond the bend apex as well as close to the point bar margin. In addition, a notable depositional area is located at the concave side of the channel at the bend exit, with a net deposition varying between 0.4 m and 0.7 m. The concave bank itself, on the other hand, experienced net erosion.
8. Discussion
We used a range of remote sensing methods to produce a seamless DTM of a river channel and flood plain. Our results show that a range of accuracies is possible, depending on the methods used. The FGI Roamer MMS system produces point cloud data with a verified accuracy of under 2 cm, whereas the UAV-based methods can deliver data with accuracies of between 10 and 20 cm. The mobile laser scanning accuracy, which has been assessed in detail in Vaaja et al. [51], compares favourably with, for instance Bitenc et al. [58], who mapped a coastal area in the Netherlands using MMS. They achieved an accuracy of between 3 mm and 5 cm, albeit relative to other points in the same data set, rather than an independent reference data set, such as the TLS point cloud used here. While mobile laser scanning can clearly out-compete the photography-based methods, it can do so only on dry land.
The UAV-photography-bathymetry model was able to deliver depth accuracies of under 10 cm, but the accuracy decreases when comparing the depths that were converted to elevation to the RTK-GNSS data. Previous studies using optical imagery-based bathymetry assessed the bathymetric data against other depth data, rather than bathymetry converted to elevation data (e.g., [40,41,45,59,60]). The decrease in accuracy when comparing under-water elevations to RTK-GNSS-measured elevations, is likely due to imprecision in the water surface model used to convert the depth values to elevation values. In 2010 in particular, the water surface was calculated as a theoretical surface based on RTK-GPS–measured shoreline points and does not represent the real water surface as accurately as the one created form the ADCP–RTK-GPS–measured water surface points. This model was used both to convert the GPS points to depth, so that the bathymetric model could be calibrated, and subsequently to convert the bathymetric model to an elevation model. In 2011 the depth points had been measured directly so the water surface model was only used at one point in the procedure, to convert the bathymetric model to an elevation model. Moreover this surface was interpolated form the water surface points measured with the RTK-GPS embarked on the ADCP. This indicates that the bathymetric model is able to produce depth estimates well, but that the water surface model used to convert the elevations to depth and the depths to elevations is of great importance when creating a DTM from a bathymetric model. Williams et al. [6] analysed the effect of different methods of water surface interpolations on the accuracy of bathymetry derived elevations and found errors in water surface models to propagate to the bed elevations derived from optical bathymetric modelling. Considering the result of the bathymetry-based DEM, the accuracy is in line with most sonar systems, while, unlike sonar, providing a raster model that does not require interpolation to create the DEM, thereby delivering spatially continuous data.
The UAV-based photogrammetry point data covers the dry and the submerged river channel. However, the refraction of light at the water surface is not taken into account in the creation of the photogrammetry point cloud, therefore the positional accuracy of the submerged points is unknown. We consider the UAV photogrammetry data only for the dry area in this study. The accuracy delivered by this method can be fairly good (sub-decimetre) but the difference in accuracy between the two flight campaigns shows that it depends on the image data. One important factor here is the number of images that can be used to create the model, and the geometric quality of the image network, that is, the relative positions of the image origins over the target area. Other factors that affect the accuracy of UAV-photogrammetry point clouds are image lens abberations and distortions and image sharpness. The 2010 images were shot using a 14 mm lens from a lower altitude and at lower resolution, leading to more distortion and less ability for the algorithm to distinguish common features in multiple images, especially on the rather low-contrast sandbank. In comparison, the 2011 images were shot from a higher altitude using a 20 mm lens, leading to less distortion that needs correcting, and at a higher resolution allowing to detect common points easier even in low-contrast areas, leading to better results. The difference in accuracy can be clearly seen in Figure 5. The 2010 point cloud shows some geometric shapes on the point bar which is reflected in the scatter plot in Figure 7 by a drastic spread of points at the higher end of the elevation spectrum.
When creating a seamless wet-dry DTM, the best result can be achieved by combining high-accuracy MLS data for the dry part with UAV-photography based bathymetric modelling. This does require a suite of expensive equipment, though, so depending on the intended use of the DTM, a UAV-only solution may be preferable, combining photogrammetry point clouds for the dry areas with bathymetric modelling for the inundated part. Given a large number of high-quality images shot from a relatively constant height and clear water conditions with uniform sediment and illumination throughout the scene, both wet and dry areas can be modelled at high resolution with around 10 cm vertical accuracy using the UAV-photography based methods we applied in this study. This level of accuracy should be satisfactory for many applications such as hydraulic modelling or habitat studies [13]. However, when the objective is to study small geomorphic features such as the dynamics of sand dunes and ripples in natural river environments, the extra level of accuracy delivered by mobile laser scanning [61–63] or terrestrial laser scanning [6,13,64] is required. Such detailed riverine processes have thus far not been studied much outside laboratory flumes, due to the previous difficulty of obtaining data that is accurate enough for this purpose in natural rivers. The combination of MMS and UAV-based high-resolution bathymetry makes detailed studies of river dynamics possible in natural environments.
The change detection in the present study reveals that, even though the seamless model is able to give a synoptic view of the river channel, the difference in accuracy of the measurement methods needs to be taken into account when analysing changes in detail. The high accuracy of the MMS measurements allows us to detect smaller (sub-decimetre) changes on the dry part of the channel than can be achieved on the inundated part of the channel, expressed as LoD (cf. Kasvi et al. [18]). Therefore, the interpretation of changes differentiates between both parts of the channel, all the while giving a more complete insight into the erosion and deposition processes taking place than a more traditional study focussing on either part of the channel alone would.
A detailed look at the coverage of the change detection map demonstrates that any lack of coverage in measurements accumulates over time and limits the change interpretation. Figure 12 shows that the part of the channel that is inundated throughout the year experienced mostly deposition, but a narrow strip of channel bed on the outside of the bend, including one slightly wider area, is missing form this map because the UAV photography mosaic had a gap in this area in 2011. The narrow irregular strip of missing data is due to overhanging trees that made bathymetric modelling in that area impossible. Any missing areas accumulate and the map of changes can only cover those areas that are covered at all time steps. For this reason, methodological redundancy is desirable since it minimises the likelihood of spatial gaps in the data. While such gaps may be tolerable to some extent in a single measurement campaign, they are accentuated in multi-temporal studies, and should therefore be minimised as much as possible. It may therefore be desirable to process and analyse the gathered data in the field as far as possible in order to immediately recognise any gaps so that these can be filled with either a modified approach of the same method, or, in case they are caused by obstructions, using other methods. In case the view of the river bed from the UAV is obstructed by overhanging trees, the no-data areas this creates in the optical bathymetric model can be filled using sonar for instance.
9. Conclusions
This study has demonstrated the creation of seamless digital elevation models in river environments by combining mobile laser scanning with UAV-photography based bathymetry modelling. We conclude that a continuous wet–dry model of the river channel can be constructed at a sub-decimetre resolution with vertical accuracy within the same range. If the accuracy requirement is in the +/− decimetre scale, we find that a UAV-only system, combining photogrammetry with optical bathymetry may be sufficient. When sub-decimetre accuracy is required, the combination of boat-based and backpack-based mobile LiDAR is the most efficient way of mapping river environments. TLS, used here as reference data, will meet even centimetre scale accuracy requirements, however the aerial coverage is more limited in that case. The methods presented in this paper lend themselves well to mapping larger areas than the test area covered in this study. The mobile LiDAR setup used here was for instance successfully employed in a study of lateral erosion of a 1.8 km stretch of river in Lotsari et al. [65]. From a logistical point of view, both methods can be efficiently employed almost simultaneously in the field, making use of the same ground target setups, thereby saving time and increasing efficiency.
Despite the contiguous data produced, the differences in measurement accuracy need to be taken into account when using these terrain models in a multi-temporal analysis of change. The combination of different high-resolution mobile remote sensing methods allows us to create seamless DTMs of decimetre to centimetre accuracy and resolution that will support two- or three-dimensional hydrodynamic modelling and fluvial geomorphological investigations.
Acknowledgments
This study was funded by the Academy of Finland (RivCHANGE research project), The Aalto Energy Efficiency research programme (project Light Energy—Efficient and Safe Traffic Environments), Research on resident-driven infill development possibilities—case study in urban areas in Finland (REPSU) and the Geography Graduate School of Finland. Fieldwork was supported by the Kevo Subarctic Research Station and the field assistance of Eliisa Lotsari is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Veijalainen, N.; Lotsari, E.; Alho, P.; Vehviläinen, B.; Käyhkö, J. National scale assessment of climate change impacts on flooding in Finland. J. Hydrol 2010, 391, 333–350. [Google Scholar]
- Lotsari, E.; Wainwright, D.; Corner, G.; Alho, P.; Käyhkö, J. Surveyed and modelled one-year morphodynamics in the braided lower Tana River. Hydrol. Process. 2013. [Google Scholar] [CrossRef]
- Alho, P.; Hyyppä, H.; Hyyppä, J. Consequence of DTM precision for flood hazard mapping: A case study in SW Finland. Nord. J. Surv. Real Estate Res 2009, 6, 21–39. [Google Scholar]
- Hicks, D.M.; Shankar, U.; Duncan, M.J.; Rebuffé, M.; Aberle, J. Use of Remote-Sensing with Two-Dimensional Hydrodynamic Models to Assess Impacts of Hydro-Operations on a Large, Braided, Gravel-Bed River: Waitaki River, New Zealand. In Braided Rivers; Smith, G.H.S., Best, J.L., Bristow, C.S., Petts, G.E., Eds.; Blackwell Publishing Ltd: Malden, MA, USA, 2009; pp. 311–326. [Google Scholar]
- Vetter, M.; Hofle, B.; Mandlburger, G.; Rutzinger, M. Estimating changes of riverine landscapes and riverbeds by using airborne LiDAR data and river cross-sections. Z. Geomorphol. Suppl. Issues 2011, 55, 51–65. [Google Scholar]
- Williams, R.; Brasington, J.; Vericat, D.; Hicks, D. Hyperscale terrain modelling of braided rivers: Fusing mobile terrestrial laser scanning and optical bathymetric mapping. Earth Surf. Process. Landf. 2013. [Google Scholar] [CrossRef]
- Allouis, T.; Bailly, J.S.; Feurer, D. Assessing Water Surface Effects on LiDAR Bathymetry Measurements in Very Shallow Rivers: A Theoretical Study. Proceedings of the Second Space for Hydrology Workshop “Surface Water Storage and Runoff: Modeling, In-Situ Data and Remote Sensing”, Geneva, Switzerland, 12–14 November 2007.
- Feurer, D.; Bailly, J.S.; Puech, C.; Le Coarer, Y.; Viau, A.A. Very-high-resolution mapping of river-immersed topography by remote sensing. Prog. Phys. Geogr 2008, 32, 403–419. [Google Scholar]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens 1981, 2, 71–82. [Google Scholar]
- Best, J. The fluid dynamics of river dunes: A review and some future research directions. J. Geophys. Res. Earth Surf. 2005, 110. [Google Scholar] [CrossRef]
- Fuller, I.C.; Large, A.R.; Charlton, M.E.; Heritage, G.L.; Milan, D.J. Reach-scale sediment transfers: An evaluation of two morphological budgeting approaches. Earth Surf. Process. Landf 2003, 28, 889–903. [Google Scholar]
- Smith, M.J.; Chandler, J.; Rose, J. High spatial resolution data acquisition for the geosciences: Kite aerial photography. Earth Surf. Process. Landf 2009, 34, 155–161. [Google Scholar]
- Heritage, G.; Hetherington, D. Towards a protocol for laser scanning in fluvial geomorphology. Earth Surf. Process. Landf 2007, 32, 66–74. [Google Scholar]
- Cobby, D.M.; Mason, D.C.; Davenport, I.J. Image processing of airborne scanning laser altimetry data for improved river flood modelling. ISPRS J. Photogramm. Remote Sens 2001, 56, 121–138. [Google Scholar]
- Bates, P. Remote sensing and flood inundation modelling. Hydrol. Process 2004, 18, 2593–2597. [Google Scholar]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens 2008, 29, 1339–1366. [Google Scholar]
- Mason, D.C.; Cobby, D.M.; Horritt, M.S.; Bates, P.D. Floodplain friction parameterization in two-dimensional river flood models using vegetation heights derived from airborne scanning laser altimetry. Hydrol. Process 2003, 17, 1711–1732. [Google Scholar]
- Kasvi, E.; Vaaja, M.; Alho, P.; Hyyppä, H.; Hyyppä, J.; Kaartinen, H.; Kukko, A. Morphological changes on meander point bars associated with flow structure at different discharges. Earth Surf. Process. Landf 2012, 38, 577–590. [Google Scholar]
- Wang, Y.; Liang, X.; Flener, C.; Kukko, A.; Kaartinen, H.; Kurkela, M.; Vaaja, M.; Hyyppä, H.; Alho, P. 3D modeling of coarse fluvial sediments based on mobile laser scanning data. Remote Sens 2013, 5, 4571–4592. [Google Scholar]
- El-Sheimy, N. An Overview of Mobile Mapping Systems. Proceedings of the From Pharaohs to Geoinformatics FIG Working Week 2005 and GSDI-8, Cairo, Egypt, 16–21 April 2005.
- Kukko, A.; Andrei, C.O.; Salminen, V.M.; Kaartinen, H.; Chen, Y.; Rönnholm, P.; Hyyppä, H.; Hyyppä, J.; Chen, R.; Haggrén, H.; et al. Road environment mapping system of the Finnish Geodetic Institute-FGI ROAMER. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2007, 36, 241–247. [Google Scholar]
- Barber, D.; Mills, J.; Smith-Voysey, S. Geometric validation of a ground-based mobile laser scanning system. ISPRS J. Photogramm. Remote Sens 2008, 63, 128–141. [Google Scholar]
- Graham, L. Mobile mapping systems overview. Photogramm. Eng. Remote Sens 2010, 76, 222–228. [Google Scholar]
- Alho, P.; Kukko, A.; Hyyppä, H.; Kaartinen, H.; Hyyppä, J.; Jaakkola, A. Application of boat-based laser scanning for river survey. Earth Surf. Process. Landf 2009, 34, 1831–1838. [Google Scholar]
- Hohenthal, J.; Alho, P.; Hyyppä, J.; Hyyppä, H. Laser scanning applications in fluvial studies. Prog. Phys. Geogr 2011, 35, 782–809. [Google Scholar]
- Jaakkola, A.; Hyyppa, J.; Kukko, A.; Yu, X.; Kaartinen, H.; Lehtomaki, M.; Lin, Y. A low-cost multi-sensoral mobile mapping system and its feasibility for tree measurements. ISPRS J. Photogramm. Remote Sens 2010, 65, 514–522. [Google Scholar]
- Haarbrink, R.; Koers, E. Helicopter UAV for Photogrammetry and Rapid Response. Proceedings of the 2nd International Workshop “The Future of Remote Sensing”, Antwerp, Belgium, 17–18 October 2006; 36, p. 1.
- Sauerbier, M.; Eisenbeiss, H. UAVs for the documentation of archaeological excavations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2010, 38, 526–531. [Google Scholar]
- Remondino, F.; Barazzetti, L.; Nex, F.; Scaioni, M.; Sarazzi, D. UAV photogrammetry for mapping and 3d modeling—Current status and future perspectives. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2011, 38, 1. [Google Scholar]
- Rosnell, T.; Honkavaara, E. Point cloud generation from aerial image data acquired by a quadrocopter type micro unmanned aerial vehicle and a digital still camera. Sensors 2012, 12, 453–480. [Google Scholar]
- Berni, J.; Zarco-Tejada, P.J.; Suárez, L.; Fereres, E. Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans. Geosci. Remote Sens 2009, 47, 722–738. [Google Scholar]
- Koljonen, S.; Huusko, A.; Mäki-Petäys, A.; Louhi, P.; Muotka, T. Assessing habitat suitability for juvenile atlantic salmon in relation to in-stream restoration and discharge variability. Restor. Ecol 2012, 21, 344–352. [Google Scholar]
- Maxwell, S.L.; Smith, A.V. Generating river bottom profiles with a Dual-Frequency Identification Sonar (DIDSON). North Am. J. Fish. Manag 2007, 27, 1294–1309. [Google Scholar]
- Sirniö, V.P. Uoman Kartoitus-Teknologia. Maankäyttö 2004, 3, 26–27. [Google Scholar]
- Kaeser, A.J.; Litts, T.L.; Tracy, T.W. Using low-cost side-scan sonar for benthic mapping throughout the Lower Flint River, Georgia, USA. River Res. Appl 2013, 29, 634–644. [Google Scholar]
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geogr 2009, 33, 103–116. [Google Scholar]
- Hilldale, R.C.; Raff, D. Assessing the ability of airborne LiDAR to map river bathymetry. Earth Surf. Process. Landf 2008, 33, 773–783. [Google Scholar]
- Winterbottom, S.J.; Gilvear, D.J. Quantification of channel bed morphology in gravel-bed rivers using airborne multispectral imagery and aerial photography. Regul. Rivers-Res. Manag 1997, 13, 489–499. [Google Scholar]
- Westaway, R.; Lane, S.; Hicks, D. Remote survey of large-scale braided, gravel-bed rivers using digital photogrammetry and image analysis. Int. J. Remote Sens 2003, 24, 795–815. [Google Scholar]
- Gilvear, D.; Hunter, P.; Higgins, T. An experimental approach to the measurement of the effects of water depth and substrate on optical and near infra-red reflectance: A field-based assessment of the feasibility of mapping submerged instream habitat. Int. J. Remote Sens 2007, 28, 2241–2256. [Google Scholar]
- Flener, C.; Lotsari, E.; Alho, P.; Käyhkö, J. Comparison of empirical and theoretical remote sensing based bathymetry models in river environments. River Res. Appl 2012, 28, 118–133. [Google Scholar]
- Legleiter, C.; Roberts, D.; Marcus, W.; Fonstad, M. Passive optical remote sensing of river channel morphology and in-stream habitat: Physical basis and feasibility. Remote Sens. Environ 2004, 93, 493–510. [Google Scholar]
- Fonstad, M.; Marcus, W. Remote sensing of stream depths with hydraulically assisted bathymetry (HAB) models. Geomorphology 2005, 72, 320–339. [Google Scholar]
- Marcus, W.A.; Fonstad, M.A. Optical remote mapping of rivers at sub-meter resolutions and watershed extents. Earth Surf. Process. Landf 2008, 33, 4–24. [Google Scholar]
- Legleiter, C.; Roberts, D.; Lawrence, R. Spectrally based remote sensing of river bathymetry. Earth Surf. Process. Landf 2009, 34, 1039–1059. [Google Scholar]
- Flener, C. Estimating deep water radiance in shallow water: Adapting optical bathymetry modelling to shallow river environments. Boreal Environ. Res 2013, 18, 488–502. [Google Scholar]
- Legleiter, C.J.; Roberts, D.A. A forward image model for passive optical remote sensing of river bathymetry. Remote Sens. Environ 2009, 113, 1025–1045. [Google Scholar]
- Legleiter, C.J.; Overstreet, B.T. Mapping gravel bed river bathymetry from space. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Alho, P.; Mäkinen, J. Hydraulic parameter estimations of a 2D model validated with sedimentological findings in the point bar environment. Hydrol. Process 2010, 24, 2578–2593. [Google Scholar]
- Mansikkaniemi, H.; Mäki, O.P. Palaeochannels and recent changes in the Pulmankijoki valley, northern Lapland. Fennia 1990, 168, 137–152. [Google Scholar]
- Vaaja, M.; Kukko, A.; Kaartinen, H.; Kurkela, M.; Kasvi, E.; Flener, C.; Hyyppä, H.; Hyyppä, J.; Järvelä, J.; Alho, P. Data processing and quality evaluation of a boat-based mobile laser scanning system. Sensors 2013, 13, 12497–12515. [Google Scholar]
- Kukko, A.; Kaartinen, H.; Hyyppä, J.; Chen, Y. Multiplatform mobile laser scanning: Usability and performance. Sensors 2012, 12, 11712–11733. [Google Scholar]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2000, 33, 111–118. [Google Scholar]
- Combrink, A. Introduction to Lidar-Based Aerial Surveys (Part 2). In PositionIT; EE Publishers: Muldersdrift, South Africa, 2011; pp. 20–24. [Google Scholar]
- Bilker, M.; Kaartinen, H. The Quality of Real-Time Kinematic (RTK) GPS Positioning; Reports of the Finnish Geodetic Institute: Masala, Finland, 2001. [Google Scholar]
- Schürch, P.; Densmore, A.L.; Rosser, N.J.; Lim, M.; McArdell, B.W. Detection of surface change in complex topography using terrestrial laser scanning: Application to the Illgraben debris-flow channel. Earth Surf. Process. Landf 2011, 36, 1847–1859. [Google Scholar]
- Milan, D.J.; Heritage, G.L.; Hetherington, D. Application of a 3D laser scanner in the assessment of erosion and deposition volumes and channel change in a proglacial river. Earth Surf. Process. Landf 2007, 32, 1657–1674. [Google Scholar]
- Bitenc, M.; Lindenbergh, R.; Khoshelham, K.; van Waarden, A.P. Evaluation of a LiDAR land-based mobile mapping system for monitoring sandy coasts. Remote Sens 2011, 3, 1472–1491. [Google Scholar]
- Marcus, W.; Legleiter, C.; Aspinall, R.; Boardman, J.; Crabtree, R. High spatial resolution hyperspectral mapping of in-stream habitats, depths, and woody debris in mountain streams. Geomorphology 2003, 55, 363–380. [Google Scholar]
- Carbonneau, P.E.; Lane, S.N.; Bergeron, N. Feature based image processing methods applied to bathymetric measurements from airborne remote sensing in fluvial environments. Earth Surf. Process. Landf 2006, 31, 1413–1423. [Google Scholar]
- Alho, P.; Vaaja, M.; Kukko, A.; Kasvi, E.; Kurkela, M.; Hyyppa, J.; Hyyppa, H.; Kaartinen, H.A. Mobile laser scanning in fluvial geomorphology: Mapping and change detection of point bars. Z. für Geomorphol 2011, 55, 31–50. [Google Scholar]
- Vaaja, M.; Hyyppä, J.; Kukko, A.; Kaartinen, H.; Hyyppä, H.; Alho, P. Mapping topography changes and elevation accuracies using a mobile laser scanner. Remote Sens 2011, 3, 587–600. [Google Scholar]
- Kasvi, E.; Alho, P.; Vaaja, M.; Hyyppä, H.; Hyyppä, J. Spatial and temporal distribution of fluvio-morphological processes on a meander point bar during a flood event. Hydrol. Res 2013, 44, 1022–1039. [Google Scholar]
- Entwistle, N.S.; Fuller, I.C. Terrestrial Laser Scanning to Derive the Surface Grain Size Facies Character of Gravel Bars. In Laser Scanning for the Environmental Sciences; Heritage, G.L.L.A., Ed.; Wiley-Blackwell: Oxford, UK, 2009; pp. 102–114. [Google Scholar]
- Lotsari, E.; Vaaja, M.; Flener, C.; Kaartinen, H.; Kukko, A.; Kasvi, E.; Hyyppä, H.; Hyyppä, J.; Alho, P. Detecting the morphological changes of banks and point bars in a meandering river using high-accuracy multi-temporal laser scanning and flow measurements. Water Resour. Res. 2013. submitted. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).