Bayesian Networks for Raster Data (BayNeRD): Plausible Reasoning from Observations
Abstract
:1. Introduction
2. Bayesian Networks
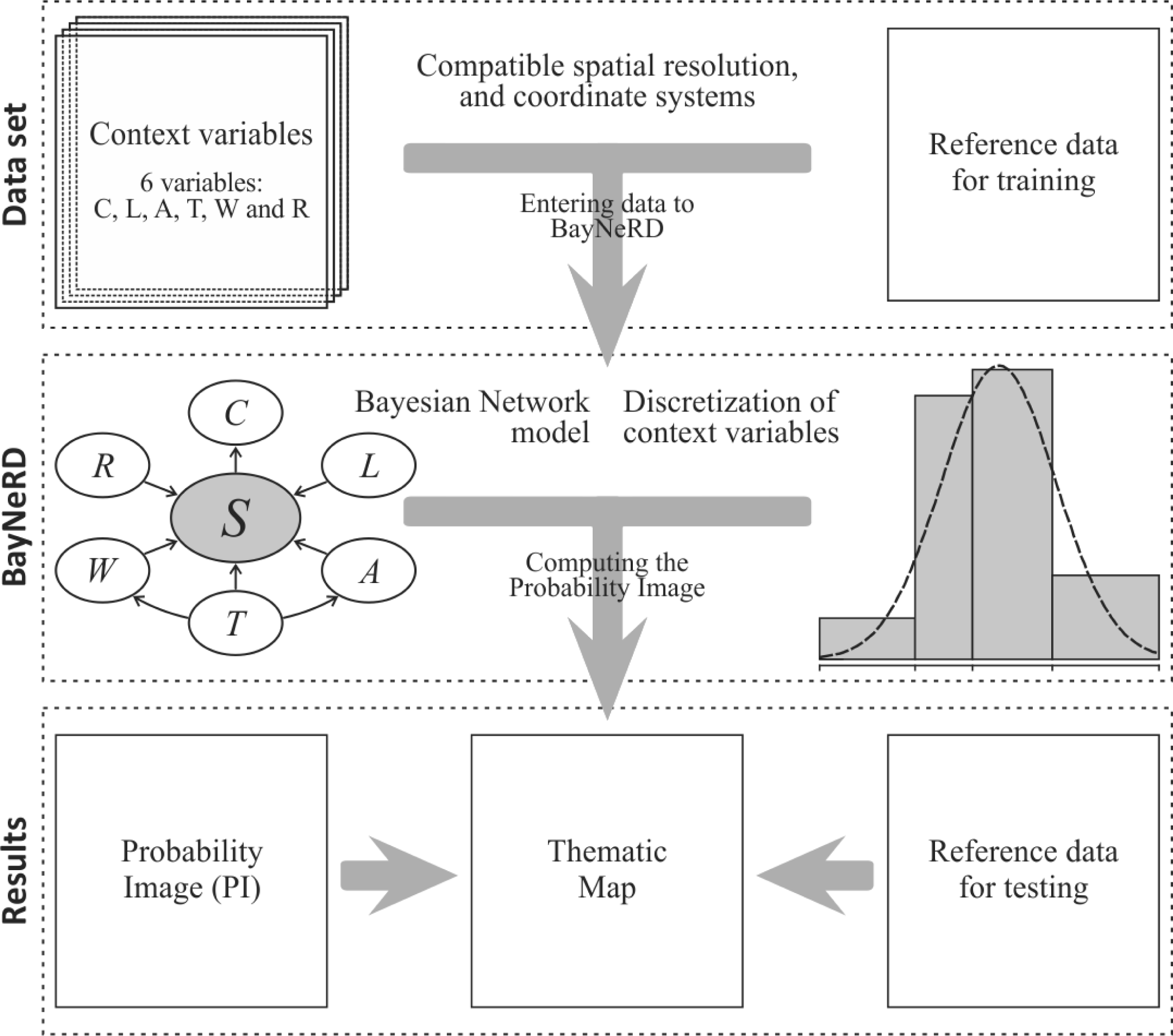
3. Framework of the Implemented BayNeRD Algorithm in R Software
3.1. Target Variable
3.2. Context Variables
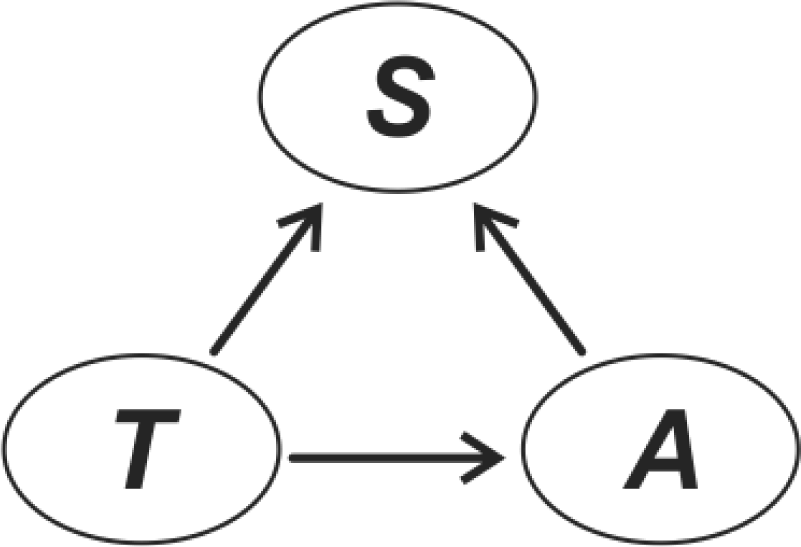
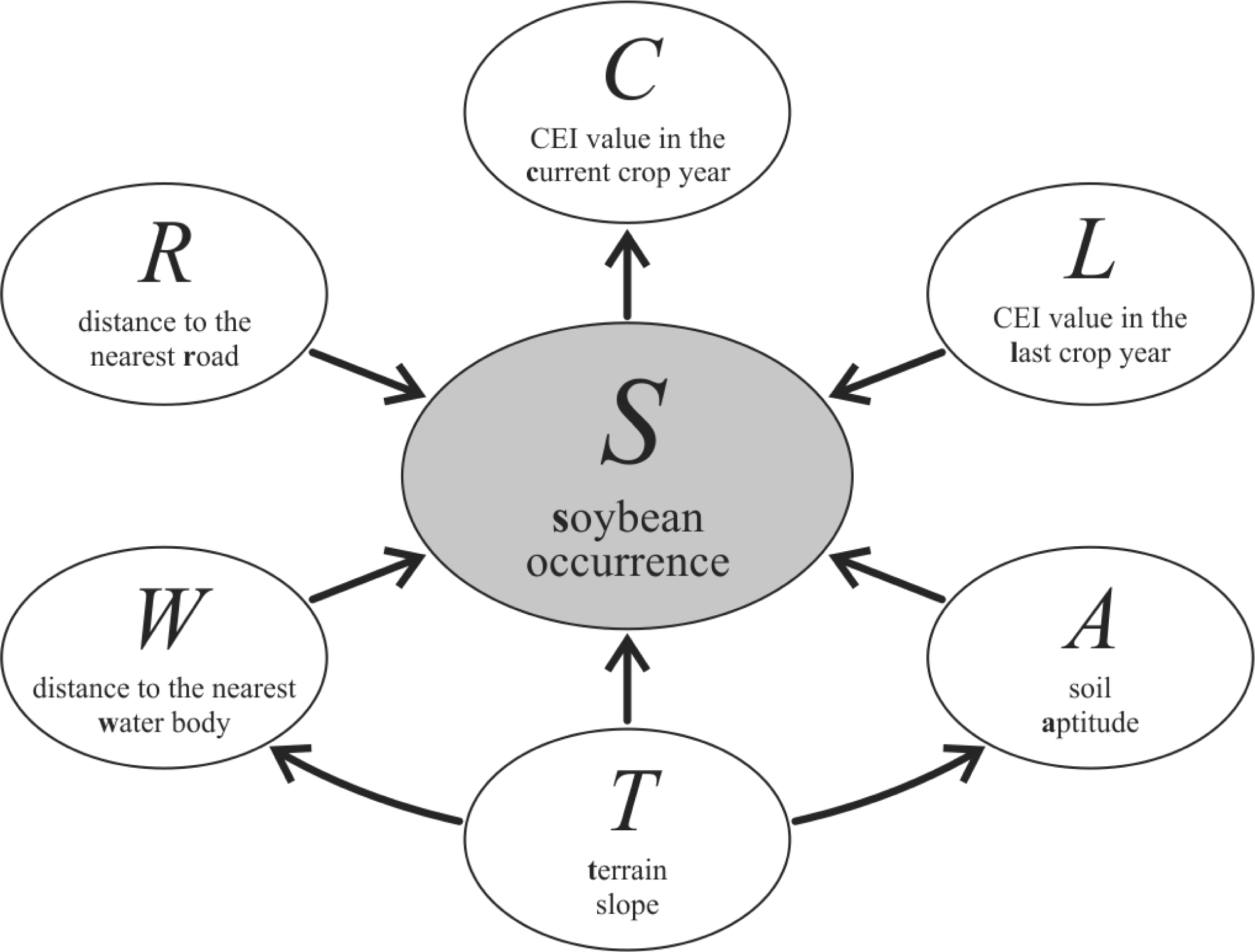
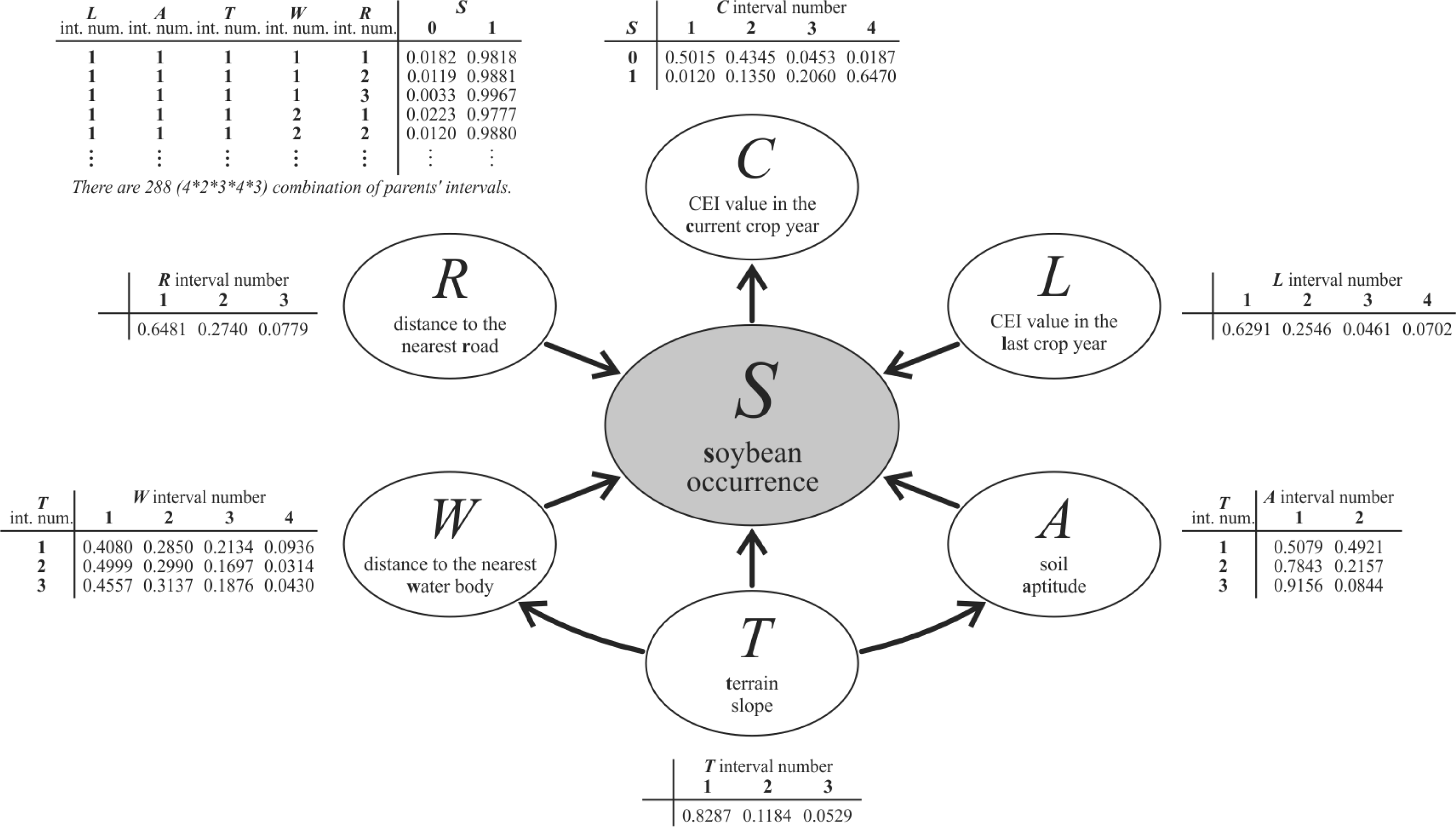
3.3. Designing the Bayesian Network Graphical Model
3.4. Discretization and Probability Functions
3.5. Computing the Probability Image
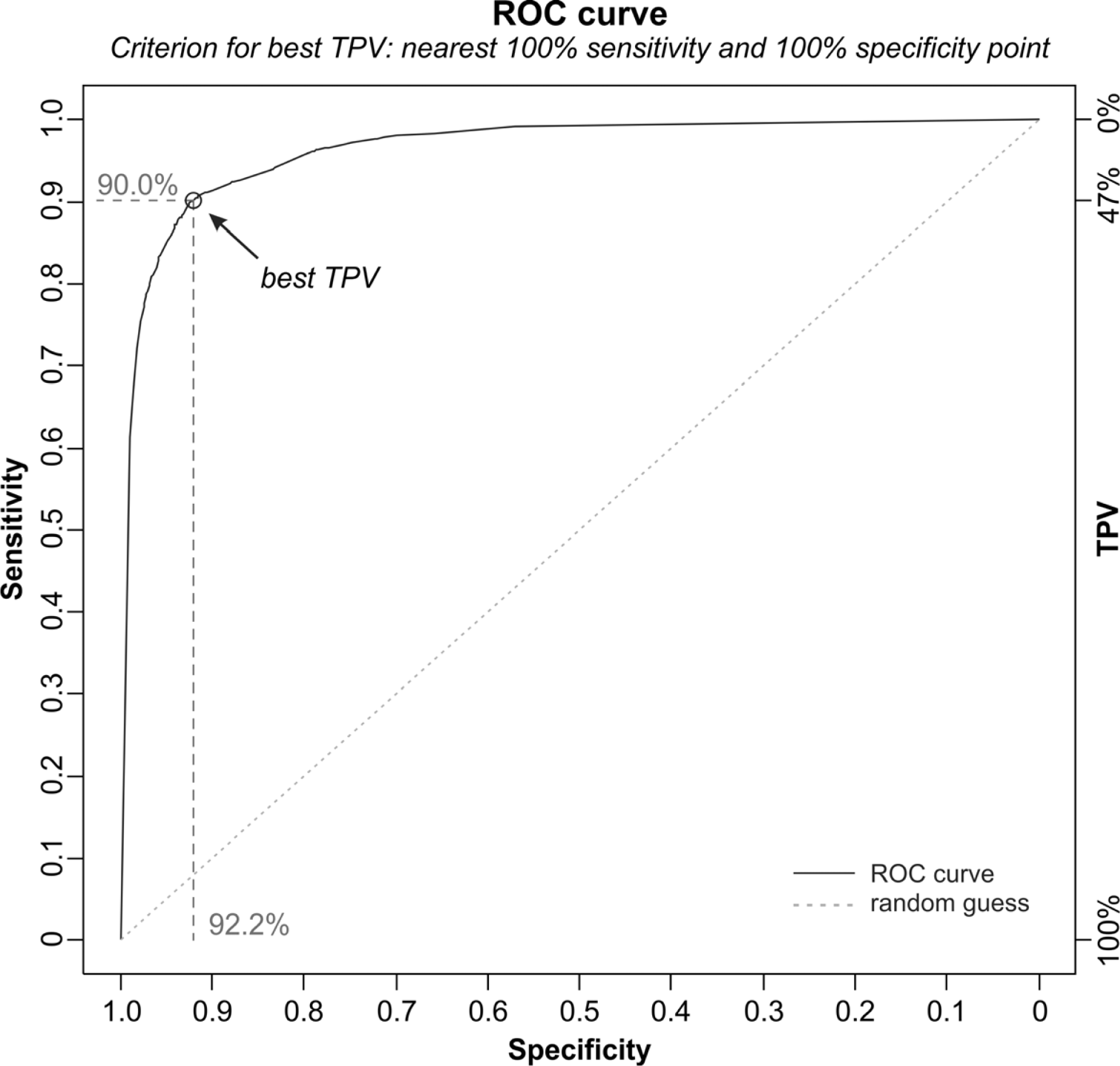
3.6. Selecting the Target Probability Value
4. Case Study of Soybean Mapping in Brazil: Materials and Research Methods
4.1. Variables
- (1)
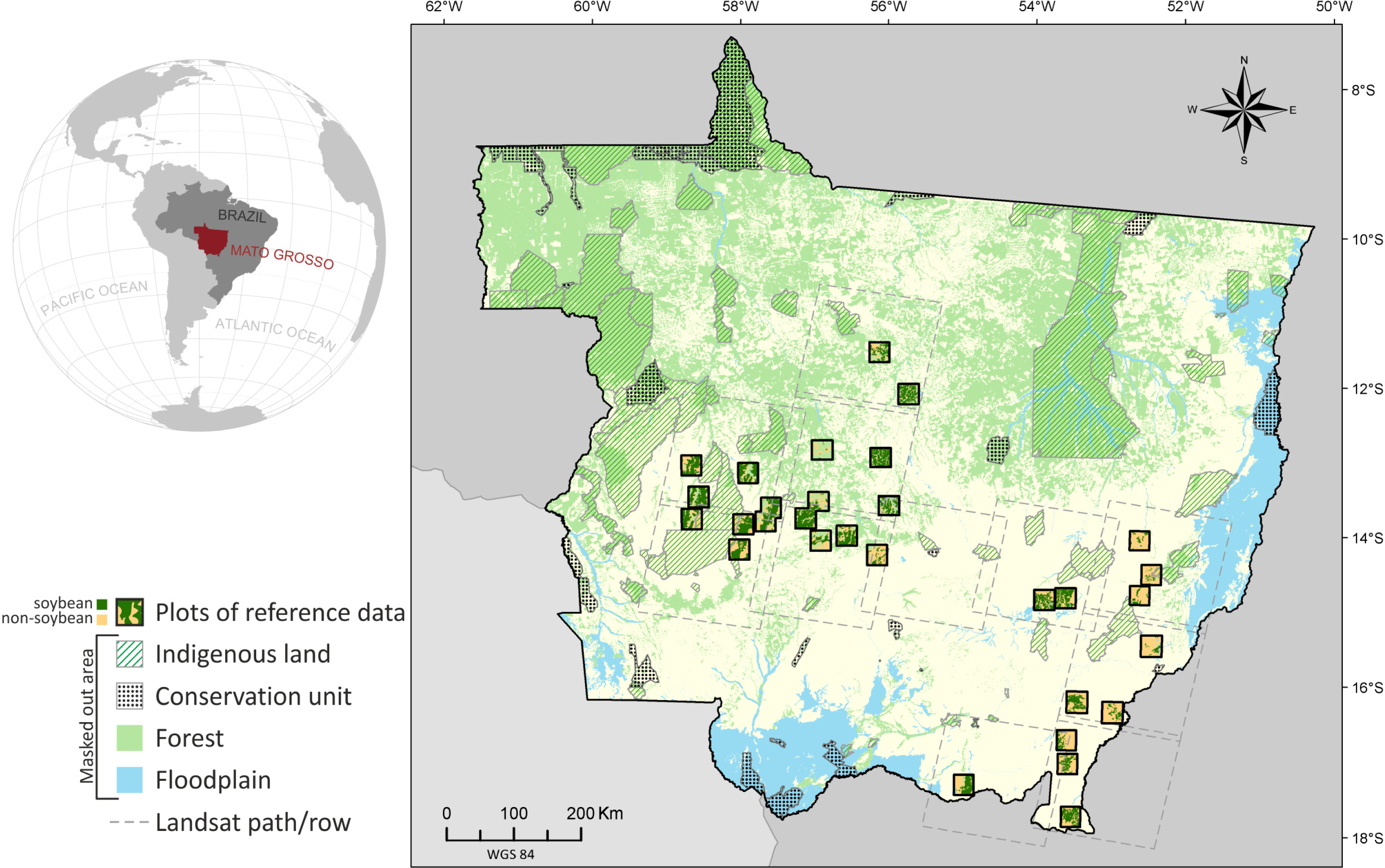
- Target variable—soybean occurrence (S) corresponding to the studied phenomenon, represented by a thematic map with four classes for the crop year 2005/2006: (i) target presence observed (i.e., soybean); (ii) target absence observed (i.e., non-soybean); (iii) missing data (i.e., no observations); and (iv) pixels outside the study area. This thematic map, produced by Epiphanio et al. [33], was used as a reference in this study. In the BayNeRD modelling, S = s, where s = 1 for soybean presence and s = 0 for soybean absence. Two thirds of the pixels in each of the thematic class soybean and non-soybean were randomly selected from the reference map to compose the reference data for training. The remaining third of the reference map pixels was set aside to be used for accuracy assessment (reference data for testing).
- (2)
- Context variables—the selected and available variables to compose the model are listed in Table 1. From expert knowledge it is known that each context variable influences soybean occurrence (S).
4.2. Bayesian Network Model
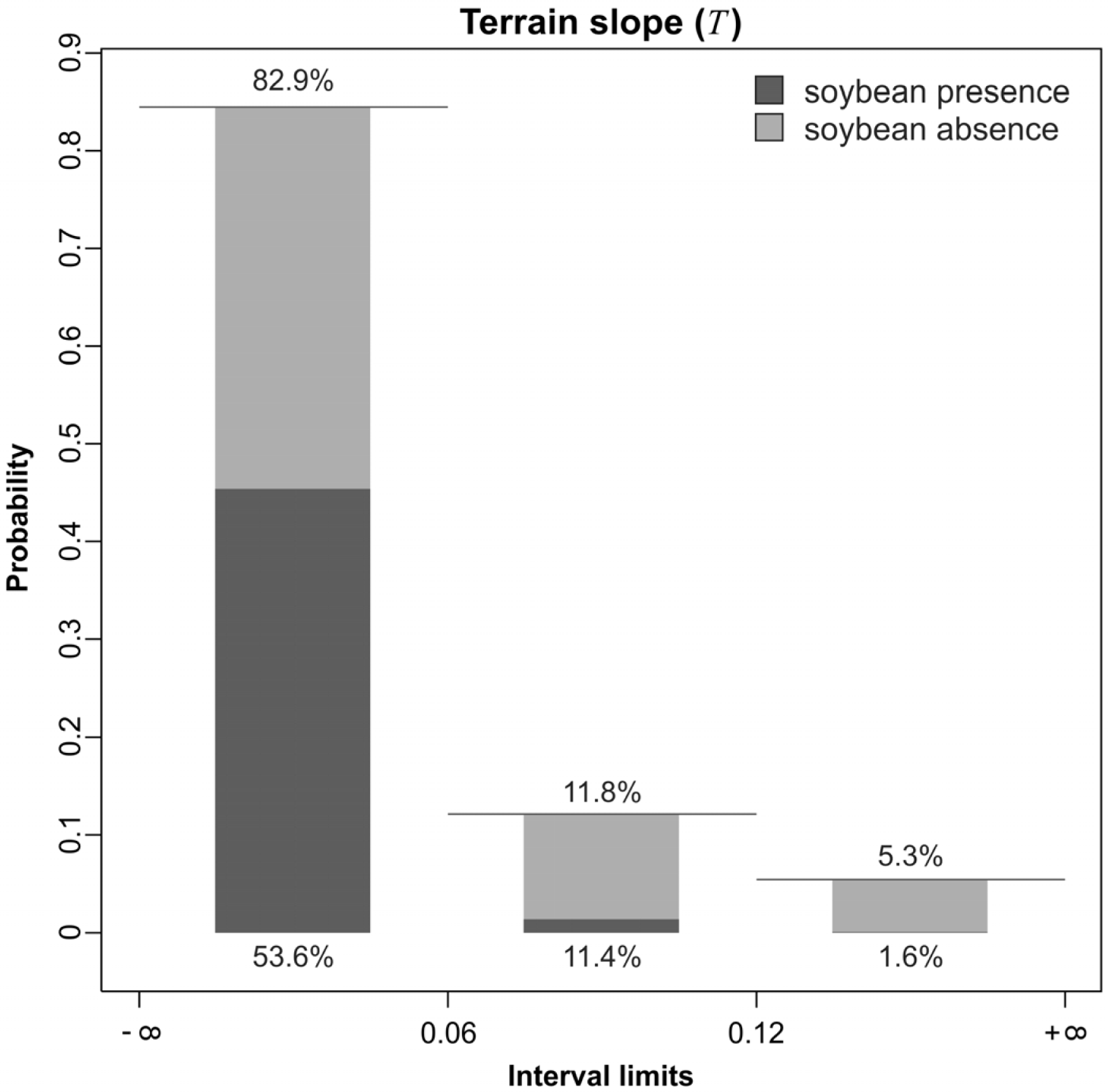
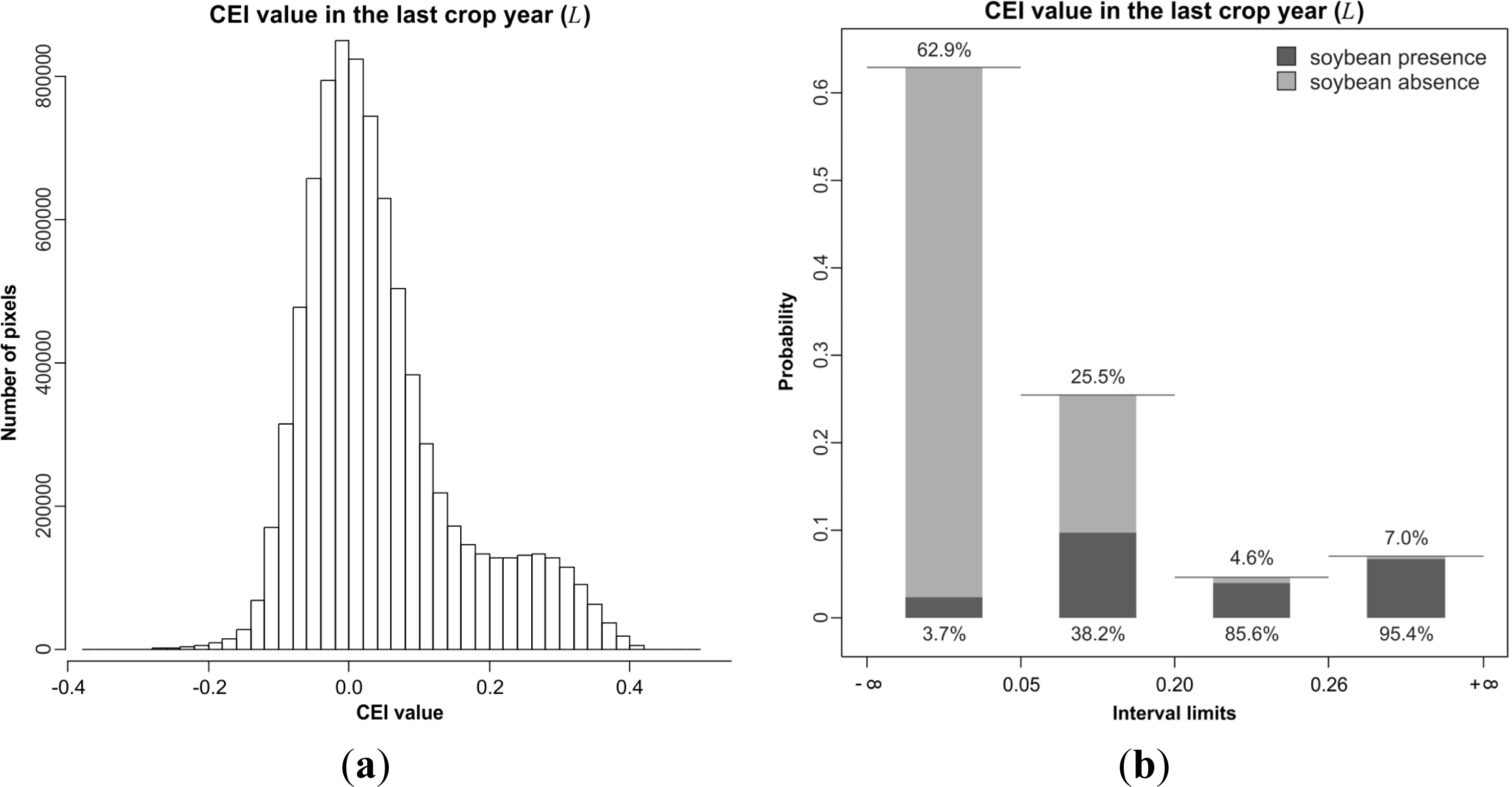
4.3. Discretization and Probability Functions
4.4. PI
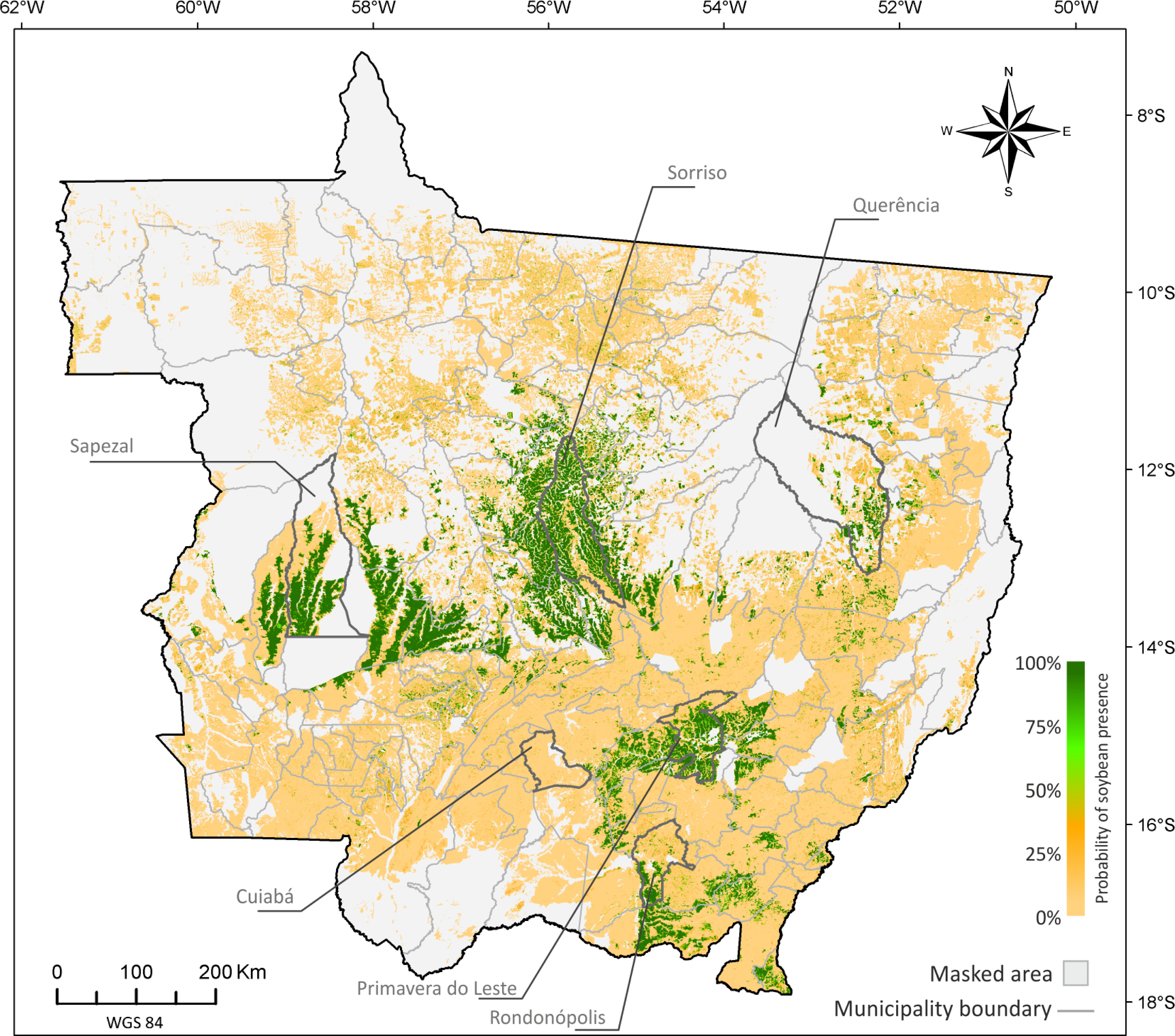
5. Results and Discussion
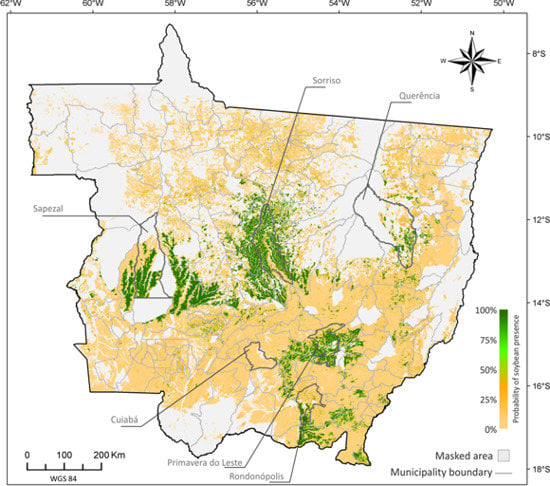
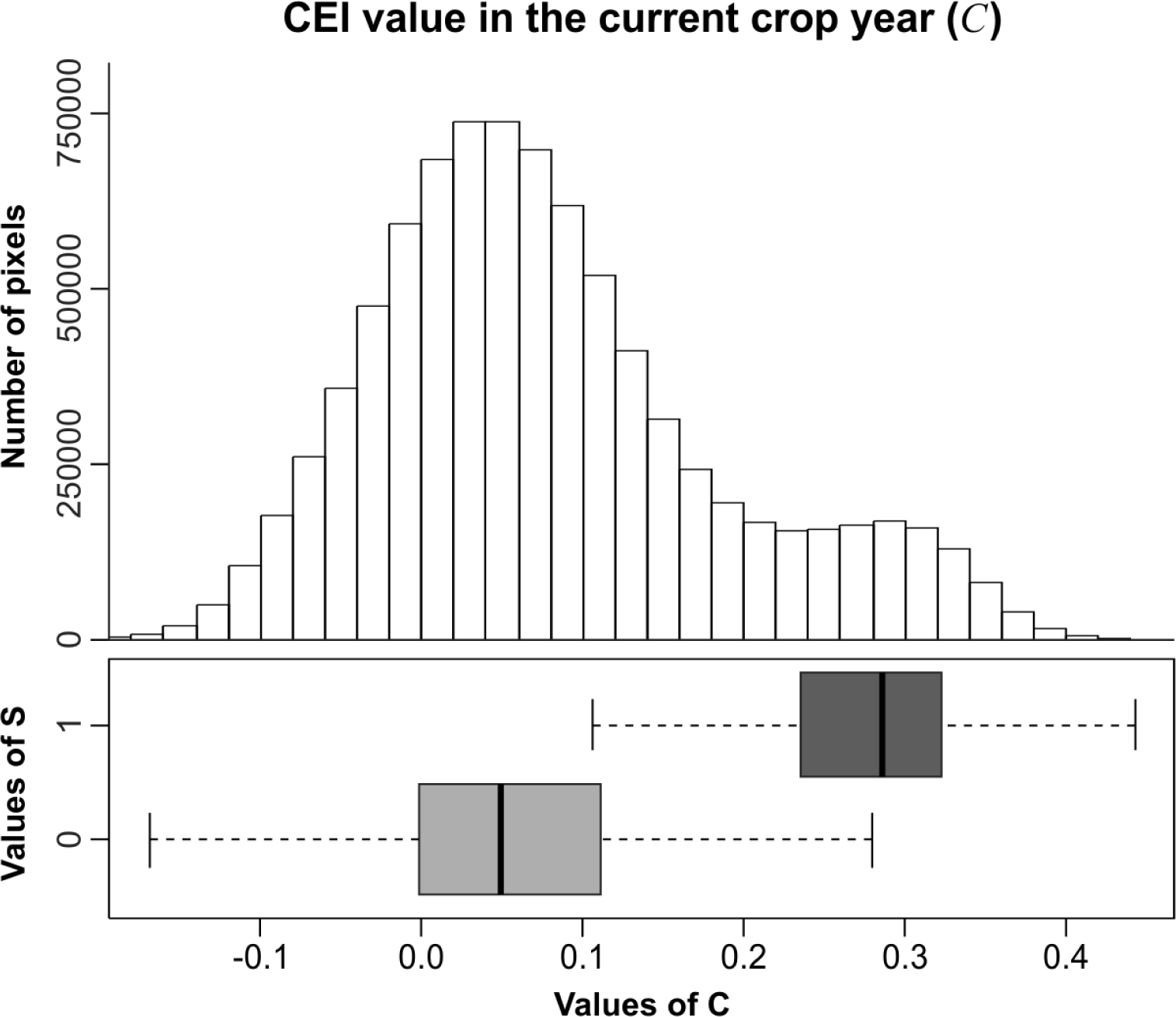
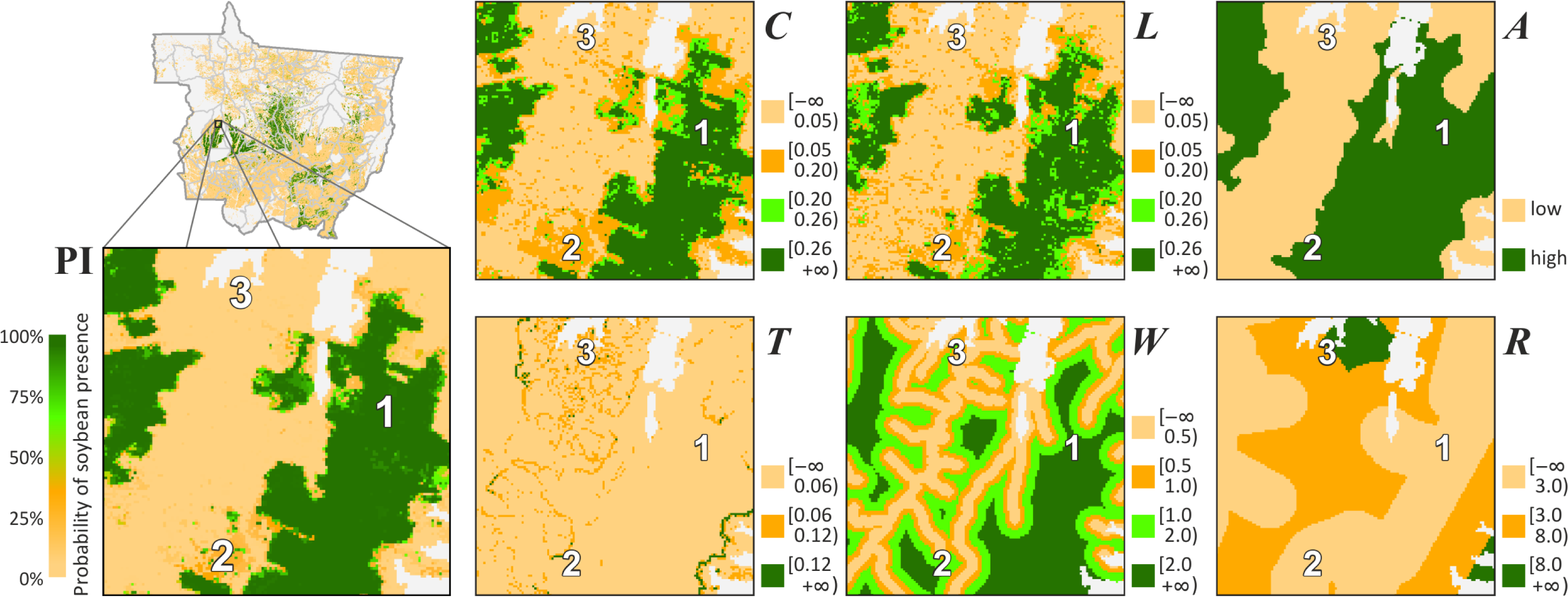
5.1. Probability Image (PI)
5.2. Creating Thematic Maps from the PI
6. Conclusion
Acknowledgments
Conflicts of Interest
References
- Melesse, A.M.; Weng, Q.; Thenkabail, P.S.; Senay, G.B. Remote sensing sensors and applications in environmental resources mapping and modelling. Sensors 2007, 7, 3209–3241. [Google Scholar]
- Donner, R.; Barbosa, S.; Kurths, J.; Marwan, N. Understanding the earth as a complex system—Recent advances in data analysis and modelling in Earth sciences. Eur. Phys. J. Spec. Top 2009, 174, 1–9. [Google Scholar]
- Li, Z.; Chen, J.; Baltsavias, E. (Eds.) Advances in Photogrammetry, Remote Sensing and Spatial Information Sciences: 2008 ISPRS Congress Book, 1st ed; CRC Press: Trowbridge, UK, 2008; Volume 23, p. 546.
- Lee, C.A.; Gasster, S.D.; Plaza, A.; Chang, C.-I.; Huang, B. Recent developments in high performance computing for remote sensing: A review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2011, 4, 508–527. [Google Scholar]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens 2007, 28, 823–870. [Google Scholar]
- Richards, J.A. Analysis of remotely sensed data: The formative decades and the future. IEEE Trans. Geosci. Remote Sens 2005, 43, 422–432. [Google Scholar]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003; p. 727. [Google Scholar]
- McGrayne, S.B. The Theory that would not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy; Yale University Press: New Haven, CT, USA, 2011; p. 336. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference, 1st ed; Morgan Kaufmann: San Francisco, CA, USA, 1988; p. 552. [Google Scholar]
- Jensen, F.V.; Nielsen, T.D. Bayesian Networks and Decision Graphs, 2nd ed; Springer: New York, NY, USA, 2007; p. 447. [Google Scholar]
- Neapolitan, R.E. Learning Bayesian Networks; Prentice Hall: Upper Saddle River, NJ, USA, 2003; p. 674. [Google Scholar]
- Darwiche, A. Modeling and Reasoning with Bayesian Networks; Cambridge University Press: New York, NY, USA, 2009; p. 560. [Google Scholar]
- Heckerman, D. Bayesian networks for data mining. Data Min. Knowl. Discov 1997, 1, 79–119. [Google Scholar]
- Uusitalo, L. Advantages and challenges of Bayesian networks in environmental modelling. Ecol. Model 2007, 203, 312–318. [Google Scholar]
- Aguilera, P.A.; Fernández, A.; Fernández, R.; Rumí, R.; Salmerón, A. Bayesian networks in environmental modelling. Environ. Model. Softw 2011, 26, 1376–1388. [Google Scholar]
- Garrett, R.D.; Lambin, E.F.; Naylor, R.L. Land institutions and supply chain configurations as determinants of soybean planted area and yields in Brazil. Land Use Policy 2013, 31, 385–396. [Google Scholar]
- Park, S.; McSweeney, K.; Lowery, B. Identification of the spatial distribution of soils using a process-based terrain characterization. Geoderma 2001, 103, 249–272. [Google Scholar]
- Cooper, G.F.; Herskovits, E. A Bayesian method for the induction of probabilistic networks from data. Mach. Learn 1992, 9, 309–347. [Google Scholar]
- Mello, M.P.; Rudorff, B.F.T.; Adami, M.; Rizzi, R.; Aguiar, D.A.; Gusso, A.; Fonseca, L.M.G. A Simplified Bayesian Network to Map Soybean Plantations. Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 351–354.
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Crawley, M.J. The R Book; John Wiley & Sons: Chichester, UK, 2007; p. 950. [Google Scholar]
- Bivand, R.S.; Pebesma, E.J.; Gómez-Rubio, V. Applied Spatial Data Analysis with R; Springer: New York, NY, USA, 2008; p. 378. [Google Scholar]
- Albert, J. Bayesian Computation with R, 2nd ed; Springer: New York, NY, USA, 2009; p. 298. [Google Scholar]
- Balov, N.; Salzman, P. catnet: Categorical Bayesian Network Inference. R Package Version 1.14.2. Available online: http://CRAN.R-project.org/package=catnet (accessed on 18 August 2013).
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat 1951, 22, 79–86. [Google Scholar]
- Zweig, M.H.; Campbell, G. Receiver-operating characteristic (ROC) plots: A fundamental evaluation tool in clinical medicine. Clin. Chem 1993, 39, 561–577. [Google Scholar]
- Altman, D.G.; Bland, J.M. Statistics notes: Diagnostic tests 1: Sensitivity and specificity. BMJ 1994, 308, 1552–1552. [Google Scholar]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Measur 1960, 20, 37–46. [Google Scholar]
- Hudson, W.D. Correct formulation of the Kappa coefficient of agreement. Photogramm. Eng. Remote Sens 1987, 53, 421–422. [Google Scholar]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Pratices, 2nd ed; CRC Press: Boca Raton, FL, USA, 2009; p. 183. [Google Scholar]
- CONAB. Séries Históricas Relativas às Safras 1976/77 a 2011/2012 de Área Plantada, Produtividade e Produção. Available online: http://www.conab.gov.br/conteudos.php?a=1252&t= (accessed on 21 March 2013).
- BRASIL. Resolução da Presidência do IBGE de n° 5 (R.PR-5/02) de 10 de outubro de 2002; Diário Oficial da União: Brasília, DF, Brazil, 2002; pp. 48–69. [Google Scholar]
- Epiphanio, R.D.V.; Formaggio, A.R.; Rudorff, B.F.T.; Maeda, E.E.; Luiz, A.J.B. Estimating soybean crop areas using spectral-temporal surfaces derived from MODIS images in Mato Grosso, Brazil. Pesquisa Agropecuária Brasileira 2010, 45, 72–80. [Google Scholar]
- FAO. FAOSTAT: FAO Statistical Database. Available online: http://faostat.fao.org (accessed on 9 April 2012).
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens 2013, 5, 949–981. [Google Scholar]
- Rudorff, B.F.T.; Aguiar, D.A.; Silva, W.F.; Sugawara, L.M.; Adami, M.; Moreira, M.A. Studies on the rapid expansion of sugarcane for ethanol production in São Paulo State (Brazil) using Landsat data. Remote Sens 2010, 2, 1057–1076. [Google Scholar]
- Rizzi, R.; Rudorff, B.F.T. Estimativa da área de soja no Rio Grande do Sul por meio de imagens Landsat. Revista Brasileira de Cartografia 2005, 57, 226–234. [Google Scholar]
- Vieira, M.A.; Formaggio, A.R.; Rennó, C.D.; Atzberger, C.; Aguiar, D.A.; Mello, M.P. Object based image analysis and data mining applied to a remotely sensed Landsat time-series to map sugarcane over large areas. Remote Sens. Environ 2012, 123, 553–562. [Google Scholar]
- Mello, M.P.; Vieira, C.A.O.; Rudorff, B.F.T.; Aplin, P.; Santos, R.D.C.; Aguiar, D.A. STARS: A new method for multitemporal remote sensing. IEEE Trans. Geosci. Remote Sens 2013, 51, 1897–1913. [Google Scholar]
- Asner, G.P. Cloud cover in Landsat observations of the Brazilian Amazon. Int. J. Remote Sens 2001, 22, 3855–3862. [Google Scholar]
- Sano, E.E.; Ferreira, L.G.; Asner, G.P.; Steinke, E.T. Spatial and temporal probabilities of obtaining cloud-free Landsat images over the Brazilian tropical savanna. Int. J. Remote Sens 2007, 28, 2739–2752. [Google Scholar]
- Arvor, D.; Jonathan, M.; Meirelles, M.S.P.; Dubreuil, V.; Durieux, L. Classification of MODIS EVI time series for crop mapping in the state of Mato Grosso, Brazil. Int. J. Remote Sens 2011, 32, 7847–7871. [Google Scholar]
- Macedo, M.N.; DeFries, R.S.; Morton, D.C.; Stickler, C.M.; Galford, G.L.; Shimabukuro, Y.E. Decoupling of deforestation and soy production in the southern Amazon during the late 2000s. Proc. Natl. Acad. Sci. USA 2012, 109, 1341–1346. [Google Scholar]
- Morton, D.C.; DeFries, R.S.; Shimabukuro, Y.E.; Anderson, L.O.; Arai, E.; del Bon Espirito-Santo, F.; Freitas, R.M.; Morisette, J. Cropland expansion changes deforestation dynamics in the southern Brazilian Amazon. Proc. Natl. Acad. Sci. USA 2006, 103, 14637–14641. [Google Scholar]
- Justice, C.; Townshend, J.R.G.; Vermote, E.; Masuoka, E.; Wolfe, R.; Saleous, N.; Roy, D.; Morisette, J. An overview of MODIS land data processing and product status. Remote Sens. Environ 2002, 83, 3–15. [Google Scholar]
- Rizzi, R.; Risso, J.; Epiphanio, R.D.V.; Rudorff, B.F.T.; Formaggio, A.R.; Shimabukuro, Y.E.; Fernandes, S.L. Estimativa da área de Soja no Mato Grosso por meio de Imagens MODIS. Proceedings of the 14th Brazilian Remote Sensing Symposium, Natal, RN, Brazil, 25–30 April 2009; INPE: São José dos Campos, SP, Brazil, 2009; pp. 387–394. [Google Scholar]
- Huete, A.R.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ 2002, 83, 195–213. [Google Scholar]
- Risso, J. Diagnóstico Espacialmente Explícito da Expansão da Soja no Mato Grosso de 2000 a 2012; National Institute for Space Research: São José dos Campos, SP, Brazil, 2013; p. 110. [Google Scholar]
- SEPLAN-MT. Sistema Interoperável de Informações Geoespaciais do Estado do Mato Grosso (SIIGEO). Available online: http://www.siigeo.mt.gov.br/ (accessed on 14 April 2012).
- Palmiere, F.; Santos, H.G.; Gomes, I.A.; Lumbreras, J.F.; Aglio, M.M.D. The Brazilian Soil Classification System. In Soil Classification: A Global Desk Reference; Rice, T., Eswaran, H., Stewart, B., Ahrens, R., Eds.; CRC Press: Boca Raton, FL, USA, 2002; pp. 127–146. [Google Scholar]
- Sistema Brasileiro de Classificação de Solos, 2nd ed; Santos, H.G.; Oliveira, J.B.; Lumbrelas, J.F.; Anjos, L.H.C.; Coelho, M.R.; Jacomine, P.K.T.; Cunha, T.J.F.; Oliveira, V.Á. (Eds.) Embrapa Solos: Rio de Janeiro, RJ, Brazil, 2006; p. 306.
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens 2003, 57, 241–262. [Google Scholar]
- Shaxson, F. New Concepts and Approaches to Land Management in the Tropics with Emphasis on Steeplands; FAO: Rome, Italy, 1999; p. 125. [Google Scholar]
- Seeruttun, S.; Crossley, C.P. Use of digital terrain modelling for farm planning for mechanical harvest of sugar cane in Mauritius. Comput. Electron. Agric 1997, 18, 29–42. [Google Scholar]
- ANEEL. Sistema de Informações Georeferenciadas do Setor Elétrico (SIGEO). Available online: http://sigel.aneel.gov.br (accessed on 20 April 2012).
- Silva, J.A.A.; Nobre, A.D.; Joly, C.A.; Nobre, C.A.; Manzatto, C.V.; Rech Filho, E.L.; Skorupa, L.A.; May, P.H.; Cunha, M.M.L.C.; Rodrigues, R.R.; et al. Brazil Forest Code and Science: Contributions to the Dialogue, 2nd ed; The Brazilian Society for the Advancement of Science—SBPC: São Paulo, SP, Brazil, 2012; p. 147. [Google Scholar]
- IBGE. Maps. Available online: http://mapas.ibge.gov.br/en/ (accessed on 29 April 2012).
- Fearnside, P.M. Soybean cultivation as a threat to the environment in Brazil. Environ. Conserv 2002, 28, 23–38. [Google Scholar]
- INPE. PRODES: Projeto de Monitoramento do Desflorestamento na Amazônia Legal. Available online: http://www.obt.inpe.br/prodes/index.php (accessed on 20 January 2012).
- Shimabukuro, Y.E.; Batista, G.T.; Mello, E.M.K.; Moreira, J.C.; Duarte, V. Using shade fraction image segmentation to evaluate deforestation in Landsat Thematic Mapper images of the Amazon Region. Int. J. Remote Sens 1998, 19, 535–541. [Google Scholar]
- FUNAI. Maps. Available online: http://mapas.funai.gov.br (accessed on 20 January 2013).
- MMA. Download de Dados Geográficos. Available online: http://mapas.mma.gov.br/i3geo/datadownload.htm (accessed on 20 January 2013).
- Galford, G.L.; Mustard, J.F.; Melillo, J.; Gendrin, A.; Cerri, C.C.; Cerri, C.E. Wavelet analysis of MODIS time series to detect expansion and intensification of row-crop agriculture in Brazil. Remote Sens. Environ 2008, 112, 576–587. [Google Scholar]
- Risso, J.; Rizzi, R.; Rudorff, B.F.T.; Adami, M.; Shimabukuro, Y.E.; Formaggio, A.R.; Epiphanio, R.D.V. Índices de vegetação Modis aplicados na discriminação de áreas de soja. Pesquisa Agropecuária Brasileira 2012, 47, 1317–1326. [Google Scholar]
- Rudorff, B.F.T.; Adami, M.; Risso, J.; de Aguiar, D.A.; Pires, B.; Amaral, D.; Fabiani, L.; Cecarelli, I. Remote sensing images to detect soy plantations in the amazon biome—The soy moratorium initiative. Sustainability 2012, 4, 1074–1088. [Google Scholar]
- Rudorff, B.F.T.; Adami, M.; Aguiar, D.A.; Moreira, M.A.; Mello, M.P.; Fabiani, L.; Amaral, D.F.; Pires, B.M. The soy moratorium in the Amazon biome monitored by remote sensing images. Remote Sens 2011, 3, 185–202. [Google Scholar]
- IBGE. Sistema IBGE de Recuperação Automática (SIDRA)—Produção Agrícola Municipal (PAM) 2012. Avaiable online: http://www.sidra.ibge.gov.br (accessed on 2 July 2012).
- Jepson, W. Producing a modern agricultural frontier: Firms and cooperatives in Eastern Mato Grosso, Brazil. Econ. Geogr 2009, 82, 289–316. [Google Scholar]
- Rizzi, R.; Rudorff, B.F.T.; Shimabukuro, Y.E.; Doraiswamy, P.C. Assessment of MODIS LAI retrievals over soybean crop in Southern Brazil. Int. J. Remote Sens 2006, 27, 4091–4100. [Google Scholar]
- Jasinski, E.; Morton, D.; DeFries, R.; Shimabukuro, Y.; Anderson, L.; Hansen, M. Physical landscape correlates of the expansion of mechanized agriculture in Mato Grosso, Brazil. Earth Interact 2005, 9, 1–18. [Google Scholar]
- Soares-Filho, B.S.; Nepstad, D.C.; Curran, L.M.; Cerqueira, G.C.; Garcia, R.A.; Ramos, C.A.; Voll, E.; McDonald, A.; Lefebvre, P.; Schlesinger, P. Modelling conservation in the Amazon basin. Nature 2006, 440, 520–523. [Google Scholar]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ 2002, 80, 185–201. [Google Scholar]
- Liu, C.; Frazier, P.; Kumar, L. Comparative assessment of the measures of thematic classification accuracy. Remote Sens. Environ 2007, 107, 606–616. [Google Scholar]
- Smits, P.C.; Dellepiane, S.G.; Schowengerdt, R.A. Quality assessment of image classification algorithms for land-cover mapping: A review and a proposal for a cost-based approach. Int. J. Remote Sens 1999, 20, 1461–1486. [Google Scholar]
- Foody, G.M. Assessing the accuracy of land cover change with imperfect ground reference data. Remote Sens. Environ 2010, 114, 2271–2285. [Google Scholar]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar]
- Krug, L.A.; Gherardi, D.F.M.; Stech, J.L.; Leão, Z.M.A.N.; Kikuchi, R.K.P.; Hruschka, E.R.; Suggett, D.J. The construction of causal networks to estimate coral bleaching intensity. Environ. Model. Softw 2013, 42, 157–167. [Google Scholar]
- Silvestrini, R.A.; Soares-Filho, B.S.; Nepstad, D.; Coe, M.; Rodrigues, H.; Assunção, R. Simulating fire regimes in the Amazon in response to climate change and deforestation. Ecol. Appl. Public. Ecol. Soc. Am 2011, 21, 1573–1590. [Google Scholar]
- Aragão, L.E.O.C.; Malhi, Y.; Barbier, N.; Lima, A.; Shimabukuro, Y.; Anderson, L.; Saatchi, S. Interactions between rainfall, deforestation and fires during recent years in the Brazilian Amazonia. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci 2008, 363, 1779–1785. [Google Scholar]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land-use planning. Eng. Geol 2008, 102, 99–111. [Google Scholar]
- Oliveira, F.S.C.; Gherardi, D.F.M.; Stech, J.L. The relationship between multi-sensor satellite data and Bayesian estimates for skipjack tuna catches in the South Brazil Bight. Int. J. Remote Sens 2010, 31, 4049–4067. [Google Scholar]
- Li, L.; Wang, J.; Leung, H.; Jiang, C. Assessment of catastrophic risk using Bayesian network constructed from domain knowledge and spatial data. Risk Anal 2010, 30, 1157–1175. [Google Scholar]
- Rodrigues, E.C.; Assunção, R. Bayesian spatial models with a mixture neighborhood structure. J. Multivar. Anal 2012, 109, 88–102. [Google Scholar]

| Variable | Description |
|---|---|
| C | CEI* value in the Current crop year (2005/2006) |
| L | CEI* value in the Last crop year (2004/2005) |
| A | Soil Aptitude |
| T | Terrain slope (given in %) |
| W | Distance to the nearest Water body (given in km) |
| R | Distance to the nearest Road (given in km) |
| Interval # | C | L | A | T | W | R |
|---|---|---|---|---|---|---|
| 1 | [−∞; 0.05) | [−∞; 0.05) | low | [−∞; 0.06) | [−∞; 0.5) | [−∞; 3.0) |
| 2 | [0.05; 0.20) | [0.05; 0.20) | high | [0.06; 0.12) | [0.5; 1.0) | [3.0; 8.0) |
| 3 | [0.20; 0.26) | [0.20; 0.26) | [0.12; +∞) | [1.0; 2.0) | [8.0; +∞) | |
| 4 | [0.26; +∞) | [0.26; +∞) | [2.0; +∞) | |||
| # of intervals | 4 | 4 | 2 | 3 | 4 | 3 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mello, M.P.; Risso, J.; Atzberger, C.; Aplin, P.; Pebesma, E.; Vieira, C.A.O.; Rudorff, B.F.T. Bayesian Networks for Raster Data (BayNeRD): Plausible Reasoning from Observations. Remote Sens. 2013, 5, 5999-6025. https://doi.org/10.3390/rs5115999
Mello MP, Risso J, Atzberger C, Aplin P, Pebesma E, Vieira CAO, Rudorff BFT. Bayesian Networks for Raster Data (BayNeRD): Plausible Reasoning from Observations. Remote Sensing. 2013; 5(11):5999-6025. https://doi.org/10.3390/rs5115999
Chicago/Turabian StyleMello, Marcio Pupin, Joel Risso, Clement Atzberger, Paul Aplin, Edzer Pebesma, Carlos Antonio Oliveira Vieira, and Bernardo Friedrich Theodor Rudorff. 2013. "Bayesian Networks for Raster Data (BayNeRD): Plausible Reasoning from Observations" Remote Sensing 5, no. 11: 5999-6025. https://doi.org/10.3390/rs5115999
APA StyleMello, M. P., Risso, J., Atzberger, C., Aplin, P., Pebesma, E., Vieira, C. A. O., & Rudorff, B. F. T. (2013). Bayesian Networks for Raster Data (BayNeRD): Plausible Reasoning from Observations. Remote Sensing, 5(11), 5999-6025. https://doi.org/10.3390/rs5115999