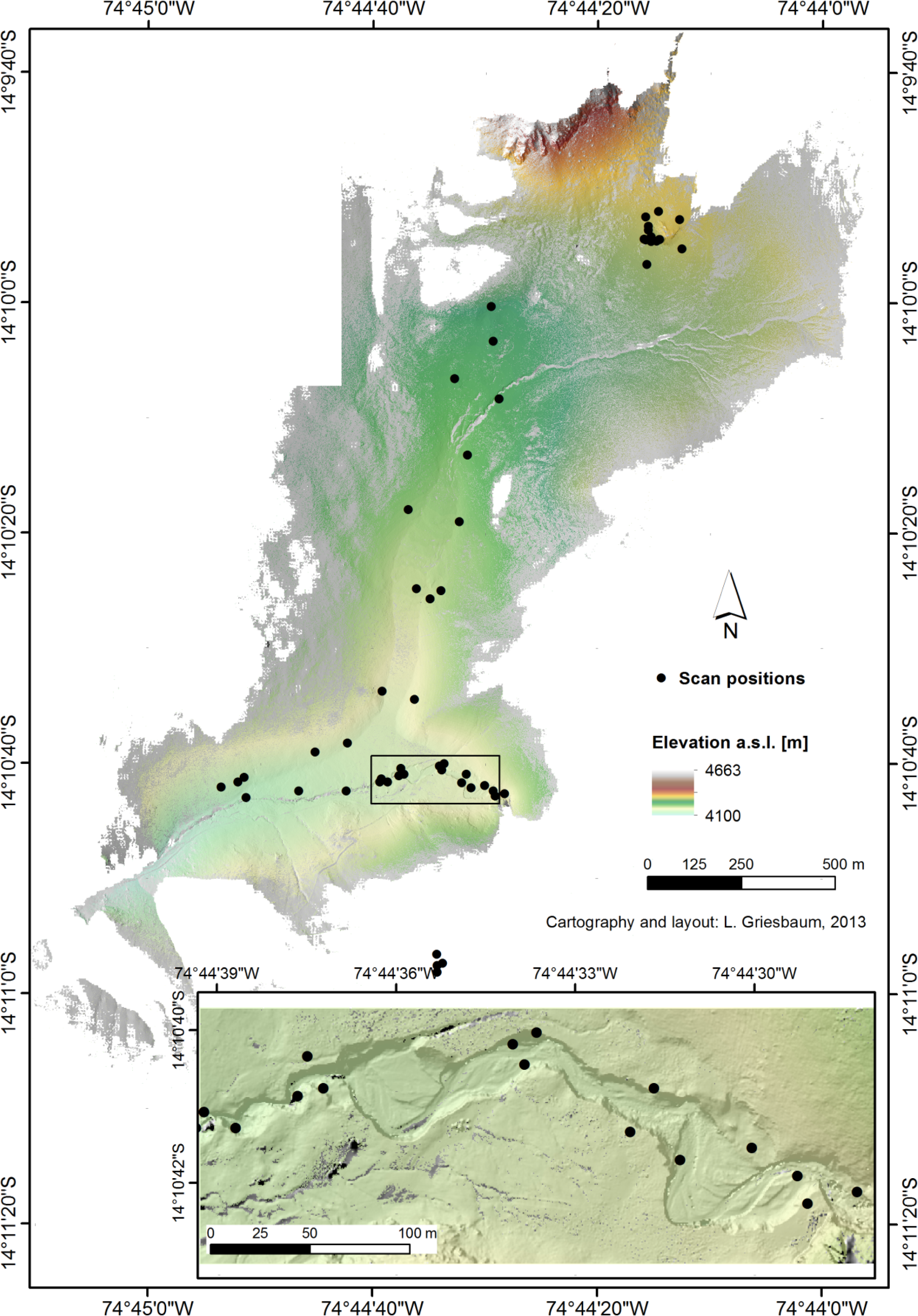
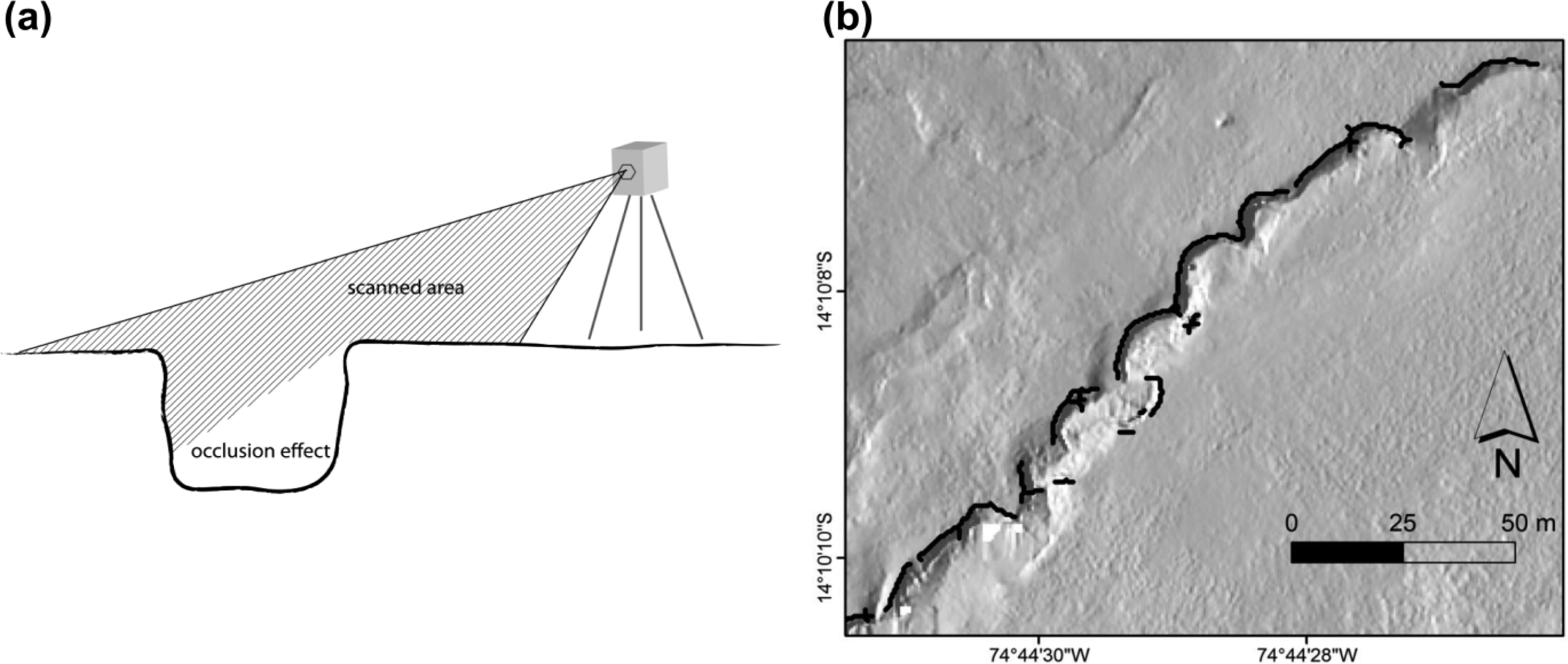
1. Introduction
Being strongly connected to climate and land use change, gully and soil erosion are an increasing problem causing major socio-economic impacts and significant loss of sediments exiting agricultural landscapes [
1]. Soil degradation requires monitoring and a full understanding of the processes and complex interrelated systems, especially in highly sensitive ecosystems [
2]. Cushion peatlands are typical elements of the high Andean vegetation zones and important ecosystems due to their water storage capacity in the mostly semiarid to arid Puna. Through rivers they also supply oases in the hyperarid coastal desert in Peru and Chile. Hence, cushion peatlands are part of the local people’s livelihood as they are used as pasture and water reservoirs, and are therefore important for agriculture [
2,
3]. In these naturally regulated ecosystems, mostly anthropogenic intervention causes gully erosion and, thus, leads to degradation and desiccation [
2,
4].
Studies on gully erosion take place mostly in semi-arid regions, since erosion mainly occurs due to sparse vegetation cover and sporadic but often heavy rainfall. Background information about characteristics, processes and morphology of gullies is found in [
1,
5–
7]. Although water erosion is not a typical process in peatlands, it is observed in various upland peats [
8–
10]. The studies of [
2,
3] provide more detailed information on these typical landforms of the Andean highland and [
4] gives insights particularly into the Llamoca peatland in Peru, the study area of this research.
Area-wide erosion monitoring and quantification in peatlands is made possible by applying remote sensing to collect detailed 3D topographic information and to derive digital elevation models (DEMs). DEMs are input to GIS-based geomorphometric analysis and the implementation of erosion models [
11]. First, to generate such a submeter resolution DEM adequate data sources are necessary. Second, to identify the affected landscape in the DEM dataset, geomorphological landform mapping through feature detection algorithms is required.
LiDAR, also referred to as laser scanning, provides reliable and accurate 3D point clouds, from which high-resolution Digital Terrain Models (DTMs) can be derived for geomorphological studies [
12,
13]. The DTM represents a DEM of the bare Earth without elevated anthropogenic objects and high vegetation. In particular ground-based LiDAR,
i.e., Terrestrial Laser Scanning (TLS), offers high point densities to derive submeter resolution DTMs. TLS is applied for the investigation of landforms with small spatial extent and processes with low magnitudes of changes over time [
14–
16]. Additionally, TLS is a suitable field method to derive DTMs in areas where high precision airborne acquisition is hampered due to difficult flight conditions (e.g., high altitude, wind conditions) or costs. Furthermore, in gully research TLS is often used as high quality reference dataset to evaluate different field methods for quantifying gully erosion in 2D and 3D (e.g., eroded gully volume) [
17,
18].
The quality of LiDAR-derived DTMs—in terms of DTM resolution, vertical and horizontal elevation accuracy—enables automatic detection of detailed natural landforms as well as man-made objects [
19]. Automatic GIS classifications are usually based on morphometric characteristics, such as slope, curvature, aspect, or other derivatives of elevation [
13,
20,
21]. Gully detection is of high importance regarding erosion monitoring and gully erosion modeling, which aims at predicting erosion rates and the impact of gully development, e.g., on hydrology and sediment budgets [
22].
The aim of our study is to present and examine the potential of a new GIS-based workflow for detecting gullies in cushion peatlands from TLS DTMs. Utilization of TLS data coupled with GIS enabling automatic gully detection is still underexploited (Section 2). Former works on gully detection concentrated mostly on the extraction of linear features to form gully networks. In contrast, this work aims at mapping gully erosion areas as polygons, which enables straightforward volumetric and multitemporal analysis of changes in morphology over time. The study area is located in the catchment area of Río Viscas at the foot of Cerro Llamoca, Peru (Section 3). Due to the high altitude of the catchment (∼4400 m a.s.l.), and its remote location, no detailed elevation information of the micro-topography has been available previous to this investigation. The objects of interests are gullies with a dimension of a few meters up to more than 50 m in width. In this study, we demonstrate for the first time the utilization of TLS for geomorphological mapping of gullies in high altitude Andean cushion peatlands for a relatively large study extent with almost 2 km2 (Section 4). The results are compared with gully outlines digitized manually by several geomorphologists (Section 5).
Apart from the methodological progress in this paper, we expect to stimulate research on cushion peatlands using LiDAR and GIS, which will help to enhance the understanding of the underlying geomorphological processes, channel response and catchment behavior including gully erosion and hydrology.
2. Related Works
Previous works mainly used satellite or aerial images for mapping of gullies. GIS-based gully monitoring using high-resolution (<0.1 m) aerial photography taken from blimp and kite platforms are performed in the study of [
23]. The monitoring over several years of two gullies located in Spain yields the capability of deriving DEMs from this data source. However, vegetation cover and the specific morphology of the gullies make fully automatic DEM derivation difficult. In [
24] IKONOS and GEOEYE-1 satellite images are used as input of an object-based image analysis (OBIA) for mapping of the gully system area in a study site in Morocco. Input features for segmentation and classification are derived from topographic, spectral, shape and contextual information. They generate a 1m-DTM from a Digital Surface Model (DSM) derived from a GEOEYE-1 stereo-pair, from which features such as slope, flow direction, specific catchment area,
etc., are derived. The detected gully system area differs only slightly (<2%) from the reference area. In the study of [
25] a multi-scale OBIA approach is developed using unmanned aerial vehicle (UAV) photographs as an input layer where image (RGB) contrast information and shape properties of segments are considered. The OBIA workflow includes a multi-resolution segmentation and knowledge-based classification designed for the investigated landform. Compared with manually detected reference landforms, gully mapping achieves detection rates of around 67%.
Recent studies make use of LiDAR data predominantly obtained from airborne platforms [
13]. In particular, LiDAR can enable geomorphological mapping of vegetated areas where passive remote sensing techniques do not provide sufficient ground information below high vegetation (e.g., [
26]). GIS-based geomorphological mapping by means of airborne LiDAR data for landform identification and delineation has been used for several years such as for fluvial morphological landforms [
27,
28] and quantification of multitemporal changes [
29,
30]. For a comprehensive review of studies using airborne LiDAR in geomorphology see [
13] and references therein.
Several studies on (semi)automatic, object-based gully detection from airborne LiDAR have already been published. In the study of [
26], a gully system in a forested area is investigated and gully morphologic information is extracted in a semi-manual procedure by looking at DTM-derived contour lines. They aim at deriving channel locations and network topological connectivity of the channels to improve channel-network maps and topological models. They conclude that the relatively low point density of terrain points and thus DTM resolution (2–4 m cell size) and, furthermore, occlusion of gully bottoms are the main limitations. This results in low mapping accuracy and poor morphological information. In [
31] the authors derive gully maps in upland peatlands from airborne LiDAR DEMs with 2 m ground resolution. They identify gully areas through low difference from mean elevation (
i.e., high-pass filter) and high positive plan curvature. Their automated workflow can be applied to large areas. The achieved accuracy of gully width and depth are within the range of the horizontal and vertical accuracy of the input LiDAR data. The results of the raster-based approach of [
32] highlight the need for adaptive thresholds for the detection of natural landforms such as channels and gullies. They use curvature and openness maps derived from a 1m-DTM from airborne LiDAR to identify the channel network via unsupervised channel pattern recognition and classification. A statistical approach is applied to derive optimum kernel sizes. The approach introduced by [
33] detects gullies in airborne LiDAR data through surface curvature in multiple scales (
i.e., varying window sizes). Furthermore, they present an algorithm to connect fragmented parts to a gully network. Gaps in the network are due to eroded shallow parts in between.
Compared to the results derived from airborne LiDAR datasets, only a few studies have assessed the potential of ground-based LiDAR for gully investigation. The analysis of [
18] is based on TLS point clouds as input to model gully cross-sections and to derive geometric parameters (e.g., cross-section area computation). Furthermore, they automatically extract the thalweg of a gully. They state the importance of data preprocessing, and identify TLS intensity correction (
cf. [
34]) and gully edge detection as future research topics. The study of [
35] assesses the effect of TLS point sampling density on the characterization of ephemeral gullies within areas of agricultural land use. They outline guidance principles for multitemporal gully LiDAR surveys in order to minimize scanning effort while keeping the required topographic details as high as possible. The authors deploy the concept of semivariograms to quantitatively assess the relationship between LiDAR point density and topographic modeling. They conclude that, due to the inherent nature of heterogeneous point density distribution of TLS, there is a large potential to optimize scan settings and planning. In particular, data acquisition has to be regarded with respect to the (i) object of interest (e.g., scale, extent), (ii) detail of maintained micro-relief, and (iii) reduction of occlusion effects. One of the first comparisons of DEMs derived from terrestrial and airborne LiDAR for gully erosion estimation is presented by [
36]. They stress the advantage of high point density of TLS and the preferable bird’s eye view from airborne LiDAR to capture data even in deeply incised gullies, which is not possible with TLS due to topographic occlusion. Thus, both LiDAR data sources are complementary. They advise to capture the main gully system area-wide with high-resolution airborne LiDAR and, additionally, apply TLS in areas with narrow gully tributaries. Furthermore, they state that TLS is a suitable and cost-effective tool to develop time-series for monitoring of gully erosion processes.
To sum up, GIS-based geomorphological mapping of cushion peatlands using TLS data is not yet fully exploited. However, TLS has already proven a large potential to become a standard tool for multitemporal monitoring of gully erosion. In particular the combination of DEMs from different data sources is increasingly gaining interest, such as airborne and terrestrial LiDAR as well as DTMs derived from images.
4. Methods
The aim of our GIS-based workflow is to detect and delineate gully channels as polygons at individual gully scale. This will enable further detailed studies on gully erosion and fluvial morphological analysis by automatic geomorphometric parameter extraction of gully systems. The resolution of the input DTM with 0.5 m cell size is sufficient for gully mapping in the Cerro Llamoca peatland, as the study site’s gullies clearly exceed 0.5 m in width. The main principle of the method is to parameterize a gully as a depression in the terrain surface (
i.e., loss of volume due to erosion), and additionally having a clear separation from the plateau depicted by a terrain discontinuity,
i.e., breakline (
Figure 2). The outline of the gully polygon shall correspond to a certain upper boundary of the gully channel, such as the border between uneroded terrain and the incision.
The chosen strategy is to make use of edge-based segmentation by breakline detection [
20] combined with filling of sinks [
39,
40]. First, the upper breaklines of the gully incision are detected and serve as potential outline of the gully. In order to derive the gully as polygon, feature sink filling is performed on a conditioned DTM. For this purpose, the thalweg at the bottom of the gully is required and extracted from the DTM. Based on the thalweg, the gully system is divided into small patches by inserting artificial “dams” orthogonally to the gully thalweg along the gully course. Thereafter, both breaklines and small artificial dams at each patch are implemented into the DTM. This conditioned DTM is then used for sink filling of each “pool”. The gully outline can be defined by using a threshold on fill depth for the artificially filled pools. The workflow is developed in GRASS GIS [
41] and the main single steps are shown in
Figure 4. Preprocessing and DTM generation have been described above in Section 3.2. The workflow is followed by a comparison with manually digitized reference data.
4.1. DTM Conditioning
Due to the nearly flat peat area and the steep gully slopes, the upper gully edges exhibit a high terrain curvature. Geomorphological breakline detection of upper gully edges is performed by the method of [
20], which is a curvature-based edge detection procedure. In this approach, a curvature raster is calculated by local surface approximation using a bivariate quadric function (
cf. [
42]). 3D breaklines can be derived by setting a threshold on high plan curvature and subsequent skeletonization of the masked areas.
The thalweg is defined as the connecting line of the lowest points inside the gully along the channel course [
43]. Several studies such as [
31,
32] assume concavity along the bottom of the gully, which does not hold for the Llamoca gullies with predominantly U-shaped erosion channels. The approach of [
43] to extracting thalweg networks combines the morphological criteria of significant curvature (
i.e., discontinuous concave areas) and topographic convergence index. To generate the thalweg we use the topographic convergence index (TCI), which is defined as the logarithm of the ratio of flow accumulation and local slope [
44]. Maximum TCI values describe regions with high chance for surface runoff. By masking areas with high TCI followed by skeletonization, the thalweg vector line is derived. In order to use the thalweg line for generating orthogonal transects, the vector line has to be smoothed to suppress effects of micro-topographic structures on the shape of the line. The final thalweg line is ready after applying vector line generalization by means of the Snakes algorithm [
44].
Orthogonal transects, representing the artificial dams to construct pools along the gully channel, are constructed every 50 m with a lateral length of 40 m on each side of the thalweg. Shorter distances between transects should be chosen if the gully system has high elevation gradients along the channel in relation to the height step at the gully edges. In case of the Llamoca gully, the elevation changes within 50 m are much lower than the heights of the gully edges. To avoid transects to overlap neighboring gully channels, overhanging transect dangles at each side of the gully edges (i.e., breaklines) are removed by intersecting the transect lines with the vectorized breaklines. In this step, only transects intersecting breaklines on both sides are trimmed automatically by keeping the middle transect part. All other transects keep their original length.
As the method of filling sinks considers multiple flow directions in the DTM, the raster breaklines and transect lines must be grown by one pixel in all directions to prevent the virtual surface water from overflowing. Both breaklines and thalweg transect lines are inserted as vertically extended objects into the DTM by adding a certain height to the DTM elevation (
Figure 5). A height value is applied that definitely exceeds the maximum expected gully depth of the study area (here 10 m). This ensures that the sink-filling algorithm fills the whole gully volume and not only small local depressions at the gully bottom. Results of this processing step are the thalweg line and the modified DTM, which is used as input in the next step.
4.2. Gully Delineation
As outlined above, the DTM conditioned with artificial barriers serves as input for sink filling as implemented in GRASS GIS [
40]. The conditioning of the DTM prior to sink filling has the advantage of providing distinct, detectable boundaries where the gully has clear edges. At the same time, due to the sink filling of the artificial gully pools, outlines can be derived even in areas where no clear edges are present. The artificially introduced sinks are filled up to the level of the sink spill point. In case of pools that are completely encompassed by breaklines and transects, the spill point corresponds to the location at the downstream orthogonal transect where the lowest gully channel elevation is present. In all other cases the spill point can be found at the gully edge with lowest elevation where no breakline was detected (
Figure 5).
Subtracting the input DTM from the filled DTM leads to a raster of fill depth values. Masking areas with a fill depth above a certain threshold marks the main gully channel areas and depressions outside gullies. The fill depth values correspond to the elevation difference between spill point elevation and original DTM elevation. Depth values of gully sections that are completely encompassed by breaklines do not have a geomorphological meaning, as they are mainly related to the height of the artificial barriers. In case of “open” pools with missing artificial barriers at the edges, the fill depths are determined by the elevation of the lowest “open” gully edge. The two possible cases can be seen in
Figure 5b.
The derived mask still contains the artificial barriers as holes between the single patches. By mathematical morphology of closing of the binary raster mask, these gaps are bridged and the patches along the gully channel are connected to the final gully polygons. Small isolated sinks can be removed by a threshold on polygon area (here <10 m2).
The medial axis of the gully is the closure of the set of points that have at least two closest points on the boundary (
cf. [
45]). It is derived from the gully polygon by applying the grassfire model. In this procedure the raster polygon area is thinned from all sides to a line with one pixel width. Resulting bifurcations are removed to derive the medial axis line vector. Analogous to the thalweg, the medial axis is smoothed for further application. The results of this step include the vector polygon of the gully areas and corresponding medial axes.
4.3. Gully Morphology
Descriptive geomorphometric parameters are necessary for understanding the erosion processes and the development of gullies in complex cushion peatland systems. The gully channel geometry is assessed and quantified through a series of cross-sections orthogonal to the medial axis [
18]. The lengths of the orthogonal cross-sections and the distance between the cross-sections along the gully course have to be chosen in relation to the geomorphological characteristics of the study object. In our case the length of the cross-section is adapted automatically as it is determined and limited by the gully polygon. The shortest reasonable distance between the cross-sections is determined by the given resolution of the DTM. By draping the cross-sections over the LiDAR DTM, 3D lines are generated which are the input for assessing the width, depth and cross-sectional area along the gully channel course. Furthermore, summarizing the single cross-sections allows for calculating the overall eroded volume.
4.4. Comparison with Manual Reference Data
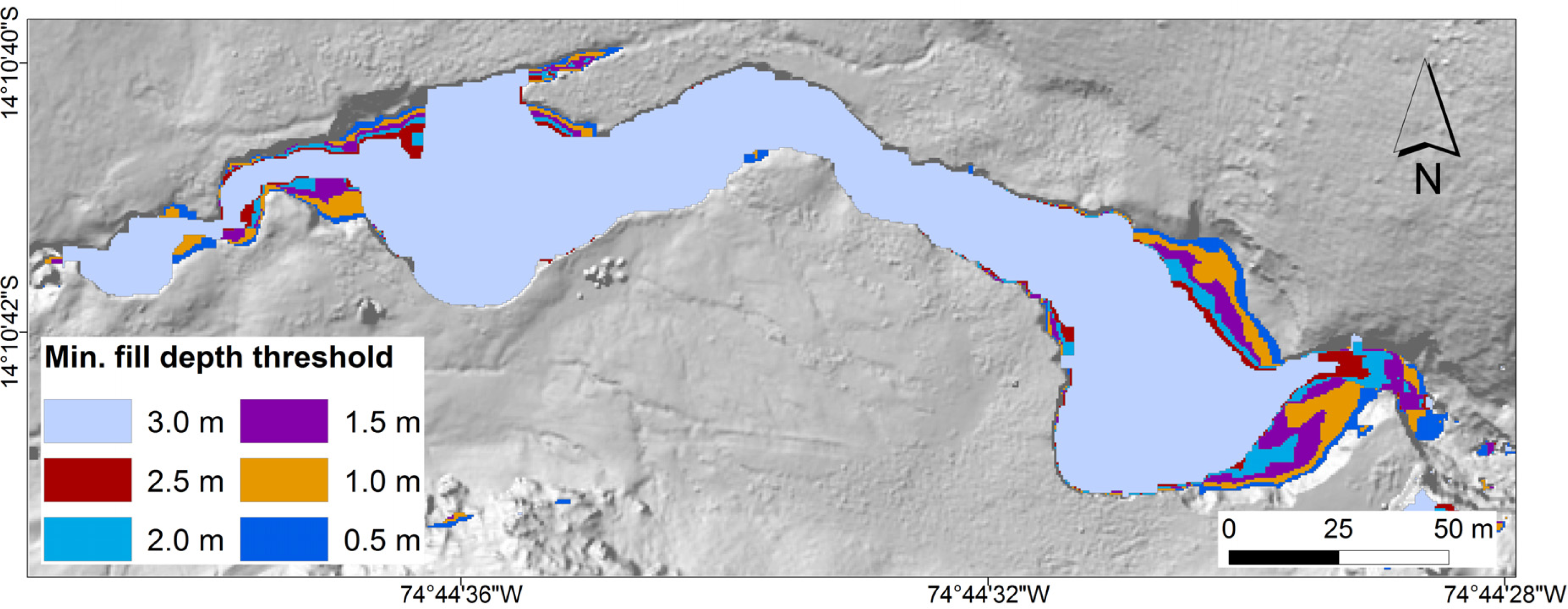
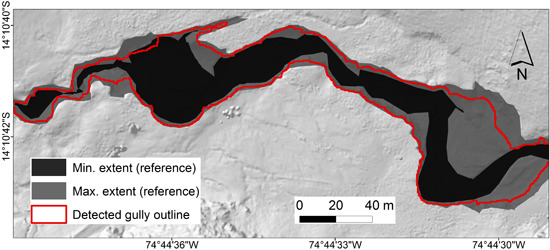
Automatic geomorphological mapping results may differ strongly from manual digitization. In order to compare and evaluate the proposed method, the approach of [
20] is applied, where a rich reference dataset is produced through manual digitization based on shaded reliefs of the LiDAR DTM. The operators were asked to digitize the outline of the gully as polygon feature. Nine reference datasets are available. The automatic delineation is performed 6 times with varying fill depth thresholds of 0.5 m, 1.0 m, 1.5 m, 2.0 m, 2.5 m, and 3.0 m.
First, the statistics of area values of the automatically detected polygons is analyzed regarding the effect of different fill depth thresholds. Second, the area values of the manually digitized reference polygons are investigated regarding different interpreters. Third, the automatic extraction with a fill depth threshold of 0.5 m is compared and spatially intersected with the maximum (by spatial union) and minimum polygon (by spatial intersection) of all reference datasets.
6. Conclusions and Future Work
Since gully erosion is a frequent phenomenon in highly sensitive ecosystems such as cushion peatlands, development of improved gully mapping methods and the derivation of geomorphometric parameters are essential. This paper presents the first study on automatic GIS and LiDAR-based detection and delineation of gully channels in a high altitude and remote cushion peatland in the Peruvian Andes.
The developed method uses a combination of breakline detection and sink filling based on a conditioned DTM. This is particularly beneficial in areas with smooth transitions and several small terraces depicting the border between gully channel and peatland plateau. Furthermore, the method can delineate channels even if gully bottoms have been captured only partly due to topographic occlusion of the laser scan. Fully occluded channel bottoms remain a challenge in terrestrial LiDAR data analysis, independently of the mapping method. The comparison of automatic gully extraction and manually digitized reference polygons reveals a high correspondence (93%) in polygon area values and in the spatial comparison derived by polygon intersection. The automatically derived gully delineation lies within the maximum and minimum digitized extents.
The introduced multi-step GIS workflow generates various results that can serve as input for multitemporal monitoring and gully system modeling. Results include the thalweg, medial axis, gully delineation and several geomorphometric channel parameters along the channel course (e.g., width, depth and cross-sectional area). In principle, the workflow can be transferred to other study areas and input DTMs with the necessity of tuning algorithm parameters and thresholds.
Future work will concentrate on the investigation of optimizing terrestrial LiDAR data acquisition for multitemporal gully channel monitoring by setting up guiding principles for field surveys. The impact of scan geometry, point sampling density and DTM resolution on gully delineation accuracy and morphometric parameters will be assessed. The full potential of TLS for cushion peatland studies is still underexploited. Radiometric backscatter values provided by full-waveform TLS offer promising complementary information to monitor geomorphology and also vegetation in cushion peatlands. Furthermore, future research should include the complementary advantages of multi-source 3D sensing, such as combining terrestrial LiDAR to capture steep slopes with airborne 3D data acquisition (e.g., UAV-based) in order to achieve a complete morphological shape of the objects of interest.