1. Introduction and System Overview
The Unmanned Systems Laboratory (USL) at Virginia Tech has developed a number of systems to facilitate rapid and safe response to an explosive event, specifically one involving the dispersal of radioactive material. In the aftermath of a serious accident, such as a nuclear power plant meltdown, response teams must quickly assess the situation to determine effective safety zones and begin evaluating both the causes of and possible responses to the disaster. The danger to personnel in such a situation suggests the use of autonomous robots to perform the initial exploration, driving the development of unmanned aerial vehicles (UAVs) carrying arrays of sensors to perform these dangerous, time-critical tasks.
Obtaining situational awareness of the post-event environment requires mapping the radiation distribution of the area and localization sources of high radioactive intensity. Conventional systems for these tasks require large, heavy, expensive equipment that necessitate the use of a full-size helicopter instead of an inexpensive, easily transportable UAV. Therefore, the USL has developed a sensing system to fit within the constraints of a small helicopter UAV platform and still complete the required mapping and localization tasks.
The complete autonomous aerial response system is shown in
Figure 1. Based on the Aeroscout B1-100 helicopter platform, this sensor system weighs 20 kg and has been designed for hardware and software modularity, which allows the system or any of its components to be installed and flown on any similar aircraft. To discover the radiation distribution of the area and localize the sources of dangerous radiation, this system employs a lightweight single-crystal radiation detector as one of its primary components, discussed in more detail in Section 2.1. In addition to this detector, the sensing system also features a stereovision system to generate terrain maps of a region of interest, a DST OTUS-L170 Gimbal camera with laser range finding functionality to geo-locate points of interest, and a Cobham NETNode COFDM radio to provide this functionality at a maximum range of seven kilometers in non-line-of-sight scenarios. In this system, an on-board generator powers the sensing system components and lithium-polymer batteries power the flight controller and communications radio.
This paper examines the utilization of an inexpensive radiation detector with novel algorithms to quickly and efficiently provide situational awareness about the radiation content of an area to response personnel. Because safety is paramount, establishing a perimeter beyond which personnel may safely work is most important. For response purposes, and especially in preparation for ingress to collect and dispose of hazardous material, accurately estimating the locations of high-intensity sources is the primary focus. The second algorithm presented in this paper opportunistically provides an estimate of the number of point sources present, though the accuracy of this estimate is of lower priority. With this low-weight, low-cost, expendable system, these personnel can rapidly acquire the information they need to plan effective response operations.
2. Autonomous Radiation Mapping
While the algorithms presented herein suffice to localize and partially map radiation sources, there exist two substantial areas of expansion explored by the USL that are outside the scope of this paper. The addition of terrain information to this system provides necessary corrections, especially when the terrain varies widely from flat; the USL system employs stereovision to develop terrain maps on the fly to aid the radiation detection algorithms. As the system collects radiation data, it generates a very sparse, irregular map of the data. Spatial deconvolution methods developed by colleagues of the USL can resolve the distribution with greater detail, so the complete system can provide not only precise point source locations but also a radiation map of the surrounding area.
This section comprises three major topics: an overview of the radiation detection system and radiation detection methodologies in general; an exhaustive Bayesian method for very accurate detection of a single source; and a more straightforward contour analysis method for localization of an arbitrary number of sources.
2.1. Radiation Detection System
The small size of the unmanned platform limits the payload weight capacity, which influences the complexities and the capabilities of the detector used. The detector employed in this system consists of a sodium-iodide scintillating crystal to convert gamma rays to visible light photons, a massive photomultiplier to amplify flashes in the crystal to voltage levels appropriate for traditional electronics, and an embedded computer to translate the analog signal to spectral information and communicate with a ground station computer. The detector returns the integrated number of counts over a one-second period. As a consequence of the nonnegligible integration period, this paper assumes that all counts returned for a period occurred at the detector’s location at the end of that period. For the purposes of this paper, the crystal is assumed to be a sphere; at the altitudes in question, its inherent directionality is negligible.
2.2. Radiation Detection Background
Because of the importance of responding appropriately and quickly to nuclear material dispersion, significant research has been done in the area of point source detection and localization. The field of radiation detection can be roughly divided into two major sub-topics, focusing on either localization or mapping. In general, localization work addresses the problem of finding a point source of radiation using the overlaying radiation distribution as a guide in the search. Radiation mapping, conversely, usually cares little about individual sources and seeks instead to generate a complete map of an area.
Before beginning any kind of radiation localization algorithm development, it is important to understand the nature of radioactive decay. As a radioactive isotope decays, it emits a variety of types of radiation, including alpha particles (
), beta particles (
β−), X-rays, and gamma rays. Unfortunately for detection purposes, alpha particles, beta particles, and X-rays suffer from self-absorption within the source, resulting in different emission characteristics for different source shapes. Therefore, radiation detection instruments rely on impingement of gamma rays [
1].
When a gamma ray intersects with a scintillator, such as the NaI scintillator in the USL’s radiation detector, one of three types of interaction occur: (1) a photoelectric interaction, where a photoelectron absorbs the energy of the gamma ray and emits a visible-light photon; (2) a Compton interaction, in which only a part of the gamma ray’s energy is absorbed and re-emitted as visible light, and a weaker gamma ray escapes the detector; or (3) a Compton interaction followed by a photoelectric interaction. Because both events in (3) occur within a single detection cycle, both (1) and (3) record the correct energy for the gamma ray. Type (2) interactions result in one or more low-energy detection events; these contribute to the gross gamma ray count but not to the correct energy peak.
A radiation detector records all of the interactions that take place within some period of time—in the USL detector, one second—and reports the total number of interactions (hereafter referred to as “counts”) as well as an energy spectrum. The algorithms in this paper utilize only the gross count, though if the isotope of the desired point source is known, the energy range used may be narrowed and the same techniques may be used.
The rate thus reported by the instrument depends on the intensity of the radiation source and its distance from the instrument. This dependency exhibits the expected inverse-square relationship and can be expressed as
where
I is the intensity of the source, (
xk, yk, zk) is the position of detector
k, (
x0, y0, z0) is the position of the source, and
λb is the background intensity at the measurement point. All measurements in this paper assume a constant altitude difference, so
zk −
z0 =
C.
The observation of nuclear decay events is appropriately modeled by the Poisson distribution [
1]. The number of counts received within a certain time period is therefore drawn from a Poisson distribution with argument
λ =
I, where
I is the average number of counts for that period of time. The discrete probability of measuring exactly
k counts from a source with
λ average counts is therefore given by the following equation:
It is useful to note that as λ becomes large, the Poisson distribution approximates the Gaussian distribution (with μ = σ2 = λ) on which many recursive Bayesian estimators (RBEs) rely.
2.3. Prior Work in Radiation Source Localization
Previous attempts at radioactive point source localization make several assumptions or exceed the constraints imposed on the USL’s mission. Using a concept familiar from global positioning system calculations, Howse
et al. evaluate level curves of potential source locations for each of four detectors placed in the corners of a room and take their intersection points as the most likely locations for the sources [
2]. They use a recursive nonlinear least squares optimization algorithm to reconcile sensor estimates of the source location into a single position estimate. The researchers assume that the intensity of their Cesium-137 source is known
a priori and successfully track the source in real time within an error of, on average, one foot, in a roughly 50 × 30 ft room.
When the trajectory of a source, but not its intensity, is known, an array of sensors may be used to detect the presence or absence of radioactive material, such as in [
3]. Brennan
et al. characterize the bounds of material detection using a network of sensors with known but randomized locations and find that real-time Bayesian classification algorithms are feasible and accurate in networks with fewer than ten nodes.
The nonlinear, non-Gaussian nature of radioactive decay suggests that the most appropriate Bayesian algorithm must go beyond the standard Kalman filter. It is tempting simply to attempt to linearize the model in the style of the extended Kalman filter (EKF), but Muske and Howse found that the nature of the nonlinearities inherent in the model can drive at least the EKF unstable [
4]. At least part of this instability results from the highly non-Gaussian shape of the Poisson model that describes radioactive sources at low count rates.
In the previous cases, either the number of sources, the intensity of the sources, or the trajectory of the source is known and multiple radiation sensors are used to perform estimation. As the proposed mission of this paper has none of those luxuries, more relevant research is found in Morelande
et al., which evaluates two methods of simultaneously estimating the number of sources present and their locations and intensities [
5]. In the first case, the maximum likelihood estimator (MLE) is used to find the source positions and intensities and a generalized maximum likelihood rule chooses the number of sources. The second technique estimates parameter values with a Bayesian algorithm very common in particle filter applications, known as importance sampling with progressive correction. The paper concludes that the MLE technique successfully estimates parameters for zero, one, or two sources, but fails when a third source is introduced, while the Bayesian method performs well in all scenarios.
The preceding work suggests that the Bayesian technique to be used must be at least as powerful in the face of nonlinearity and non-Gaussian distributions as the particle filter. Focusing again on the case in which the number and intensity of the sources are known, Brewer uses the USL platform and a particle filter to successfully localize a single point source within a 250 × 250 m box [
6]. The algorithms presented in this paper relax both assumptions Brewer makes about prior knowledge available to the algorithm; they also extend the search area, increase estimation accuracy, and decrease estimation time.
3. Recursive Bayesian Estimation Method
The grid-based RBE method is in some ways a “regression” from the particle-filtering method that solves some problems while introducing others. Notably, it suffers from the “curse of dimensionality”, where an increase in any dimension of the search space results in an exponential increase in the time and memory required by the search process. The problems solved, however, are those of heuristics: where a particle filter must be tuned in terms of collapse rate, degeneracy, and redistribution, the grid-based search avoids moving particles at all in favor of static grid points. Therefore, no tuning is necessary and the problem may be approached without reservation or concern for tuning parameters. With even inexpensive computers, now containing sufficiently powerful processors, and efficient matrix multiplication and convolution algorithms implemented in environments such as Matlab, a grid-based search is made possible in real time on commodity hardware.
The basic operation of a recursive Bayesian estimator is discussed in detail in literature [
7], so this section highlights only the specific operation of this type of RBE in the context of localizing a radioactive source. To employ a grid-based RBE, a search field must be selected and discretized into a number of grid cells. The grid resolution should be chosen according to the needs of the search (for example, if the source is thought to be on a vehicle, centimeter accuracy is unnecessary, as an estimate within two meters will effectively localize the vehicle) and the available computational power.
3.1. Localization Algorithm
The prior is drawn from the uniform distribution such that the sum is 1; that is,
With the prior grid established,
Algorithm 1 shows the process of localizing the source. Note that the detection model used for all simulations in this section,
getS
ourceC
ounts, is a procedure to estimate the mean number of counts expected to be observed given a sensor location and the location, isotope, and activity of the source. The procedures
poisspdf and
poisscdf return the probability distribution function (PDF) and cumulative distribution function (CDF), respectively, of the Poisson distribution given a value
x and Poisson parameter
λ.
At each iteration (which occurs each time a new observation is available from the radiation detector, or when the previous iteration concludes, whichever comes second), the observation is checked against a known background count level for the area of interest and altitude of the sensor (line 3). If the observation is higher than the background, it is assumed the source has been detected. In this case, the expected number of counts for each grid cell, assuming the source is in that cell, is calculated (line 5). The likelihood that the source is in that cell is then the probability that the true observation was drawn from a Poisson distribution with a mean of the expected counts for that cell (line 6).
If the observed count level is less than or equal to the background count level, the source is assumed not to have been observed. The expected count level for each cell is again computed, but the next calculation is different. Because the source was not detected, the likelihood is computed by the information provided by that fact. Simply, if the sensor did not detect the source, the source is most likely not in a cell within the maximum detection range of the sensor. The likelihood for those cells is therefore set very low, while likelihood for all other cells is set at or close to one to avoid changing the prior value when no new information is available. This calculation is accomplished by computing the probability of detection for each cell, which is the probability that the observation would be less than or equal to the background count level if the source were in fact in that cell (line 11).
Algorithm 1.
2-D Grid-Based RBE Localization
Algorithm 1.
2-D Grid-Based RBE Localization
| repeat |
| observedCounts ← current observation |
| if observedCounts > background then {the source is detected} |
| for all cell ∈ grid do |
| 5: | expectedCounts ← getSourceCounts (sensor, cell) |
| cellLikelihood ← poisspdf (x = observedCounts, λ = expectedCounts) |
| end for |
| else {the source is not detected} |
| for all cell ∈ grid do |
| 10: | expectedCounts ← getSourceCounts (sensor, cell) |
| probabilityOfDetection ← 1 − poisscdf(x = background, λ = expectedCounts) |
| cellLikelihood ← 1 − probabilityOfDetection |
| end for |
| end if |
| 15: | prior ← prior · gridLikelihood {update prior} |
| {normalize prior to PDF |
| confidence ← max (prior) |
| sensor ← moveSensor (sensor, target) |
| until confidence ≥ 90% |
The likelihood is one minus that value (line 12), as shown by examining the extreme values. If the probability of detection for a cell is 1, the sensor definitely would have detected a source in that cell; because it did not, the source is definitely not in that cell, so the likelihood is 0. If the probability of detection for a cell is 0, the sensor could never have detected a source in that cell; because it did not detect the source, it has no information about the presence or absence of a source in that cell, so the likelihood is 1.
The prior is updated by the likelihood grid and re-normalized so it remains a PDF. Because the value for each cell in the prior is the probability that the source is in that cell, the cell with the highest value is the most likely location for the source given the information collected so far. That cell’s probability is also the algorithm’s confidence in its estimate: because the sum of all the cells is 1, a low value indicates either a few other cells with similarly high probabilities or many cells with lower, but non-zero, probabilities. The former scenario suggests several likely locations for the source; the latter indicates a lack of precision, or “fuzziness,” in the estimate. Further observations will correct both issues and increase the confidence calculated by the algorithm.
With a mobile sensor, it is desirable to move the sensor after each iteration in a manner that maximizes the information gained in the next iteration. It is intuitive that moving orthogonally, in some sense, to the source estimate should accomplish this improvement. In addition, it is easily observed that a sensor moving along a straight line can create “ghost” estimates, as a nondirectional sensor cannot distinguish between its left side and its right. Moving orthogonally to the vector between the sensor and the source estimate maximizes the difference between the likelihoods at the positions of the true and “ghost” estimates; this motion is equivalent to moving along a path tangent to the circle centered at the source estimate and passing through the sensor position.
3.2. Grid-Based Localization Results
In the absence of availability of unshielded radioactive sources against which to test this algorithm, a stochastic simulation was developed to test the algorithm against randomized source locations and initial sensor positions. In addition, the same trials were carried out for several different isotopes: 75Se at 1.7 Ci, 60Co at 0.3 Ci (about half as strong as the selenium source), and 192Ir at 6.7 Ci (about twice as strong as the selenium source). The background radiation detected by the sensor was set at a constant 1,000 counts, a reasonable average value for an open field in southwest Virginia. For all trials, the field was a 160,000-square-meter area with a resolution of 1 m for a total of 160,801 grid cells. The source was randomly placed exactly on a grid cell within a 100 m radius of the center to ensure detection during the localization flight and the sensor was initially located randomly without restriction within the search area. The sensor velocity was limited to 4 m/s, which is the maximum horizontal velocity of the Aeroscout B1-100 in an assisted stability flight mode. The helicopter can move at 10 m/s straight forward, but in these simulations, it was allowed to move in any direction, necessitating the constraint. The sensor altitude was maintained at 60 m for all simulations.
Of interest in these simulations is the number of iterations required to completely localize the source after the source is initially detected. “Completely localize” in this case is defined as having greater than 90% confidence in the solution, a situation guaranteed in these simulations by placing the source exactly in a grid cell. A real localization flight would not have knowledge of the source’s true location, so it could not check its error and would have to rely on the confidence measure; however, simulation allows error calculation, so those results are reported as well. The number of iterations between the beginning of the search and the detection of the source is irrelevant to the analysis of the operation of the filter itself.
The simulation was run 500 times for each isotope and analysis of the results appears in
Table 1 for iterations from detection to high confidence (
>90%) and from detection to zero error (where “zero error” is defined as the minimum error possible given the grid resolution). Because the initial sensor and source locations in the simulation were completely randomized, occasionally the sensor started within detection range of the source. The data for these cases is not reported in the tables because initial detection provides a significant advantage over searching for the source. In these trials, the advantage has a mean of 4.66 iterations. The trials analyzed here therefore provide the most “fair” comparisons between trials.
In almost 1200 simulations, none took more than 38 iterations between initially detecting a source and localizing it to a very high level of confidence; most (75%) took 28 or fewer iterations. In the real detector, these iterations occur at 1 Hz, so most localization would occur within 30 s of detection. The most important observation from the statistics presented is this: attaining zero error takes many fewer iterations than achieving 90% confidence in the position estimate. In fact, zero error is always attained before 90% confidence. This relationship makes intuitive sense: if the correct position has p > 0.5, it is guaranteed to be the reported estimate (because Σi,j pi,j = 1), but raising that confidence to p = 0.9 may take many more iterations. As a result, the two events may occur simultaneously, but it is guaranteed that because of this relationship, once the algorithm declares itself finished, the error is zero. The results of these simulations demonstrate that the algorithm is both very fast and very accurate.
Recall that these simulations require prior knowledge of the isotope and activity of the source and that only one source exists for each trial. The contour mapping technique removes these constraints.
4. Radiation Contour Mapping
Removing the prior knowledge constraints imposed by the computation requirements of recursive Bayesian estimation algorithms requires completely re-posing the problem. Instead of considering the localization of a point source via estimating its effects and calculating probabilities, the techniques described in this chapter utilize a mapping approach. Assuming no prior knowledge of the situation dictates an algorithm that intelligently observes the area and draws conclusions about the presence or absence of radioactive sources based on the resulting map. This approach requires three basic steps, as detailed in this subsection: initially locating a particular level set of radiation contours; following the contour to obtain a useful map of the area; and translating the resulting map into source position estimates.
4.1. Algorithm Overview
Before exploring the steps of this algorithm individually, it will be helpful to summarize its operation. The contour analysis localization algorithm, as indicated by its name, operates by mapping level sets of radiation counts and analyzing them to localize radioactive sources.
Consider the field of radioactive intensity created by the presence of one or more radioactive sources in an area. Just as a topographical map presents elevation contours measured in meters, this radiation field exhibits similar level sets in radiation intensity measured in counts per second. Under the assumption that air is a homogeneous medium (changes in the density of air can invalidate this assumption, especially in the presence of changing humidity, differing air pressure as altitude increases, or thermoclines), level contours of radioactive intensity form perfect concentric spheres centered on the center of mass of the source. The intersection of that sphere with a plane, in this case the plane of constant altitude in which the sensor travels, is therefore a perfect circle. Accurately tracing that circle would reveal the location of the source at the circle’s horizontal center. Because the relationship between distance and received intensity is known (
Equation (1)), if the received intensity at each point on the circle is known and constant, the intensity of the source may also be estimated.
Adding additional sources to the first changes the contour shape predictably. Specifically, because the contribution from each source is perfectly spherical (assuming a homogeneous medium), the combined contour can be considered as the sum of those circles with some distortion of each circle by the contribution of the other source. The amount of distortion varies from zero for relatively weak sources far away from each other to intractably extreme for sources of similar positions or extremely disparate magnitudes. (The more intense source will “shadow” the smaller source entirely, making detection extremely difficult or impossible. Changing the altitude of the search will change the shape of the contour and, if the sensor is brought sufficiently close to one source, localization may become possible again.)
If the source is not a point source, but is instead an extended source composed of radioactive material spread over several square meters, the traced contours would become less clear. While no simulations were done using extended sources, a similar amount of radioactive material spread over a small area relative to the search area should provide similar results. It is expected that the position results would be less precise, but a larger source requires less precision to locate accurately; the estimated source strength would be incorrect for a point source, but because the actual received counts would still be accurate, a safety perimeter could still be properly established with no additional computation. A source so spread out as to be detected as multiple sources should not pose additional difficulties; the source count would be too high, but the location estimates would still give valid locations for radioactive material.
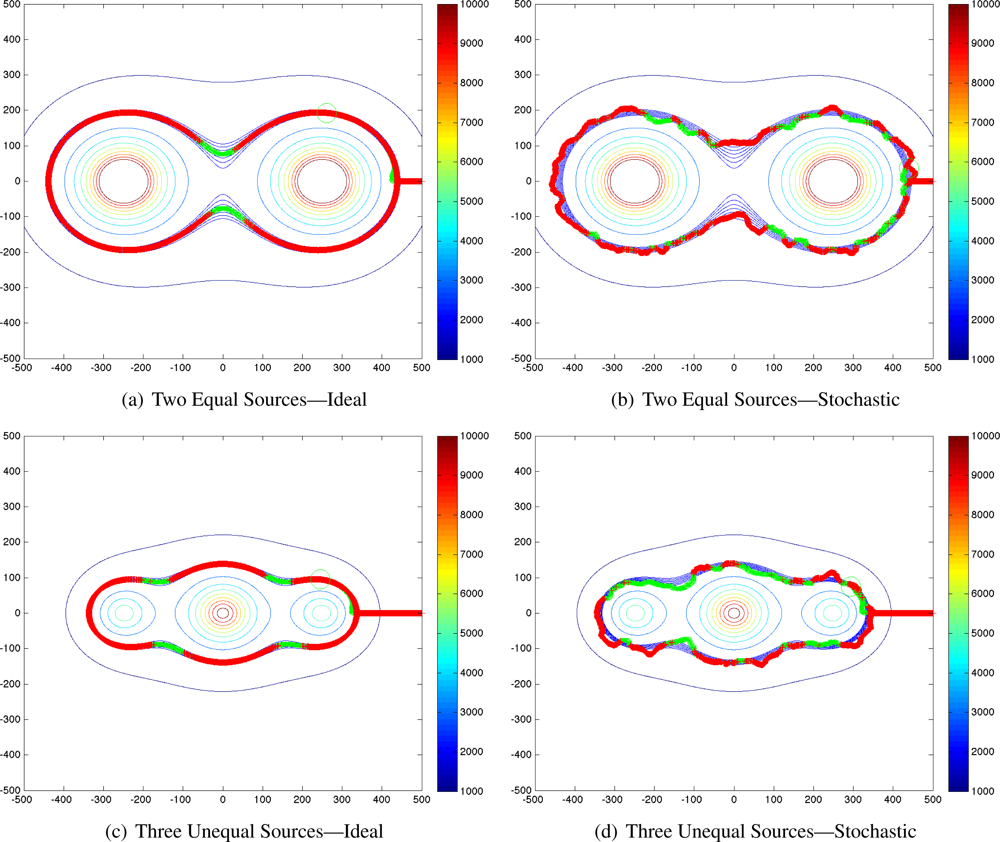
Five combinations of radioactive sources were simulated using generic sources with strength measured in received counts at 60 m. The combinations are listed in
Table 2 and their contours are shown in
Figure 2.
All the contours presented in
Figure 2 are as seen by a sensor at a constant altitude of 60 m. For comparison among the source combinations, the outermost contour in each image is 1,000 counts, and the next inner contour is 2,000 counts, but the remainder (all interior contours) represent different count levels for each combination.
Though this analysis technique removes the major constraints on source localization [the limit of one source and the need for prior knowledge of the source’s strength (and by extension, its isotope)], one (weak) requirement for prior knowledge remains. Because the algorithm maps a particular contour level, that contour level must be chosen somehow. The choice of contour level has a great effect on the shape of the contour in multi-source situations, as easily seen in
Figure 2(b–d).
4.2. Contour Detection
Because of the time-limited nature of the mission prescribed for this system, rapidly detecting the designated contour level is a necessity. This task comprises searching the area of interest using the most efficient flight path in terms of both fuel and time. Both requirements suggest using the vehicle’s maximum speed, which is possible only when moving forward. Maintaining this speed requires moving in large, smooth curves instead of more traditional patterns such as the lawnmower coverage pattern and the ladder search pattern. The obvious choice of path resulting from these considerations is a spiral; specifically, an Archimedean spiral. Parameterized by
the Archimedean spiral maintains a constant separation between its rings, ideal for a search pattern. The spiral shape also allows the helicopter to move in large, sweeping curves and thereby maintain a high forward velocity.
To implement this search path, the maximum detection range of the sensor for the desired contour intensity is first calculated. The distance between the arms of the spiral is slightly less than twice this distance—uncertainty grows at the edge of the detection range, so the swaths will overlap at the edges.
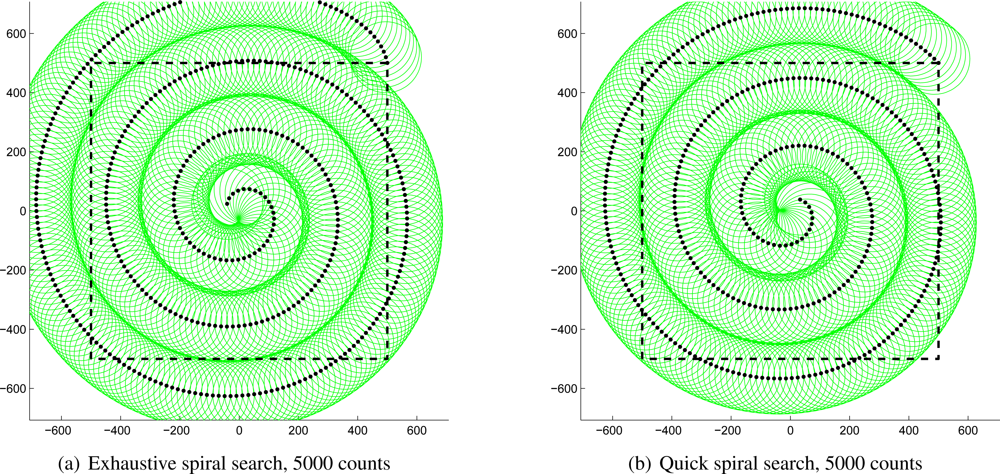
As an example,
Figure 3(a) shows a complete spiral path generated with this algorithm with the helicopter moving at 10 m/s attempting to detect a 5,000-count source against 1,000-count background radiation on a one-square-kilometer field. The black dots show the path of the helicopter, which starts at the top-right corner of the square; the green circles show the detection range of the sensor at each position; and the dashed square denotes the boundaries of the field of interest. Note that the entire field of interest has been observed at some point and almost all of it has been observed for several seconds. As mentioned above, the edges of the circles overlap along the curves of the spiral to make up for the lack of certainty at the edges of the detection range. The entire spiral requires 812 s, or about 13.5 min, to search the entire area; if a source existed in the area, the spiral would have terminated when the source was first detected and the contour would then be followed as described below.
It is clear that the path in
Figure 3(a) is not perfectly efficient. In fact, the first several locations do not observe the area of interest at all; this shortcoming is a consequence of requiring that 100% of the field be observed at some point. Relaxing that restriction very slightly permits the path shown in
Figure 3(b), which is the same scenario without the absolute coverage requirement. Note the small areas on the bottom-right and top-right of the square that are never observed. The benefit of allowing the algorithm to ignore those small areas is that the incomplete coverage spiral can be completed in only 694 s, or about 11.5 min, nearly two minutes faster than the first path above. A contour would have to be extremely small to exist within the area of interest and avoid detection; such a weak source would not likely be detected above background radiation. Note, however, that the entire contour need not exist within the prescribed boundaries. If any part of it does, the contour mapping algorithm will follow the entire contour irrespective of its size or position.
4.3. Contour Following
Once the specified contour level has been detected, the helicopter must map the entire contour for analysis. Detection is defined as measuring at least
counts, where λd is the desired contour count level. The adjustment is necessary to ensure the algorithm begins on the inside of the contour and it serves as a safeguard against receiving an anomalously-high count and beginning the contour mapping prematurely.
The contour following algorithm operates in a very simple manner: if a measured count is greater than λd, the helicopter turns to the right; if a measured count is less than λd, the helicopter turns to the left. The result is that the helicopter follows the contour in a counterclockwise direction. The forward speed of the helicopter is set at the beginning of the test, and should be adjusted by the operator for the size of the search area, the desired speed of the search, and the desired accuracy and completeness of the finished contour. A faster search will result in less accuracy in the analysis step, but some loss of accuracy may be acceptable for the time saved. A large search area or physically large contours (a low λd for a strong source, for example) allow much higher forward speeds, while tight contours (relatively high λd) require a slower scan to follow the contour properly. The limiting factor from the helicopter for these considerations is the maximum turn rate. The Aeroscout B1-100 has a maximum yaw rate of 30°/s in its assisted stability flight mode, but such a high yaw rate coupled with high forward speeds may result in sideslip, which would draw the vehicle off the contour and result in a lower turn rate than the commanded yaw rate. For this reason, yaw rates in this chapter are limited to 15°/s, which simulations have shown can be translated directly into turn rates.
The helicopter’s turn rate is determined by a proportional-integral-derivative (PID) controller that takes as input the latest received count rate
ck and the contour level
λd and returns the desired helicopter yaw rate
ψd:
where
kp,
kd, and
ki are PID controller constants, derived below. Proportional error differs from the simple error from
λd to adjust for the 1
/R2 relationship of radiation emission intensity to distance. For extremely high contour levels, an error of as little as 1 m may result in hundreds or thousands of counts of error; an extreme turn will take the vehicle off the contour. Conversely, for very low contour levels, a displacement of several meters may result in tens of counts of error, so the helicopter must react quickly.
The PID constants
kp,
kd, and
ki are modified by
σλ so that the same constants may be used for any desired contour level. An unconstrained nonlinear optimization method was used to generate error-optimal PID constants using the 2,000-count contour of
Figure 2(d) with an update rate of 1 Hz at 1 m/s. The resulting values are presented in
Table 3.
The controller output
ψd undergoes several checks before it is applied to the helicopter. It is first limited to the maximum yaw rate
ψmax:
In addition to constraining the yaw for any individual iteration, the total amount of consecutive yaw allowed is also limited to 180°. This restriction prevents the helicopter, in extreme circumstances, from turning in circles either inside or outside the contour. The vehicle may not execute more than 180° of yaw without crossing the contour; as a consequence, the helicopter must always re-intersect the contour.
To determine when the contour has been completed, the helicopter waits until it has completed at least 180° of yaw from its heading when it first encountered the contour, and then stops when it has achieved 360°, a full rotation. Because all radiation contours are known to be closed, these conditions must be met for every contour eventually.
4.4. Contour Following Results
To examine the efficacy of the contour-following algorithm, simulations were run where the measured counts were calculated exactly according to
Equation (1) and where the counts were drawn from the Poisson distribution as described above. The ideal simulations were performed with a yaw rate limit of 6°/s to maintain precise flight paths at high speeds; the stochastic simulations relaxed the limit to 15°/s to give the controller more flexibility to correct for widely-varying responses.
Representative results of the simulations are given in
Figure 4, comparing the ideal contour following and the stochastic version.
4.5. Source Localization
Once a level contour of radiation counts has been mapped, the positions and intensities of the radioactive sources that generated the contour may be estimated. The Hough transform, traditionally used for line detection but here adapted to detect circles, is the central algorithm in this step of the process. The procedure outline is presented as
Algorithm 2.
The contour points are first converted into a binary image to simplify later calculations (line 1). Because the Hough transform can be extremely computationally intensive, the image may be downsampled to halve or quarter the resolution and correspondingly decrease computation time. Defining the search space (the set of (x, y, radius) tuplets to analyze) provides another opportunity to save cycles. This analysis is based on the above contour mapping, so each image contains an entire contour; therefore, the maximum radius of any circle contained in the image must be no larger than half the size of the smaller dimension of the image. Further, a circle with a radius less than about one-eighth the smaller dimension of the image represents a source that is almost always too weak to localize accurately, providing a convenient radial lower bound.
Algorithm 2.
Hough Transform-based Contour Analysis
Algorithm 2.
Hough Transform-based Contour Analysis
| cImage ← getImage(contourPoints) |
| cImage ← downsample(cImage) |
| |
| |
| 5: | cand ← houghCircles(cImage; minRadius; maxRadius) |
| cand ← deleteInvalidCandidates(cand; cImage) |
| cand ← upsample(cand) |
| while length(cand) > 0 do |
| bestCand ← cand(cand.c = = max(cand.c)) |
| 10: | for all cand s.t. cand:center is within bestCand:radius of bestCand:center do |
| delete from cand |
| end for |
| end while |
| repeat |
| 15: | for all est ∈ estimates do |
| est.intensity ← estimateIntensity(est) |
| estimates ← adjustCounts(estimates) |
| end for |
| maxChange ← max(estimates:adjustment) |
| 20: | until maxChange = = 0 |
Given these constraints, the image is analyzed with the Hough transform, returning a set of candidate estimates. When the traced contour is not strictly convex (that is, in almost every possible combination of two or more interacting sources), some of the estimated centers will be outside the contour. They are obviously invalid, so the procedure deleteInvalidCandidates (line 6) eliminates them. Because the Hough transform returns all possible circles within its constraints, the list of candidates is usually long; the algorithm therefore analyzes the initial transform’s confidence results and further eliminates all but the most likely circles.
Two sources that fall within the contour radius of each other are usually indistinguishable with the given contour. (This assumption does not hold true in all cases, but the vast majority of source combinations validate it.) Holding this assumption true suggests the process by which spurious source estimates are eliminated: the most-likely candidate is accepted and all nearby candidates are eliminated (line 8).
Given a list of source estimates, the intensity may be estimated as suggested previously. The equation for received intensity,
Equation (1), changes form to accommodate the different definition of source intensity in this chapter. Specifically, because source intensity is defined as the received counts at 60 m, the equation may be rearranged as follows to solve for
Isource if
rsource is redefined as the radius associated with a source estimate:
In the presence of more than one source, each source impacts the contour at all points, requiring the compensation of each intensity estimate for each other source intensity. This algorithm, hereafter referred to as iterative intensity correction, is outlined by the loop starting at line 14. For each estimate, the intensity is initially estimated according to
Equation (3) using the original contour level for
Icontour. Once an intensity estimate is derived for a source, its effect on each of the other sources is calculated; the corrected estimate replaces
Icontour and the loop repeats until each estimate converges.
4.6. Contour-Based Localization Results
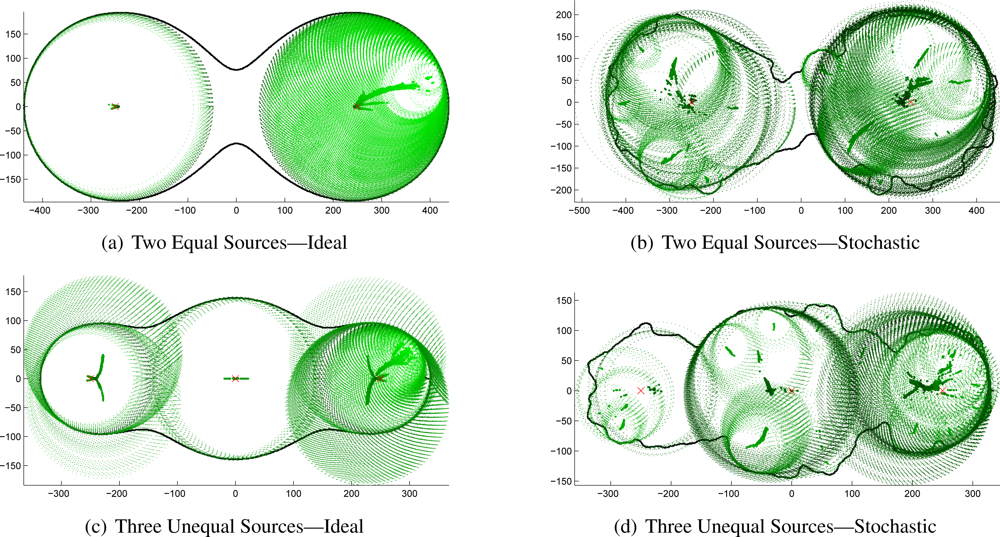
The Hough transform-based source localization algorithm presented above was applied to the previously-generated idealized and stochastic contours. The output of the Hough transform is an extremely long list of candidate source locations that must be culled to the best possible source estimates. The initial results for the three-source configuration are shown in
Figure 5 to demonstrate the problem to be solved. The thick line is the traced contour, the green dots are the centers of all the estimates returned, and the dotted green circles show the radii associated with each estimate. Darker center dots and circles indicate higher confidence. The correct source locations are shown by red “×” marks.
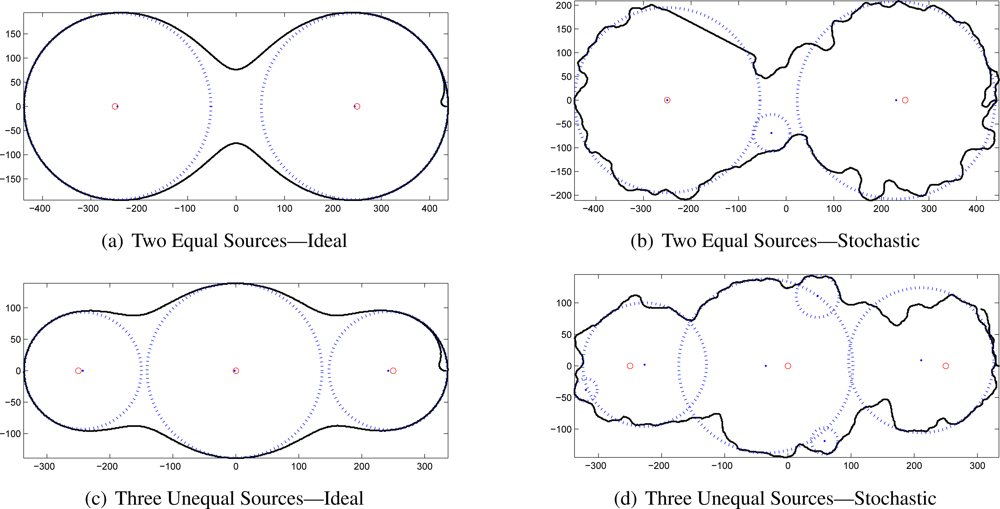
These plots reveal that even with idealized contours, the signal-to-noise ratio of the returned candidate source estimates is extremely low. Clearly, nearly all of the returned candidates must be eliminated. The remaining best-choice estimates for each of these source-combinations are shown in
Figure 6. The black line is again the contour; blue dots and circles indicate the best estimate source locations and radii; and the red circles show the true location of the targets.
Despite the relatively low quality of the traced contours, the algorithms developed above successfully localized each of the sources. In some cases, the position estimate for the stochastic case is almost as accurate as for the ideal contours. The numerical results for this analysis are presented in
Table 4 for the two equal sources and in
Table 5 for three unequal sources. (This analysis was performed for five different cases: one small source, one large source, two equal sources, two unequal sources, and three unequal sources. Only representative results, those of the third and fifth, are presented here for brevity.)
It is obvious that in the stochastic case, not all of the spurious source location estimates could be rejected. However, the tables demonstrate that the confidence estimates clearly indicate which estimates should be ignored: correct estimates have very high confidences, near 1.0, while spurious estimates have confidence well below 0.5.
While the position errors for the ideal contours are quite low, at or near zero in most cases, the errors for the stochastic contours are much higher—sometimes unusably so, as in the 40 m error for the right-hand source of three. However, the field is a square kilometer and the contour itself is nearly 700 m long. This algorithm has therefore reduced the search area from 1,000,000 m2 to just over 5000 m2, a reduction of 99.5%. The result is even more useful when determining safety perimeters for rescue personnel: slightly larger inaccuracies do not affect perimeter assignment nearly as much as search efforts. The safety zone will certainly include a buffer that will easily correct for this worst-case inaccuracy of less than 50 m.
The data also clearly show that the iterative intensity correction routine (
Algorithm 2, line 14) radically reduces error in most cases. In the case of spurious source estimates, it actually makes the estimates worse, providing an even stronger indicator of their extraneous nature. And in some cases, the improvement is extreme: the stochastic contour estimate of the intensity of the left-hand source in the three-source configuration was originally 46.7% high; it was corrected to only 6.7% high. A full statistical analysis of the position errors for both cases is shown in
Figure 7 and the combined improvements offered by the iterative correction algorithm are shown in
Table 6.
These results clearly demonstrate that the techniques presented in this chapter rapidly, effectively, and accurately localize one, two, or three sources of unknown intensity without prior knowledge of the number of sources or their strengths. The mean position error for tracing contours using realistic Poisson distribution-based simulation parameters was 17.86 m. Furthermore, the algorithms presented here estimate the source intensity with reasonable accuracy. The mean relative intensity error in the analysis of the Poisson distribution-based simulation was 15.07%, as improved from a raw estimated intensity relative error of 36.74%. These algorithms give accurate, useful information regarding the number of radioactive sources present in an area, their positions, and their intensities, without the unacceptably high computation requirements or the “curse of dimensionality” suffered by both the particle filter of Brewer and the grid-based RBE.
5. Conclusions
The localization techniques presented above provide a major component of a complete unmanned radiological disaster response system. Though the small UAV platform presents a unique set of constraints with respect to its size, payload capacity, and endurance limits, these algorithms successfully operate within them.
The first algorithm, based on the grid-based RBE method localizes a single radioactive source in less than a minute over a field 0.4 km on a side to within an arbitrary grid resolution. The second algorithm, based on a novel contour analysis technique, localizes an arbitrary number of radioactive point sources over an arbitrary field and estimates their intensity.
Both algorithms were proven in simulation, giving the results presented above. Applying appropriate statistical noise simulates the most non-ideal difference between simulation and field testing, under which conditions the algorithms still perform well, but these results should nevertheless be understood as upper bounds of algorithm performance. True field testing of this system requires a radiological source. Unfortunately, radioactive gamma ray emission does not follow the radiation pattern of a radio antenna, nor does a gamma ray detector have the directionality limitations of an electro-optical or electromagnetic sensor, so simulating a source proves very difficult. Given a sufficiently-dense mapping of a radiation field and appropriate interpolation, the algorithms could be field-tested on the system in a different location using real data collected previously. The USL has performed preliminary experiments of this type, but no complete system test with unshielded radioactive sources has been performed.
Including the other pieces of the USL system—specifically, the stereovision terrain mapping component—generalizes these algorithms to any terrain mappable by the system. Most importantly, employing the complete system including the above algorithms allows first responders to determine regions of high radiation intensity and areas to focus their response operations. In this way, response efforts can be expedited while maintaining rescue personnel safety.