Abstract
The objective of this study was to determine whether leaf area index (LAI) in temperate mixed forests is best estimated using multiple-return airborne laser scanning (lidar) data or dual-band, single-pass interferometric synthetic aperture radar data (from GeoSAR) alone, or both in combination. In situ measurements of LAI were made using the LiCor LAI-2000 Plant Canopy Analyzer on 61 plots (21 hardwood, 36 pine, 4 mixed pine hardwood; stand age ranging from 12–164 years; mean height ranging from 0.4 to 41.2 m) in the Appomattox-Buckingham State Forest, Virginia, USA. Lidar distributional metrics were calculated for all returns and for ten one meter deep crown density slices (a new metric), five above and five below the mode of the vegetation returns for each plot. GeoSAR metrics were calculated from the X-band backscatter coefficients (four looks) as well as both X- and P-band interferometric heights and magnitudes for each plot. Lidar metrics alone explained 69% of the variability in LAI, while GeoSAR metrics alone explained 52%. However, combining the lidar and GeoSAR metrics increased the R2 to 0.77 with a CV-RMSE of 0.42. This study indicates the clear potential for X-band backscatter and interferometric height (both now available from spaceborne sensors), when combined with small-footprint lidar data, to improve LAI estimation in temperate mixed forests.
1. Introduction
Leaf area index (LAI) is an important canopy descriptor used to estimate growth and productivity in forest ecosystems. Watson [1] stated one of the early definitions of LAI as the total one-sided area of leaf tissue per unit of ground surface area. Thus, LAI is a dimensionless index that represents an important method to quantify the amount of photosynthesizing tissue in forests. Leaves are radiation receivers (depending on the amount of productive leaves and their specific surface area, they absorb between 80 to 90% of the light assimilated by forests). Leaves are the main photosynthesizing organ in forest stands, thus variations in leaf production and light interception are directly related to forests growth and development. Accordingly, LAI is a key variable that can be used to monitor current forest stand growth and has become a key explanatory variable for ecosystem process models.
Remote sensing estimation of LAI has been mostly based on empirical modeling, using vegetation indices, generally developed with the spectral reflectance from the near-infrared and red wavelengths, and their correlations with ground-truth estimates. However, the use of optical imagery carries some disadvantages, as follows: (1) it is only suitable when evaluating horizontal variation; (2) optical passive sensors are unable to obtain data from the ground when it is obscured by clouds, and most importantly; (3) vegetation indices calculated using optical imagery tend to reach a saturation point when LAI values are above 3 [2–4]. This last limitation can be particularly important when estimating LAI in the eastern US hardwood and mixed forests where reported estimations have ranged from 3.9 to 7.3 [5] and from 3.5 to 5.1 [6].
Two fairly recent technologies could potentially improve the estimate of LAI in these forests where canopies can vary greatly not only horizontally but also vertically, and the likelihood of reaching a reflectance saturation point is high. Light detection and ranging (lidar) sensors measure the time between the emission and reception of laser pulses to estimate the location and height of the target feature. They thus acquire information in three dimensions (x, y, and z coordinates) and provide the means to evaluate variation across a vertical profile. Previous studies in which LAI was estimated, in mixed forests (distributed around the world) using lidar data, have reported R2’s between 0.37 and 0.93 related to a number of indices and lidar metrics. For a coniferous and mixed beech forest in Italy, the laser penetration index (LPI, taking into account the transmission of the laser beams through the canopy, as the proportion of laser pulses that hit the ground to the total number of pulses) was created explaining 89% of the variation of LAI [7]. Later, Kwak et al. [8] using the LPI and an interception index (LII) could explain 86% of the variation in a South Korean mixed forest. In Japan, using the ground fraction of returns, Sasaki et al. [9] reported an adjusted R2 of 0.80 for an evergreen and broad-leaved forest. Solberg et al. [10] reported correlations with laser penetration from 0.37 to 0.93 (depending on plot size), in a mixed forest in Norway. Hopkinson and Chasmer [11] evaluated coniferous and mixed forests in Canada, and found R2’s ranging from 0.58 to 0.78, when using either lidar returns ratios or intensity of returns ratios. In United States, Zhao and Popescu [12] found an R2 of 0.84 in a mixed hardwoods and coniferous (including plantations) from Texas, and Richardson et al. [13] reported R2 values from 0.49 to 0.66 for a Pacific Northwest mixed forest. Other efforts to estimate LAI with lidar, using different approaches than LPI and in either coniferous or hardwood forests only, have shown similar promising results [14–19]. In addition, none of these prior studies have reported a maximum LAI or saturation problem using lidar.
Dual-band interferometric synthetic aperture radar (DBInSAR) can now be collected using the geographic synthetic aperture radar (GeoSAR) airborne radar mapping system. GeoSAR acquires X-band (VV, 9.7 GHz) and P-band (HH, 0.35 GHz) simultaneously over 11 km swaths [20]. GeoSAR has emerged as a potential instrument to be used to estimate forest attributes, such as canopy height [21] and biomass [20,22]. Long wavelengths from the P-band (0.85 m) penetrate the upper canopy and can reach the ground; short wavelengths (0.03 m) from the X-band are scattered at the top of the canopy. This technology has been widely used in tropical regions where forest canopies are usually under clouds most of the year [23,24].
Previous attempts to estimate LAI using SAR (Synthetic Aperture Radar) data have found low correlations between ERS-2 (European Remote Sensing Satellite-2) SAR backscatter and LAI or biomass, but significant correlations between a green leaf biomass index (calculated using ERS-2 SAR backscatter) and LAI, in Mediterranean vegetation [25]. Sun et al. [26] evaluated the correlations of biomass with the Laser Vegetation Imaging Sensor (LVIS) and with SAR signatures. Their results showed that the predictive models that used both lidar samples and radar imagery explained between 63% and 71% of the variability in biomass. In addition, as an effort to simulate the X-band interferometric heights using airborne lidar, Solberg et al. [27] reproduced InSAR heights with an R2 of 0.78 by using a simulator that could be used for understanding how vegetation changes may affect the InSAR data. Other researchers have found saturation problems for the C-band (radar band that operates at a wavelength of 4–8 cm) backscatter with high values of LAI in tundra ecosystems and plantation forests [28,29]. Manninen et al. [30] used a C-band backscatter ratio from ENVISAT (ENVIroment SATellite)/ASAR (Advanced Synthetic Aperture Radar) in a mixed forest obtaining an RMSE of 0.27.
While these and other studies have used radar backscatter to estimate LAI, none to date has assessed the potential utility of interferometric heights for LAI estimation. Given that lidar data have been shown to enable robust LAI estimation, and both lidar and DBInSAR can be used to estimate canopy heights, we posited that the DBInSAR data from GeoSAR could be useful for remote sensing of LAI. As such, the objective of this study was to determine whether leaf area index in temperate mixed forests is best estimated using multiple-return airborne laser scanning (lidar) data or dual-band, single-pass interferometric synthetic aperture radar data (from GeoSAR) alone or both in combination.
2. Methods
2.1. Study Site
The study area was located in the Appomattox-Buckingham State Forest in Virginia, at 37°25′9″N and 78°40′30″W (Figure 1). This state forest is the largest in Virginia, covering approximately 8,094 ha. It is located within the Piedmont physiographic region. The elevation in the area ranges between 159 to 238 m, with a gentle relief often described as rolling slopes and flat terrain. The mean annual precipitation is between 78 to 120 mm; and the mean annual temperatures can vary from −4 (winter) to 31 °C (summer). The state forest is managed as multiple use, with forestry and hunting the predominant activities. It is divided in 27 compartments that include 1,244 stands. This forest is composed of coniferous, hardwoods, and mixed stands. Three pine species are present, as follows: loblolly pine (Pinus taeda L.), shortleaf pine (Pinus echinata Mill.), and Virginia pine (Pinus virginiana Mill.). Among the deciduous trees are northern red oak (Quercus rubra L.), white oak (Quercus alba L.), red maple (Acer rubrum L.), yellow poplar (Liriodendron tulipifera L.), blackgum (Nyssa sylvatica Marsh.), and American beech (Fagus grandifolia Ehrh.). The forest stands had been previously classified based on the species groups and their relative stoking [31], in six forest vegetation types: bottomland hardwoods, upland hardwoods, pine-hardwoods, loblolly pine, shortleaf pine, and Virginia pine.
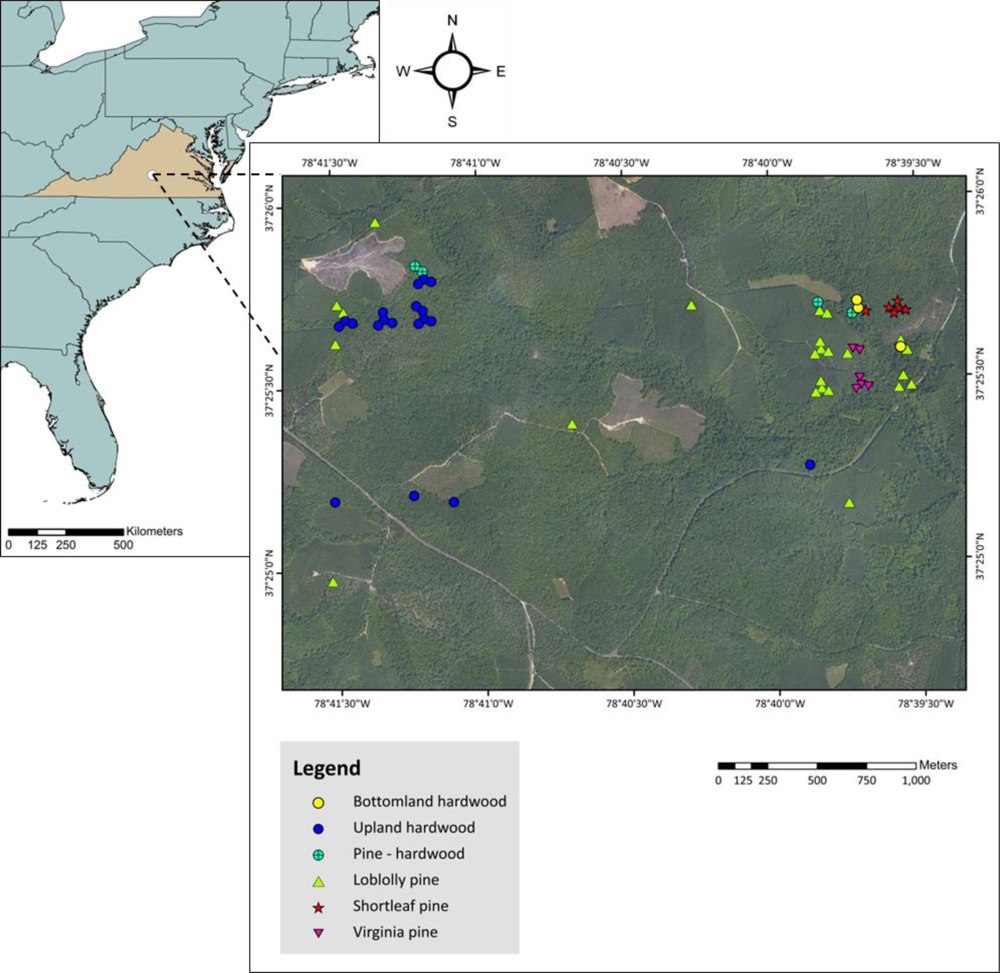
Figure 1.
Geographic distribution of plots in Appomattox Buckingham State Forest, Virginia, USA. Plots are displayed over a true color aerial photo.
The measurement plots were installed following the US National Forest Inventory and Analysis (FIA) guidelines [32] and were of two types: fixed radius plots and variable radius plots, the latter based on basal area guidelines. The fixed radius plots were installed in 1999 and the variable radius plots were installed in 2002 using a basal area factor of 10 (BAF) and following a grid of 201.17 m [33]. The plots were composed of 4 circular sub-plots (one in the center and three in a triangle shape around the center); each sub-plot has a radius of 7.32 m (for tree measurement), and they are 36.58 m apart from each other. For more details about this study design (see [34]). The center of the plots was found using GPS navigation. All plots (fixed and variable radius) were measured during the 2008 dormant season. Out of the 81 fixed radius plots initially installed, only 51 were measured for this research, since 12 of them had been harvested. Additionally, from the 219 variable radius plots already installed, only 30 could be measured, and those were distributed mainly near the access roads (Figure 1). The plots measured were distributed among 25 stands covering over 405 ha.
Total tree height (ht) and diameter at breast height (DBH) were assessed for every individual with a DBH > 2.54 cm within the measurement plots using a Haglöf Vertex hypsometer and diameter tape. A 20 m buffer was applied to each plot (from its center) to generate circular plots of 1,256.6 m2 of size.
2.2. Field Data Collection and Analysis
2.2.1. Leaf Area Measured with an Optical Sensor
Leaf area index was indirectly estimated during late summer (23–25 September 2008), using the LiCor LAI-2000 Plant Canopy Analyzer. Although, the ground data collection was undertaken in September, the vegetation was mostly green at all levels of the forest vertical profile. The LAI-2000 measures the gap fraction (the probability that a ray of light will go through the canopy without intercepting any plant element), and applies the Beer-Lambert law to estimate leaf area, assuming that the foliage elements (independent of whether they are leaves, needles or shoots) are randomly distributed, and that the leaf size is small compared to the size of the canopy. Thus, when these assumptions are not met, underestimations can occur. However, this instrument has been widely used in previous research, due to it being one of the non-destructive methods to estimate leaf area index, and due to its portability, especially when sampling plots with high amount of understory located in remote areas. Above-canopy readings were recorded remotely every 15 s by placing an instrument in an open field adjacent to the stand during the same date and time that measurements were taken inside the stand. The measurements inside the stand, below-canopy readings, were made holding the instrument at the height of 1 m facing upwards. This same procedure was repeated in every plot regardless of the presence of understory or mid-story vegetation. Due to the instrument design, measurements were taken under diffuse sky conditions to ensure that the sensor used indirect light only. Thus, measurements were taken during the dawn and pre-dusk periods, with the above instrument facing north and using a 90° view cap. Sampling points were distributed in the following manner: one reading at the center of the plot, and one reading at 5 m away from the center in each cardinal direction (north, south, east and west), for a total of 5 readings per plot. The calculation of LAI was accomplished using the FV-2000 software which averaged all the readings per plot. The canopy model used to calculate LAI was Horizontal [35]; the ring number 5 was masked to reduce the error introduced by the stem and branches of trees; and the option of skipping records with transmittance >1 was used in order to avoid bad readings that can alter the mean values of LAI per plot. The above and below canopy records were matched by time [36].
2.2.2. Lidar Data
Small footprint lidar data were acquired in late August 2008. The system was an Optech ALTM 3100 with an integrated Applanix DSS 4K × 4K DSS camera. The data have multiple returns with a sampling density of 5 pulses per square meter, with 4 or fewer returns per pulse. The scan angle was less than 15 degrees. Instrument vertical accuracy over bare ground is 15 cm, and horizontal accuracy is 0.5 m. The inverse distance weighted interpolation method was used to generate a digital elevation model (DEM) with the data classified as ground returns [34]. Vegetation returns were classified using a 1 m threshold because the instrument used to estimate LAI in situ was held at approximately 1 m above the ground. The metrics derived from the ground returns class (Gr) were: frequency (count) of returns and frequency (count) of pulses (Table 1). The metrics derived from the all returns class (All) were: frequency (count), mean height, standard deviation, coefficient of variation, minimum, maximum, percentiles (10, 20, 25, 40, 50, 75, and 90; as the height or value at which a percentage—10, 20, etc.—of the total number of returns are below that value), and frequency (count) of pulses [34,37]. The metrics derived from the vegetation returns class (Veg) were the same described for the all returns class with the addition of the mode. The distribution of intensity values (I) were described using the mean, minimum, maximum, standard deviation, and coefficient of variation. First, second, third and fourth returns were classified as such and divided by the total number of “vegetation returns” (R). The Laser Penetration Index (LPI) [38] was calculated per plot as the proportion of ground pulses to the total pulses. Density metrics (d) were calculated following [39], as the proportion of returns found on each of 10 sections equally divided within the range of heights of vegetation returns for each plot. Additionally, another set of metrics, crown density slices (Cd), was calculated using the mode value of vegetation returns. Ten 1-m sections of vegetation returns (5 above and 5 below the mode value) were classified and proportion of returns to the total number of returns, mean, standard deviation, and coefficient of variation were calculated (Figure 2).

Table 1.
Explanatory variables derived from lidar and GeoSAR. Return hag refers to the return height above the ground. Statistics in subscripts were as follows: frequency (total), mean, mode, standard deviation (stdv), coefficient of variation (cv), minimum (min), maximum (max), and height percentiles (10th, 20th, …, 90th). The metrics Grtotal, Alltotal, Vegtotal, Grreturns, Allpulses, and Vegpulses were determined for calculation of other metrics (i.e., proportions of returns), but were not used for model development.
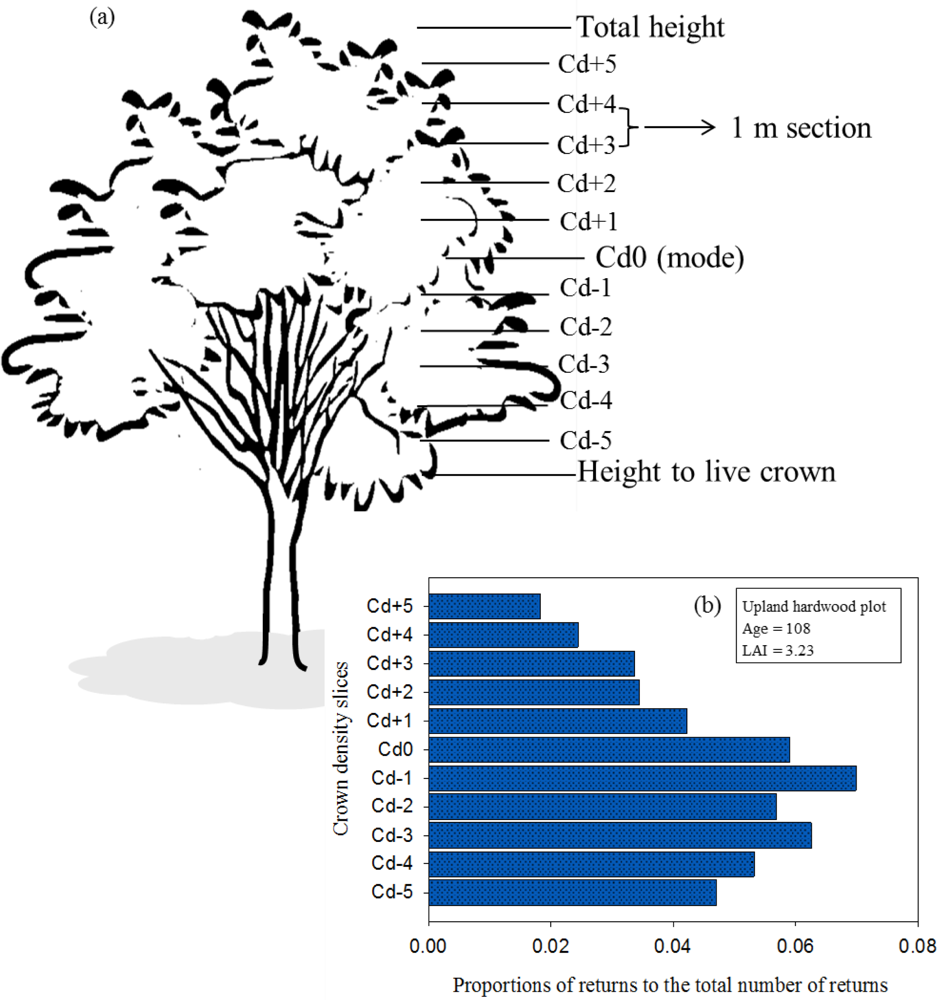
Figure 2.
(a) Hypothetical representation of crown density slices derived from lidar Vegmode value (height to live crown was not measured on the ground). Five 1-m sections above and below the mode were defined, and the descriptive statistics (i.e., frequency, mean, standard deviation, and coefficient of variation) from the returns within each section were obtained. See Table 1 for variable names and how they were calculated. (b) Crown density values for an upland hardwood plot.
Frequency of returns (count), calculated from each of the lidar data point classes, was used only to estimate other metrics, such as proportions of returns, but was not used in the development of the models (Table 1). Ground plots were overlaid on digital orthophotographs acquired at the same time as the lidar data. Sixteen plots partially encompassed roads or herbaceous areas. These plots were eliminated from the dataset.
2.2.3. GeoSAR Data
GeoSAR data were acquired in late summer 2008. The system recorded data from two microwave bands, X (VV, 9.7 GHz) with a 0.03 m wavelength and P (HH, 0.35 GHz) with a 0.85 m wavelength, in single passes. Postings from the X-band were 3 m; those from the P-band were 5 m. GeoSAR X-band interferometry yields a digital surface model (DSM) and P-band interferometry is used to create a digital elevation model (DEM). Previous research has used the difference between the DSM and DEM to create a canopy height model used to estimate forest biomass [20]. The provider (Fugro EarthData, Inc.) performed the preprocessing, including both the interferometry and generation of two orthorectified magnitude images: (1) the magnitude from bands X and P, expressed as the square root of the intensity values and (2) the sigma-0 (σ0) or backscatter coefficient from all four looks (North, South, East, West), defined as the backscatter power per unit area on the ground. Analogous to those used with lidar-derived heights and intensities, GeoSAR metrics were developed using the following approach (see also Table 1):
- In order to evaluate the vegetation height, the difference between X-band (mostly backscattered from the vegetation/canopy surface) and P-band (mostly from the ground and lower tree branches) interferometric heights was calculated. In addition, the X-band was divided by the P-band with the purpose of evaluating any other relationship between the two bands.
- The high resolution DEM created from the lidar data was used to generate the heights above ground for the X and P bands.
- No changes were made to the magnitude or the σ0 bands.
- The cell values from all the rasters created (10 in total) were extracted and the frequency, mean, standard deviation, coefficient of variation, minimum, maximum, and percentiles (10th to 90th) were calculated for all plots.
2.2.4. Statistical Analysis
A dataset of 81 plots was compiled for all lidar-derived, GeoSAR-derived and ground-truth metrics. However, after deleting plots for proximity to roads and for being outliers (but not influential), the number of plots was reduced to 61. Pearson correlation coefficients were used to evaluate relationships among lidar metrics, GeoSAR metrics and ground estimated LAI. Multiple regressions were used to fit the dataset. Best subset regression models were examined using the RSQUARE method for best subsets model identification [40]. This method generates a set of best models for each number variables (1, 2,…,6, etc.). The criterion to choose the models with the best group of variables was a combination of several conditions, as follows:
- High coefficient of determination (R2) value.
- Low residual mean square (RMSE).
- Similarity between the adjusted coefficients of determination R2adj’ and R2 values. The R2adj’ is a rescaling of R2 by degrees of freedom, hence involves the ratio of mean squares instead of sum of squares.
- Mallows’ Cp statistic values [41]. When the model is correct, the Cp is close to the number of variables in the model.
- Low values from two information criteria, the [42] Information Criterion (AIC) and [43] Bayesian Criterion (SBC). The AIC is known for its tendency to select larger subset sizes than the true model; hence the SBC was used for comparison, since it penalizes models with larger number of explanatory variables more heavily than AIC.
The best models chosen per each subset size (based on number of variables in the models) were evaluated for collinearity issues. Near-linear dependencies between the explanatory variables were evaluated using computational stability diagnostics. In order to make independent variables orthogonal to the intercept and therefore remove any collinearity that involves the intercept, independent variables were centered by subtracting their mean values [44,45]. The variance inflation factor (VIF) with a threshold of 10 was used to quantify how much the variance of an estimated regression coefficient was inflated. However, VIF neither detects multiple near-singularities nor identifies the source of singularities. Hence, the condition index (CI), as the square root of the ratio of the largest eigenvalue to the corresponding eigenvalue from the dataset matrix, was also evaluated for all variables within the models. Similar to VIF, the CI indicates weak dependencies when higher than 10 but lower than 30, and severe dependencies when higher than 30 [46].
Additional data to test the models were not available, thus cross-validation analysis was performed using the prediction sum of squares (PRESS), which is the sum of squares of the difference between each observation and its prediction when that observation was not used in the prediction equation [47]. The root mean square error from the cross validation analysis (CV-RMSE, also known as RMSEpred) was then calculated as the square root of the ratio between the PRESS statistic and the number of observations. The CV-RMSE is an indicator of the predictive power of the model. The significance level used for all the statistical tests was α = 0.05 (p-value < 0.05). This p-value was used to evaluate if the variables included in the model were statistically significant as well. The squared semipartial correlation coefficients (SSCC) were calculated using partial sum of squares to determine the contribution from each variable to the models, while controlling the effects of other independent variables within the model. These coefficients represent the proportion of the variance of the dependent variable associated uniquely with the independent variable.
Although the statistical analyses applied to the dataset of 61 plots did not show the presence of outliers, three of these plots with measured low LAI values (1.34 to 1.43) could potentially be influencing the dependent vs. independent variable relationships. Therefore, best subset analyses were also applied to the dataset after removing these three observations (n = 58).
3. Results
3.1. Summary Statistics from Ground Measurements and Lidar Metrics
The 61 plots were distributed within the different forest types as follows: 3 in bottomland hardwoods, 18 in upland hardwoods, 4 in mixed pine-hardwoods, 24 in loblolly pine, 6 in shortleaf pine, and 6 in Virginia pine. For all forest types, stand age ranged between 10 and 164 years.
Mean tree height ranged from 13 m to 16 m, and mean dbh from 13 cm to 24 cm. Mean leaf area index values estimated on the ground, for all forest types, were between 3.1 to 4.1 (Table 2). For all groups of forest types, the mean number of lidar ground returns ranged between 222 and 555 returns/plot area (1,256.6 m2), and for all returns (hag > 0.2 cm) from 4,343 to 5,278 returns/plot area. Mean lidar heights above ground were between 9.9 m to 13.2 m, with standard deviations ranging from 4.5 m to 6.8 m (Table 3).

Table 2.
Descriptive statistics for tree height, tree dbh, and leaf area index (LAI) at plots per forest type classes. Statistics for total were calculated based on plot means. Column annotation: n (number of observations or plots), ht (mean tree height), dbh (diameter at breast height), and Stdv (standard deviation).

Table 3.
Means of lidar returns per forest type and per plot area (1,256.6 m2). Minimum values for all returns heights above ground were set at 0.2 m. Intensity minimum value was 1 for all plots (n = 61). Column annotation: n (number of observations or plots), Grtotal (total number of ground returns), Alltotal (total number of all returns), Stdv (standard deviation), Max (maximum value), and LPI (Laser Penetration Index).
Minimum heights were set to 0.2 m, and maximum values ranged from 25.3 m to 37.6 m. Intensity mean values from vegetation returns (hag > 1 m) were observed between 37 to 51 watts/plot. Standard deviations from the intensity values were over 20 watts/plot for all groups of plots. Laser penetration index (LPI) was lowest (0.003) for the pine-hardwoods and shortleaf pine group of plots, and highest (0.039) for the upland hardwood plots.
The mean number of cells per plot from the GeoSAR P-band was 49, and for the X-band was 138. Mean heights from the P-band ranged from 5.46 m to 10.48 m, while for the X-band they ranged from 10.84 m to 16.06 m (Table 4). Mean heights from the X-band were always higher than lidar returns, except for the upland hardwood plots. However, maximum values from the lidar returns were as much as 10 m higher than the maximum values from the X-band. P-band mean height values were high (up to 18 m) from the ground, which made the difference of X and P bands to be low, sometimes as low as half the mean height observed from the lidar returns. A comparison between lidar returns and GeoSAR heights for an upland hardwood plot can be visualized in Figure 3. The range of magnitude values from the P-bands was larger than from the X-band, as shown by the standard deviation. The vertical profile (distribution of heights vs. frequency) from lidar returns (Figure 4) showed two peaks, one at the mode value (13 m) and a second one at lower height. The latter might be related to a well-defined understory stratum in the forest stands. Also, a graph was obtained from the distribution of GeoSAR X-band heights, showing two peaks. Although, the highest peak (corresponding to the overstory vegetation) was at a similar height than the peak from lidar, the lower peak (corresponding to the understory vegetation) was a few meters higher than the peak acquired from lidar (Figure 4). This could be due to the level (height) at which the X-band penetrates to the forest, which unavoidably misses a large amount of vegetation present in the understory.

Table 4.
Means of GeoSAR cell values per forest type. P and X band heights were calculated by subtracting the values from a DEM created from the lidar returns (n = 61). Column annotation: X − P (X-band minus P-band), Pmag (P-band magnitude values), Xmag (X-band magnitude values), n (number of observations or plots), Stdv (standard deviation), and Max (maximum value).
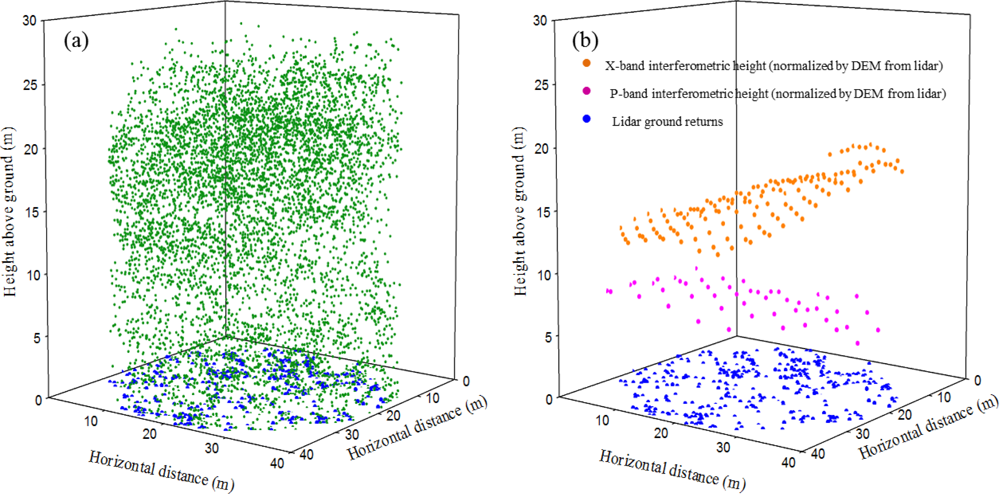
Figure 3.
Lidar returns and GeoSAR X- and P-band heights from a 108 yr-old upland hardwood plot with LAI = 3.23. Three-dimensional plots are: (a) Lidar returns (from ground and vegetation), and (b) GeoSAR interferometric heights from bands X and P, after having been subtracted from a DEM created from the lidar data. Lidar ground returns are drawn for reference.
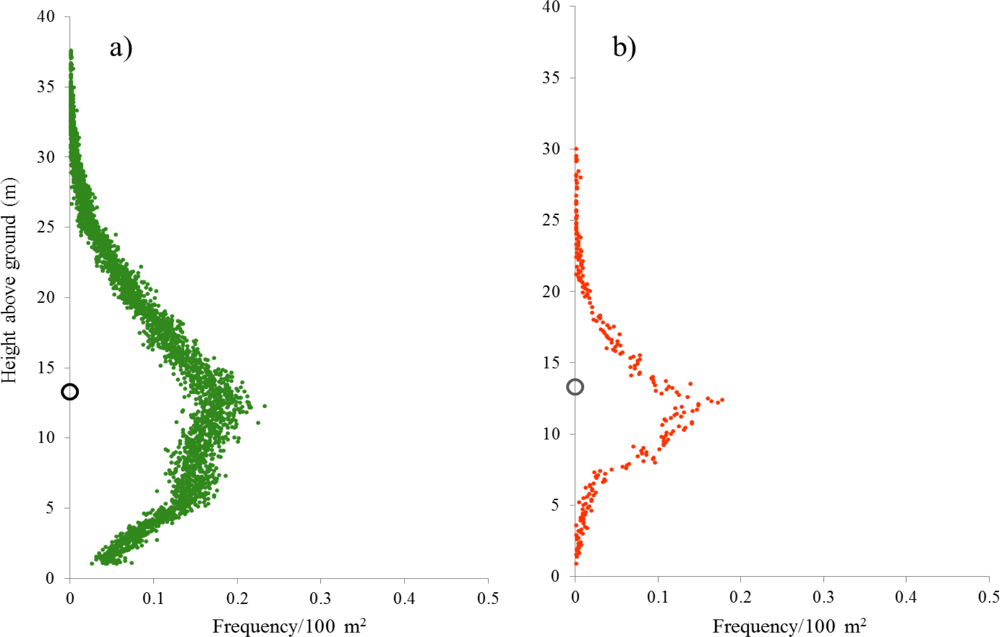
Figure 4.
Vertical profiles for all plots: (a) lidar vegetation returns (hag > 1 m) and (b) heights generated from GeoSAR X-band (cells), after corrected by a DEM generated from lidar returns. The mode calculated from the lidar vegetation returns is circled on the y axis: (a) black, (b) gray, drawn as a reference for visual comparison.
Pearson correlation coefficients were summarized for the variables included in the best models (Table 5). Laser penetration index (LPI) had the highest correlation with LAI (−0.698), followed by All10th (0.638) and X50th (0.609). Also, d2 (−0.347) and Xcv (−0.485) were statistically significant. The 10th and 20th percentiles (height values) were the only percentiles of any type significantly correlated with LAI. It is important to mention that in the past, the relationship between LAI and LPI has been reported as linear [38] and as curvilinear (as the logarithmic transformation of LPI) [48]. In this research, we evaluated both relationships as variables in the models. The Pearson correlation values were similar, −0.689 for the curvilinear model vs. −0.698 for the linear approach. Also, the results from the subset analyses showed consistently similar or higher R2’s values when using the linear relationship than when using the logarithmic transformation of LPI. This is probably due to a combination of factors, such as ecosystem type and range of LAI values. As a result, the models reported include the variable from the linear relationship only, which not only performed similarly to the curvilinear, but also makes the models easier to use and interpret.

Table 5.
Pearson correlation coefficients for the independent variables used to predict leaf area index (LAI) (n = 61). For a description of the variable names refer to Table 1. LAI was measured on the ground. Bold values were significant at α = 0.05.
The best models from lidar metrics had R2 values up to 0.69 with 4 variables in the model. Adding more variables increased the R2 and resulted in no collinearity problems. However, there was always at least one variable not contributing significantly to the model. Hence, only models with 2 and 4-variables were reported (Table 6). Common variables in these models were LPI and All10th, the increase in R2 (from 0.58 to 0.69) was given by the d10 and Cd-3 metrics. The largest contribution in both models was from the LPI (0.174 and 0.202), and in the 4-variable model the other three variables (All10th, d10, and Cd-3) had a similar contribution (0.053, 0.064, and 0.059). Predicted values from the 4-variable model were plotted against the measured LAI (Figure 5). The results from the best subset analyses for GeoSAR metrics showed that although the R2 values increased when adding more variables to the model, the R2adj’ did not, therefore only a 4-variable model with an R2 of 0.52 is shown in Table 6. The variable that contributed the most was X50th (0.127), followed by Xcv (0.098), sn01xlcv (0.047), and Xmagstdv (0.035). All variables included in the lidar only and GeoSAR only models had a VIF and CI lower than 5.

Table 6.
Best predictive models of LAI using lidar metrics only and GeoSAR metrics only, n = 61. The statistics R2adj’, CV-RMSE, SSCC, VIF, and CI are the adjusted coefficient of determination, the RMSE from the cross validation analysis, the squared semipartial correlation coefficient from partial sum of squares, the variance inflation factor and the condition index, respectively. For a description of the variable names refer to Table 1. All variables in the models were highly significant at a p-value < 0.001.
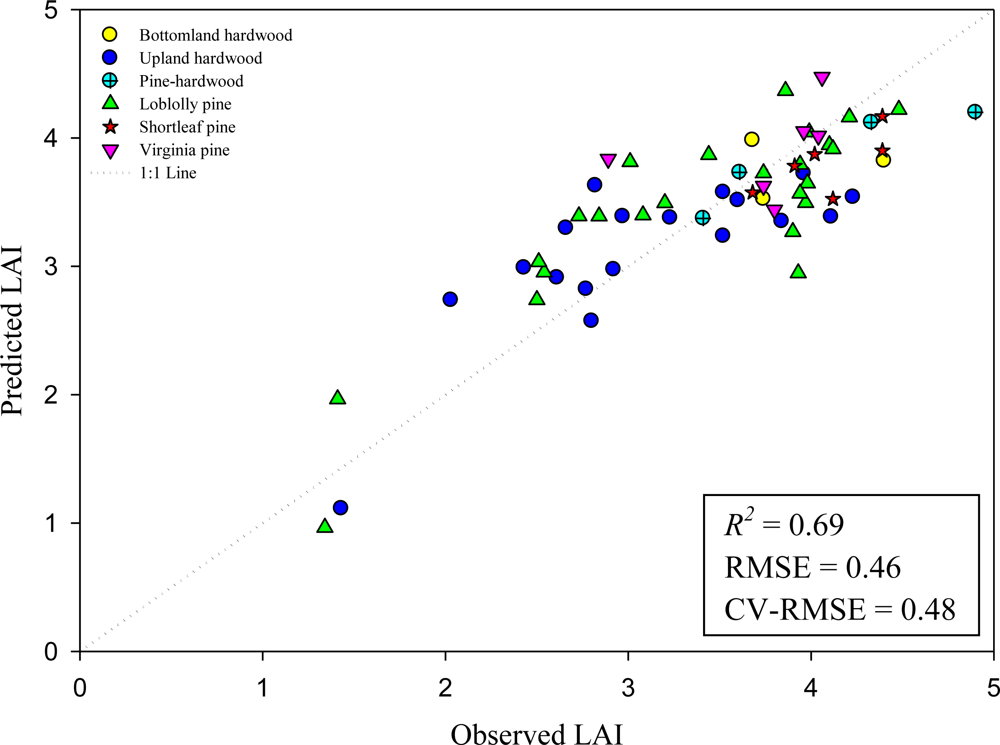
Figure 5.
Relationship between estimated LAI and measured LAI using the 4-variable model with lidar metrics only (n = 61). Plots were classified by forest type. Model (refer to Table 1 for variable names): LAI = 3.405 − 7.480(LPI) + 0.134(All10th) − 12.498(d10) − 15.113(Cd-3).
3.2. Variable Selection and Modeling
The best-performing models from the best subsets regressions using the metrics from lidar and GeoSAR combined are reported in Table 7. The R2 values ranged from 0.66 from a 2-variable model to 0.77 from a 6-variable model. The All50th and X50th variables were included in all models; the latter was the only variable from GeoSAR that was included. Other variables included in these models from lidar were LPI, d2, and two crown density metrics (Cd-1, and Cd-3stdv). The largest contributions (always higher than 0.1) were from the All50th and X50th variables. Between the 5 and 6-variable model, the R2 and R2adj’ increased and the RMSE decreased with an extra variable, but the CV-RMSE stayed the same.

Table 7.
Best predictive models of LAI using lidar metrics (including crown density slices) and GeoSAR metrics, n = 61. The statistics R2adj’, CV-RMSE, SSCC, VIF, and CI are the adjusted coefficient of determination, the RMSE from the cross validation analysis, the squared semipartial correlation coefficient from partial sum of squares, the variance inflation factor and the condition index, respectively. All variables in the models were highly significant at a p-value < 0.0001. For a description of the variable names refer to Table 1.
There were no collinearity issues flagged by the VIF and CI, which were under 5 for all variables. Predicted values from the 4-variable model and 6-variable model are shown in Figures 6 and 7 for comparison. The difference in R2 values between these two is only 0.04, but the observations from the 6-variable model are distributed closer to the 1:1 line, suggesting a better fit.
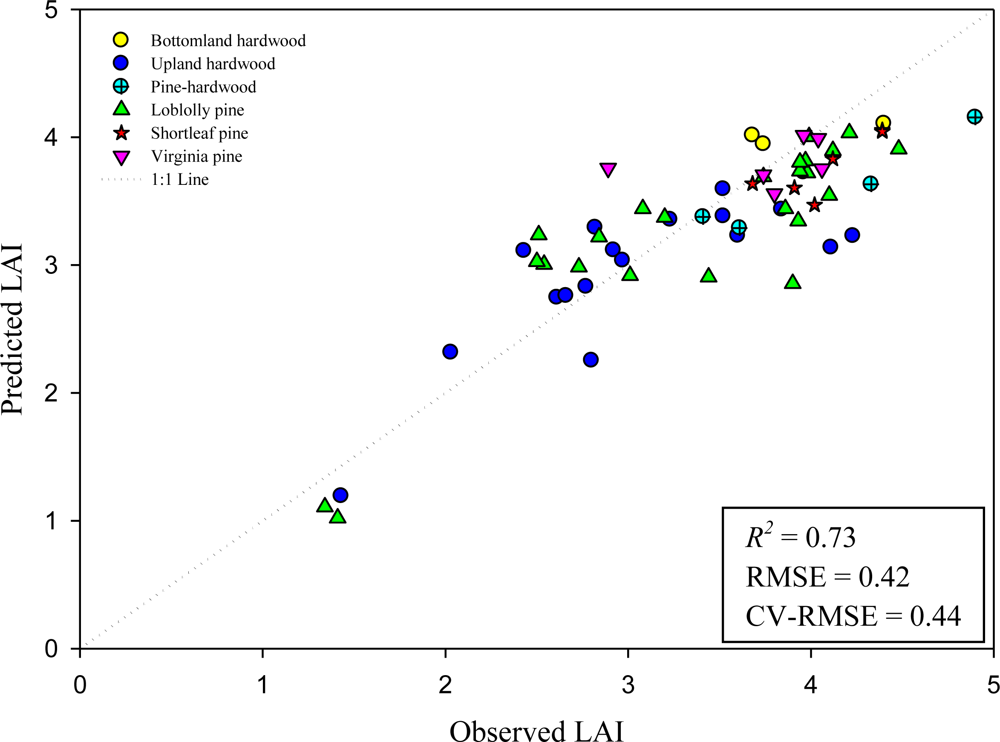
Figure 6.
Relationship between estimated LAI and measured LAI using the 4-variable model with lidar and GeoSAR metrics (n = 61). Plots were classified by forest type. Model (refer to Table 1 for variable names): LAI = 3.391 − 3.044 (LPI) − 0.147 (All50th) − 3.027 (d2) + 0.201 (X50th).
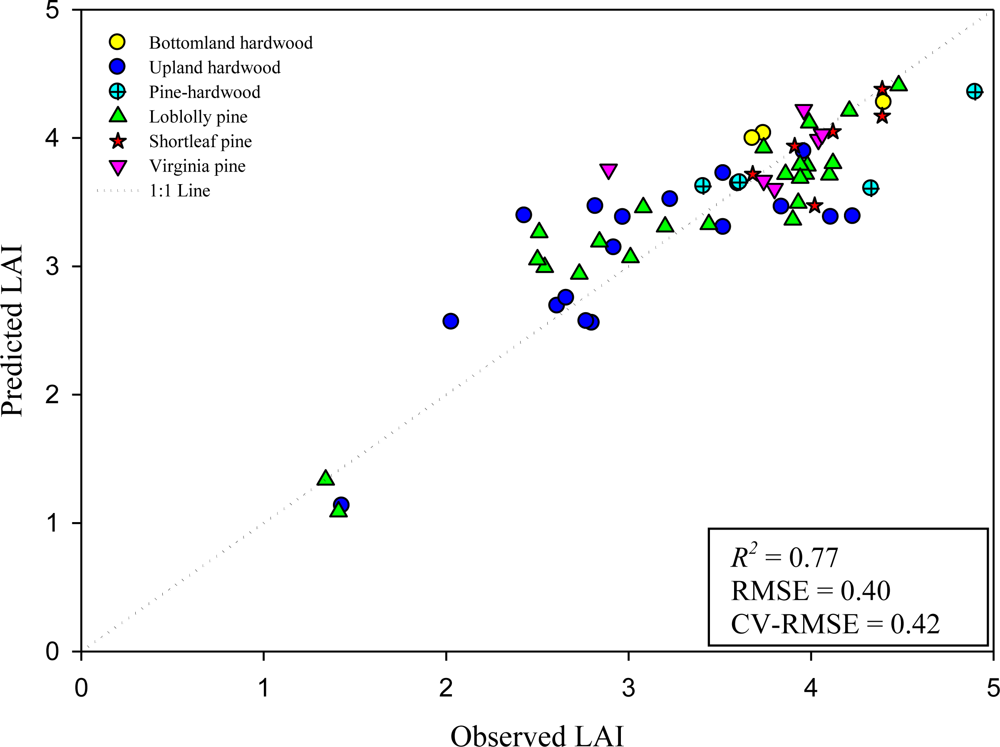
Figure 7.
Relationship between estimated LAI and measured LAI using the 6-variable model with lidar and GeoSAR metrics (n = 61). Plots were classified by forest type. Model (refer to Table 1 for variable names): LAI = 3.475 − 4.246 (LPI) − 0.185 (All50th) − 4.979 (d2) + 0.208 (X50th) − 14.977 (Cd-3stdv) − 7.805 (Cd-1).
The best models obtained from the best subset regression analyses applied to the dataset without the low LAI plots (n = 58), consistently included the same variables as the best models obtained when using the dataset of 61 plots. The R2 values were lower (0.1 lower) than the R2 values observed when using the 61 plots (Figure 8), however, this reduction of the R2 values can be attributed to the reduced number of plots representing the low levels of the LAI range. In addition, the fact that the best models included the exact same variables than the models from the 61 plots, and that the reduction of the R2 values is only 0.1 confirms that such plots are not influential enough to drive the relationship in the models. Therefore, since the exclusion of these three plots did not affect the relationship of measured LAI with the lidar and GeoSAR metrics, most of the results reported in this research used the dataset with 61 plots.
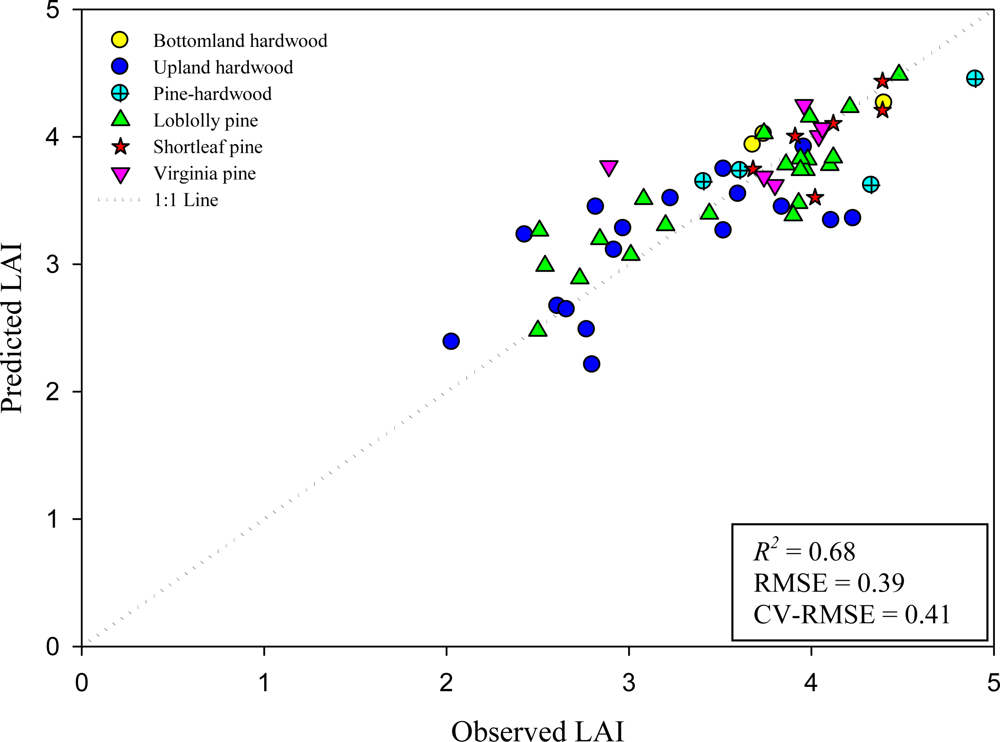
Figure 8.
Relationship between estimated LAI and measured LAI using the 6-variable model with lidar and GeoSAR metrics and excluding the three plots of low LAI values from the dataset (n = 58). Plots were classified by forest type. Model (refer to Table 1 for variable names): LAI = 3.658 − 8.933 (LPI) − 0.193 (All50th) − 4.800 (d2) + 0.211 (X50th) − 18.042 (Cd-3stdv) − 8.531 (Cd-1).
Crown density metrics were included in the best models using 5 or more variables. These were removed as independent variables, and the data re-analyzed. The results from these analyses are shown in Table 8. It was noticeable that in the absence of the crown metrics from lidar, more variables from GeoSAR were included in the models, to the point of obtaining R2 and RMSE values comparable to the models in Table 7. The additional metrics from GeoSAR were Pmagstdv and Pmagmax. The VIF values from these two models increased to 7.6 compared to the models with the crown metrics, due to the high correlation between Pmagstdv and Pmagmax (0.931).

Table 8.
Best predictive models of LAI using lidar metrics (excluding crown density slices) and GeoSAR metrics, n = 61. The statistics R2adj’, CV-RMSE, SSCC, VIF, and CI are the adjusted coefficient of determination, the RMSE from the cross validation analysis, the squared semipartial correlation coefficient from partial sum of squares, the variance inflation factor and the condition index, respectively. All variables in the models were highly significant at a p-value < 0.0001. For a description of the variable names refer to Table 1.
4. Discussion
The LAI range of values, among all plots, was large enough to develop a relationship with lidar metrics. There were few representatives (3) at the low range of LAI. These three plots were influential, and therefore, were not deleted from the dataset. It is important to highlight that even when the estimations from the LiCor LAI-2000 could be conservative and underestimating the actual values of LAI for the plots sampled [49–51], there was consistency in the estimates acquired and the amount of vegetation observed (especially, in the extremes of the LAI range). Therefore, the prediction models developed using these estimations can capture relative differences in LAI among the observed forest conditions.
In the past, models for LAI prediction in mixed hardwood and coniferous forests using only lidar data have reported R2 values ranging from 0.8 to 0.9, using either very few plots (between 10 to 18) or small plot sizes (400 m2 to 500 m2) [8,9,12,38]. The results reported in this research, using 61 plots of 1,257 m2 size, reveal an R2 of 0.69 (CV-RMSE = 0.48) for lidar only models, and an increased R2 value of 0.77 (CV-RMSE = 0.42) when using lidar and GeoSAR data together.
The high correlation of LPI with leaf area index was expected [7]. Laser penetration index, defined as the proportion of ground returns to the total number of pulses, is directly related to the amount of leaves and canopy thickness. The more open the canopy the more pulses reach the ground, and vice versa. This variable was included in the models that were developed with either lidar metrics alone or with the combination of lidar and GeoSAR metrics. There were two models where LPI was not included, in which the 50th percentile of lidar returns took its place.
Lidar return percentiles are height values calculated based on the vertical density of returns [39]. They describe the height of the vegetation density across the stand vertical profiles. In other words, such heights relate to the target heights on the ground, as more targets (i.e., branches, leaves, etc.) the laser encounters at certain height or section from the ground, more returns are obtained from that section of the stand. For example, the 50th percentile value means that 50% of the return heights are above or below that height. In addition, the 10th percentile was included in the lidar only models, this metric ranged from 0.40 m to 8.08 m, with a mean of 3.54 m for all 61 plots. At this height (of the vertical profile) in the measured forest stands, mostly understory was present, making this stratum an important contributor to the LAI value of the plot.
Similar to the 10th percentile of the lidar returns, the density metric d10 [39], defined as the proportion of returns found at the top of the canopy with respect to the total number of returns from the vegetation, was included in the lidar metric models only. The top of the canopy is directly related to tree crowns, and hence LAI. Almost opposite to d10, the density metric d2 was selected in the models using lidar and GeoSAR metrics together. This variable relates to the low section of the vertical profile of the stand.
Crown density slice metrics are descriptors of tree crowns, and metrics related with the proportions of returns and standard deviation of the return heights at 1 and 3 meters below the mode value were included in the models. These variables contributed as much as the density metrics. Interestingly, the combination of all returns percentiles, densities, and crown density metrics in the models managed to describe the vegetation at the top, medium, and low level of the vertical profile. For instance, d10, Cd-3, and All10th were together in the 4-variable model for lidar metrics only.
The interferometric heights from the X-band, after being corrected by the DEM developed from lidar data, showed the largest correlations with LAI. The 50th percentile of the height values per plot was positively correlated with LAI. The coefficient of variation from all the height values within a plot correlated negatively, suggesting more variability among the height values in plots with low LAI values. In addition, the metrics of the layer generated from the difference between X-band and P-band (X- minus P-band), and the metrics from the P-band interferometry showed significant correlations with LAI but they were not included in the best models. Moreover, the coefficient of variation obtained from the values of one of the σ0 layers contributed significantly to the model when only GeoSAR data were used.
5. Conclusions
The results from this study support previous success in estimating LAI in mixed forests using lidar metrics [11–13], R2 values were 0.58 (CV-RMSE=0.53) and 0.69 (CV-RMSE=0.48) for two and four lidar metrics in the model, respectively. Our evaluation showed that the sole use of dual-band synthetic aperture radar to estimate LAI is not as promising as the sole use of lidar data, since the best model had an R2 of 0.52 (CV-RMSE=0.58) by including four metrics in the model. However, the evaluation of the two technologies together showed an important synergistic gain in the explanation of LAI variability, the R2 values increased up to 0.77 with a CV-RMSE of 0.42. The most important metric in the combined model was the 50th percentile of the X-band interferometric height from DBInSAR The set of plots used in this research, comprised a broad range of stand ages (10 to 164 year old), forest types (21 plots of hardwoods, 36 plots of pure pine, and 4 plots of pine-hardwood), and measured LAI values (1.3 to 4.9). Considering this variability, the models developed represent a robust and accurate way to estimate LAI in the temperate mixed forests of Virginia.
Ideally, the future inclusion of additional sampled plots covering a wider range of species associations and LAI values for this particular forest type would increase the robustness and accuracy of these models and result in a more trustworthy tool for the estimation and monitoring of leaf area in other states or regions. In addition, X-band interferometry is currently possible using spaceborne sensors, which shows clear utility for LAI estimation at landscape to regional scales.
At present, the growing hardwood utilization industry requires decision support tools that can accommodate a diverse set of management, planning, and policy-making strategies and goals. Leaf area index is a key variable for the estimation of wood production and carbon storage when using such tools. Consequently, robust and accurate models to remotely estimate this variable are essential. The results of our research demonstrate that lidar and DBInSAR data can be important factors in the development and improvement of such models, particularly when the datasets are used in tandem.
Acknowledgments
This research was possible thanks to support from the Virginia Tech Department of Forest Resources and Environmental Conservation and the help in field data collection provided by Jessica Walker (Virginia Tech), Rupesh Shrestha (Boise State University), Nilam Kayastha (Virginia Tech), Asim Banskota (Conservation International), Wayne Bowman (Virginia Department of Forestry), and John Scrivani (Virginia Information Technology Agency).
References
- Watson, D.J. Comparative physiological studies in the growth of field crops. I. Variation in net assimilation rate and leaf area between species and varieties, and within and between years. Ann. Bot 1947, 41–76. [Google Scholar]
- Spanner, M.A.; Pierce, L.L.; Running, S.W.; Peterson, D.L. The seasonality of AVHRR data of temperate coniferous forests: Relationship with leaf area index. Remote Sens. Environ 1990, 33, 97–112. [Google Scholar]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between leaf area index and Landsat TM spectral vegetation indices across three temperate zone sites. Remote Sens. Environ 1999, 70, 52–68. [Google Scholar]
- Anderson, M.C.; Neale, C.M.U.; Li, F.; Norman, J.M.; Kustas, W.P.; Jayanthi, H.; Chavez, J. Upscaling ground observations of vegetation water content, canopy height, and leaf area index during SMEX02 using aircraft and Landsat imagery. Remote Sens. Environ 2004, 92, 447–464. [Google Scholar]
- Vose, J.M.; Sullivan, N.H.; Clinton, B.D.; Bolstad, P.V. Vertical leaf area distribution, light transmittance, and application of the Beer-Lambert law in four mature hardwood stands in the southern Appalachians. Can. J. For. Res 1995, 25, 1036–1043. [Google Scholar]
- Sampson, D.A.; Vose, J.M.; Allen, H.L. A Conceptual Approach to Stand Management Using Leaf Area Index as the Integral of Site Structure, Physiological Function, and Resource Supply. Proceedings of Ninth Biennial Southern Silvicultural Research Conference, Clemson, SC, USA, 25–27 February 1997; pp. 447–451.
- Barilotti, A.; Turco, S.; Alberti, G. LAI Determination in Forestry Ecosystem by Lidar Data Analysis. Proceedings of International Workshop 3D Remote Sensing in Forestry, Vienna, Austria, 14–15 February 2006; pp. 248–252.
- Kwak, D.-A.; Lee, W.-K.; Cho, H.-K. Estimation of LAI Using Lidar Remote Sensing in Forest. Proceedings of ISPRS Workshop on Laser Scanning and SilviLaser, Espoo, Finland; 2007; pp. 248–252. [Google Scholar]
- Sasaki, T.; Imanishi, J.; Ioki, K.; Morimoto, Y.; Kitada, K. Estimation of leaf area index and canopy openness in broad leaved forest using an airborne laser scanner in comparison with high-resolution near-infrared digital photography. Landscape Ecol. Eng 2008, 4, 47–55. [Google Scholar]
- Solberg, S.; Brunner, A.; Hanssen, K.H.; Lange, H.; Næsset, E.; Rautiainen, M.; Stenberg, P. Mapping LAI in a Norway spruce forest using airborne laser scanning. Remote Sens. Environ 2009, 113, 2317–2327. [Google Scholar]
- Hopkinson, C.; Chasmer, L. Testing LiDAR models of fractional cover across multiple forest ecozones. Remote Sens. Environ 2009, 113, 275–288. [Google Scholar]
- Zhao, K.; Popescu, S. Lidar-based mapping of leaf area index and its use for validating GLOBCARBON satellite LAI product in a temperate forest of the southern USA. Remote Sens. Environ 2009, 113, 1628–1645. [Google Scholar]
- Richardson, J.J.; Moskal, L.M.; Kim, S.-H. Modeling approaches to estimate effective leaf area index from aerial discrete-return LIDAR. Agr. For. Meteorol 2009, 149, 1152–1160. [Google Scholar]
- Jensen, J.L.R.; Humes, K.S.; Vierling, L.A.; Hudak, A.T. Discrete return lidar-based prediction of leaf area index in two conifer forests. Remote Sens. Environ 2008, 112, 3947–3957. [Google Scholar]
- Solberg, S. Mapping gap fraction, LAI and defoliation using various ALS penetration variables. Int. J. Remote Sens 2010, 31, 1227–1244. [Google Scholar]
- Riaño, D.; Valladares, F.; Condes, S.; Chuvieco, E. Estimation of leaf area index and covered ground from airborne laser scanner (lidar) in two contrasting forests. Agr. For. Meteorol 2004, 124, 269–275. [Google Scholar]
- Korhonen, L.; Korpela, I.; Heiskanen, J.; Maltamo, M. Airborne discrete-return LIDAR data in the estimation of vertical canopy cover, angular canopy closure and leaf area index. Remote Sens. Environ 2011, 115, 1065–1080. [Google Scholar]
- Thomas, V.; Noland, T.; Treitz, P.; McCaughey, J.H. Leaf area and clumping indices for a boreal mixed-wood forest: lidar, hyperspectral, and Landsat models. Int. J. Remote Sens 2011, 32, 8271–8297. [Google Scholar]
- Cerrillo, R.M.N.; de la Orden, M.S.; Bonilla, J.G.; Garcia-Ferrer, A.; Clemente, R.H.; Lanjeri, S. LIDAR-based estimation of leaf area index on Holm oak Quercus ilex L. subsp ballota (Desf.) Samp. trees. For. Syst 2010, 19, 61–69. [Google Scholar]
- Williams, M.L.; Milne, T.; Tapley, I.; Reis, J.J.; Sanford, M.; Kofman, B.; Hensley, S. Tropical Forest Biomass Recovery Using GeoSAR Observations. Proceedings of 2009 IEEE International Geoscience and Remote Sensing Symposium, Capte Town, South Africa, 12–17 July 2009; pp. IV-173–IV-176.
- Sexton, J.O.; Bax, T.; Siqueira, P.; Swenson, J.J.; Hensley, S. A comparison of lidar, radar, and field measurements of canopy height in pine and hardwood forests of southeastern North America. For. Ecol. Manage 2009, 257, 1136–1147. [Google Scholar]
- Williams, M.L.; Silman, M.; Saatchi, S.; Hensley, S.; Sanford, M.; Yohannan, A.; Kofman, B.; Reis, J.; Kampes, B. Analysis of GeoSAR Dual-Band InSAR Data for Peruvian Forest. Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1398–1401.
- Carson, T.M. Topographic mapping in the equatorial belt using dual-frequency airborne IFSAR (GeoSAR). Photogramm. Eng Reote Sensing 2008, 74, 939–944. [Google Scholar]
- Williams, M.L.; Jenkins, L.G. GeoSAR and DBInSAR: Combining “X” With “P” for Tropical Forest “C”. Photogramm. Eng. Reote Sensing 2009, 75, 738–743. [Google Scholar]
- Svoray, T.; Shoshany, M.; Curran, P.J.; Foody, G.M.; Perevolotsky, A. Relationship between green leaf biomass volumetric density and ERS-2 SAR backscatter of four vegetation formations in the semi-arid zone of Israel. Int. J. Remote Sens 2001, 22, 1601–1607. [Google Scholar]
- Sun, G.Q.; Ranson, K.J.; Guo, Z.; Zhang, Z.; Montesano, P.; Kimes, D. Forest biomass mapping from lidar and radar synergies. Remote Sens. Environ 2011, 115, 2906–2916. [Google Scholar]
- Solberg, S.; Weydahl, D.J.; Naesset, E. Simulating X-Band Interferometric Height in a Spruce Forest From Airborne Laser Scanning. IEEE Trans. Geosci. Remote Sens 2010, 48, 3369–3378. [Google Scholar]
- Durden, S.L.; Morrissey, L.A.; Livingston, G.P. Microwave backscatter and attenuation dependence on leaf area index for flooded rice fields. IEEE Trans. Geosci. Remote Sens 1995, 33, 807–810. [Google Scholar]
- Paloscia, S. An empirical approach to estimating leaf area index from multifrequency SAR data. Int. J. Remote Sens 1998, 19, 361–366. [Google Scholar]
- Manninen, T.; Stenberg, P.; Rautiainen, M.; Voipio, P.; Smolander, H. Leaf area index estimation of boreal forest using ENVISAT ASAR. IEEE Trans. Geosci. Remote Sens 2005, 43, 2627–2635. [Google Scholar]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States tree species. For. Sci 2003, 49, 12–35. [Google Scholar]
- Means, J.E.; Acker, S.A.; Harding, D.J.; Blair, J.B.; Lefsky, M.A.; Cohen, W.B.; Harmon, M.E.; McKee, W.A. Use of large-footprint scanning airborne lidar to estimate forest stand characteristics in the Western Cascades of Oregon. Remote Sens. Environ 1999, 67, 298–308. [Google Scholar]
- van Aardt, J.; Wynne, R.H.; Oderwald, R.G. Forest volume and biomass estimation using small-footprint lidar-distributional parameters on a per-segment basis. For. Sci 2006, 52, 636–649. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Nelson, R. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Electron. Agr 2002, 37, 71–95. [Google Scholar]
- LI-COR, FV2000 the LAI-2000 Data File Viewer; LI-COR Biosciences: Lincoln, NE USA, 2010; p. 73.
- Welles, J.M.; Norman, J.M. Instrument for indirect measurement of canopy architecture. Agron. J 1991, 83, 818–825. [Google Scholar]
- Holmgren, J. Prediction of tree height, basal area and stem volume in forest stands using airborne laser scanning. Scand. J. Forest Res 2004, 19, 543–553. [Google Scholar]
- Barilotti, A.; Turco, S.; Napolitano, R.; Bressan, E. La Tecnologia LiDAR per lo Studio Della Biomassa Negli Ecosistemi Forestali. Proceedings of 15th Meeting of the Italian Society of Ecology, Torino, Italy, 12–14 September 2005.
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ 2002, 80, 88–99. [Google Scholar]
- SAS, The SAS System for Windows Release 9.1.3; SAS Institute Inc: Cary, NC, USA, 2010.
- Hocking, R. The analysis and selection of variables in linear regression. Biometrics 1976, 32, 1–49. [Google Scholar]
- Akaike, H. Fitting autoregressive models for prediction. Ann. Inst. Stat. Math 1969, 21, 243–247. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat 1978, 6, 461–464. [Google Scholar]
- Belsley, D.A. Demeaning conditioning diagnostics through centering (with discussion). Amer. Statistician 1984, 38, 73–77. [Google Scholar]
- Marquart, D.W. Comment: you should standarize the predictor variables in your regression models. J. Amer. Stat. Assoc 1980, 75, 87–91. [Google Scholar]
- Rawlings, J.O.; Pantula, S.G.; Dickey, D.A. Applied Regression Analysis: A Research Tool, 2nd ed.; Springer: Ann Arbor, MI, USA, 2001; p. 657. [Google Scholar]
- Allen, D. The Prediction Sum of Squares as a Criterion for Selection of Predictor Variables; Tech. Report 23. Department of Statistics, University of Kentucky: Lexington, KY, USA, 1971.
- Solberg, S.; Næsset, E.; Hanssen, K.H.; Christiansen, E. Mapping defoliation during a severe insect attack on Scots pine using airborne laser scanning. Remote Sens. Environ 2006, 102, 364–376. [Google Scholar]
- Nasahara, K.N.; Muraoka, H.; Nagai, S.; Mikami, H. Vertical integration of leaf area index in a Japanese deciduous broad-leaved forest. Agr. Forest Meteorol 2008, 148, 1136–1146. [Google Scholar] [Green Version]
- Gower, S.T.; Norman, J.M. Rapid Estimation of Leaf Area Index in Conifer and Broad-Leaf Plantations. Ecology 1991, 72, 1896–1900. [Google Scholar]
- Sampson, D.A.; Allen, H.L. Direct and indirect estimates of leaf-area index (LAI) for lodgepole and loblolly-pine stands. Trees-Struct. Funct 1995, 9, 119–122. [Google Scholar]