Assessing the Accuracy of Georeferenced Point Clouds Produced via Multi-View Stereopsis from Unmanned Aerial Vehicle (UAV) Imagery
Abstract
:1. Introduction
1.1. Structure from Motion - Photogrammetry Meets Computer Vision
1.2. UAVs for 3D Reconstruction of Natural Landscapes
1.3. Georeferenced Point Clouds and Reference Data
2. Methods
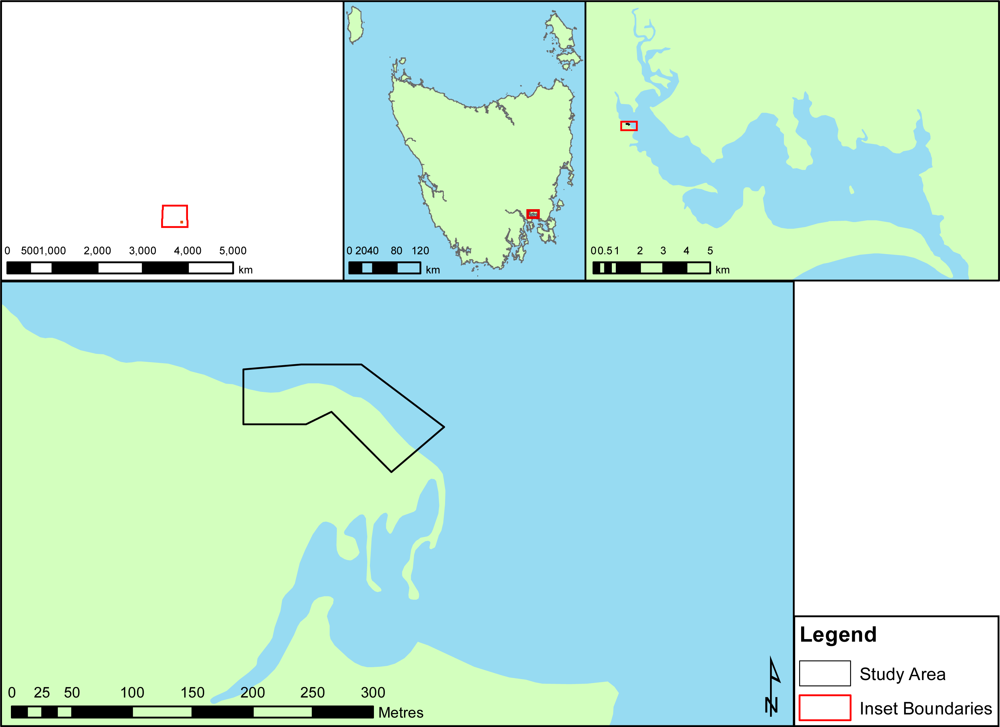
2.1. Study Area
2.2. Hardware
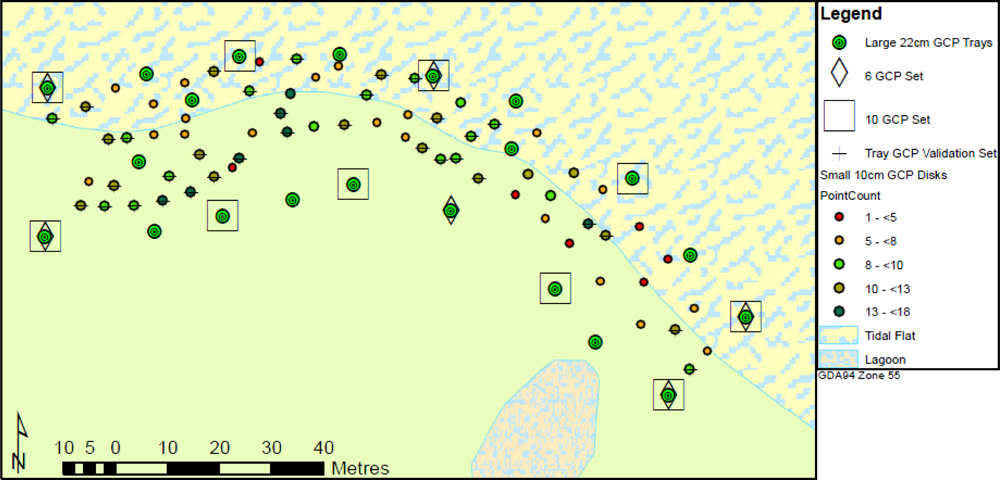
2.3. Data Collection
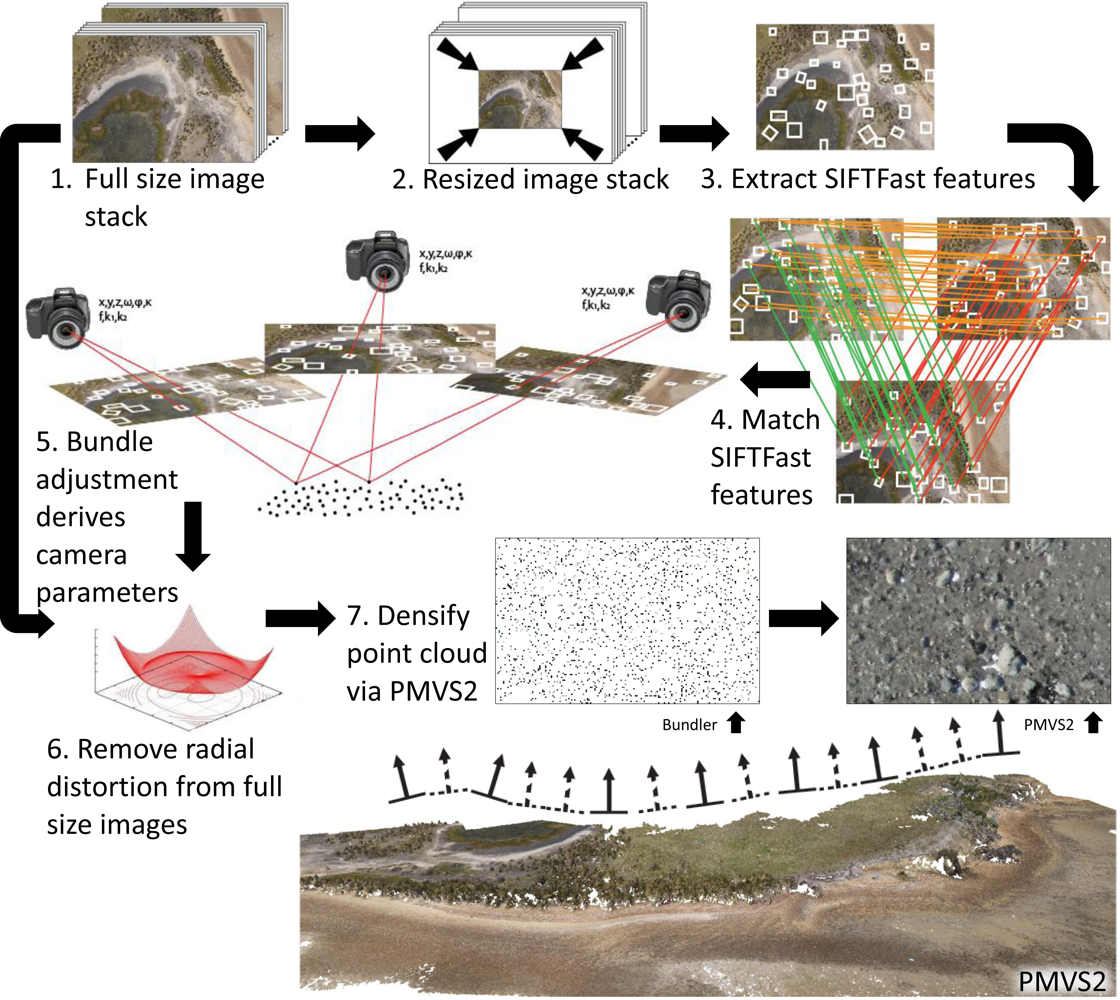
2.4. UAV-MVS
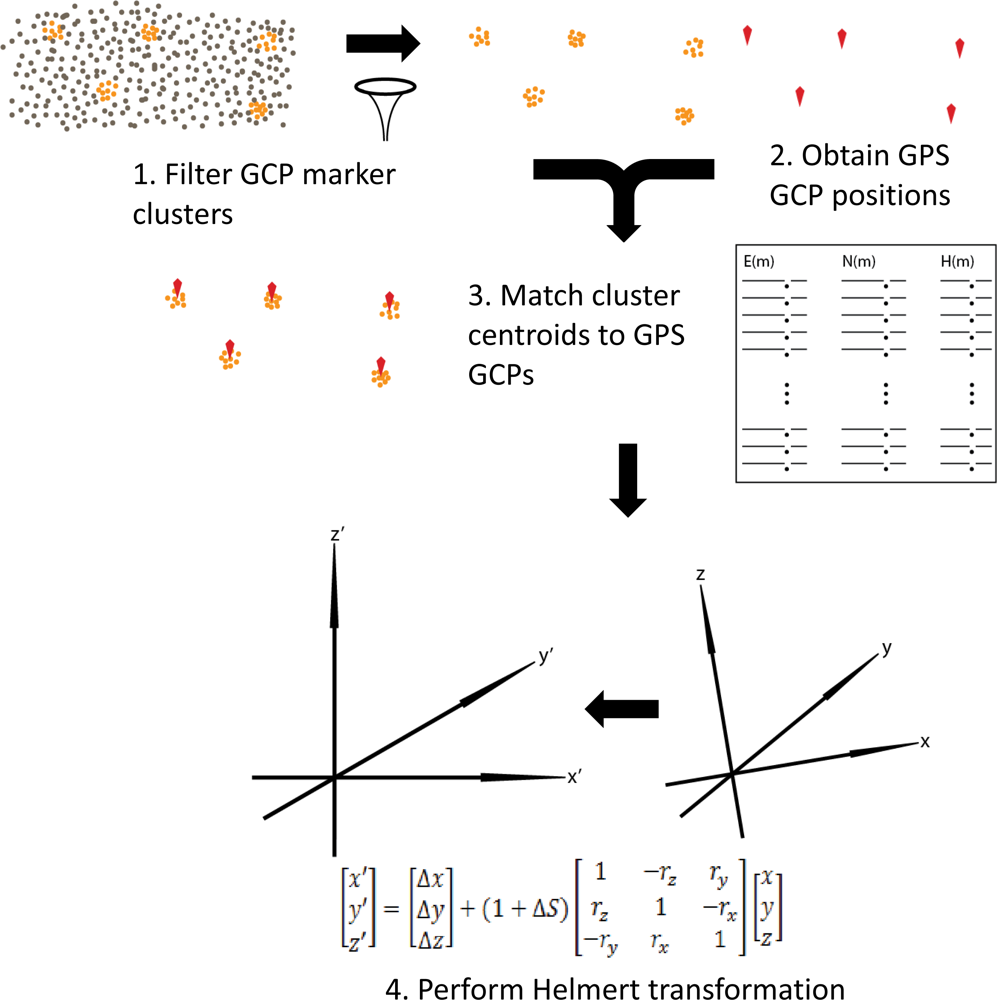
2.5. Accuracy Assessment
3. Results and Discussion
3.1. Cluster Centres—Centroid or Mean?
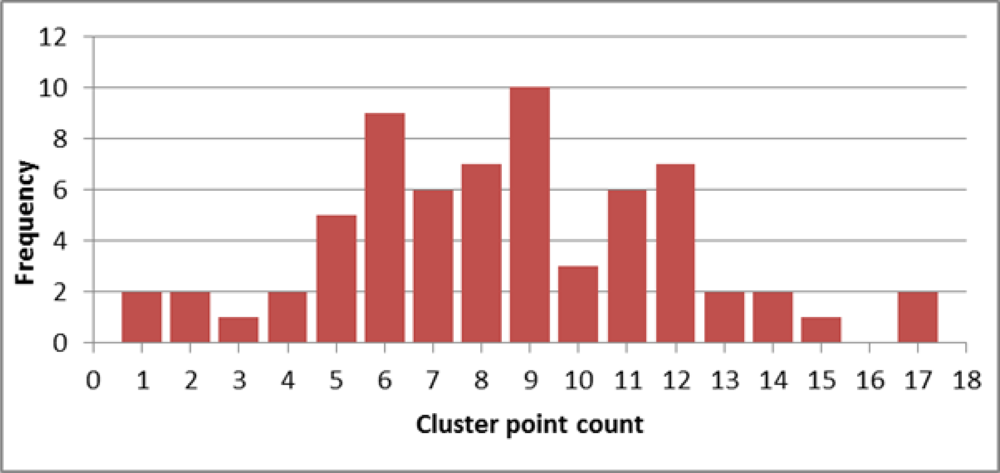
3.2. Automated GCP Disk Cluster Extraction Performance
3.3. Scenario 1 and 2
3.4. Scenario 3
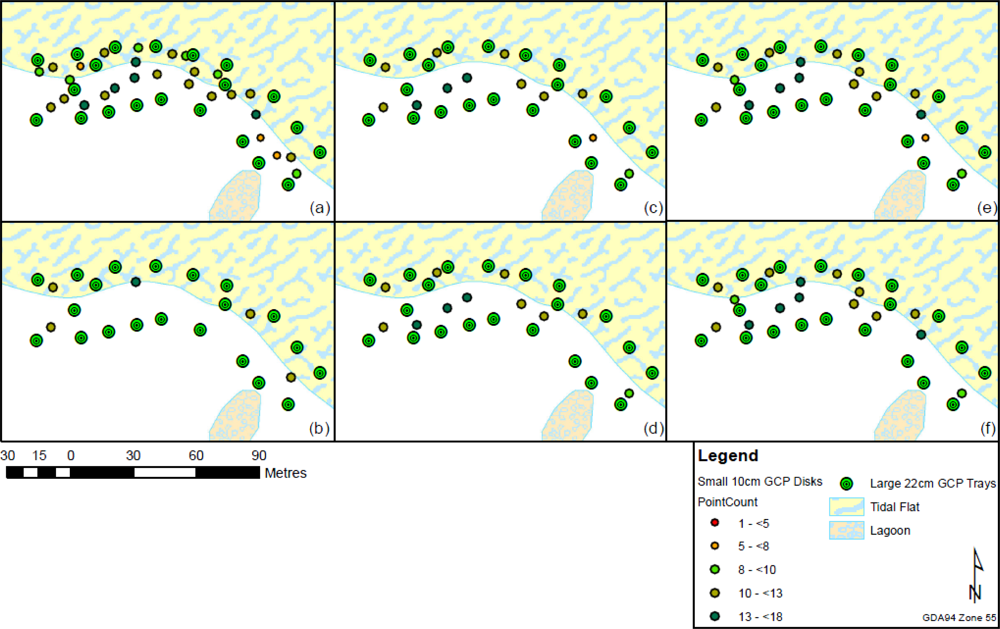
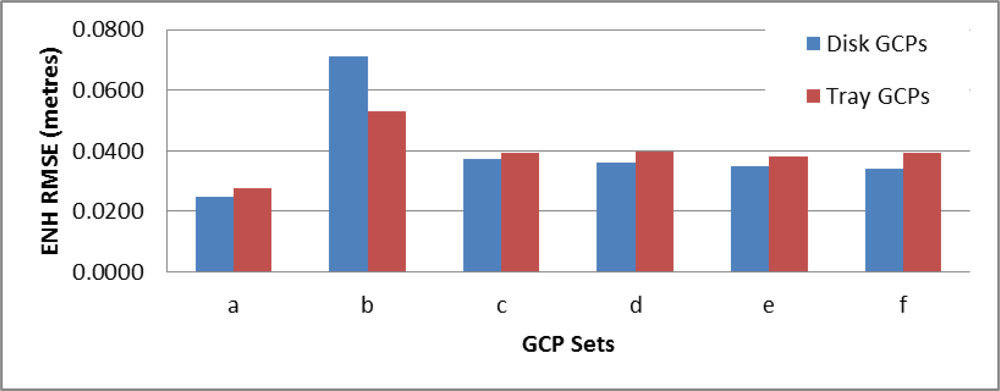
3.5. GCP Distribution
3.6. Applications and Limitations
4. Conclusions
Acknowledgments
References
- Laliberte, A.; Herrick, J.; Rango, A.; Winters, C. Acquisition, orthorectification, and object-based classification of unmanned aerial vehicle (UAV) imagery for rangeland monitoring. Photogramm. Eng. Remote Sensing 2010, 76, 661–672. [Google Scholar]
- Coulter, L.; Lippitt, C.; Stow, D.; McCreight, R. Near Real-Time Change Detection for Border Monitoring. In Proceedings of the ASPRS Annual Conference, Milwaukee, WI, USA, 1–5 May 2011; pp. 9–17.
- Chao, H.; Cao, Y.; Chen, Y. Autopilots for small unmanned aerial vehicles: A survey. Int. J. Control Autom. Syst 2010, 8, 36–44. [Google Scholar]
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multi-View Stereopsis. Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 18–23 June 2007; 1, pp. 1–8.
- Neitzel, F.; Klonowski, J. Mobile 3D mapping with a low-cost UAV system. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2011, 38, 1–6. [Google Scholar]
- Rosnell, T.; Honkavaara, E. Point cloud generation from aerial image data acquired by a quadrocopter type micro unmanned aerial vehicle and a digital still camera. Sensors 2012, 12, 453–480. [Google Scholar]
- Turner, D.; Lucieer, A.; Watson, C. Development of an Unmanned Aerial Vehicle (UAV) for Hyper Resolution Vineyard Mapping Based on Visible, Multispectral, and Thermal Imagery. Proceedings of the 34th International Symposium on Remote Sensing of Environment (ISRSE34), Sydney, Australia, 11–15 April 2011.
- Dandois, J.P.; Ellis, E.C. Remote sensing of vegetation structure using computer vision. Remote Sens 2010, 2, 1157–1176. [Google Scholar]
- Lucieer, A.; Robinson, S.; Turner, D. Unmanned Aerial Vehicle (UAV) Remote Sensing for Hyperspatial Terrain Mapping of Antarctic Moss Beds Based on Structure from Motion (SfM) Point Clouds. Proceedings of the 34th International Symposium on Remote Sensing of Environment (ISRSE34), Sydney, Australia, 11–15 April 2011.
- Monserrat, O.; Crosetto, M. Deformation measurement using terrestrial laser scanning data and least squares 3D surface matching. ISPRS J. Photogramm 2008, 63, 142–154. [Google Scholar]
- Hartley, R.; Mundy, J. The relationship between photogrammetry and computer vision. Proc. SPIE 1993, 14, 92–105. [Google Scholar]
- Remondino, F.; El-Hakim, S. Image-based 3D modelling: A review. Photogramm. Rec 2006, 21, 269–291. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis 2004, 60, 91–110. [Google Scholar]
- Juan, L.; Gwun, O. A comparison of SIFT, PCA-SIFT and SURF. Int. J. Image Process 2009, 3, 143–152. [Google Scholar]
- Mikolajczyk, K.; Schmid, C. Scale & affine invariant interest point detectors. Int. J. Comput. Vis 2004, 60, 63–86. [Google Scholar]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up Robust Features. Proceedings of 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417.
- Strecha, C.; Bronstein, A.; Bronstein, M.; Fua, P. LDAHash: Improved matching with smaller descriptors. IEEE Trans. Pattern Anal. Mach. Intell 2011, 34, 66–78. [Google Scholar]
- Ke, Y.; Sukthankar, R. PCA-SIFT: A More Distinctive Representation for Local Image Descriptors. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; pp. 506–513.
- Triggs, B.; McLauchlan, P.; Hartley, R.; Fitzgibbon, A. Bundle Adjustment—A Modern Synthesis. Proceedings of the ICCV ’99 Vision Algorithms: Theory and Practice, Corfu, Greece, 20–21 September 1999; pp. 153–177.
- Snavely, N. Bundler: Structure from Motion (SfM) for Unordered Image Collections. Available online: http://phototour.cs.washington.edu/bundler/ (accessed on 15 March 2011).
- Snavely, N.; Seitz, S.M.; Szeliski, R. Photo tourism: Exploring photo collections in 3D. ACM Trans. Graph 2006, 25, 835–846. [Google Scholar]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the world from internet photo collections. Int. J. Comput. Vis 2007, 80, 189–210. [Google Scholar]
- Microsoft Corporation. Photosynth. Available online: http://photosynth.net/ (accessed on 25 October 2010).
- AgiSoft. Agisoft PhotoScan. Available online: http://www.agisoft.ru/products/photoscan/ (accessed on 1 November 2010).
- Eos Systems Inc. PhotoModeler. Available online: http://www.photomodeler.com/products/photomodeler.htm (accessed on 1 October 2011).
- Furukawa, Y.; Ponce, J. Patch-Based Multi-View Stereo Software. Available online: http://grail.cs.washington.edu/software/pmvs/ (accessed on 1 June 2010).
- Furukawa, Y. Clustering Views for Multi-View Stereo (CMVS). Available online: http://grail.cs.washington.edu/software/cmvs/ (accessed on 3 December 2010).
- Furukawa, Y.; Ponce, J. Accurate, dense, and robust multi-view stereopsis. IEEE Trans. Pattern Anal. Mach. Intell 2010, 32, 1362–1376. [Google Scholar]
- Seitz, S.; Curless, B.; Diebel, J. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; 1, pp. 519–528.
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. Multi-View Stereo. Available online: http://vision.middlebury.edu/mview/ (accessed on 12 April 2012).
- Strecha, C.; von Hansen, C.; Gool, L.V.; Fua, P.; Thoennessen, U. On Benchmarking Camera Calibration and Multi-View Stereo for High Resolution Imagery. Proceedins of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 24–26 June 2008.
- Strecha, C.; Fransens, R. Wide-Baseline Stereo from Multiple Views: A Probabilistic Account. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; pp. I:552–I:559.
- Strecha, C.; Fransens, R.; van Gool, L. Combined Depth and Outlier Estimation in Multi-View Stereo. Proceedins of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; 2, pp. 2394–2401.
- Hirschmuller, H. Accurate and Efficient Stereo Processing by Semi-Global Matching and Mutual Information. Proceedins of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; 2, pp. 807–814.
- Hirschmüller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell 2008, 30, 328–341. [Google Scholar]
- Baillard, C.; Zisserman, A. A plane-sweep strategy for the 3D reconstruction of buildings from multiple images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2000, 33, 56–62. [Google Scholar]
- Vu, H.H.; Labatut, P.; Pons, J.P.; Keriven, R. High accuracy and visibility-consistent dense multi-view stereo. IEEE Trans. Pattern Anal. Mach. Intell 2011, 34, 889–901. [Google Scholar]
- Eisenbeiss, H.; Sauerbier, M. Investigation of uav systems and flight modes for photogrammetric applications. Photogramm. Rec 2011, 26, 400–421. [Google Scholar]
- Küng, O.; Strecha, C.; Beyeler, A.; Zufferey, J.C.; Floreano, D.; Fua, P.; Gervaix, F. The Accuracy of Automatic Photogrammetric Techniques on Ultra-Light UAV Imagery. In IAPRS, Proceedings of the International Conference on Unmanned Aerial Vehicle in Geomatics (UAV-g), Zurich, Switzerland, 14–16 September 2011; 2011; 38. [Google Scholar]
- Vallet, J.; Panissod, F.; Strecha, C. Photogrammtric Performance of an Ultralightweight Swinglet UAV. In IAPRS, Proceedings of the International Conference on Unmanned Aerial Vehicle in Geomatics (UAV-g), Zurich, Switzerland, 14–16 September 2011; 2011; 38. [Google Scholar]
- Hirschmüller, H. Semi-Global Matching Motivation, Developments and Applications. Proceedins of the Invited Paper at the 54th Photogrammetric Week, Stuttgart, Germany, 5–11 September 2011; pp. 173–184.
- Pix4D. Available online: http://pix4d.com/ (accessed on 12 April 2012).
- BAE Systems. Next-Generation Automatic Terrain Extraction (NGATE). Available online: http://www.socetgxp.com/docs/products/modules/ss_ngate.pdf (accessed on 11 December 2011).
- Rosnell, T.; Honkavaara, E.; Nurminen, K. On geometric processing of multi-temporal image data collected by light UAV systems. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2011, 38, 1–6. [Google Scholar]
- Walker, J.P.; Willgoose, G.R. A comparative study of australian cartometric and photogrammetric digital elevation model accuracy. Photogramm. Eng. Remote Sensing 2006, 72, 771–779. [Google Scholar]
- Shrestha, R.L.; Carter, W.E.; Lee, M.; Finer, P.; Sartori, M. Airborne laser swath mapping: ALSM. Civil Eng 1999, 59, 83–94. [Google Scholar]
- Töyrä, J.; Pietroniro, A.; Hopkinson, C.; Kalbfleisch, W. Assessment of airborne scanning laser altimetry (lidar) in a deltaic wetland environment. Can. J. Remote Sens 2003, 29, 718–728. [Google Scholar]
- Farah, A.; Talaat, A.; Farrag, F. Accuracy assessment of digital elevation models using GPS. Artif. Satellites 2008, 43, 151–161. [Google Scholar]
- Hodgson, M.; Bresnahan, P. Accuracy of airborne lidar-derived elevation: Empirical assessment and error budget. Photogramm. Eng. Remote Sensing 2004, 70, 331–339. [Google Scholar]
- Vaaja, M.; Hyyppä, J.; Kukko, A.; Kaartinen, H.; Hyyppä, H.; Alho, P. Mapping topography changes and elevation accuracies using a mobile laser scanner. Remote Sens 2011, 3, 587–600. [Google Scholar]
- Mikrokopter. Available online: http://www.mikrokopter.de/ucwiki/en/MikroKopter (accessed on 28 May 2012).
- Geoscience Australia. Available online: http://www.ga.gov.au/geodesy/ausgeoid/nvalcomp.jsp (accessed on 11 December 2010).
- Farenzena, M.; Fusiello, A.; Gherardi, R. Structure-and-Motion Pipeline on a Hierarchical Cluster Tree. Proceedings of the IEEE Computer Vision Workshops (ICCV Workshops), 2009 IEEE 12th International Conference, Kyoto, Japan, 27 September–4 October 2010; pp. 1489–1496.
- Libsift Sourceforge Project. Available online: http://libsift.sourceforge.net/ (accessed on 10 September 2010).
- Zhang, Y.; Zhang, Z.; Zhang, J.; Wu, J. 3D building modelling with digital map, lidar data and video image sequences. Photogramm. Rec 2005, 20, 285–302. [Google Scholar]
- Zhang, Z.; Wu, J.; Zhang, Y.; Zhang, J. Multi-view 3D city model generation with image sequences. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2003, 34, 351–356. [Google Scholar]
- Kocaman, S.; Zhang, L.; Gruen, A.; Poli, D. 3D City Modeling from High-Resolution Satellite Images. Proceedings of ISPRS Workshop on Topographic Mapping from Space, Ankara, Turkey, 14–16 February 2006; XXXVI. Part 1/W41.
- Hanley, H. Geopositioning accuracy of IKONOS imagery: Indications from two dimensional transformations. Photogramm. Rec 2001, 17, 317–329. [Google Scholar]
- Myriax. Available online: http://www.eonfusion.com (accessed on 2 October 2009).
- Lu, F.; Ji, X.; Dai, Q.; Er, G. Multi-View Stereo Reconstruction with High Dynamic Range Texture. Proceedings of the Computer Vision—ACCV 2010, Queenstown, New Zealand, 8–12 November 2011; Springer: Berlin, Heidelberg, Germany, 2011; 6493/2011, pp. 412–425. [Google Scholar]
- Mičušík, B.; Košecká, J. Multi-view superpixel stereo in urban environments. Int. J. Comput. Vis 2010, 89, 106–119. [Google Scholar]




| ERMSE | NRMSE | HRMSE | ENRMSE | ENHRMSE | |
|---|---|---|---|---|---|
| Centroid based transformations | 15.2 | 14.4 | 53.1 | 14.8 | 34.4 |
| Mean based transformations | 18.0 | 15.4 | 49.0 | 16.7 | 33.5 |
| Description | Tx | ± | Ty | ± | Tz | ± | Rx | ± | Ry | ± | Rz | ± | Scale | +/− |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All trays | 536, 154.565 | 61.1 | 5, 262, 637.035 | 98.2 | 30.916 | 68.6 | −6.216 | 1.1 | −18.8783 | 2.5 | −32.9718 | 0.9 | 9.4409 | 8.2 |
| 10 trays | 536, 154.522 | 108.6 | 5, 262, 636.977 | 169.9 | 30.837 | 118.6 | 34.6250 | 1.9 | 9.4528 | 4.3 | −73.8128 | 1.4 | 9.4383 | 13.4 |
| 6 trays | 536, 154.401 | 154.2 | 5, 262, 636.794 | 244.2 | 30.6975 | 165.2 | 3.2108 | 2.5 | −3.1168 | 6.2 | −48.6806 | 1.9 | 9.4352 | 17.8 |
| Description | Tx | ± | Ty | ± | Tz | ± | Rx | ± | Ry | ± | Rz | ± | Scale | ± |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All trays | 536, 154.554 | 60.7 | 5, 262, 637.027 | 97.6 | 30.947 | 68.1 | −56.4816 | 1.1 | −31.4445 | 2.5 | −32.9719 | 0.9 | 9.4415 | 8.1 |
| 10 trays | 536, 154.511 | 108.1 | 5, 262, 636.970 | 169.1 | 30.870 | 118.1 | −40.7732 | 1.8 | 3.1694 | 4.3 | −42.3968 | 1.4 | 9.4389 | 13.4 |
| 6 trays | 536, 154.392 | 152.8 | 5, 262, 636.792 | 242.0 | 30.732 | 163.7 | 3.2107 | 2.5 | −3.1168 | 6.1 | −48.6806 | 1.9 | 9.4358 | 17.6 |
| Description | GCP Count | Test Count | ERMSE | NRMSE | HRMSE | ENRMSE | EN HRMSE |
|---|---|---|---|---|---|---|---|
| All trays | 21 | 34 | 28.1 | 18.7 | 49.2 | 23.4 | 34.4 |
| 10 trays | 10 | 34 | 67.5 | 43.8 | 102.9 | 55.6 | 75.4 |
| 6 trays | 6 | 34 | 143.0 | 97.0 | 171.0 | 120.0 | 140.4 |
| Description | GCP Count | Test Count | ERMSE | NRMSE | HRMSE | ENRMSE | EN HRMSE |
|---|---|---|---|---|---|---|---|
| All trays | 21 | 34 | 36.8 | 19.6 | 21.0 | 28.2 | 27.0 |
| 10 trays | 10 | 34 | 76.9 | 43.8 | 73.6 | 60.3 | 66.5 |
| 6 trays | 6 | 34 | 153.2 | 97.5 | 143.7 | 125.3 | 133.7 |
| Description | Tx | ± | Ty | ± | Tz | ± | Rx | ± | Ry | ± | Rz | ± | Scale | ± |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dense GCP coverage | 536; 154.462 | 39.3 | 5;262; 636.876 | 73.4 | 30.905 | 46.4 | −6.2140 | 0.8 | −18.8730 | 2.0 | −58.1048 | 0.6 | 9.4474 | 5.9 |
| Very sparse GCP coverage | 536; 154.393 | 94.9 | 5;262; 636.718 | 193.5 | 30.812 | 104.6 | 0.0695 | 1.8 | −0.0215 | 5.4 | −45.5388 | 1.4 | 9.4445 | 13.1 |
| GCPs along edge (≥6 cluster points) | 536; 154.484 | 64.5 | 5;262; 636.881 | 117.0 | 30.935 | 73.9 | −15.6391 | 1.3 | 9.4484 | 3.3 | −36.1137 | 1.0 | 9.4451 | 9.7 |
| GCPs along edge (≥8 cluster points) | 536; 154.483 | 68.4 | 5;262; 636.875 | 125.5 | 30.941 | 79.1 | 0.0689 | 1.4 | −0.0236 | 3.5 | −39.2554 | 1.2 | 9.4465 | 11.0 |
| GCPs along edge and within (≥6 cluster points) | 536; 154.468 | 50.9 | 5;262; 636.866 | 96.1 | 30.928 | 59.4 | 12.6356 | 1.0 | −6.3064 | 2.7 | −26.6889 | 0.8 | 9.4479 | 7.7 |
| GCPs along edge and within (≥8 cluster points) | 536; 154.466 | 53.0 | 5;262; 636.860 | 101.7 | 30.934 | 62.1 | −12.4972 | 1.1 | −6.3063 | 2.8 | −58.1050 | 0.9 | 9.4495 | 8.5 |
| Description | Map | GCP Count | Test Count | ERMSE | NRMSE | HRMSE | ENRMSE | ENHRMSE |
|---|---|---|---|---|---|---|---|---|
| Dense GCP coverage | a | 27 | 13 | 15.2 | 3.0 | 40.0 | 9.1 | 24.8 |
| Very sparse GCP coverage | b | 5 | 31 | 87.9 | 77.6 | 38.7 | 82.7 | 71.3 |
| GCPs along edge (≥6 cluster points) | c | 12 | 24 | 15.5 | 1.3 | 63.1 | 8.4 | 37.5 |
| GCPs along edge (≥8 cluster points) | d | 11 | 24 | 9.6 | 1.7 | 61.7 | 5.7 | 36.1 |
| GCPs along edge and within (≥6 cluster points) | e | 16 | 21 | 6.6 | 2.8 | 59.9 | 4.7 | 34.8 |
| GCPs along edge and within (≥8 cluster points) | f | 15 | 21 | 0.7 | 1.3 | 59.1 | 1.0 | 34.1 |
| Description | Map | GCP Count | Test Count | ERMSE | NRMSE | HRMSE | ENRMSE | EN HRMSE |
|---|---|---|---|---|---|---|---|---|
| Dense GCP coverage | a | 27 | 21 | 8.1 | 22.6 | 41.0 | 15.4 | 27.5 |
| Very sparse GCP coverage | b | 5 | 21 | 64.8 | 47.7 | 44.0 | 56.3 | 53.0 |
| GCPs along edge(≥6 cluster points) | c | 12 | 21 | 6.3 | 25.4 | 62.9 | 15.9 | 39.3 |
| GCPs along edge(≥8 cluster points) | d | 11 | 21 | 13.8 | 28.9 | 61.0 | 21.3 | 39.8 |
| GCPs along edge and within (≥6 cluster points) | e | 16 | 21 | 17.0 | 22.8 | 59.7 | 19.9 | 38.2 |
| GCPs along edge and within (≥8 cluster points) | f | 15 | 21 | 24.6 | 24.5 | 58.5 | 24.5 | 39.3 |
Share and Cite
Harwin, S.; Lucieer, A. Assessing the Accuracy of Georeferenced Point Clouds Produced via Multi-View Stereopsis from Unmanned Aerial Vehicle (UAV) Imagery. Remote Sens. 2012, 4, 1573-1599. https://doi.org/10.3390/rs4061573
Harwin S, Lucieer A. Assessing the Accuracy of Georeferenced Point Clouds Produced via Multi-View Stereopsis from Unmanned Aerial Vehicle (UAV) Imagery. Remote Sensing. 2012; 4(6):1573-1599. https://doi.org/10.3390/rs4061573
Chicago/Turabian StyleHarwin, Steve, and Arko Lucieer. 2012. "Assessing the Accuracy of Georeferenced Point Clouds Produced via Multi-View Stereopsis from Unmanned Aerial Vehicle (UAV) Imagery" Remote Sensing 4, no. 6: 1573-1599. https://doi.org/10.3390/rs4061573
APA StyleHarwin, S., & Lucieer, A. (2012). Assessing the Accuracy of Georeferenced Point Clouds Produced via Multi-View Stereopsis from Unmanned Aerial Vehicle (UAV) Imagery. Remote Sensing, 4(6), 1573-1599. https://doi.org/10.3390/rs4061573






