Extracting More Data from LiDAR in Forested Areas by Analyzing Waveform Shape
Abstract
:1. Introduction
1.1. Potential Benefits of Identifying LiDAR Pulses for Forestry
1.2. Waveform LiDAR
2. Method
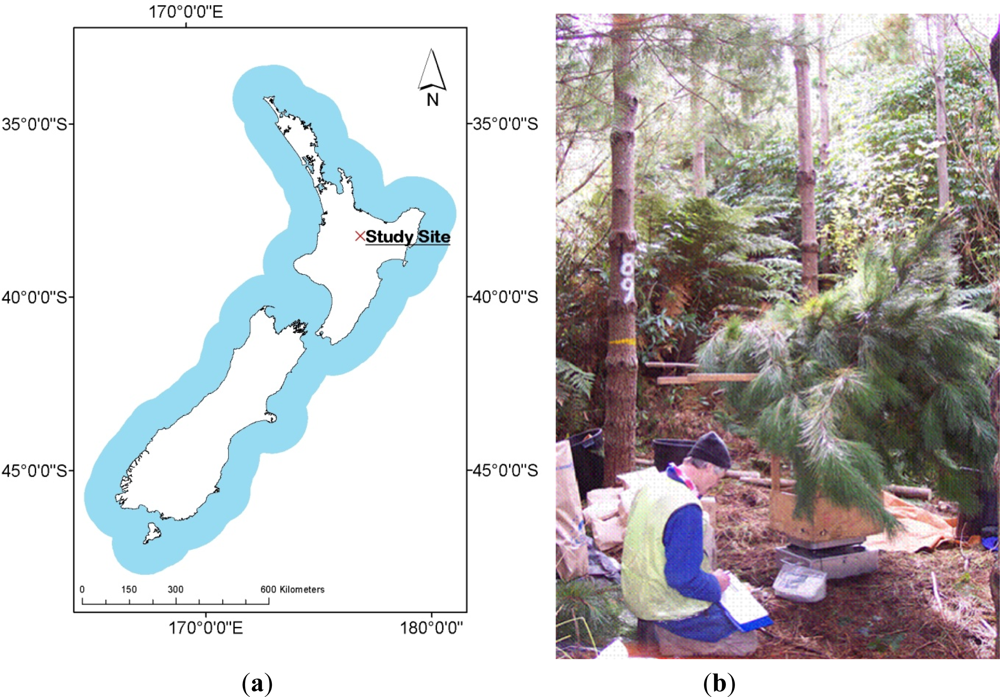
2.1. Data Collection
2.2. Waveform Analysis
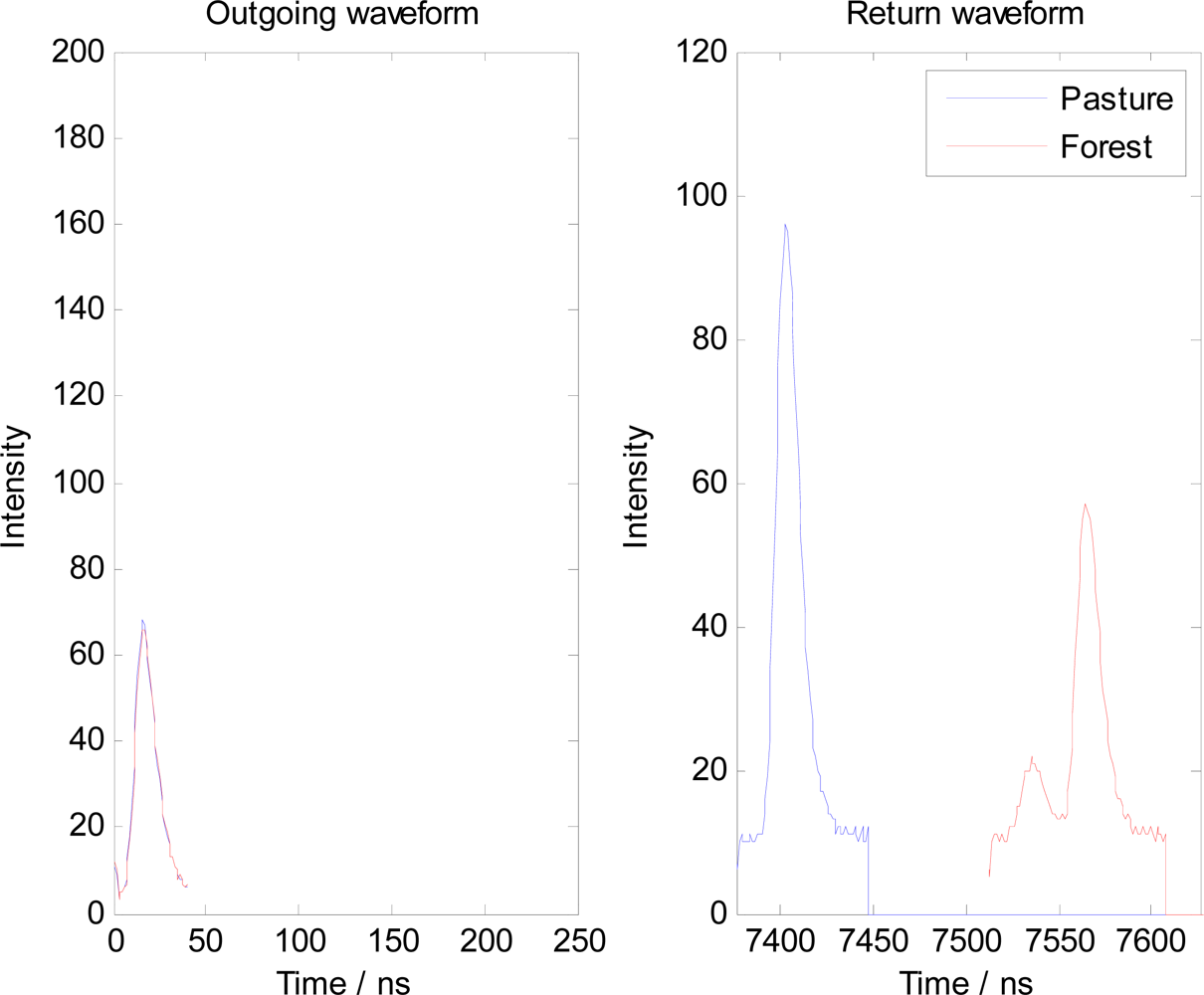
- The forest waveform consists of multiple peaks (returns)
- The peak intensities (in arbitrary units defined by the hardware) of the forest waveform are less than the open pasture.
- Georeference every 1 ns waveform sample to determine which waveforms (or part waveforms) fall into the field plots.
- Determine a ground surface for the field plots.
- Employ Gaussian fitting to describe each peak with a peak height and half-height width.
- Employ exponential curve-fitting to determine the exponential decay rate of each peak.
- Determine the above ground height of each peak (for comparison with field measured foliage data).
- was achieved using the methods and code in Parrish [21], adapted for the New Zealand NZGD2000 coordinate system. The field plots were located using a high-grade, differentially-corrected GPS unit, and the selection of waveform samples simply consisted of any that fell into the vertical space above the field plots.
- was achieved by using the discrete LiDAR data set for the area flown. The ground-filtering algorithm (GroundFilter.exe) in FUSION [24] was used to select only ground returns (based on the linear filtering method of Kraus and Pfeifer [25]). These ground returns were interpolated into a raster using FUSION’s GridSurfaceCreate.exe algorithm.
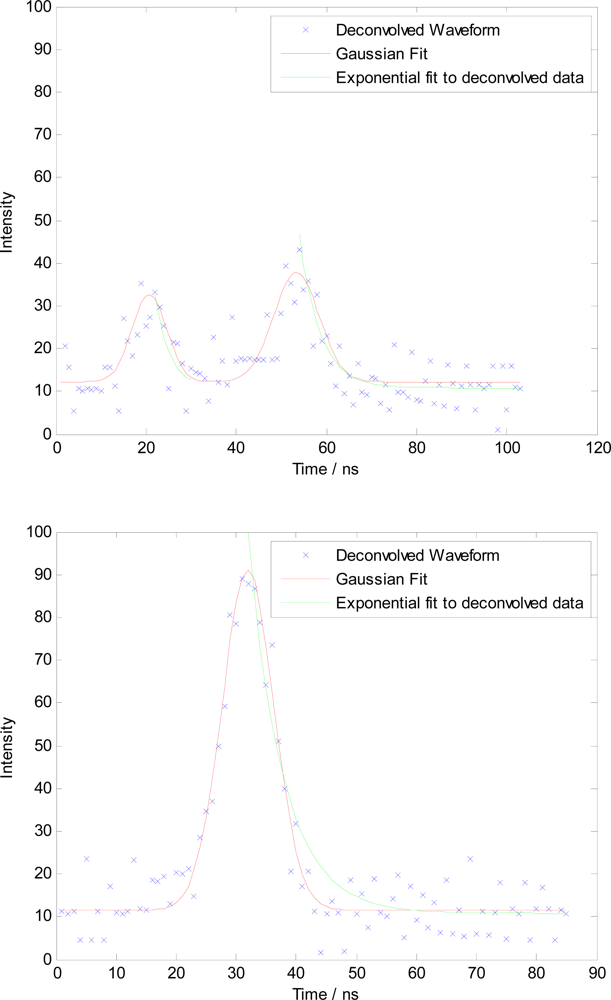
- As we are interested in decay rates of waveform peaks in (4), we do not need to search for additional ‘hidden’ peaks as other authors have. Peaks that are hidden through close proximity to another or low peak amplitude will not have sufficient data points after the peak to give a good decay. As such, we only select peaks in the waveform data with a corresponding discrete return. Gaussians were fit using Matlab’s fminsearch function, a simplex search method given in [26]. This is a direct search method that does not use numerical or analytic gradients. The number of Gaussians and a first-guess of their locations could be specified by the number and location of returns in the discrete datset. The peak height and half-height width of each Gaussian is recorded, as well as the R2 value of the fit.
- In (3), the location of each peak to be analyzed will have been determined. An exponential curve fit of the type y = Ce−λx was applied from the peak maximum to the following local minima (either before the end of the waveform or before the next peak). The exponential curve was determined, also using Matlab’s fminsearch algorithm, taking the peak maximum as a start point for C, and 0.2 as a start point for λ. The final value for λ is recorded along with the R2 value of the fit.
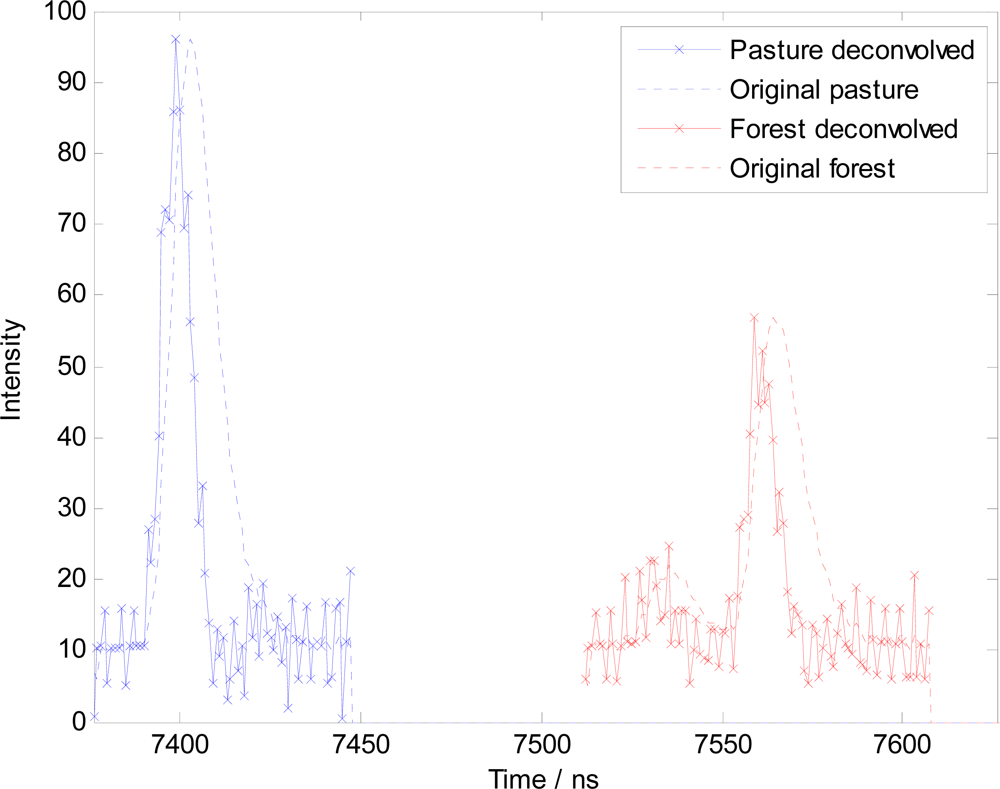
- As this study is a proof of concept, only peaks that corresponded to a return in the discrete data set were analyzed (see step 3). Ground height was obtained by linear interpolation of the ground surface generated in (2) to the discrete return’s x, y coordinates. Height above ground was the discrete return height, minus the interpolated ground height. We made the assumption that the waveform peak was coincident with the discrete return, which is appropriate, as the ALTM discrete return data and waveform data were generated from the same input signal. Using the coordinates from the well-calibrated discrete return data eliminated small potential errors from georeferencing the waveform, as the ranging calculation was calibrated on the convolved peak, and not the translated peak observed in the deconvolution. Waveform LiDAR is known to give many more returns than discrete LiDAR, so by only selecting returns with a corresponding discrete return we are limiting our results to only the strongest peaks available. This should demonstrate any correlations most clearly, which may be hidden when including additional peaks with limited data due to close proximity to another peak or very low amplitudes.
2.3. Metric Analysis
3. Results and Discussion
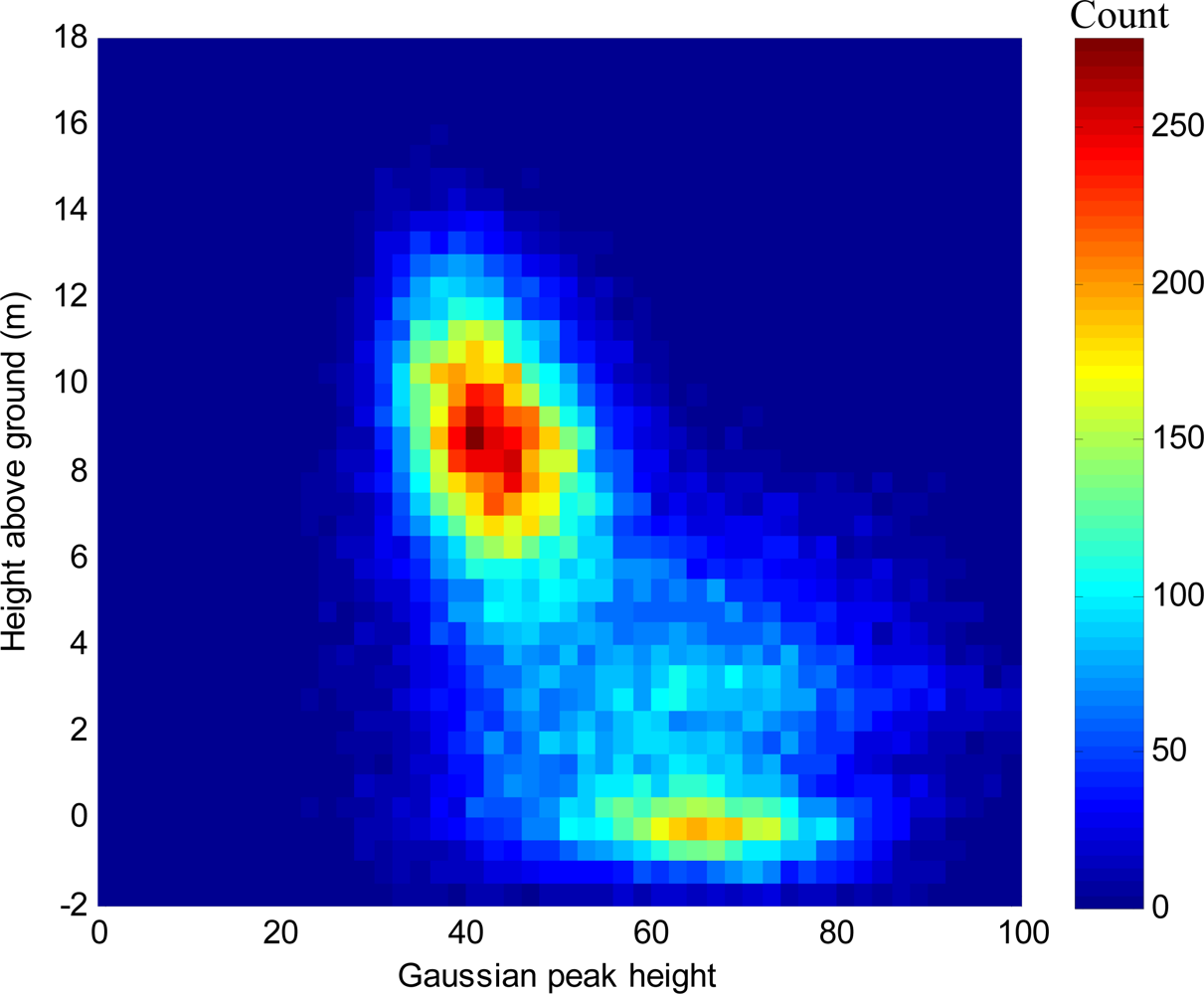
3.1. Gaussian Peak Height
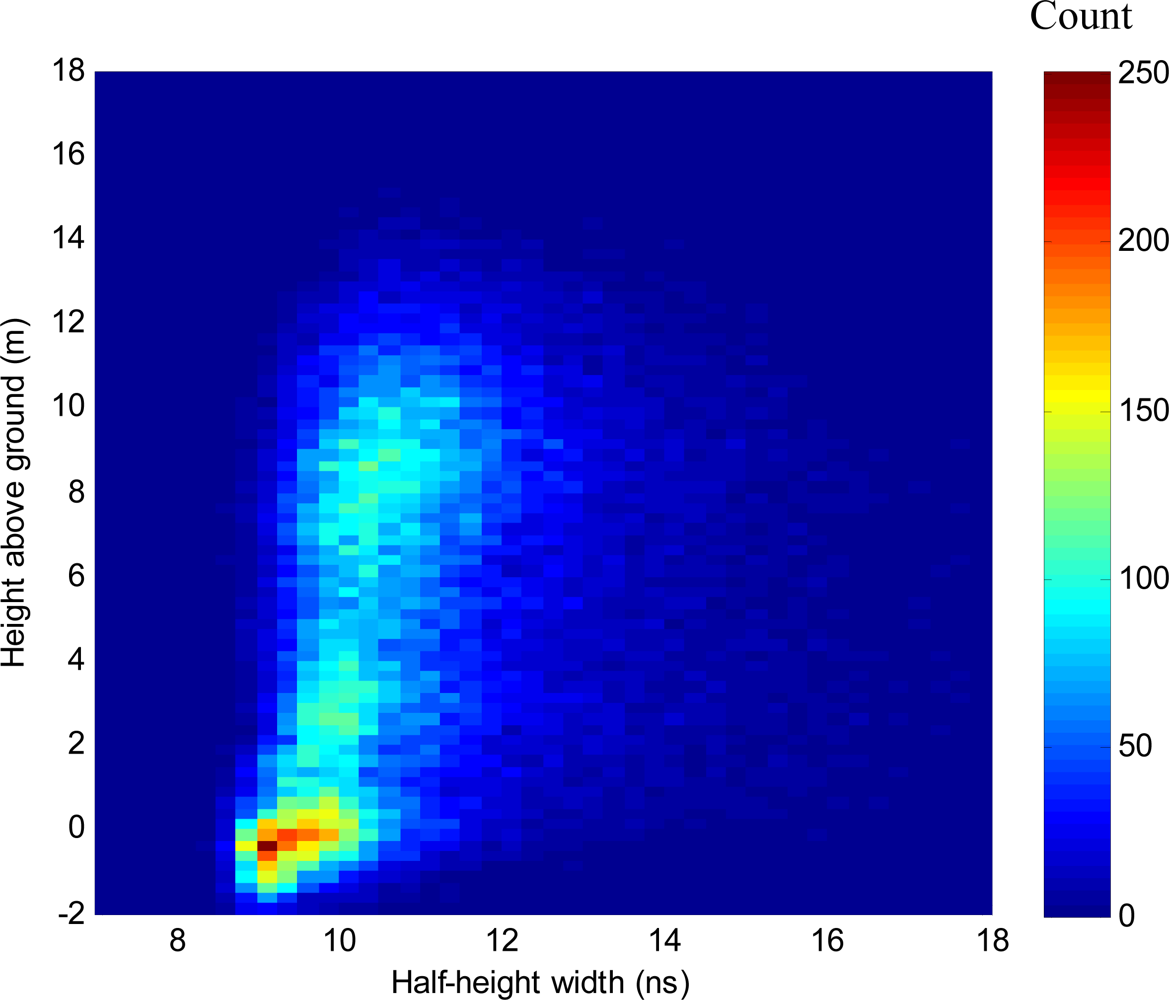
3.2. Gaussian Half-Height Width
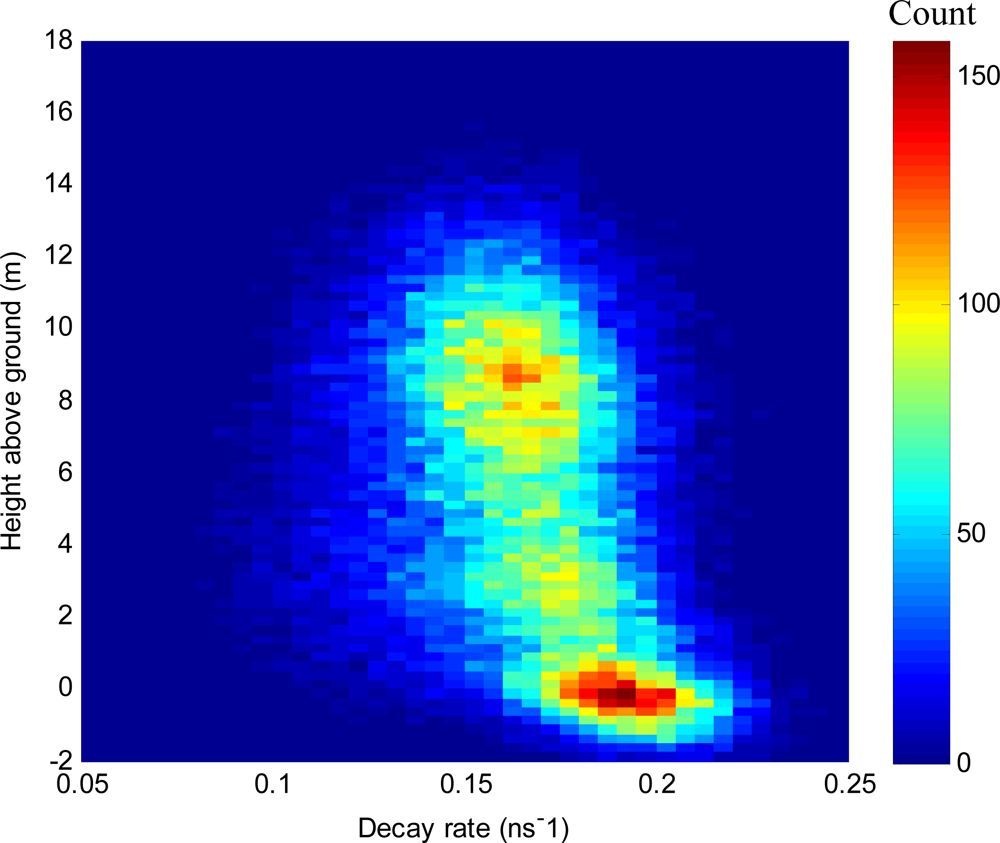
3.3. Pulse Decay Rate
3.4. Comparison with Foliage Density
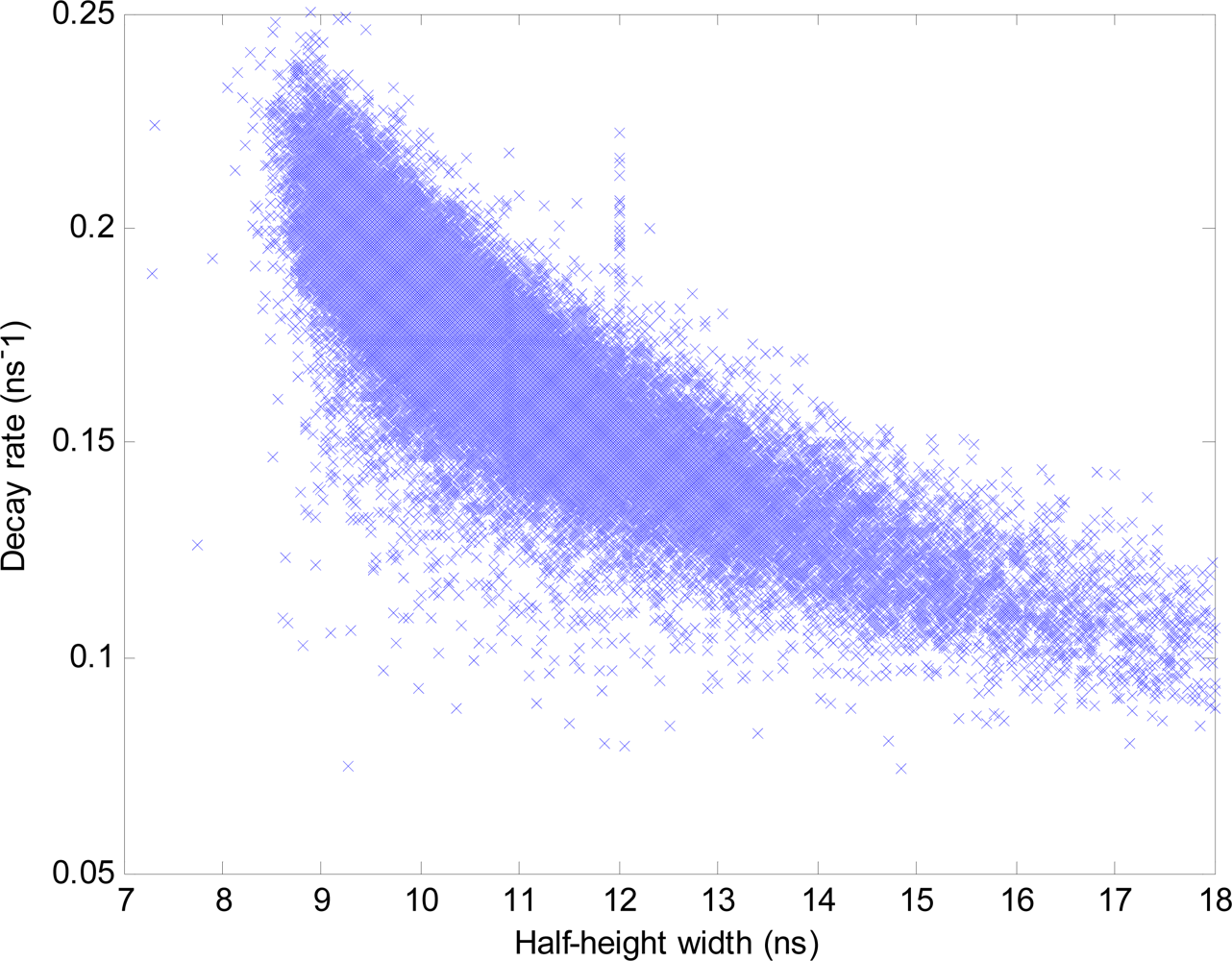
3.5. Models for Interpreting Waveform Shape
- The standard interpretation is as the result of a series of discrete ‘hard’ returns, such as may be achieved by well-separated layers of foliage. These supposed layers are of a thickness equal to or less than the return distance travelled by the laser pulse in one sampling period (0.15 m for 1 ns sampling).
- As the result of transmission and reflectance from a volume of semi-transparent foliage which attenuates the radiation exponentially.
4. Conclusions
Acknowledgments
References
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm 2004, 59, 85–101. [Google Scholar]
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne lidar data: A review of critical issues. Remote Sens 2010, 2, 833–860. [Google Scholar]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Espirito-Santo, F.D.B.; Hunter, M.O.; de Oliveira, R., Jr. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett 2005, 32, L22S02. [Google Scholar]
- Naesset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ 1997, 61, 246–253. [Google Scholar]
- Maclean, G.; Krabill, W. Gross-merchantable timber volume estimation using an airborne lidar system. Can. J. Remote Sens 1986, 12, 7–18. [Google Scholar]
- Beets, P.N.; Reutebuch, S.; Kimberley, M.O.; Oliver, G.R.; Pearce, S.H.; McGaughey, R.J. Leaf area index, biomass carbon and growth rate of radiata pine genetic types and relationships with lidar. Forests 2011, 2, 637–659. [Google Scholar]
- Stephens, P.R.; Watt, P. J.; Loubser, D.; Haywood, A.; Kimberley, M.O. Estimation of Carbon Stocks in New Zealand Planted Forests Using Airborne Scanning Lidar. ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007; pp. 389–394.
- Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D segmentation of single trees exploiting full waveform lidar data. ISPRS J. Photogramm 2009, 64, 561–574. [Google Scholar]
- Morsdorf, F.; Kotz, B.; Meier, E.; Itten, K.; Allgower, B. Estimation of LAI and fractional cover from small footprint airborne laser scanning data based on gap fraction. Remote Sens. Environ 2006, 104, 50–61. [Google Scholar]
- Chasmer, L.; Hopkinson, C.; Treitz, P. Investigating laser pulse penetration through a conifer canopy by integrating airborne and terrestrial lidar. Can. J. Remote Sens 2006, 32, 116–125. [Google Scholar]
- Jutzi, B.; Stilla, U. Characteristics of the measurement unit of a full-waveform laser system. Revue Française de Photogrammétrie et de Télédétection 2006, 182, 17–22. [Google Scholar]
- Reitberger, J.; Krzystek, P.; Stilla, U. Analysis of full waveform lidar data for the classification of deciduous and coniferous trees. Int. J. Remote Sens 2008, 29, 1407–1431. [Google Scholar]
- Parrish, C.E.; Jeong, I.; Nowak, R.D.; Smith, R. Empirical comparison of full-waveform lidar algorithms: Range extraction and discrimination performance. Photogramm. Eng. Remote Sensing 2011, in press. [Google Scholar]
- Chauve, A.; Vega, C.; Durrieu, S.; Bretar, F.; Allouis, T.; Deseilligny, P.; Puech, W. Processing full-waveform lidar data in an alpine coniferous forest: Assessing terrain and tree height quality. Int. J. Remote Sens 2009, 30, 27. [Google Scholar]
- Hofton, M.A.; Minster, J.B.; Blair, J.B. Decomposition of laser altimeter waveforms. IEEE Trans. Geosci. Remote Sens 2000, 38, 1989–1996. [Google Scholar]
- Reitberger, J.; Krzystek, P.; Stilla, U. Analysis of Full Waveform Lidar Data for Tree Species Classification. In International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Symposium of ISPRS Commission III “Photogrammetric Computer Vision PCV '06”, Bonn, Germany, 20–22 September 2006; 2006; 36, pp. 228–233. [Google Scholar]
- Persson, Å.; Söderman, U.; Töpel, J.; Ahlberg, S. Visualization and Analysis of Full-Waveform Airborne Laser Scanner Data. In International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, ISPRS WG III/3, III/4, V/3 Workshop “Laser scanning 2005”, Enschede, The Netherlands, 12–14 September 2005; 2005; 36, pp. 103–108. [Google Scholar]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitizing airborne laser scanner. ISPRS J. Photogramm 2006, 60, 100–112. [Google Scholar]
- Jupp, D.; Culvenor, D.S.; Lovell, J.L.; Newnham, G.J.; Strahler, A.H.; Woodcock, C.E. Estimating forest LAI profiles and structural parameters using a ground-based laser called ‘Echidna®. Tree Physiol 2009, 29, 171–181. [Google Scholar]
- Drake, J.B.; Dubayah, R.; Clark, D.B.; Knox, R.G.; Blair, J.B.; Hofton, M.A.; Chazdon, R.L.; Weishampel, J.F.; Prince, S. Estimation of tropical forest structural characteristics using large-footprint lidar. Remote Sens. Environ 2002, 79, 305–319. [Google Scholar]
- Parrish, C.E. Vertical Object Extraction from Full-Waveform Lidar Data Using a 3D Wavelet-Based Approach. Ph.D. Thesis, The University of Wisconsin-Madison, Madison, WI, USA; 2007. [Google Scholar]
- Beets, P.; Lane, P. Specific leaf area of pinus radiata as influenced by stand age, leaf age, and thinning. New Zealand J. Forest. Sci 1987, 17, 283–291. [Google Scholar]
- Madgwick, H. Above-ground dry-matter content of a young close-spaced pinus radiata stand. New Zealand J. Forest. Sci 1981, 11, 203–209. [Google Scholar]
- McGaughey, R.J. Fusion. US Pacific Northwest Research Station, Forest Service: Salt Lake City, UT, USA, 2010. Available online: http://www.fs.fed.us/eng/rsac/fusion/ (accessed on 7 December 2011).
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm 1998, 53, 193–203. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the nelder-mead simplex method in low dimensions. SIAM J. Optimiz 1999, 9, 112–147. [Google Scholar]

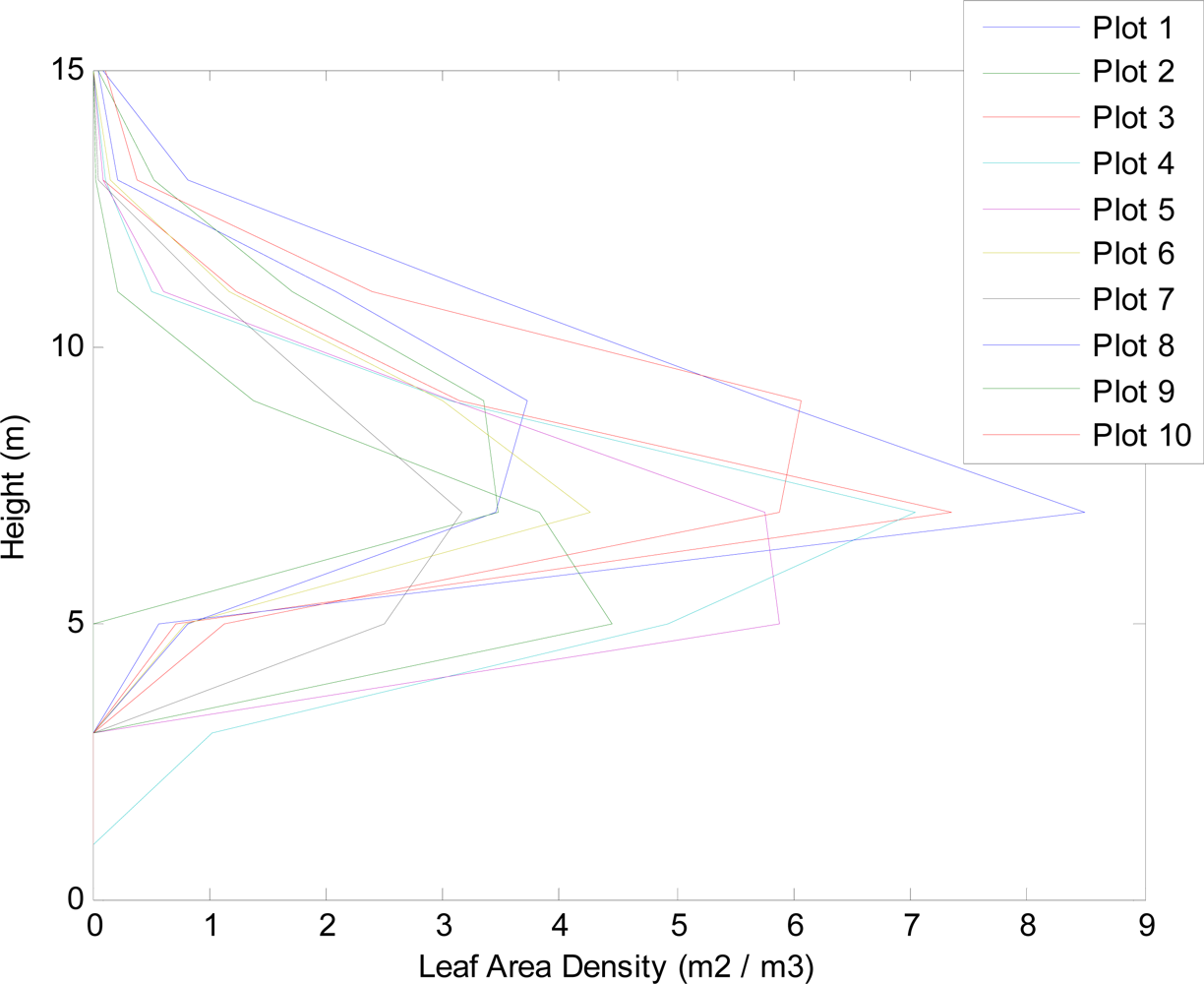
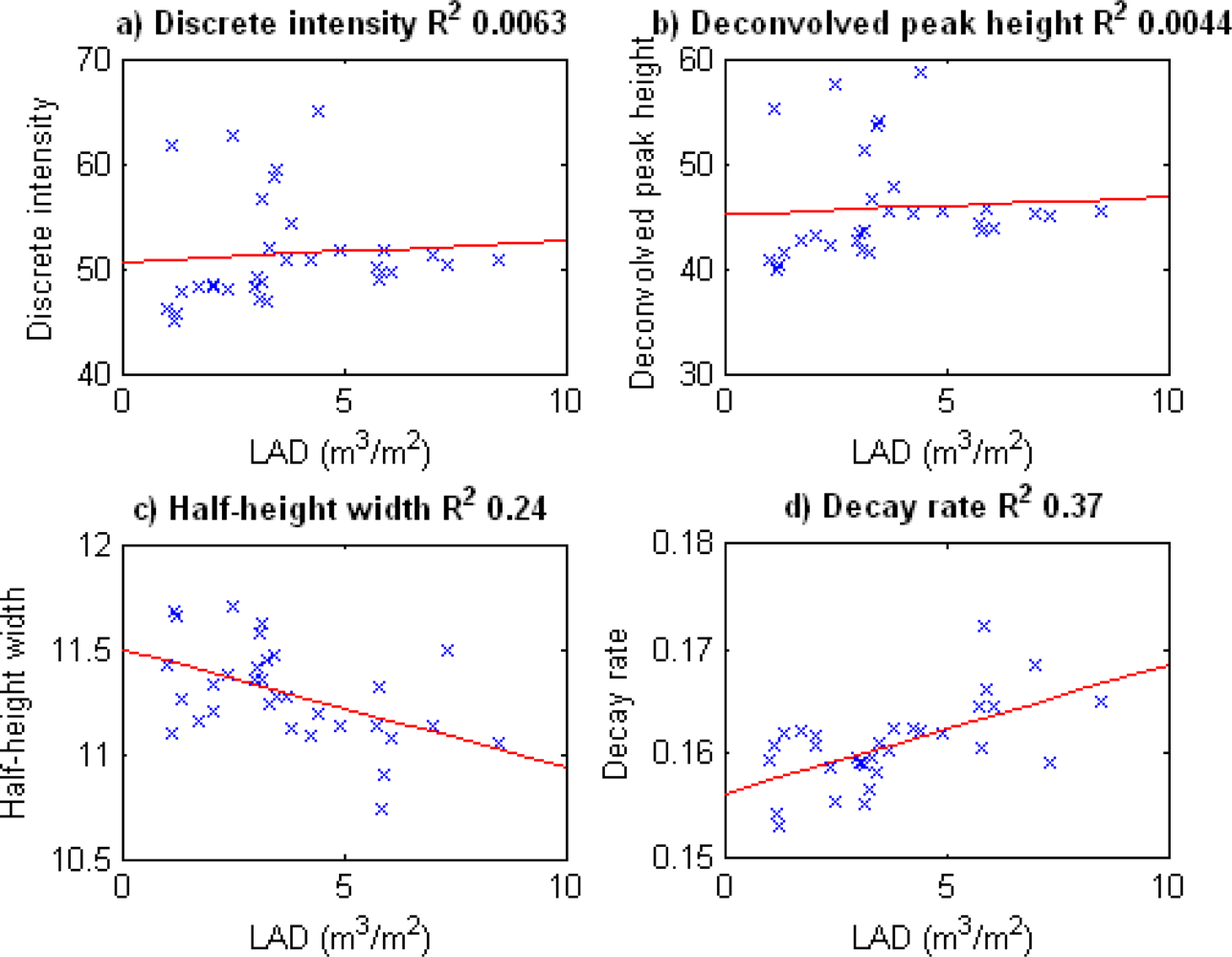
| Plot | Number of Waveforms with Peak Intensity > 25 | Number of Returns | Number of Returns with Good Quality Fits and Intensity > 25 | Percentage Used |
|---|---|---|---|---|
| 1 | 12,558 | 11,616 | 4,570 | 28% |
| 2 | 16,150 | 14,939 | 5,608 | 27% |
| 3 | 12,305 | 11,261 | 4,942 | 33% |
| 4 | 11,332 | 10,286 | 4,207 | 29% |
| 5 | 12,326 | 11,075 | 4,541 | 31% |
| 6 | 13,810 | 13,130 | 5,488 | 32% |
| 7 | 12,687 | 11,992 | 4,598 | 27% |
| 8 | 14,849 | 14,210 | 4,847 | 25% |
| 9 | 15,862 | 15,145 | 8,746 | 45% |
| 10 | 14,312 | 13,513 | 4,531 | 24% |
| Total | 136,191 | 127,167 | 52,078 | 30% |
Share and Cite
Adams, T.; Beets, P.; Parrish, C. Extracting More Data from LiDAR in Forested Areas by Analyzing Waveform Shape. Remote Sens. 2012, 4, 682-702. https://doi.org/10.3390/rs4030682
Adams T, Beets P, Parrish C. Extracting More Data from LiDAR in Forested Areas by Analyzing Waveform Shape. Remote Sensing. 2012; 4(3):682-702. https://doi.org/10.3390/rs4030682
Chicago/Turabian StyleAdams, Thomas, Peter Beets, and Christopher Parrish. 2012. "Extracting More Data from LiDAR in Forested Areas by Analyzing Waveform Shape" Remote Sensing 4, no. 3: 682-702. https://doi.org/10.3390/rs4030682
APA StyleAdams, T., Beets, P., & Parrish, C. (2012). Extracting More Data from LiDAR in Forested Areas by Analyzing Waveform Shape. Remote Sensing, 4(3), 682-702. https://doi.org/10.3390/rs4030682




