1. Introduction
A general aim of forest inventory projects is to form a basis for decision-making and sustainable use of forest resources in the form of objective statistics at the national and regional levels and for administrative units. Conventionally, the statistics are obtained for pre-defined areas for the species-specific measures of the total volume of living and dead trees and merchantable volume characteristics. Questions and issues raised by the United Nations Framework Convention on Climate Change (UNFCCC) through its “Reducing Emissions from Deforestation and Forest Degradation” (REDD) program have increased the need for forest resource inventories and widened the application of their results. Countries already having suitable national forest inventory (NFI) frameworks can harness their NFIs to support also the assessment of green house gas (GHG) emissions. When developing countries, such as Nepal, for instance, are addressing this kind of task, technical and methodological support provided for assessing the forest resources may become even more important than before [
1]. Due to the repetition requirements and temporal and geographical consistency conditions, the possibilities for utilizing remote sensing technology together with field inventory data are increasingly gaining the interest of the organizations responsible for the forest inventory activities related to the REDD mechanism (e.g., [
2,
3]). The operative inventory project “Forest Resource Assessment of Nepal” (FRA Nepal) belongs to the Finnish Government’s development aid toolkit. The FRA Nepal project is an example of an action that aims to develop cost-efficient inventory techniques based on information obtained from both conventional field inventories and remote sensing materials.
Biometrical modeling is also needed for inventory calculations that make use of remote sensing: for example, the calculation system for the FRA Nepal project consists of models for height or volume by tree species, which are necessary for imputing the values missing from the field data. Obtaining data from the tree level to the stand or plot level, or to the regional, level is a process by which inventory calculations and reporting modules are developed. To put all of this together, a forest inventory database is needed.
To combine field sample plot observations, digital map data and satellite image data, for classification or prediction purposes, multi-source forest inventory (MSFI) techniques have been developed [
4,
5]. Even if the pure inventory results are directly derived from the characteristics measured by the field sample plots, a multi-source approach aiming at the wall-to-wall mapping of forest characteristics requires remote sensing data. The necessary input data,
i.e., the ground-truth data, comes from the inventory calculation system and from the Forest Inventory Database. Tools for processing GIS and image data are further utilized, for example, when classifying satellite image pixels and performing overlaying analysis.
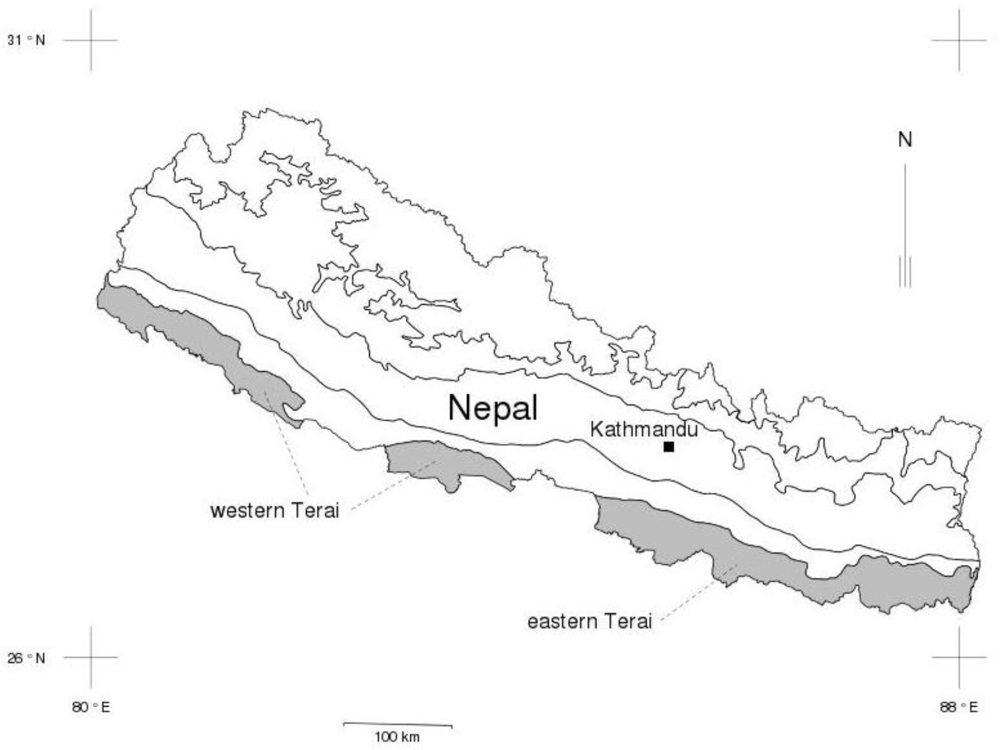
A representative and large enough field sample for MSFI is a prerequisite, so that the estimation results are of a satisfactory quality and accurate enough. However, if only a small or very sparse sample of field plots is available, it must be possible to not only utilize plots on the same image, but also on neighboring images. For the FRA Nepal project, at minimum, it would be necessary to have a relative calibration procedure that would make it possible to combine several satellite images with respect to the target inventory areas. In our study case in Terai region, the main factors affecting the availability and the usability of Landsat TM images are cloudiness and seasonal variations. If cloud-free images are available, one alternative for relative calibration is then to adjust the radiometric properties of a subject image to those of a reference image [
6–
11]. Seasonal variation effects between images can partly be decreased by aiming to use images from the same time of year [
6]. For tackling the problems caused by cloudiness, gap-filling approaches have been presented, where several images are used to cover the gaps in a selected image [
12].
The aim of this study was to produce thematic maps of forest cover (forest/non-forest) and total stand volume for the Terai region in southern Nepal using a non-parametric,
k-nearest neighbor technique. The pre-processing of Landsat TM images was conducted by using MODIS satellite data as a reference in a local correction approach. Mixed modeling was utilized for the generalization of sample tree characteristics that was conducted as a part of calculating the stand volumes by sample plots (see
Appendix). The approach used to create the forest cover map was based on a combination of Landsat TM satellite data and visual interpretation data,
i.e., a sample grid of visual interpretation plots by which we obtained the land use classification according to the FAO standard. For the volume mapping procedure, we utilized Landsat TM data, the forest cover map and the total stand volumes obtained by the field measured sample plots.
3. Methods
3.1. Building a Satellite Image Mosaic
The FAO NAFORMA project has produced a technique for creating image mosaics for the purposes of forest inventory planning [
8]. A MODIS (MYD09A1) image,
i.e., an atmospherically corrected image with a 500-m pixel size, was used as a reference for atmospherically correcting the Landsat images. The basic principle was to match the mean and the variance of the data in both images by taking into account the difference in the pixel sizes [
8]. In the technique developed by Tomppo
et al.[
8], simple linear mapping was calculated for each band and the correction was calculated separately for each Landsat image when making the mosaics. The averaging was used for the Landsat data to account for the larger resolution in the MODIS data.
The approach developed by Tomppo
et al.[
8], which they initially used in Tanzania, is close to that of the one developed by Tuominen and Pekkarinen [
7] for local radiometric correction to assist with the multi-source forest inventory. In their study, the idea was to adjust the BRDF-affected intensities in digitized aerial photography to match the local intensities of the reference imagery,
i.e., the Landsat 5 TM satellite data. Thus, the reference imagery needs to be independent of the BRDF. The local calibration was based on adjusting the mean values in a correction unit, for example, a moving circle with a radius of 40 m. Using a moving window, an adaptive correction based on the reference image digital numbers became possible; likewise, the parameters for the method were defined empirically.
In the case of Terai, approaches developed by both Tomppo
et al.[
8] and Tuominen and Pekkarinen [
7] were combined to create a local correction model. The separate Landsat TM images were corrected by applying the correction function below (see
Equation (1)) and by using MODIS image data as the underlying reference image. The objectives of the procedure presented here are as follows: (1) to match the mean and the variance of the data in both images by taking into account the differences in pixel sizes [
8] and (2) to apply the correction locally [
7] by using raster map algebra and a moving window approach to calculate the parameter values for the model.
The correction function (see Tomppo
et al.[
8]) applied for a pixel (
x,
y) was as follows:
where
f̂i (
x,
y) is the corrected data for the pixel (
x,
y) in band
i,
fi (
x,
y) is the uncorrected data in band
i, and
ai (
x,
y) and
bi (
x,
y) are the parameters computed for the given pixel (
x,
y) in band
i.
To calculate the parameters for the correction function (
Equation (1)), averaging was first used to transform the Landsat image data to match the resolution of the MODIS reference image. The common pixel size of the images after averaging is later denoted by
c. This study used the
c-value of 500 m. The raster maps “
avgLi”, “
sdLi”,
avgMj” and “
sdMj”—which represent the mean and standard deviation values of the Landsat TM data and the MODIS data in the compatible spectral wavelength bands
i and
j, respectively—were thereafter calculated using a moving window approach with a window size of
w ×
w pixels. Here, a 21 × 21 window neighborhood was utilized (
w = 21), representing approximately a 10 km neighborhood for each pixel with the size of
c. The raster maps with a pixel size of
c were computed for both image datasets: target images (Landsat TM) and reference images (MODIS).
Parameters
ai and
bi in the correction function (
Equation (1)) were calculated for each pixel (
x,
y) as follows:
where
i denotes a Landsat TM band and
j denotes a MODIS band that is compatible with
i. This study used the MODIS bands 3, 4, 1, 2, 6 and 7 as compatible bands for the Landsat TM bands 1, 2, 3, 4, 5 and 7.
Finally, the correction model (
Equation (1)) was applied in the original Landsat TM image data to produce locally corrected Landsat data in a MODIS reflectance value scale and at the original 30-m resolution. The coefficients
ai and
bi (see
Equation (2)) of the correction function (
Equation (1)) were local, being based on statistics from the neighborhood of each pixel (
x,
y). As a result, the Landsat TM pixel values were rescaled according to the local distribution parameters (mean and standard deviation) of the pixel values in the reference image bands.
In the correction approach of this study, each Landsat TM image had to first be processed separately, after which a mosaic of the corrected Landsat TM images was created. This mosaic was used as input for the forest/non-forest classification and the wall-to-wall map generation of a forest variable (stand volume, m3·ha−1).
The resolution (c) of the raster maps representing the mean and standard deviation and the size of the moving window (w) are user-defined parameters. Here, we used a resolution corresponding to that of the reference MODIS image, i.e., averaging was used only for Landsat images, as mentioned above. The size of the moving window (w) determines the flexibility of local correction. However, the window size (w) should be large enough to enable valid computations of the mean and standard deviation. In this case, it was not possible to conduct an exhaustive search for the resolution and neighborhood size (w), and therefore, we evaluated the result by checking the visual appearance of the resulting image mosaic. A good-quality reference image without any extreme pixel values is needed for a successful result.
3.2. Nearest Neighbors Techniques
A non-parametric, multi-source forest inventory method based on the
k-nearest neighbor (
k-NN) estimation (see Tomppo [
4], Tomppo
et al.[
5]), an approach recently reviewed by McRoberts [
25], was applied in the production of forest cover and volume maps in the Terai region. In this study, the population units (the target set of pixels) were the pixels in the satellite image. The satellite image bands were used as the ancillary variables (feature variables) with observations for all units of the population. The forest variables with observations only available for a sample (the reference set of pixels) were denoted as response variables. In practice, the reference set is built by querying the satellite image in the locations of sample plots, whereas the aim of the nearest neighbors approach is to impute the response variable values to the target set elements.
The classification was based on a pixel-by-pixel analysis, where the nearest neighbors for a target pixel among all the reference pixels (the pixels covering the center point of a sample plot) were determined using weighted Euclidean distance in spectral feature space (see Tokola [
26]; for this in matrix form, see, e.g., McRoberts [
25]):
where
nb is the number of bands,
i is the target set element for which a prediction is sought and
j is a reference set element,
bih and
bjh are spectral band values for the pixels
i and
j on band
h, respectively, and
ph is the empirical parameter for band
h.
For the target pixel
i, the
k-nearest neighbors (
i.e., a set of
k reference pixels to which the Euclidean distance in spectral feature space from the target pixel
i is smallest,
K(
i)={
j1(
i),…,
jk(
i)}) were sought. In the case of categorical variables, the mode value of a response variable from among the
k-nearest neighbors was the predicted class for a target pixel. In the case of continuous response variables, on the contrary, the weight
wij of each neighbor
j ∈
K(
i) was determined to be inversely proportional to its distance to target pixel
i:
where
t is a user-defined parameter (
t ≥ 0).
In this study, a small positive number was given for zero distances and a value
t = 2 was used in
Equation (4). It follows that for target pixel
i,
. A
k-nearest neighbor prediction (
ŷi) target pixel
i was calculated as follows:
where
yj is the observed value of the response variable in reference pixel
j ∈
K(
i).
In forest cover mapping, the set of spectral features contained values of the image mosaic bands from 1 to 6, corresponding to the Landsat TM image bands from 1 to 5 and 7, and we used the Euclidean distance as the measure of distance (the band weight (ph) was set to 1 for all bands). The mode value of a response variable, i.e., the FAO land use class, among the k-nearest neighbors was the predicted class for the given target pixel. We selected pixels from the Landsat TM mosaic from Terai as the set of target pixels using the physiographic zone raster map as a mask in the GRASS GIS package. The reference set consisted of the pixels covered by the center points of the 1st phase plots, where the observed value (FAO land use class) was known based on the visual interpretation. In order to clarify forest classification, the plots belonging to the land use categories “Agricultural area with tree cover” or “Built-up area with tree cover” were dropped out from the reference set, whereas the category “Roads”, having a very small number of observations, was combined with the category “Built-up land without tree cover”.
The post-processing phase of the classification included three steps. First, we applied a spatial 3 × 3 mode filter to reduce the salt-and-pepper effect in the pixel-by-pixel classification. Second, we constructed a forest/non-forest raster map (denoted as a forest cover raster map later) by reclassifying non-forest categories into a single class. Third, we converted the resulting forest cover raster map into a vector format and excluded forest segments with an area of less than 0.5 ha.
3.3. Validation of Results
For the category variable,
i.e., forest cover, the value for
k was selected by examining the classification accuracy of the forest cover predictions obtained using different values of
k. For classification accuracy, indicators based on the confusion matrices were used [
27] and included: (1) producer’s accuracy (FPA, forest), (2) user’s accuracy (FUA, forest), (3) overall accuracy (OA) and (4) the Kappa statistic (KHAT); the KHAT was computed because the OA results are too optimistic if the proportion of a single class is high (see Hyvönen and Anttila [
28]).
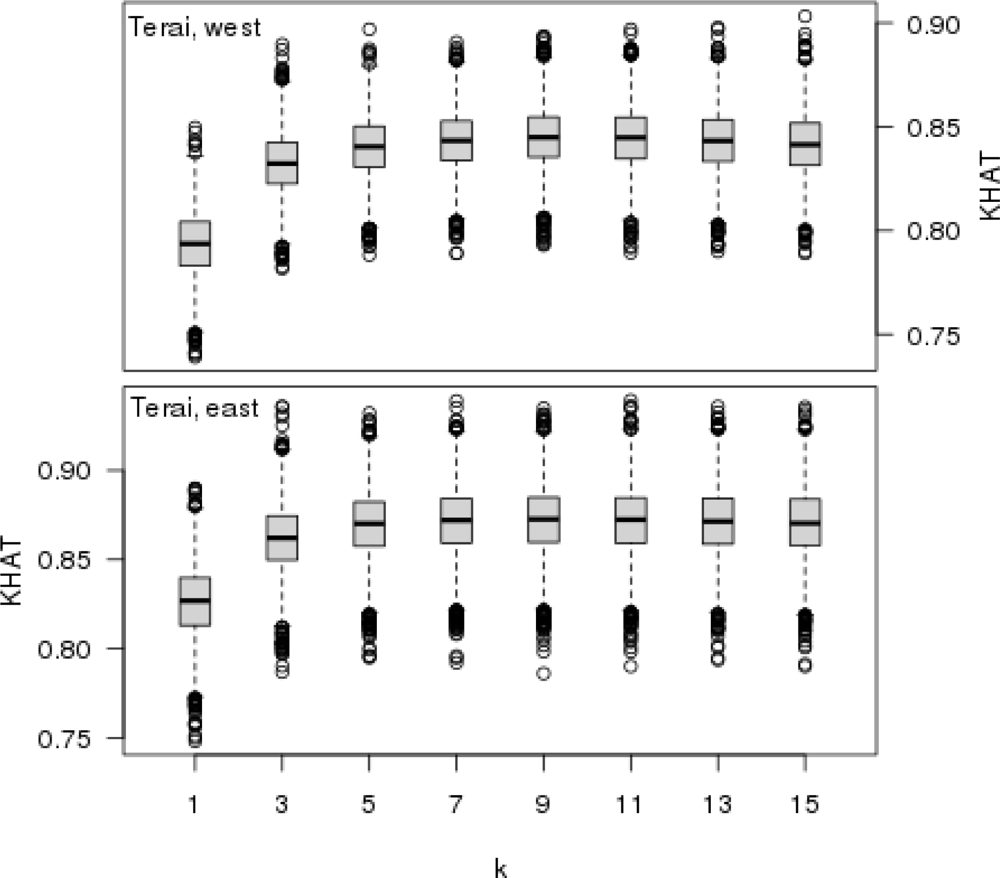
The Monte Carlo technique, including the random sampling of test samples, was applied when selecting k, i.e., the number of neighbors. For each k ∈ {1, 3, 5,...,15}, 5,000 test samples were randomly selected from the entire reference element set. Each sample contained 1,000 elements (1st phase sample plots of visual inspection), which were classified as test material, whereas all the remaining elements not included in the sample comprised the reference. The aforementioned classification accuracy indicators were calculated for each test sample. As a result, an empirical distribution of each test indicator with a varying value of k was produced. This approach was applied in the two parts of Terai separately. At the end, the forest cover delineations derived from the visual interpretation and the forest cover map were also checked by their classification accuracy using the field observed values for the field sample plots.
A leave-one-out analysis was conducted, and common cross-validation criteria,
i.e., RMSE and bias, were calculated for the continuous variable,
i.e., the total stand volume, in the reference set (e.g., Tokola [
26]; Katila and Tomppo [
29]). In this study, the RMSEs and biases were determined as follows:
where
yi is the observed value,
ŷi the predicted value of the given characteristic, and
n is the number of observations. The relative,
i.e., percent, RMSEs (RMSE
%) and biases (bias
%) were calculated by dividing the absolute RMSEs and biases by the means of the respective values from the observations (
ȳ) and multiplying the resulting quotients by 100.
Cross-validation and feature selection were carried out using a genetic algorithm-based approach (e.g., Haapanen and Tuominen [
30]) that has been compiled in with the “genalg” package of R software [
31]. The value for
k was simultaneously determined in the feature selection and weight search. Several runs were made in order to find the best combination of features and parameter value for
k for the volume estimation. The parameter values of population size, number of iterations, elitism and mutation chance that we used for the algorithm were 500, 1,000, 40% and 0.05, respectively, and the goal was to minimize the sum of RMSE and bias obtained for the stand volume. The features that we tested for the model included band values (
b1,…,
b6) in the Landsat TM mosaic (referring to TM wavelength bands 1,..,5 and 7) together with the ratios of the band values and the value of the Normalized Difference Vegetation Index (NDVI).
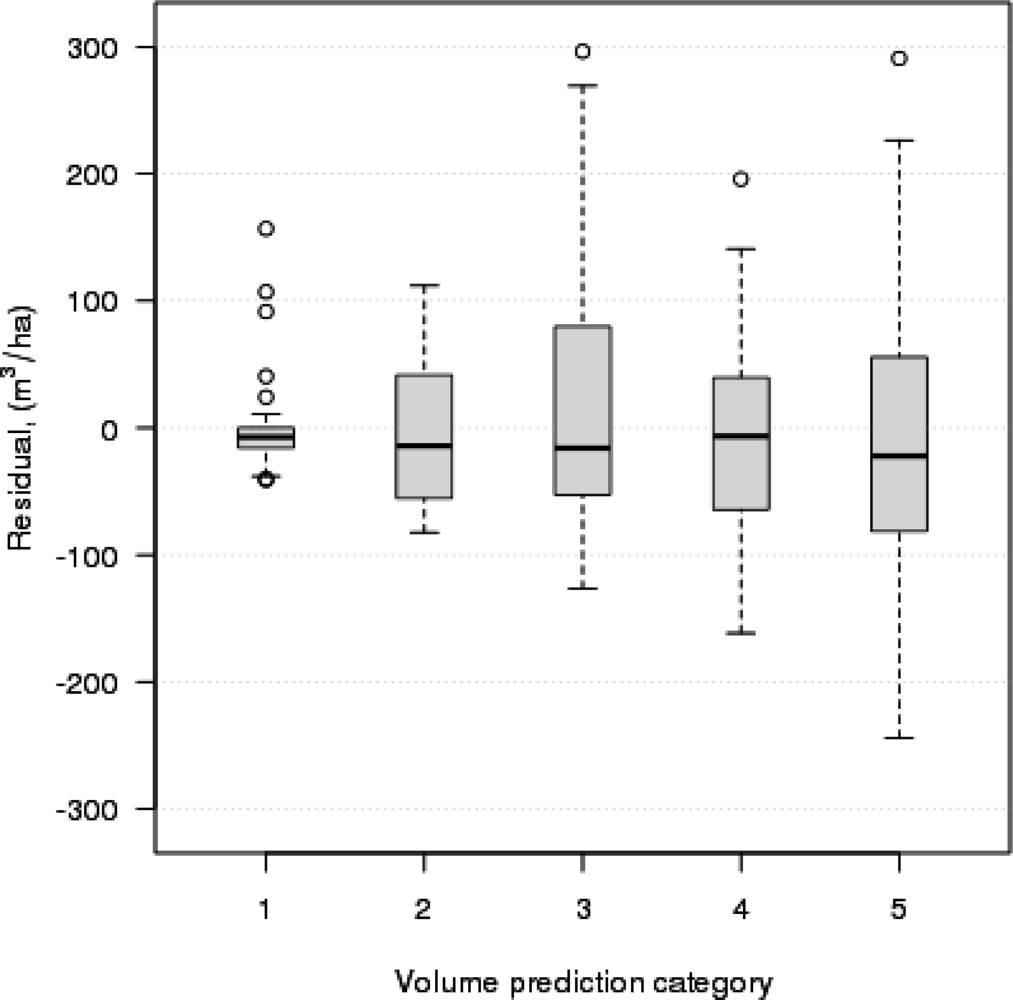
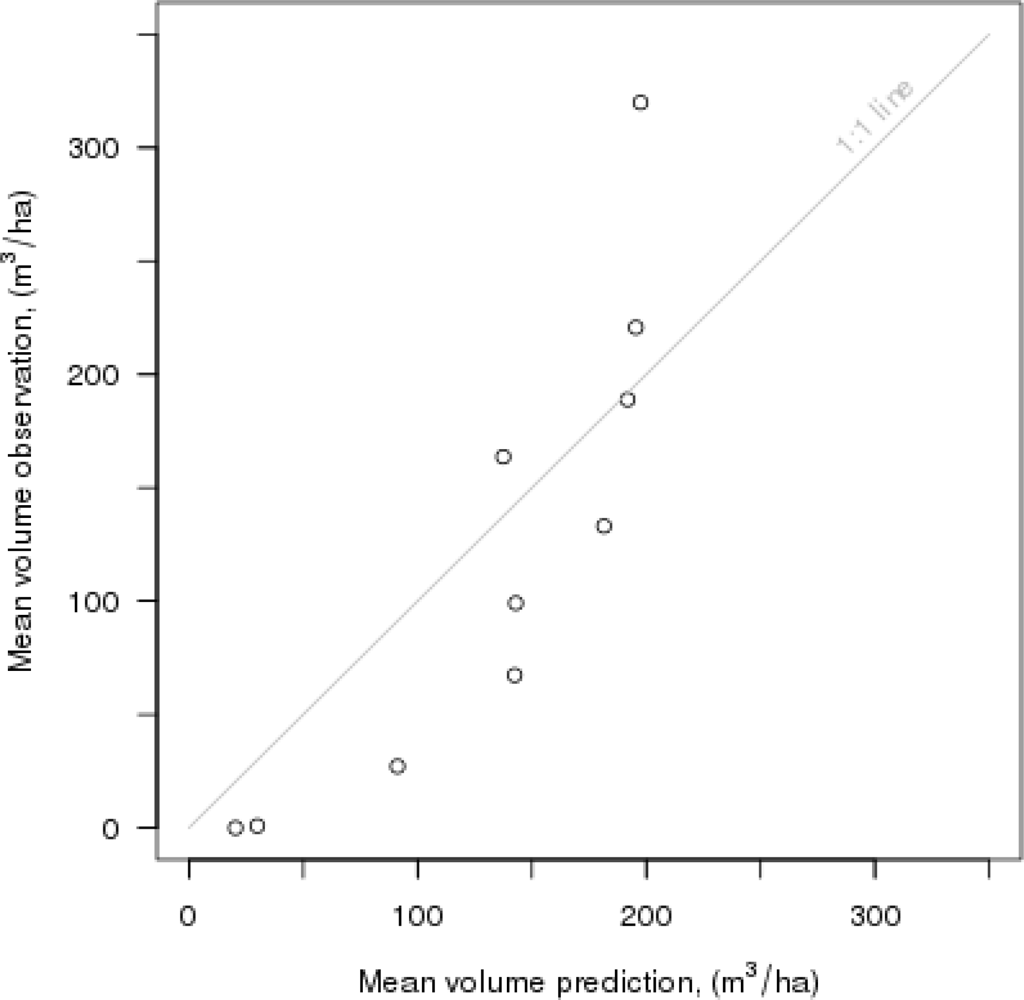
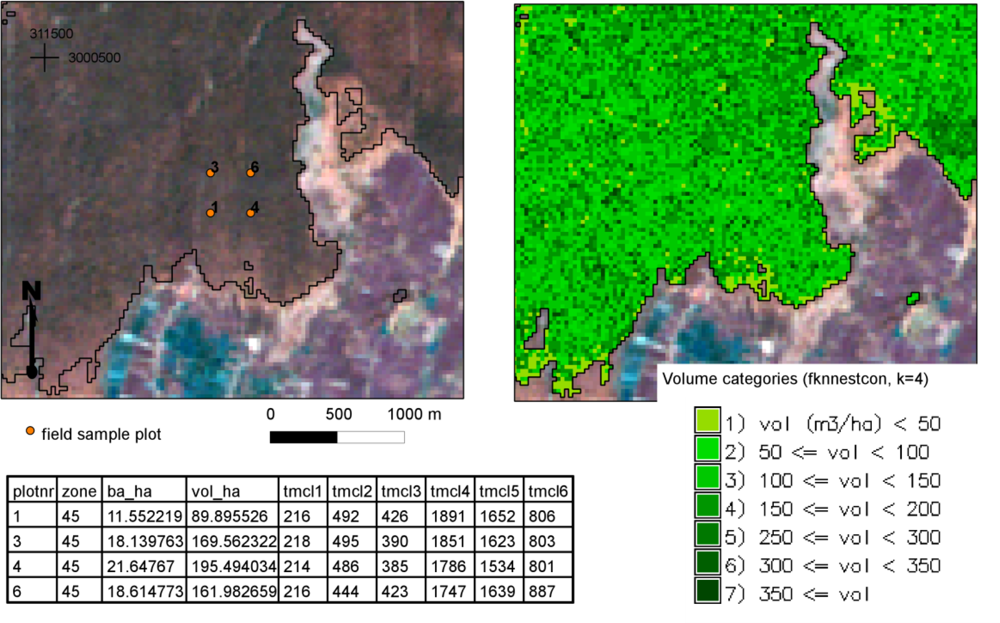
When creating thematic wall-to-wall maps for growing stock volume, we selected a set of target pixels using the forest cover map as a mask in the GRASS GIS package. The reference set consisted of the pixels covered by the center points of the field plots (
Table 2). For composing the thematic map of volume, we classified the volume predictions for the pixels into classes of 50 m
3·ha
−1.
5. Discussion
In the case of the Terai region, it was not possible to apply the nearest neighbor’s techniques for each Landsat image separately, because the number of plots was inadequate. This meant that we needed to apply relative calibration for the Landsat images, despite the fact that there could be quite a long amount of time between the dates for the available good-quality images. For this purpose, we applied a pre-processing approach based on using a reference image covering the whole region. For aiming at a seamless result, the potential overlapping area of the neighboring target images (Landsat TM images in our case) needs to be utilized when the raster maps representing means and standard deviations are computed. By detecting pixels having extreme values (outlier pixels) in the images and excluding them from this stage, one can improve the result of this local approach. Depending on image materials, this method also allows one to apply a pixel size c different than the original pixel size in the reference image.
A robust regression approach would offer another empirically oriented approach for a relative calibration of image materials. Regressing the images for the selected reference image would make it possible to concurrently use neighboring images. In the case of the geographically wide Terai region, the robust regression approach was less applicable. However, in a multi-temporal case, a regression approach for relative radiometric calibration could possibly be applied when detecting changes in landscape, such as cuttings (e.g., [
11,
34,
35]).
The agreement between the
k-NN forest cover classification and the visual interpretation in Terai was strong, since the resulting value of KHAT was greater than 0.80 (see, e.g., Congalton [
27] and Green [
32]). The OA values were also high, which can at least be partly explained by the high proportion of the non-forest category. It is worth noting that we did not examine the effect of the post-processing phase (steps 1 to 3) when calculating the accuracy measures in the test samples for the selected value of
k. Also, the classification accuracy of the forest cover map evaluated against field observed values showed that the agreement between these forest cover delineations is substantial (western Terai) or strong (eastern Terai).
The visual land use class interpretation process was conducted using Google Earth satellite imagery viewer [
21], where the background imagery originated from the period between 2003 and 2010, together with additional RapidEye imagery from the year 2010. Due to shaded areas, haze and cloudiness, the visual interpretation work proved difficult in the case of some RapidEye images, and then, the interpretation was supported using satellite imagery available in Google Earth. Therefore, the time difference between these image materials could make a source of uncertainty to the interpretation process itself. In this study, an unwanted mixing of the forest class and the land use classes with some tree cover was tackled by dropping out the plots in classes “Agricultural area with tree cover” and “Built-up area with tree cover” from the reference set. For classification accuracy checking, a correct matching of the locations between field plots and the visual interpretation plots on the image is also crucial. Unfortunately, information to check this location accuracy was not available.
Besides RMSE and bias, robust measures for the quality of the
k-NN-based estimation in terms of feature selection and cross-validation could be useful, especially in cases where the number of plots is small, which corresponds to this study (
n = 217). For instance, in the
k-nearest neighbor analysis for stand volume, the most extreme observations may also have affected the model parameter search, because the number of field plots was quite small. Therefore, the diagnostic approach suggested by McRoberts [
33] for detecting outliers and influential observations could be very important for our work in the future.
The
k-nearest neighbor technique, applied to the mapping of forest cover and stand volume in the Terai region of Nepal, is a straightforward procedure that has been efficiently utilized in Finland (see, e.g., Tomppo
et al.[
5] and Tomppo [
4]). Moreover, this technique was also applied earlier by Tokola
et al.[
36] for classifying land use and for estimating timber volume and biomass in Nepal.
This was, however, one of the first forest mapping studies completely conducted using Open Source software tools and free packages. In this respect, it was natural that substantial efforts were needed to incorporate appropriate data processing techniques and suitable procedures and, especially, that the techniques and procedures were compatible for processing the remote sensing and inventory data.
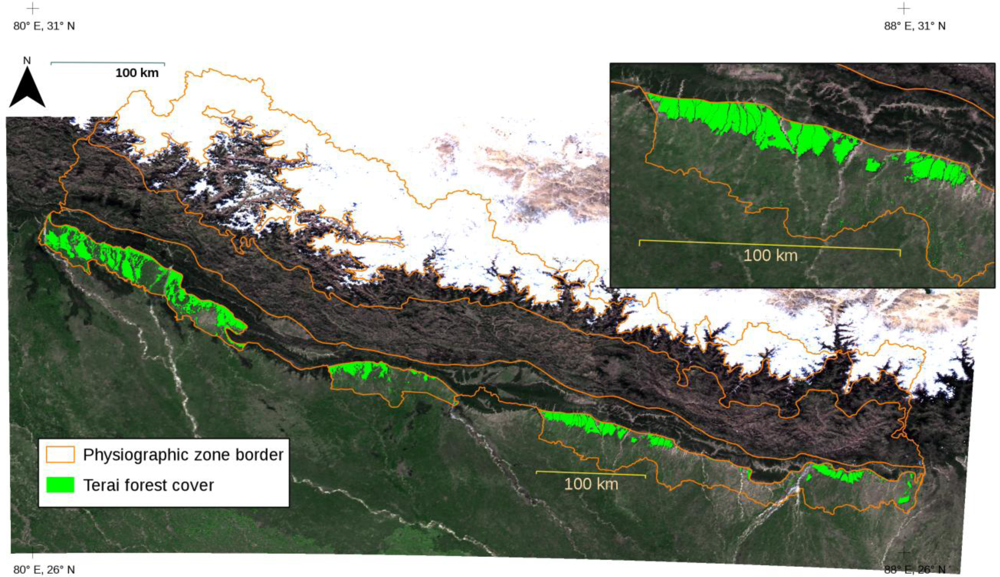
The forest cover map now available for Terai (
Figure 5) is one source of information that can be utilized when estimating above-ground forest volumes and biomasses based on the LiDAR data as part of the ongoing survey conducted by the FRA Nepal project in the central parts of Terai. In the future, similar forest cover maps will also be needed for other physiographic zones beyond Terai, where the LiDAR-oriented estimations of forest attributes will be conducted. Later, experience will show if the forest cover maps prove useful in other fields of forestry. Potential applications in Nepalese conditions include inventory planning and monitoring practices. The forest cover and volume maps (
Figure 8) estimated using the
k-NN method and inventory data from the FRA Nepal project are already appropriate and valuable data for research purposes and for planning forthcoming forest inventories when testing optimal inventory designs (see [
37]).
Spatially explicit biomass maps could also form a basis for the forthcoming greenhouse gas inventory,
i.e., the REDD-related estimation of gross primary production and soil carbon change. The
k-NN-based forest biomass mapping technique, which corresponds to that of stand volume mapping, has already been demonstrated by Tuominen
et al.[
38] in Finnish conditions. One shared feature between the approach by Tuominen
et al.[
38] and the one in this study has to do with the data-efficient, mixed-effects modeling-based generalization of sample tree characteristics. This study, however, used an NLME model for generalizing the sample tree heights (see
Appendix), whereas the model utilized by Tuominen
et al.[
38] made use of an LME model provided by Eerikäinen [
39].
Adapting the methods and techniques and applying the Open Source software tools presented here requires capacity building in Nepal: development work and education measures have already been launched by the ICI project, which is an inter-institutional development cooperation project between Nepalese, Vietnamese and Finnish governmental institutes and that was initiated with the support of the Ministry for Foreign Affairs (MFA) of Finland. The development activities of the project have been designed and implemented with a special focus on human capacity development within the governmental forest research organizations participating in the project. Special emphasis has therefore been given to hands-on training periods and workshops and to disseminating information on forest inventory-related techniques and procedures. Of these objectives, the latter covers the goal of the present study: to increase and share knowledge about the existing techniques and procedures and to make it easier to adapt them to the conditions in, for instance, Nepal.
Local expertise is always required for the most pivotal part of the forest inventory, that is to say, the work conducted in the field and, at the moment, by the FRA Nepal project in Nepal. Through scientific work and collaboration, however, it is possible to achieve more diverse and detailed results in terms of conventional statistics and advanced electronic maps of the forest attributes of interest. This study is also one example of how to improve the use of field inventory data and exploit them together with additional remote sensing data in order to satisfy the new reporting requirements set for large-scale forest inventories.
6. Conclusions
In this study, we introduced an approach for a MODIS-based relative calibration of Landsat TM images to enable the use of a mosaic of several Landsat TM images in a
k-nearest neighbor (
k-NN) estimation. The presented approach for relative calibration combined aspects presented earlier by Tuominen and Pekkarinen [
7] and Tomppo
et al.[
8]. The method relies only on image data (see [
7]) and is easy to implement. Optionally, the reference image could have been converted to a reflectance scale, but for the
k-NN estimation method that was not necessary. A prerequisite for the success of the local correction approach for the relative calibration of images is that the target images and the good-quality reference image material need to be temporally and seasonally close to each other. However, more studies are needed on selecting the parameters for the approach when using image resolution scales other than the ones used in the Terai case, which utilized Landsat TM and MODIS.
The k-nearest neighbor technique was very applicable to the forest cover mapping in Terai using visual interpretation plots as a reference material. There was a strong agreement (KHAT > 0.80) between the forest cover delineations based on visual interpretation and field observations. The agreement between the forest cover delineation in the forest cover map and the one derived from the field observed values was substantial in Western Terai (KHAT 0.745) and strong in Eastern Terai (KHAT 0.825).
One feature related to the development of the multi-source technique and, especially, to its application to different geographical conditions in Nepal in the future has to do with using digital elevation models (DEMs). In the case of Terai,
i.e., within the lowlands of Nepal, no radiometric corrections were conducted using DEMs (e.g., Tomppo
et al.[
5]; Tokola
et al.[
36]), neither was the DEM-based moving geographical vertical reference area used in the
k-NN method (see Katila and Tomppo [
29]). It is therefore recommended that the significance of DEM be tested in other physiographic vegetation zones north of Terai, where the topography is very mountainous compared to the southernmost region of Nepal.