Simulating Forest Cover Changes of Bannerghatta National Park Based on a CA-Markov Model: A Remote Sensing Approach
Abstract
:1. Introduction
2. Material and Methods
2.1. Site Description
2.2. Data Sources
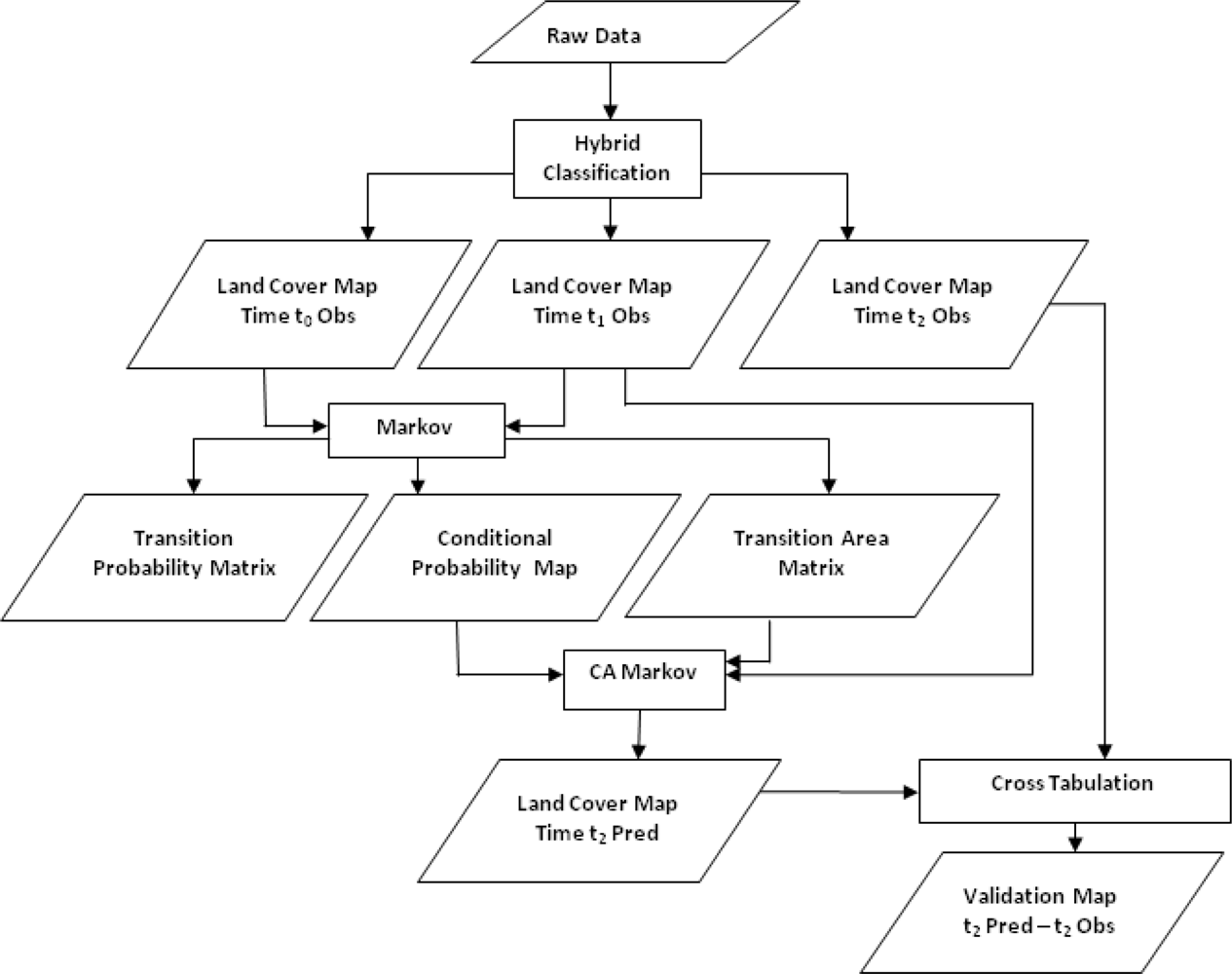
2.3. Research Methods
2.3.1 Land-Use and Land-Cover Change Detection Analysis
2.3.2 Markov Chain Analysis
- Vi × Pij = Proportion of land cover of second date,
- Pij = Matrix of probability of land cover transition,
- Vi = Proportion of land cover of first date (Vector),
- i = type of land cover in first date,
- j = type of land cover in second date,
- P11 = the probability that a land cover 1 at first date will change into land cover 1 by second date,
- P12 = the probability that a land cover 1 at first date will change into land cover 2 by second date and so on,
- m = the number of land cover types in the study area.
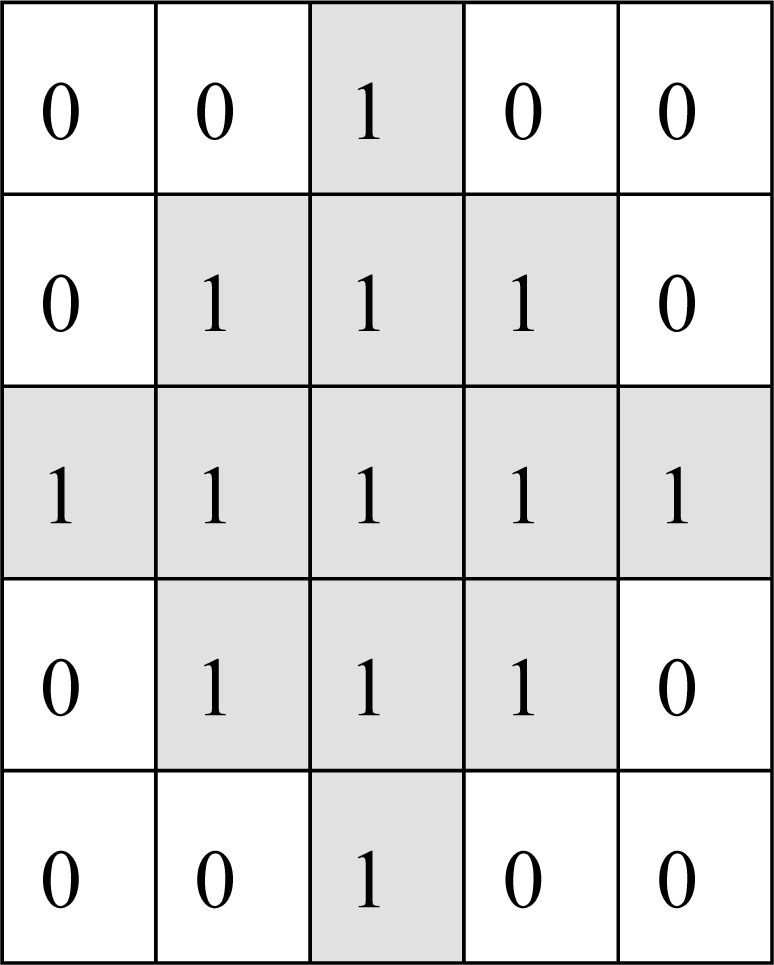
2.3.3. Cellular Automata (CA)
2.3.4. CA Markov Model
3. Results
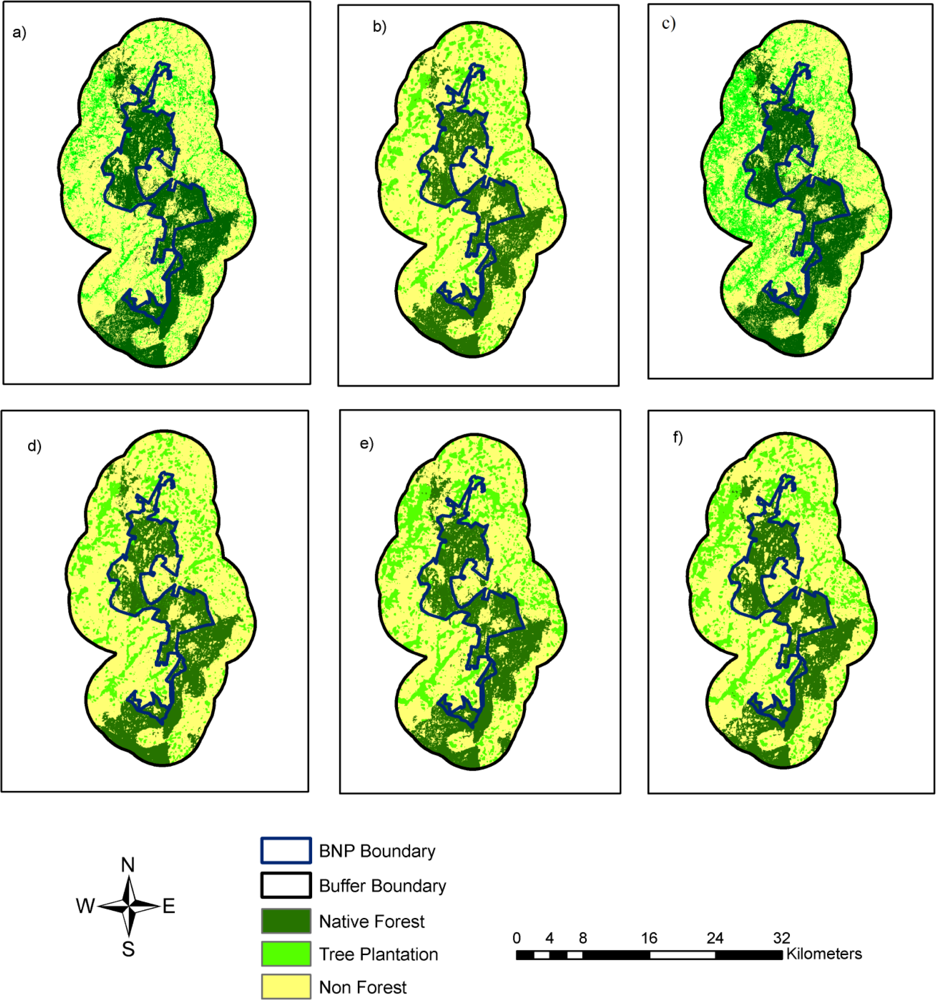
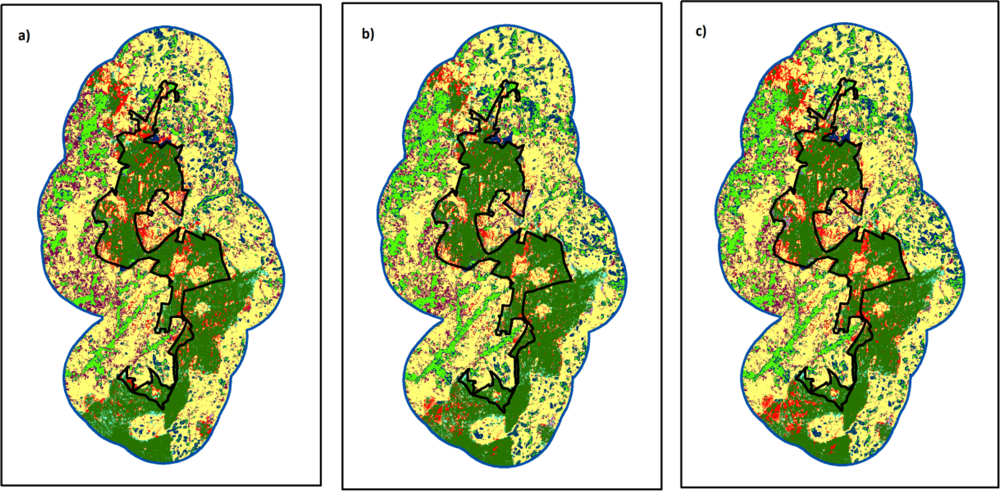
3.1. Land-Use and Land-Cover Projection—Before–After/Inside–Outside
3.2. Change Trajectories Projection
3.3. Model Validation
4. Discussion
5. Conclusions
Acknowledgments
References and Notes
- National Research Council (NRC). Trends and Transitions. In Our Common Journey: A Transition toward Sustainability; National Academy Press: Washington, DC, USA, 1999; pp. 59–132. [Google Scholar]
- Geist, H.J.; Lambin, E.F. Proximate causes and underlying driving forces of tropical deforestation. BioScience 2002, 52, 143–150. [Google Scholar]
- Brambilla, M.; Casale, F.; Bergero, V.; Bogliani, G.; Crovetto, G.M.; Falco, R.; Roati, M.; Negri, I. Glorious past, uncertain present, bad future? Assessing effects of land-use changes on habitat suitability for a threatened farmland bird species. Biol. Conserv 2010, 143, 2770–2778. [Google Scholar]
- Angelsen, A.; Kaimowitz, D. Rethinking the causes of deforestation: lessons from economic models. World Bank Res. Obs 1999, 14, 73–98. [Google Scholar]
- Food and Agriculture Organization (FAO). Global Forest Resources Assessment 2010; Food and Agriculture Organization of the United Nations: Rome, Italy, 2010. Available online: http://www.fao.org/forestry/fra/fra2010/en/ (accessed on 12 September 2012).
- Rodrigues, A.S.L.; Andelman, S.J.; Bakarr, M.I.; Boitani, L.; Brooks, T.M.; Cowling, R.M.; Fishpool, L.D.C.; da Fonseca, G.A.B.; Gaston, K.J.; Hoffmann, M.; et al. Effectiveness of the global protected area network in representing species diversity. Nature 2004, 428, 640–643. [Google Scholar]
- Chape, S.; Harrison, J.; Spalding, M.; Lysenko, I. Measuring the extent and effectiveness of protected areas as an indicator for meeting global biodiversity targets. Phil. T. Roy. Soc. B 2005, 360, 443–455. [Google Scholar]
- Loucks, C.; Ricketts, H.T.; Naidoo, R.; Lamoreux, J.; Hoekstra, J. Explaining the global pattern of protected area coverage: Relative importance of vertebrate biodiversity, human activities and agricultural suitability. J. Biogeogr 2008, 35, 1337–1348. [Google Scholar]
- United Nations Environment Programme-World Conservation Monitoring Centre. State of the World’s Protected Areas 2007: An Annual Review of Global Conservation Progress; UNEP-WCMC: Cambridge, UK, 2008. [Google Scholar]
- Jenkins, C.N.; Joppa, L. Expansion of the global terrestrial protected area system. Biol. Conserv 2009, 142, 2166–2174. [Google Scholar]
- Lele, N.; Nagendra, H.; Southworth, J. Accessibility, demography and protection: drivers of forest stability and change at multiple scales in the Cauvery Basin, India. Remote Sens 2010, 2, 306–332. [Google Scholar]
- Tattoni, C.; Ciolli, M.; Ferretti, F.; Cantiani, M.G. Monitoring spatial, temporal pattern of Paneveggio forest (Northern Italy) from 1859 to 2006. iForest 2010, 3, 72–80. [Google Scholar]
- Tattoni, C.; Ciolli, M.; Ferretti, F. The fate of priority areas for conservation in protected areas: A fine-scale Markov chain approach. Environ. Manage 2011, 47, 263–278. [Google Scholar]
- Bracchetti, L. Land-cover changes in a remote area of central Apennines (Italy) and management directions. Landsc. Urban Plan 2012, 104, 157–170. [Google Scholar]
- Cabral, P.; Zamyatin, A. Markov processes in modeling land use and land cover changes in Sintra-Cascais, Portugal. Dyna 2009, 158, 191–198. [Google Scholar]
- Pfaff, A.S.P. What drives deforestation in the Brazilian Amazon?: Evidence from satellite and socioeconomic data. J. Environ. Econ. Manage 1999, 37, 26–43. [Google Scholar]
- Zimmerer, K.S.; Galt, R.E.; Buck, M.V. Globalization and multi-spatial trends in the coverage of protected-area conservation (1980 to 2000). Ambio 2004, 33, 520–529. [Google Scholar]
- Nagendra, H. Do parks work? Impact of protected areas on land cover clearing. Ambio 2008, 37, 330–337. [Google Scholar]
- Brandon, K.; Redford, K.; Sanderson, S. Parks in Peril: People, Politics and Protected Areas; Island Press: Washington, DC, USA, 1998; pp. 1–23. [Google Scholar]
- Bates, D.; Rudel, T.K. The political ecology of conserving tropical rain forests: A cross-national analysis. Soc. Natur. Resour 2000, 12, 619–634. [Google Scholar]
- Nagendra, H.; Southworth, J.; Tucker, C.M.; Karmacharya, M.; Karna, B.; Carlson, L. Monitoring parks through remote sensing: Studies in Nepal and Honduras. Environ. Manage 2004, 33, 1–13. [Google Scholar]
- Agrawal, A.; Ostrom, E. Collective action, property rights, and decentralization in resource use in India and Nepal. Polit. Soc 2001, 29, 485–514. [Google Scholar]
- Briggs, J. The biogeographic and tectonic history of India. J. Biogeogr 2003, 30, 381–388. [Google Scholar]
- Mittermeier, R.A.; Mittermeier, C.G. Megadiversity: Earth’s Biologically Wealthiest Nations, 1st ed; Cemex-Conservation International: Monterrey, Mexico, 2005; pp. 1–501. [Google Scholar]
- Karanth, K.K.; Defries, R. Conservation and management in human-dominated landscapes: Case studies from India. Biol. Conserv 2010, 143, 2865–2869. [Google Scholar]
- Rangarajan, M. India’s Wildlife History; Permanent Black and Ran Thambhore Foundation: New Delhi, India, 2001; pp. 1–135. [Google Scholar]
- Guha, R. Dietrich Brandis and Indian Forestry: A Vision Revisited and Reaffirmed. In Village Voices, Forest Choices: Joint Forest Management in India; Poffenberger, M., McGean, B., Eds.; Oxford University Press: New Delhi, India, 1996; pp. 86–100. [Google Scholar]
- Bandopadhaya, S.; Soumya, S.B.; Shah, P.J. Briefing Paper on Forest Policy: Community Stewardship and Management; Center for Civil Society: New Delhi, India, 2005; pp. 3–6. [Google Scholar]
- Guha, R. Forestry in British and post-British India: A historical analysis in two parts. Econ. Polit. Wkly 1983, 27, 1883. [Google Scholar]
- Saxena, N.C. Policy and Joint Forest Management Series 1: Forest Policy in India; WWF India and International Institute for Environment and Development (IIED): London, UK; p. 1999.
- Arora, D. From state regulation to people’s participation: case of forest management in India. Econ. Polit. Wkly 1994, 29, 691–98. [Google Scholar]
- Karanth, K.K.; Kramer, R.; Qian, S.; Christensen, N.L. Conservation attitudes, perspectives and challenges in India. Biol. Conserv 2008, 141, 2357–2367. [Google Scholar]
- Nagendra, H.; Pareeth, S.; Paul, S.; Dutt, S. Landscapes of protection: Forest change and fragmentation in northern West Bengal, India. Environ. Manage 2009, 44, 853–864. [Google Scholar]
- Balmford, A.; Bennun, L.; Brink, B.T.; Cooper, D.; Côte, I.M.; Crane, P.; Dobson, A.; Dudley, N.; Dutton, I.; Green, R.E.; et al. Ecology: The convention on biological diversity’s 2010 target. Science 2005, 307, 212–213. [Google Scholar]
- Carr, D.L. A tale of two roads: Land tenure, poverty, and politics on the Guatemalan frontier. Geoforum 2006, 37, 94–103. [Google Scholar]
- Oliveira, P.J.C.; Asner, G.P.; Knapp, D.E.; Almeyda, A.; Galvan-Gildemeister, R.; Keene, S.; Raybin, R.F.; Smith, R.C. Land-use allocation protects the peruvian amazon. Science 2007, 317, 1233–1236. [Google Scholar]
- Andam, K.S.; Ferraro, P.J.; Pfaff, A.; Sanchez-Azofeifa, G.A.; Robalino, J.A. Measuring the effectiveness of protected area networks in reducing deforestation. PNAS 2008, 105, 16089–16094. [Google Scholar]
- Pffaf, A.; Robalino, J.A.; Sanchez-Azofeifa, G.A.; Andam, K.S.; Ferraro, P.J. Park location affects forest protection: land characteristics cause differences in park impacts across Costa Rica. B.E. J. Econom. Anal. Policy 2009, 9, 1–24. [Google Scholar]
- Bruner, A.G.; Gullison, R.E.; Rice, R.E.; da Fonseca, G.A.B. Effectiveness of parks in protecting tropical biodiversity. Science 2001, 291, 125–128. [Google Scholar]
- Sanchez-Azofeifa, G.A.; Daily, G.C.; Pfaff, A.S.P.; Busch, C. Integrity and isolation of Costa Rica’s national parks and biological reserves: Examining the dynamics of land-cover change. Biol. Conserv 2003, 109, 123–135. [Google Scholar]
- Naughton-Treves, L.; Holland, M.B.; Brandon, K. The role of protected areas in conserving biodiversity and sustaining local livelihoods. Annu. Rev. Environ. Resour 2005, 30, 219–252. [Google Scholar]
- Nepstad, D.; Schwartzman, S.; Bamberger, B.; Santilli, M.; D, R.A.Y.; Schlesinger, P.; Lefebvre, P.; Alencar, A.; Prinz, E.; Fiske, G.; Rolla, A. Inhibition of Amazon deforestation and fire by parks and indigenous lands. Conserv. Biol 2006, 20, 65–73. [Google Scholar]
- Joppa, L.N.; Loarie, S.R.; Pimm, S.L. On the protection of “protected areas”. PNAS 2008, 105, 6673–6678. [Google Scholar]
- Joppa, L.; Pfaff, A. Reassessing the forest impacts of protection. Ann. N.Y. Acad. Sci 2010, 1185, 135–149. [Google Scholar]
- Gadgil, M.; Prasad, S.N.; Ali, R. Forest management and forest policy in India: A critical review. Soc. Action (N.Y.) 1983, 33, 127–155. [Google Scholar]
- Hartter, J.; Southworth, J. Dwindling resources and fragmentation of landscapes around parks: Wetlands and forest patches around Kibale National Park, Uganda. Landsc. Ecol 2009, 24, 643–656. [Google Scholar]
- Hudak, A.T.; Wessman, C.A. Textural analysis of historical aerial photography to characterise woody plant encroachment in South African savanna. Remote Sens. Environ 1998, 66, 317–330. [Google Scholar]
- Lambin, E.F. Modelling and monitoring land-cover change processes in tropical regions. Prog. Phys. Geog 1997, 21, 375–393. [Google Scholar]
- Mertens, B.; Lambin, E.F. Land cover change trajectories in Southern Cameroon. Ann. Assoc. Am. Geogr 2000, 90, 467–494. [Google Scholar]
- Southworth, J.; Nagendra, H.; Munroe, D.K. Are parks working? Exploring human–environment tradeoffs in protected area conservation. Appl. Geogr 2006, 26, 87–95. [Google Scholar]
- Cheong, So-Min.; Brown, D.; Kok, K.; López-Carr, D. Mixed Methods in Land Change Research: Towards Integration. Trans.Inst. Br. Geogr 2012, 37, 8–12. [Google Scholar]
- Mondal, P.; Southworth, J. Evaluation of conservation interventions using a cellular Automata-Markov model. For. Ecol. Manage 2010, 260, 1716–1725. [Google Scholar]
- Liu, M.; Hu, Y.; Chang, Y.; He, X.; Zhang, W. Land use and land cover change analysis and prediction in the upper reaches of the Minjiang River, China. Environ. Manage 2009, 43, 899–907. [Google Scholar]
- Houet, T.; Hubert-Moy, L. Modelling and projecting land-use and land-cover changes with a cellular automaton in considering landscape trajectories: an improvement for simulation of plausible future states. EARSeL eProc 2006, 5, 6–76. [Google Scholar]
- Weinstein, D.; Shugart, H. Ecological Modeling of Landscape Dynamics. In Disturbance and Ecosystems; Mooney, H.A., Gordon, M., Eds.; Springer-Verlag: New York, NY, USA, 1983; pp. 29–45. [Google Scholar]
- Baker, L.W. A review of models of landscape change. Landsc. Ecol 1989, 2, 111–133. [Google Scholar]
- Sklar, F.H.; Costanza, R. The Development of Dynamic Spatial Models for Landscape Ecology: A Review. In Quantitative Methods in Landscape Ecology; Turner, M.G., Gardner, R.H., Eds.; Springer-Verlag: New York, NY, USA, 1991; pp. 239–288. [Google Scholar]
- Brown, D.G.; Walker, R.; Manson, S.; Seto, K.C. Modeling Land Use and Land Cover Change. In Land Change Science: Observing, Monitoring, and Understanding Trajectories of Change on the Earth’s Surface; Gutman, G., Janetos, A., Justice, C., Moran, E., Mustard, J., Rindfuss, R., Skole, D., Turner, B.L., II., Cochrane, M.A., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 395–409. [Google Scholar]
- Pontius, R.G.J.; Malanson, J. Comparsion of the structure and accuracy of two land change models. Int. J. Geogr. Inf. Sci 2005, 19, 243–265. [Google Scholar]
- Mertens, B.; Lambin, E.F. Spatial modeling of deforestation in southern Cameroon: Spatial disaggregation of diverse deforestation processes. Appl. Geogr 1997, 17, 143–162. [Google Scholar]
- Hastie, T.; Tibshirani, R. Generalized additive models. Stat. Sci 1986, 1, 297–318. [Google Scholar]
- Brown, D.G.; Goovaerts, P.; Burnicki, A.; Li, M.Y. Stochastic simulation of land-cover change using geostatistics and generalized additive models. Photogramm. Eng. Remote Sensing 2002, 68, 1051–1061. [Google Scholar]
- Tewolde, M.G.; Cabral, P. Urban sprawl analysis and modeling in Asmara, Eritrea. Remote Sens 2011, 3, 2148–2165. [Google Scholar]
- Fitz, H.C.; DeBellevue, E.B.; Costanza, R.; Boumans, R.; Maxwell, T.; Wainger, L.; Sklar, F.H. Development of a general ecosystem model for a range of scales and ecosystems. Ecol. Model 1996, 88, 263–295. [Google Scholar]
- Wu, Y.; Sklar, F.H.; Gopu, K.; Rutchey, K. Fire simulations in the Everglades landscape using parallel programming. Ecol. Model 1996, 93, 113–124. [Google Scholar]
- Voinov, A.; Costanza, R.; Wainger, L.; Boumans, R.; Villa, F.; Maxwell, T.; Voinov, H. Patuxent landscape model: Integrated ecological economic modeling of a watershed. Environ. Modell. Softw 1999, 14, 473–491. [Google Scholar]
- Clarke, K.C.; Gaydos, L.J. Loose-coupling a cellular automation model and GIS: Long-term urban growth prediction for San Francisco and Washington/Baltimore. Int. J. Geogr. Inf. Sci 1998, 12, 699–714. [Google Scholar]
- Parker, C.D.; Manson, M.S.; Janssen, A.M.; Hoffmann, J.M.; Deadman, P. Multi-Agent Systems for the simulation of land-use and land-cover change: A review. Ann. Assoc. Am. Geogr 2003, 93, 314–337. [Google Scholar]
- Manson, S.M. Agent-Based Dynamic Spatial Simulation of Land-Use/Cover Change in the Yucatán Peninsula, Mexico. Proceedings of the Fourth International Conference on Integrating GIS and Environmental Modeling (GIS/EM4), Banff, Canada, 2– 8 September 2000.
- Urban, D.L.; Wallin, D.O. Introduction to Markov Models. In Learning Landscape Ecology: A Practical Guide to Concepts and Techniques; Gergel, S.E., Turner, M.G., Eds.; Springer-Verlag: New York, NY, USA, 2002; pp. 35–48. [Google Scholar]
- Muller, R.M.; Middleton, J. A Markov model of land-use change dynamics in the Niagara region, Ontario, Canada. Landsc. Ecol 1994, 9, 151–157. [Google Scholar]
- Qihao, W. Land use change analysis in the Zhujiang Delta of China using satellite remote sensing, GIS and stochastic modeling. J. Environ. Manage 2002, 64, 273–284. [Google Scholar]
- Usher, M.B. Statistical Models of Succession. In Plant Succession: Theory and Prediction; Gelnn-Lewin, D.C., Peet, R.K., Veblen, T.T., Eds.; Chapman and Hall: London, UK, 1992; pp. 215–248. [Google Scholar]
- Briassoulis, H. Analysis of Land Use Change: Theoretical and Modelling Approaches. In The Web Book of Regional Science; Loveridge, S., Ed.; Regional Research Institute, West Virginia University: Morgantown, WV, USA, 2000. [Google Scholar]
- Barringer, T.H.; Robinson, V.B. Stochastic Models of Cover Class Dynamics. Proceedings of the 15th International Symposium on Remote Sensing of the Environment, Ann Arbor, MI, USA, 1 January 1981; pp. 125–144.
- Alig, R.J. Modeling Acreage Changes in Forest Ownerships and Cover Types in the Southeast, 3rd ed; US Department of Argriculture, Forest Service, Rocky Mountain Forest and Range Experiment Station: Fort Collins, CO, USA, 1985; pp. 1–14. [Google Scholar]
- Silvertown, J.; Holtier, S.; Johnson, J.; Dale, P. Cellular Automaton models of interspecific competition for space-the effect of pattern on process. J. Ecol. 1992, 80, 527–533. [Google Scholar]
- Clark Labs. IDRISI Geographic Information Systems and Remote Sensing Software; Clark Labs: Worcester, MA, USA, 2006. [Google Scholar]
- Li, H.; Reynolds, J.F. Modeling Effects of Spatial Pattern, Drought, and Grazing on Rates of Rangel and Degradation: A Combined Markov and Cellular Automaton Approach. In Scale in Remote Sensing and GIS; Quattrochi, D.A., Goodchild, M.F., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1997; pp. 211–230. [Google Scholar]
- Radha Devi, A. Karnataka Forest Department Master Plan for Consolidation of Bannerghatta National Park Boundaries and Elephant Corridors; Government of Karnataka: Kalkere, Bangalore, 2003; p. 2. [Google Scholar]
- Green, G.M.; Schweik, C.M.; Randolf, J.C. Retrieving Land-Cover Change Information from Landsat Satellite Images by Minimizing Other Sources of Reflectance Variability. In Seeing the Forest and the Trees: Human-Environment Interactions in Forest Ecosystems; Moran, E.F., Ostrom, E., Eds.; MIT Press: Cambridge, MA, USA, 2005; pp. 131–160. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Champion, H.G.; Seth, S.K. A Revised Survey of Forest Types of India; Government of India: New Delhi, India, 1968. [Google Scholar]
- Pontius, R.G. Quantification error versus location error in comparison of categorical maps. Photogramm. Eng. Remote Sensing 2000, 66, 1011–1016. [Google Scholar]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ 2002, 80, 185–201. [Google Scholar]
- Petit, C.; Scudder, T.; Lambin, E. Quantifying processes of land-cover change by remote sensing: resettlement and rapid land-cover changes in south-eastern Zambia. Int. J. Remote Sens 2001, 22, 3435–3456. [Google Scholar]
- Southworth, J.; Munroe, D.K.; Nagendra, H. Land cover change and landscape fragmentation: Comparing the utility of continuous and discrete analyses for a western Honduras region. Agric. Ecosyst. Environ 2004, 101, 185–205. [Google Scholar]
- Lambin, E.F. Modeling Deforestation Processes: A Review; European Commission: Luxemburg, 1994; pp. 1–113. [Google Scholar]
- Verburg, P.H.; de Nijs, T.C.M.; Ritsema van Eck, J.; Visser, H.; de Jong, K.; A. Method to analyse neighbourhood characteristics of land use patterns. Comput. Environ. Urban Syst 2004, 28, 667–690. [Google Scholar]
- Messina, J.P.; Walsh, S.J. 2.5D Morphogenesis: Modeling landuse and landcover dynamics in the Ecuadorian Amazon. Plant Ecol 2001, 156, 75–88. [Google Scholar]
- Haefner, J.W. Modeling Biological Systems: Principles and Applications; Chapman and Hall: New York, NY, USA, 1996; pp. 144–177. [Google Scholar]
- Pontius, R.G.; Huffaker, D.; Denman, K. Useful techniques of validation for spatially explicit land-change models. Ecol. Model 2004, 179, 445–461. [Google Scholar]
- Ministry of Environment and Forests (MOEF). National Forest Policy 1988; Government of India: New Delhi, India, 1988. [Google Scholar]
- McNeely, J.A. Expanding Partnerships in Conservation; Island Press: Washington DC, USA, 1995; pp. 1–302. [Google Scholar]
- Chape, S.; Harrison, J.; Spalding, M.; Lysenko, I. Measuring the extent and effectiveness of protected areas as an indicator for meeting global biodiversity targets. Phil. T. Roy. Soc. B 2005, 360, 443–455. [Google Scholar]
- Hocking, M.; Stolton, S.; Dudley, N. Evaluating Effectiveness: A Framework for Assessing Management of Protected Areas; IUCN: Gland, Switzerland, and Cambridge, UK, 2000; pp. 1–105. [Google Scholar]
- Nagendra, H. Drivers of regrowth in South Asia’s human impacted forests. Curr. Sci 2009, 97, 1586–1592. [Google Scholar]
- Pressey, R.L.; Whish, G.L.; Barrett, T.W.; Watts, M.E. Effectiveness of protected areas in north-eastern New South Wales: recent trends in six measures. Biol. Conserv 2002, 106, 57–69. [Google Scholar]
- Nagendra, H.; Pareeth, S.; Ghate, R. People within parks—forest villages, land-cover change and landscape fragmentation in the Tadoba Andhari Tiger Reserve, India. Appl. Geogr 2006, 26, 96–112. [Google Scholar]
- Rudel, T.K.; Coomes, O.T.; Moran, E.; Achard, F.; Angelsen, A.; Xu, J.; Lambin, E. Forest transitions: Towards a global understanding of land use change. Global Environ. Change A 2005, 15, 23–31. [Google Scholar]
- Grainger, A. The Bigger Picture-Tropical Forest Change in Context, Concept and Practice. In Reforesting Landscapes: Linking Pattern and Process, Landscape Series 10; Nagendra, H., Southworth, J., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 15–44. [Google Scholar]
- DeFries, R.S.; Hansen, A.; Newton, A.C.; Hansen, M.C. Increasing isolation of protected areas in tropical forests over the past twenty years. Ecol. Appl 2005, 15, 19–26. [Google Scholar]
- Southworth, J.; Nagendra, H. Reforestation: Challenges and Themes in Reforestation Research. In Reforesting Landscapes: Linking Pattern and Process, Landscape Series 10; Nagendra, H., Southworth, J., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 1–14. [Google Scholar]
- Munroe, D.K.; Southworth, J.; Tucker, C.M. Modeling spatially and temporally complex land cover change: The case of Western Honduras. Prof. Geogr 2004, 56, 544–559. [Google Scholar]
- Nagendra, H.; Pareeth, S.; Sharma, B.; Schweik, C.M.; Adhikari, K.R. Forest fragmentation and regrowth in an institutional mosaic of community, government and private ownership in Nepal. Landsc. Ecol 2008, 23, 41–54. [Google Scholar]
- Sitzia, T.; Semenzato, P.; Trentanovi, G. Natural reforestation is changing spatial patterns of rural mountain and hill landscapes: A global overview. For. Ecol. Manage 2010, 259, 1354–1362. [Google Scholar]
- Alonso, D.; Sole, R.V. The DivGame simulator: A stochastic cellular automata model of rainforest dynamics. Ecol. Model 2000, 133, 131–141. [Google Scholar]
- Srinivasan, S. Linking land use and transportation in a rapidly urbanizing context: A study in Delhi, India. Transportation 2005, 32, 87–104. [Google Scholar]
- García-Frapolli, E.; Ayala-Orozco, B.; Bonilla-Moheno, M.; Espadas-Manrique, C.; Ramos-Fernandez, G. Biodiversity conservation, traditional agriculture and ecotourism: Land cover/land use change projections for a natural protected area in the northeastern Yucatan Peninsula, Mexico. Landsc. Urban Plan 2007, 83, 137–153. [Google Scholar]
- Peterson, L.K.; Bergen, K.M.; Brown, D.G.; Vashchuk, L.; Blam, Y. Forested land-cover patterns and trends over changing forest management eras in the Siberian Baikal region. For. Ecol. Manage 2009, 257, 911–922. [Google Scholar]
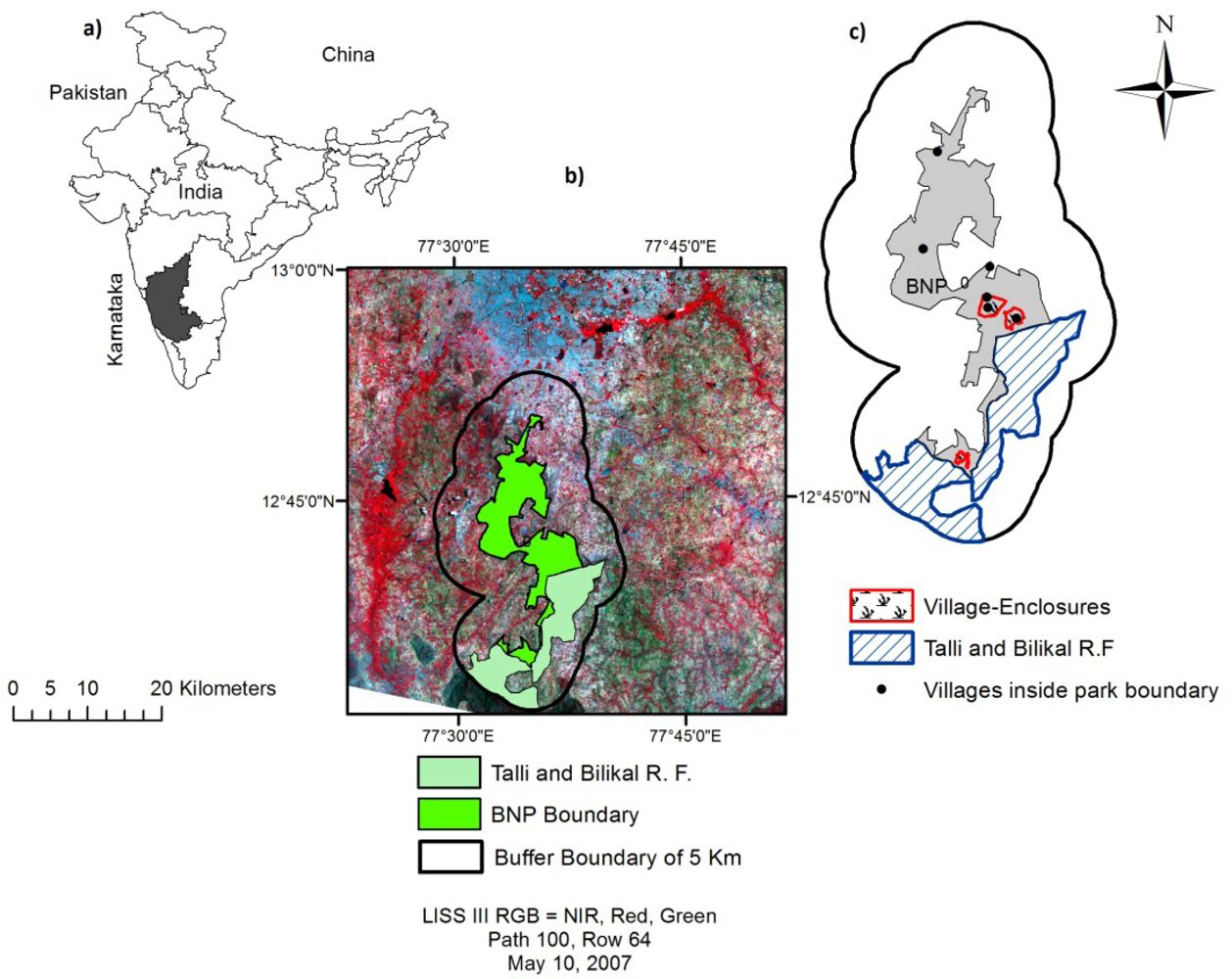
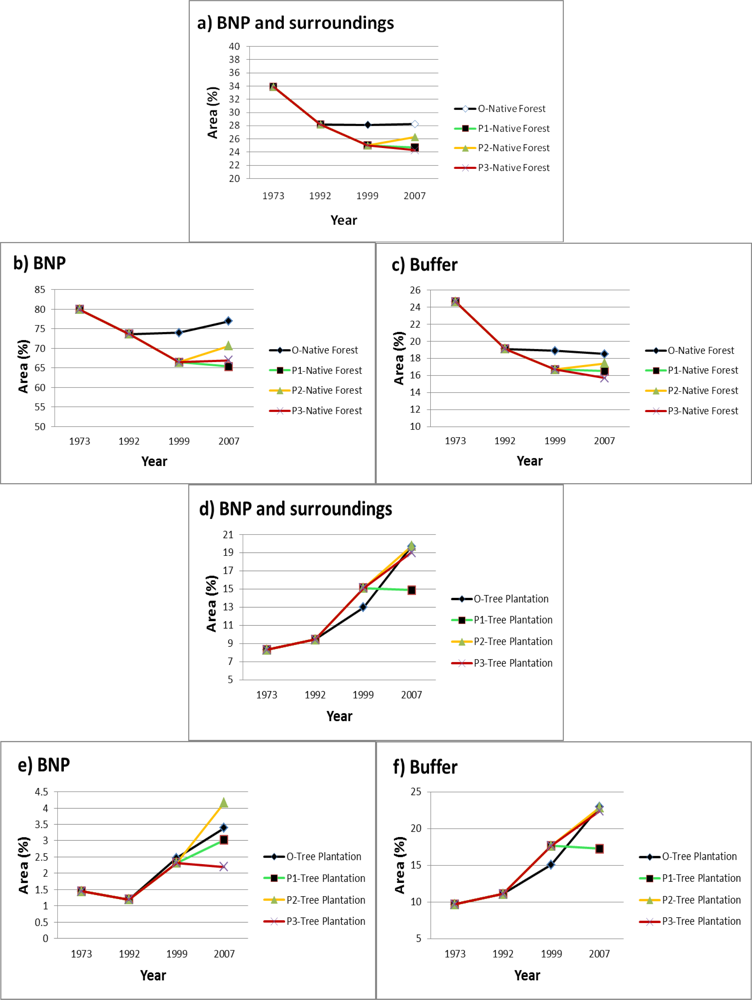
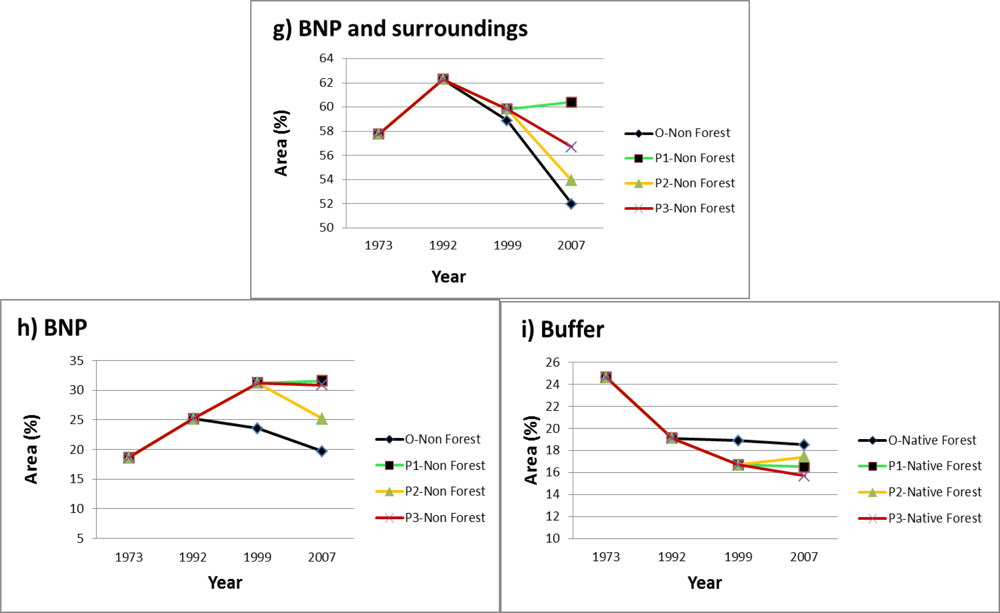
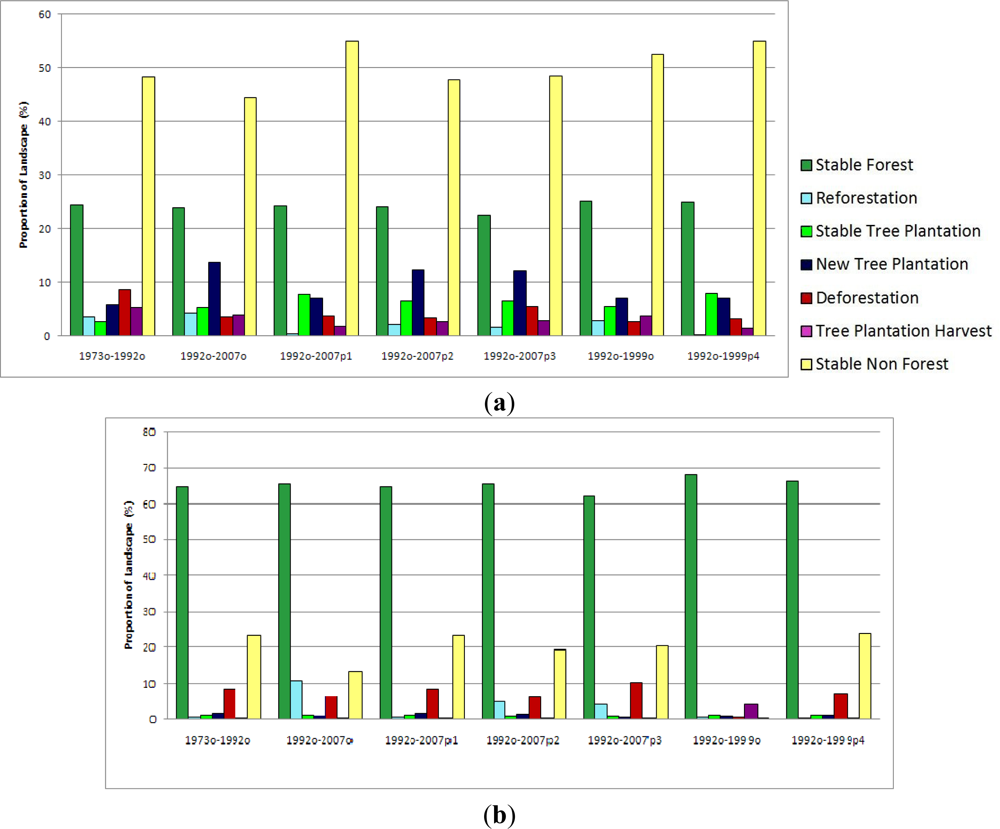
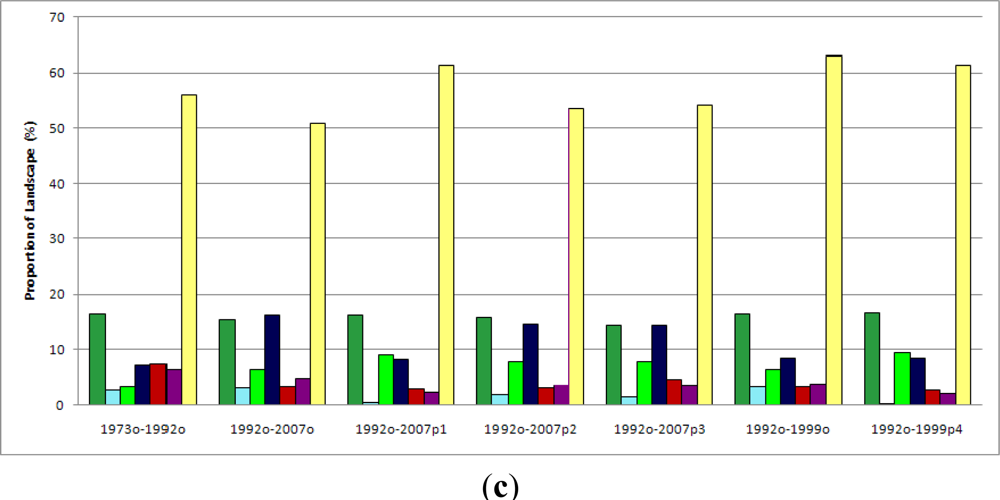


| Sensors | Month/Day | Year | Spatial Resolution (m) | Path/Row |
|---|---|---|---|---|
| Landsat MSS | 02/27 | 1973 | 60 | 154/51 |
| Landsat TM | 01/14 | 1992 | 28.5 | 144/51 |
| Landsat TM | 02/02 | 1999 | 30 | 144/51 |
| IRS LISS III | 05/10 | 2007 | 23.5 | 100/64 |
| Step 1 of Markov Chain Analysis
| ||||
|---|---|---|---|---|
| Time T0 | Time T1 | Land Cover Characteristics | Time T2 | |
| Model 1 | 1973obs | 1992obs | No Policy Intervention | 2007pred1 |
| Model 2 | 1992obs | 1999obs | Policy Intervention | 2007pred2 |
| Model 3 | 1973obs | 1999obs | Combined policy Intervention and non policy intervention | 2007pred3 |
| Model 4 | 1973obs | 1992obs | No Policy Intervention | 1999pred4 |
| Probability of Change to Land Cover: | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Change from Given | Model 1 | Model 2 | Model 3 | Model 4 | ||||||||
| Land Cover: | F | P | NF | F | P | NF | F | P | NF | F | P | NF |
| F | 0.650 | 0.027 | 0.321 | 0.741 | 0.037 | 0.220 | 0.749 | 0.000 | 0.250 | 0.716 | 0.013 | 0.269 |
| P | 0.024 | 0.321 | 0.654 | 0.038 | 0.425 | 0.534 | 0.002 | 0.462 | 0.535 | 0.007 | 0.392 | 0.600 |
| NF | 0.097 | 0.178 | 0.724 | 0.084 | 0.223 | 0.692 | 0.0541 | 0.220 | 0.725 | 0.076 | 0.176 | 0.747 |
| Land-cover | Observed-99 | Observed-07 | Model 1 Predicted-07 | Model 2 Predicted-07 | Model 3 Predicted-07 | Model 4 Predicted-99 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) | Area (km2) | Total Area (%) | Area (km2) | Total Area (%) | Area (km2) | Total Area (%) | Area (km2) | Total Area (%) | Area (km2) | Total Area (%) | Area (km2) | Total Area (%) |
| Native Forest | 177.15 | 28.13 | 178.19 | 28.29 | 155.56 | 24.70 | 165.79 | 26.32 | 153.04 | 24.30 | 157.75 | 25.05 |
| Tree Plantation | 81.9 | 13.00 | 124.22 | 19.72 | 93.84 | 14.90 | 124.36 | 19.75 | 119.78 | 19.02 | 95.20 | 15.12 |
| Non Forest | 370.76 | 58.86 | 327.40 | 51.98 | 380.42 | 60.40 | 339.67 | 53.93 | 356.99 | 56.68 | 376.86 | 59.84 |
| (b) | ||||||||||||
| Native Forest | 78.03 | 73.98 | 81.10 | 76.90 | 68.95 | 65.37 | 74.49 | 70.63 | 70.60 | 66.94 | 70.09 | 66.45 |
| Tree Plantation | 2.61 | 2.47 | 3.58 | 3.39 | 3.19 | 3.03 | 4.39 | 4.16 | 2.31 | 2.19 | 2.45 | 2.33 |
| Non Forest | 24.82 | 23.82 | 20.79 | 19.71 | 33.33 | 31.60 | 26.59 | 25.21 | 32.56 | 30.87 | 32.93 | 31.23 |
| (c) | ||||||||||||
| Native Forest | 99.12 | 18.90 | 97.09 | 18.52 | 86.61 | 16.52 | 91.30 | 17.41 | 82.44 | 15.72 | 87.67 | 16.72 |
| Tree Plantation | 79.28 | 15.12 | 120.64 | 23.01 | 90.65 | 17.29 | 119.97 | 22.88 | 117.47 | 22.40 | 92.75 | 17.69 |
| Non Forest | 345.93 | 65.97 | 306.61 | 58.48 | 347.09 | 66.19 | 313.07 | 59.71 | 324.43 | 61.87 | 343.93 | 65.59 |
Share and Cite
Adhikari, S.; Southworth, J. Simulating Forest Cover Changes of Bannerghatta National Park Based on a CA-Markov Model: A Remote Sensing Approach. Remote Sens. 2012, 4, 3215-3243. https://doi.org/10.3390/rs4103215
Adhikari S, Southworth J. Simulating Forest Cover Changes of Bannerghatta National Park Based on a CA-Markov Model: A Remote Sensing Approach. Remote Sensing. 2012; 4(10):3215-3243. https://doi.org/10.3390/rs4103215
Chicago/Turabian StyleAdhikari, Sanchayeeta, and Jane Southworth. 2012. "Simulating Forest Cover Changes of Bannerghatta National Park Based on a CA-Markov Model: A Remote Sensing Approach" Remote Sensing 4, no. 10: 3215-3243. https://doi.org/10.3390/rs4103215
APA StyleAdhikari, S., & Southworth, J. (2012). Simulating Forest Cover Changes of Bannerghatta National Park Based on a CA-Markov Model: A Remote Sensing Approach. Remote Sensing, 4(10), 3215-3243. https://doi.org/10.3390/rs4103215





