Next Article in Journal
Urban Heat Island Analysis Using the Landsat TM Data and ASTER Data: A Case Study in Hong Kong
Next Article in Special Issue
Identification of Mangrove Areas by Remote Sensing: The ROC Curve Technique Applied to the Northwestern Mexico Coastal Zone Using Landsat Imagery
Previous Article in Journal
Sensitivity of Depth-Integrated Satellite Lidar to Subaqueous Scattering
Previous Article in Special Issue
Remote Sensing of Shallow Coastal Benthic Substrates: In situ Spectra and Mapping of Eelgrass (Zostera marina) in the Gulf Islands National Park Reserve of Canada
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 3
Issue 7
10.3390/rs3071516
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Shoreline Change along Sheltered Coastlines: Insights from the Neuse River Estuary, NC, USA

by
Lisa Cowart
1,
D. Reide Corbett
1,2,* and
J.P. Walsh
1,2
1
Department of Geological Sciences, East Carolina University, Greenville, NC 27858, USA
2
Institute for Coastal Science & Policy, East Carolina University, Greenville, NC 27858, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2011, 3(7), 1516-1534; https://doi.org/10.3390/rs3071516
Submission received: 1 June 2011 / Revised: 29 June 2011 / Accepted: 29 June 2011 / Published: 12 July 2011
(This article belongs to the Special Issue Remote Sensing in Coastal Ecosystem)
Browse Figures
Versions Notes

Abstract

:
Coastlines are constantly changing due to both natural and anthropogenic forces, and climate change and associated sea level rise will continue to reshape coasts in the future. Erosion is not only apparent along oceanfront areas; shoreline dynamics in sheltered water bodies have also gained greater attention. Additional estuarine shoreline studies are needed to better understand and protect coastal resources. This study uses a point-based approach to analyze estuarine shoreline change and associated parameters, including fetch, wave energy, elevation, and vegetation, in the Neuse River Estuary (NRE) at two contrasting scales, Regional (whole estuary) and Local (estuary partitioned into eight sections, based on orientation and exposure). With a mean shoreline-change rate of –0.58 m yr−1, the majority (93%) of the NRE study area is eroding. Change rates show some variability related to the land-use land-cover classification of the shoreline. Although linear regression analysis at the Regional Scale did not find significant correlations between shoreline change and the parameters analyzed, trends were determined from Local Scale data. Specifically, erosion rates, fetch, and wave exposure increase in the down-estuary direction, while elevation follows the opposite trend. Linear regression analysis between mean fetch and mean shoreline-change rates at the Local Scale provide a first-order approach to predict shoreline-change rates. The general trends found in the Local Scale data highlight the presence of underlying spatial patterns in shoreline-change rates within a complex estuarine system, but Regional Scale analysis suggests shoreline composition also has an important influence.

1. Introduction

Due to the significance of estuaries as fish nurseries [1] and with a higher density of people residing in coastal counties [2], considerable interest surrounds the health of the estuarine shoreline [3]. Previous research has focused extensively on oceanfront, sandy beach shorelines, including analysis of the influence of offshore shoals [4], longshore sediment transport [5], and erosion [6]. Although the estuarine environment is located within the coastal area, in close proximity to oceanfront beaches, estuarine shorelines are generally more protected and not as exposed to the vast ocean fetches and high wave energy. However, these protected estuarine shorelines are impacted by a variety of factors, including high energy events, such as storm tides and wind waves. The estuarine environment is complex and an important refuge for juvenile fish and filter for waste, pollution, and excess nutrients [1,7]. Estuarine shoreline change has been calculated in several previous studies [8,9,10,11,12,13,14,15,16]; however, only a few studies have quantitatively analyzed the influence of physical parameters on estuarine shoreline change [8,10,14]. The objective of this study is to further understand the influence of physical parameters (elevation, vegetation, fetch, wave exposure) associated with estuarine shoreline change over a large area using readily available datasets and techniques.
Shoreline change analysis has been conducted utilizing different approaches, including field observations and transect-based, and point-based approaches in a GIS [8,10,11,14,16,17,18,19,20,21,22,23]. Field-based methods are costly, requiring much manpower and resources. Additionally, historical or long-term shoreline-change analysis is not attainable solely through field observations unless monitoring programs began previously. The transect-based and point-based approaches can both be used with remotely sensed data to calculate short- and long-term shoreline change. The transect-based approach has been implemented since its inception with attempts to automate the process dating back to Dolan et al. [24]. Extraction and application of the transect-based approach became more easily executable with the Digital Shoreline Analysis System, created by the USGS [25]. However, recent research has unveiled the ease and application of a point-based approach in estuarine shoreline change analysis [26]. In addition to calculating shoreline change, Cowart et al. [26] describes how the point-based approach allows the user to easily associate parameters or variables (e.g., vegetation, elevation, and fetch) to the shoreline change occurring at each point along the shoreline.
This study applies the point-based approach of Cowart et al. [26] to the analysis of shoreline change at a large-scale (fine-resolution) along the Neuse River Estuary (NRE), North Carolina (Figure 1). In addition to shoreline change, parameters commonly associated with shoreline erosion (elevation, fetch, wave exposure, shoreline vegetation) are determined and statistically analyzed with the objective of identifying controls on the patterns of shoreline change. To facilitate the analysis, the estuary is analyzed at two scales: the Regional Scale (the estuary as a whole) and the Local Scale (the estuary partitioned into eight sections, based on orientation and exposure).
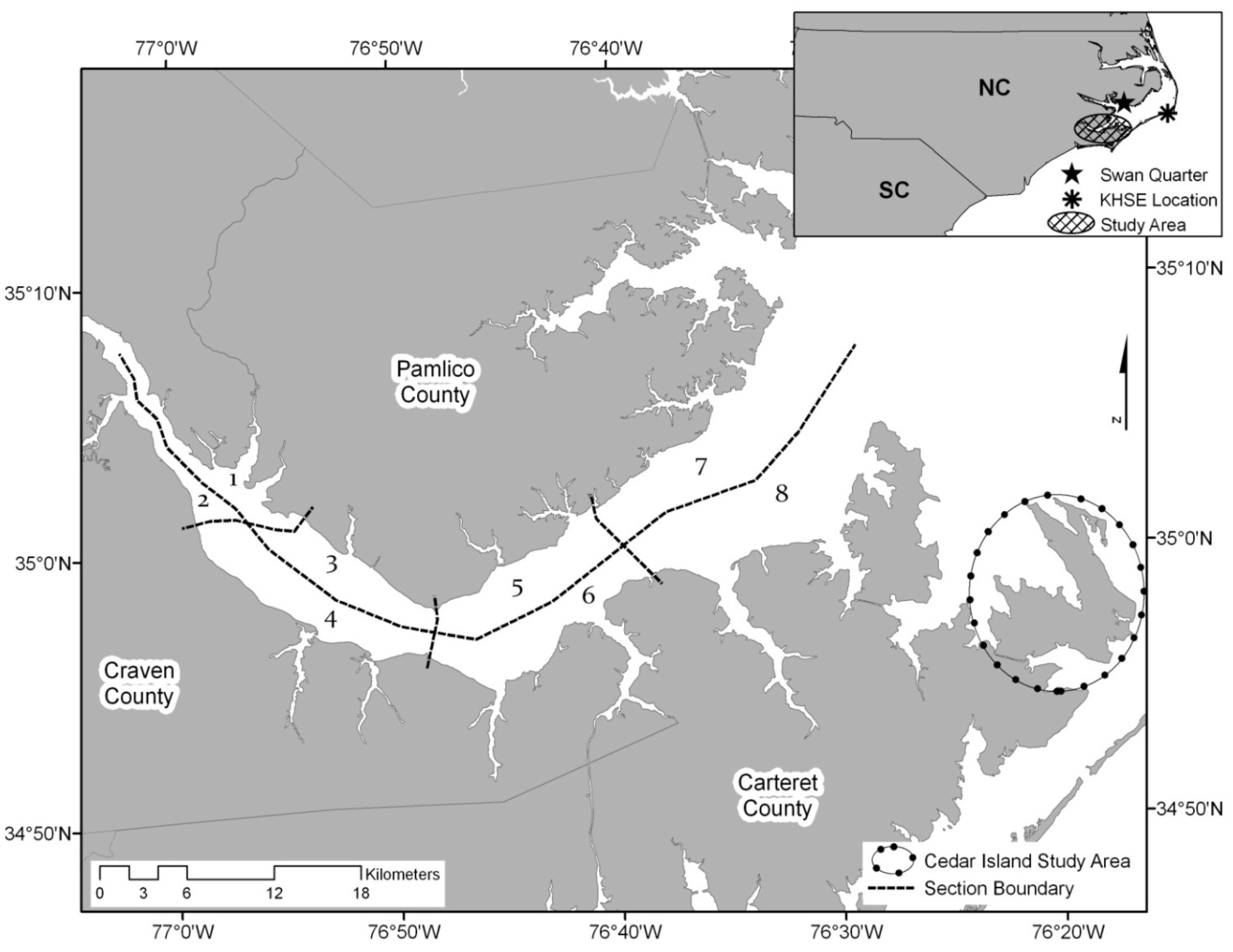
Remotesensing 03 01516 g001 1024
Figure 1. Location map of Neuse River Estuary study area located in North Carolina (inset). Meteorological data were obtained from the KHSE site (inset). The dashed line and corresponding numbers refer to the Local Scale sections.
Figure 1. Location map of Neuse River Estuary study area located in North Carolina (inset). Meteorological data were obtained from the KHSE site (inset). The dashed line and corresponding numbers refer to the Local Scale sections.
Remotesensing 03 01516 g001

2. Study Area

Coastal North Carolina contains the Albemarle-Pamlico Estuarine System (APES), which is the second largest estuary in the United States and is considered one of the 28 “nationally significant” estuaries [1]. The Neuse River Estuary (NRE) is the southernmost sub-estuary contained within the APES. The NRE is shaped like a bent arm with the elbow approximately 30 km from the mouth of the river and is a drowned river valley, approximately 70-km long, 6.5-km wide, and has an average depth of 3.5 m [27,28]. It is fed by the Neuse River, which drains a moderately sized basin that originates in the Piedmont, flows through the Coastal Plain and empties into Pamlico Sound. The average annual discharge of the Neuse River to the NRE is 150 m3 s−1, supplying a large portion of freshwater flow to Pamlico Sound [29]. The estuary is dominated by river flow and is characterized by wind-tide-driven mixing and occasionally strong stratification.
The APES is separated from the Atlantic Ocean on the eastern side by the Outer Banks, a series of barrier islands. The tidal influence of the Atlantic Ocean is restricted by four inlets resulting in an astronomical tidal variation of ≤10 cm [27]. Due to the low tidal influence, the major force driving water flow is the wind [30], and the large fetches of Pamlico Sound (>1 km) make the NRE susceptible to large waves during strong winds (e.g., storms).

3. Methods

3.1. Determining Shoreline Change Rates

Shoreline-change rates (SCRs) were calculated using 1998 Digital Orthophoto Quarter Quadrangles (DOQQs) and 1958 black and white aerial photographs. The 1998 DOQQs with 1 m × 1 m image pixel resolution, in NAD 1983 State Plane NC FIPS 3200 projection, were obtained from the USGS in digital format. The 1958 aerial photographs were obtained from the North Carolina Geological Survey, but were originally collected by Aerial Park Surveys, Inc. for the United States Department of Agriculture Commodity Stabilization Service. The 9 cm × 9 cm positive contact prints of the 1958 photographs were scanned using a Microtek ScanMaker 9800XL at 8-bit pixel resolution with a 600-dpi image resolution and were saved in tiff format. Once in digital form, the 1958 photographs were rectified using the 1998 DOQQs and the georeferencing tools within ArcGIS®. Ninety 1958 aerial photographs were rectified using a minimum of four ground control points. The mean number of ground control points used in rectification was 9.5, and depending on the number of ground control points, the aerial photographs were rectified with a first- or second-order polynomial transformation. In areas where less than six ground control points were identified, the first-order polynomial transformation was needed; otherwise, the second-order polynomial transformation was used. The mean root-mean-square error of the 1958 aerial photograph rectifications was 1.51 m.
Once the aerial photographs were rectified, the wet/dry line was delineated on sediment shorelines (see [31] and references therein), whereas the apparent shoreline was digitized on vegetated shorelines, i.e., the vegetation boundary [32]. The shorelines were on-screen digitized as a series of polylines using a zoom tolerance of 1:500 to 1:3,000 [33]. The polyline segments were then routed, using the CREATE ROUTES linear referencing tool within ArcGIS®. After the shorelines were digitized and routed, points were created every 50 meters along the 1998 shoreline using the ArcGIS® DIVIDE function and saved as a point shapefile. A polygon shapefile was generated from the 1958 shoreline polyline to define the initial land area. By intersecting the 1998 shoreline points with the 1958 polygon land area, the shoreline points that had moved landward were identified, i.e., indicating erosion or negative shoreline change. Then, the end-point rate method was used to calculate the SCR at each point [17,26]. Distances from the 1998 shoreline points to the 1958 shoreline were determined using the NEAR tool in ArcGIS®. The distance value was then divided by 40 years, to calculate the SCR over the four decade time period between photographs.
The total positional uncertainty (UT) of the shorelines and SCRs determined within this study was calculated based on the work performed by Genz et al. [34] and Fletcher et al. [35]. Of the error variables used by Genz et al. [34] and Fletcher et al. [35], three were utilized to calculate UT for this study, including digitization error of the 1998 shoreline (Ed1), digitization error of the 1958 shoreline (Ed2), and rectification error (Er).
U T = ± E d 1 2 + E d 2 2 + E r 2
For shoreline change analysis using aerial photography the tidal fluctuation error can be incorporated; however, since the tidal fluctuation within the study area is minimal (≤10 cm; [27]), this variable was not included in the positional uncertainty analysis. Through multiple digitization of the same area, a digitization error of 0.55 m was calculated for the 1998 and 1958 shorelines. To reduce uncertainty, all shoreline digitization in this study was completed by a single digitizer. As stated previously, the 1958 rectified aerials had a mean RMSE of 1.51 m; therefore, the UT of the shorelines and SCR data is ±1.70 m, which is 0.04 m yr−1 over the 40 year period.

3.2. Evaluating Parameters that Influence Shoreline-Change Rates

To evaluate controls of SCR, some of the parameters identified in previous studies that have been considered relevant to estuarine erosion were determined at the 1998 shoreline points, including fetch, wave exposure, elevation, and shoreline vegetation. Fetch is the unobstructed distance over open water. Relative Exposure Index (REI) was used as a proxy for wave exposure. The fetch and REI values were calculated using a Wave Exposure Model (WEMo). WEMo is an ArcGIS® tool developed by and available from the NOAA and has been used as a measure of wave exposure in submerged-aquatic-vegetation research [36]. In WEMo, fetch was determined by radiating 32 lines at 11.25° angle increments from the point of interest. The fetch lines were clipped to the area occupied by the bathymetric dataset. To create a single representative value of fetch, the 32 fetch lengths were averaged to calculate the “mean fetch” value at each shoreline point. The fetch, bathymetry, and wind data were used to calculate REI within WEMo. The bathymetry data, used to calculate REI, was extracted from the NOAA TopoDigital Elevation Model (TDEM) that was created from North Carolina Federal Emergency Management Agency LIDAR data, Shuttle Radar Topographic Mission data, the USGS National Elevation Dataset, National Ocean Service soundings, United States Army Corps of Engineers soundings, Coastal Relief Model data, and digitized NOAA paper nautical charts [37]. The NOAA TDEM has a 6 m horizontal resolution and 20 cm vertical accuracy on land and lower resolution for bathymetric data due to varying age and acquisition of data (NAVD 88 datum). To create the bathymetry dataset, values less than zero were extracted (i.e., below sea level), using the ArcGIS® spatial analyst extension. Hourly wind data were obtained from the KHSE weather station, located in Hatteras, NC (35°14'N 75°37'W, see Figure 1), for the four-decade period (1958 to 1998).
Additionally, elevation and shoreline vegetation were determined at the shoreline points. Shoreline elevation is the elevation of the area surrounding each shoreline point and was determined using the topographic data within the NOAA TDEM. Values greater than zero (land) were extracted within the NOAA TDEM using the ArcGIS® spatial analyst extension. Because the shoreline points were spaced 50 m apart, and to avoid a spurious value for the shoreline elevation, a 25 m buffer was used to calculate a mean elevation for each shoreline point. The mean elevation values within the 25 m buffer were determined using the ZONAL STATISTICS function within Hawth’s Tools© [38]. Shoreline vegetation is a categorical variable that was determined using the 1997 NOAA land-use land-cover (LULC) Coastal Change Analysis Program (C-CAP) dataset, which has a 30 m resolution [39]. Because shoreline points did not perfectly overlie the LULC data, the nearest value was assigned to each shoreline point. This was accomplished by converting the LULC raster dataset to a point shapefile and then using the NEAR tool. While each of these datasets and approaches have their potential limitations and inaccuracies, it is believed the gross trends and variability will be captured in the analysis because of the numerous measurements of shoreline change and the associated parameters.

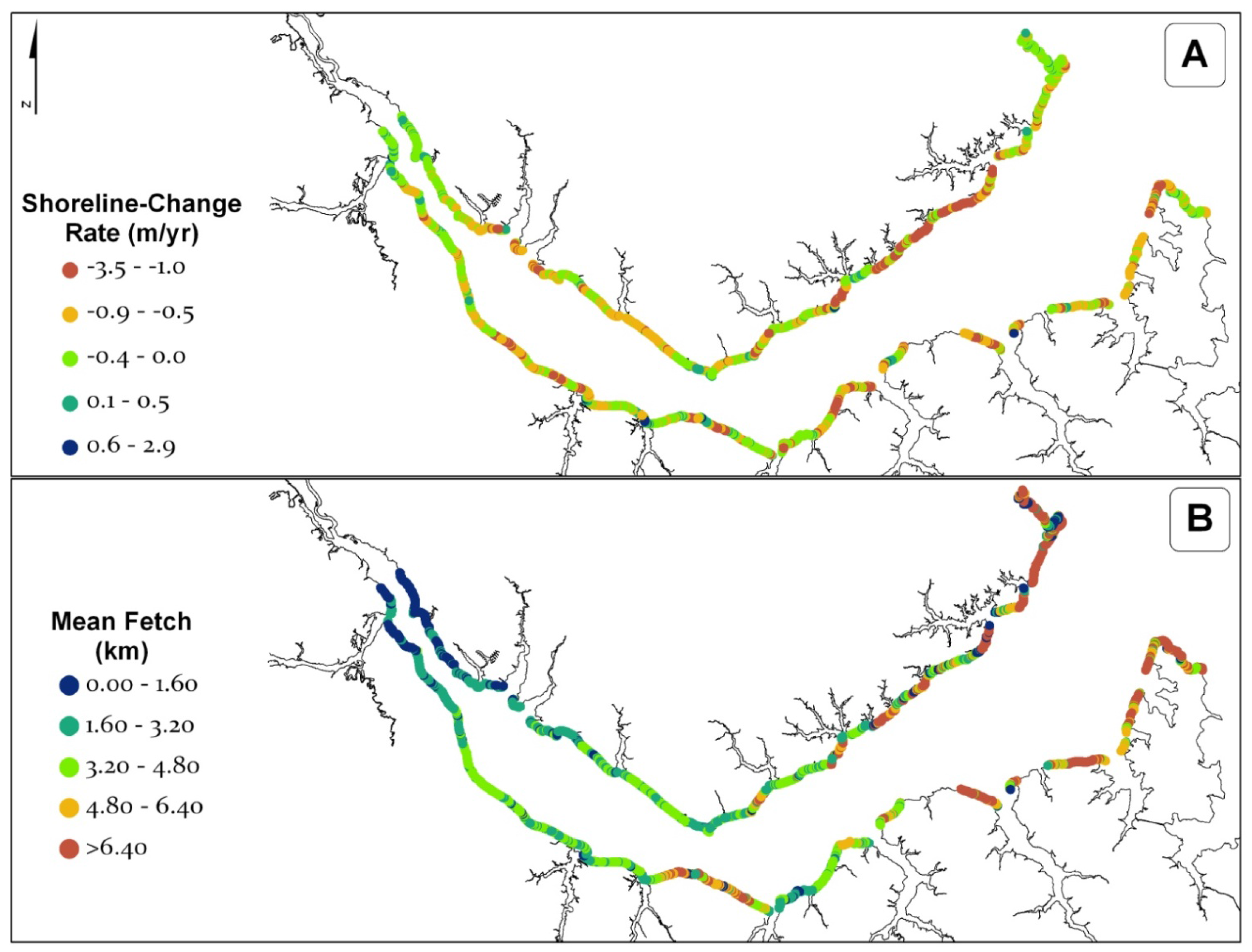
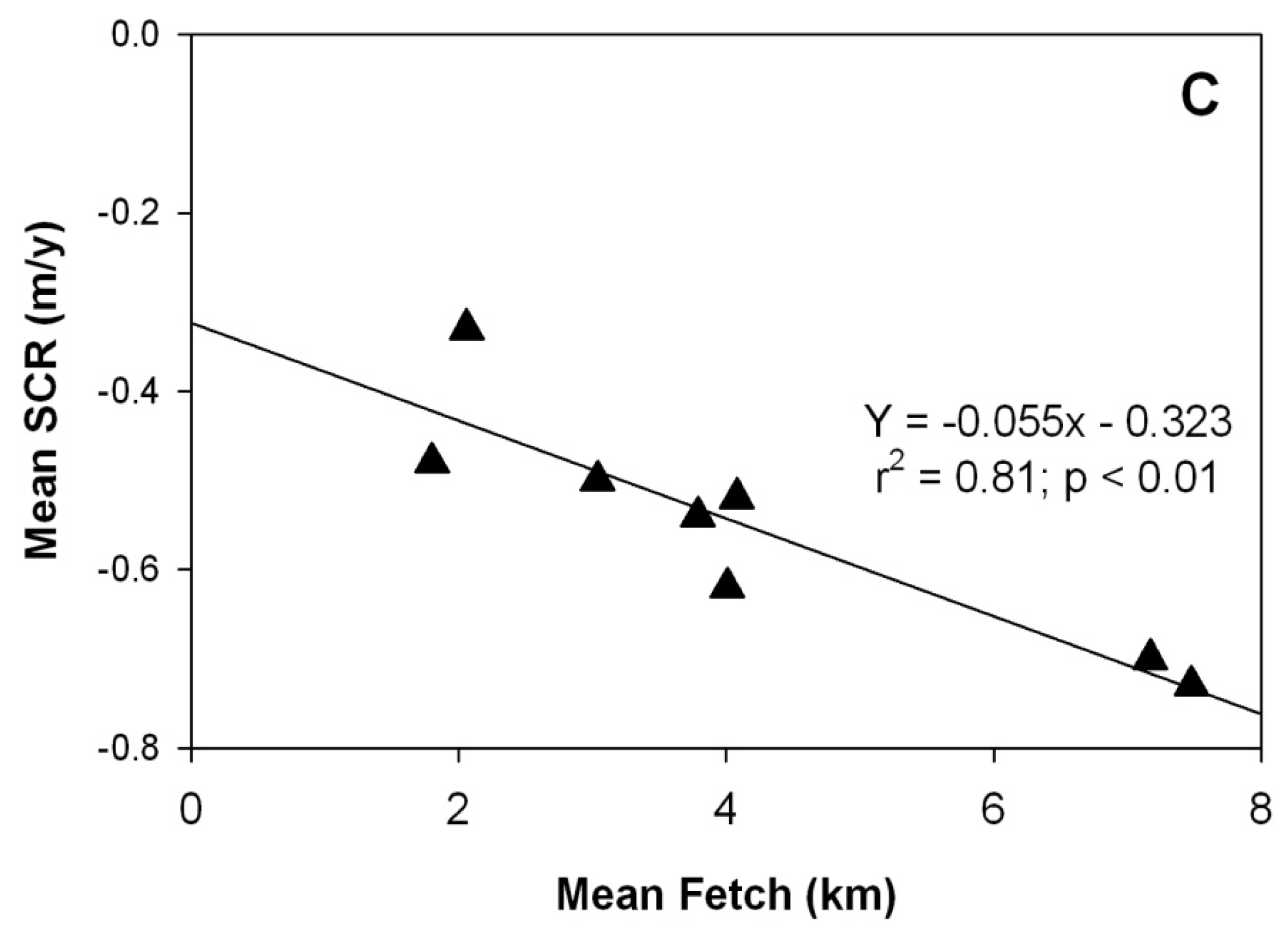
4. Results

4.1. Regional Scale

Of the 156 km of shoreline analyzed, 93.0% eroded, 6.6% accreted, and 0.4% did not experience a measured change over the 40 year period. The average SCR of the entire NRE trunk was −0.58 m yr−1 for the 40 year time period and ranged from −3.48 to 2.89 m yr−1 (Table 1). Higher erosion rates (lower SCRs) were determined down-estuary where the NRE opens to Pamlico Sound, whereas the upper estuary, where the Neuse River enters the system, had lower erosion rates (higher SCRs) on average, as shown in Figure 2(A).
Table
Table 1. Descriptive statistics of parameters measured within the Neuse River Estuary.
Table 1. Descriptive statistics of parameters measured within the Neuse River Estuary.
ParameterMinimumMaximumMeanStandard Deviation
Shoreline Change Rate (m yr−1)−3.482.89−0.580.54
Elevation (m)0.047.200.960.80
Fetch(km)East064.18.81
Northeast01007.51
North038.84.63
Northwest025.93.14
West019.02.47
Southwest022.61.82
South016.62.66
Mean Fetch (km)018.84.653.66
Relative Exposure Index (103)011.61.822.51
The mean shoreline elevation of the study area was 0.96 m with a range of 7.20 m (Table 1). The majority (70%) of the shoreline had a mean elevation value less than 1 m. Because the vertical accuracy of the DEM used to derive the mean elevation values is 20 cm, the mean shoreline elevation values were binned into 30 cm intervals (Figure 3). The mean SCRs of the elevation intervals were all negative, but generally ranged from −1 to −0.5 m yr−1. Interestingly, no clear trends were evident between shoreline elevation and SCR.
Of the dominant eight compass heading directions (north, northeast, east, southeast, south, southwest, west, and southwest), the lowest average fetch direction within the NRE was southwest (1.8 km), and the highest average fetch direction was east (8.8 km, Table 1). The mean fetch value of the study area was 4.6 km with a range of 18.8 km. Generally, larger mean fetch values were located down-estuary and in the middle of the NRE on the southern shoreline, where long northeast fetches occur. Smaller mean fetches were located in embayed areas and on the up-estuary shorelines of the NRE (Figure 2(B)). Similar to fetch values, REI values had a large range (11.6 × 103), while the mean REI value for the entire study area was relatively low (1.82 × 103; Table 1).
Remotesensing 03 01516 g002 1024
Figure 2. (A) Map of shoreline-change rate distribution along the Neuse River Estuary study area. Areas with higher erosion rates are denoted in warmer colors (yellow to red), and areas that have accreted are represented in cooler colors (blues). (B) Map of mean fetch distribution along the Neuse River Estuary shoreline. High mean fetch values are represented in red and low mean fetch values are denoted as blue.
Figure 2. (A) Map of shoreline-change rate distribution along the Neuse River Estuary study area. Areas with higher erosion rates are denoted in warmer colors (yellow to red), and areas that have accreted are represented in cooler colors (blues). (B) Map of mean fetch distribution along the Neuse River Estuary shoreline. High mean fetch values are represented in red and low mean fetch values are denoted as blue.
Remotesensing 03 01516 g002
Remotesensing 03 01516 g003 1024
Figure 3. Plot of mean shoreline-change rate (±1 standard error) for the binned 30 cm elevation intervals.
Figure 3. Plot of mean shoreline-change rate (±1 standard error) for the binned 30 cm elevation intervals.
Remotesensing 03 01516 g003
Figure 4 shows scatterplots that display the distribution of parameter values related to SCRs. Linear regression analysis indicated elevation, fetch, and REI were not correlated with SCRs; mean elevation, fetch, and REI values only explained 1.5% of the variation in the SCR values. A significant relationship was calculated between the parameters and SCR values (p = 0.000), largely due to the large number of values in the dataset, but this does not explain much of the variation in SCRs (e.g., low correlation coefficient). The majority of SCR points were located at a mean elevation less than or equal to 1.00 m (70%), with approximately one quarter of the shoreline within the study area being less than or equal to 0.50 m (24%, Figure 4(A)). The distribution of SCR points decreases at higher REI values, and there was no direct correlation between the exposure at the shoreline and SCRs using a 50 m sampling interval with the entire dataset (i.e., at the Regional Scale, Figure 4(B)). The SCRs within the 0 to 1.00 m mean elevation had a wide SCR distribution, ranging from 2.89 to −3.48 m yr−1. Also, SCRs had a broad distribution over the range of mean fetches (Figure 4(C)).
Remotesensing 03 01516 g004 1024
Figure 4. Scatterplots of (A) shoreline-change rates and mean elevation, (B) relative exposure index, and (C) mean fetch values calculated at 50 m spacing along the Neuse River Estuary shoreline.
Figure 4. Scatterplots of (A) shoreline-change rates and mean elevation, (B) relative exposure index, and (C) mean fetch values calculated at 50 m spacing along the Neuse River Estuary shoreline.
Remotesensing 03 01516 g004
Of the 16 LULC types within the C-CAP dataset, 14 are located on the shoreline of the NRE study area, including bare land, cultivated land, deciduous forest, estuarine emergent wetland, evergreen forest, grassland, high intensity developed, low intensity developed, mixed forest, palustrine emergent wetland, palustrine forested wetland, palustrine scrub/shrub wetland, scrub/shrub, and unconsolidated shore. Of these LULC types, estuarine emergent wetland is the most dominant, composing 46% of the shoreline. Deciduous forest is the least abundant (<1%) of the 14 LULC types present.
To further evaluate the affect of shoreline composition on SCRs, the LULC types were grouped into 4 categories: Wetland (palustrine emergent wetland, palustrine forested wetland, palustrine scrub/shrub wetland, estuarine emergent wetland), Sediment Bank (unconsolidated shore, bare land, grassland, scrub/shrub), Forest (deciduous forest, mixed forest, evergreen forest), and Other (high intensity developed, low intensity developed, cultivated land). Because of some non-normality and heteroscedasticity of the data, a non-parametric Kruskal-Wallis test was employed to confirm the importance of LULC in explaining the variance. When the 4 LULC categories were compared with an ANOVA, the mean SCR of the Sediment Bank shoreline (−0.70 m yr−1) was found to be the lowest (most erosive) and significantly different from the Wetland, Forest, and Other LULC categories (Table 2). Related to this, Forest shorelines had the highest mean elevation while Wetland areas had the lowest mean elevation. Mean elevation values of the Forest and Wetland LULC categories were significantly different from the other three LULC categories. Additionally, larger and significantly different mean fetch values were calculated on Wetland and Sediment Bank shorelines compared to Forest and Other LULC categories. Although the Wetland areas had the highest mean fetch value, these areas had the lowest mean elevation and least amount of erosion (highest SCR). However, because of some non-normality and heteroscedasticity, the robustness of these results may be viewed with caution.
Table
Table 2. Mean parameter values of the four Land-Use Land-Cover (LULC) categories within the Neuse River Estuary study area. Symbols denote the LULC categories that are significantly different for the specified parameters.
Table 2. Mean parameter values of the four Land-Use Land-Cover (LULC) categories within the Neuse River Estuary study area. Symbols denote the LULC categories that are significantly different for the specified parameters.
ParameterLULC Category
WetlandForestSediment BankOther
MeanShoreline Change Rate (m yr−1)−0.53 †−0.57 †−0.70 ‡−0.56 †
Elevation (m)0.85 †1.40 ‡1.09 #1.09 #
Fetch (km)4.9 †3.5 ‡4.6 †3.7 ‡
Relative Exposure Index (103)2.0 †1.0 ‡1.7 †,#1.3 ‡,#

4.2. Local Scale

The Local Scale data were generated by binning the shoreline points into eight sections based on orientation and exposure (Figure 1). Section 1 is the northwesternmost shoreline, with section numbers increasing eastward. Odd sections are located along the northern shoreline, and even sections are found along the southern shoreline. The highest mean erosion rates (lowest SCRs) are calculated for Sections 7 and 8 (−0.73 and −0.70 m yr−1), and Section 2 has the lowest erosion rate (−0.33 m yr−1; Table 3). The mean SCR decreases (becomes more erosive) on the northern and southern shoreline moving from west to east. The inverse relationship is seen for mean fetch values, with the lowest mean fetch calculated for Section 1 (1.80 km) and Section 7 having the highest mean fetch (7.48 km). Excluding Section 1, the mean elevation values decreases moving from west to east, with Section 2 having the highest mean elevation (1.63 m), and the lowest mean elevation is calculated for Section 8 (0.58 m).
Through an ANOVA, the mean SCR and parameter values are compared between the eight sections (Table 3). The lowest erosion rate (highest SCR) is calculated for Section 2, and it is found to be significantly different from the other seven sections. The mean SCRs of the other sections displayed a general trend of increasing erosion down-estuary with Sections 1 and 2 being significantly different from Sections 6–8. Mean elevation values also varied significantly down-estuary, where Sections 7 and 8 have the lowest mean elevations and are significantly different from Sections 2–6. Excluding Section 1, the mean elevation values decrease moving down-estuary. The inverse relationship is present for the mean fetch values of the sections, with the lowest mean fetch values calculated for Sections 1 and 2 and the largest mean fetch values in Sections 7 and 8. The mean fetch values up-estuary (Sections 1 and 2) and down-estuary (Sections 7 and 8) are significantly different from the other six sections.
Wetland is the dominate LULC type in each of the eight sections (≥44%, Table 4). Excluding Section 2, Sediment Bank is the second most abundant LULC type, ranging from 11 to 36% in the eight sections. The lowest erosion rate (highest value of SCR) of Wetland shorelines between the eight sections is calculated for Section 2 (−0.30 m yr−1) and is significantly different from the mean SCRs of the other seven sections (Table 4). The Wetland shoreline in Section 8, which has the highest erosion rate (−0.70 m yr−1), is also significantly different from the other seven sections (Figure 5).
Table
Table 3. Mean parameter values of the eight Local Sections within the study area. Sections 1, 3, 5, and 7 are located on the northern shoreline, and Sections 2, 4, 6, and 8 are located on the southern shoreline (see Figure 1 for section locations). Symbols denote values that are significantly different for the specified parameters.
Table 3. Mean parameter values of the eight Local Sections within the study area. Sections 1, 3, 5, and 7 are located on the northern shoreline, and Sections 2, 4, 6, and 8 are located on the southern shoreline (see Figure 1 for section locations). Symbols denote values that are significantly different for the specified parameters.
ParameterLocal Section Number
12345678
MeanShoreline Change Rate (m yr−1)−0.48 †−0.33 ‡−0.50 †,#−0.54 †,#−0.52 †,#−0.62 #,$−0.73 $−0.70 $
Elevation (m)0.62 †1.63 ‡1.30 #1.51 ‡1.00 $0.90 $0.64 †0.58 †
Fetch (km)1.80 †2.06 †3.04 ‡3.79 #4.08 #4.01#7.48 $7.17 $
Relative Exposure Index (103)0.10 †0.13 †0.29 †0.78 ‡1.11 ‡1.65#3.71 $4.03 $
Table
Table 4. Mean shoreline-change rate (SCR) and percent (%) of the LULC categories for each Local Section. Significantly different values of SCR are denoted by different symbols.
Table 4. Mean shoreline-change rate (SCR) and percent (%) of the LULC categories for each Local Section. Significantly different values of SCR are denoted by different symbols.
Local SectionLand-Use Land-Cover Category
WetlandForestSediment BankOther
SCR(%)SCR(%)SCR(%)SCR(%)
1−0.52(82)−0.57(1)−0.27(11)−0.18(6)
2−0.30 †,‡(39)−0.43 †(16)−0.37 †,‡(21)−0.27 ‡(24)
3−0.52(60)−0.43(2)−0.53(29)−0.31(9)
4−0.63 †(44)−0.59 †(16)−0.46 †(35)−0.14 ‡(5)
5−0.45(44)N/AN/A−0.61(36)−0.51(20)
6−0.52(47)−0.65(10)−0.72(31)−0.69(11)
7−0.49 †(70)−1.17 ‡(1)−1.24 ‡(24)−1.50 ‡(5)
8−0.70(68)−0.74(1)−0.67(25)−0.79(6)
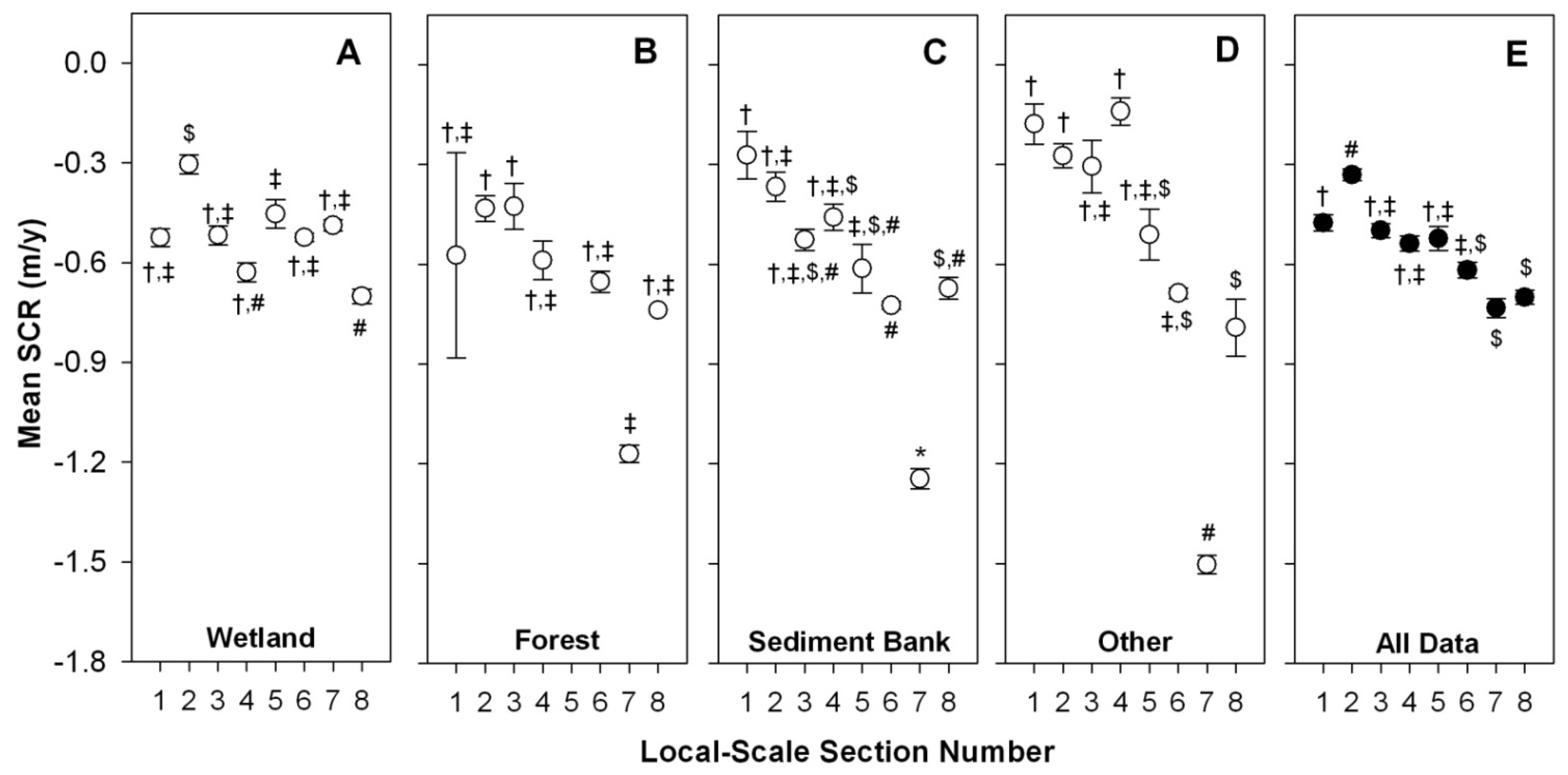
Remotesensing 03 01516 g005 1024
Figure 5. Plot of mean shoreline-change rate values (±1 standard error) for each of the eight sections grouped by land-use land-cover type (LULC) category, displaying the (A) Wetland, (B) Forest, (C) Sediment Bank, (D) other, and (E) the entire dataset. Significantly different values are denoted by different symbols between sections within each plot.
Figure 5. Plot of mean shoreline-change rate values (±1 standard error) for each of the eight sections grouped by land-use land-cover type (LULC) category, displaying the (A) Wetland, (B) Forest, (C) Sediment Bank, (D) other, and (E) the entire dataset. Significantly different values are denoted by different symbols between sections within each plot.
Remotesensing 03 01516 g005
When the mean SCRs and parameter values (elevation, REI, fetch) of the eight Local Sections are regressed, all three parameters are significantly correlated (Figure 6). Mean elevation is positively correlated with the mean SCRs (Figure 6(A)), explaining 51% of the variation in shoreline change (p < 0.05). A more highly correlated, inverse relationship is present between mean REI values and mean SCRs of the eight Local Sections (Figure 6(B)), where mean REI values explains 80% of the variation in SCRs (p < 0.01). Mean fetch values have the highest correlation, explaining 81% of the variation in SCRs (p < 0.01) (Figure 6(C)).
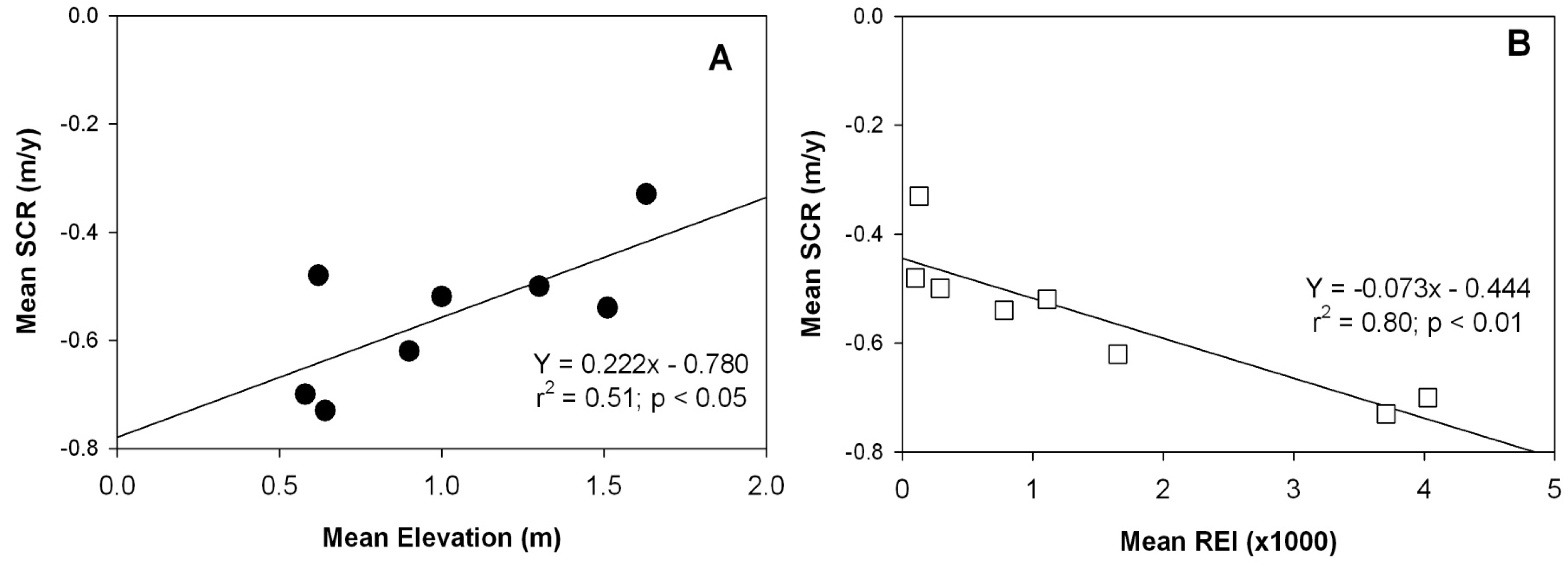
Remotesensing 03 01516 g006a 1024Remotesensing 03 01516 g006b 1024
Figure 6. Scatterplots and linear regression of shoreline-change rate and (A) mean elevation, (B) mean relative exposure index, and (C) mean fetch values of the eight Local Sections.
Figure 6. Scatterplots and linear regression of shoreline-change rate and (A) mean elevation, (B) mean relative exposure index, and (C) mean fetch values of the eight Local Sections.
Remotesensing 03 01516 g006aRemotesensing 03 01516 g006b

5. Discussion

5.1. Regional Scale Relationships

In previous research, SCRs of protected areas range from −0.16 m yr−1 along the western shoreline in the Chesapeake Bay, MD [9] to −3.21 m yr−1 in Delaware Bay, NJ [10]. Within the sub-estuaries of the APES, the highest SCRs (least erosional) calculated for wetland shorelines are determined along Cedar Island (−0.24 m yr−1; Cowart et al. 2010) and the lowest wetland SCRs (most erosive) along the shoreline of Swan Quarter (−0.91 m yr−1; [13]). Despite the variability of shoreline vegetation composition and fetch, it is not surprising that the mean SCR of the entire NRE trunk (−0.58 m yr−1) is within the range of wetland SCRs previously calculated in the APES and other studies. Similar to the findings of Cowart et al. [26], the Wetland areas are shown to be eroding less, compared to the other shoreline LULC types; however, the mean SCR of the Wetland shoreline data of the NRE trunk (i.e., this study, −0.53 m yr−1) is eroding at more than double the rate of the wetland shoreline points analyzed along Cedar Island, NC (−0.22 m yr−1). A higher mean erosion rate is likely due to the wave energy of the NRE trunk compared to Cedar Island, NC.
There is no linear correlation between the parameters analyzed (i.e., using all elevation, fetch, and REI data) and SCRs. A similar lack of correlation was found along the shoreline of Cedar Island, NC [26]. However, Cowart et al. [26] did observe a significant difference between mean SCRs of different LULC types (i.e., estuarine emergent wetland, scrub/shrub, evergreen forest). Similar to the findings in Cowart et al. [26], the highest mean SCRs (lowest erosion rate) occur at Wetland shorelines, and the lowest mean SCRs (highest erosion rate) occur at Sediment Bank shorelines along the NRE shoreline; however, unlike the Cedar Island study, the mean SCRs are not significantly different between each of the LULC types. Discrepancies between the findings of the two studies may be due to the spatial distribution of the LULC types within the NRE trunk. For example, the majority (42%) of the Wetland is located down-estuary in the NRE, which experiences the largest fetch and is at a lower mean elevation. Although 63% of the shoreline in the upper estuary is Wetland, it represents only 23% of the Wetland shoreline within the NRE and almost half of the amount located further down-estuary.
Conflicting results between the Cedar Island study and the findings from this study may also be due to spatial autocorrelation. Spatial autocorrelation occurs when values located near each other are more similar compared to those farther apart. When values located close together are similar, they are considered spatially dependent (see [10,40]). For example, shoreline change is expected to be consistent in areas with less geomorphological complexity compared to a more geomorphologically complex area. This is illustrated in previous research on linear oceanfront shorelines which determined that SCRs can be averaged over 6 to 10 km along the Atlantic coast of North Carolina [40] whereas the more geomorphologically complex Delaware Bay, NJ shoreline must be sampled at 3-km stretches to avoid spatial autocorrelation [10]. To minimize the potential impact of spatial autocorrelation on the analysis of the NRE data, shoreline change was further analyzed at the Local Scale.

5.2. Local Scale Trends

Phillips [10] analyzed up-bay and down-bay sites within the Delaware Bay, NJ at three scales (6.5, 10.4, and 17.4 km). Up-bay sites were more protected and were located further from the open water of the Atlantic Ocean, similar to Sections 1 and 2 within the NRE. The down-bay area was more exposed and comparative to Sections 7 and 8 within the NRE. Similar to the general trends determined at the Local Scale within the NRE, Phillips [41] found lower erosion rates up-bay and higher erosion rates down-bay. The trends may reflect the influence of shoreline vegetation type and exposure on shoreline change.
The general trend of increasing erosion moving from more protected areas, (up-estuary, Sections 1 and 2) to more exposed areas (down-estuary, Sections 7 and 8) is also shown in the LULC-separated data at the Local Scale. The Forest, Sediment Bank, and Other categories all show a general trend of increasing erosion down-estuary. However, Wetland SCRs (Figure 5(A)) display only a subtle, if any, trend down-estuary (i.e., with increasing Section number), suggesting this shoreline type may be more independent of fetch compared to the other vegetation types. For example, large fetches may create wind waves that overtop the shoreline, having a reduced influence on wetlands, and as water floods onto the wetland vegetation, the baffling of marsh grasses may aid vertically accretion [42]. Previous research has suggested the strong potential influence of storm processes on estuarine-forest and sediment-bluff recession [43,44]. In the NFE, higher erosion rates down-estuary in the Forest and Sediment Bank shorelines may be due to its orientation relative to storm conditions. Nor'easters occur along the Atlantic coast from October to April and can generate large waves causing considerable erosion and property damage [45]. At the Local Scale, the lowest mean SCRs (highest erosion) are calculated for Sections 7 and 8, which are more susceptible to the influence of wind waves generated from the nor'easters. However, because the imagery utilized within this study spans a 40 year time period, the impact of individual storm events cannot be elucidated.

5.3. Predicting Erosion Rates

The regression of fetch and SCR was used to provide a first-order predictive tool. Although the corresponding equation (Figure 6(C)) does not calculate accretion, applying this to the Regional Scale allows the influence of fetch on eroding estuarine shorelines within the NRE to be ascertained. A similar approach was conducted for marsh shorelines in Rehoboth Bay, Delaware using wave power [14]. By log transforming average erosion rates and estimated wave power calculated for nine sites, Schwimmer [14] determined a positive correlation (R2 = 0.80). As wave power increased, the erosion rate also increased. Like this study, no sizeable areas of accretion were present.
Remotesensing 03 01516 g007 1024
Figure 7. Maps displaying (A) the predicted shoreline-change rate values using the linear regression equation of Mean Fetch versus SCR (see Figure 6(C)) and (B) the residual shoreline-change rate values. Box 1 a nd 2 (inset) are areas of larger residuals.
Figure 7. Maps displaying (A) the predicted shoreline-change rate values using the linear regression equation of Mean Fetch versus SCR (see Figure 6(C)) and (B) the residual shoreline-change rate values. Box 1 a nd 2 (inset) are areas of larger residuals.
Remotesensing 03 01516 g007
The predicted SCRs have a mean of −0.58 m yr−1 with a range of 1.68 and a variance of 0.04. The predicted SCRs (Figure 7(A)) can be compared spatially from those measured (Figure 2(A)), or mathematically through the residual values (Figure 7(B)). The residuals are determined by subtracting the predicted SCR from the measured SCR. Note, few erosion shoreline points have large residuals, indicating that this predictive tool reasonably performs at the system-wide scale. However, the equation generally overestimates shoreline change on Wetland shorelines with large exposure, like those within Sections 7 and 8 (see Box 1, Figure 7(B)), and underestimates on Sediment Bank shorelines with large fetches. This suggests that there is a significant influence by the shoreline composition, and this is most evident in Figure 5A, which shows little variation in Wetland SCRs from the Local Scale data (Figure 5(A)). Larger residual values were determined on the western part of Section 7 (see Box 2, Figure 7(B)), where the shoreline is predominantly Sediment Bank. It appears shoreline change may be underestimated for this LULC type, especially with the large fetch associated with this section. This is in part due to the dominance of Wetland in this area (~70%; Table 4) and the presumed difference in influence of fetch on SCR between these two LULC (Figure 5(A,C)). Previous research has identified the resilient and baffling nature of wetland vegetation because of its binding roots and cohesive sediments [42]; these properties aid in their ability to vertically accrete through sediment and organic matter accumulation [46,47,48]. Since there is little SCR change in Wetlands regardless of fetch, elevation or REI, it may be more appropriate to assign an average SCR to all Wetland shorelines if one was attempted to model shoreline change in this system. Regardless of its limitations, this predictive, linear relationship signifies the notable influence of fetch and, ultimately wave energy (e.g., REI), on estuarine shoreline change within the NRE and a similar prediction approach may be suitable on other estuarine shorelines exposed to moderate fetch. Additional analysis based on fetch and vegetation type may clarify the response of estuarine shoreline change and should be pursued in further research.

5.4. Additional Influences on Shoreline Change

There are additional parameters that were not addressed within this study that may affect shoreline change. One possible affect on shoreline change that was not analyzed within this study is shoreline modification. A field excursion performed in the winter of 2007 revealed large areas of shoreline modification structure, i.e., bulkhead, riprap, groin, or a combination. However, installation dates of these modification structures are not accessible; therefore, the influence of these modification structures on the shoreline change rates could not be determined. The modified shorelines and surrounding areas are retained within the study and may contribute to some of the variability in long-term SCRs. Previous research has concluded that shoreline modification structures along the Texas Gulf of Mexico coast altered the sediment budget and caused the largest amount of long-term shoreline change [49]. For this reason, shoreline modification is another potential explanation for the discrepancies between the Cedar Island study [26] and this study discussed above. Cedar Island is part of the National Wildlife Refuge, and there are no shoreline modification structures within the study. The influence of shoreline hardening on estuarine SCRs should be investigated in future work.

6. Summary and Conclusions

Using the point-based approach and a sampling interval of 50 m, the shoreline of the NRE was analyzed at two spatial scales (Regional and Local). The Regional Scale was the largest, encompassing the main trunk of the NRE shoreline. The majority of the NRE trunk shoreline is eroding (93%) and the mean SCR of the study area is −0.58 m yr−1. Sediment Bank shorelines had a significantly different SCR compared to other LULC classes, but no significant linear correlations were distinguishable between shoreline-change rates and the parameters analyzed (elevation, fetch, and REI) at the Regional (whole estuary) Scale. However, based on orientation and exposure, the NRE shoreline was partitioned into eight Local Sections. At the Local Scale, significant correlation trends were evident with erosion rates increasing down-estuary along with increasing mean fetch and decreasing mean elevation. Predicted SCR using the correlation equation overpredicted erosion in Wetland areas with large fetches and underestimated SCRs on corresponding Sediment Bank shorelines. Overall, the equation conservatively and reasonably predicts erosion based on fetch. Further analysis of shoreline change with a procedure that collectively considers shoreline type, wave energy and shoreline modification should offer improved insight into and predictive ability for shoreline change.

Acknowledgments

Funding for this project was provided by NOAA Coastal Ocean Program (NA05 NOS 4781182). The authors would like to thank Dave Kunz, Jason Prior, Jeremy Brandsen, Haley Cleckner, Dorothea Ames, Amit Malhotra, and Tom Crawford for their contributions and assistance.

References

  1. Martin, D.M.; Morton, T.; Dobrzynski, T.; Valentine, B. Estuaries on the Edge: The Vital Link Between Land and Sea; The American Oceans Campaign: Washington, DC, USA, 1996; p. 297. [Google Scholar]
  2. Crossett, K.M.; Culliton, T.J.; Wiley, P.C.; Goodspeed, T.R. Population Trends along the Coastal United States: 1980–2008; 2004. Available online: http://www.oceanservice.noaa.gov/programs/mb/pdfs/coastal_pop_trends_complete.pdf (accessed on 12 January 2011).
  3. Benoit, J.; Hardaway, C.S., Jr.; Hernansez, D.; Holman, R.; Koch, E.; McLellan, N.; Peterson, S.; Reed, D.; Suman, D. Mitigating Shore Erosion Along Sheltered Coasts; The National Academies Press: Washington, DC, USA, 2007. [Google Scholar]
  4. McNinch, J.E. Geologic control in the nearshore: Shore-oblique sandbars and shoreline erosional hotspots, Mid-Atlantic Bight, USA. Mar. Geol. 2004, 211, 121–141. [Google Scholar] [CrossRef]
  5. Miller, H.C. Field measurements of longshore sediment transport during storms. Coastal Eng. 1999, 36, 301–321. [Google Scholar] [CrossRef]
  6. Zhang, K.; Douglas, B.C.; Leatherman, S.P. Global warming and coastal erosion. Climate Change 2004, 64, 41–58. [Google Scholar] [CrossRef]
  7. Day, J.W.J.; Hall, C.A.S.; Kemp, W.M.; Yàñez-Arancibia, A. Estuarine Ecology; John Wiley & Sons, Inc.: New York, NY, USA, 1989; p. 258. [Google Scholar]
  8. Gibson, G. An Analysis of Shoreline Change at Little Lagoon, Alabama. M.Sc. Thesis, Department of Geography, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2006. [Google Scholar]
  9. Hennessee, E.L.; Halka, J.P. Hurricane Isabel and erosion of Chesapeake Bay shorelines, Maryland. In Hurricane Isabel in Perspective; Sellner, K.G., Ed.; Chesapeake Research Consortium: Edgwater, MD, USA, 2005; Volume 05-160, pp. 81–88. [Google Scholar]
  10. Phillips, J.D. Spatial Analysis of Shoreline Erosion, Delaware Bay, New Jersey. Ph.D. Dissertation, Department of Geography, Rutgers-The State University, New Brunswick, NJ, USA, 1985. [Google Scholar]
  11. Price, F.D. Quantification, Analysis, and Management of Intracoastal Waterway Channel Margin Erosion in the Guana Tolomato Matanzas National Estuarine Research Reserve, Florida; National Estuarine Research Reserve Technical Report Series 2006:1; National Estuarine Research Reserve: Apalachicola, FL, USA, 2006. [Google Scholar]
  12. Riggs, S.R. Shoreline Erosion in North Carolina Estuaries; Publication No. UNC-SG-01-11; North Carolina Sea Grant Raleigh: Raleigh, NC, USA, 2001. [Google Scholar]
  13. Riggs, S.R.; Ames, D.V. Drowning the North Carolina Coast: Sea Level Rise and Estuarine Dynamics; Publication No. UNC-SG-03-04; North Carolina Sea Grant Raleigh: Raleigh, NC, USA, 2003. [Google Scholar]
  14. Schwimmer, R.A. Rates and processes of marsh shoreline erosion in Rehoboth Bay, Delaware, USA. J. Coast. Res. 2001, 17, 672–683. [Google Scholar]
  15. Swisher, M.L. The Rates and Causes of Shore Erosion around a Transgressive Coastal Lagoon, Rehoboth Bay, Delaware. M.Sc. Thesis, College of Marine Studies, University of Delaware, Newark, DE, USA, 1982. [Google Scholar]
  16. Thieler, E.R.; O’Connell, J.F.; Schupp, C.A. The Massachusetts Shoreline Change Project: 1800s to 1994; US Geological Survey Administrative Report 2001; USGS: Woods Hole, MA, USA, 2001. [Google Scholar]
  17. Dolan, R.; Fenster, M.S.; Holme, S.J. Temporal analysis of shoreline recession and accretion. J. Coast. Res. 1991, 7, 723–744. [Google Scholar]
  18. Douglas, B.C.; Crowell, M.; Leatherman, S.P. Considerations for shoreline position prediction. J. Coast. Res. 1998, 14, 1025–1033. [Google Scholar]
  19. Fenster, M.S.; Dolan, R.; Morton, R.A. Coastal storms and shoreline change: Signal or noise? J. Coast. Res. 2001, 17, 714–720. [Google Scholar]
  20. Forbes, D.L.; Parkes, G.S.; Manson, G.K.; Ketch, L.A. Storms and shoreline retreat in the southern Gulf of St. Lawrence. Mar. Geol. 2004, 210, 169–204. [Google Scholar] [CrossRef]
  21. Morton, R.A.; Miller, T.; Moore, L. Historical shoreline changes along the US gulf of Mexico: A summary of recent shoreline comparisons and analyses. J. Coast. Res. 2005, 21, 704–709. [Google Scholar] [CrossRef]
  22. Rozynski, G. Long-term shoreline response of a nontidal, barred coast. Coastal Eng. 2005, 52, 79–91. [Google Scholar] [CrossRef]
  23. Thieler, E.R.; Danforth, W. Historical shoreline Mapping(II): Applications of the digital Shoreline mapping and analysis systems (DSMS/DSAS) to shoreline change mapping in Puerto Rico. J. Coast. Res. 1994, 10, 600–620. [Google Scholar]
  24. Dolan, R.; Hayden, B.; Heywood, J. A new photogrammetric method for determining shoreline erosion. Coastal Eng. 1978, 2, 21–39. [Google Scholar] [CrossRef]
  25. Thieler, E.R.; Danforth, W.W. Digital Shoreline Analysis System (DSAS) User’s Guide, Version 1.0; Open-File Report No. 92-355; United States Geological Survey Reston: Reston, VA, USA, 1992; p. 42. [Google Scholar]
  26. Cowart, L.C.; Walsh, J.P.; Corbett, D.R. Analyzing estuarine shoreline change: A case study of Cedar Island, NC. J. Coast. Res. 2010, 26, 817–830. [Google Scholar] [CrossRef]
  27. Benninger, L.K.; Wells, J.T. Sources of sediment to the Neuse River estuary, North Carolina. Mar. Chem. 1993, 3, 137–156. [Google Scholar] [CrossRef]
  28. Luettich, R.A.; Carr, S.D.; Reynolds-Fleming, J.V.; Fulcher, C.W. Semi-diurnal seiching in a shallow, micro-tidal lagoonal estuary. J. Cont. Res. 2002, 22, 1669–1681. [Google Scholar] [CrossRef]
  29. Wells, J.T.; Kim, S. Sedimentation in the Albemarle-Pamlico Lagoonal System: Synthesis and hypothesis. Mar. Geol. 1989, 88, 263–284. [Google Scholar] [CrossRef]
  30. Luettich, R.A.; McNinch, J.E.; Paerl, H.W.; Peterson, C.H.; Wells, J.T.; Alperin, M.; Martens, C.S.; Pinckney, J.L. Neuse River Estuary Modeling and Monitoring Project Stage 1: Hydrography and Circulation, Water Column Nutrients and Productivity, Sedimentary Processes and Benthic-Pelagic Coupling, Report UNC-WRRI-2000-325B; Water Resources Research Institute of the University of North Carolina: Raleigh, NC, USA, 2000; p. 172. [Google Scholar]
  31. Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 12, 688–703. [Google Scholar] [CrossRef]
  32. Ellis, M.Y. Coastal Mapping Handbook; Department of the Interior, US Geological Survey and U.S. Department of Commerce, National Ocean Service and Office of Coastal Zone Management: Washington, DC, USA, 1978. [Google Scholar]
  33. Poulter, B. Interactions between Landscape Disturbances and Gradual Environmental Change: Plant Community Migration and Response to Fire and Sea-Level Rise. Ph.D. Thesis, Duke University, Durham, NV, USA, 2005. [Google Scholar]
  34. Genz, A.S.; Fletcher, C.H.; Dunn, R.A.; Frazer, N.; Rooney, J.J. The predictive accuracy of shoreline change rate methods and alongshore beach variation on Maui, Hawaii. J. Coast. Res. 2007, 23, 87–105. [Google Scholar] [CrossRef]
  35. Flecher, C.; Rooney, J.; Barbee, M.; Lim, S.C.; Richmnond, B. Mapping shoreline change using digital orthophotogrammetry on Maui, Hawaii. J. Coast. Res. 2003, 38, 106–124. [Google Scholar]
  36. Fonseca, M.S.; Robbins, B.D.; Whitfield, P.E.; Wood, L.; Clinton, P. Evaluating the Effect of Offshore Sandbars on Seagrass Recovery and Restoration in Tampa Bay through Ecological Forecasting and Hindcasting of Exposure to Waves; Tampa Bay Estuary Program: St. Petersburg, FL, USA, 2002. [Google Scholar]
  37. Hess, K.W.; White, S.A.; Sellars, J.; Spargo, E.A.; Wong, A.; Gill, S.K.; Zervas, C. North Carolina Sea Level Rise Project: Interim Technical Report; NOAA Technical Memorandum NOS CS 5; NOAA: Silver Spring, MD, USA, 2004; p. 26. [Google Scholar]
  38. Beyer, H.L. Hawth’s Analysis Tools for ArcGIS; Version 3.26; 2007; Available online: http://www.spatialecology.com (accessed on 12 January 2011).
  39. Dobson, J.E.; Bright, E.A.; Ferguson, R.L.; Field, D.W.; Wood, L.L.; Haddad, K.D.; Iredale, H., III; Jensen, J.R.; Klemas, V.V.; Orth, R.J.; Thomas, J.P. NOAA Coastal Change Analysis Program (C-CAP): Guidance for Regional Implementation; NOAA Technical Report NMFS 123; NOAA NMFS: Seattle, WA, USA, 1995; p. 140. [Google Scholar]
  40. Dolan, R.; Fenster, M.S.; Holme, S.J. Spatial analysis of shoreline recession and accretion. J. Coast. Res. 1992, 8, 263–285. [Google Scholar]
  41. Phillips, J.D. Spatial analysis of shoreline erosion, Delaware Bay, New Jersey. Ann. Assoc. Am. Geogr. 1986, 76, 50–62. [Google Scholar] [CrossRef]
  42. Goodbred, S.L.; Hine, A.C. Coastal storm deposition: Salt-marsh response to a severe extratropical storm, March 1993, West-Central Florida. Geology 1995, 23, 679–682. [Google Scholar] [CrossRef]
  43. Kirwin, M.L.; Kirwin, J.L.; Copenheaver, C.A. Dynamics of an estuarine forest and its response to rising sea level. J. Coast. Res. 2007, 23, 457–463. [Google Scholar] [CrossRef]
  44. Phillips, J.D. Even timing and sequence on coastal shoreline erosion: Hurricanes Bertha and Fran and the Neuse Estuary. J. Coast. Res. 1999, 15, 616–623. [Google Scholar]
  45. Davis, R.E.; Dolan, R. Nor’ easters. Am. Sci. 1993, 81, 428–439. [Google Scholar]
  46. Nyman, J.A.; Delaune, R.D.; Patrick, W.H.J. Wetland soil formation in the rapidly subsiding Mississippi River deltaic plain: Mineral and organic matter relationships. Estuar. Coast. Shelf Sci. 1990, 31, 57–69. [Google Scholar] [CrossRef]
  47. Nyman, J.A.; Walters, R.J.; Deluane, R.D.; Patrick, W.H.J. Marsh vertical accretion via vegetative growth. Estuar. Coast. Shelf Sci. 2006, 69, 370–380. [Google Scholar] [CrossRef]
  48. Craft, C.B.; Seneca, E.D.; Broome, S.W. Vertical accretion in microtidal regularly and irregularly flooded estuarine marshes. Estuar. Coast. Shelf Sci. 1993, 37, 371–386. [Google Scholar] [CrossRef]
  49. Gibeaut, J.C.; White, W.A.; Hepner, T.; Gutiérrez, R.; Tremblay, T.A.; Smyth, R.C.; Andrews, J.R. Texas Shoreline Change Project: Gulf of Mexico Shoreline Change from the Brazos River to Pass Cavallo; Report prepared for the Texas Coastal Coordination Council pursuant to National Oceanic and Atmospheric Administration Award No. NA870Z0251; Bureau of Economic Geology, The University of Texas at Austin: Austin, TX, USA, 2000; p. 32. [Google Scholar]

Share and Cite

MDPI and ACS Style

Cowart, L.; Corbett, D.R.; Walsh, J.P. Shoreline Change along Sheltered Coastlines: Insights from the Neuse River Estuary, NC, USA. Remote Sens. 2011, 3, 1516-1534. https://doi.org/10.3390/rs3071516

AMA Style

Cowart L, Corbett DR, Walsh JP. Shoreline Change along Sheltered Coastlines: Insights from the Neuse River Estuary, NC, USA. Remote Sensing. 2011; 3(7):1516-1534. https://doi.org/10.3390/rs3071516

Chicago/Turabian Style

Cowart, Lisa, D. Reide Corbett, and J.P. Walsh. 2011. "Shoreline Change along Sheltered Coastlines: Insights from the Neuse River Estuary, NC, USA" Remote Sensing 3, no. 7: 1516-1534. https://doi.org/10.3390/rs3071516

Article Metrics

Back to TopTop