Regional Mapping of the Geoid Using GNSS (GPS) Measurements and an Artificial Neural Network
Abstract
:1. Introduction
2. Data and Methodology
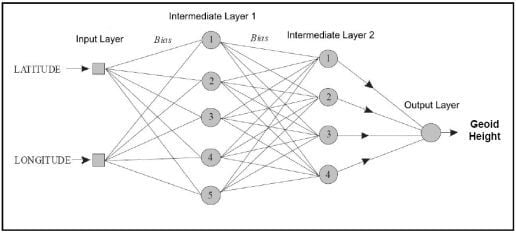
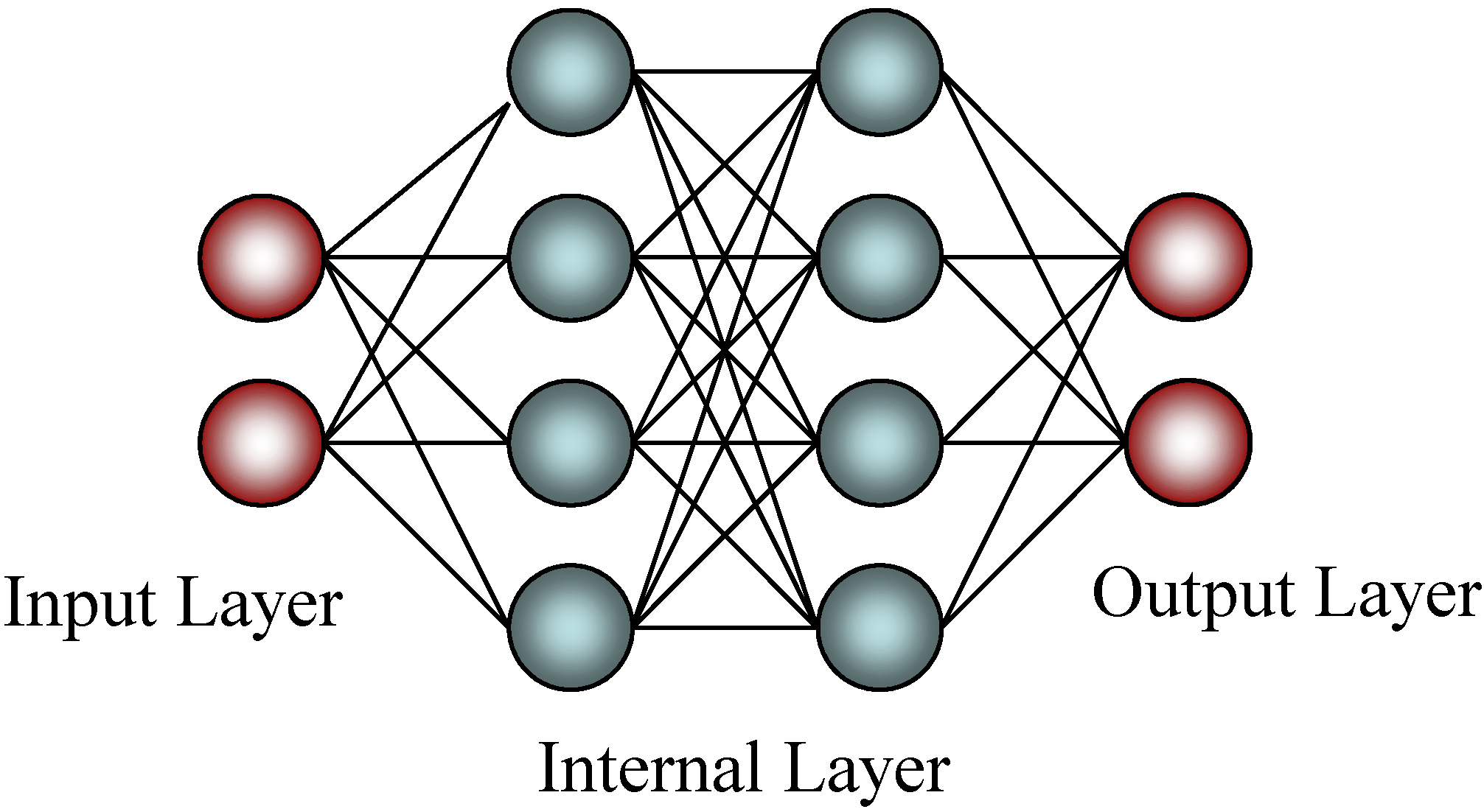
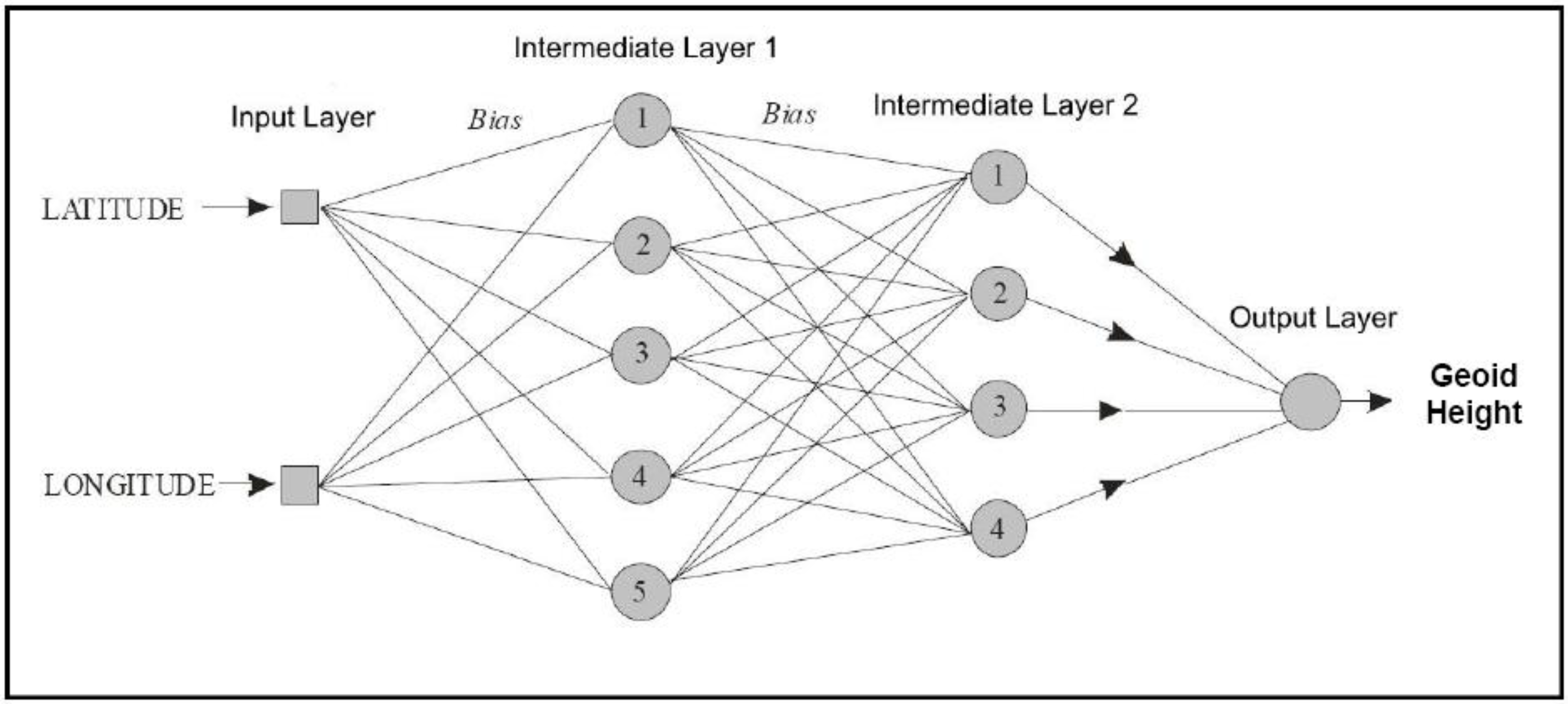
2.1. Structure of Neural Networks
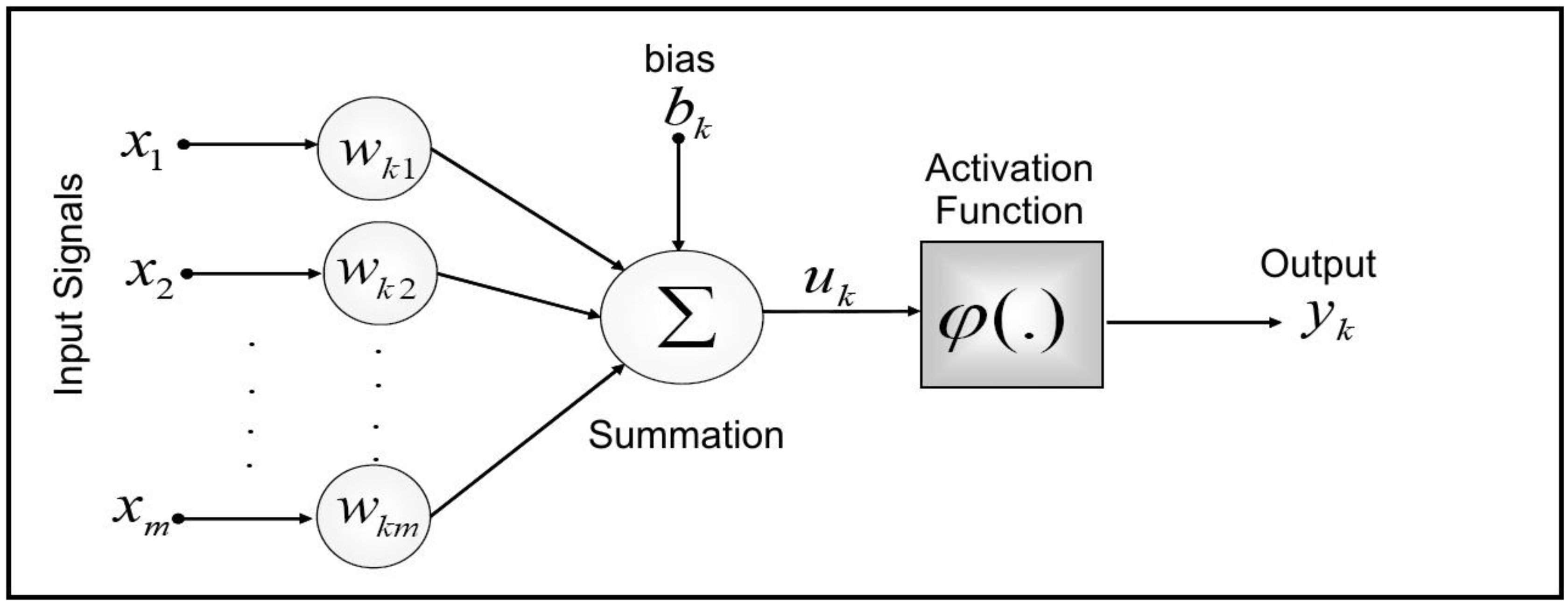
- Input signals (x1, x2 and xm) or input information, which might come from the environment or from the activation of other neurons.
- A set of weights (wk1, wk2, wkm), which describe the connection forces; that can be positive, representing excitatory junctions; or negative, inhibiting the activation of the neuron. When there is no connection between two neurons the synaptic weight is null.
- Sum function (Σ), which represents the summation of the input signals multiplied by their respective weights, constituting a linear combiner.
- Activation function [(.)], which restricts the output amplitude of the neuron, in an interval normalized between [0;1] or [−1,1].
- Output signal (yk), which is the result generated by the neuron.
2.2. Geoid Height for Training and Simulation of Neural Network
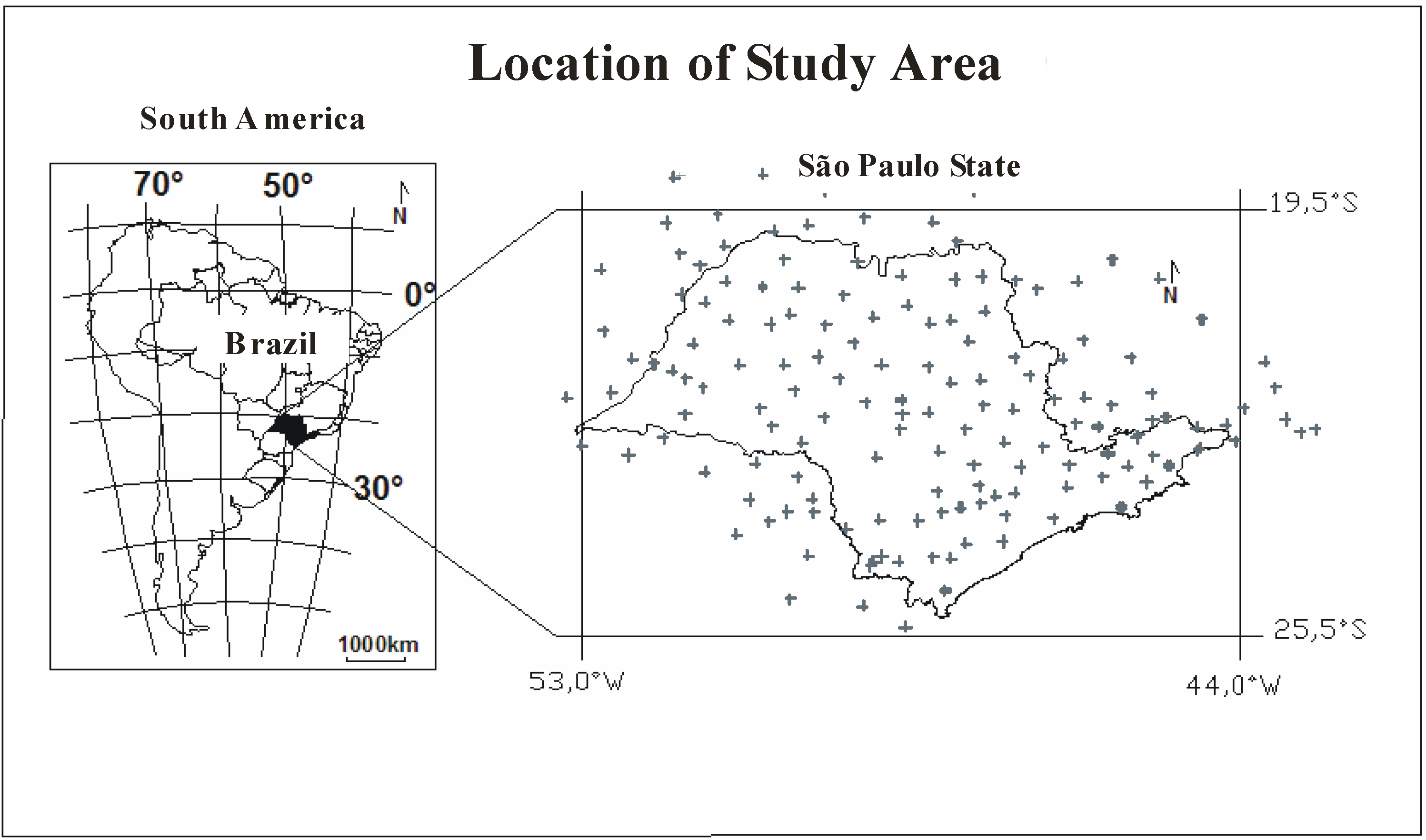
- Average Helmert Anomalies on a 10′ × 10′ grid in continental areas, obtained from Brazilian Geography and Statistic Institute (IBGE) and other organizations in Brazil or neighboring countries.
- Free-air anomalies derived from satellite altimetry data in oceanic areas.
- Digital terrain model with 1′ × 1′ resolution obtained from topographic map digitisation.
- The EGM96 geopotential model to degree and order 180 [33].
3. Results and Discussion
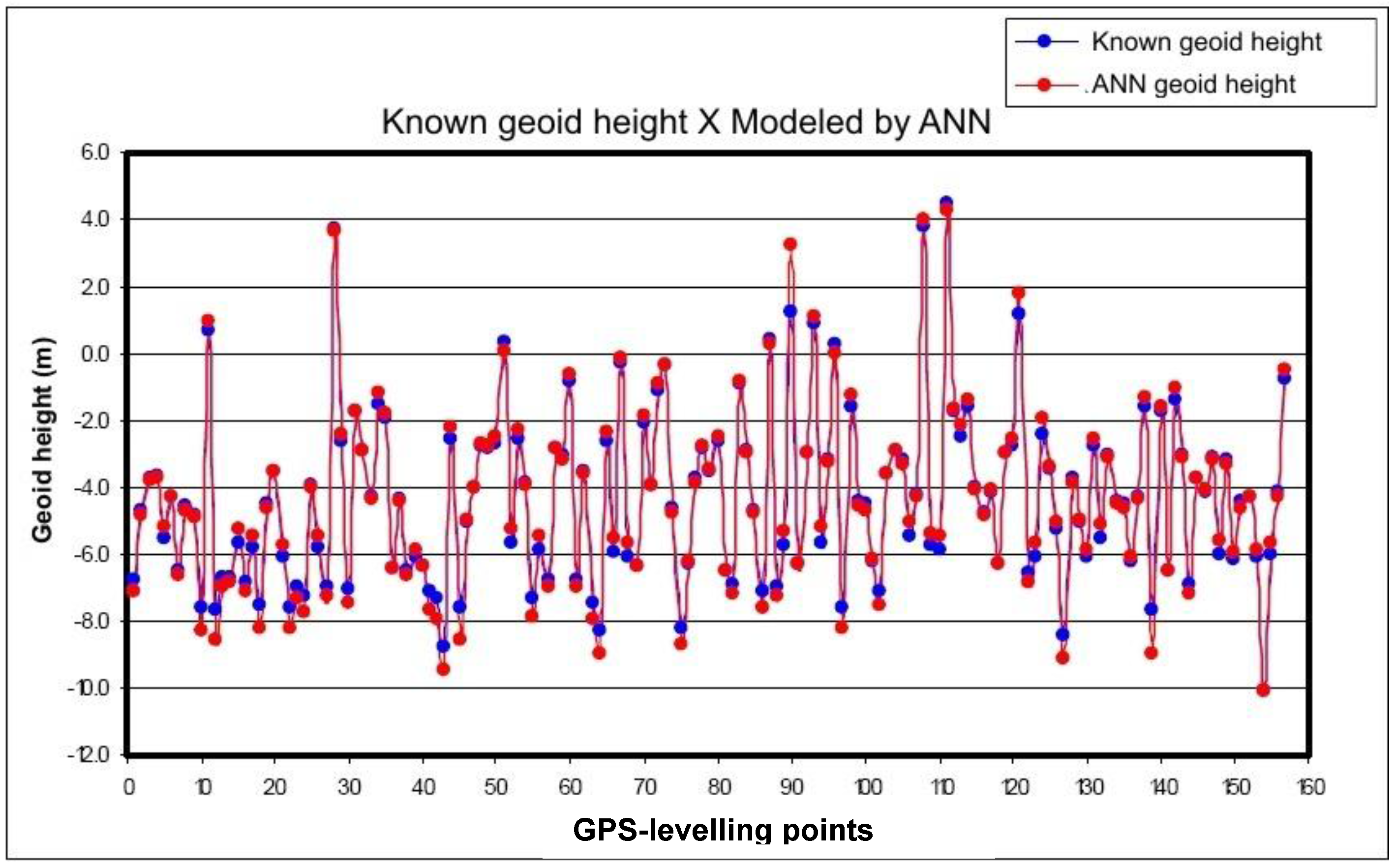
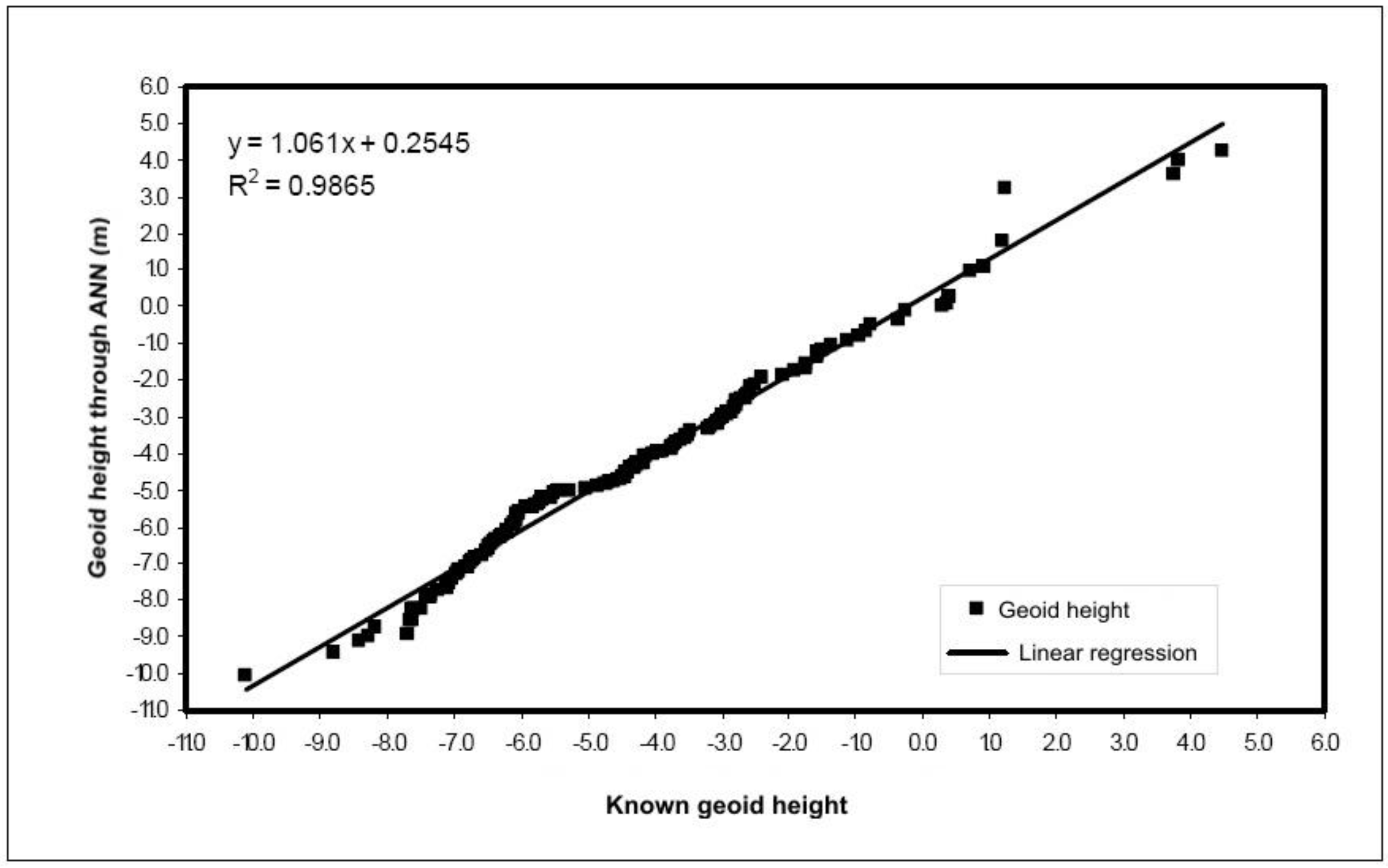
| Equation(1) | R2 (2) | SQR(3) |
|---|---|---|
| y = 1.061x + 0.2545 | 0.9865 | 18.86 |
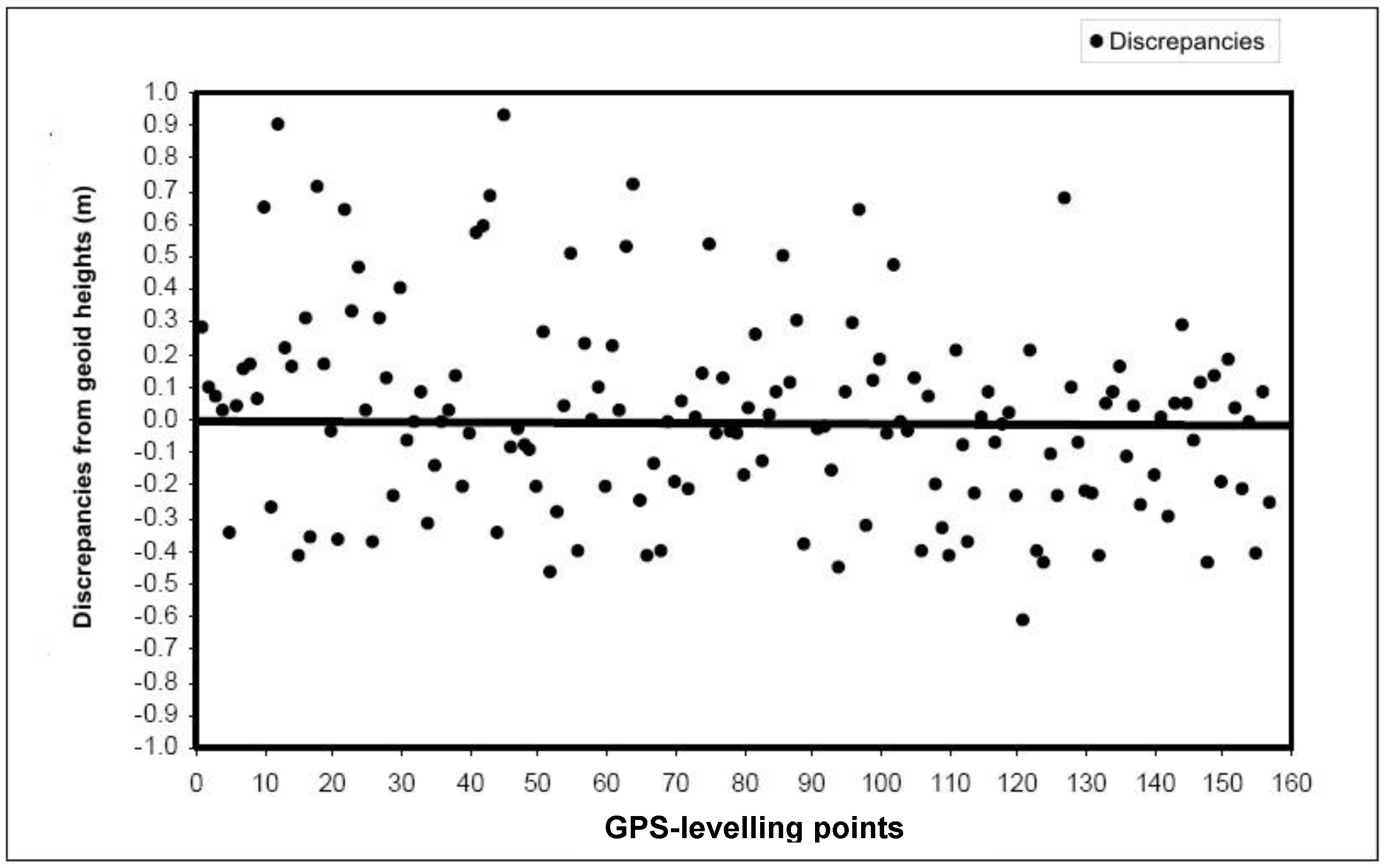
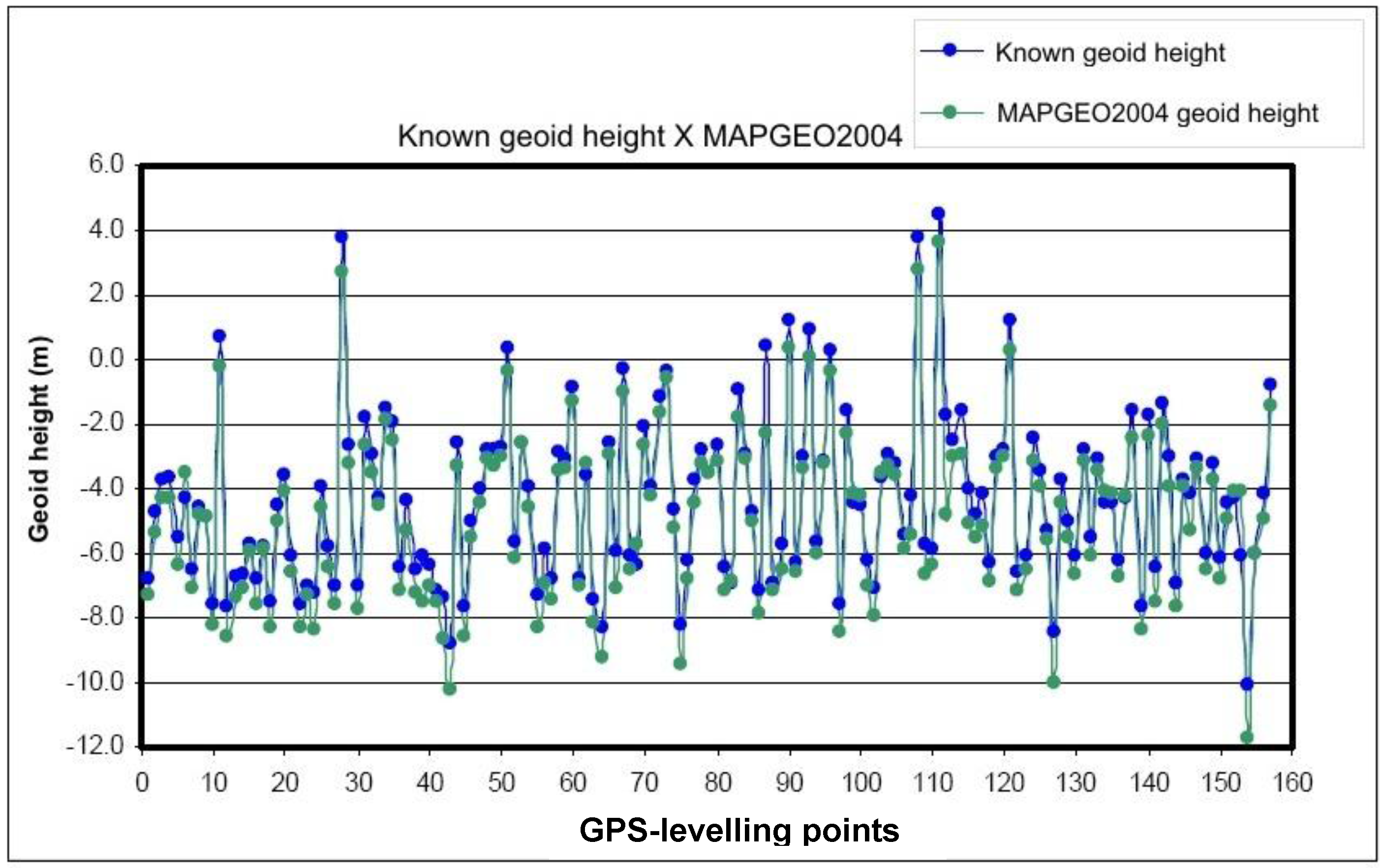
| Equation(1) | R2 (2) | SQR(3) |
|---|---|---|
| y = 0.9918x – 0.6087 | 0.9607 | 92.39 |
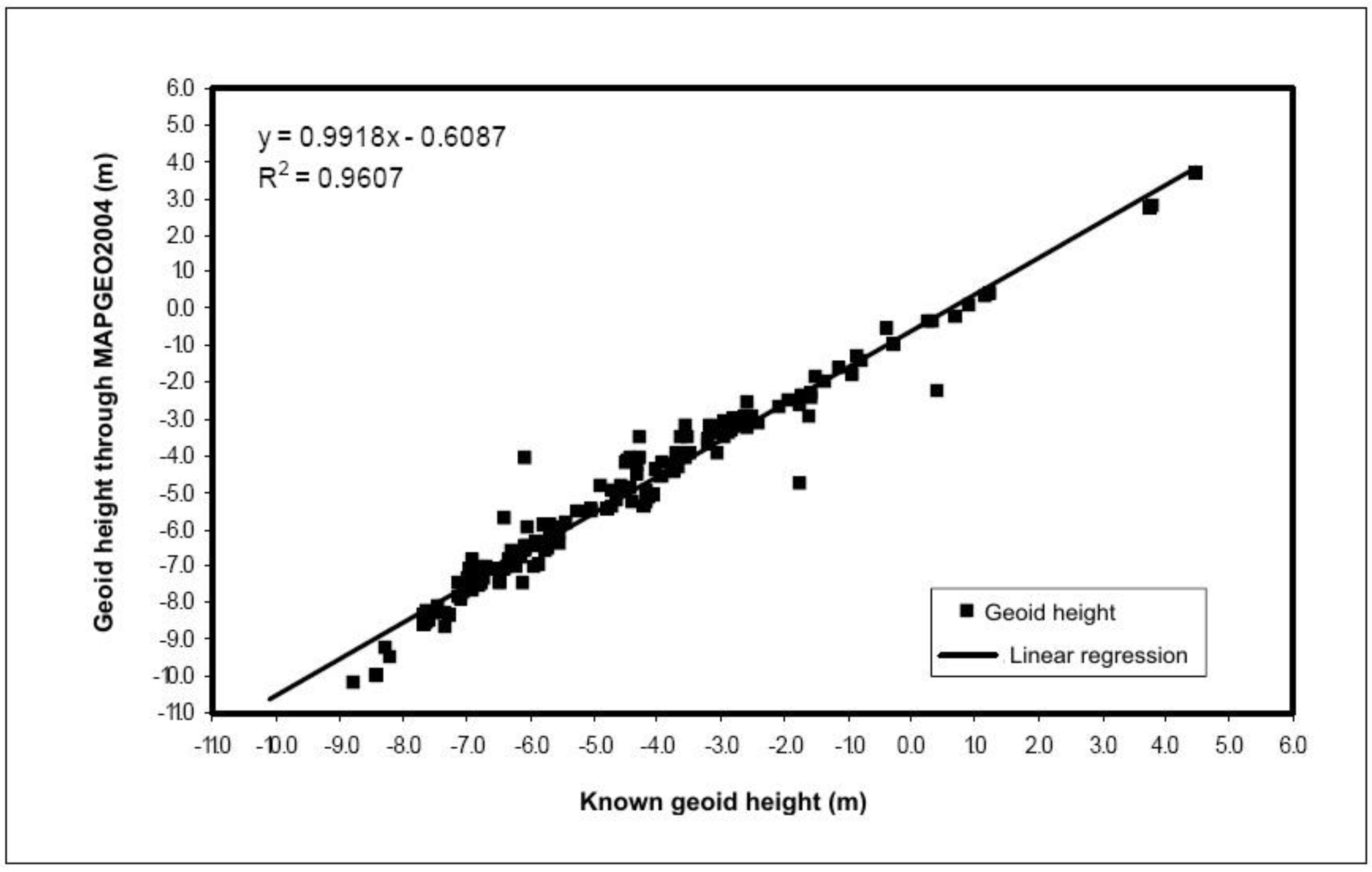
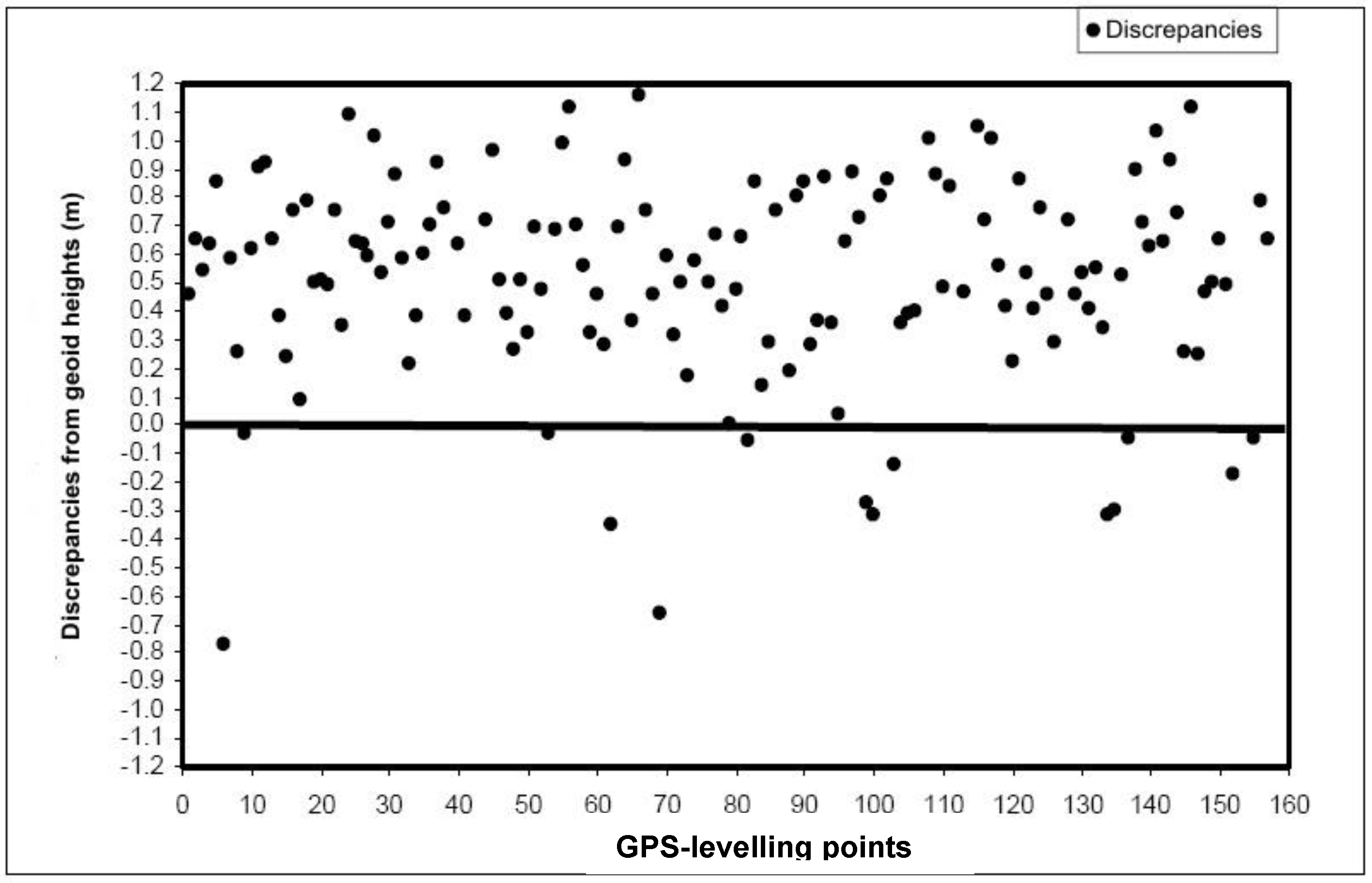
4. Conclusions
References and Notes
- Müller, M.; Fill, H.D. Redes Neurais aplicadas na programação de vazões. In Proceedings of Simpósio Brasileiro de Recursos Hídricos, Curitiba, Brazil, 23–27 November 2003.
- Haykin, S. Redes Neurais: Princípios e prática; Bookman: Porto Alegre, Brazil, 2001. [Google Scholar]
- Galvão, C.O.; Valença, M.J.S. Sistemas inteligentes: Aplicações a recursos hídricos e ciências ambientais; UFRGS/ABRH: Porto Alegre, Brazil, 1999. [Google Scholar]
- Atluri, V.; Hung, C.C.; Coleman, T.L. An artificial neural network for classifying and predicting soil moisture and temperature using Levenberg-Marquat algorithm. In Proceedings of IEEE Southeastcon ’99, Lexington, KY, USA, 25–28 March 1999; pp. 10–13.
- George, R.K. Prediction of soil temperature by using artificial neural networks algorithms. Nonlinear Analysis 2001, 47, 1737–1748. [Google Scholar] [CrossRef]
- Kumar, M.; Sousa, E.F.; Oliveira, V.P.S.; Almeida, F.T.; Bernardo, S. Estimating evapotranspiration using artificial neural network. J. Irrig. Drainage Eng. 2002, 128, 224–233. [Google Scholar] [CrossRef]
- Mao, K.; Shi, J.A. Neural network technique for separating land surface emissivity and temperature from ASTER imagery. IEEE Trans. Geosci. Remote Sens. 2008, 46, 200–208. [Google Scholar] [CrossRef]
- Veronez, M.R.; de Souza, S.F.; Matsuoka, M.T.; Reinhardt, A.O. Estimativa de alturas geoidais para o estado de São Paulo baseada em redes neurais artificiais. Revista Brasileira de Geofísica 2009, 27, 583–593. [Google Scholar] [CrossRef]
- Yang, C.C.; Prasher, S.O.; Mehuys, G.R.; Patni, N.K. Application of artificial neural networks for simulations of soil temperature. Trans. ASAE 1997, 40, 649–656. [Google Scholar] [CrossRef]
- Zanetti, S.S.; Sousa1, E.F.; de Carvalho, D.F.; Bernardo, S. Estimação da evapotranspiração de referência no Estado do Rio de Janeiro usando redes neurais artificiais. Revista Brasileira de Engenharia Agrícola e Ambiental 2008, 12, 174–180. [Google Scholar] [CrossRef]
- Andrade, A.J.N. Aplicação de redes neurais artificiais na interpretação de perfis de poço aberto. Ph.D. Thesis, Curso de Pós-graduação em Geofísica, Universidade Federal do Pará, Belém, Brazil, 1997. [Google Scholar]
- Bhatt, A. Reservoir Properties from Well Logs Using Neural Networks. Ph.D. Thesis, Department of Petroleum Engineering and Applied Geophysics, Norwegian University of Science and Technology, Trondheim, Norway, 2002. [Google Scholar]
- Da Cunha, E.S.; Oliveira, K.A.; Herman, M.G. Investigação do treinamento de uma rede neural para o conhecimento de litofácies combinando dados de testemunhos e perfis de poços de petróleo. Congresso Brasileiro de P&S em Petróleo & Gas 2003, 2, 1–6. [Google Scholar]
- Hsieh, B.; Lewis, C.; Lin, Z. Lithology of aquifers from geophysical well logs and fuzzy logic analysis: Shui-Lin Area, Taiwan. Comput. Geosci. 2005, 31, 263–275. [Google Scholar] [CrossRef]
- da Silva, A.N.R.; Ramos, R.A.R.; de Souza, L.C.L.; Rodrigues, D.S.; Mendes, J.F.G. SIG: Uma plataforma para introdução de técnicas emergentes no planejamento urbano regional e de transportes; EESC/USP: São Carlos, Brazil, 2004. [Google Scholar]
- Siripitayananon, P.; Chen, H.C.; Hart, B.S. A new technique for lithofacies prediction: Back-propagation neural network. In Proceedings of ACMSE: The 39th Association of Computing and Machinery South Eastern Conference, Atlanta, GA, USA, 16–17 March 2001; pp. 31–38.
- Yang, Y.; Aplin, A.C.; Larter, S.R. Quantitative assessment of mudstone lithology using geophysical wireline logs and artificial neural networks. Petroleum Geosci. 2004, 10, 141–151. [Google Scholar] [CrossRef]
- Jana, R.B. Multiscale pedotransfer functions for soil water retention. Vadose Zone J. 2007, 6, 868–878. [Google Scholar] [CrossRef]
- Parasueaman, K.; Elshorbagy, A.; Si, B.C. Estimating saturated hydraulic conductivity using genetic programming. Soil Sci. Soc. Am. J. 2007, 71, 1676–1684. [Google Scholar] [CrossRef]
- Zacharias, S.; Wessolek, G. Excluding organic matter content from pedotransfer predictors of soil water retention. Soil Sci. Soc. Am. J. 2007, 71, 43–50. [Google Scholar] [CrossRef]
- Da Silva, C.A.U. Um método para estimar observáveis GPS usando redes neurais artificiais. Ph.D. Thesis, Escola de Engenharia de São Carlos, Universidade de São Paulo, São Paulo, Brazil, 2003. [Google Scholar] [Green Version]
- Hernández-Pajares, P.M. Neural network modeling of ionospheric electron content at global scale using GPS data. Radio Science 1997, 32, 1081–1089. [Google Scholar] [CrossRef]
- Gemael, C. Introdução à Geodésia Física; UFPR: Curitiba, Brazil, 1999. [Google Scholar] [Green Version]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W.H. Freeman and Company: San Francisco, CA, USA, 1967. [Google Scholar] [Green Version]
- Schwarz, K.P.; Sideris, M.G.; Forsberg, R. The use of FFT techniques in physical geodesy. Geophys. Int. J. 1989, 110, 485–514. [Google Scholar] [CrossRef]
- Maia, T.C.B. Utilização de redes neurais artificiais na determinação de modelos geoidais. Ph.D. Thesis, Escola de Engenharia de São Carlos, Universidade de São Paulo, São Paulo, Brazil, 2003. [Google Scholar] [Green Version]
- Miranda, F.A.; De Freitas, S.R.C.; Fraggion, P.L. Integração e interpolação de dados de anomalias ar livre utilizando-se a técnica de RNA e krigagem. In Simpósio Brasileiro de Geomática, Presidente Prudente, Brazil, 24–27 July 2007. [Green Version]
- Seager, J.; Collie, P.; Kirb, J. Modelling geoid undulations with an artificial neural network. In Proceedings of 1999 International Joint Conference on Neural Networks, Washington, DC, USA, 10–16 July 1999; Volume 5, pp. 3332–3335. [Green Version]
- Tierra, A.; De Freitas, S.R.C. Predicting free-air gravity anomaly using artificial neural network. In Proceedings of International Association of Geodesy Symposia: Vertical Reference Systems, Cartagena, Colombia, 20–23 February 2001; Volume 124, pp. 215–218. [Green Version]
- Lemoine, F.G.; Kenyon, S.C.; Factor, J.K.; Trimmer, R.G.; Pavlis, N.K.; Chinn, D.S.; Cox, C.M.; Klosko, S.M.; Luthcke, S.B.; Torrence, M.H.; et al. The Development of the joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96; NASA/TP-1998-206861; NASA Goddard Space Flight Center: Greenbelt, MD, USA, July 1998. [Google Scholar] [Green Version]
- Reinke, M.; Veronez, M.R.; Thum, A.B.; De Souza, G.C.; Segantine, P.C.L. Determinação da superfície geoidal através de redes neurais artificiais. GAEA 2007, 3, 27–36. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. An earth gravitational model to degree 2160: EGM2008. Geophys. Res. Abs. 2008, 10. EGU2008-A-01891. [Google Scholar] [Green Version]
- Souza, S.F. Contribuição do GPS pra Aprimoramento do Geóide no Estado de São Paulo. Ph.D. Thesis, IAG, Universidade de São Paulo, São Paulo, Brazil, 2002. [Google Scholar] [Green Version]
- IBGE. Instituto Brasileiro de Geografia e Estatística. Geosciências. Available on line: http://www.ibge.gov.br/home/geociencias/geodesia/modelo_geoidal.shtm (accessed on 2 September 2008). [Green Version]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Veronez, M.R.; Florêncio de Souza, S.; Matsuoka, M.T.; Reinhardt, A.; Macedônio da Silva, R. Regional Mapping of the Geoid Using GNSS (GPS) Measurements and an Artificial Neural Network. Remote Sens. 2011, 3, 668-683. https://doi.org/10.3390/rs3040668
Veronez MR, Florêncio de Souza S, Matsuoka MT, Reinhardt A, Macedônio da Silva R. Regional Mapping of the Geoid Using GNSS (GPS) Measurements and an Artificial Neural Network. Remote Sensing. 2011; 3(4):668-683. https://doi.org/10.3390/rs3040668
Chicago/Turabian StyleVeronez, Mauricio Roberto, Sérgio Florêncio de Souza, Marcelo Tomio Matsuoka, Alessandro Reinhardt, and Reginaldo Macedônio da Silva. 2011. "Regional Mapping of the Geoid Using GNSS (GPS) Measurements and an Artificial Neural Network" Remote Sensing 3, no. 4: 668-683. https://doi.org/10.3390/rs3040668
APA StyleVeronez, M. R., Florêncio de Souza, S., Matsuoka, M. T., Reinhardt, A., & Macedônio da Silva, R. (2011). Regional Mapping of the Geoid Using GNSS (GPS) Measurements and an Artificial Neural Network. Remote Sensing, 3(4), 668-683. https://doi.org/10.3390/rs3040668