Airborne Lidar: Advances in Discrete Return Technology for 3D Vegetation Mapping
Abstract
:1. Introduction
2. Background
2.1. Discrete Return and Full Waveform Systems
2.2. Vertical Target Discrimination Distance
3. Enhancing Capabilities of DR Technology for 3D Vegetation Mapping
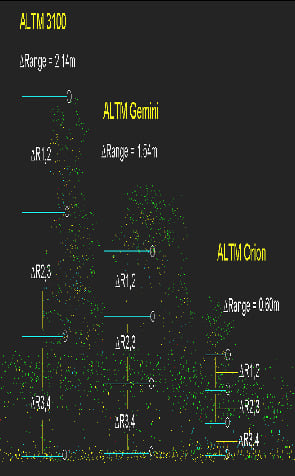
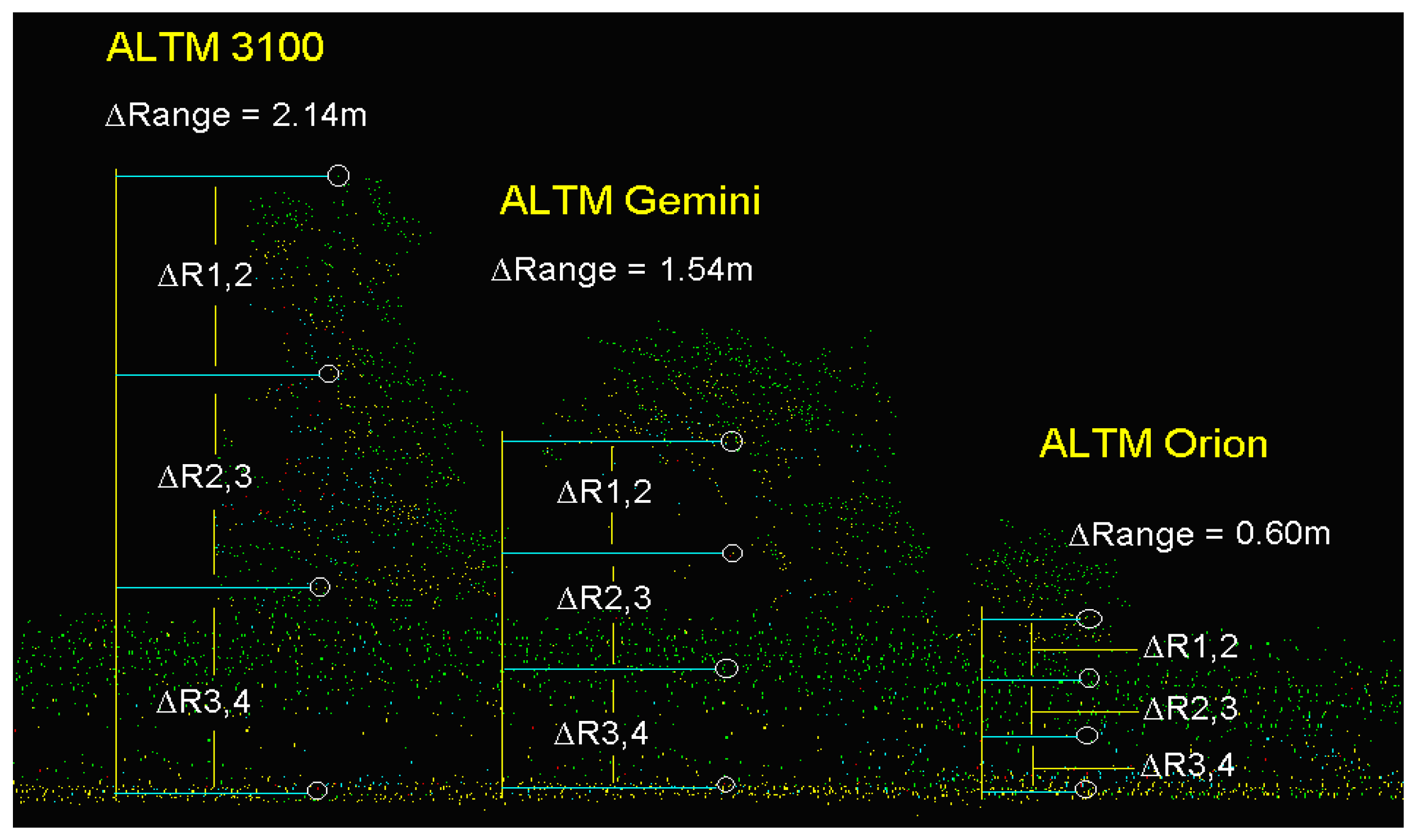
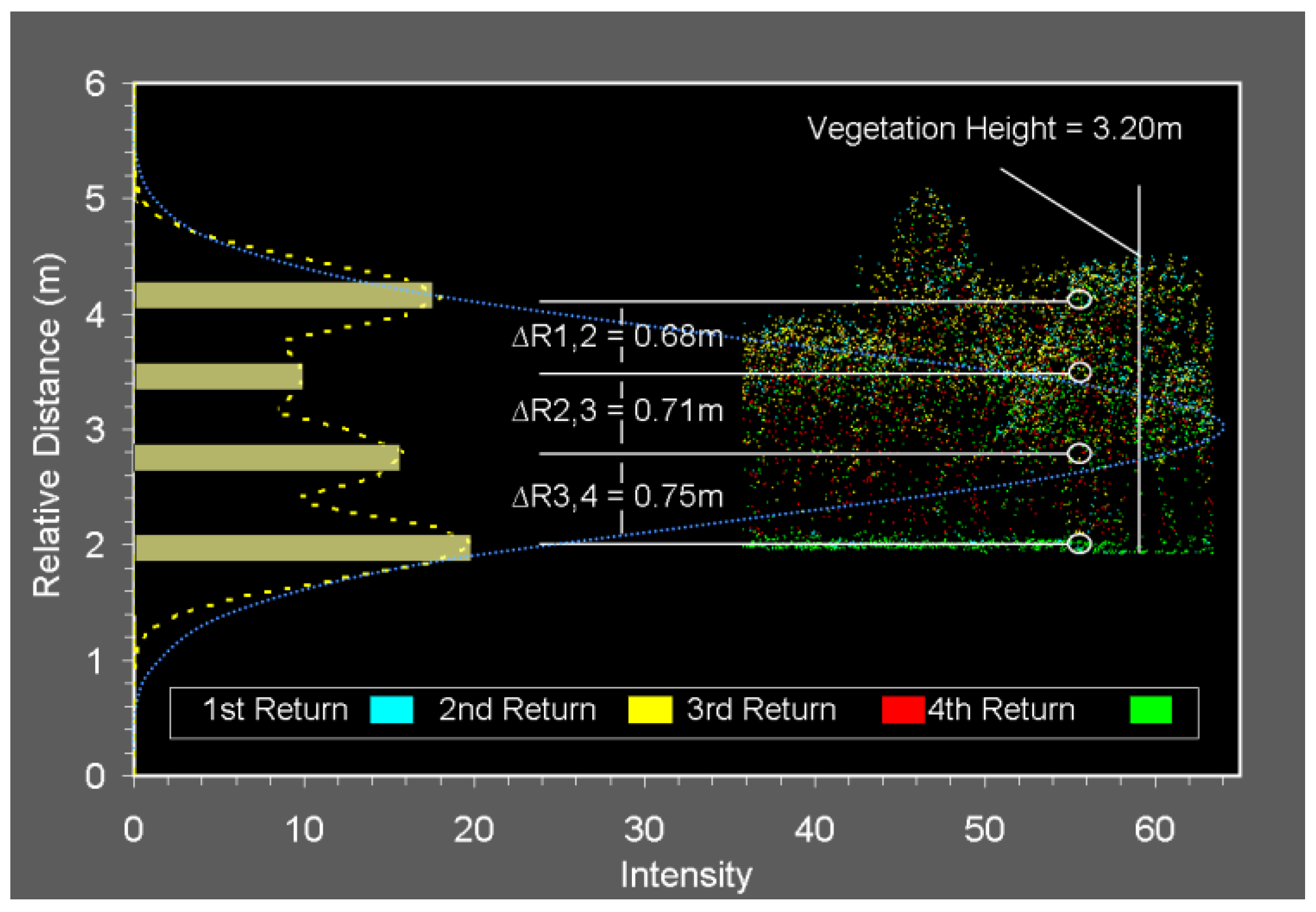
3.1. Objectives and Methodology
- Empirical evaluation of the minimum vertical target discrimination distance for ALTM-Orion data using statistical analysis of the field data collected over selected types of vegetation targets.
- Analysis of the capabilities of ALTM-Orion to represent the vertical structure of vegetation targets: number and distribution of multiple returns, typical vertical target discrimination values, correlation of number of multiple returns with vegetation height, signal penetration to the ground.
- Comparison of the results of 1–2 to a similar analysis based on ALTM-Gemini data.
- Investigate the potential of return signal waveform modeling for DR data.
3.2. Results and Discussion

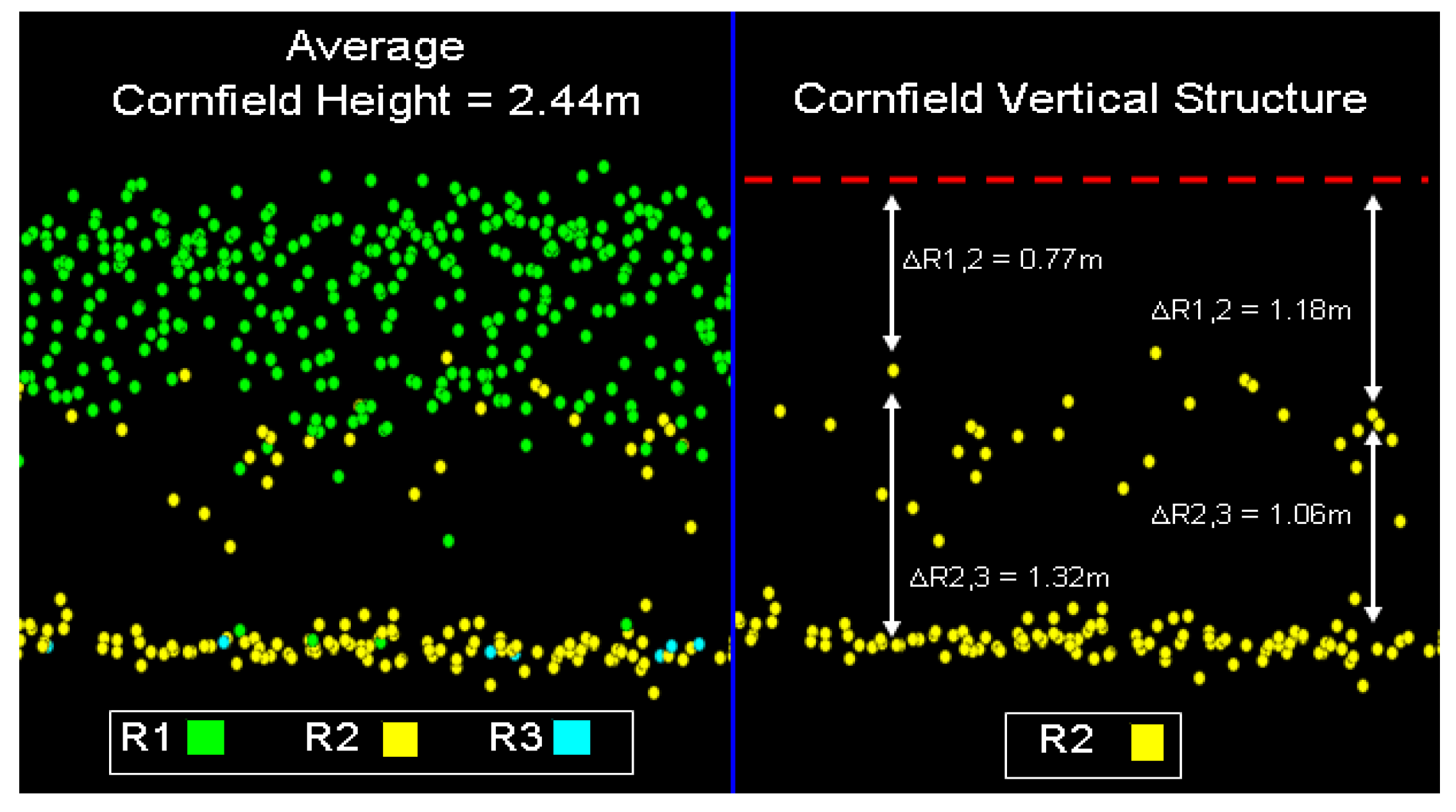
| Sample | Avg ∆R1,2 (m) | Avg ∆R2,3 (m) | Avg ∆R3,4 (m) | Avg height (m) |
|---|---|---|---|---|
| 1 | 1.36 | 1.06 | n/a | 2.31 |
| 2 | 1.25 | 0.99 | n/a | 1.92 |
| 3 | 1.34 | 1.00 | n/a | 2.12 |
| Sample | Min ∆R1,2 (m) | Min ∆R2,3 (m) | Min ∆R3,4 (m) | Avg height (m) |
| 1 | 0.67 | 0.69 | n/a | 2.31 |
| 2 | 0.64 | 0.65 | n/a | 1.92 |
| 3 | 0.66 | 0.67 | n/a | 2.12 |
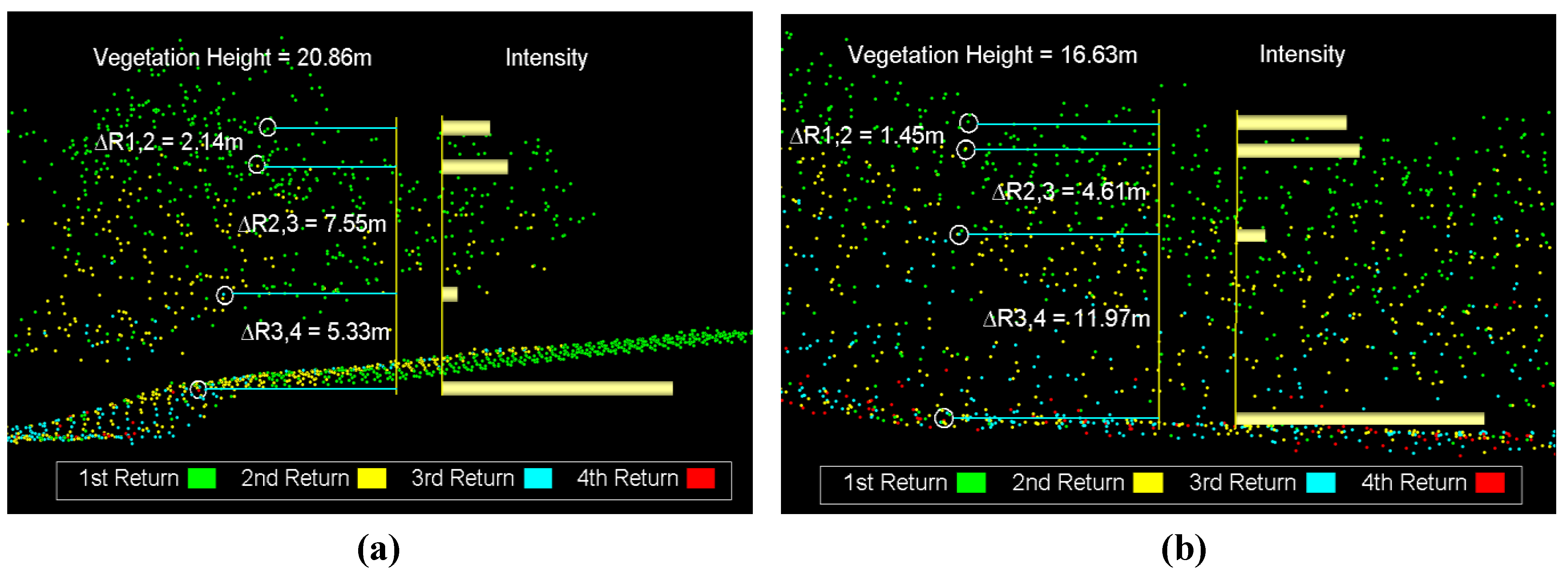
| Sample | Avg ∆R1,2 (m) | Avg ∆R2,3 (m) | Avg ∆R3,4 (m) | Avg height (m) |
|---|---|---|---|---|
| 1 | 2.54 | 2.10 | 1.91 | 6.0 |
| 2 | 3.64 | 3.92 | 4.26 | 22.5 |
| 3 | 3.44 | 3.50 | 3.69 | 20.0 |
| Sample | Min ∆R1,2 (m) | Min ∆R2,3 (m) | Min ∆R3,4 (m) | Avg height (m) |
| 1 | 0.68 | 0.71 | 0.73 | 6.0 |
| 2 | 0.70 | 0.70 | 0.64 | 22.5 |
| 3 | 0.65 | 0.61 | 0.68 | 20.0 |
| Sample | Pulse Return | % of Total |
|---|---|---|
| Sample 1 Average height 6 m | 1 | 55.88 |
| 2 | 33.03 | |
| 3 | 9.38 | |
| 4 | 1.71 | |
| Sample 2 Average height 22.5 m | 1 | 43.22 |
| 2 | 31.6 | |
| 3 | 17.71 | |
| 4 | 7.47 | |
| Sample 3 Average height 20 m | 1 | 44.8 |
| 2 | 31.91 | |
| 3 | 16.79 | |
| 4 | 6.51 |

| Pulse Return | Sample | % of Total | Sample | % of Total |
|---|---|---|---|---|
| 1 | Sample 1 Average height 6–7 m | 84.5 | Sample 4 Average height 22–27 m | 43.5 |
| 2 | 15.3 | 35.3 | ||
| 3 | 0.2 | 16.9 | ||
| 4 | 0.0 | 4.3 | ||
| 1 | Sample 2 Average height 6–7 m | 85.7 | Sample 5 Average height 22–27 m | 39.8 |
| 2 | 14.1 | 31.9 | ||
| 3 | 0.2 | 21.4 | ||
| 4 | 0.0 | 6.9 | ||
| 1 | Sample 3 Average height 6–7 m | 83.6 | Sample 6 Average height 22–27 m | 42.1 |
| 2 | 15.8 | 34.0 | ||
| 3 | 0.6 | 18.7 | ||
| 4 | 0.0 | 5.2 |
4. Waveform Modeling for DR Data
- Pi is the received signal power for i-return
- Pt is the transmitted laser pulse power
- Dr is the diameter of the lidar receiver aperture
- Q is the optical efficiency of the lidar system
- is the laser beam divergence
- Tatm is the atmospheric transmittance factor
- Ri is the range from the sensor to i-target
- σi is the effective backscattering cross-section of i-target

4. Conclusions
Acknowledgements
References
- Aldred, A.; Bonner, M. Application of Airborne Lasers to Forest Surveys; Information Report PI‑X-51; Petawawa National Forestry Centre, Canadian Forestry Service: Petawawa, ON, Canada, 1987; p. 62. [Google Scholar]
- Nelson, R.; Krabill, W.; Maclean, G. Determining forest canopy characteristics using airborne laser data. Remote Sens. Environ. 1984, 15, 201–212. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Drake, J.B. Lidar remote sensing for forestry. J. Forestry 2000, 98, 44–46. [Google Scholar]
- Nelson, R.; Parker, G.; Hom, M. A portable airborne laser system for forest inventory. Photogramm. Eng. Remote Sensing 2003, 69, 267–273. [Google Scholar] [CrossRef]
- Roberts, S.D.; Dean, T.J.; Evans, D.L.; McCombs, J.W.; Harrington, R.L.; Glass, P.A. Estimating individual tree leaf area in loblolly pine plantations using LiDAR-derived measurements of height and crown dimensions. Forest Ecol. Manage. 2005, 213, 54–70. [Google Scholar] [CrossRef]
- Hudak, A.T.; Evans, J.S.; Smith, A.M.S. Review: LiDAR utility for natural resource managers. Remote Sens. 2009, 1, 934–951. [Google Scholar] [CrossRef]
- Ussyshkin, V.; Theriault, L. Advances in Airborne Lidar Technology for Forestry and Other 3D Mapping Applications. In Proceedings of the Regional ISPRS Conference: Latin American Remote Sensing Week (LARS), Santiago, Chile, 4–7 October 2010.
- Hopkinson, C.; Sitar, M.; Chasmer, L.; Treitz, P. Mapping snowpack depth beneath forest canopies using airborne lidar. Photogramm. Eng. Remote Sensing 2004, 70, 323–330. [Google Scholar] [CrossRef]
- Alharthy, A.; Bethel, J. Heuristic Filtering and 3D Feature Extraction from Lidar Data. In Proceedings of ISPRS Commission III, Symposium 2002 “Photogrammetric Computer Vision”, Graz, Austria, 9–13 September 2002.
- Bates, P.D.; Pappenberger, F.; Romanowicz, R. Uncertainty and risk in flood inundation modeling. In Flood Forecasting; Beven, K., Hall, J., Eds.; Wiley & Co.: New York, NY, USA, 1999. [Google Scholar]
- Raber, G.T.; Jensen, J.R.; Schill, S.R.; Schuckman, K. Creation of digital terrain models using an adaptive Lidar vegetation point removal process. Photogramm. Eng. Remote Sensing 2002, 68, 1307–1316. [Google Scholar]
- Renslow, M.; Greenfield, P.; Guay, T. Evaluation of Multi-Return LIDAR for Forestry Applications; RSAC-2060/4810-LSP-0001-RPT1; US Department of Agriculture Forest Service-Engineering: Salt Lake City, UT, USA, 2000. Available online: http://www.ndep.gov/USDAFS_LIDAR.pdf (accessed on 19 November 2010).
- Ussyshkin, V.; Sitar, M. Advantages of Airborne Lidar Technology for Power Line Asset Management. In Proceedings of 5th Annual CIGRÉ Canada Conference: Innovation and Renewal-Building the New Power System, Vancouver, BC, Canada, 17–19 October 2010. [CDROM].
- Chauve, A.; Mallet, C.; Bretar, F.; Durrieu, S.; Pierrot-Deseilligny, M.; Puech, W. Processing Full-Waveform Lidar Data: Modelling Raw Signals. In Proceedings of ISPRS Workshop on Laser Scanning 2007, Espoo, Finland, 12 September 2007; Volume 36, Part 3/W52. pp. 102–107.
- Korpela, I.; Ørka, H.O.; Maltamo, M.; Tokola, T.; Hyyppä, J. Tree species classification using airborne LiDAR—Effects of stand and tree parameters, downsizing of training set, intensity normalization, and sensor type. Silva Fennica 2010, 44, 319–339. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Progr. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Parrish, C.E.; Scarpace, F.L. Investigation of Full Waveform Lidar Data for Detection and Recognition of Vertical Objects. In Proceedings of ASPRS 2007 Annual Conference, Tampa, FL, USA, 7–11 May 2007.
- Chauve, A.; Vega, C.; Bretar, F.; Durrieu, S.; Allouis, T.; Pierrot-Deseilligny, M.; Puech, W. Processing full-waveform lidar data in an alpine coniferous forest: assessing terrain and tree height quality. Int. J. Remote Sens. 2009, 30, 5211–5228. [Google Scholar] [CrossRef]
- Magruder, L.A.; Neuenschwander, A.L.; Marmillion, S.P.; Tweddale, S.A. Obstruction detection comparison of small-footprint full-waveform and discrete return lidar. Proc. SPIE 2010, 7684, 768410. [Google Scholar] [CrossRef]
- Chauve, A.; Bretar, F.; Pierrot-Deseilligny, M.; Puech, W. Full Analyze: A Research Tool for Handling, Processing and Analyzing Full-Waveform Lidar Data. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 12–17 July 2009.
- Ussyshkn, V.; Theriault, L. ALTM-Orion: Bridging Conventional Lidar and Full Waveform Digitizer Technology. In ISPRS TC VII Symposium “100 Years ISPRS”, Vienna, Austria, 5–7 July 2010; Volume 38, Part7B. pp. 606–611, [CDROM].
- Bretar, F.; Chauve, A.; Mallet, C.; Jutzi, B. Managing Full Waveform Lidar Data: A Challenging Task for the Forthcoming Years. In Proceeding sof XXIst ISPRS Congress, Beijing, China, 3–11 July 2008; Volume 37, Part B1. pp. 415–420.
- Neuenschwander, A.L.; Magruder, L.A.; Tyler, M. Landcover classification of small-footprint, full-waveform lidar data. J. Appl. Remote Sens. 2009, 3, 033544. [Google Scholar] [CrossRef]
- Wagner, W.; Hollaus, M.; Briese, C.; Ducic, V. 3D vegetation mapping using small-footprint full‑waveform airborne laser scanners. Int. J. Remote Sens. 2008, 29, 1433–1452. [Google Scholar] [CrossRef]
- Petrie, G. Current Developments in Airborne Laser Scanning Technologies. In Proceedings of IX International Scientific & Technical Conference—From Imagery to Map: Digital Photogrammetric Technologies, Attica, Greece, 5–8 October 2009.
- Jutzi, B.; Stilla, U. Characteristics of the Measurement Unit of a Full-Waveform Laser System. In Symposium of ISPRS Commission I: From Sensors to Imagery, Paris, France, May 2006; Volume 36. Part 1/A [CDROM].
- Reitberger, J.; Krzystek, P.; Stilla, U. Analysis of Fullwaveform LiDAR Data for Tree Species Classification. In Proceedings of ISPRS Symposium of Commission III “Photogrammetric Computer Vision and Image Analysis”, Bonn, Germany, 20–22 September 2006; Volume 36, pp. 228–233.
- Jutzi, B.; Stilla, U. Range determination with waveform recording laser systems using a Wiener Filter. ISPRS J. Photogramm. Remote Sens. 2006, 61, 95–107. [Google Scholar] [CrossRef]
- Hofton, M.A.; Blair, J.B. Laser altimeter return pulse correlation: A method for detecting surface topographic change. J. Geodyn. 2002, 34, 477–489. [Google Scholar] [CrossRef]
- Hussein, M.; Tripp, J.; Hill, B. An ultra compact laser terrain mapper for deployment onboard unmanned aerial vehicles. Proc. SPIE 2009, 7307, 73070B. [Google Scholar]
- Ussyshkin, V.; Theriault, L. Precise Mapping: ALTM Orion Establishes a New Standard in Airborne Lidar Performance. In Proceedings of ASPRS Annual Conference, San Diego, CA, USA, 26–30 April 2010.
- Ussyshkin, V.; Theriault, L. Empirical Evaluation of the Resolution of Range Measurements in ALTM-Gemini; Internal Optech Document; Optech: Vaughan, ON, Canada, 2010. [Google Scholar]
- Measures, R.M. Laser Remote Sensing, Fundamentals and Applications; Wiley Interscience: New York, NY, USA, 1984. [Google Scholar]
- Jelalian, A.V. Laser Radar Systems; Artech House: Boston, MA, USA, 1992. [Google Scholar]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Wagner, W.; Ullrich, A.; Melzer, T.; Briese, C.; Kraus, K. From Single-Pulse to Full-Waveform Airborne Laser Scanners: Potential and Practical Challenges. In Proceedings of the International Society for Photogrammetry and Remote Sensing 20th Congress Commission 3, Istanbul, Turkey, 12–23 July 2004; Volume 35, Part B/3. pp. 6–12.
- Schaer, P.; Skaloud, J.; Landtwing, S.; Legat, K. Accuracy Estimation for Laser Point Cloud Including Scanning Geometry. In Proceedings of The 5th International Symposium on Mobile Mapping Technology, Padua, Italy, 29–31 May 2007.
- Jutzi, B.; Gross, H. Normalization of Lidar Intensity Data Based on Range and Surface Incidence Angle. In Proceedings of Laserscanning 09, Paris, France, 1–2 September 2009; Volume 38, Part 3/W8. pp. 213–218.
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ussyshkin, V.; Theriault, L. Airborne Lidar: Advances in Discrete Return Technology for 3D Vegetation Mapping. Remote Sens. 2011, 3, 416-434. https://doi.org/10.3390/rs3030416
Ussyshkin V, Theriault L. Airborne Lidar: Advances in Discrete Return Technology for 3D Vegetation Mapping. Remote Sensing. 2011; 3(3):416-434. https://doi.org/10.3390/rs3030416
Chicago/Turabian StyleUssyshkin, Valerie, and Livia Theriault. 2011. "Airborne Lidar: Advances in Discrete Return Technology for 3D Vegetation Mapping" Remote Sensing 3, no. 3: 416-434. https://doi.org/10.3390/rs3030416
APA StyleUssyshkin, V., & Theriault, L. (2011). Airborne Lidar: Advances in Discrete Return Technology for 3D Vegetation Mapping. Remote Sensing, 3(3), 416-434. https://doi.org/10.3390/rs3030416