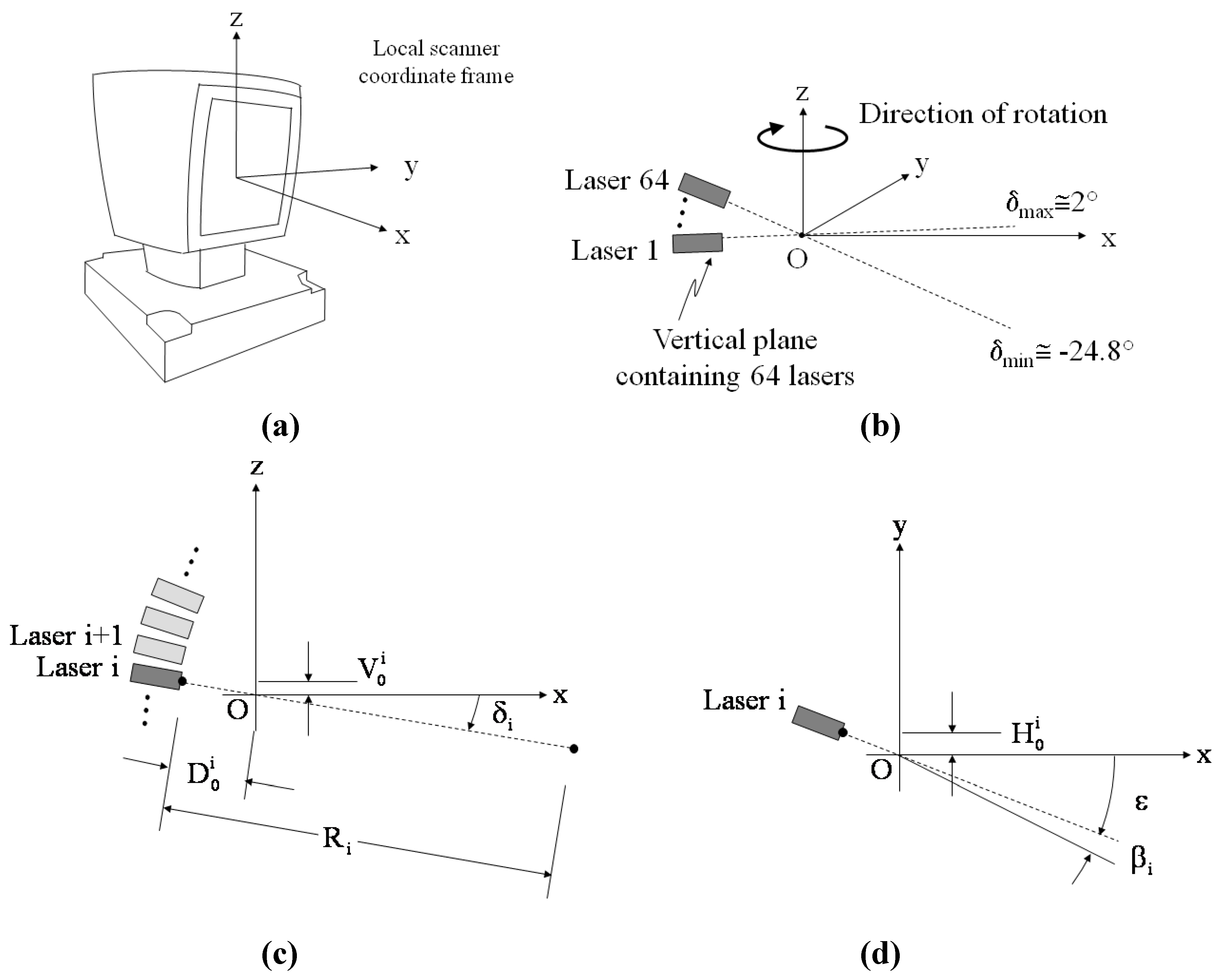
5.2. Measurement Residual Analysis
In addition to examining the overall improvement in the planar misclosure, it is also instructive to examine the measurement residuals from the adjustment. For the Velodyne laser, there are two measurements per point, a range and an encoder angle.
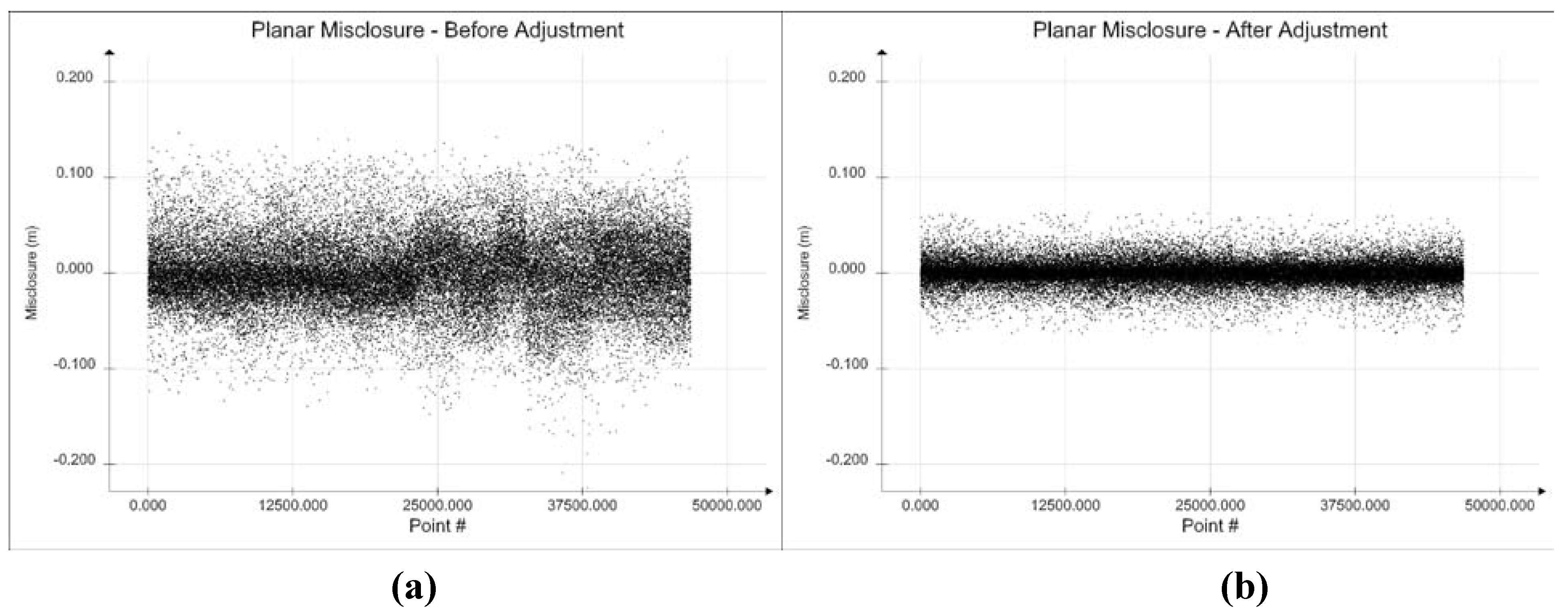
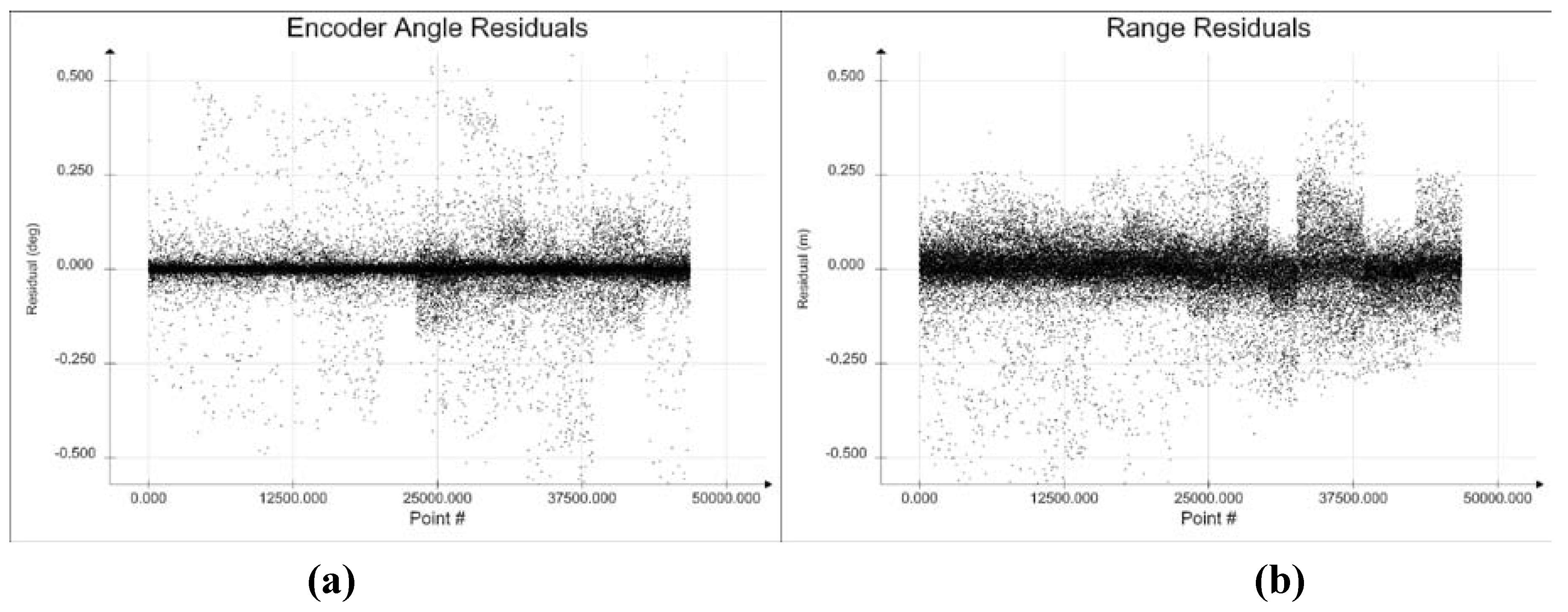
Figure 5 shows plots of the final measurement residuals for the least squares adjustment for both range and encoder angles.
Figure 5.
(a) Encoder Angle Residuals. (b) Range Residuals for Least Squares Adjustment.
Figure 5.
(a) Encoder Angle Residuals. (b) Range Residuals for Least Squares Adjustment.
Figure 5 shows that there are still some unmodelled systematic effects since the range and encoder angle residuals do not appear to be normally-distributed random errors. To further examine these apparent systematic errors, the residuals are plotted in
Figure 6 with respect to the laser beam incidence angle on the planar surface. Please note that for all figures, no post adjustment outlier removal procedure has been performed.
Figure 6.
Residuals Versus Planar Incidence Angle (a) Encoder Angle (b) Range.
Figure 6.
Residuals Versus Planar Incidence Angle (a) Encoder Angle (b) Range.
In examining the residuals for the range measurements in
Figure 6, the overall noise level and distribution of the residuals appears fairly consistent and regular up to an incidence angle of approximately 60° to 65°. The encoder angle residuals also show a sharp increase in value at approximately the same incidence angle. These results are consistent with other static scanner adjustments found in literature. For example, [
5] showed that for an AM-CW scanner, the larger residuals were nearly always isolated to points with incidence angles greater than 65° or 70°, while [
13] found critical angles of 65° to 75° for reflectorless total stations. The slightly lower incidence angle threshold found here may be due to the much larger beam divergence for the Velodyne (2.0 mrad)
versus the AM-CW scanner in [
5], (0.2 mrad) and the instruments in [
13] (0.4 mrad and 1 mrad). This pattern suggests that the calibration procedure should reject points with high incidence angles, or alternatively the weighting of the range and encoder angle measurements should be modified to relax the accuracy of observations at higher angles of incidence.
It should also be noted that the encoder angle residuals presented in
Figure 6 do not appear to have a uniform distribution across the incidence angle range from 0° to 60°. The residuals at low incidence angles are much smaller than those at higher incidence. However, this pattern is likely not due to any unmodelled error in the encoder angle. At very low incidence angle, the planar misclosure of a point is dominated by range errors and has very low correlation with the encoder angle. Therefore for lower incidence angle points the calculated encoder angle residuals are smaller.
Finally, it is also instructive to compare the range and encoder angle residuals to the manufacturer specifications for ranging and angular accuracy of the HDL-64E S2.
Table 4 displays the residuals of both measurements, for all incidence angles, and for incidence angles less than 65°.
Table 4.
Range and Encoder Angle Residuals (All Points and Points With Planar Incidence < 65°).
Table 4.
Range and Encoder Angle Residuals (All Points and Points With Planar Incidence < 65°).
| All Measurements | Incidence Angle < 65 deg |
| Range (m) | Encoder (deg) | Range (m) | Encoder (deg) |
| Minimum | −1.058 | −0.940 | −0.232 | −0.298 |
| Maximum | 0.498 | 0.710 | 0.204 | 0.298 |
| Mean | 0.001 | −0.001 | 0.000 | 0.000 |
| RMSE | 0.084 | 0.063 | 0.037 | 0.027 |
From
Table 1, the manufacturer specifications for the unit give a 1σ value for the range at 15 mm, and an encoder angular resolution at 0.09° (0.026° quantization noise standard deviation). The encoder angle residuals in
Table 3 are well below the angular resolution of the encoder, and in fact the RMSE of residuals with constrained incidence angles actually approaches the quantization noise level of the scanner. The RMSE of the range residuals however are significantly higher than the manufacturer’s specification for the lasers. Even with the constrained incidence angles the resultant RMSE of the range residuals is still twice the expected value.
The discrepancy between observed and expected range accuracy is significantly larger than expected. Therefore, the range residuals were more closely examined to discover if there was any correlation between the residuals and any other measureable parameters. Analyses of the residuals as a function of laser return intensity did not reveal any dependencies. In addition, the range residuals did not exhibit any apparent correlation with encoder angle, which would suggest that there isn’t a misalignment between the scanner and encoder axes.
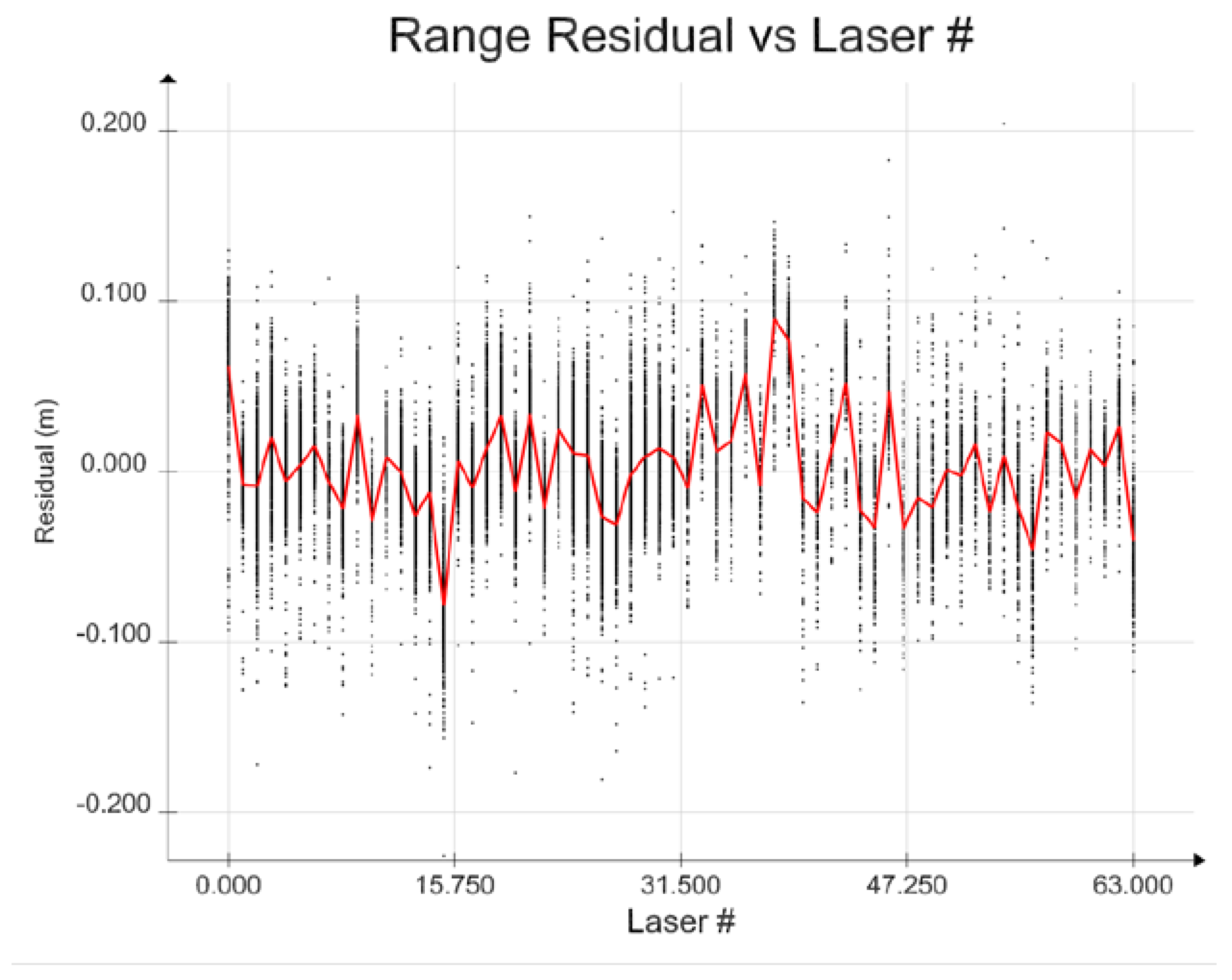
Figure 7 shows range residuals plotted for each individual laser in the 64-laser array excluding observations having planar incidence angles greater than 65°.
Figure 7.
Range Residuals versus Laser # (Red Line = Mean Value).
Figure 7.
Range Residuals versus Laser # (Red Line = Mean Value).
Figure 7 shows what appears to be a systematic error in the ranges. The red line in the figure connects the mean residual values for each laser’s residuals. As is evident from the graph, the lasers do not individually have zero mean residuals. To further investigate this phenomenon, the mean range residuals are plotted in
Figure 8, this time
versus the vertical angle, δ, of the laser.
Figure 8.
Magnitude of Mean Range Residual vs Laser Vertical Angle.
Figure 8.
Magnitude of Mean Range Residual vs Laser Vertical Angle.
With the exception of one outlier, the mean biases tend to be in the range of 1 to 3 cm, except for a cluster of lasers with the largest vertical angle offsets. In examining
Figure 1 it is noted that the lenses for each of the laser emitter and receiver blocks are arranged in order to focus the outgoing laser beams, and to focus the returned energy on the detectors. It is reasonable to assume that the lasers with the highest vertical angle are most likely passing through the emitter and/or receiver mirrors near their edges and are perhaps being distorted in a manner that is not properly modeled by the six coefficients given in Equation (1), or are contributing additional noise to the raw range measurements. This effect will need further study to see if the root cause can be isolated. Nevertheless, even if the five lasers with large mean range residual biases are removed from the computation, the overall RMSE of the range residuals is still only 29 mm (for incidence angles < 65°). This is nearly twice the manufacturer specification. The standard deviations of the individual laser’s ranges however vary between 15 and 25 mm, which is closer to the manufacturer specification, although still slightly higher. It is apparent that there is still an unmodelled component of the laser ranges which is the cause of the non-zero mean residuals, and perhaps for the slightly higher than specification standard deviations.
5.3. Parameter Correlation
A good indication of the strength of the solution and the observability of the individual calibration parameters can be obtained by examining the correlation coefficients between the estimated unknown parameters.
Table 5 presents the correlation coefficients for the adjustment. In general, the correlation between the scanner position and orientation parameters between station (e.g., Setup 1
vs. Setup 5) was quite low (<0.1), therefore the light green values in the table are averages over all stations, but only considering correlation with the unknowns from the same station. Similarly, the correlation between the laser parameters of different lasers was quite low (<0.1), and therefore, the values in the grey area of the table are averages over all lasers, but only considering correlation with the other 5 parameters from the same laser. Values in white, correlations between stations and laser unknowns, have been averaged over all stations and all lasers.
Table 5.
Correlation Coefficients Between Estimated Unknowns.
Table 5.
Correlation Coefficients Between Estimated Unknowns.
| Correlation Coefficients |
| Y | Z | OMEGA | PHI | KAPPA | □ | □ | Dio | Hio | Vio | s |
| X | 0.113 | 0.064 | 0.072 | 0.153 | 0.19 | 0.012 | 0.045 | 0.018 | 0.011 | 0.018 | 0.029 |
| Y | xx | 0.114 | 0.071 | 0.083 | 0.227 | 0.023 | 0.015 | 0.022 | 0.01 | 0.022 | 0.145 |
| Z | xx | xx | 0.459 | 0.195 | 0.042 | 0.038 | 0.013 | 0.039 | 0.014 | 0.035 | 0.019 |
| OMEGA | xx | xx | xx | 0.157 | 0.188 | 0.098 | 0.017 | 0.025 | 0.021 | 0.094 | 0.021 |
| PHI | xx | xx | xx | xx | 0.17 | 0.078 | 0.021 | 0.019 | 0.021 | 0.076 | 0.021 |
| KAPPA | xx | xx | xx | xx | xx | 0.022 | 0.068 | 0.023 | 0.024 | 0.018 | 0.021 |
| δ | xx | xx | xx | xx | xx | xx | 0.127 | 0.491 | 0.095 | 0.909 | 0.454 |
| β | xx | xx | xx | xx | xx | xx | xx | 0.132 | 0.879 | 0.111 | 0.193 |
| Dio | xx | xx | xx | xx | xx | xx | xx | xx | 0.112 | 0.593 | 0.754 |
| Hio | xx | xx | xx | xx | xx | xx | xx | xx | xx | 0.091 | 0.154 |
| Vio | xx | xx | xx | xx | xx | xx | xx | xx | xx | xx | 0.493 |
Overall, the station unknown coordinates and orientations exhibit fairly low correlation with themselves, and with the laser unknown parameters. This is to be expected, but also confirms that scanning from unknown locations to targets with unknown absolute locations does not appear to significantly hinder the estimation of the unknown laser parameters.
For the individual laser unknown parameters (grey area in
Table 5), the correlation coefficients are in general higher than for the station unknowns. The most troubling are the three correlations highlighted in yellow. The highest correlation, with an average of 0.909, is found between the vertical rotation correction δ
i, and the vertical offset parameter
. The correlation ranges from 0.78 to 0.9 for lasers with a vertical angle between +2° and −12° and from 0.9 to 0.94 for the lasers with larger vertical angles between −12° and −27° degrees. This increase in correlation with increased vertical angle is to be expected because the larger the vertical angle the larger the vertical component of the distance measurement. Although the laser was tilted for 8 of the collected scans, it was only tilted at an angle of 30° with respect to the ground plane. In retrospect, this amount of tilt was likely not enough to completely separate the vertical angle and vertical offset components. This correlation can likely be mitigated in future calibrations by collecting additional data with the scanner tilted 90° (
i.e., collecting laser data in a vertical plane), along with the horizontal and elevated scans collected in this study.
The horizontal rotation βi, and horizontal offset , also had a high degree of correlation for the solution, an average of 0.879. The correlation is of approximately the same magnitude for all of the lasers in the scanner array. However, this correlation coefficient increases significantly if the scan stations with 30° of tilt are removed from the solution. Without the tilted scans, this correlation averages 0.94. Therefore, it is reasonable to assume that the addition of scans with the laser tilted at 90° would also help to de-correlate the horizontal rotation and offset components.
Finally, the distance offset, , and distance scale, si, parameters also show fairly high correlation with an average of 0.754. This correlation component varies, and is generally a function of the number of longer ranges observed for the particular laser. The maximum range observed in the calibration dataset was approximately 50 m, and the scale factors for the lasers averaged about 1.0006 (i.e., 3 cm at 50 m), so even at the maximum range the scale factor was still only at the RMSE level of the ranges. Given that the maximum range for the scanners is approximately 125 m, future calibrations should attempt to incorporate longer ranges, up to the scanner maximum, to be able to reliably estimate the scale factor and also decouple it from the distance offset parameter.
5.4. Accuracy of Estimated Parameters
The internal calibration parameters for the laser scanner (and the scanner position and orientation unknowns) were solved for simultaneously in a least square adjustment, and therefore, via error propagation, estimates of the accuracy of the unknown parameters estimated in the adjustment can be calculated.
Table 6 presents the maximum, minimum and average correction values for each unknown parameter in the adjustment, along with the average calculated accuracy for that parameter estimate. Given the large number of stations (16), and the large number of lasers (64), an average correction and estimated accuracy was computed for the position and orientation unknowns of the stations, and the 6 laser parameter corrections and estimated accuracies were also averaged over all 64 lasers.
Table 6.
Maximum, Minimum and Average Correction and Accuracy Estimates for Unknown Values.
Table 6.
Maximum, Minimum and Average Correction and Accuracy Estimates for Unknown Values.
| Unknown | Maximum
Correction | Minimum
Correction | Average | Units |
| Correction | Estimated Accuracy |
| X | 0.0022 | −0.0014 | 0.0007 | 0.0012 | m |
| Y | 0.0115 | −0.0051 | 0.0035 | 0.0019 | m |
| Z | 0.0004 | −0.0006 | −0.0001 | 0.0004 | m |
| OMEGA | 0.0133 | −0.0075 | 0.0006 | 0.0038 | deg |
| PHI | 0.0058 | −0.0077 | −0.0003 | 0.0046 | deg |
| KAPPA | 0.0037 | −0.0068 | −0.0005 | 0.0053 | deg |
| V ROT | 0.3967 | −0.1299 | 0.1118 | 0.0124 | deg |
| H ROT | 0.1703 | −0.1941 | −0.0517 | 0.0167 | deg |
| D OFF | 0.1640 | −0.0140 | 0.0657 | 0.0046 | m |
| H OFF | 0.0351 | −0.0238 | −0.0006 | 0.0039 | m |
| V OFF | 0.0601 | −0.0203 | 0.0223 | 0.0028 | m |
| D SCALE | 0.0009 | −0.0022 | −0.0006 | 0.0003 | unitless |
The results presented in
Table 6 have not been scaled by the estimated variance factor for the adjustment. The estimated variance factor was calculated as 6.587. This inflated values is due to the larger than expected noise level of the range measurements as discussed in
Section 5.2. Overall the estimated accuracies in
Table 6 show an acceptable level of confidence in the estimated parameters. Internal calibration distances are resolved to the order of a few mm, and angular calibration values are resolved to a couple hundredths of a degree—both of which are better than the observed noise levels of the individual range and encoder angle measurements. Therefore, the planar based adjustment procedure utilized seems to give an acceptable level of results and accuracy for calibration of the HDL-64E S2 scanner.