Hydraulic Geometry, GIS and Remote Sensing, Techniques against Rainfall-Runoff Models for Estimating Flood Magnitude in Ephemeral Fluvial Systems
Abstract
:1. Introduction
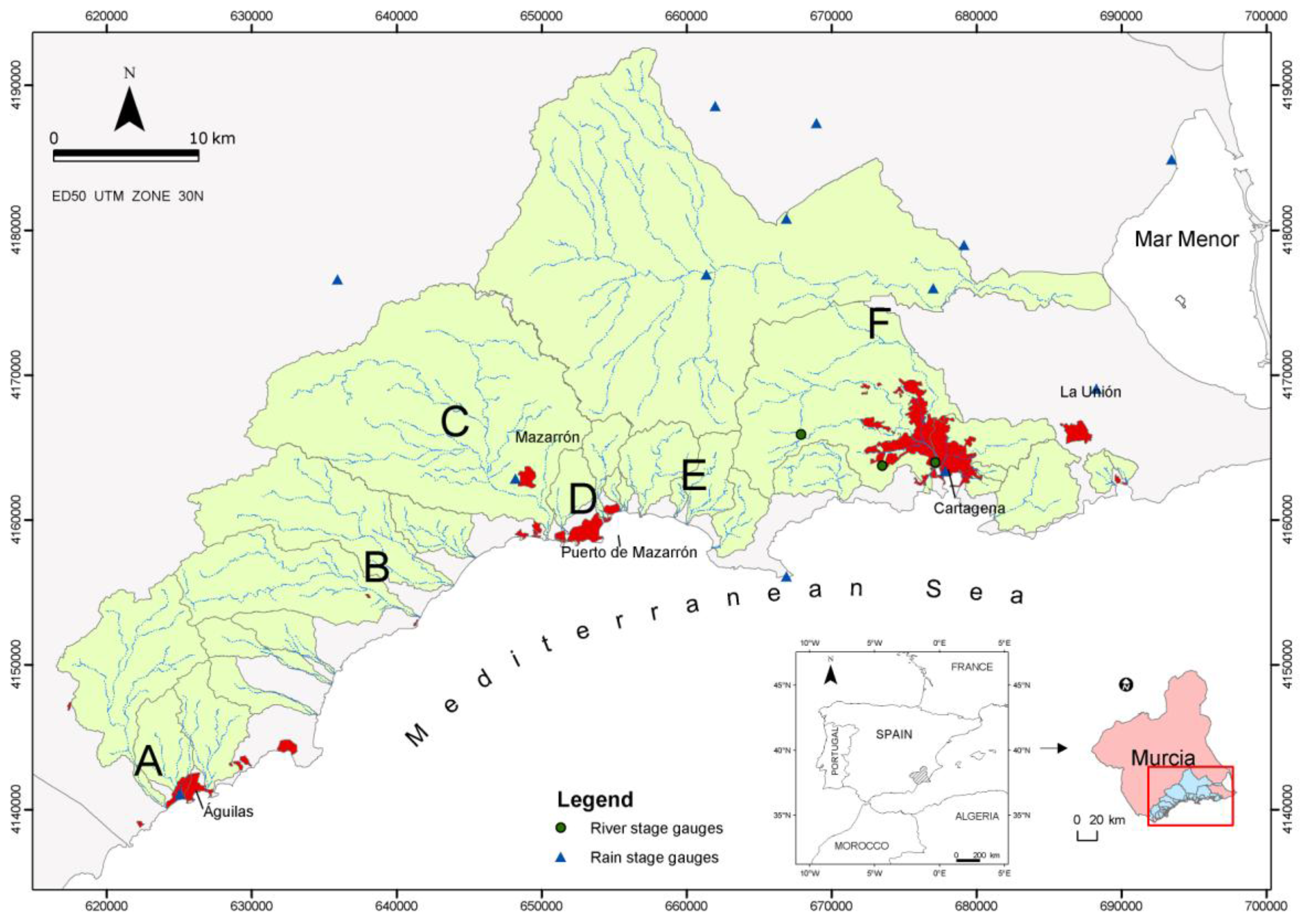
2. Study Area
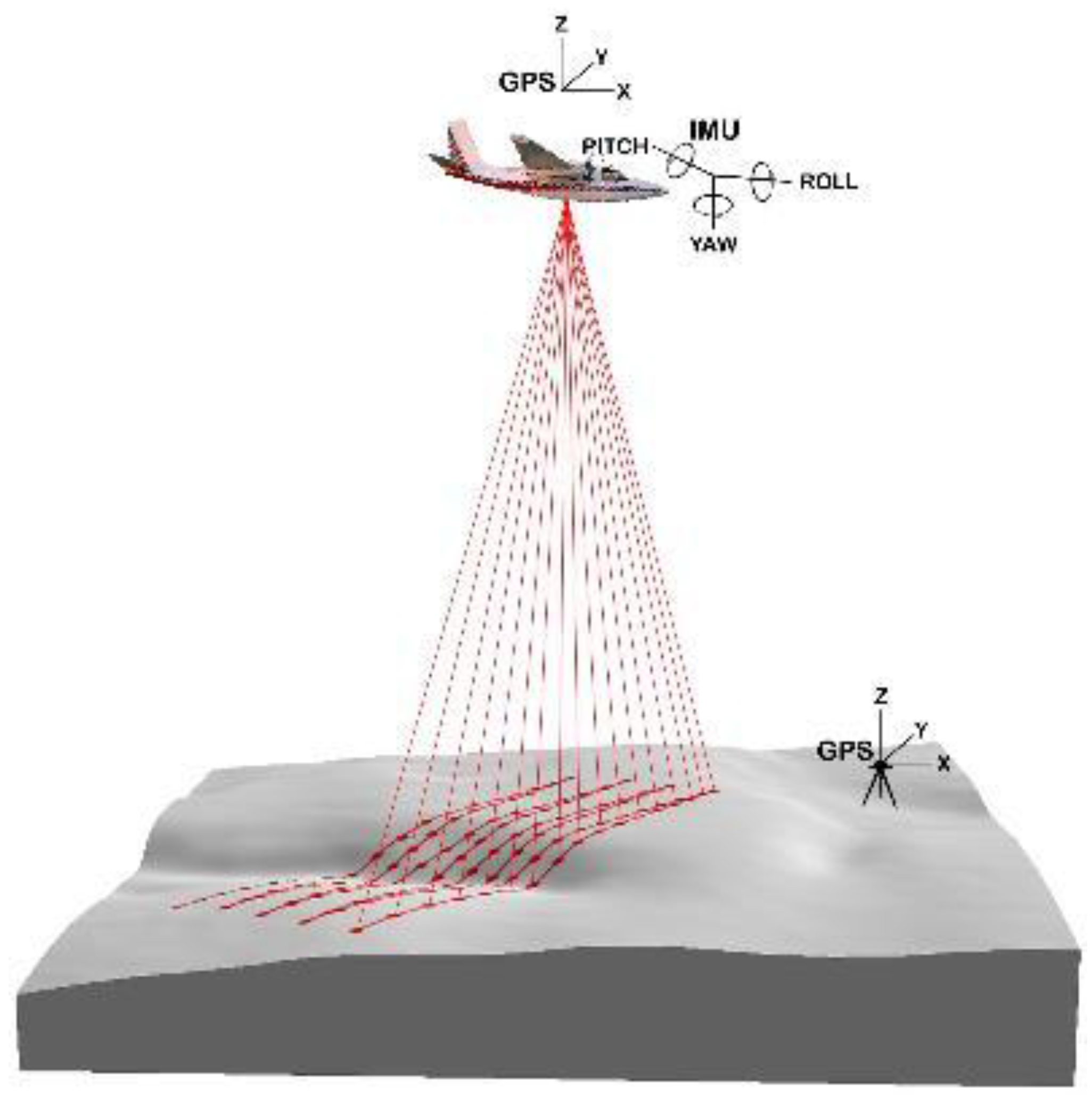
3. Methodology
3.1. The Hydraulic Geometry Method (HGM) Compared to Hydrometeorological Methods for Calculating Flood Discharges
3.1.1. Hydrometeorological Models
3.1.2. Channel Hydraulic Geometry Methods
3.2. Combination of Hydraulic Geometry Methods (HGM) with Remote Sensing Methods for Recent Floods
| Type of Channel and Description | Minimum | Normal | Maximum |
|---|---|---|---|
| A. Natural Streams | |||
| 1. Main Channels | |||
| a. Clean, straight, full, no rifts or deep pools | 0.025 | 0.030 | 0.033 |
| b. Same as above, but more stones and weeds | 0.030 | 0.035 | 0.040 |
| c. Clean, winding, some pools and shoals | 0.033 | 0.040 | 0.045 |
| d. Same as above, but some weeds and stones | 0.035 | 0.045 | 0.050 |
| e. Same as above, lower stages, more ineffective slopes and sections | 0.040 | 0.048 | 0.055 |
| f. Same as “d” but more stones | 0.045 | 0.050 | 0.060 |
| g. Sluggish reaches, weedy, deep pools | 0.050 | 0.070 | 0.080 |
| h. Very weedy reaches, deep pools, or floodways with heavy stands of timber and brush | 0.070 | 0.100 | 0.150 |
| 2. Flood Plains | |||
| a. Pasture no brush | |||
| 1. Short grass | 0.025 | 0.030 | 0.025 |
| 2. High grass | 0.030 | 0.035 | 0.050 |
| b. Cultivated areas | |||
| 1.No crop | 0.020 | 0.030 | 0.040 |
| 2. Mature row crops | 0.025 | 0.035 | 0.045 |
| 3. Mature field crops | 0.030 | 0.040 | 0.050 |
| c. Brush | |||
| 1. Scattered brush, heavy weeds | 0.035 | 0.050 | 0.070 |
| 2. Light brush and trees, in winter | 0.035 | 0.050 | 0.060 |
| 3. Light brush and trees, in summer | 0.040 | 0.060 | 0.080 |
| 4. Medium brush and trees, in winter | 0.045 | 0.070 | 0.110 |
| 5. Medium brush and trees, in summer | 0.070 | 0.100 | 0.160 |
| d. Trees | |||
| 1. Cleared land with tree stumps, no sprouts | 0.030 | 0.040 | 0.050 |
| 2. Same as above, but heavy sprouts | 0.050 | 0.060 | 0.080 |
| 3. Heavy stand of timber, few down trees, little undergrowth, flow below branches | 0.080 | 0.100 | 0.120 |
| 4. Same as above, but with flow into branches | 0.100 | 0.120 | 0.160 |
| 5. Dense willows, summer, straight | 0.110 | 0.150 | 0.200 |
| 3. Mountain Streams, no vegetation in channel, banks steep, with trees and brush on banks submerged | |||
| a. Bottom: gravels, cobbles and few boulders | |||
| b. Bottom: cobbles with large boulders | |||
| B. Lined or Built-Up Channels | |||
| 1. Concrete | |||
| a. Trowel finish | 0.011 | 0.013 | 0.015 |
| b. Float Finish | 0.013 | 0.015 | 0.016 |
| c. Finished, with gravel bottom | 0.015 | 0.017 | 0.020 |
| d. Unfinished | 0.014 | 0.017 | 0.020 |
| e. Gunite, good section | 0.016 | 0.019 | 0.023 |
| f. Gunite, wavy section | 0.018 | 0.022 | 0.025 |
| g. On good excavated rock | 0.017 | 0.020 | |
| h. On irregular excavated rock | 0.022 | 0.027 | |
| 2. Concrete bottom float finished with sides of: | |||
| a. Dressed stone in mortar | 0.015 | 0.017 | 0.020 |
| b. Random stone in mortar | 0.017 | 0.020 | 0.024 |
| c. Cement rubble masonry, plastered | 0.016 | 0.020 | 0.024 |
| d. Cement rubble masonry | 0.020 | 0.025 | 0.030 |
| e. Dry rubble on riprap | 0.020 | 0.030 | 0.035 |
| 3. Gravel bottom with sides of: | |||
| a. Formed concrete | 0.017 | 0.020 | 0.025 |
| b. Random stone in mortar | 0.020 | 0.023 | 0.026 |
| c. Dry rubble or riprap | 0.023 | 0.033 | 0.036 |
| 4. Brick | |||
| a. Glazed | 0.011 | 0.013 | 0.015 |
| b. Incement mortar | 0.012 | 0.015 | 0.018 |
| 5. Vegetal lining | 0.030 | 0.050 | |
| C. Excavated or Dredged Channels | |||
| 1. Earth, straight and uniform | |||
| a. Clean, recently completed | 0.016 | 0.018 | 0.020 |
| b. Clean, after weathering | 0.018 | 0.022 | 0.025 |
| c. Gravel, uniform section, clean | 0.022 | 0.025 | 0.030 |
| d. With short grass, few weeds | 0.022 | 0.027 | 0.033 |
| 2. Earth, winding and sluggish | |||
| a. No vegetation | 0.023 | 0.025 | 0.030 |
| b. Grass, some weeds | 0.025 | 0.030 | 0.033 |
| c. Dense weeds or aquatic plants | 0.030 | 0.035 | 0.040 |
| d. Earth bottom and rubble side | 0.028 | 0.030 | 0.035 |
| e. Stony bottom and weedy banks | 0.025 | 0.035 | 0.040 |
| f. Cobble bottom and clean sides | 0.030 | 0.040 | 0.050 |
| 3. Dragline-excavated or dredged | |||
| a. No vegetation | 0.025 | 0.028 | 0.033 |
| b. Light brush on banks | 0.035 | 0.050 | 0.060 |
| 4. Rock cuts | |||
| a. Smooth and uniform | 0.025 | 0.035 | 0.040 |
| b. Jagged and irregular | 0.035 | 0.040 | 0.050 |
| 5. Channels not maintained, weeds and brush | |||
| a. Clean bottom, brush on sides | 0.040 | 0.050 | 0.080 |
| b. Same as above, highest flow stage | 0.045 | 0.070 | 0.110 |
| c. Dense weeds, high as flow depth | 0.050 | 0.080 | 0.120 |
| d. Dense brush, high stage | 0.080 | 0.100 | 0.140 |
3.3. Using Bankfull Stage and Flood-Prone Area as Thresholds of Flood Hazard
4. Results and Discussion
4.1. Validation of the Hydraulic Geometry Method compared to the Rainfall-Runoff Models
| Basin | Watershed area (km2) | Basin slope (m/m) | Channel length (km) | Channel slope (m/m) | P0 (mm) | CN |
|---|---|---|---|---|---|---|
| Benipila | 97.10 | 0.1370 | 22.84 | 0.016 | 34.3 | 81.4 |
| Benipila+Dolores | 144.64 | 0.1145 | 24.35 | 0.013 | 26.9 | 84.8 |
| Nogalte | 128.65 | 0.1943 | 32.40 | 0.022 | 23.2 | 86.6 |
| Rambla | Tc (h) | Lt (h) | Bt (h) | Tp (h) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ASCS | Tγ | MRM | ASCS | Tγ | MRM | ASCS | Tγ | MRac | ASCS | Tγ | MRM | |
| Benipila | 4.33 | 7.09 | 7.09 | 2.60 | 2.48 | 2.60 | 13.19 | 15.15 | 7.57 | 2.68 | 2.57 | 2.68 |
| Benipila + Dolores | 4.45 | 7.75 | 7.75 | 2.67 | 2.71 | 2.67 | 13.54 | 16.52 | 8.23 | 2.71 | 2.75 | 2.71 |
| Nogalte | 4.02 | 8.71 | 8.71 | 2.41 | 3.05 | 2.83 | 12.27 | 18.54 | 9.15 | 2.45 | 3.09 | 2.45 |
| Rambla | Date | Peak discharge (m3/s) | basin P (mm) | Q AHIS (m3/s) | |||
|---|---|---|---|---|---|---|---|
| SCSD | Tγ | MRM | HGM | ||||
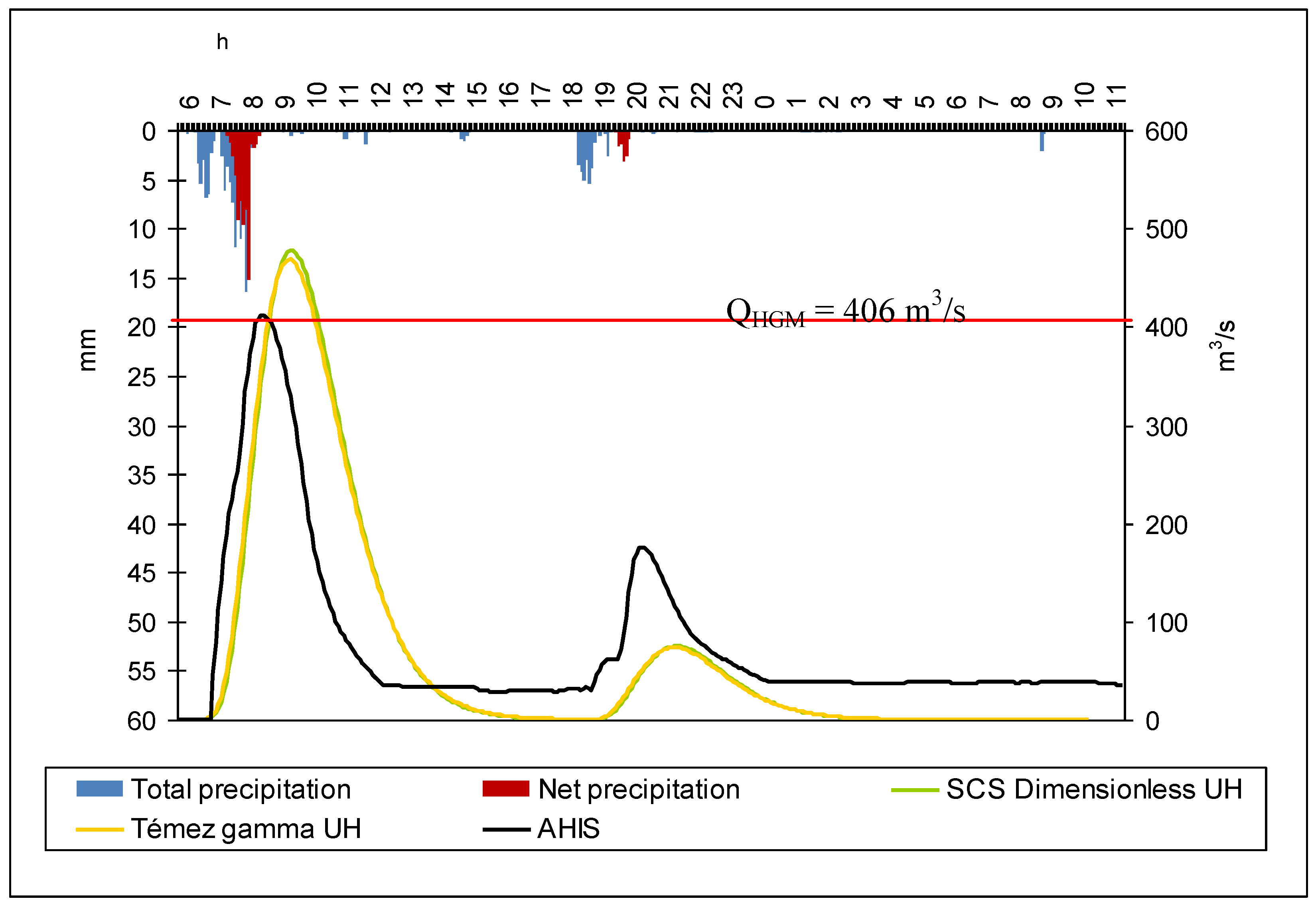
| Benipila | 30/09/1997 | 9.5 | 9.3 | 16.8 | 2.3 | 54.7 | 2.9 |
| 23/10/2000 | 477.0 | 468.1 | 272.7 | 405.9 | 162.8 | 430.7 | |
| 18/11/2003 | 282.8 | 277.6 | 208.4 | 57.5 | 141.1 | 1.2 | |
| 16/04/2004 | 68.8 | 67.7 | 99.5 | 3.1 | 98.7 | 5.5 | |
| 09/10/2008 | 184.9 | 183.1 | 88.7 | 9.6 | 93.8 | 0.9 | |
| Benipila+Dolores | 09/10/2008 | 294.1 | 282.5 | 164.1 | 9.6 | 93.8 | 0.9 |
| 28/09/2009 | 288.5 | 275.7 | 525.9 | 258.2 | 176.8 | 271.6 | |
| Nogalte | 29/09/1997 | 50.7 | 40.3 | 77.3 | 45.7 | 67.1 | 53.9 |
| 09/10/2008 | -- | -- | 18.8 | 24.1 | 39.2 | 28.3 | |
| 13/09/2009 | 1.4 | 1.0 | 15.0 | 29.9 | 36.7 | 37.6 | |
| Rambla | Date | Q | h (m) | W (m) | A (m2) | wP (m) | V (m/s) | S (m/m) | n |
|---|---|---|---|---|---|---|---|---|---|
| Benipila | 30/09/1997 | SCSD | 0.28 | 20.5 | 5.71 | 20.6 | 1.66 | 0.0025 | 0.04 |
| Tγ | 0.28 | 20.4 | 5.64 | 20.5 | 1.65 | 0.0025 | 0.04 | ||
| Benipila | 23/10/2000 | SCSD | 2.18 | 47.8 | 103.24 | 48.0 | 4.61 | 0.0025 | 0.04 |
| Tγ | 2.16 | 47.2 | 101.97 | 47.9 | 4.58 | 0.0025 | 0.04 | ||
| Benipila - Dolores | 28/09/2009 | SCSD | 1.59 | 46.0 | 73.10 | 46.5 | 3.93 | 0.0025 | 0.04 |
| Tγ | 1.55 | 45.8 | 70.90 | 46.3 | 3.88 | 0.0025 | 0.04 |
4.2. Application of the Proposed Methodology
| ID | W (fp) | hm (m) | A (m2) | h max (m) | S | n | Vm (m/s) | Q(fp) (m3/s) | QHGM* (m3/s) | QHGM*/Q (fp) |
|---|---|---|---|---|---|---|---|---|---|---|
| R4 | 138 | 0.77 | 106.3 | 1.78 | 0.0100 | 0.053 | 1.59 | 168.4 | 277.0 | 1.64 |
| Vi3 | 38 | 0.45 | 17.1 | 1.66 | 0.0191 | 0.052 | 1.56 | 26.6 | 42.4 | 1.59 |
| L3 | 59 | 0.49 | 28.9 | 0.62 | 0.0069 | 0.029 | 1.79 | 51.8 | 104.6 | 2.02 |
| B19 | 178 | 0.95 | 169.1 | 2.13 | 0.0025 | 0.040 | 1.21 | 204.3 | 405.9 | 1.99 |
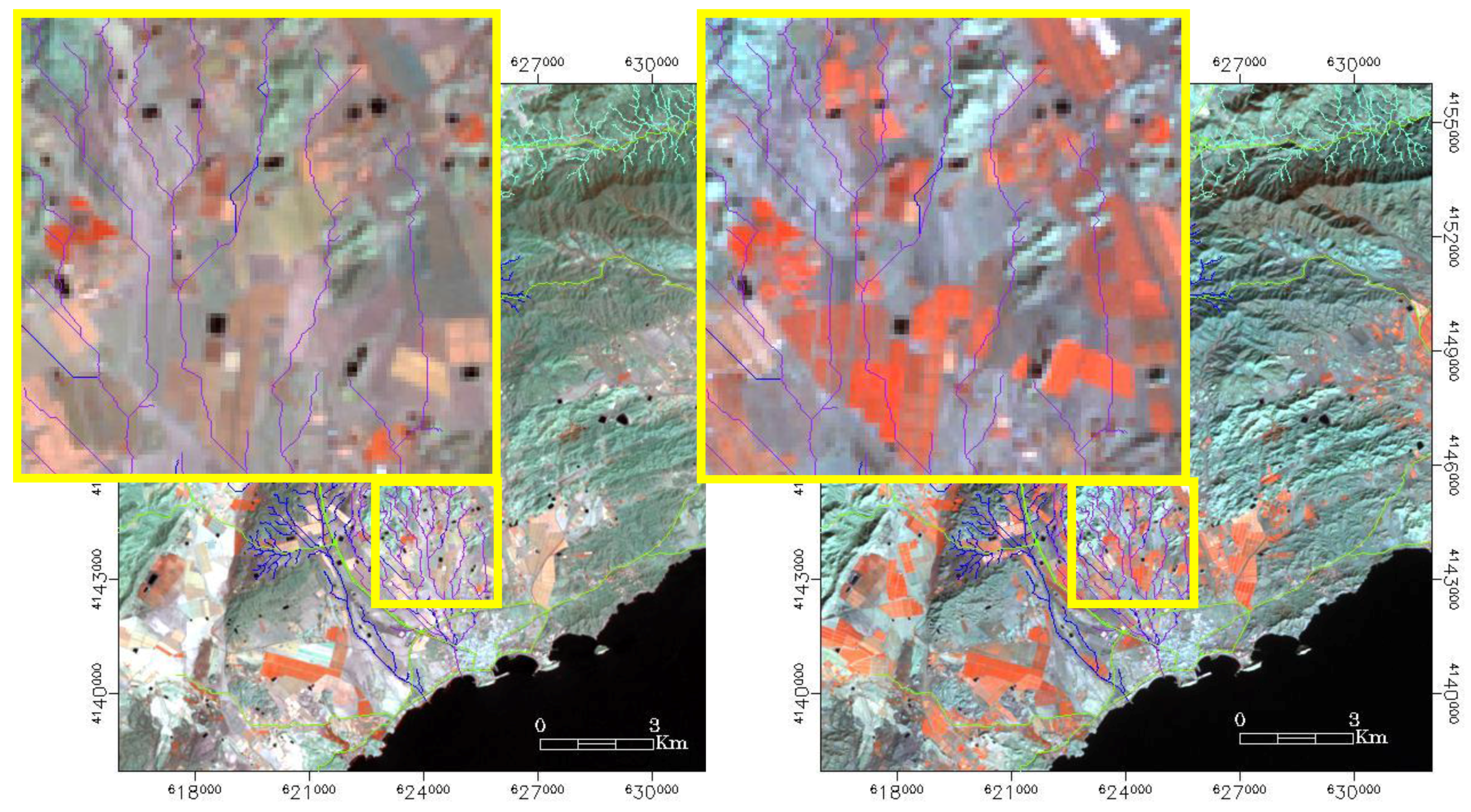
| Flooded sector | h (m) | W (m) | W/h | Rh (m) | Vi (m/s) | Re (1·104) | Fr | A (Ha) | Volume (m3) |
|---|---|---|---|---|---|---|---|---|---|
| A.1Cañarete | 0.30 | 133.1 | 447 | 0.30 | 1.5 | 33,51 | 0.86 | 21.96 | 65331 |
| A.2 Charco | 0.27 | 138.1 | 512 | 0.27 | 0.6 | 13,43 | 0.39 | 13.32 | 35964 |
| B. Moreras | 0.37 | 97.1 | 260 | 0.37 | 1.7 | 51,75 | 0.90 | 8.17 | 30556 |
| C. Ramonete | 0.74 | 162.3 | 220 | 0.74 | 1.2 | 69,12 | 0.45 | 7.36 | 54219 |
| D. Lorentes | 1.09 | 75.7 | 70 | 0.96 | 0.9 | 66,81 | 0.28 | 10.26 | 111720 |
| E.1. Honda (iz) | 0.95 | 192.5 | 203 | 0.81 | 1.9 | 118,29 | 0.68 | 11.16 | 105797 |
| E.2. Honda (der) | 1.34 | 246.5 | 183 | 1.20 | 0.9 | 159,48 | 0.18 | 4.5 | 60450 |
| F.1. Dolores (iz) | 0.06 | 98.4 | 1575 | 0.06 | 0.6 | 2,81 | 0.73 | 3.15 | 1969 |
| F.2. Dolores (der) | 0.54 | 80.1 | 147 | 0.54 | 2.6 | 104,86 | 1.12 | 5.4 | 29391 |
5. Conclusions
Acknowledgments
References and Notes
- Lacey, G. Stable channels in alluvium. ICE Minutes Proc. 1930, 229, 259–284. [Google Scholar] [CrossRef]
- Lacey, G. Uniform flow in alluvial rivers and canals. ICE Minutes Proc. 1934, 237, 421–453. [Google Scholar] [CrossRef]
- Tinkler, K.J. A hydraulic geometry of rockbed channels based on critical flow. In Proceedings of Geological Society of America Annual Meeitng, Toronto, ON, Canada, October 25–29, 1998.
- Dingman, S.L.; Sharma, K.P. Statistical development and validation of discharge equations for natural channels. J. Hydrol. 1997, 199, 13–35. [Google Scholar] [CrossRef]
- Leopold, L.B.; Wolman, M.G.; Miller, J.P. Fluvial Processes in Geomorphology; W.H. Freeman: New York, NY, USA, 1964. [Google Scholar]
- Koblinsky, C.J.; Clarke, R.T.; Brenner, A.C.; Frey, H. Measurement of river level with satellite altimetry. Water Resour. Res. 1993, 29, 1839–1848. [Google Scholar] [CrossRef]
- Smith, L.C.; Isacks, B.L.; Bloom, A.L.; Murray, A.B. Estimation of discharge from three braided rivers using synthetic aperture radar satellite imagery. Water Resour. Res. 1996, 32, 2021–2034. [Google Scholar] [CrossRef]
- Massonet, D. Satellite radar interferometry. Sci. Amer. Mag. 1997, February, 46–53. [Google Scholar] [CrossRef]
- Riggs, H.C. Flash flood potential from channel measurements. In Proceedings of Flash Floods Symposium, Paris, France, September 1974; International Association of Hydrological Sciences Publication No. 112. 1974; pp. 52–56. [Google Scholar]
- Osterkamp, W.R.; Hedman, E.R. Perennial-Streamflow Characteristics Related to Channel Geometry in Missouri River Basin; Professional Paper 1242; United States Geological Survey: Washington, DC, USA, 1982. [Google Scholar]
- Wharton, G. Flood estimation from channel size: Guidelines for using the channel-geometry method. Appl. Geogr. 1992, 12, 339–359. [Google Scholar] [CrossRef]
- Wharton, G. The channel-geometry method: Guidelines and applications. Earth Surf. Process. Landf. 1995, 20, 649–660. [Google Scholar] [CrossRef]
- Bustamante, J.; Díaz-Delgado, R.; Aragonés, D. Determinación de las características de masas de agua someras en las marismas de Doñana mediante teledetección. Revista de Teledetección 2005, 24, 107–111. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Hidrología aplicada; McGraw-Hill: Madrid, Spain, 1994. [Google Scholar]
- SCS (Soil Conservation Service). National Engineering Handbook; Section 4; U.S. Department of Agriculture: Washington, DC, USA, 1972.
- SCS (Soil Conservation Service). Hydrology. In National Engineering Handbook; Section 4; U.S. Department of Agriculture: Washington, DC, USA, 1985. [Google Scholar]
- Solís, L. Hidrología, 2005. Available online: http://212.81.159.185:8080/hidrologia/index.html (accessed on 10 September 2009).
- Nanía, L.S.; Gómez Valentín, M. Ingeniería Hidrológica, Segunda Edición ed; Grupo Editorial Universitario: Granada, Spain, 2006; p. 280. [Google Scholar]
- Témez, J.R. Cálculo hidrometeorológico de caudales máximos en pequeñas cuencas naturales; Dirección General de Carreteras, MOPU: Madrid, Spain, 1987. [Google Scholar]
- Ferrer, J. Recomendaciones para el cálculo hidrometeorológico de avenidas; CEDEX M-37; CEDEX: Madrid, Spain, 1993. [Google Scholar]
- Singh, S.K. Transmuting synthetic unit hydrograph into gamma distribution. J. Hydrol. Eng. 2000, 5, 380–385. [Google Scholar] [CrossRef]
- Témez, J.R. Extended and Improved Rational Method: Version of the Highways Administration of Spain. In Proceedings of XXIV Congress of IAHR, Madrid, Spain, September 1991; Volume A, pp. 33–40.
- MOPU. Norma 5,1-I.C. Instrucción de carreteras. Dirección General de Carreteras, MOPU: Madrid, Spain, 1990. [Google Scholar]
- Benito, G.; Grodek, T.; Enzel, Y. The geomorphic and hydrologic impacts of the catastrophic failure of flood-control-dams during the 1996-Biescas flood (Central Pyrenees, Spain). Zeitschrift für Geomorphologie 1998, 42, 417–437. [Google Scholar]
- Rico, M.; Benito, G. Estimación de caudales de crecida en pequeñas cuencas de montaña: Revisión metodológica y aplicación a la cuenca de Montardit (Pirineos Centrales, España). Cuaternario & Geomorfología 2002, 16, 127–138. [Google Scholar]
- Benito, G.; Thorndycraft, V.R. Palaeoflood hydrology and its role in applied hydrological sciences. J. Hydrol. 2005, 313, 3–15. [Google Scholar] [CrossRef]
- Jarrett, R.D. Hydraulics of high-gradient streams. J. Hydraul. Div. Am. Soc. Civ. Eng. 1984, 110, 1519–1539. [Google Scholar] [CrossRef]
- Jarrett, R.D. Determination of Roughness Coefficient for Streams in Colorado; USGS Water Resources Investigations Report 85-4004; 1985.
- Jarrett, R.D. Errors in slope-area computations of peak discharges in mountain streams. J. Hydrol. 1987, 96, 53–67. [Google Scholar] [CrossRef]
- Jarrett, R.D. Hydrologic and hydraulic research in mountain rivers. Water Resour. Bull. 1990, 26, 419–429. [Google Scholar] [CrossRef]
- Manning’s n Information Table. In HEC-RAS; Version 3.1.1.; U.S. Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2003.
- Conesa-García, C.; García-Lorenzo, R.; López Bermúdez, F. Bed stability variations after check dam construction in torrential channels (South-East Spain). Earth Process. Landf. 2007, 32, 2165–2184. [Google Scholar] [CrossRef]
- Conesa-García, C. Les ‘ramblas’ du Sud-est Espagnol: systèmes hydromorphologiques en milieu méditerranéen sec. Zeitschrift für Geomorphologie 2005, 49, 205–224. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Conesa-Garcia, C.; Caselles-Miralles, V.; Sanchez Tomas, J.M.; Garcia-Lorenzo, R. Hydraulic Geometry, GIS and Remote Sensing, Techniques against Rainfall-Runoff Models for Estimating Flood Magnitude in Ephemeral Fluvial Systems. Remote Sens. 2010, 2, 2607-2628. https://doi.org/10.3390/rs2112607
Conesa-Garcia C, Caselles-Miralles V, Sanchez Tomas JM, Garcia-Lorenzo R. Hydraulic Geometry, GIS and Remote Sensing, Techniques against Rainfall-Runoff Models for Estimating Flood Magnitude in Ephemeral Fluvial Systems. Remote Sensing. 2010; 2(11):2607-2628. https://doi.org/10.3390/rs2112607
Chicago/Turabian StyleConesa-Garcia, Carmelo, Vicente Caselles-Miralles, Juan M. Sanchez Tomas, and Rafael Garcia-Lorenzo. 2010. "Hydraulic Geometry, GIS and Remote Sensing, Techniques against Rainfall-Runoff Models for Estimating Flood Magnitude in Ephemeral Fluvial Systems" Remote Sensing 2, no. 11: 2607-2628. https://doi.org/10.3390/rs2112607
APA StyleConesa-Garcia, C., Caselles-Miralles, V., Sanchez Tomas, J. M., & Garcia-Lorenzo, R. (2010). Hydraulic Geometry, GIS and Remote Sensing, Techniques against Rainfall-Runoff Models for Estimating Flood Magnitude in Ephemeral Fluvial Systems. Remote Sensing, 2(11), 2607-2628. https://doi.org/10.3390/rs2112607




