Analysis of a Least-Squares Soil Moisture Retrieval Algorithm from L-band Passive Observations
Abstract
:1. Introduction
- The use of no a priori information in the vs. the use of a priori information about all the auxiliary parameters excluding on the cost function.
- The effect of the presence of a vegetation canopy.
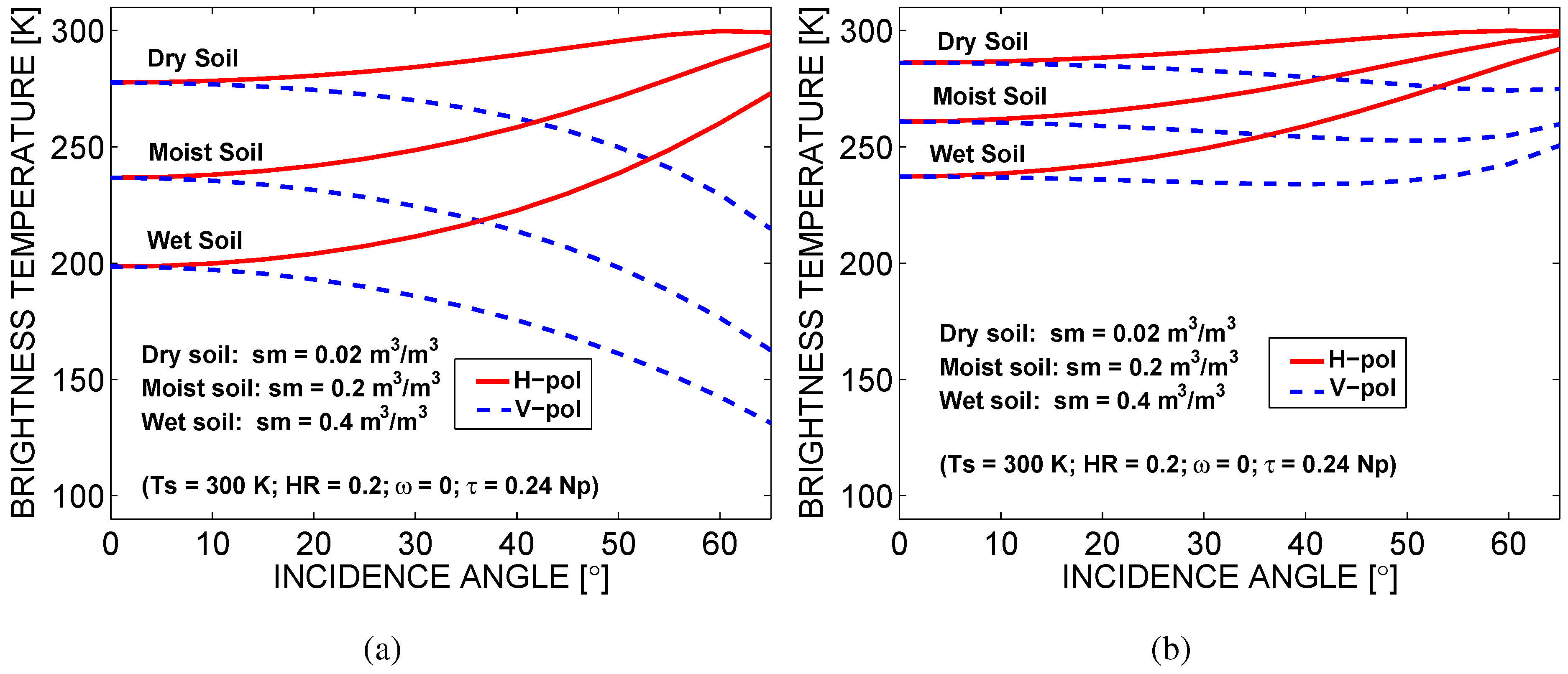
- The effect of the soil moisture content (dry/moist/wet).
- The retrieval formulation using the vertical and horizontal polarizations separately or using the first Stokes parameter.
2. Methodology
2.1. Scenario Definition
| [m/m] | [K] | ω | τ [Np] | |||
| () | () | () | () | () | ||
| Bare | dry soil | 0.02 | 0.2 | 300 | 0 | 0 |
| moist soil | 0.2 | 0.2 | 300 | 0 | 0 | |
| wet soil | 0.4 | 0.2 | 300 | 0 | 0 | |
| Vegetation-covered | dry soil | 0.02 | 0.2 | 300 | 0 | 0.24 |
| moist soil | 0.2 | 0.2 | 300 | 0 | 0.24 | |
| wet soil | 0.4 | 0.2 | 300 | 0 | 0.24 |
2.2. Forward Model
2.3. Retrieval Algorithm
| [m/m] | [K] | [Np] | |||
| 100 | 100 | 100 | 100 | 100 | |
| 100 | 0.05 | 2 | 0.1 | 0.1 |
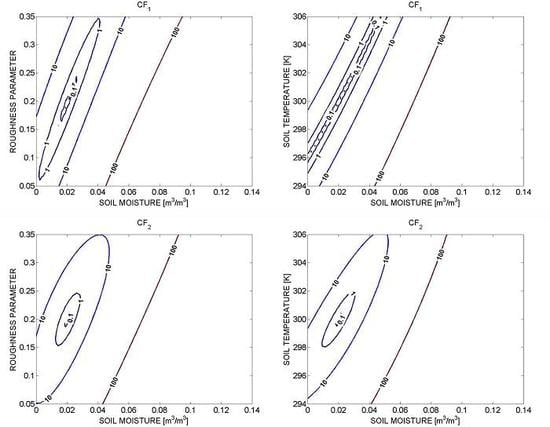
3. Sensitivity Analysis
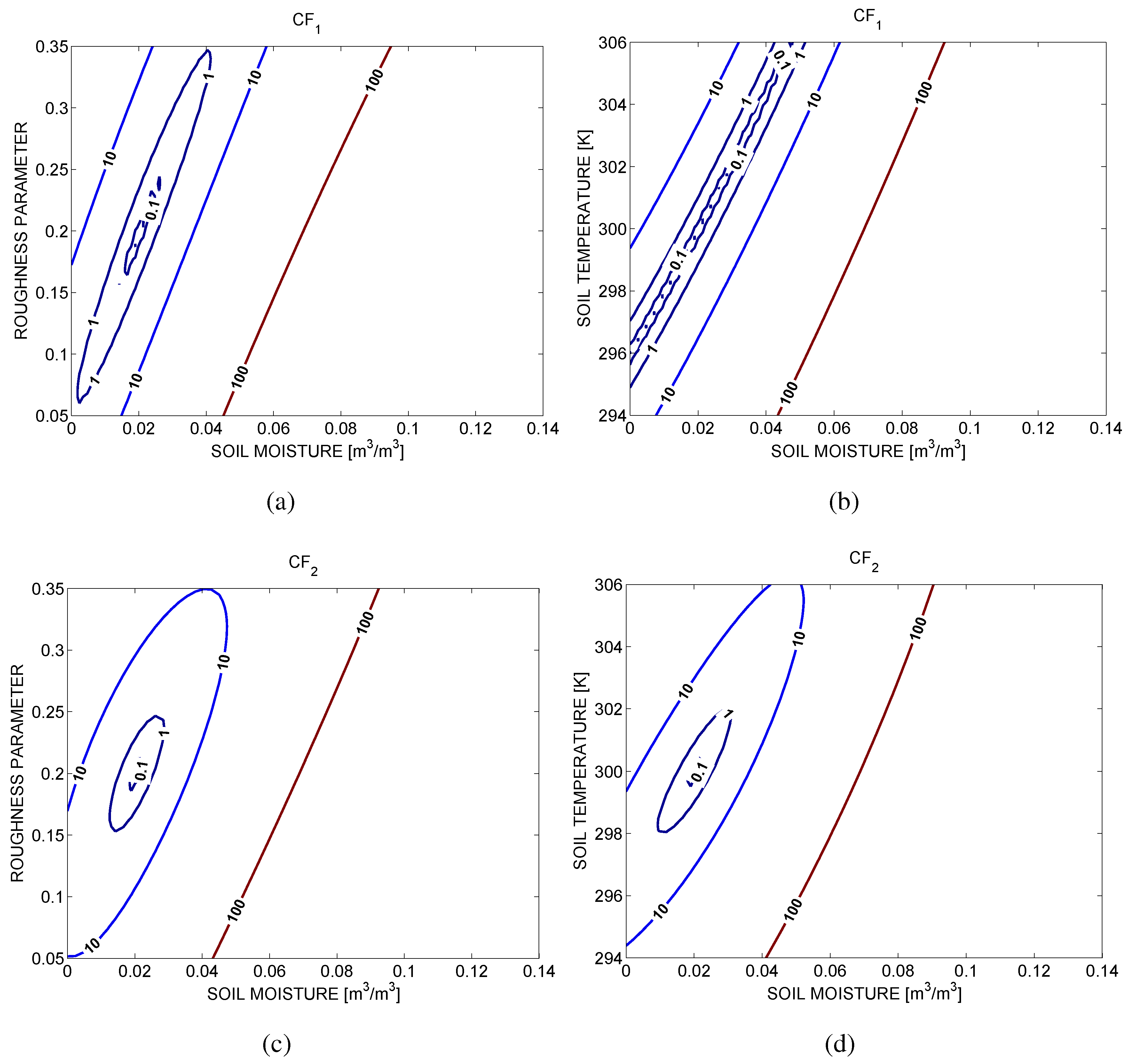
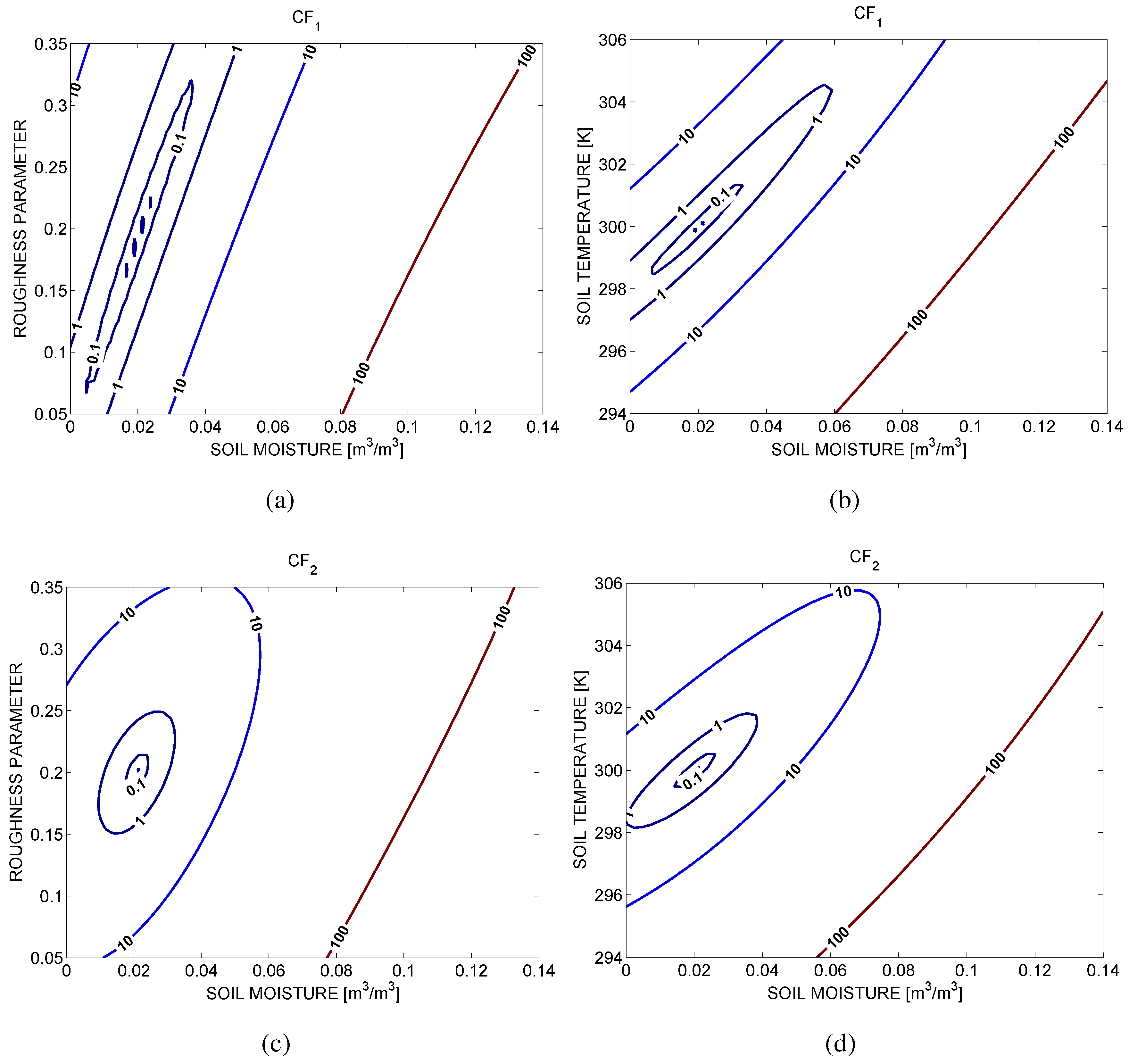
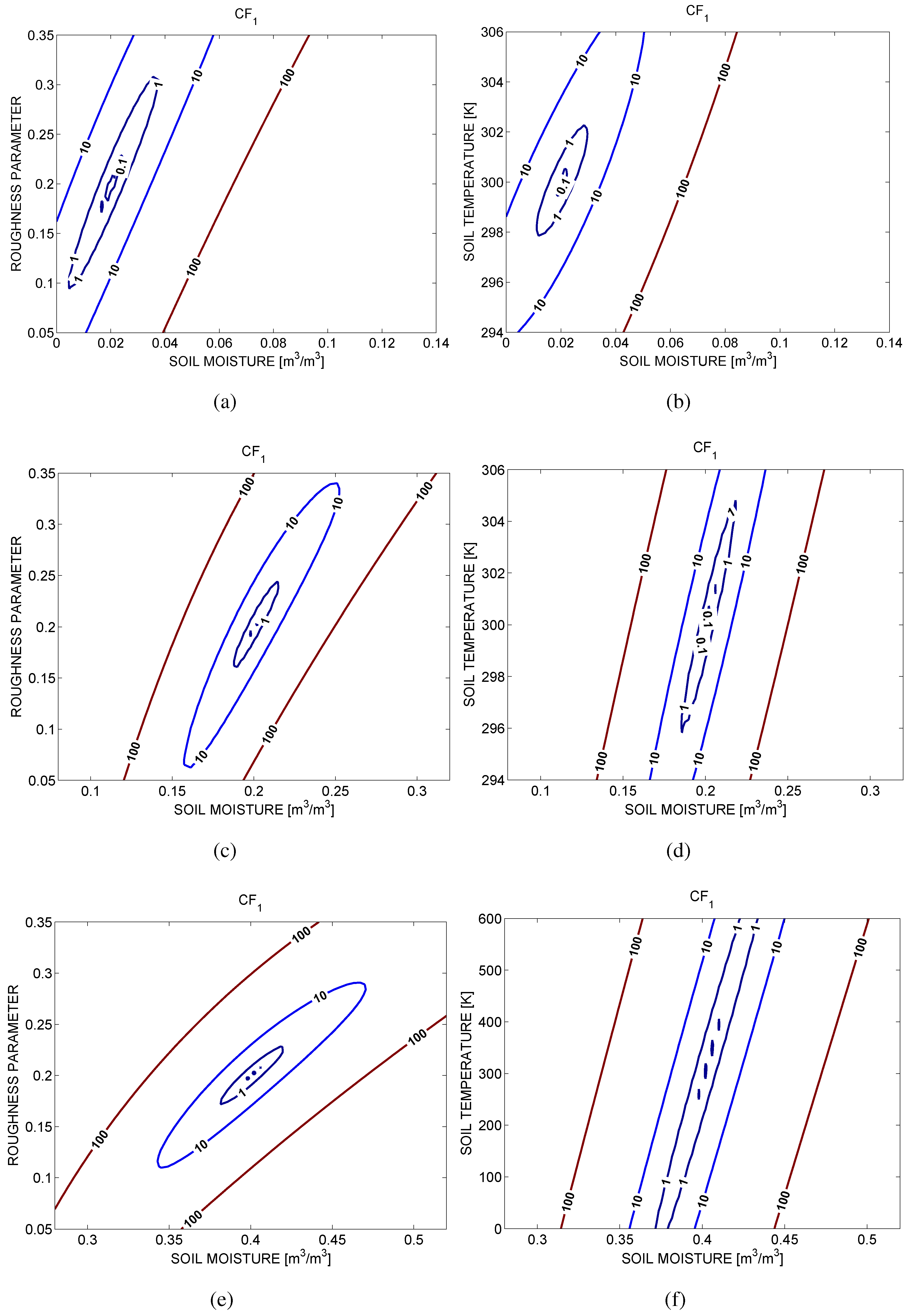
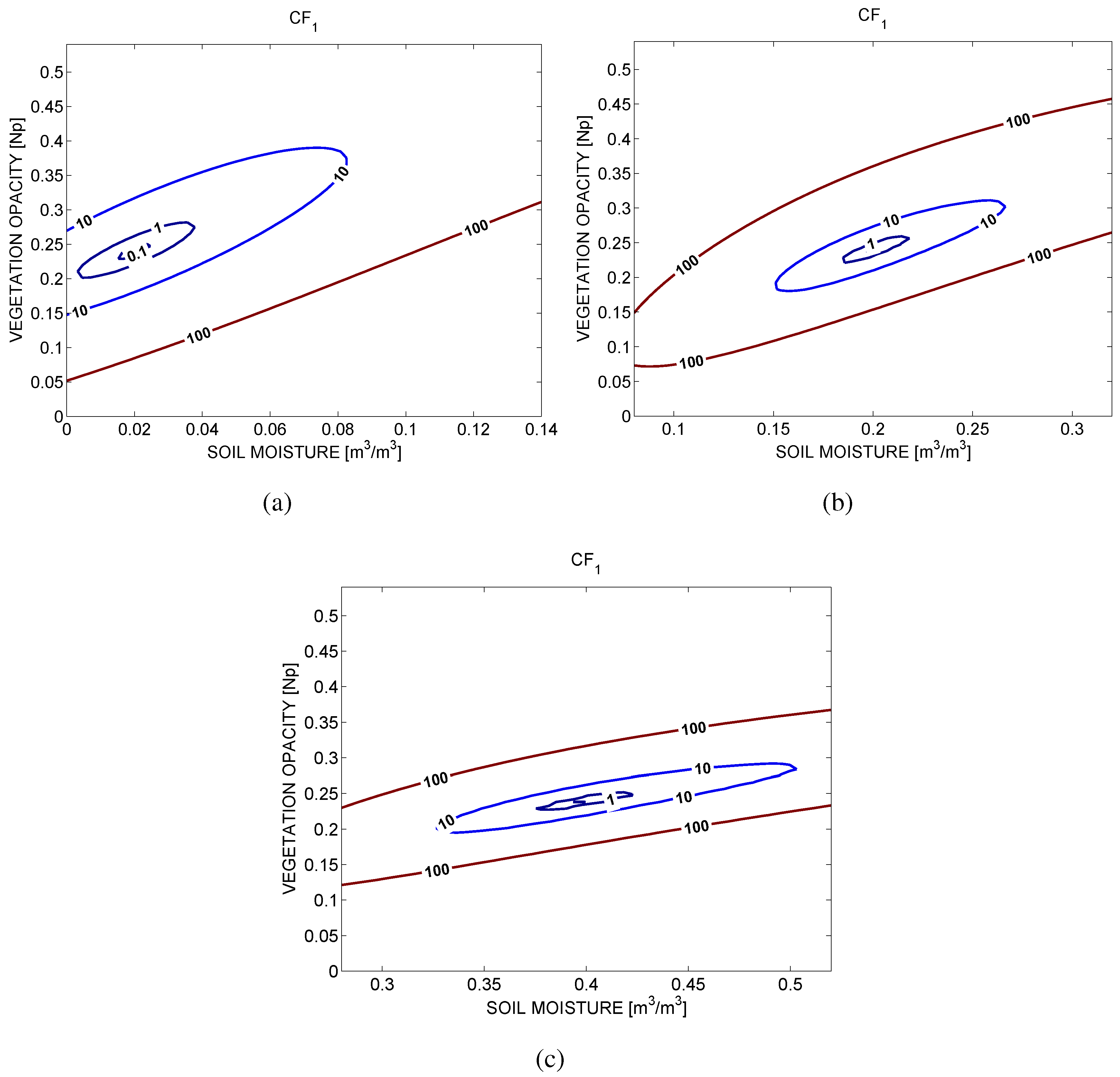
4. Analysis with Simulated SMOS Data
4.1. Simulation Strategy
- –
- The geophysical models and the ancillary data used in the L2 Processor Simulator are the same as in SEPS, so that the effect of the model used is not affecting the results.
- –
- The performance of the configuration is not dependent on , since the absolute accuracy of the radiometric measurements is available on the SEPS output and is used in L2 Processor Simulator.
- –
- To reduce the computational time, the search limits of the retrieved variables in the have been reduced within reasonable bounds, namely m/m, K, , Np, and [23].
- –
- The reference values of the parameters on the () are randomly determined from a normal distribution with the nominal standard deviations on Table 1, added to the original values.
- –
- Homogeneous pixels have been assumed in the simulations to evidence the contribution of each parameter in the results and facilitate the analysis. However, further studies will be required to assess the limitations imposed by heterogeneity of vegetation cover and soil characteristics within a satellite footprint.
4.2. Simulation Results
| Scenario | Retrieved error | () | () | ||
| Earth | Stokes | Earth | Stokes | ||
| Bare Dry Soil | Mean | ||||
| Std. dev. | |||||
| RMS | |||||
| Bare Moist Soil | Mean | ||||
| Std. dev. | |||||
| RMS | |||||
| Bare Wet Soil | Mean | ||||
| Std. dev. | |||||
| RMS | |||||
| Scenario | Retrieved error | ||||
| Earth | Stokes | Earth | Stokes | ||
| Dry Soil + Canopy | Mean | 0.169 | 0.170 | 0.060 | 0.049 |
| Std. dev. | 0.162 | 0.169 | 0.116 | 0.053 | |
| RMS | 0.235 | 0.240 | 0.131 | 0.072 | |
| Moist Soil + Canopy | Mean | 0.076 | 0.095 | 0.003 | 0.048 |
| Std. dev. | 0.143 | 0.121 | 0.120 | 0.076 | |
| RMS | 0.162 | 0.153 | 0.120 | 0.090 | |
| Wet Soil + Canopy | Mean | -0.062 | -0.040 | -0.061 | -0.021 |
| Std. dev. | 0.119 | 0.102 | 0.093 | 0.050 | |
| RMS | 0.134 | 0.109 | 0.111 | 0.054 | |
| Scenario | Retrieved τ error | ||||
| Earth | Stokes | Earth | Stokes | ||
| Dry Soil + Canopy | Mean | 0.439 | 0.369 | 0.110 | 0.036 |
| Std. dev. | 0.888 | 0.606 | 0.307 | 0.085 | |
| RMS | 0.991 | 0.709 | 0.326 | 0.092 | |
| Moist Soil + Canopy | Mean | 0.224 | 0.100 | 0.049 | 0.025 |
| Std. dev. | 0.732 | 0.342 | 0.267 | 0.078 | |
| RMS | 0.765 | 0.356 | 0.272 | 0.082 | |
| Wet Soil + Canopy | Mean | 0.187 | 0.019 | 0.053 | -0.029 |
| Std. dev. | 0.714 | 0.208 | 0.274 | 0.056 | |
| RMS | 0.738 | 0.209 | 0.279 | 0.063 | |
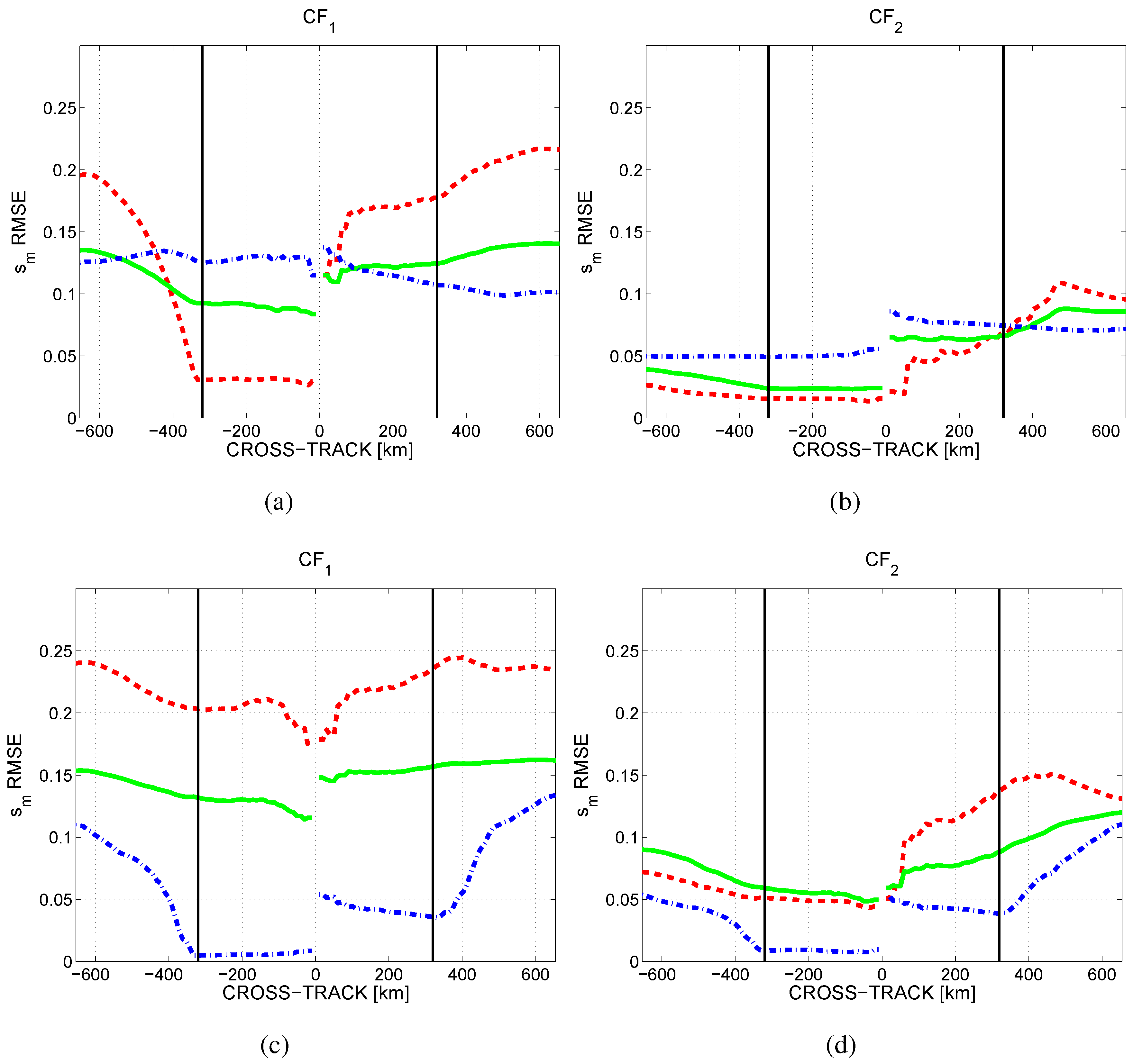
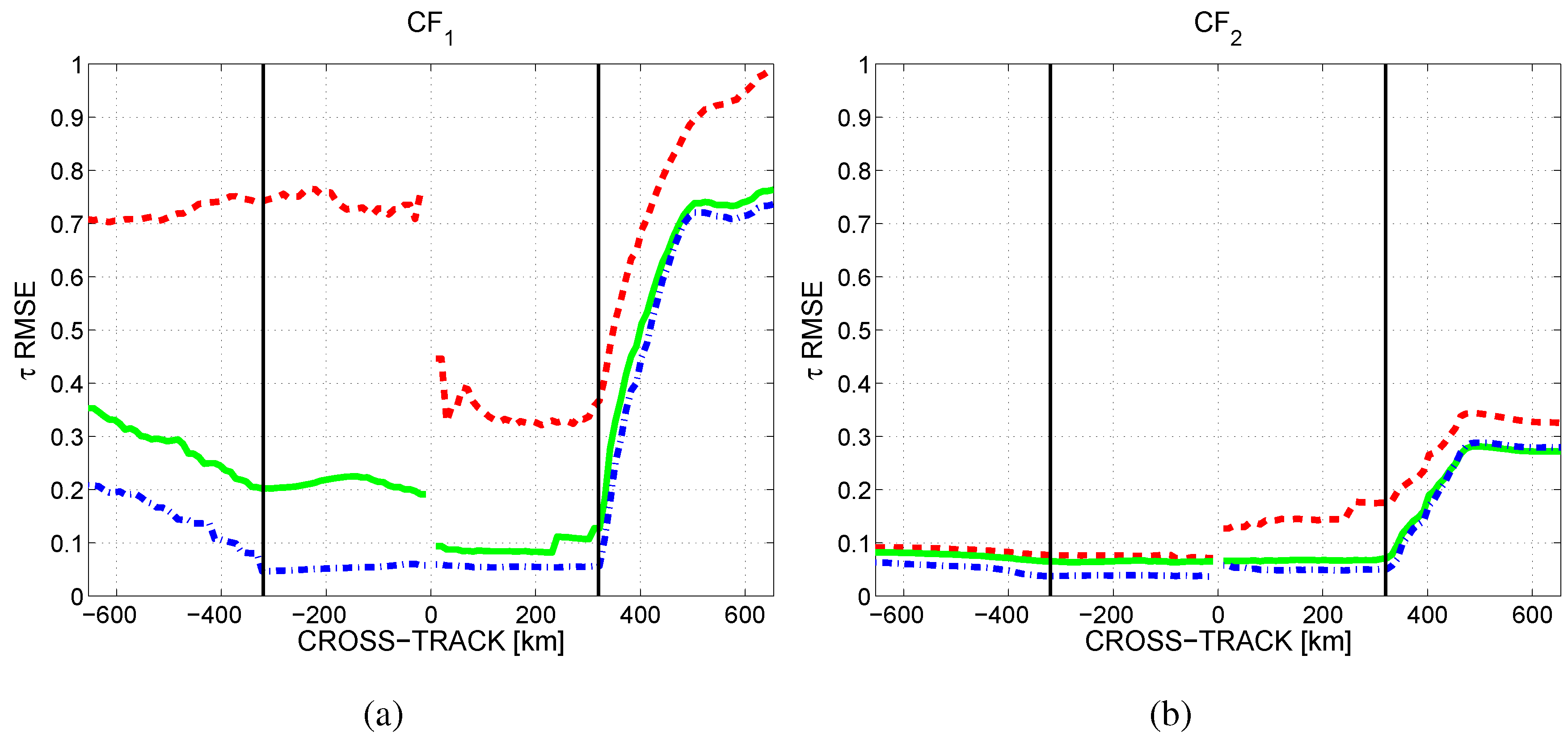
5. Conclusions and Discussion
- –
- The use of adequate ancillary information on the cost function significantly improves the accuracy of retrievals, and is needed to satisfy the SMOS science requirement of 0.04 m/m. Using constraints (Table 2), RMSE retrievals of ≈ 0.07 to 0.09 m/m are obtained using , and of ≈ 0.03 to 0.05 m/m using over bare soil scenarios. As expected, there is a strong decrease of the brightness temperatures sensitivity to in the presence of vegetation, and RMSE retrievals of ≈ 0.11 to 0.13 m/m are obtained using , and of ≈ 0.05 to 0.09 m/m using (with ).
- –
- The use of adequate constraints on the cost function () highly improves the accuracy of τ estimations and is therefore critical to derive VWC maps from SMOS at the required accuracy of 0.2 kg/m; Preliminary calculations indicate that VWC maps with an accuracy of ≈ 1.9 to 2.2 kg/m could be estimated from τ retrievals using , and of ≈ 0.4 to 0.6 kg/m using .
- –
- More accurate soil moisture estimates have been obtained over wet soils than over dry soils (bare and with low vegetation), except for the case of retrievals using and . Regarding τ retrievals, more accurate estimates have been obtained over wet soils than over dry soils in all the configurations.
- –
- Better retrievals have been obtained when using than when using . Also, the formulation in terms of leads to better τ retrievals in all the configurations. These results suggest that, although is the formulation generally adopted in most studies, the use of should not be disregarded. In addition, is more robust in the presence of geometric rotations and Faraday rotation (at any spatial scale) than . These effects have been perfectly corrected on the simulations, but are critical from an operational point of view.
- –
- Due to SMOS observation geometry, better accuracies could be obtained if only the Narrow Swath (640-km, the central part of the FOV) is used. The use of adequate constraints () and the retrieval formulation in terms of provide the most accurate and τ retrievals over all scenarios in the case of considering either the nominal or the Narrow Swath.
Acknowledgements
References
- Entekhabi, D.; Asrar, G.; Betts, A.; Beven, K.; Bras, R. An agenda for land surface hydrology research and a call for the Second International Hydrological Decade. Bull. Amer. Meteor. Soc. 1999, 80, 2043–2058. [Google Scholar] [CrossRef]
- Krajewski, W.; Anderson, M.; Eichinger, W.; Entekhabi, D.; Hornbuckle, B.; Houser, P.; Katul, G.; Kustas, W.; Norman, J.; Peters-Lidard, C.; Wood, E. A remote sensing observatory for hydrologic sciences: a genesis for scaling to continental hydrology. J. Water Resour. Res. 2006. [Google Scholar] [CrossRef]
- Wagner, W.; Blsch, G.; Pampaloni, P.; Calvet, J.; Bizarri, B.; Wigneron, J.P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Nord. Hydrol. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Njoku, E.; Entekhabi, D. Passive microwave remote sensing of soil moisture. J. Hydrol. 1996, 184, 101–129. [Google Scholar] [CrossRef]
- Schmugge, T.; Kustas, W.; Ritchie, J.; Jackson, T.; Rango, A. Remote sensing in hydrology. Adv. Water Resour. 2002, 25, 1367–1385. [Google Scholar] [CrossRef]
- Ulaby, F.; Moore, R.; Fung, A. Microwave Remote Sensing Active and Passive, Vol. 1 and 2; Artech House: Norwood, MA, USA, 1981. [Google Scholar]
- Shi, J.; Wang, J.; Hsu, A.; ONeill, P.; Engman, E.T. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar]
- Jackson, T.; Schmugge, T.; Engman, E. Remote sensing applications to hydrology: soil moisture. Hydrol. Sci. J.-J. Des. Sci. Hydrol. 1996, 41, 517–530. [Google Scholar] [CrossRef]
- Kerr, Y.; Waldteufel, P.; Wigneron, J.P.; Font, J.; Berger, M. Soil moisture retrieval from space: the soil moisture and ocean salinity (SMOS) mission. IEEE Trans. Geosci. and Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- National Research Council. Earth Science and Applications from Space: National Imperatives for the next Decade and Beyond; Technical report, Space Studies Board, National Academies Press: Washington, DC, WA, USA, 2007. [Google Scholar]
- Martín-Neira, M.; Ribó, S.; Martín-Polegre, A.J. Polarimetric mode of MIRAS. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1755–1768. [Google Scholar] [CrossRef]
- Mission Objectives and Scientific Requirements of the SMOS Mission. MRD, version 5; Technical report, European Space Agency: Paris, France, 2003.
- Pellarin, T.; Wigneron, J.P.; Calvet, J.; Waldteufel, P. Global soil moisture retrieval on a synthetic L-band brightness temperature data set. J. Geophys. Res. 2003, 108, 4364. [Google Scholar] [CrossRef]
- Pardé, M.; Wigneron, J.P.; Waldteufel, P.; Kerr, Y. N-parameter retrievals from L-band microwave observatinos acquired over a variety of crop fields. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1168–1178. [Google Scholar] [CrossRef]
- Camps, A.; Vall-llossera, M.; Duffo, N.; Torres, F.; Corbella, I. Performance of sea surface salinity and soil moisture retrieval algorithms with different auxiliary datasets in 2-D L-band aperture synthesis interferometric radiometers. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1189–1200. [Google Scholar] [CrossRef]
- Wang, J.R.; Schmugge, T. An empirical model for the complex dielectric permittivity of soils as a function of water content. IEEE Trans. Geosci. Remote Sens. 1980, GRS-18, 288–295. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M.A. Microwave dielectric behavior of wet soil-Part II: Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- van de Griend, A.; Wigneron, J.P. The b-factor as a function of frequency and canopy type at H-polarization. IEEE Trans. Geosci. Remote Sens. 2004, 42, 786–794. [Google Scholar] [CrossRef]
- Camps, A.; Corbella, I.; Vall.llossera, M.; Duffo, N.; Marcos, F.; Martinez-Fadrique, F.; Greiner, M. The SMOS end-to-end performance simulator: description and scientific applications. Proc. IEEE IGARSS 2003, 1, 13–15. [Google Scholar]
- Talone, M.; Camps, A.; Mourre, B.; Sabia, R.; Vall-llossera, M.; Gourrion, J.; Gabarró, C.; Font, J. Simulated SMOS levels 2 and 3 products: the effect of introducing ARGO data in the processing chain and its impact on the error induced by the vicinity of the coast. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3041–3050. [Google Scholar] [CrossRef]
- Sabia, R.; Camps, A.; Talone, M.; Vall-llossera, M.; Font, J. Determination of sea surface salinity error budget in the soil moisture and ocean salinity mission. IEEE Trans. Geosci. Remote Sens. 2010, in press. [Google Scholar] [CrossRef]
- Monerris, A. Experimental estimation of soil emissivity and its application to soil moisture retrieval in the SMOS mission. PhD thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2009. [Google Scholar]
- Algorithm Theoretical Bases Document; ATBD, Issue 3.a; Technical report; European Space Agency: Paris, France, 2007; Available online: http://www.cesbio.ups-tlse.fr/ (accessed on 10 December 2009).
- Masson, V.; Champeaux, J.L.; Chauvin, F.; Meriguet, C. A global database of land surface parameters at 1-km resolution in meteorological and climate models. J. Climate 2003, 16, 1261–1282. [Google Scholar] [CrossRef]
- Choudhury, B.; Schmugge, T.; Chang, A.; Newton, R. Effect of surface roughness on the microwave emission from soils. J. Geophys. Res. 1979, 84, 5699–5706. [Google Scholar] [CrossRef]
- Mo, T.; Choudhury, B.; Schmugge, T.; Jackson, T. A model for microwave emission from vegetation-covered fields. J. Hydrol. 1982, 184, 101–129. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Wilson, A.E. Microwave attenuation properties of vegetation canopies. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 746–753. [Google Scholar] [CrossRef]
- Wang, J.; Choudhury, B. Remote sensing of soil moisture content over bare field at 1.4 GHz frequency. J. Geophys. Res. 1981, 86, 5277–5282. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Laguerre, L.; Kerr, Y. A simple parameterization of the L-band microwave wmission from rough agricultural soils. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1696–1707. [Google Scholar] [CrossRef]
- Jackson, T.J.; Vine, D.M.L.; Hsu, A.Y.; Oldak, A.; Starks, P.J.; Swift, C.T.; Isham, J.D.; Haken, M. Soil moisture mapping at regional scales using microwave radiometry: the Southern Great Plains hydrology experiment. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2136–2151. [Google Scholar] [CrossRef]
- Wigneron, J.; Kerr, Y.; Waldteufel, P.; Saleh, K.; Escorihuela, M.-J.; Richaume, P.; Ferrazzoli, P.; Grant, J.P.; Hornbuckle, B.; de Rosnay, P.; Calvet, J.-C.; Pellarin, T.; Gurney, R.; Matzler, C. L-band Microwave Emission of the Biosphere (L-MEB) Model: description and calibration against experimental data sets over crop fields. Remote Sens. Environ. 2007, 107, 639–655. [Google Scholar] [CrossRef]
- Panciera, R.; Walker, J.P.; Kalma, J.D.; Kim, E.J.; Saleh, K.; Wigneron, J.P. Evaluation of the SMOS L-MEB passive microwave soil moisture retrieval algorithm. Remote Sens. Environ. 2009, 113, 435–444. [Google Scholar] [CrossRef]
- Saleh, K.; Kerr, Y.; Richaume, P.; Escorihuela, M.J.; Panciera, R.; Delwart, S.; Boulet, G.; Maisongrande, P.; Walker, J.P.; Wursteisen, P.; Wigneron, J.P. Soil moisture retrievals at L-band using a two-step inversion approach (COSMOS/NAFE’05 Experiment). Remote Sens. Environ. 2009, 113, 1304–1312. [Google Scholar] [CrossRef]
- Schneeberger, K.; Schwank, M.; Stamm, C.; de Rosnay, P.; Mätzler, C.; Flühler, H. Topsoil structure influencing soil water retrieval by microwave radiometry. Vadose Zone J. 2004, 3, 1169–1179. [Google Scholar] [CrossRef]
- Escorihuela, M.; Kerr, Y.; de Rosnay, P.; Wigneron, J.; Calvet, J.; Lemaitre, F. A simple model of the bare soil microwave emission at L-band. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1978–1987. [Google Scholar] [CrossRef]
- Kirdiashev, K.P.; Chukhantsev, A.A.; Shutko, A.M. Microwave radiation of the earth’s surface in presence of vegetation cover. Radio Eng. Elect. 1979, 24, 256–264. [Google Scholar]
- Wigneron, J.P.; Chanzy, A.; Calvet, J.; Bruguier, N. A simple algorithm to retrieve soil moisture and vegetation biomass using passive microwave measurements over crop fields. Remote Sens. Environ. 1995, 51, 331–341. [Google Scholar] [CrossRef]
- Hornbuckle, B.K.; England, A.W.; de Roo, R.D.; Fischman, M.A.; Boprie, D.L. Vegetation canopy anisotropy at 1.4 GHz. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2211–2222. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Walker, J.P. A methodology for surface soil moisture and vegetation optical depth retrieval using the microwave polarization difference index. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1643–1654. [Google Scholar] [CrossRef]
- Hornbuckle, B.K.; England, A.W. Diurnal variation of vertical temperature gradients within a field of maize: implications for stellite microwave radiometry. IEEE Geosc. Remote Sens. Lett. 2005, 2, 74–77. [Google Scholar] [CrossRef]
- Jackson, T.; Schmugge, T. Vegetation effects on the microwave emission from soils. Remote Sens. Environ. 1991, 36, 203–212. [Google Scholar] [CrossRef]
- Marquardt, D. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Randa, J.; Lahtinen, J.; Camps, A.; Gasiewski, A.; Hallikainen, M.; Vine, D.L.; Martín-Neira, M.; Piepmeier, J.; Rosenkranz, P.; Ruf, C.; Shiue, J.; Skou, N. Recommended Terminology for Microwave Radiometry; Technical report; National Institution of Standards and Tecnology: Gaithersburg, MA, USA, 2008. [Google Scholar]
- Piles, M.; Camps, A.; Vall-llossera, M.; Monerris, A.; Talone, M.; Sabater, J.M. Performance of Soil Moisture Retrievals using Multi-angular L-band Brightness Temperatures. Water Resour. Res. 2010, in press. [Google Scholar] [CrossRef]
- Portabella, M.; Stoffelen, A. A probabilistic approach for seawinds data assimilation. Q. J. R. Meteorol. Soc. 2004, 130, 127–152. [Google Scholar] [CrossRef]
- Gabarró, C.; Portabella, M.; Talone, M.; Font, J. Toward an Optimal SMOS Ocean Salinity Inversion Algorithm. IEEE Geosci. Remote. Sens. 2009, 6, 509–513. [Google Scholar] [CrossRef]
- Davenport, I.J.; Fernandez-Galvez, J.; Gurney, R.J. A sensitivity analysis of soil moisture retrieval from the tau-omega microwave emission model. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1304–1316. [Google Scholar] [CrossRef]
- SEPS Architectural Detailed Design Document; ADDD V5.0; Technical report; European Space Agency: Paris, France, 2006; Available online: http://cassiopea.estec.esa.int/SEPS/Documents/ (accessed on 10 December 2009).
- de Jeu, R.; Wagner, W.; Holmes, T.; Dolman, H.; van de Giesen, N.; Friesen, J. Global soil moisture patterns observed by space borne microwave radiometers and scatterometers. Surv. Geophys. 2008, 29, 399–420. [Google Scholar] [CrossRef]
- Barre, H.M.J.; Duesmann, B.; Kerr, Y. SMOS: the mission and the system. IEEE Trans. Geosci. Remote Sens. 2008, 46, 587–593. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Piles, M.; Vall-llossera, M.; Camps, A.; Talone, M.; Monerris, A. Analysis of a Least-Squares Soil Moisture Retrieval Algorithm from L-band Passive Observations. Remote Sens. 2010, 2, 352-374. https://doi.org/10.3390/rs2010352
Piles M, Vall-llossera M, Camps A, Talone M, Monerris A. Analysis of a Least-Squares Soil Moisture Retrieval Algorithm from L-band Passive Observations. Remote Sensing. 2010; 2(1):352-374. https://doi.org/10.3390/rs2010352
Chicago/Turabian StylePiles, María, Mercè Vall-llossera, Adriano Camps, Marco Talone, and Alessandra Monerris. 2010. "Analysis of a Least-Squares Soil Moisture Retrieval Algorithm from L-band Passive Observations" Remote Sensing 2, no. 1: 352-374. https://doi.org/10.3390/rs2010352
APA StylePiles, M., Vall-llossera, M., Camps, A., Talone, M., & Monerris, A. (2010). Analysis of a Least-Squares Soil Moisture Retrieval Algorithm from L-band Passive Observations. Remote Sensing, 2(1), 352-374. https://doi.org/10.3390/rs2010352