Next Article in Journal
Monitoring Maize Phenology Using Multi-Source Data by Integrating Convolutional Neural Networks and Transformers
Previous Article in Journal
Boosting All-in-One UAV Image Restoration via Degradation-Aware Frequency Prompt State Space Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 18
Issue 2
10.3390/rs18020355
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Parsing the Relative Contributions of Leaf and Canopy Traits in Airborne Spectrometer Measurements

by
Franklin B. Sullivan
1,*,
Jack H. Hastings
1,2,
Scott V. Ollinger
1,2,
Andrew Ouimette
1,3,
Andrew D. Richardson
4,5 and
Michael Palace
1,6
1
Earth Systems Research Center, Institute of Earth, Oceans, and Space, University of New Hampshire, Durham, NH 03824, USA
2
Department of Natural Resources, University of New Hampshire, Durham, NH 03824, USA
3
United States Forest Service, Northern Research Station, Durham, NH 03824, USA
4
Center for Ecosystem Science and Society, Northern Arizona University, Flagstaff, AZ 86011, USA
5
School of Informatics, Computing, and Cyber Systems, Northern Arizona University, Flagstaff, AZ 86011, USA
6
Department of Earth Sciences, University of New Hampshire, Durham, NH 03824, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2026, 18(2), 355; https://doi.org/10.3390/rs18020355
Submission received: 29 October 2025 / Revised: 15 January 2026 / Accepted: 16 January 2026 / Published: 21 January 2026
Browse Figures
Versions Notes

Highlights

What are the main findings?
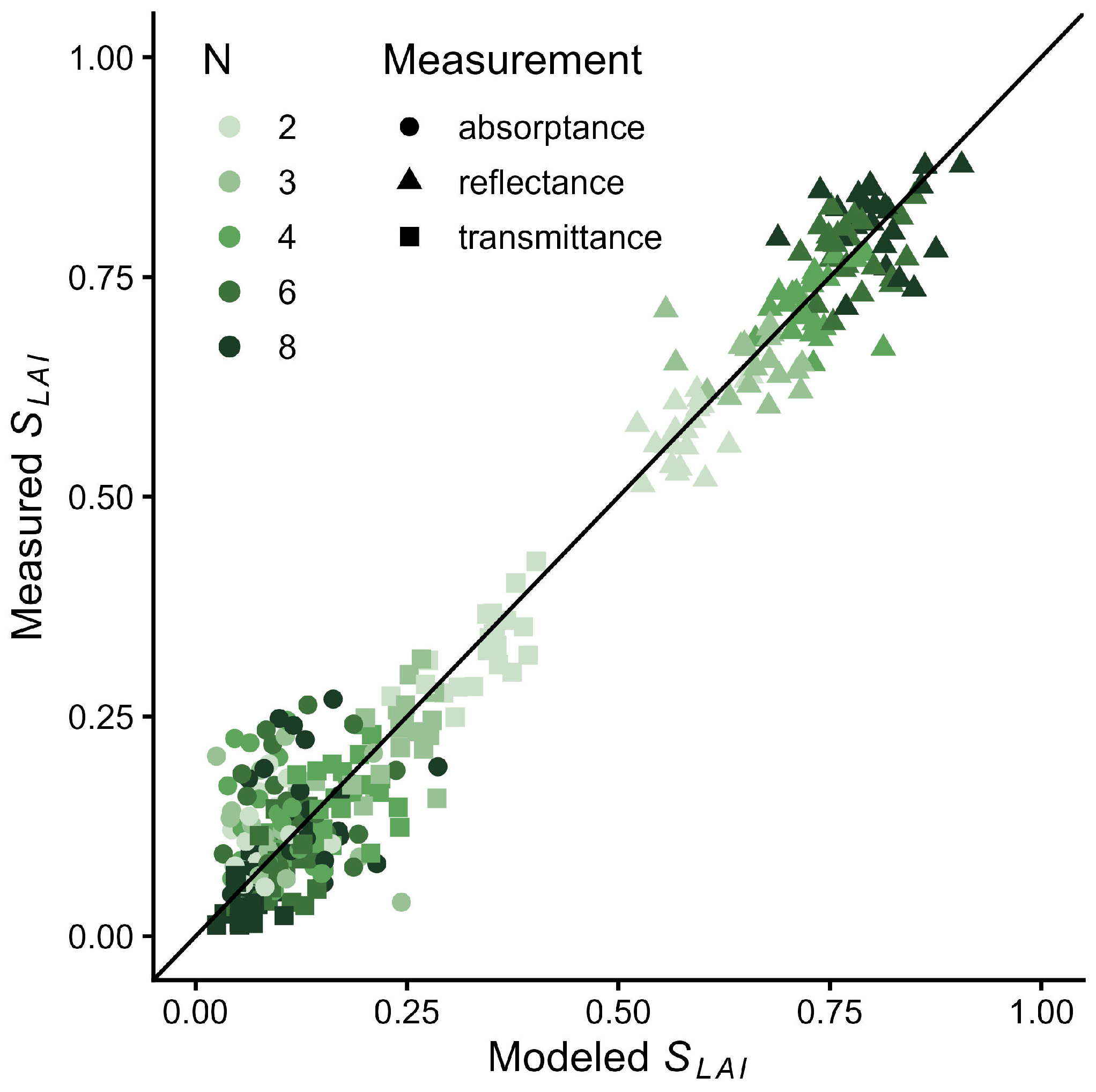
  • We validated a model of potential canopy reflectance representing a structural simplified canopy using LAI-weighted optical properties, and showed a strong positive relationship with canopy %N.
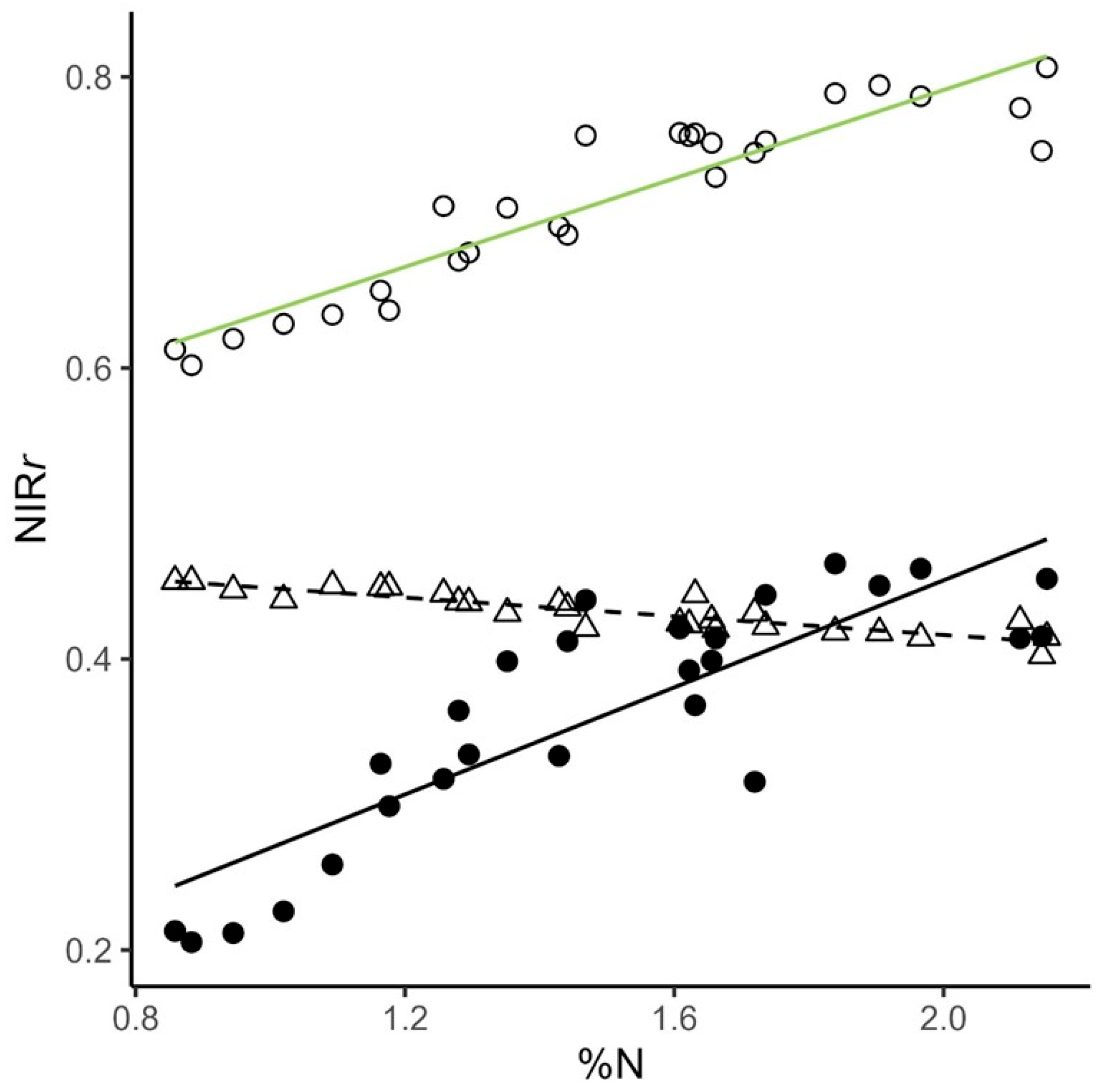
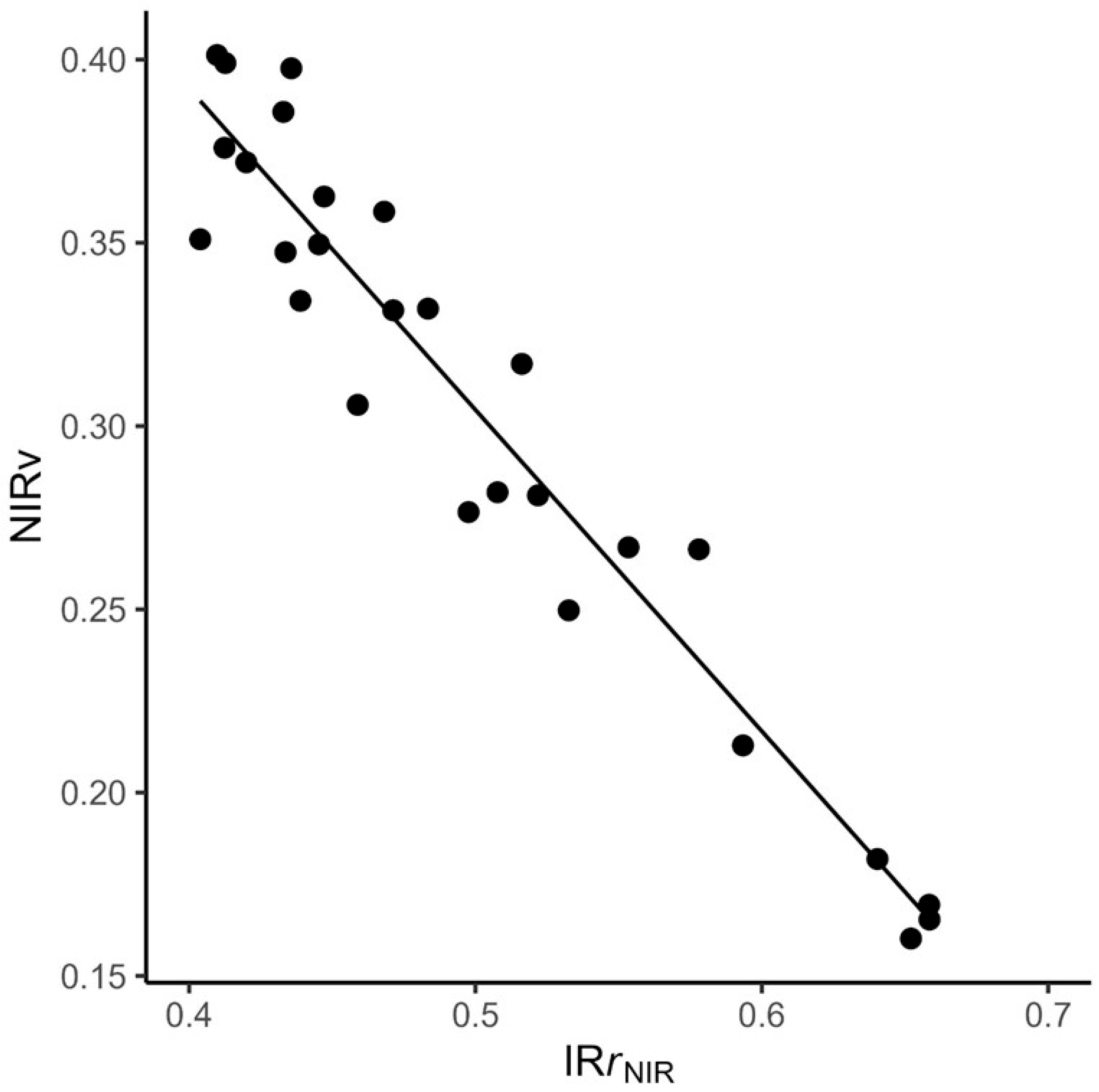
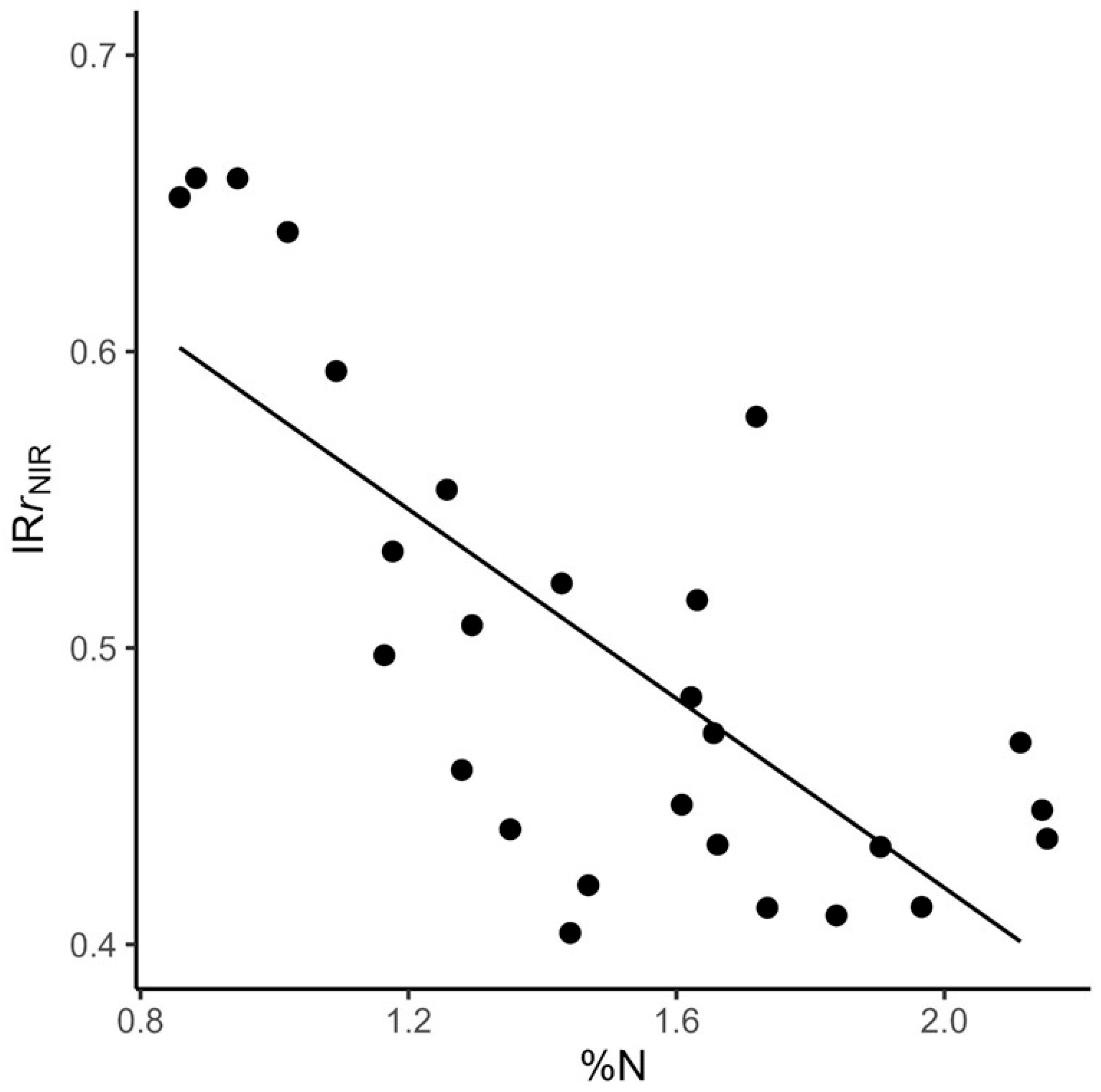
  • We derived an index of relative reflectance to quantify the effect of canopy structural complexity on whole-canopy reflectance and found that complexity reduces potential canopy NIR reflectance more in low %N stands high %N stands.
What are the implications of the main findings?
  • The positive correlation between canopy %N and LAI-weighted leaf NIR reflectance suggests that the relationship between canopy %N and canopy NIR reflectance arises from the integrated effects of canopy complexity acting on differences in leaf-level optical traits.
  • The physical mechanism or mechanisms underlying the relationship between canopy complexity and canopy %N require further study, but implies existing links between ecosystem biochemistry, leaf traits, and canopy growth patterns.

Abstract

Forest canopy near-infrared reflectance and mass-based canopy nitrogen concentration (canopy %N) have been shown to be positively correlated. While the mechanisms underpinning this relationship remain unresolved, the broad range of wavelengths involved points to structural properties that influence scattering and covary with %N. Despite this, efforts that have focused on commonly measured structural properties such as leaf area index (LAI) have failed to identify a causal mechanism. Here, we sought to understand how lidar-derived canopy traits related to additional properties of foliar arrangement and structural complexity modulate the effects of leaf spectra and leaf area index (LAI) on canopy reflectance. We developed a leaf layer spectra model to explore how canopy reflectance would change if complex foliage arrangements were removed, compressing the canopy into optically dense, uniform stacked layers while maintaining the same leaf area index. Model results showed that LAI-weighted leaf reflectance saturates at a leaf area index of approximately two for needleleaf species and four for broadleaf species. When upscaled to estimate plot-level canopy reflectance in the absence of structural complexity (NIRrLAI), results showed a strong positive relationship with canopy %N (r2 = 0.86), despite a negative relationship for individual leaves or “big-leaf” canopies with an LAI of one (NIRrL, r2 = 0.78). This result implies that the relationship between canopy near-infrared reflectance and canopy %N results from the integrated effects of canopy complexity acting on differences in leaf-level optical properties. We introduced an index of relative reflectance (IRr) that shows that the relative contribution of structural complexity to canopy near-infrared reflectance (NIRrC) is related to canopy %N (r2 = 0.55), with a three-fold reduction from potential canopy near-infrared reflectance observed in stands with low %N compared to a two-fold reduction in stands with high %N. These findings support the hypothesis that the correlation between canopy %N and canopy reflectance is the result of interactions between leaf traits and canopy structural complexity.

1. Introduction

Remote estimation of forest canopy chemistry has proven useful for upscaling ecosystem models to regional, continental, and global scales [1,2,3]. One result of these efforts is the observation of a positive correlation between mass-based canopy nitrogen concentration (canopy %N) and reflectance of incident solar radiation over broad portions of the near-infrared region (NIRr), a relationship that has been shown regionally [4,5] and more broadly [6,7,8]. In addition, recent work has shown strong relationships between vegetation NIRr and canopy photosynthesis at regional and global scales [9,10,11]. Although useful, the full potential of these relationships requires a better understanding of their underlying mechanisms. A growing body of literature has demonstrated complex interrelationships among foliar nitrogen, canopy and branch structure, solar radiation absorption, and NIRr that are likely related to the strategies employed by species for optimizing photosynthetic capacity of forest canopies through the interaction of light harvesting strategies and plant nutrition [5,9,10,11,12,13].
Although biochemical constituents of leaves directly affect narrow portions of the solar reflectance spectrum [14], their influence on the structure of leaves and whole plants may cause variability outside of those regions. Ollinger [12] hypothesized that the correlation between canopy %N and canopy NIRr may be the result of indirect causal relationships between biochemical and structural traits with underpinnings in evolutionary biology. Specifically, leaf nitrogen concentration exerts a primary constraint on carbon assimilation, which influences structural characteristics related to light harvesting, leaf clumping, water content, lateral branching, and crown structure, all of which are known to affect scattering and canopy reflectance. Although a number of leaf traits are known to influence NIRr [15,16], studies that have examined the leaf-level relationship between %N and NIRr have yielded mixed results. Bartlett et al. [17] and Wicklein et al. [18] found a negative relationship between leaf %N and NIRr that persisted for measurements collected on single leaves and stacks of leaves, leading to the conclusion that leaf reflectance, at least among broadleaf species, did not drive the relationship observed for forest canopies. Sullivan et al. [5] found that, when broadleaf and needleleaf species were pooled, a weak positive relationship between leaf %N and NIRr emerged. However, when the two foliage types were evaluated separately, the relationship among needleleaf species was positive, while broadleaf species exhibited a neutral to negative relationship. Collectively, these results suggest that the relationship between canopy %N and NIRr is the direct result of canopy structural complexity traits (e.g., porosity, rugosity; hereafter referred to as canopy complexity) that interact and covary with leaf traits in a predictable, albeit poorly understood, manner across a range of ecosystems [5,12].
Other recent studies have converged on links between canopy complexity and net primary production (NPP) [19,20]. From a canopy structural perspective, Gough et al. [21] suggested that the primary constraint on complexity, and therefore NPP, is canopy volume. Relatedly, Atkins et al. [22] found that canopy light absorption and canopy structural complexity are related. Earlier studies have explored the role of resource limitation on finer-scale structural variation, such as branch and shoot architecture. For example, clumping of needles within shoots has been shown to be correlated with site nutrient status [23,24], and in eucalyptus seedlings, leaf angle and nitrogen were linked [25]. More recently, Béland and Baldocchi [26] showed that clumping of foliage on branches is related to two resource limitations; in water-limited sites in their study, foliage clumping was random throughout the canopy, but in light-limited sites, foliage was increasingly aggregated towards the top of the canopy, theoretically maximizing photon penetration and light use efficiency in light-limited forest canopies. Using a radiative transfer model, Béland and Kobayashi [27] found that leaf clumping within shoots, leaf angle at the tops of canopies, and leaf absorptance are the primary drivers of NIRr of whole canopies.
Although our understanding of forest–light interactions has rapidly developed with the increased availability of very-high-resolution remote sensing data sets, one outstanding challenge in forest remote sensing is our ability to disentangle the relative effects of leaf traits and canopy complexity on whole-canopy reflectance using field-based measurements. This represents a persistent limitation to resolving the nature of the relationship between canopy %N and NIRr. Here, we present a method to disentangle the influence of leaf reflectance and canopy complexity on whole-canopy reflectance by using a simple plate reflectance model based on the PROSPECT and LIBERTY leaf reflectance models to simulate canopy reflectance if foliage were presented as uniform stacked layers rather than distributed throughout the canopy. We then introduce an index of relative reflectance to establish the relative effects of leaf and canopy traits on whole-canopy reflectance observations. We use this approach to evaluate our hypothesis that NIRr arises from a combination of leaf and canopy complexity traits that are related to nitrogen concentration of leaves and canopies. Specifically, we hypothesize that (1) the NIRr-%N relationship arises due to leaf-level optical traits and, therefore, LAI-weighted leaf reflectance, in the absence of canopy complexity, correlates positively with canopy %N from the effects of multiple scattering and leaf absorption; and (2) canopy complexity has a relatively more pronounced effect on observed canopy NIRr in low %N plots dominated by needleleaf species than in high %N plots dominated by broadleaf species due to more complex structure.

2. Materials and Methods

2.1. Study Site

Bartlett Experimental Forest (BEF) is a temperate mixed deciduous forest located in the White Mountain National Forest in Bartlett, New Hampshire, United States (44.05°N, −71.29°W). Elevation throughout the study site ranges from 207 m to approximately 915 m. Species composition varies throughout the site, with northern hardwood species at lower elevations and spruce and fir at higher elevations. 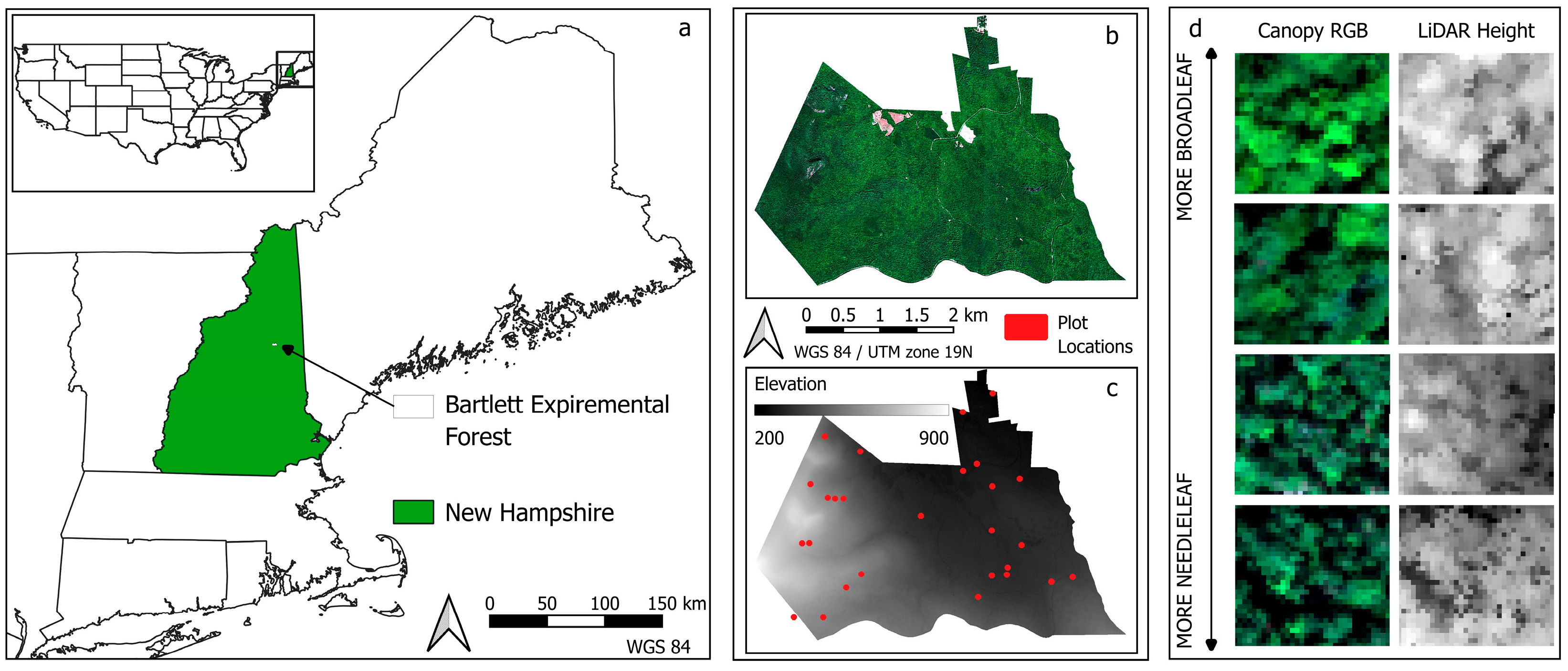The BEF inventory plot network consists of 437 square 0.25-acre plots located on a north-to-south and east-to-west grid regularly spaced throughout the extent of the study site [28]. We used a stratified sampling approach to randomly select twenty-seven of the inventory plots across a gradient of structure, canopy %N, reflectance, and elevation based on the results of a cluster analysis of field and remote sensing data (Figure 1). This effort helped us to limit collinearity between these traits and functional type and elevation, as confirmed by the variance inflation factors test using the function vif in the R (v. 4.3.1) package car (v. 3.1-3), by selecting plots that were representative of the full range of these combined traits. Unless otherwise noted, all analyses were performed in R.

2.2. Field and Lab Measurements

We conducted a field campaign to sample foliar traits (EDI: 1369.1, ref. [29]) and plot characteristics between 26 July 2017 and 9 August 2017. At each plot, we collected foliage samples from species that had leaves in the upper canopy, resulting in 8–15 trees sampled for each plot. Samples were retrieved from throughout the canopy and stratified across species on the plot based on a visual assessment of the canopy cover and an inventory-based estimate of species composition. We used a shotgun to collect a minimum of 15 leaves per tree, and we estimated the sample collection height using a Trimble® TruPulse 360R laser rangefinder (Laser Technology, Inc., Centennial, CO, USA). Samples were kept cool and moist prior to lab processing within one day of collection.
We measured leaf area from each broadleaf sample on 8–10 undamaged leaves using a portable leaf area meter (LiCOR LI-3000C, LiCOR, Lincoln, NE, USA). For each needleleaf sample, 20 needles were removed from each branch and scanned on a flatbed scanner. Total needle area was later calculated from the images using ImageJ (v. 1.50) [30]. All samples were weighed after scanning and within 12 h of excision to determine a fresh weight. Finally, foliage samples were dried in an oven at 70 °C until a stable dry weight was reached. Moisture content was calculated as the difference between the sample fresh weight and dry weight divided by the fresh weight. Leaf mass per unit area (LMA) was calculated as the dry weight divided by the total area of the sample. Dry foliage samples were ground and chemically analyzed on an Elementar Americas Pyrocube elemental analyzer (Elementar Americas, Inc., Mt. Laurel, NJ, USA) at the University of New Hampshire Stable Isotope Laboratory for leaf nitrogen content.
Leaf area index (LAI), gap fraction (GF), and vertical species-specific leaf area distribution were estimated by making measurements across 49 gridded points on each plot. LAI and GF estimates were made using a LiCOR LAI 2200C Plant Canopy Analyzer (LiCOR, Lincoln, NE, USA) in a paired two-wand configuration. We placed one wand “above-canopy” in a large clearing to automatically log open sky measurements, while we manually logged below-canopy measurements at each of the grid points. Both sensors were outfitted with a 270° view cap to restrict the field of view from operator obstruction, and we performed a sensor match calibration before beginning measurements. LiCOR’s FV2200 software (v. 2.1.1) was used to pair the above- and below-canopy readings and calculate LAI and GF.
Camera point-quadrat sampling [31] was conducted to characterize leaf area-based canopy species composition. Briefly, at each grid point, a 35 mm camera with a 135 mm telephoto lens calibrated to distance was set facing up toward the canopy on a 1 m tripod. We manually adjusted the focus to determine the height and species of the lowest leaf at 15 grid points within the camera field of view (for 49 × 15 = 735 total observations per plot). Open sky readings were recorded if no leaves were present at the grid intersection. These data were used to calculate relative LAI and area- and mass-weighted leaf traits for dominant species at 2 m increments throughout the canopy.
Mixed effects modeling of leaf traits was performed using the mlm function in the lme4 package (v. 1.1-33). We assigned random effects of plot and species, as well as functional type (needleleaf or broadleaf), and used height as a fixed effect. Models were selected using Akaike Information Criterion (AIC), and plot and species effects were assessed using a pseudo coefficient of determination [32,33]. We derived a significant relationship between sample height and LMA, which was used to estimate LMA for the 2 m height classes. Relative LAI for each species was converted to mass-based canopy species composition by multiplying by species-specific LMA at each height. Finally, we estimated canopy %N by weighting leaf-level chemistry measurements by mass-based canopy species composition.

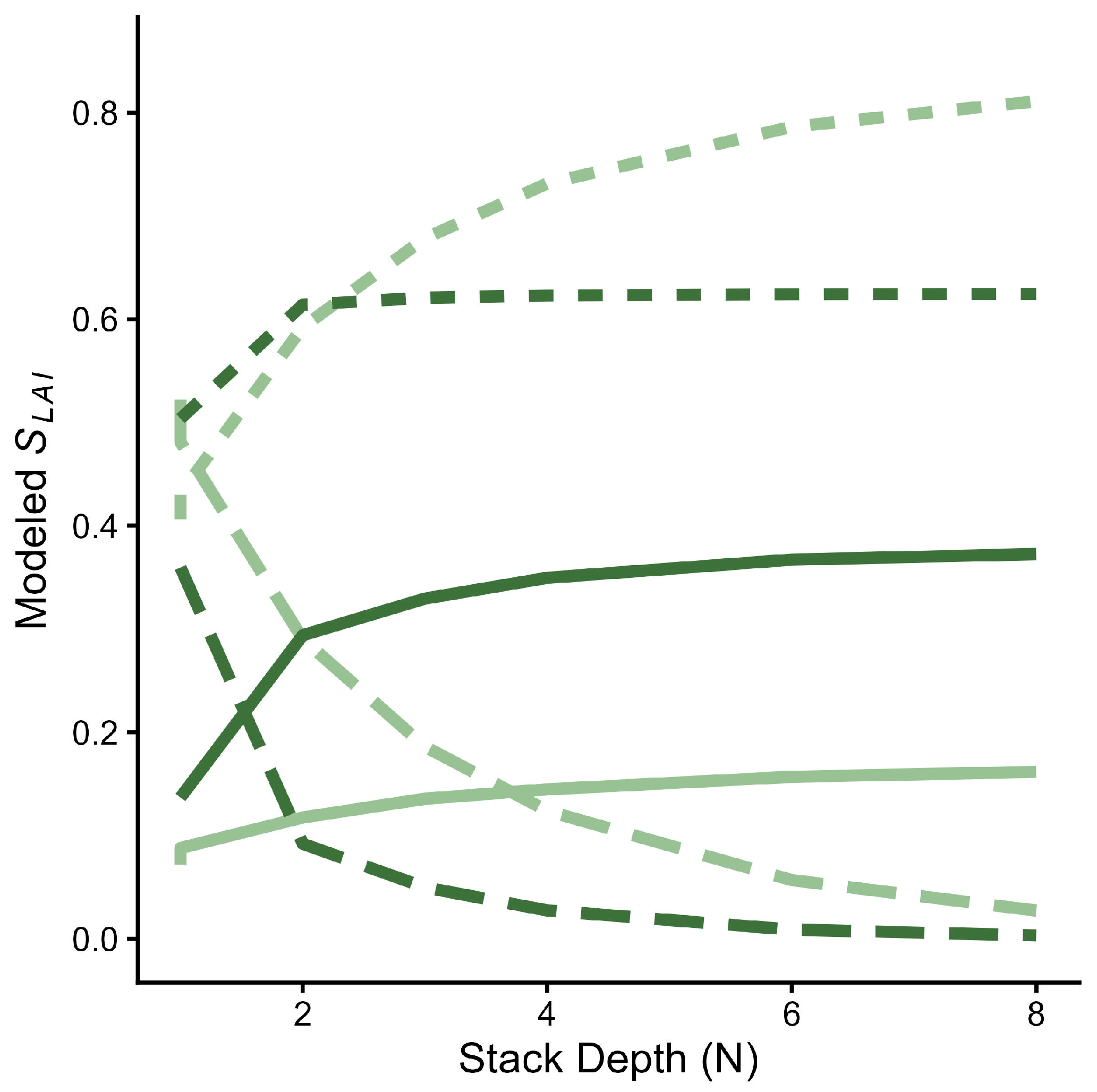
2.3. Leaf Stack Reflectance Model

We modeled the reflectance (r), transmittance (t), and absorptance (a) of a stack of leaves with a depth equal to the LAI of a plot. These simulated spectra were calculated to represent the potential whole canopy reflectance in the absence of foliage distribution and arrangement. We used the modeled spectra, from here on referred to as LAI-weighted leaf reflectance, to better understand the effects of leaf traits on measured whole-canopy reflectance and to evaluate their role in the relationship between canopy %N and NIRr. To do this, we first compiled a spectral library of the species present at our study area from the Ecological Spectral Information System (EcoSIS) database (https://ecosis.org). We included leaf reflectance and transmittance spectra measured using an ASD FieldSpec equipped with either an integrating sphere or a leaf clip. We then modeled the transmittance for the stack of leaves equal to plot LAI, given measurements of reflectance and transmittance for one leaf.
For broadleaf species, we estimated stack transmittance using the plate model approach [34]. The plate model served as the basis for the structure parameter in PROSPECT to account for the effects of cellular structure organization and intercellular airspace on the elementary reflectance and transmittance, estimated from leaf pigment concentrations and water content [16]. Here, rather than estimate reflectance and transmittance spectra from leaf constituents, we assumed leaf spectra from the spectral library as the elementary spectral measurements. We then estimated transmittance for stack depth, n, assuming the spectra for each layer are the same as the previous, as described by Jacquemoud and Ustin [35] (ch. 9):
tn = (∝ − ∝−1)/(∝βn − ∝−1 β−n),
where
∝ = (1 + r12 − t12 + ∆)/2r1,
β = (1 − r12 + t12 + ∆)/2t1∆ = √((r12 − t12 + 1)2 − 4r1),
Although the plate model is used to estimate rn as well, we parsed the total transmittance lost for a given leaf stack depth to absorptance and reflectance by the proportions measured for a single leaf. We validated modeled spectra using measurements of reflectance and transmittance for stacks of leaves collected from specimens of several broadleaf tree species [17]. Our validation focused on the NIR region (850–1050 nm), where the effect of structure, in this case the number of leaves in a stack, on reflectance and transmittance is more readily apparent because absorption is low [15,16].
For needleleaf species, we estimated stack transmittance and reflectance using the approach described by Benford [36] and later implemented in the LIBERTY model to estimate spectra of conifer needles [37]. Like the plate model, this approach estimates reflectance and transmittance of a medium at different thicknesses, given a unit reflectance and transmittance. Benford [36] showed that transmittance and reflectance can be estimated continuously between 0 and infinite units of thickness using the transmittance and reflectance measurements of one unit. Here, we consider a single needle as our measurement unit and assume that each needle in a stack has the same spectral characteristics. The calculations can be made for a continuous thickness using three sets of functions: first, between one and two units of thickness (1 + f) as
t1+f = t11+f × (1 + t12 − r12)1−f,
r1+f = 1 + r12 − t12 − (1 + r12 − t12)2 − 4r12 × (1 − t1+f2)/2r1,
then using (r1+f, t1+f) to calculate for greater than two units of thickness as
ti+f = ti−1 × t1+f/(1 − r1+f × ri−1),
ri+f = ri−1 + ti−12 r1+f/(1 − r1+f × ri−1),
which requires first solving for the whole parts, ti−1 and ri−1. We can also solve for less than one unit of thickness as
a = r12 × t12 + t12 − t14 − 2t1+f2 × r12,
b = 4r12 × (t12 − r12 × t1+f2) × (t12 − t1+f2),
rf = (a − √(a2 − b))/2r12 (t12 − r12 t1+f2),
tf = (t1+f/t1) × (1 − r1 × rf),
where (rn, tn) are equal to (rf, tf), (r1+f, t1+f), or (ri+f, ti+f), depending on whether n is less than 1, between 1 and 2, or greater than 2.
We upscaled measurements from the leaf spectral library to estimate plot-level canopy reflectance in the absence of canopy complexity (LAI-weighted leaf spectra) using area-based canopy composition and the leaf layering model for each plot as
SLAI = ∑spp SsppPspp,
where SLAI is r, t, and a modeled for n equal to field-measured LAI; Pspp is the area-based species proportion estimated from camera point-quadrat sampling; and Sspp is the LAI-weighted spectra derived for the species. Input spectra were averages for the species, or for the genus or functional type if the species spectra did not exist in the spectral library. We calculated NIRrLAI (LAI-weighted mean NIR reflectance) and NIRrL (the area-weighted single-leaf mean NIR reflectance) as the arithmetic mean of reflectance between 850 and 1050 nm.

2.4. Remote Sensing Characterization of Study Plots

We used the hyperspectral L3 data from the NEON Airborne Observatory Platform collected in August 2019 (National Ecological Observatory Network (NEON) [38], 3 April 2023, [39]). Our field campaign was intended to coincide with NEON AOP data acquisition during the summer of 2017 over BEF (NEON D01 site: BART), but due to poor weather and atmospheric conditions, hyperspectral data was not acquired over the field site. We used hyperspectral data acquired in August 2019, as it was the nearest high-quality data available. Although the temporal mismatch is not ideal because of interannual variability in leaf and canopy %N, previous studies have demonstrated strong linear relationships in between-year canopy %N at our field site over a three-year period [40], though a reduction in the strength of the relationship is possible. To further ensure its suitability, we compared LiDAR-derived vegetation profiles and canopy height models from 2017 and 2019 and identified no significant stand structural changes between field sampling and hyperspectral acquisition (Figure S1).
The hyperspectral sensor deployed was the NEON imaging spectrometer (NASA JPL, La Cañada Flintridge, CA, USA), which is a pushbroom scanner outfitted with a 2D focal plane array of 480 spectral and 640 spatial pixels. The L3 reflectance data consists of 426 bands between 380 and 2510 nm, with a nominal spectral resolution of 5 nm. The spectrometer data are converted to at-sensor radiance using sensor calibration parameters and then atmospherically corrected, georeferenced, orthorectified, stacked, mosaicked, and provided as 1 km2 tiles with 1 m spatial resolution. Data were retrieved from HDF files using Python (v. 2.7) and subsequently clipped to the extents of the Bartlett Experimental Forest site boundary. From within the extents of each plot, data were extracted using GDAL (v. 2.2) and Gippy (v. 1.0.0). All spectra from an average of 47 pixels on each plot were averaged to produce canopy spectral curves. NIRrC for each plot was calculated as the average percent reflectance of spectral bands with wavelengths between 850 nm and 1050 nm.
We calculated an index of relative reflectance (IRr), which can be interpreted as the proportion of radiation that is lost to structure (i.e., foliage distribution and arrangement) and non-photosynthetic components of the canopy and soil, as
IRr = (rLAIω − rCω)/rLAIω,
where the reflectance of the canopy, rC, is subtracted from the LAI-weighted leaf reflectance, rLAI, then divided by rLAI at each wavelength, ω. In general, values closer to 1 are indicative of a relatively higher contribution of canopy complexity to total absorption. rLAI spectra were downsampled to match the sampled wavelengths of NEON AOP data. We calculated IRrNIR as the average of IRr from 850 nm to 1050 nm to estimate the proportion of NIR radiation absorbed by the canopy because of foliage distribution and arrangement.
We used the LiDAR L1 discrete return point cloud data from NEON AOP (National Ecological Observatory Network (NEON), 3 April 2023, ref. [39]). Lidar data were collected using an Optech Gemini lidar sensor (Teledyne Geospatial, Vaughan, Ontario, Canada) flown at approximately 1000 m with a pulse density of up to 8 pulses/m2, which produced a return density of approximately 6–8 returns/m2 within our plots. We voxelized data at a horizontal grain size of 5 m and vertical grain size of 1 m and calculated a set of canopy structural complexity metrics [41,42,43] and canopy light metrics [44,45]. Lidar metrics were calculated in R using the libraries lidR (v. 4.0.3), sf (v. 1.0-14), and terra (v. 1.7-39). For a summary of derived remote sensing metrics and their calculations, see Table 1.
Statistical analysis of canopy chemistry and hyperspectral and lidar metrics was performed using the lm function for univariate models. Multiple regression modeling was performed using AIC to compare model strength [46].

3. Results

For both broadleaf and needleleaf species, modeled NIRr and absorptance increased logarithmically towards saturation with the number of layers, while total transmittance decayed toward zero (Figure 2). For broadleaf tree species, modeled r, t, and a were in good agreement with measurements made by Bartlett et al. [17] for stacks of leaves (Figure 3; RMSE 0.049, 0.042, and 0.073, respectively).
At the plot scale, the application of the leaf layering model using LAI modified the direction of the relationship between NIRr and %N from slightly negative for NIRrL to strongly positive for NIRrLAI (Figure 4). Relationships between canopy %N and NIRrL and NIRrLAI were both significant (r2 0.78 and r2 0.86, respectively). NIRrC was also strongly positively correlated with %N with a similar slope to NIRrLAI but a lower intercept (r2 0.73; Figure 4).
Strong relationships were found between IRrNIR and NIRv (r2 0.93, Figure 5), IRrNIR and canopy %N (r2 0.55, Figure 6), and IRrNIR and NIRrC (r2 0.94). We found correlations between IRrNIR, NIRrC, and canopy %N and numerous canopy structural complexity and canopy light interception metrics derived from remote sensing and field methods (Table 2, Figure S2). Among these, the strongest relationship between IRrNIR, a proxy for canopy complexity, and a complexity metric was with canopy porosity (r2 0.57), which was also correlated with canopy %N (r2 0.42). A multiple regression analysis to predict NIRrC using canopy %N, mean leaf NIR absorption, and canopy porosity (in place of IRrNIR) resulted in a two-variable model to predict NIRrC using absorption and porosity (r2 0.85).

4. Discussion

4.1. Effects of Leaf Traits on Leaf and Leaf Stack Reflectance

In forest canopies, the fate of photons, and thus whole-canopy reflectance, is influenced by the number of leaf interactions, the optical properties of both leaves and the ground, and the overall canopy structure and complexity [47,48,49]. We developed a simple leaf layer spectra model to explore how canopy reflectance would change if foliage arrangement—such as leaf angle, clumping, and leaf area distribution—were removed, compressing the canopy into uniform stacked layers while maintaining the same leaf area index. Forest canopy structural traits are hypothesized to contribute to the relationship between NIRr, canopy %N, and photosynthesis [5,8,12,27,50]. These same associations underpin efforts to leverage canopy complexity via vegetation-specific NIR reflectance to estimate canopy photosynthetic traits [8,9,51]. Yet, efforts to disentangle the relative contributions of leaf and canopy properties in the relationship between NIRr and canopy %N are ongoing [27].
While validation of needleleaf stack spectra was not possible because methods for measuring needle spectra are not readily portable to stacks of needles [52,53,54], modeled leaf stack spectra for broadleaf species aligned well with empirical studies of leaf stack reflectance [17,18,55]. We found that total leaf stack reflectance is governed by the balance of absorption and transmittance of individual leaves, which is consistent with an interpretation that greater stack depth corresponds to more interactions between photons and leaf cellular structures [15,16,38]. Due to differences in the relative rates of reflectance and absorptance of individual leaves, transmittance attenuates and reflectance saturates more quickly in needleleaf stacks, whereas absorptance reaches saturation more rapidly in broadleaf stacks. This modeling exercise underscores the critical importance of measuring both leaf reflectance and transmittance to understand the fate of NIR radiation in forest canopies, as even subtle variations in single-leaf absorptance can significantly impact whole-canopy reflectance [27,56].
For individual leaves, the relative rates of NIR absorption, reflectance, and transmittance are primarily governed by structural variation that may be related to leaf economics [12]. For example, internal leaf structure and foliar %N both affect photosynthetic capacity of leaves through the capture and conversion of photosynthetically active radiation into chemical energy [57]. In deciduous broadleaf species, nitrogen is more readily allocated to rubisco for carbon fixation [58,59], as opposed to non-photosynthetic components that maximize leaf longevity, a necessary investment for needleleaf species to retain their needles for multiple years [57,60]. Broadleaf species typically have a larger surface area of mesophyll cells exposed to intercellular air space, which facilitates enhanced gas exchange and supports more efficient photosynthesis. A result of this structure is an increase in NIR radiation scattering from leaves [15], which also acts as a thermoregulatory mechanism to optimize leaf temperature in high-light upper-canopy environments [61].
Internal structure also affects the optical signals of needleleaf species [62]. For example, Rock et al. [63] showed that anatomical changes as needles age cause increases in NIR absorption. They attributed changes in needle spectra to declines in intercellular airspace and increases in cell size and water volume as needles age. However, in needleleaf species, light capture and scattering are thought to be controlled more by the shape of needle surfaces and their arrangement along shoots [64,65]. This configuration causes shoots to function as “photon traps” [66] through the effects of photon recollision probability [67] and has led previous studies to evaluate needleleaf shoots as the elementary foliage unit in conifer canopies [56,68]. Needle packing on shoots may have evolved for surviving harsh winter conditions [69] but has also been linked to leaf temperature increases that optimize photosynthesis in cold climates [70]. There is also evidence that shoot traits are related to plant nitrogen status [24,71], demonstrating a potential link between nitrogen, carbon assimilation, plant morphology, and spectra in needleleaf species. Despite these observations, we treated individual needles as the elementary foliage unit in our leaf layer spectra model because we sought to understand the integrated effects of canopy complexity—including the distribution of needles on shoots—on the relationship between canopy %N and NIRrC.

4.2. Using IRr to Evaluate Links Between Canopy %N, NIRr, and Canopy Complexity

We modeled potential whole-canopy reflectance (i.e., NIRrLAI, LAI-weighted leaf reflectance) using field measurements of canopy LAI. However, we found that reflectance and absorptance are nearly saturated, while transmittance is nearly attenuated at a stack depth of two for needleleaf species and four for broadleaf species, with most of our plots having an LAI of at least five. As a result, our NIRrLAI estimates approximate an optically dense canopy. Assuming canopy transmission and ground optical properties have a minimal influence on canopy reflectance across our closed canopy plots [66], we can interpret the difference between modeled potential canopy reflectance and measured canopy reflectance as representing the effects of canopy foliage arrangement [51]. We observed that the slopes of the %N-NIRr relationship were nearly identical for both NIRrC and NIRrLAI (Figure 4). However, when expressed as a relative reduction (i.e., our index of relative reflectance, Figure 6), we found that canopy complexity has an absorptance effect that is more pronounced for lower %N plots. Specifically, canopy complexity results in a 3-fold decrease in NIRr in the lowest %N plots but only a 2-fold decrease at the highest %N plots.
Canopy complexity has been linked to both canopy reflectance and nutrient status [23,26,50]. We found that lidar-derived canopy porosity covaried positively with NIRrC across a %N gradient at the Bartlett Experimental Forest. We interpret higher porosity on high %N plots as a result of higher %N species allocating foliage toward high-light environments to facilitate higher rates of photosynthesis [72], resulting in increased NIRrC. Branching patterns are plastic, driven by light availability [73], nutrients and carbon allocation [74], competition [75], and wood specific gravity [33,76]. At our study site, this manifests in more open volume below the canopy surface (i.e., more porous canopy volume) for higher %N plots, as compared to lower %N plots with more shade-tolerant mid- and understory layers and constrained canopy architecture [77]. This is supported by evidence of the strong relationship between IRrNIR and NIRv (Figure 5), as NIRv is thought to be a comprehensive index of light capture [9]. Further, both %N [78] and NIRv [9] have been found to be related to light use efficiency. That IRrNIR is both grounded in direct measurements of leaf and canopy spectra and so strongly correlated with NIRv demonstrates its potential for exploring the complex relationships between plant and site nutrient status, canopy complexity, and light attenuation.
Recent work by Béland and Kobayashi [27] used terrestrial laser scanning and a ray tracing radiative transfer model to explore potential drivers of the relationship between canopy %N and NIRr in broadleaf stands. Their results highlighted leaf clumping and top-of-canopy leaf angle as important canopy traits driving NIRr. In broadleaf species, variation in leaf angle distribution (LAD) has been observed between species with differing foliage qualities [79,80,81]. Although its relationship to nutrient status in mature forests remains less resolved, there is growing evidence that LAD is a dynamic plant trait, exhibiting both tropic and nastic responses to water and light [50,82,83,84], which may confound empirical models [85,86]. This suggests that while LAD likely contributes to the relationship between canopy %N and NIRr, more stable canopy traits related to growth habits, such as clumping and crown shape, may have a stronger influence on its persistence and serve as a better link across species functional types.
Exploring these relationships at the individual tree scale would be illuminating. This effort would benefit from the automation of field measurements [80,87], alongside very high spatial and temporal resolution remote sensing data, such as those acquired by sensors deployed on unoccupied aerial vehicles [88,89,90] or fixed cameras [50,91], which can be used to acquire data with a repetition rate that better aligns with the high-frequency temporal variability of environmental conditions and specific canopy traits, such as leaf angle. Understanding the extent to which canopy traits vary within and between species, and to what extent those traits are dynamic, may be necessary for fully resolving the nature of the relationship between canopy %N and whole-canopy reflectance. Nonetheless, both LAD and clumping influence light penetration, scattering, canopy light use efficiency, and thermoregulation, and along with leaf traits and other canopy architecture traits, influence canopy photosynthesis and canopy reflectance [8,9,11,12,26,27,50,87].

5. Conclusions

In this study, we evaluated the modulating effects of individual leaf optical traits and canopy complexity on whole-canopy reflectance by using a simple model of leaf stack reflectance to simulate reflectance of mixed-species forest canopies in the absence of canopy complexity. To date, few studies have used direct measurements to explore the integrated effects of leaf and canopy traits on whole-canopy reflectance. Here, we have demonstrated an approach that can be used to resolve the relative contributions of both to understand complex relationships between forests and light. We showed that, across a species composition gradient, the direction and slope of the relationship between canopy %N and modeled potential canopy reflectance is consistent with canopy %N and canopy reflectance. This outcome suggests that the relationship between canopy %N and canopy reflectance may arise from traits of individual leaves that influence the rates of reflectance and absorptance, especially in the NIR, despite a neutral to negative relationship between leaf %N and NIR reflectance of individual leaves. We demonstrated the index of relative reflectance in the NIR (IRrNIR) to isolate the contribution of canopy complexity to the total canopy reflectance by comparing total canopy reflectance to simulated leaf reflectance for a depth equal to LAI. We showed that this proxy measurement of canopy complexity is related to canopy %N and that both IRrNIR and canopy %N are related to canopy porosity. The results of our approach showed that a combination of leaf traits and canopy structural traits that are associated with plant nutrient status and light harvesting strategies drives whole-canopy reflectance in mixed temperate forests. Future studies might explore these relationships and models in other ecosystems.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs18020355/s1, Figure S1: Example of diagnostic plots used to evaluate canopy structural change between 2017 and 2019; Figure S2: Scatter plot matrix of lidar and field data.

Author Contributions

Conceptualization, F.B.S., S.V.O. and A.O.; methodology, F.B.S., J.H.H., S.V.O. and A.O.; software, F.B.S.; formal analysis, F.B.S.; investigation, F.B.S., S.V.O. and A.O.; data curation, A.D.R.; writing—original draft preparation, F.B.S. and J.H.H.; writing—review and editing, S.V.O., A.O., A.D.R. and M.P.; project administration, S.V.O. and M.P.; funding acquisition, S.V.O. and M.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by NSF Macrosystems (NSF Grant #1638688), NSF EPSCoR (NSF Grant #1923004), NASA RST (#80NSSC20K1730), NSRC (23-DG-11242311-020), and NHAES (USDA-NIFA 1006997).

Data Availability Statement

Data used for this research were accessed from the NEON AOP Data Portal, www.neonscience.org/data (accessed on 28 September 2023) and the EcoSIS Spectral Library, data.ecosis.org (accessed on 14 November 2023). Leaf trait data from the 2017 field campaign at Bartlett Experimental Forest are openly available and published at EDI: 1369.1. Additional data and code supporting the conclusions of this article will be made available by the authors upon request.

Acknowledgments

The authors are grateful to numerous researchers and field assistants for invaluable contributions in the field and lab. This work was conducted at the Bartlett Experimental Forest, which is operated and maintained by the USDA Forest Service, Northern Research Station. The findings and conclusions are those of the authors and should not be construed to represent any official USDA or U.S. Government determination or policy.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing Canopy Biochemistry from Imaging Spectroscopy and Its Application to Ecosystem Studies. Remote Sens. Environ. 2009, 113, S78–S91. [Google Scholar] [CrossRef]
  2. Loozen, Y.; Rebel, K.T.; de Jong, S.M.; Lu, M.; Ollinger, S.V.; Wassen, M.J.; Karssenberg, D. Mapping Canopy Nitrogen in European Forests Using Remote Sensing and Environmental Variables with the Random Forests Method. Remote Sens. Environ. 2020, 247, 111933. [Google Scholar] [CrossRef]
  3. Ollinger, S.V.; Smith, M.-L. Net Primary Production and Canopy Nitrogen in a Temperate Forest Landscape: An Analysis Using Imaging Spectroscopy, Modeling and Field Data. Ecosystems 2005, 8, 760–778. [Google Scholar] [CrossRef]
  4. Lepine, L.C.; Ollinger, S.V.; Ouimette, A.P.; Martin, M.E. Examining Spectral Reflectance Features Related to Foliar Nitrogen in Forests: Implications for Broad-Scale Nitrogen Mapping. Remote Sens. Environ. 2016, 173, 174–186. [Google Scholar] [CrossRef]
  5. Sullivan, F.B.; Ollinger, S.V.; Martin, M.E.; Ducey, M.J.; Lepine, L.C.; Wicklein, H.F. Foliar Nitrogen in Relation to Plant Traits and Reflectance Properties of New Hampshire Forests. Can. J. For. Res. 2013, 43, 18–27. [Google Scholar] [CrossRef]
  6. Hollinger, D.Y.; Ollinger, S.V.; Richardson, A.D.; Meyers, T.P.; Dail, D.B.; Martin, M.E.; Scott, N.A.; Arkebauer, T.J.; Baldocchi, D.D.; Clark, K.L.; et al. Albedo Estimates for Land Surface Models and Support for a New Paradigm Based on Foliage Nitrogen Concentration. Glob. Change Biol. 2010, 16, 696–710. [Google Scholar] [CrossRef]
  7. Martin, M.E.; Plourde, L.C.; Ollinger, S.V.; Smith, M.-L.; McNeil, B.E. A Generalizable Method for Remote Sensing of Canopy Nitrogen across a Wide Range of Forest Ecosystems. Remote Sens. Environ. 2008, 112, 3511–3519. [Google Scholar] [CrossRef]
  8. Ollinger, S.V.; Richardson, A.D.; Martin, M.E.; Hollinger, D.Y.; Frolking, S.E.; Reich, P.B.; Plourde, L.C.; Katul, G.G.; Munger, J.W.; Oren, R.; et al. Canopy Nitrogen, Carbon Assimilation, and Albedo in Temperate and Boreal Forests: Functional Relations and Potential Climate Feedbacks. Proc. Natl. Acad. Sci. USA 2008, 105, 19336–19341. [Google Scholar] [CrossRef]
  9. Badgley, G.; Anderegg, L.D.L.; Berry, J.A.; Field, C.B. Terrestrial Gross Primary Production: Using NIRV to Scale from Site to Globe. Glob. Change Biol. 2019, 25, 3731–3740. [Google Scholar] [CrossRef] [PubMed]
  10. Badgley, G.; Field, C.B.; Berry, J.A. Canopy Near-Infrared Reflectance and Terrestrial Photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef]
  11. Baldocchi, D.D.; Ryu, Y.; Dechant, B.; Eichelmann, E.; Hemes, K.; Ma, S.; Sanchez, C.R.; Shortt, R.; Szutu, D.; Valach, A.; et al. Outgoing Near-Infrared Radiation from Vegetation Scales with Canopy Photosynthesis Across a Spectrum of Function, Structure, Physiological Capacity, and Weather. J. Geophys. Res. Biogeosci. 2020, 125, e2019JG005534. [Google Scholar] [CrossRef]
  12. Ollinger, S.V. Sources of Variability in Canopy Reflectance and the Convergent Properties of Plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef]
  13. Ollinger, S.V.; Reich, P.B.; Frolking, S.; Lepine, L.C.; Hollinger, D.Y.; Richardson, A.D. Nitrogen Cycling, Forest Canopy Reflectance, and Emergent Properties of Ecosystems. Proc. Natl. Acad. Sci. USA 2013, 110, E2437. [Google Scholar] [CrossRef] [PubMed]
  14. Bolster, K.L.; Martin, M.E.; Aber, J.D. Determination of Carbon Fraction and Nitrogen Concentration in Tree Foliage by near Infrared Reflectances: A Comparison of Statistical Methods. Can. J. For. Res. 1996, 26, 590–600. [Google Scholar] [CrossRef]
  15. Gates, D.M.; Keegan, H.J.; Schleter, J.C.; Weidner, V.R. Spectral Properties of Plants. Appl. Opt. 1965, 4, 11–20. [Google Scholar] [CrossRef]
  16. Jacquemoud, S.; Baret, F. PROSPECT: A Model of Leaf Optical Properties Spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
  17. Bartlett, M.K.; Ollinger, S.V.; Hollinger, D.Y.; Wicklein, H.F.; Richardson, A.D. Canopy-Scale Relationships between Foliar Nitrogen and Albedo Are Not Observed in Leaf Reflectance and Transmittance within Temperate Deciduous Tree Species. Botany 2011, 89, 491–497. [Google Scholar] [CrossRef]
  18. Wicklein, H.F.; Ollinger, S.V.; Martin, M.E.; Hollinger, D.Y.; Lepine, L.C.; Day, M.C.; Bartlett, M.K.; Richardson, A.D.; Norby, R.J. Variation in Foliar Nitrogen and Albedo in Response to Nitrogen Fertilization and Elevated CO2. Oecologia 2012, 169, 915–925. [Google Scholar] [CrossRef]
  19. Gough, C.M.; Atkins, J.W.; Fahey, R.T.; Hardiman, B.S. High Rates of Primary Production in Structurally Complex Forests. Ecology 2019, 100, e02864. [Google Scholar] [CrossRef]
  20. Scheuermann, C.M.; Nave, L.E.; Fahey, R.T.; Nadelhoffer, K.J.; Gough, C.M. Effects of Canopy Structure and Species Diversity on Primary Production in Upper Great Lakes Forests. Oecologia 2018, 188, 405–415. [Google Scholar] [CrossRef]
  21. Gough, C.M.; Atkins, J.W.; Fahey, R.T.; Hardiman, B.S.; LaRue, E.A. Community and Structural Constraints on the Complexity of Eastern North American Forests. Glob. Ecol. Biogeogr. 2020, 29, 2107–2118. [Google Scholar] [CrossRef]
  22. Atkins, J.W.; Fahey, R.T.; Hardiman, B.S.; Gough, C.M. Forest Canopy Structural Complexity and Light Absorption Relationships at the Subcontinental Scale. J. Geophys. Res. Biogeosci. 2018, 123, 1387–1405. [Google Scholar] [CrossRef]
  23. Niinemets, Ü. A Review of Light Interception in Plant Stands from Leaf to Canopy in Different Plant Functional Types and in Species with Varying Shade Tolerance. Ecol. Res. 2010, 25, 693–714. [Google Scholar] [CrossRef]
  24. Niinemets, Ü.; Cescatti, A.; Lukjanova, A.; Tobias, M.; Truus, L. Modification of Light-Acclimation of Pinus Sylvestris Shoot Architecture by Site Fertility. Agric. For. Meteorol. 2002, 111, 121–140. [Google Scholar] [CrossRef]
  25. Close, D.C.; Beadle, C.L. Leaf Angle Responds to Nitrogen Supply in Eucalypt Seedlings. Is It a Photoprotective Mechanism? Tree Physiol. 2006, 26, 743–748. [Google Scholar] [CrossRef]
  26. Béland, M.; Baldocchi, D. Is Foliage Clumping an Outcome of Resource Limitations within Forests? Agric. For. Meteorol. 2020, 295, 108185. [Google Scholar] [CrossRef]
  27. Béland, M.; Kobayashi, H. Drivers of Deciduous Forest Near-Infrared Reflectance: A 3D Radiative Transfer Modeling Exercise Based on Ground Lidar. Remote Sens. Environ. 2024, 302, 113951. [Google Scholar] [CrossRef]
  28. Ducey, M.J.; Fraser, O.L.; Yamasaki, M.; Belair, E.P.; Leak, W.B. Eight Decades of Compositional Change in a Managed Northern Hardwood Landscape. For. Ecosyst. 2023, 10, 100121. [Google Scholar] [CrossRef]
  29. Baillargeon, K.A.; Ouimette, A.P.; Hastings, J.H.; Sanders-DeMott, R.; Ollinger, S.V. Regional and Local Variation in Chemical, Structural, and Physical Leaf Traits for Tree Species in the Northeastern United States; Environmental Data Initiative: Albuquerque, NM, USA, 2023. [Google Scholar]
  30. Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 Years of Image Analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
  31. Aber, J.D. Foliage-Height Profiles and Succession in Northern Hardwood Forests. Ecology 1979, 60, 18–23. [Google Scholar] [CrossRef]
  32. Cragg, J.G.; Uhler, R.S. The Demand for Automobiles. Can. J. Econ. Rev. Can. d’Econ. 1970, 3, 386–406. [Google Scholar] [CrossRef]
  33. Sullivan, F.B.; Ducey, M.J.; Orwig, D.A.; Cook, B.; Palace, M.W. Comparison of Lidar- and Allometry-Derived Canopy Height Models in an Eastern Deciduous Forest. For. Ecol. Manag. 2017, 406, 83–94. [Google Scholar] [CrossRef]
  34. Stokes, G.G. On the Intensity of the Light Reflected from or Transmitted through a Pile of Plates. Proc. R. Soc. Lond. 1860, 11, 545–556. [Google Scholar] [CrossRef]
  35. Jacquemoud, S.; Ustin, S. Modeling Leaf Optical Properties: Prospect. In Leaf Optical Properties; Jacquemoud, S., Ustin, S., Eds.; Cambridge University Press: Cambridge, UK, 2019; pp. 265–291. ISBN 978-1-108-48126-7. [Google Scholar]
  36. Benford, F. Radiation in a Diffusing Medium. J. Opt. Soc. Am. 1946, 36, 524–554. [Google Scholar] [CrossRef] [PubMed]
  37. Dawson, T.P.; Curran, P.J.; Plummer, S.E. LIBERTY—Modeling the Effects of Leaf Biochemical Concentration on Reflectance Spectra. Remote Sens. Environ. 1998, 65, 50–60. [Google Scholar] [CrossRef]
  38. National Ecological Observatory Network (NEON). Spectrometer Orthorectified Surface Directional Reflectance—Mosaic (DP3.30006.001): RELEASE-2023; National Ecological Observatory Network (NEON): Boulder, CO, USA, 2023. [Google Scholar]
  39. National Ecological Observatory Network (NEON). Discrete Return LiDAR Point Cloud (DP1.30003.001), RELEASE-2023; National Ecological Observatory Network (NEON): Boulder, CO, USA, 2023. [Google Scholar]
  40. Smith, M.-L.; Martin, M.E.; Plourde, L.; Ollinger, S.V. Analysis of hyperspectral data for estimation of temperate forest canopy nitrogen concentration: Comparison between an airborn (AVIRIS) and a spaceborne (Hyperion) sensor. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1332–1337. [Google Scholar] [CrossRef]
  41. Hardiman, B.S.; Bohrer, G.; Gough, C.M.; Curtis, P.S. Canopy Structural Changes Following Widespread Mortality of Canopy Dominant Trees. Forests 2013, 4, 537–552. [Google Scholar] [CrossRef]
  42. Kane, V.R.; Bakker, J.D.; McGaughey, R.J.; Lutz, J.A.; Gersonde, R.F.; Franklin, J.F. Examining Conifer Canopy Structural Complexity across Forest Ages and Elevations with LiDAR Data. Can. J. For. Res. 2010, 40, 774–787. [Google Scholar] [CrossRef]
  43. Parker, G.G.; Russ, M.E. The Canopy Surface and Stand Development: Assessing Forest Canopy Structure and Complexity with near-Surface Altimetry. For. Ecol. Manag. 2004, 189, 307–315. [Google Scholar] [CrossRef]
  44. Kamoske, A.G.; Dahlin, K.M.; Serbin, S.P.; Stark, S.C. Leaf Traits and Canopy Structure Together Explain Canopy Functional Diversity: An Airborne Remote Sensing Approach. Ecol. Appl. 2021, 31, e02230. [Google Scholar] [CrossRef]
  45. Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. Lidar Remote Sensing of the Canopy Structure and Biophysical Properties of Douglas-Fir Western Hemlock Forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
  46. Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Statistics and Computing, Statistics, Computing Venables, W.N.: Statistics w.S-PLUS; Springer: New York, NY, USA, 2002; ISBN 978-0-387-95457-8. [Google Scholar]
  47. Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL Models: A Review of Use for Vegetation Characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
  48. Knyazikhin, Y.; Martonchik, J.V.; Myneni, R.B.; Diner, D.J.; Running, S.W. Synergistic Algorithm for Estimating Vegetation Canopy Leaf Area Index and Fraction of Absorbed Photosynthetically Active Radiation from MODIS and MISR Data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
  49. Stenberg, P.; Mõttus, M.; Rautiainen, M. Photon Recollision Probability in Modelling the Radiation Regime of Canopies—A Review. Remote Sens. Environ. 2016, 183, 98–108. [Google Scholar] [CrossRef]
  50. McNeil, B.E.; Fahey, R.T.; King, C.J.; Erazo, D.A.; Heimerl, T.Z.; Elmore, A.J. Tree Crown Economics. Front. Ecol. Environ. 2023, 21, 40–48. [Google Scholar] [CrossRef]
  51. Zeng, Y.; Badgley, G.; Dechant, B.; Ryu, Y.; Chen, M.; Berry, J.A. A Practical Approach for Estimating the Escape Ratio of Near-Infrared Solar-Induced Chlorophyll Fluorescence. Remote Sens. Environ. 2019, 232, 111209. [Google Scholar] [CrossRef]
  52. Daughtry, C.S.T.; Biehl, L.L.; Ranson, K.J. A New Technique to Measure the Spectral Properties of Conifer Needles. Remote Sens. Environ. 1989, 27, 81–91. [Google Scholar] [CrossRef]
  53. Mesarch, M.A.; Walter-Shea, E.A.; Asner, G.P.; Middleton, E.M.; Chan, S.S. A Revised Measurement Methodology for Conifer Needles Spectral Optical Properties: Evaluating the Influence of Gaps between Elements. Remote Sens. Environ. 1999, 68, 177–192. [Google Scholar] [CrossRef]
  54. Noda, H.M.; Motohka, T.; Murakami, K.; Muraoka, H.; Nasahara, K.N. Accurate Measurement of Optical Properties of Narrow Leaves and Conifer Needles with a Typical Integrating Sphere and Spectroradiometer. Plant Cell Environ. 2013, 36, 1903–1909. [Google Scholar] [CrossRef] [PubMed]
  55. Neuwirthová, E.; Lhotáková, Z.; Albrechtová, J. The Effect of Leaf Stacking on Leaf Reflectance and Vegetation Indices Measured by Contact Probe during the Season. Sensors 2017, 17, 1202. [Google Scholar] [CrossRef]
  56. Hovi, A.; Schraik, D.; Hanuš, J.; Homolová, L.; Juola, J.; Lang, M.; Lukeš, P.; Pisek, J.; Rautiainen, M. Assessment of a Photon Recollision Probability Based Forest Reflectance Model in European Boreal and Temperate Forests. Remote Sens. Environ. 2022, 269, 112804. [Google Scholar] [CrossRef]
  57. Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornelissen, J.H.; Diemer, M.; et al. The Worldwide Leaf Economics Spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef]
  58. Field, C.; Mooney, H.A. Leaf Age and Seasonal Effects on Light, Water, and Nitrogen Use Efficiency in a California Shrub. Oecologia 1983, 56, 348–355. [Google Scholar] [CrossRef]
  59. Hikosaka, K.; Hanba, Y.T.; Hirose, T.; Terashima, I. Photosynthetic Nitrogen-Use Efficiency in Leaves of Woody and Herbaceous Species. Funct. Ecol. 1998, 12, 896–905. [Google Scholar] [CrossRef]
  60. Poorter, H.; Evans, J.R. Photosynthetic Nitrogen-Use Efficiency of Species That Differ Inherently in Specific Leaf Area. Oecologia 1998, 116, 26–37. [Google Scholar] [CrossRef]
  61. Guo, Z.; Yan, Z.; Majcher, B.M.; Lee, C.K.F.; Zhao, Y.; Song, G.; Wang, B.; Wang, X.; Deng, Y.; Michaletz, S.T.; et al. Dynamic Biotic Controls of Leaf Thermoregulation across the Diel Timescale. Agric. For. Meteorol. 2022, 315, 108827. [Google Scholar] [CrossRef]
  62. Rautiainen, M.; Lukeš, P.; Homolová, L.; Hovi, A.; Pisek, J.; Mõttus, M. Spectral Properties of Coniferous Forests: A Review of In Situ and Laboratory Measurements. Remote Sens. 2018, 10, 207. [Google Scholar] [CrossRef]
  63. Rock, B.N.; Williams, D.L.; Moss, D.M.; Lauten, G.N.; Kim, M. High-Spectral Resolution Field and Laboratory Optical Reflectance Measurements of Red Spruce and Eastern Hemlock Needles and Branches. Remote Sens. Environ. 1994, 47, 176–189. [Google Scholar] [CrossRef]
  64. Knapp, A.; Carter, G. Variability in Leaf Optical Properties among 26 Species from a Broad Range of Habitats. Am. J. Bot. 1998, 85, 940. [Google Scholar] [CrossRef]
  65. Niinemets, U.; Al Afas, N.; Cescatti, A.; Pellis, A.; Ceulemans, R. Petiole Length and Biomass Investment in Support Modify Light Interception Efficiency in Dense Poplar Plantations. Tree Physiol. 2004, 24, 141–154. [Google Scholar] [CrossRef]
  66. Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Mõttus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Latorre Carmona, P.; Kaufmann, R.K.; Lewis, P.; et al. Hyperspectral Remote Sensing of Foliar Nitrogen Content. Proc. Natl. Acad. Sci. USA 2013, 110, E185–E192. [Google Scholar] [CrossRef]
  67. Rautiainen, M.; Stenberg, P. Application of Photon Recollision Probability in Coniferous Canopy Reflectance Simulations. Remote Sens. Environ. 2005, 96, 98–107. [Google Scholar] [CrossRef]
  68. Smolander, S.; Stenberg, P. A Method to Account for Shoot Scale Clumping in Coniferous Canopy Reflectance Models. Remote Sens. Environ. 2003, 88, 363–373. [Google Scholar] [CrossRef]
  69. Smith, W.K.; Brewer, C.A. The Adaptive Importance of Shoot and Crown Architecture in Conifer Trees. Am. Nat. 1994, 143, 528–532. [Google Scholar] [CrossRef]
  70. Smith, W.K.; Carter, G.A. Shoot Structural Effects on Needle Temperatures and Photosynthesis in Conifers. Am. J. Bot. 1988, 75, 496–500. [Google Scholar] [CrossRef]
  71. Niinemets, Ü.; Lukjanova, A. Needle Longevity, Shoot Growth and Branching Frequency in Relation to Site Fertility and within-Canopy Light Conditions in Pinus Sylvestris. Ann. For. Sci. 2003, 60, 195–208. [Google Scholar] [CrossRef]
  72. Ellsworth, D.S.; Reich, P.B. Canopy Structure and Vertical Patterns of Photosynthesis and Related Leaf Traits in a Deciduous Forest. Oecologia 1993, 96, 169–178. [Google Scholar] [CrossRef]
  73. Valladares, F.; Niinemets, Ü. Shade Tolerance, a Key Plant Feature of Complex Nature and Consequences. Annu. Rev. Ecol. Evol. Syst. 2008, 39, 237–257. [Google Scholar] [CrossRef]
  74. Litton, C.M.; Raich, J.W.; Ryan, M.G. Carbon Allocation in Forest Ecosystems. Glob. Change Biol. 2007, 13, 2089–2109. [Google Scholar] [CrossRef]
  75. Dybzinski, R.; Farrior, C.E.; Pacala, S.W. Increased Forest Carbon Storage with Increased Atmospheric CO2 despite Nitrogen Limitation: A Game-Theoretic Allocation Model for Trees in Competition for Nitrogen and Light. Glob. Change Biol. 2015, 21, 1182–1196. [Google Scholar] [CrossRef]
  76. Ducey, M.J. Evergreenness and Wood Density Predict Height–Diameter Scaling in Trees of the Northeastern United States. For. Ecol. Manag. 2012, 279, 21–26. [Google Scholar] [CrossRef]
  77. Cohen, Y.; Pastor, J. Interactions Among Nitrogen, Carbon, Plant Shape, and Photosynthesis. Am. Nat. 1996, 147, 847–865. [Google Scholar] [CrossRef]
  78. Kergoat, L.; Lafont, S.; Arneth, A.; Le Dantec, V.; Saugier, B. Nitrogen Controls Plant Canopy Light-Use Efficiency in Temperate and Boreal Ecosystems. J. Geophys. Res. Biogeosci. 2008, 113, G04017. [Google Scholar] [CrossRef]
  79. Chianucci, F.; Pisek, J.; Raabe, K.; Marchino, L.; Ferrara, C.; Corona, P. A Dataset of Leaf Inclination Angles for Temperate and Boreal Broadleaf Woody Species. Ann. For. Sci. 2018, 75, 50. [Google Scholar] [CrossRef]
  80. Kattenborn, T.; Richter, R.; Guimarães-Steinicke, C.; Feilhauer, H.; Wirth, C. AngleCam: Predicting the Temporal Variation of Leaf Angle Distributions from Image Series with Deep Learning. Methods Ecol. Evol. 2022, 13, 2531–2545. [Google Scholar] [CrossRef]
  81. McNeil, B.E.; Pisek, J.; Lepisk, H.; Flamenco, E.A. Measuring Leaf Angle Distribution in Broadleaf Canopies Using UAVs. Agric. For. Meteorol. 2016, 218–219, 204–208. [Google Scholar] [CrossRef]
  82. King, D.A. The Functional Significance of Leaf Angle in Eucalyptus. Aust. J. Bot. 1997, 45, 619–639. [Google Scholar] [CrossRef]
  83. Reaves, V.C.; Elmore, A.J.; Nelson, D.M.; McNeil, B.E. Drivers of Spatial Variability in Greendown within an Oak-Hickory Forest Landscape. Remote Sens. Environ. 2018, 210, 422–433. [Google Scholar] [CrossRef]
  84. Zhu, C.G.; Chen, Y.N.; Li, W.H.; Chen, X.L.; He, G.Z. Heliotropic Leaf Movement of Sophora alopecuroides L.: An Efficient Strategy to Optimise Photochemical Performance. Photosynthetica 2015, 53, 231–240. [Google Scholar] [CrossRef]
  85. Kattenborn, T.; Wieneke, S.; Montero, D.; Mahecha, M.D.; Richter, R.; Guimarães-Steinicke, C.; Wirth, C.; Ferlian, O.; Feilhauer, H.; Sachsenmaier, L.; et al. Temporal Dynamics in Vertical Leaf Angles Can Confound Vegetation Indices Widely Used in Earth Observations. Commun. Earth Environ. 2024, 5, 550. [Google Scholar] [CrossRef]
  86. Neuwirthová, E.; Lhotáková, Z.; Červená, L.; Lukeš, P.; Campbell, P.; Albrechtová, J. Asymmetry of Leaf Internal Structure Affects PLSR Modelling of Anatomical Traits Using VIS-NIR Leaf Level Spectra. Eur. J. Remote Sens. 2024, 57, 2292154. [Google Scholar] [CrossRef]
  87. Yang, X.; Li, R.; Jablonski, A.; Stovall, A.; Kim, J.; Yi, K.; Ma, Y.; Beverly, D.; Phillips, R.; Novick, K.; et al. Leaf Angle as a Leaf and Canopy Trait: Rejuvenating Its Role in Ecology with New Technology. Ecol. Lett. 2023, 26, 1005–1020. [Google Scholar] [CrossRef]
  88. Cho, E.; Hunsaker, A.G.; Jacobs, J.M.; Palace, M.; Sullivan, F.B.; Burakowski, E.A. Maximum Entropy Modeling to Identify Physical Drivers of Shallow Snowpack Heterogeneity Using Unpiloted Aerial System (UAS) Lidar. J. Hydrol. 2021, 602, 126722. [Google Scholar] [CrossRef]
  89. Hastings, J.H.; Ollinger, S.V.; Ouimette, A.P.; Sanders-DeMott, R.; Palace, M.W.; Ducey, M.J.; Sullivan, F.B.; Basler, D.; Orwig, D.A. Tree Species Traits Determine the Success of LiDAR-Based Crown Mapping in a Mixed Temperate Forest. Remote Sens. 2020, 12, 309. [Google Scholar] [CrossRef]
  90. Sullivan, F.B.; Hunsaker, A.G.; Palace, M.W.; Jacobs, J.M. Evaluating the Effects of UAS Flight Speed on Lidar Snow Depth Estimation in a Heterogeneous Landscape. Remote Sens. 2023, 15, 5091. [Google Scholar] [CrossRef]
  91. Hilker, T.; Gitelson, A.; Coops, N.C.; Hall, F.G.; Black, T.A. Tracking Plant Physiological Properties from Multi-Angular Tower-Based Remote Sensing. Oecologia 2011, 165, 865–876. [Google Scholar] [CrossRef] [PubMed]
Remotesensing 18 00355 g001
Figure 1. The location of Bartlett Experimental Forest is shown in (a) within the state of New Hampshire in the United States. NEON AOP RGB color composite from hyperspectral data (b) and digital surface model (c) were acquired in August 2019. RGB and lidar canopy surface data for plots ranging from predominantly broadleaf (top row) to predominantly needleleaf (bottom row) are shown in (d).
Figure 1. The location of Bartlett Experimental Forest is shown in (a) within the state of New Hampshire in the United States. NEON AOP RGB color composite from hyperspectral data (b) and digital surface model (c) were acquired in August 2019. RGB and lidar canopy surface data for plots ranging from predominantly broadleaf (top row) to predominantly needleleaf (bottom row) are shown in (d).
Remotesensing 18 00355 g001
Remotesensing 18 00355 g002
Figure 2. Leaf stack model results showing estimates of transmittance (long dash), absorptance (solid line), and reflectance for broadleaf (light green) and needleleaf (dark green) species averaged over the NIR region of the electromagnetic spectrum (850–1050 nm) at stack depths (N) of 1, 2, 3, 4, 6, and 8 leaves.
Figure 2. Leaf stack model results showing estimates of transmittance (long dash), absorptance (solid line), and reflectance for broadleaf (light green) and needleleaf (dark green) species averaged over the NIR region of the electromagnetic spectrum (850–1050 nm) at stack depths (N) of 1, 2, 3, 4, 6, and 8 leaves.
Remotesensing 18 00355 g002
Remotesensing 18 00355 g003
Figure 3. Validation scatter plot of leaf stack model for transmittance (squares), absorptance (circles), and reflectance (triangles) using measurements made on broadleaf species for stack depth (N) of 2 (lightest green), 3, 4, 6, and 8 (darkest green) leaves.
Figure 3. Validation scatter plot of leaf stack model for transmittance (squares), absorptance (circles), and reflectance (triangles) using measurements made on broadleaf species for stack depth (N) of 2 (lightest green), 3, 4, 6, and 8 (darkest green) leaves.
Remotesensing 18 00355 g003
Remotesensing 18 00355 g004
Figure 4. Linear relationships between canopy %N and weighted mean NIR leaf reflectance of plots for individual leaves (open triangles, dashed line, r2 = 0.78), LAI-weighted leaf reflectance (open circles, green line, r2 = 0.86), and NEON AOP directional reflectance (solid circles, black line, r2 = 0.73) for the NIR region between 850 and 1050 nm.
Figure 4. Linear relationships between canopy %N and weighted mean NIR leaf reflectance of plots for individual leaves (open triangles, dashed line, r2 = 0.78), LAI-weighted leaf reflectance (open circles, green line, r2 = 0.86), and NEON AOP directional reflectance (solid circles, black line, r2 = 0.73) for the NIR region between 850 and 1050 nm.
Remotesensing 18 00355 g004
Remotesensing 18 00355 g005
Figure 5. Relationship between IRrNIR and NIRv (black circles) with overlaid linear trendline (black line, r2 = 0.93).
Figure 5. Relationship between IRrNIR and NIRv (black circles) with overlaid linear trendline (black line, r2 = 0.93).
Remotesensing 18 00355 g005
Remotesensing 18 00355 g006
Figure 6. Relationship between canopy %N and IRrNIR (black circles) with overlaid linear trendline (black line, r2 = 0.55).
Figure 6. Relationship between canopy %N and IRrNIR (black circles) with overlaid linear trendline (black line, r2 = 0.55).
Remotesensing 18 00355 g006
Table 1. Remote sensing derived metrics.
Table 1. Remote sensing derived metrics.
Data TypeAbbreviationDescription
HyperspectralNIRrCNIR reflectance of incident solar radiation of forest canopies
NIRrLAILAI-weighted NIR reflectance of leaves
NIRrLNIR reflectance of leaves, weighted by canopy composition
IRrIndex of relative reflectance
Lidar-derived structural metricsRumpleSurface roughness; surface area divided by projected area (Kane et al. [42])
RugositySurface roughness; standard deviation of canopy height model (Parker & Russ [43])
Canopy rugosityLeaf area density variability of voxels; horizontal standard deviation of vertical standard deviation (Hardiman et al. [41])
Canopy porosityProportion of closed gap (empty) voxels within the canopy (Hardiman et al. [41])
Euphotic depthPlot mean height difference between euphotic (high-light) and oligophotic (low-light) voxels within a column (Lefsky et al. [45], Kamoske et al. [44])
Table 2. Coefficient of determination values for relationships between structural metrics and IRrNIR, NIRrC, and canopy %N.
Table 2. Coefficient of determination values for relationships between structural metrics and IRrNIR, NIRrC, and canopy %N.
Structural MetricIRrNIRNIRrC%N
Rumple0.380.30.1
Rugosity0.210.140.02
Canopy rugosity0.120.130.1
Canopy porosity0.570.560.42
Euphotic depth0.230.170.04
LAI 2200C0.440.55 *0.49 *
p < 0.001, p < 0.01, p < 0.05; * Intercept not significant.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sullivan, F.B.; Hastings, J.H.; Ollinger, S.V.; Ouimette, A.; Richardson, A.D.; Palace, M. Parsing the Relative Contributions of Leaf and Canopy Traits in Airborne Spectrometer Measurements. Remote Sens. 2026, 18, 355. https://doi.org/10.3390/rs18020355

AMA Style

Sullivan FB, Hastings JH, Ollinger SV, Ouimette A, Richardson AD, Palace M. Parsing the Relative Contributions of Leaf and Canopy Traits in Airborne Spectrometer Measurements. Remote Sensing. 2026; 18(2):355. https://doi.org/10.3390/rs18020355

Chicago/Turabian Style

Sullivan, Franklin B., Jack H. Hastings, Scott V. Ollinger, Andrew Ouimette, Andrew D. Richardson, and Michael Palace. 2026. "Parsing the Relative Contributions of Leaf and Canopy Traits in Airborne Spectrometer Measurements" Remote Sensing 18, no. 2: 355. https://doi.org/10.3390/rs18020355

APA Style

Sullivan, F. B., Hastings, J. H., Ollinger, S. V., Ouimette, A., Richardson, A. D., & Palace, M. (2026). Parsing the Relative Contributions of Leaf and Canopy Traits in Airborne Spectrometer Measurements. Remote Sensing, 18(2), 355. https://doi.org/10.3390/rs18020355

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop