Electromagnetic Scattering Characteristic-Enhanced Dual-Branch Network with Simulated Image Guidance for SAR Ship Classification

Highlights

What are the main findings?

• We propose a multi-parameter adjustable spaceborne SAR image simulation method and innovatively introduce the concept of BNM.
• We propose SeDSG, which achieves the efficient extraction and adaptive fusion of SAR image features and BNM features.

What are the implications of the main findings?

• The proposed simulation method significantly expands training sample diversity and mitigates the shortage of labeled SAR images.
• The proposed network enhances detail recognition capability and structural perception accuracy, offering a practical solution for spaceborne SAR ship classification.

Abstract

Synthetic aperture radar (SAR), with its unique imaging principle and technical characteristics, has significant advantages in surface observation and thus has been widely applied in tasks such as object detection and target classification. However, limited by the lack of labeled SAR image datasets, the accuracy and generalization ability of the existing models in practical applications still need to be improved. In order to solve this problem, this paper proposes a spaceborne SAR image simulation technology and innovatively introduces the concept of bounce number map (BNM), establishing a high-resolution, parameterized simulated data support system for target recognition and classification tasks. In addition, an electromagnetic scattering characteristic-enhanced dual-branch network with simulated image guidance for SAR ship classification (SeDSG) was designed in this paper. It adopts a multi-source data utilization strategy, taking SAR images as the main branch input to capture the global features of real scenes, and using simulated data as the auxiliary branch input to excavate the electromagnetic scattering characteristics and detailed structural features. Through feature fusion, the advantages of the two branches are integrated to improve the adaptability and stability of the model to complex scenes. Experimental results show that the classification accuracy of the proposed network is improved on the OpenSARShip and FUSAR-Ship datasets. Meanwhile, the transfer learning classification results based on the SRSDD dataset verify the enhanced generalization and adaptive capabilities of the network, providing a new approach for data classification tasks with an insufficient number of samples.

1. Introduction

Synthetic aperture radar (SAR) plays a crucial role in Earth observation with all-weather and all-time capability [1]. As an advanced remote sensing technology, it can acquire high-resolution images of the Earth’s surface. Through microwave emission and echo reception, synthetic aperture technology, and signal processing, SAR achieves a fine description of the surface of the Earth. It is well-suited to monitor dynamic processes on the Earth’s surface in a reliable, continuous and global way [2], with its keen ability to capture phenomena such as the movement of ships at sea, topographic changes on land, and the melting of glaciers in polar regions.

The classification of ships in SAR images is a bridge that connects the original data and the action of decision-making. Not only does it solve the problem of efficiency and accuracy in marine monitoring, but it also provides key intelligence support for military, economic, scientific research, and other fields. For example, in the military field, accurate ship classification can help identify the types and quantities of enemy vessels, thereby offering strong decision-making support for military operations. In terms of the marine economy, it facilitates the monitoring of maritime transportation, fishery activities, and so on, ensuring the healthy development of the marine economy.

Traditional SAR ship classification methods are mainly based on features, including geometric size, contour features, scattering characteristics, etc. With the development of deep learning, the classification methods for ships have become increasingly diverse. Deep learning models can automatically learn complex data features, substantially improving classification accuracy and immediacy, and exhibiting tremendous application prospects, which has led to an increasing demand for datasets. Currently, although a large number of SAR image classification datasets have been successively released and widely used, several key challenges still exist. To begin with, data diversity is insufficient, manifesting in single-scene coverage, unbalanced distributions of categories, and limited polarization modes. Beyond that, annotation quality and standardization need improvement, as issues such as poor annotation consistency, inconsistent or missing attribute labels, and a lack of standardized evaluation indicators remain prevalent. Additionally, adaptability to practical application scenarios is insufficient, given that sensor parameters vary widely, environmental robustness is weak, and real-time performance fails to meet practical needs.

In summary, taking into account the current practical needs, this paper achieves two innovations:

(1)

To enhance the adaptability of the dataset to actual scenarios, this paper proposes a ship image simulation technology for spaceborne SAR systems. By constructing a multi-parameter adjustable simulation framework, it can flexibly generate simulation images covering different ship types, namely bulk carriers, container ships, and tankers, under diverse satellite imaging parameters, such as resolution, incident angle, and polarization mode, effectively solving the problems of the lack of labeled SAR image data and the imbalance of category distribution. On this basis, this paper innovatively introduces the concept of BNM. By recording the average reflection times of rays in the corresponding area of each pixel point in the image, this paper constructs an enhanced feature map capable of precisely characterizing the three-dimensional structural features and local scattering characteristics of the ship.

(2)

To systematically verify the practical value of simulation images and deeply explore their multi-dimensional feature information, this paper proposes an electromagnetic scattering characteristic-enhanced dual-branch network with simulated image guidance for SAR ship classification (SeDSG). This framework achieves the fusion of SAR image features and the structural features of BNM by constructing a parallel architecture of the main branch and the auxiliary branch. The main branch adopts the improved ResNet-50 backbone network to extract the grayscale, contour, and texture features of the image, while the auxiliary branch leverages the SlimHRNet-Backbone to prioritize the electromagnetic scattering characteristics within the BNM and establish the correlation between it and the 3D structural attributes of the target. Finally, multi-scale feature fusion is achieved through the cross-branch feature pyramid fusion module. Experiments show that the simulation images generated by the proposed method not only significantly expand the diversity of training samples, but also effectively improve the detail identification ability and structure perception accuracy of the ship classification model, which provides key data support and technical innovation for spaceborne SAR ship classification.

The remainder of this article is structured as follows. Section 2 introduces the related work of ship classification based on SAR images, covering the latest progress in traditional algorithms and deep learning algorithms, as well as the application status of multimodal methods and electromagnetic simulation-assisted methods. Section 3 describes the simulation-classification collaboration framework, introduces the multi-parameter controllable SAR simulation image generation method, and elaborates on the design of SeDSG including BNM feature extraction and the cross-branch fusion mechanism. In Section 4, based on the OpenSARShip, FUSAR-Ship, and SRSDD datasets, the significant auxiliary capability of simulated images in enhancing model performance was successfully verified. Furthermore, with the aid of comprehensive ablation experiments, a meticulous and systematic analysis was carried out to evaluate the effectiveness of each module in the network. The conclusions are drawn in Section 5.

2. Related Works

2.1. Ship Classification Methods Based on SAR Images

In recent years, with the widespread application of high-resolution satellites, research on ship detection and classification based on spaceborne SAR images has become increasingly abundant. Improvements have been made to the accuracy, efficiency, and generalization performance of ship classification from different perspectives.

In traditional methods of ship classification, feature parameters are extracted from detected ship target chips using appropriate image processing approaches, and then these parameters are classified by machine learning classifiers. The commonly utilized features fall into two main categories: geometric features and electromagnetic scattering characteristics. Geometric features can accurately reflect characteristics such as the aspect ratio, shape contour, rectangularity, principal axis, and fractal dimension of the target. Chen W T et al. [3] summarized the geometric features of ship targets in SAR images and introduced the calculation methods and significance of commonly used geometric features. However, due to the influence of sidelobe effects from strong scattering targets in SAR images, the performance of geometric feature extraction is not very satisfactory. To address this issue, Hongliang Zhu et al. [4] proposed a method to eliminate the sidelobes of strong scattering points in the original SAR images of ships. By extracting the visual model contour of the ship and removing the grayscale information outside the hull, the classification accuracy was improved. Electromagnetic scattering characteristics include permanent symmetric scatterers [5], polarization characteristics [6], local radar cross-section density [7], 2D comb features [8], and other relevant features.

To improve the accuracy of ship classification tasks, researchers have proposed various machine learning classifiers based on the characteristics of targets. Zhi Zhao et al. [9] proposed a ship classification scheme, which uses the analytic hierarchy process (AHP) to evaluate and select features, fuse classification results, and then applies the K-Nearest Neighbor (KNN) algorithm to classify ships based on the selected features. Chao Wang et al. [10] proposed a hierarchical ship classifier for COSMO-SkyMed dataset. After preprocessing ship target chips, the classifier achieves classification by combining geometric features and backscattering characteristics. These methods primarily enhance classification performance through feature selection optimization. However, they also render the classification task excessively reliant on features and classifiers. To address this issue, researchers have improved performance by reducing feature dependence or optimizing classifiers. Makedonas et al. [11] proposed a two-stage hierarchical feature selection algorithm, which can more accurately determine the optimal feature combination suitable for the final classification. In addition, improvements have been made to dictionary construction methods. Xiangwei Xing et al. [7] aimed to more accurately describe ship features and reduce the dimension of the dictionary in sparse representation classification (SRC). To achieve this, they selected representative feature vectors to construct the dictionary instead of directly using pixel information. Huiping Lin et al. [12] obtained features through an active learning strategy. Within the task-driven dictionary learning (TDDL) framework, they jointly trained the discriminative dictionary and linear classifier. This approach significantly enhances the adaptability, effectiveness, and robustness of the method.

With the continuous development of deep learning technology, research on ship classification is shifting to methods based on deep learning principles. In early studies, shallow convolutional neural networks (CNNs) were employed to classify ship targets. Carlos Bentes et al. [13] proposed a multiple input resolution CNN model, constructed a complete process for marine target detection and classification in TerraSAR-X images, and verified the effectiveness of the CNN model in SAR image classification tasks. To further explore the classification performance and existing problems of convolutional networks, Ryan J. Soldin [14] used ResNet-18 to classify 10 types of targets based on the MSTAR dataset. Additionally, he explored the impact of newly emerging categories with extremely limited training samples on the classifier. Compared with traditional methods, classifiers based on convolutional neural networks have improved classification accuracy. However, most models are overly reliant on the abstract features extracted by deep networks. To further enhance the classification performance, Tianwen Zhang et al. [15] explored the fusion of traditional handcrafted features and CNN models, which further improved the accuracy. Nevertheless, existing models have low efficiency when processing satellite data and cannot achieve real-time processing. Moreover, deep neural networks themselves have potential vulnerabilities, which may lead to serious security threats when facing various adversarial attacks. This issue is equally prominent in SAR ship detection tasks, and to address it, H. Ke et al. [16] proposed a Laplace & LBP feature-guided SAR ship detection method with an adaptive feature enhancement block, which integrates traditional and adaptive enhanced features to achieve superior accuracy on the open SSDD dataset compared to other detectors. In addition to these improved methods, a progressive approaching SAR ship detection paradigm named COPO, following the principle of divergence to Concentration and POpulation to individual, has been proposed for subsequent ship classification tasks [17].

To address the issue of low efficiency, Teng Xu et al. [18] proposed a network called MobileShuffle that combines hardware-friendly modules and structural reparameterization techniques to accelerate the inference process. To tackle the problem of poor robustness, Hai-Nan Wei et al. [19] proposed a multi-objective adversarially robust CNN, namely MoAR-CNN, achieving a balance between data accuracy and adversarial robustness. To address the challenges of SAR ship classification caused by complex maritime conditions and ship imaging variations, Jinglu He et al. [20] proposed the cross-polarimetric interaction network (CPINet). It leverages deep learning strategies to explore the abundant polarization information of dual-pol SAR images. With its innovative feature extraction and fusion mechanisms, it achieves high-performance ship classification and provides an effective solution for related tasks.

2.2. Methods Assisted by Electromagnetic Simulation

When conducting target recognition and classification tasks on SAR images, a series of challenges are often encountered, such as a scarcity of samples in the dataset, limited image resolution, missing label information, and uneven distribution of samples across different categories. To improve the effectiveness of target recognition and classification, it is highly necessary to expand the existing dataset. Currently, most algorithms employ strategies like image scaling, cropping, flipping, and color transformation for data augmentation. However, these methods do not fundamentally enhance the quality of the dataset. In view of this, some scholars have begun to explore data augmentation strategies based on 3D models. Specifically, they construct computational models and simulate radar imaging processes to generate simulated images with various parameters.

For Automatic Target Recognition (ATR), Anders Kusk et al. [21] used commercial electromagnetic simulation software to calculate the radar cross section (RCS) of targets and combined it with SAR systems and terrain models to generate simulated SAR images based on the CAD model of a T90 tank. On this basis, David Malmgren-Hansen et al. [22] further generated a simulated dataset, SARSIM, which includes 14 vehicle CAD models at 7 different depression angles. Experimental results show that conducting transfer learning based on this simulated dataset can significantly improve the performance of ATR models on SAR datasets, especially in situations where real data is scarce, providing an effective solution for small-sample situations and also validating the effectiveness of simulated images in dataset expansion. Yan, Y. et al. [23] generated simulated images by superimposing 3D models with the same scale as real ships onto real background images and trained a Faster R-CNN based on the ResNet-101 using a dataset that includes both simulated and real images, further confirming that data augmentation methods based on simulated images can enhance detection performance.

To integrate scattering features into deep networks and characterize ship target features more comprehensively, X. Zhang et al. [24] propose a multiscale global scattering feature association network (MGSFA-Net) for SAR ship target recognition. It separates targets from the background to achieve effective extraction of scattering features, thereby enriching the diversity of ship features. Aiming at the limitation of ignoring the complex feature of images in SAR target recognition, P. Ni et al. [25] innovatively proposed EFMM-Net. It integrates electromagnetic features into the dual-stream manifold multiscale network, achieves parallel feature extraction based on the scattering-guided manifold multiscale (SGMM) backbone, and achieves enhanced feature fusion through the location awareness feature fusion (LAFF) recognition module, providing an effective new approach for recognizing SAR targets with high visual similarity.

Although this augmentation method can quickly generate simulated images with different parameters, there are still significant differences between simulated and real images. To address this issue, many scholars have proposed feasible solutions from different perspectives, mainly divided into two categories.

The first category of methods focuses on dataset augmentation techniques, directly optimizing the differences between simulated and real images without considering the recognition and classification networks. For example, Feng, S. et al. [26] constructed the SingleScene-SAR Simulator, combining electromagnetic simulation with the CycleGAN network to generate simulated images with high similarity to SAR images. Zongyong Cui et al. [27] proposed a global feature compensation network based on Generative Adversarial Networks (GANs). It effectively addressed the issue where simulated images exhibited similarity yet failed to meet usability requirements, thereby enhancing their capacity to better support SAR target recognition.

The second category of methods is based on model fine-tuning strategies or transfer learning methods, designing more suitable network structures. For example, Chen Zhang et al. [28] proposed a multi-similarity fusion classifier to address the problem of accurately recognizing targets using only simulated images for network training. Based on unsupervised domain adaptation, Lyu Xiaoling et al. [29] proposed a classification method assisted by simulation images. In implementing the method, they conducted domain adversarial training between the feature extractor and domain discriminator and used multi-kernel maximum mean distance for domain difference calculation, thus optimizing the classification model. On this basis, they further proposed a novel network integrating dual-branch image reconstruction and subdomain alignment [30], focusing more attention on the target area and effectively reducing the dependence on sample labels in classification tasks.

Although there are various methods that can generate simulated images efficiently and at a low time cost, differences still exist between these simulated images and SAR images, limiting their ability to improve recognition and classification performance. To solve this problem, existing research mainly focuses on two directions. The one is to use GANs to enhance the similarity between simulated and measured images. The other is to improve network models for effective feature extraction from simulated images, thereby enhancing recognition and classification performance. However, when confronting different datasets and classification tasks, existing methods still lack the ability to effectively extract useful information from simulated data, leading to poor generalization performance, and their accuracy and efficiency in recognition and classification still need further improvement.

3. Materials and Methods

3.1. Generation of Bounce Number Map (BNM)

In practical applications, SAR images are constrained by imaging quality, which increases the difficulty of extracting scattering characteristics. In addition, structural differences among ships of the same type, as well as feature variations of the same ship under different incident angles, azimuth angles, and polarization modes, all affect classification performance.

To address this issue, this paper proposes the definition of BNM, which aims to mitigate the aforementioned challenges by visualizing structure-related scattering characteristics. The physical significance of the BNM lies in quantifying the direct mapping relationship between typical geometric structural components of ships such as flat decks and dihedral superstructures and corresponding electromagnetic scattering behaviors including surface scattering and multiple scattering by means of the statistical distribution of scattering counts. It serves as a crucial foundation for ship classification tasks based on SAR images.

As illustrated in Figure 1, flat or smooth curved surface areas of the ship, such as decks and hull sides, are dominated by surface scattering, which is associated with relatively weak echo energy, resulting in these regions generally appearing darker in SAR images. In contrast, superstructures such as cockpits and cranes form dihedral and trihedral angle structures, leading to multiple scattering and thus appearing as brighter regions in SAR images.

Among traditional scattering features, RCS merely serves to characterize the energy distribution of echo signals, bearing no direct correlation with the geometric structure of targets. As for polarization characteristics, their core function lies in reflecting the differential scattering responses of terrain objects to incident waves with distinct polarization modes, and they only maintain an indirect association with structural information. In contrast, BNM achieves the visual and quantitative unification of structural morphology and scattering mechanisms, thereby functioning as a significant feature underpinned by physical principles for ship classification tasks.

To generate the BNM, this paper adopts the shooting and bouncing ray (SBR) method [31], a high-frequency approximation technique that integrates geometrical optics (GO) and physical optics (PO). It leverages the GO method for rapid ray path tracing and the PO method for efficient scattering field intensity calculation, thus boasting the advantages of fast computation speed and high accuracy. The calculation of RCS for electrically large-scale targets involves the following steps:

• Extract key information such as dimensions and structure from the target model file, and represent it using an appropriate data structure to facilitate computer processing;
• Construct a ray pool based on conditions including resolution and satellite parameters, and complete the accurate determination of target incidence points;
• Trace all ray tubes using the GO method until the rays no longer intersect the target or reach the preset upper limit of reflection times, and synchronously record the number of ray reflections during the tracing process to provide data support for generating the BNM;
• Based on the calculation results of the electromagnetic field when the rays depart from the target surface, comply with the electromagnetic field equivalence principle, and combine the polarization directions of electromagnetic wave transmission and reception to calculate the RCS of the entire target using the PO method.

3.1.1. Target Modeling and Incidence Point Determination

To enable computers to better calculate the electromagnetic scattering characteristics of a target, it is necessary to segment the target. The model file is in the stereolithography (STL) format, with small triangular facets as the basic unit. Each facet is represented by a normal vector and the three vertices of the triangle, and it is used to discretely approximate and describe the surface of the 3D model. In this paper, the STL file is stored in binary format. Figure 2 shows the actual oil tanker model and its corresponding binary STL file.

In consideration of runtime efficiency, we generate a spatially ordered index array of triangular facets in the mesh. Based on the array, a bounding volume hierarchy (BVH) [32] is constructed to efficiently support intersection point determination and ray tracing operations.

At the stage of index construction, the centroid position of each facet in the STL file is calculated firstly based on its vertex coordinates, followed by normalization and discretization. These centroid coordinates then serve as the basis for generating Morton codes, converting three-dimensional spatial coordinates into one-dimensional codes. The method preserves the correlation of original spatial positions through sorting.

To facilitate ray intersection computation, this paper generates and optimizes the structure of BVH. Its core principle is to convert the geometry into a binary tree, thereby quickly eliminating irrelevant spatial regions. Division starts from the root node and proceeds sequentially until each node contains at most one triangular facet. At the optimization phase, a post-order traversal algorithm is used to process nodes layer by layer from leaf nodes to the root node, removing empty nodes and adjusting the indices of the remaining nodes. In the simplified BVH array, leaf nodes store data of the corresponding triangular facets, while branch nodes store node status, parent node index, child node indices, and bounding box information.

When determining the intersection point of a ray on the model, traversal starts from the root node of the BVH following the depth-first principle. That is, first perform an intersection test between the ray and the axis-aligned bounding box of the current node. If there is no intersection, the branch is directly eliminated. If an intersection exists, the test proceeds to the next layer, continuing until a leaf node is reached, where the corresponding triangular facet contains the intersection point. If no intersecting node is found after traversing the entire BVH structure, it indicates that the ray does not intersect the target model. Based on this algorithm, assuming the total number of triangular facets is N, the time complexity of the search process is only $O\left({log}_{2}N\right)$, which is a logarithmic time cost and much lower than $O\left(N\right)$ for direct traversal.

3.1.2. Ray Tracing Algorithm

The ray tracing algorithm based on GO accurately tracks the optical path of each ray tube. It can fully take into account the multiple reflection of rays, thereby improving the integrity and effectiveness of RCS calculation for complex targets. In practical applications, it is necessary to construct reflected ray tubes to clarify the complete optical path of all rays. According to the reflection law, the reflection angle of the ray on the target surface is equal to the incident angle. Thus, the reflection direction can be expressed by the normal vector and the incident direction as follows:

$$k_r=k_i-2\left(k_i · n\right)· n$$

(1)

To facilitate the recording of reflection counts, the surface of the target model is discretized into a point-array target. Based on the model dimensions and the set resolution parameters, the number of points in the range direction $N_r$ and azimuth direction $N_a$ can be derived, with their calculation formulas given respectively as:

$$N_r=⌊{\displaystyle \frac{\parallel (x_{max},y_{max},z_{max})\parallel +\parallel (x_{min},y_{min},z_{min})\parallel }{{\rho }_r}}⌋+1$$

(2)

$$N_a=⌊{\displaystyle \frac{\parallel (x_{max},y_{max},z_{max})\parallel +\parallel (x_{min},y_{min},z_{min})\parallel }{{\rho }_a}}⌋+1$$

(3)

where $(x_{max},y_{max},z_{max})$ and $(x_{min},y_{min},z_{min})$ represent the boundary point coordinates of the target model region. $\parallel (x_{max},y_{max},z_{max})\parallel$ and $\parallel (x_{min},y_{min},z_{min})\parallel$ denote the Euclidean distances from these two vertices to the coordinate origin, which are used to characterize the spatial extent of the target model. Respectively, ${\rho }_r$ and ${\rho }_a$ represent the resolution in the range direction and azimuth direction. Adjusting these parameters can control the density of the point array and generate simulated images with different resolutions. The grid coordinates in the range and azimuth directions can be calculated as follows:

$$x_r\left(i\right)=-\parallel (x_{min},y_{min},z_{min})\parallel +(i-1)·{\rho }_r,i=1,2,\dots ,N_r$$

(4)

$$y_a\left(j\right)=-\parallel (x_{min},y_{min},z_{min})\parallel +(j-1)·{\rho }_a,j=1,2,\dots ,N_a$$

(5)

When generating the discrete point-array target, estimating the span of the target region using boundary point coordinates ensures full target coverage by the grid and enhances robustness. To collect sufficient data points within the synthetic aperture time to meet the requirements of imaging resolution and the sampling theorem, the formula for the azimuth sampling number is expressed as:

$$K=\lfloor T_{syn}·PRF\rfloor +1$$

(6)

where $PRF$ is the pulse repetition frequency, which needs to satisfy the Nyquist sampling theorem to avoid azimuth ambiguity. $T_{syn}$ is the synthetic aperture time, and its expression is:

$$T_{syn}={\displaystyle \frac{L_{syn}}{v_{radar}}}={\displaystyle \frac{2R_{ref}tan\left(\frac{{\theta }_a}{2}\right)}{v_{radar}}}$$

(7)

where $L_{syn}$ is the synthetic aperture length, which is determined by the reference slant range $R_{ref}$ from the radar to the target and the azimuth scanning angle ${\theta }_a$. $v_{radar}$ is the effective velocity of the radar platform, which can be calculated from satellite orbit parameters.

Despite structural differences among different models of the same type of ship, functional consistency leads to similar component types and positional distributions. Thus, classifying targets based on the unique differences in geometric dimensions, shape contours, and scattering characteristics exhibited in SAR images is a practically effective approach. Figure 3, Figure 4, and Figure 5 respectively show the ship models and their simulated images for the bulk carrier, container ship and tanker. The relevant simulation parameters are summarized in

Table 1. SAR simulation parameters.

Parameter	Symbol	Value
Incident angle	${\theta }_i$	20∼50 °
Z-axis rotation angle	${\theta }_z$	242°
Azimuth scanning angle	${\theta }_a$	0.7554°
Range resolution	${\rho }_r$	$0.5\mathrm{m}$
Azimuth resolution	${\rho }_a$	$0.5\mathrm{m}$
Central operating frequency	$f_0$	$9.6\times {10}^9\mathrm{Hz}$
Pulse repetition frequency	$f_{\mathrm{PRF}}$	$5.7078\times {10}^3\mathrm{Hz}$
Satellite reference slant range	$R_{\mathrm{ref}}$	633,990 m

.

In practical applications, during ray tracing, it is essential to record the number of reflections of each ray along its propagation path, thereby generating a bounce number map under specified parameters. The process is specifically implemented as follows:

• Based on the pre-divided grid structure, adjacent triangular facets are assigned to their corresponding grid cells to clarify the reflection positions of rays, thereby establishing the mapping relationship between rays and the grid.
• In the ray tracing phase, a bidirectional path tracing algorithm is employed to record the propagation path of each ray in real time. Upon the intersection of a ray with the target surface, the reflection count statistic of the corresponding grid point is updated. This ensures that each reflection process is accurately recorded.
• After the completion of ray tracing, for each grid point, the reflection counts of all rays passing through that location are summed. The average bounce number is then calculated by dividing this total by the number of valid rays, which is subsequently used as the bounce number index for the grid point.
• By generating a bounce number distribution map on the target surface, the computed data is visualized to facilitate a more intuitive presentation of the scattering counts at different positions on the target.

As clearly shown in the figures, scattering distributions vary significantly across different ship types. Specifically, multiple scattering of tankers is mainly concentrated in the stern and middle cargo oil pipe areas. For container ships, the regular arrangement of cargo makes multiple scattering prone to occur in the slits between containers. Bulk carriers feature a simpler structure, so multiple scattering primarily appears at specific positions such as cranes and the stern wheelhouse. The distribution of these multiple scattering areas aligns closely with the unique structural characteristics of different ship types, and this thus serves as an important basis for ship classification. Moreover, for a more intuitive demonstration of BNM’s parameter-dependent feature representation, Figure 6 displays its visualization results of typical ship models under varied incident and Z-axis rotation angles.

3.1.3. Electromagnetic Calculation

After tracing all rays, the scattered field integral is evaluated via Physical Optics based on the illuminated region. Each ray tube’s contribution to far-field scattering is calculated, and the target’s total scattered field is obtained by superimposing all rays’ contributions.

During the ray tube’s propagation and continuous reflection, its internal electric field intensity and phase change. The relationship for the ray’s field intensity variation after reflection is given by:

$$\mathbf{E}\left({\mathbf{r}}_{n+1}\right)=DF·\mathsf{\Gamma }·\mathbf{E}\left({\mathbf{r}}_n\right)exp\left(-jk|{\mathbf{r}}_{n+1}-{\mathbf{r}}_n|\right)$$

(8)

where $|{\mathbf{r}}_{n+1}-{\mathbf{r}}_n|$ denotes the propagation path of the reflected ray, $DF$ is the ray divergence factor that quantifies the degree of electric field intensity attenuation caused by the wavefront expansion, and $\mathsf{\Gamma }$ is the target surface reflection coefficient. Due to different reflection coefficients in vertical and horizontal directions, the incident wave is decomposed into horizontally and vertically polarized wave, with their reflection coefficients calculated via Fresnel equations respectively.

For a monostatic radar, since transmission and reception are performed by the same base station, ray tubes with large deviations between the exit direction and the incident direction contribute little to the total scattered field. Calculating only rays within the adjacent angular range will introduce significant errors. Thus, all ray tubes need to be superimposed to compute the total scattered field. Figure 7 illustrates the electromagnetic scattering of a facet on the target surface, where $\mathbf{i}$ is the unit vector of the incident wave direction, and P is the position of the receiving antenna.

After calculating the reflected field, the expression for the scattered field at point P is derived from the Stratton-Chu integral [33] as follows:

$$\mathbf{E}\left(\mathbf{r}\right)={\oint }_S\left\{-j\omega \mu [\mathbf{n}\times \mathbf{H}\left({\mathbf{r}}^{\prime }\right)]G+[\mathbf{n}·\mathbf{E}\left({\mathbf{r}}^{\prime }\right)]{\nabla }^{\prime }G+[\mathbf{n}\times \mathbf{E}\left({\mathbf{r}}^{\prime }\right)]\times {\nabla }^{\prime }G\right\}d{S}^{\prime }$$

(9)

$$\mathbf{H}\left(\mathbf{r}\right)={\oint }_S\left\{j\omega \epsilon [\mathbf{n}\times \mathbf{E}\left({\mathbf{r}}^{\prime }\right)]G+[\mathbf{n}·\mathbf{H}\left({\mathbf{r}}^{\prime }\right)]{\nabla }^{\prime }G+[\mathbf{n}\times \mathbf{H}\left({\mathbf{r}}^{\prime }\right)]\times {\nabla }^{\prime }G\right\}d{S}^{\prime }$$

(10)

where S denotes a curved surface that encompasses the exit aperture plane of the ray tube and encloses the entire scatterer, and $\mathbf{r}$ and ${\mathbf{r}}^{\prime }$ respectively represent the position vectors of the receiving antenna and the boundary surface S. Since the spaceborne radar satisfies the far-field condition, the Green’s function can be expressed as:

$$G(\mathbf{r},{\mathbf{r}}^{\prime })={\displaystyle \frac{exp\left(ik\right|\mathbf{r}-{\mathbf{r}}^{\prime }\left|\right)}{4\pi |\mathbf{r}-{\mathbf{r}}^{\prime }|}}\approx {\displaystyle \frac{exp\left(ikr\right)}{4\pi r}}exp(-ik\mathbf{r}·{\mathbf{r}}^{\prime })$$

(11)

According to the simplified Green’s function, the calculation expression for the scattered field used in practical engineering is derived as follows:

$$\mathbf{E}\left(\mathbf{r}\right)={\oint }_S\left\{-j\omega \mu \left[\mathbf{n}\times \mathbf{H}\left({\mathbf{r}}^{\prime }\right)\right]-jk\mathbf{E}\left({\mathbf{r}}^{\prime }\right)\left(\mathbf{n}·\mathbf{r}\right)\right\}Gd{S}^{\prime }$$

(12)

$$\mathbf{H}\left(\mathbf{r}\right)={\oint }_S\left\{j\omega \epsilon \left[\mathbf{n}\times \mathbf{E}\left({\mathbf{r}}^{\prime }\right)\right]-jk\mathbf{H}\left({\mathbf{r}}^{\prime }\right)\left(\mathbf{n}·\mathbf{r}\right)\right\}Gd{S}^{\prime }$$

(13)

where $\mathbf{E}\left({\mathbf{r}}^{\prime }\right)$ and $\mathbf{H}\left({\mathbf{r}}^{\prime }\right)$ are respectively the electric field and magnetic field after the superposition of the incident field and the reflected field.

A radar has two polarization directions for both transmission and reception: vertical polarization (V-polarization) and horizontal polarization (H-polarization). Based on the calculated scattered field, the electric field is expressed as:

$$\mathbf{E}\left(\mathbf{r}\right)=E_r^H\widehat{\theta }+E_r^V\widehat{\phi }$$

(14)

where $E_r^H$ and $E_r^V$ respectively correspond to the horizontal and vertical polarization components of the scattered electric field. The expressions of RCS under four different polarization conditions are presented in

Table 2. Definitions of RCS under four different polarization conditions.

Incident Polarization Form	Horizontal Polarization	Vertical Polarization
Co-polarization	${\mathrm{RCS}}_{HH}=4\pi r^2{\displaystyle \frac{|E_r^H{|}^2}{|E_i^H{|}^2}}$	${\mathrm{RCS}}_{VV}=4\pi r^2{\displaystyle \frac{|E_r^V{|}^2}{|E_i^V{|}^2}}$
Cross-polarization	${\mathrm{RCS}}_{HV}=4\pi r^2{\displaystyle \frac{|E_r^V{|}^2}{|E_i^H{|}^2}}$	${\mathrm{RCS}}_{VH}=4\pi r^2{\displaystyle \frac{|E_r^H{|}^2}{|E_i^V{|}^2}}$

.

3.2. Design of Dual-Branch Network Architecture

In recent years, deep learning networks have emerged as the mainstream technology in the field of image classification. However, existing algorithms lack effective classification strategies for ship categories with scarce samples. Meanwhile, the problems of obvious differences within the same category and high similarity between different categories of ships in SAR images remain unresolved. To overcome this challenge, some scholars have attempted to expand the dataset scale using simulated images [26,27,28,29].

Although the simulation process has been optimized through various approaches, significant discrepancies still exist between simulated images and measured images of the same target. The main reasons are as follows:

(1)

Deviations exist in the fine structures and material properties between 3D models and real ships, and the computer processing technology for the models requires further improvement;

(2)

Dynamic changes in spatiotemporal conditions lead to uncertain fluctuations in ship loading states, which undermines the adaptability of simulated images to actual scenarios;

(3)

Simulated images lack sufficient accuracy in simulating imaging noise and complex background elements, such as the sea surface environment, making it difficult to fully cover various practical application scenarios.

To solve these issues, this paper proposes an electromagnetic scattering characteristic-enhanced dual-branch network with simulated image guidance for SAR ship classification (SeDSG) from the perspective of network architecture optimization. Figure 8 illustrates the architecture. While significantly reducing model complexity, the network achieves classification performance comparable to that of much deeper networks. Specifically, it adopts a parallel feature extraction strategy. By fully exploiting the feature information of both types of images and integrating attention mechanisms with feature fusion technology, the accuracy and robustness of classification are effectively enhanced. This differentiated processing design not only avoids the inherent discrepancies between simulated and measured images that are difficult to eliminate completely but also strengthens the ship classification capability of SAR images using features extracted from simulated images. It is equivalent to indirectly achieving dataset augmentation through feature transfer, thereby ultimately improving the overall classification performance.

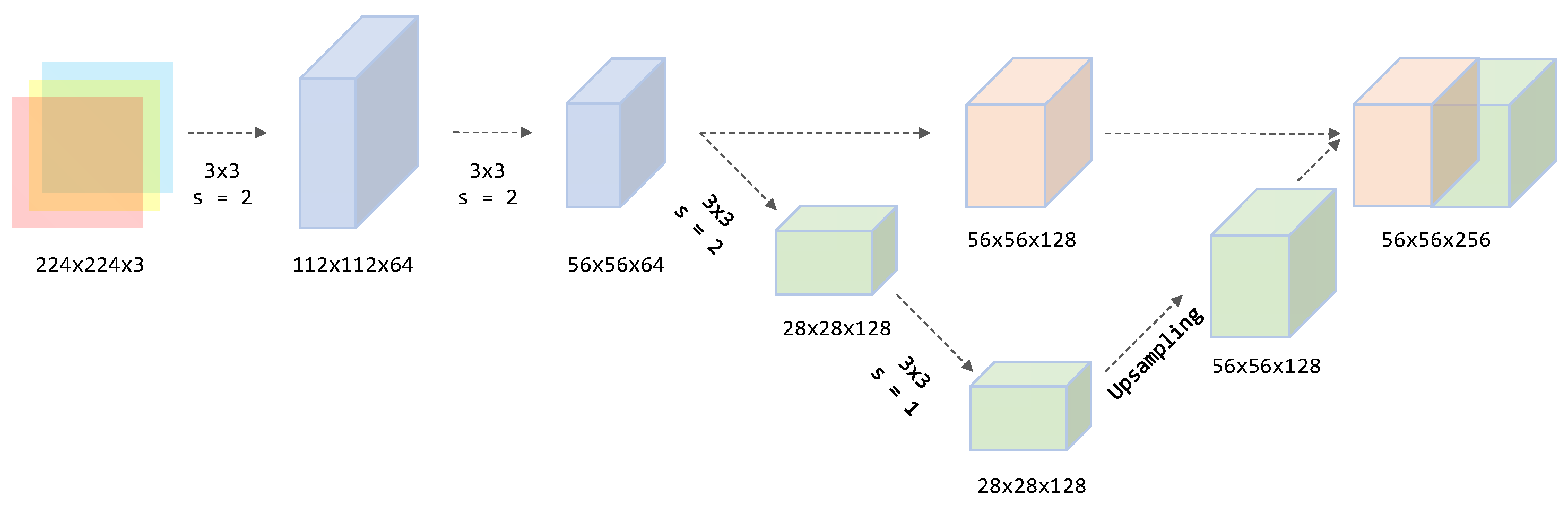
3.2.1. Main Branch Network

Through parallel design, this paper enables the auxiliary branch network to be easily integrated with different classification networks, thereby constructing a general dual-branch architecture for simulation-aided classification. Therefore, the core of network design focuses on the construction of the auxiliary branch. The main branch takes SAR images as input. After preprocessing the dataset, ResNet-50 Backbone is adopted for feature extraction. Composed of multiple ResBlocks, this network alleviates the gradient vanishing phenomenon by adding the output of each layer to the residual of that layer. Based on the traditional ResNet-50 network [34], this paper removes the global average pooling layer and fully connected layer after Layer4, outputting feature maps with a size of [2048,7,7].

This preserves spatial information and facilitates subsequent feature processing, with its core formula as follows:

$$H\left(x\right)=F\left(x\right)+x$$

(15)

where $H\left(x\right)$ is the expected output, x is the input of the residual block, and $F\left(x\right)$ is a composite function composed of three convolutional layers.

In classification tasks, CNNs are typically employed for feature extraction. However, direct utilization of these extracted features often results in unsatisfactory classification performance. The underlying reason is that shallow features primarily emphasize spatial details but lack sufficient semantic representation, while deep features, despite being rich in semantic information, suffer from low spatial resolution [35]. To better preserve boundary information and detailed features, this paper processes the feature maps extracted by ResNet-50 through the convolutional block attention module (CBAM) [36], thereby achieving efficient fusion of features at different scales and levels and enhancing the model’s ability to represent target characteristics.

When processed by the CBAM, the input feature map undergoes a two-stage refinement, namely the channel attention module and the spatial attention module. Through dynamic weight adjustment, effective integration of the feature map in both channel and spatial dimensions is achieved, enabling the model to focus more on feature maps that provide more information while suppressing the impact of invalid information on deep convolutional networks.

The attention mechanisms of the two stages are mutually independent. The calculation formula for the output of the channel attention module is as follows:

$${\mathit{M}}_c\left(\mathit{F}\right)=\sigma \left(\mathrm{MLP}\left(\mathrm{AvgPool}\right(\mathit{F}\left)\right)+\mathrm{MLP}\left(\mathrm{MaxPool}\right(\mathit{F}\left)\right)\right)$$

(16)

where $\mathit{F}$ is the input feature map, MLP denotes a multi-layer perceptron, and $\sigma$ is a Sigmoid activation function. The calculation formula for the output of the spatial attention module is as follows:

$${\mathit{M}}_s\left(\mathit{F}\right)=\sigma \left(f^{7\times 7}\left(\left[\mathrm{AvgPool}\left(\mathit{F}\right);\mathrm{MaxPool}\left(\mathit{F}\right)\right]\right)\right)$$

(17)

where $f^{7\times 7}$ represents a $7\times 7$ convolution operation, and $\left[\mathrm{AvgPool}\left(\mathit{F}\right);\mathrm{MaxPool}\left(\mathit{F}\right)\right]$ denotes the concatenation of global average pooling and max pooling results along the channel axis, thereby enhancing feature representation.

After the module, the features are compressed into a 2048-dimensional vector through adaptive average pooling, serving as a part of the input for the subsequent classifier. The main branch architecture adopted in this paper utilizes residual structures and attention mechanisms to enhance the perceptual capability of the model, providing a robust feature representation for image classification.

3.2.2. Auxiliary Branch Network

The dual-branch network adopts a mixed sample construction strategy overall. During data loading, measured images and simulated data are input synchronously, and each sample is explicitly labeled with category information to facilitate model differentiation. The auxiliary branch network takes the simulated BNM dataset as input. In the training phase, the preprocessing operations for simulated images are completely consistent with those of the main branch. By contrast, in the validation phase, simulated data is not used, and only measured images are adopted. This design enables the model to actively learn the differential features of the two types of images during training and possess the ability to classify targets using real data or simulated data independently, avoiding performance degradation caused by a single input type in practical applications. In addition, if simulated data is mixed into the validation process, the input type will be inconsistent, making it impossible to distinguish whether performance fluctuations originate from the model itself or changes in input type. Using the same data as in the prediction phase can more accurately determine the practical applicability of the model and achieve precise and stable evaluation of the network’s classification performance.

After preprocessing the input images, feature extraction needs to be performed on them. To address the problem of detail loss in traditional networks due to resolution downsampling operations during feature extraction, K. Sun et al. innovatively proposed the High-Resolution Network (HRNet) [37]. This network adopts a design where the number of channels in low-resolution branches is doubled while high-resolution branches maintain a low number of channels, enabling more efficient capture of target detail information and global features. Since the auxiliary branch needs to effectively extract detailed features of simulated images, this paper simplifies the structure of HRNet based on the task requirements of ship classification and proposes SlimHRNet-Backbone.

Figure 9 shows its network structure. It retains the core ideas of multi-resolution parallelism and feature fusion from the original network but is streamlined in terms of the number of resolution branches, phase design, and feature interaction complexity. Specifically, the four stages of the original network are simplified into two branches (high-resolution and low-resolution) without multi-stage expansion. The overall structure consists of three parts: a Stem subnetwork, a dual-branch feature extraction module, and channel fusion. In the classification task, the feature maps extracted by this network can not only capture the detailed information of ship structures such as masts and cockpits, but also be easily fused with those of SAR images, thereby effectively supplementing the information of the main branch.

The main reasons for selecting this network as the feature extractor of the auxiliary branch are as follows:

(1)

Adaptation to ship scale differences. There are significant differences in the sizes of different types of ships, and the classification of the auxiliary branch mainly relies on specific structures. The details of small ships can be clearly presented at 1/4 resolution, while the global features of large ships can still be completely retained at 1/8 resolution. The dual-branch design can accurately cover this scale range, avoiding noise introduced by excessive downsampling in HRNet due to information loss. It can not only extract the detailed features of ships but also capture the global geometric features of the entire hull, such as shape and contour.

(2)

Reduction of computational complexity. Compared with the original network, the proposed SlimHRNet-Backbone has much fewer parameters and lower computational complexity, reducing the requirement for device memory. It can be efficiently trained on ordinary GPUs, avoiding out-of-memory errors and improving feature extraction efficiency.

(3)

Compatibility with subsequent modules. The output channel number of this backbone network is uniformly 256, which fully matches the input channel requirement of the subsequent network. Meanwhile, streamlining the number of branches and the phase design reduces the difficulty of dimension alignment and channel matching during feature fusion.

To fully mine effective information from the features extracted from simulated images, this paper introduces a multi-scale pooling and feature fusion strategy, with the core of this idea drawing on the technical advantages of relevant classic methods. Specifically, spatial pyramid pooling (SPP) [38] proposed by Kaiming He et al. not only breaks the fixed limitation of CNNs on input image size, but also can simultaneously capture local details and global features through multi-scale pooling, retain the spatial structure information of images, and thereby improve the network’s recognition robustness for targets of different scales. On this basis, Hengshuang Zhao et al. further proposed the pyramid scene parsing network (PSPNet) [39], which focuses on the lack of global context information in complex scenes, establishes the association between targets and scenes through multi-scale pooling branches, and effectively improves classification accuracy. Combined with the core requirement of fusing detailed features and global features in the auxiliary branch of this paper, a pyramid pooling net (PPNet) is proposed. This module achieves efficient fusion of features at different scales through multi-scale pooling, serving as a key bridge connecting the feature extraction module and the classification module.

Figure 10 depicts the architecture of PPNet. This network synergistically captures global and local information via four pooling branches with distinct scales, and is hierarchically decomposed into four core modules: multi-scale pooling, channel dimensionality reduction, upsampling, and feature concatenation. Its core functionality lies in accepting input feature maps with 256 channels, and generating enhanced feature maps with 512 channels after undergoing multi-scale pooling and feature fusion operations.

In the multi-scale pooling module, global pooling with a 1 × 1 window focuses on global structures such as ship outlines. Medium-scale pooling with a 2 × 2 window is designed to capture larger local structures including decks, while fine-scale pooling with a 3 × 3 window extracts relatively small-scale structures like cranes. Ultra-fine-scale pooling with a 6 × 6 window further mines tiny details such as masts. After being output by all pooling branches, the feature maps undergo size unification via an upsampling layer, which ensures seamless concatenation with the original feature maps to achieve effective feature fusion.

Additionally, considering that the proposed network is tailored for ship classification tasks, pixel-level accuracy requirements here are less stringent compared to semantic segmentation tasks. Instead, greater emphasis is placed on balancing global semantics and detailed information, prompting two targeted optimizations to be implemented on the original PSPNet. Firstly, the upsampling layer abandons the strategy of aligning to 1/8 of the input size and instead aligns to the original input size, which better meets the demand for feature integrity in classification tasks. Secondly, the channel compression ratio is reduced. Although this leads to a slight increase in parameter complexity, it remarkably enhances the feature representation capability and model fitting performance. This enables accurate exploitation of the essential common features of homogeneous ships, ultimately achieving a significant improvement in classification accuracy.

3.2.3. Dual-Branch Feature Fusion Module and Classifier

The main branch and auxiliary branch are independent of each other during feature extraction, ensuring that the characteristics of each type of data can be fully learned. In the feature fusion stage, the 2048-dimensional SAR image feature maps extracted by the main branch are concatenated with the 512-dimensional BNM feature maps extracted by the auxiliary branch. The model is compatible with different input types and can output fused features with 2560 channels regardless of whether the input is single-type or multi-type data. This concatenation-based fusion strategy enables the complementary integration of global semantic information from real SAR datasets and fine-grained structural details from simulated BNM datasets. It allows the model to leverage the strengths of both datasets without requiring strict sample pairing between them, which significantly improves the robustness of ship classification, especially for low-quality or noise-corrupted SAR images.

To optimize the feature fusion performance, this paper employs an approach based on single-classification loss calculation and dynamic weight adjustment, replacing the traditional dual-branch independent loss design, so as to indirectly guide the model to learn the class discriminative value between real data and simulated data. During the fusion process, a single cross-entropy loss function is adopted. By computing the predicted probabilities of all classes and normalizing them using the Softmax function, the expression for the probability distribution of each class is derived as follows:

$$p_i={\displaystyle \frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}}},i=1,2,\dots ,K$$

(18)

where $z_i$ is the logit for the i-th class. The expression for calculating the loss corresponding to the true class y is as follows:

$$\mathrm{CrossEntropyLoss}=-log\left(p_y\right)$$

(19)

where $p_y$ represents the predicted probability of class y. The loss value reflects the classification error of the fused features, and through the dynamic adjustment of feature weights, the model is indirectly trained to better learn the effective features of the two types of data.

To address the issue of branch weight allocation in feature fusion, this paper introduces the fusion attention method [40]. A two-layer fully connected network is utilized to process the fused features, generating dynamic attention weights that sum to 1, thereby achieving adaptive importance allocation for the concatenated dual-branch features. In contrast to traditional fusion approaches relying on direct concatenation or manual fixed weight setting, this attention-based weighting strategy actively filters complementary effective information captured by the auxiliary branch while suppressing noise and redundant features [41]. For SAR ship classification, it emphasizes the correlation between the detailed scattering features of the auxiliary branch and the global semantic features of the main branch, thereby improving the class discriminability of fused features. Specifically, when simulated images provide effective discriminative information, their weight proportion is automatically enhanced, whereas their weight is reduced to minimize interference with the classifier when the information is invalid. The underlying rationales are elaborated as follows:

(1)

Adapting to differences between simulated images and SAR images. Generally speaking, compared with measured images, the BNM generated in this paper is characterized by higher resolution and more sufficient detail representation, and moreover, it achieves higher image clarity due to being free from noise interference. This enables the model to automatically increase the auxiliary branch feature weight to ensure classification performance when real images have low resolution or severe interference.

(2)

Addressing the scenario where the simulated image dataset is unavailable. Only measured SAR images are input in both validation and inference phases, rendering auxiliary branch features invalid and requiring the model to achieve excellent classification results using only the measured dataset. Therefore, during training, the model proactively optimizes the feature extraction capability of the main branch, enhances the discriminative power of SAR image features, increases their weight proportion, and guides the main branch to actively learn the local scattering features of the auxiliary branch. This enables the main branch to fully internalize the effective information from the auxiliary branch, ensuring accurate classification even in the absence of simulated data.

Notably, the core value of the auxiliary branch lies exclusively in providing additional supervision, guidance, and category feature references during training. Its extracted clear and detailed structural features prompt the main branch to mine corresponding discriminative features from low-quality SAR images and strengthen the learning of category-specific features. Since the auxiliary branch does not participate in the core task execution during inference, it can be reasonably removed at this stage. By enhancing the main branch’s independent discriminative capability, this design ultimately endows the model with superior robustness and adaptability in the inference phase.

After feature fusion, the model maps each sample to the corresponding category based on concatenated features and dynamic weights, outputting the final ship classification results. The innovation of this work is that it does not require pairing real and simulated images nor rely on their high similarity. It only needs the two image types to share category commonalities, such as the rectangular container structure exhibited by container ships in both.

4. Results

4.1. Experimental Data Description

This training process was conducted on an RTX 4090 GPU. For the software environment, the proposed method used C++, Python 3.10, PyTorch 2.6, and CUDA 11.8. To verify the feature effectiveness of simulated data and the performance of the proposed dual-branch network, three representative real SAR datasets were adopted: OpenSARShip 2.0 [42], FUSAR-Ship [43], and SRSDD-v1.0 [44]. Following the settings of previous studies [45,46,47], samples from three ship categories with high proportions in the international shipping market (bulk carriers, container ships, and tankers) were selected. Each dataset is selected based on its distinct characteristics. OpenSARShip offers a low-resolution data scenario, FUSAR-Ship represents a data-scarce benchmark, and SRSDD shares the same spotlight mode as the simulated data. In addition, to enhance the persuasiveness of the results, data augmentation was performed on the images. After processing, each category in the FUSAR-Ship and SRSDD datasets corresponds to 1000 samples, while each category in the OpenSARShip dataset corresponds to 2000 samples. Each dataset was split into training, validation, and test sets at a ratio of 7:2:1.

Table 3. Distribution of ship samples by category in different datasets.

Dataset	Category	# Training	# Validation	# Test	# All
OpenSARShip	Bulk carrier	1230	352	176	1758
	Container ship	1395	399	200	1994
	Tanker	783	224	113	1120
FUSAR-Ship	Bulk carrier	171	49	25	245
	Container ship	26	8	4	38
	Tanker	54	16	8	78
SRSDD	Bulk carrier	1437	410	206	2053
	Container ship	62	18	9	89
	Tanker	116	33	17	166
BNM (Simulated images)	Bulk carrier	135	–	–	135
	Container ship	135	–	–	135
	Tanker	135	–	–	135

Note: The symbol # denotes the number of samples.

presents the original number of ship samples per category in the three datasets and the simulated dataset.

The OpenSARShip 2.0 dataset is built on Sentinel-1 data and developed from the OpenSARShip [48] dataset with optimized annotation information and refined categories. It contains 34,528 SAR ship target slices integrated with AIS data, with samples mainly collected from major ports such as Shanghai Port, Singapore Port, Port of Thames, and Yokohama Port. The spatial resolution is approximately 20 m × 22 m in range and azimuth directions, and each image slice covers two polarization modes (VV and VH), corresponding to a single ship accurately. All category labels are obtained by querying the corresponding AIS information and applying spatiotemporal interpolation algorithms, ensuring annotation accuracy. Due to its relatively low resolution, this dataset can be used to verify the auxiliary classification performance of simulated images for low-resolution datasets. Figure 11 shows some SAR ship samples in the OpenSARShip 2.0 dataset.

The FUSAR-Ship dataset is constructed based on 126 GF-3 satellite scenes, containing more than 5,000 ship slices integrated with AIS information. It covers 15 main ship categories, which are further divided into 98 subcategories. With single-polarization SAR imaging technology adopted, the dataset encompasses two polarization modes, namely DH and DV, with a resolution of 1.124 m × 1.728 m, which enables clear visualization of the detailed features of ships. Due to the scarce number of container ship category samples within this dataset, it can be used to verify the classification performance of the network proposed in this paper under the scenario of insufficient dataset samples. Figure 12 shows some SAR ship samples in the FUSAR-Ship dataset.

The SRSDD-v1.0 dataset is built on images acquired under the spotlight mode of GF-3 satellites, with 666 slices of 1 m resolution and 1024 × 1024 pixel size extracted from 30 scenes. It contains 2884 ship samples, covering 6 different types of ships. Based on the Anchor Boxes from the object detection results, this paper crops and categorizes the original images to obtain ship slices of different categories. Owing to the consistent spotlight mode between this dataset and the simulated images, the two demonstrate enhanced similarity, thereby enabling effective verification of the simulated images’ effectiveness. Additionally, the classification results of this dataset enable the assessment of the compatibility between existing classification algorithms and object detection methods. Figure 13 shows some SAR ship samples in the SRSDD-v1.0 dataset.

4.2. Evaluation Metrics

To assess model performance in classification tasks, we adopt multiple standard evaluation metrics, namely precision, recall, F1-score, and accuracy.

Precision reflects the ratio of correctly predicted positive samples to all predicted positive samples, signifying how accurate positive predictions are. It is formulated as:

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(20)

Recall quantifies the proportion of actually positive samples that are accurately identified as positive by the model. Its mathematical formulation is expressed as follows:

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(21)

F1-Score balances the trade-off between Precision and Recall through the computation of their harmonic mean. Its mathematical formulation is given as follows:

$$F1=2\times {\displaystyle \frac{Precision\times Recall}{Precision+Recall}}$$

(22)

Accuracy, which is employed to assess the classification precision of all samples, quantifies the proportion of correctly predicted samples relative to the total number of samples. Its mathematical formula given as follows:

$$Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(23)

where true positive ($TP$) denotes correctly predicted positive samples, true negative ($TN$) denotes correctly predicted negative samples, false positive ($FP$) denotes incorrectly predicted positive samples, and false negative ($FN$) denotes incorrectly predicted negative samples.

Due to the imbalance in the distribution of ship types in SAR images, this paper employs weighted metrics to objectively and fairly evaluate the model’s performance. The overall precision, recall, and F1-score are all calculated via the weighted average of their category-specific counterparts. Taking weighted recall as an example, its calculation formula is as follows:

$$Weightedrecall=\sum _{i=1}^C\left({\displaystyle \frac{N_i}{N}}\times Recal{l}_i\right)$$

(24)

where N denotes the total number of SAR images, $N_i$ represents the number of images belonging to category i, and C is the total number of categories. confirm These metrics collectively enable a comprehensive evaluation of the model’s performance across various classification scenarios, and weighted metrics, in particular, play a crucial role in alleviating the problem of class imbalance.

4.3. Performance of SeDSG

This section presents the classification performance of the proposed method across three different SAR ship classification tasks.

Table 4. Classification confusion matrix of OpenSARShip.

	Predicted	Bulk Carrier	Container Ship	Tanker	Recall (%)
True
Bulk Carrier		154	16	6	87.50
Container ship		22	171	7	85.50
Tanker		12	6	95	84.07
Precision (%)		81.91	88.60	87.96	Accuracy = 85.89%
F1-Score (%)		84.62	87.02	85.97

,

Table 5. Classification confusion matrix of OpenSARShip enhanced.

	Predicted	Bulk Carrier	Container Ship	Tanker	Recall (%)
True
Bulk Carrier		165	19	16	82.50
Container ship		25	168	7	84.00
Tanker		4	3	193	96.50
Precision (%)		85.05	88.42	89.35	Accuracy = 87.67%
F1-Score (%)		83.76	86.15	92.79

,

Table 6. Classification confusion matrix of FUSAR-Ship.

	Predicted	Bulk Carrier	Container Ship	Tanker	Recall (%)
True
Bulk Carrier		24	1	0	96.00
Container ship		1	3	0	75.00
Tanker		1	0	7	87.50
Precision (%)		92.31	75.00	100.00	Accuracy = 91.89%
F1-Score (%)		94.12	75.00	93.33

,

Table 7. Classification confusion matrix of FUSAR-Ship Enhanced.

	Predicted	Bulk Carrier	Container Ship	Tanker	Recall (%)
True
Bulk Carrier		96	3	1	96.00
Container ship		0	99	1	99.00
Tanker		0	0	100	100.00
Precision (%)		100.00	97.06	98.04	Accuracy = 98.33%
F1-Score (%)		97.96	98.02	99.01

,

Table 8. Classification confusion matrix of SRSDD.

	Predicted	Bulk Carrier	Container Ship	Tanker	Recall (%)
True
Bulk Carrier		203	0	3	98.54
Container ship		1	8	0	88.89
Tanker		2	0	15	88.24
Precision (%)		98.54	100.00	83.33	Accuracy = 97.41%
F1-Score (%)		98.54	94.12	85.71

and

Table 9. Classification confusion matrix of SRSDD Enhanced.

	Predicted	Bulk Carrier	Container Ship	Tanker	Recall (%)
True
Bulk Carrier		100	0	0	100.00
Container ship		0	100	0	100.00
Tanker		3	0	97	97.00
Precision (%)		97.09	100.00	100.00	Accuracy = 99.00%
F1-Score (%)		98.52	100.00	98.48

present the three-class confusion matrices of the proposed SeDSG on the original FUSAR-Ship, OpenSARShip and SRSDD datasets and their augmented versions.

Experimental results on the original datasets demonstrate that the SRSDD dataset achieves the optimal classification performance with 97.41% accuracy, reflecting strong sample feature discriminability and a remarkable auxiliary training effect when synthetic and measured datasets are highly similar. The FUSAR-Ship dataset achieves a classification accuracy of 91.89%, with only 38 container ship samples in total, indicating the model’s excellent classification capability under scarce samples. The overall classification accuracy of the OpenSARShip dataset is 85.89%, with recall rates for the three ship categories spanning 84.07% to 87.50%. This outcome attests to the model’s robust performance stability and highlights its efficacy in low-resolution dataset scenarios.

After data augmentation operations such as random cropping and rotation, the classification performance of the three datasets has been significantly improved. Specifically, the classification accuracy of the FUSAR-Ship dataset increased from 91.89% to 98.33% after augmentation, basically achieving accurate classification of all samples. The SRSDD dataset reached a post-augmentation accuracy of 99.00%, with both bulk carriers and container ships attaining 100% precision and recall. For the OpenSARShip dataset, the accuracy rose to 87.67% after augmentation, and the recall rate of tankers increased sharply from 84.07% to 96.50%, effectively alleviating the class imbalance issue.

4.4. Comparison with Other Models

To evaluate the effectiveness and performance improvement of the proposed SeDSG in SAR ship classification tasks, typical deep learning networks and current state-of-the-art models are selected as comparative baselines. Among them, the former adopts the same dataset as the proposed method, while the sample size of the dataset used by the latter is significantly larger than that of this paper. Experiments were conducted on the FUSAR-Ship, OpenSARShip, and SRSDD datasets to assess the performance of the three-classification task, with the results presented in

Table 10. Comparison Results with Other Models.

Model	OpenSARShip				FUSAR-Ship				SRSDD
	P (%)	R (%)	F1 (%)	Acc (%)	P (%)	R (%)	F1 (%)	Acc (%)	P (%)	R (%)	F1 (%)	Acc (%)
AlexNet [49]	82.42	82.41	82.35	82.41	82.68	75.68	78.41	75.68	95.38	95.26	95.31	95.26
VGG-16 [50]	82.12	82.00	81.97	82.00	88.89	89.19	88.73	89.19	95.94	95.69	95.76	95.69
GoogleNet [51]	83.52	83.44	83.43	83.44	81.98	78.38	79.61	78.38	96.36	96.12	96.19	96.12
MobileNet-v2 [52]	80.71	80.37	80.35	80.37	84.94	86.49	84.98	86.49	95.52	94.83	95.03	94.83
SqueezeNet-v1.0 [53]	82.50	82.41	82.37	82.41	85.00	86.49	85.65	86.49	95.96	95.26	95.45	95.26
Wide-ResNet-50 [54]	84.54	84.46	84.45	84.46	80.54	78.38	79.34	78.38	97.06	96.98	96.99	96.98
SE-LPN-DPFF [55]	76.45	78.83	77.62	79.25	–	–	–	–	–	–	–	–
PFGFE-Net [56]	80.23	79.88	78.00	79.84	–	–	–	–	–	–	–	–
DPIG-Net [41]	85.02	82.88	83.93	81.28	–	–	–	–	–	–	–	–
HOG-ShipCLSNet [45]	72.42	77.87	75.04	78.18	–	–	–	–	–	–	–	–
HDSS-Net [46]	81.16	80.66	80.91	83.23	–	–	–	–	–	–	–	–
DBDN [47]	87.31	86.32	86.74	87.62	–	–	–	–	–	–	–	–
SeDSG (Ours)1	86.05	85.89	85.91	85.89	92.10	91.89	91.88	91.89	97.49	97.41	97.43	97.41
	(87.61)	(87.67)	(87.57)	(87.67)	(98.37)	(98.33)	(98.33)	(98.33)	(99.03)	(99.00)	(99.00)	(99.00)

¹ The values in parentheses are the results of the datasets after data augmentation.

. The comparative results demonstrate that SeDSG, through the design of a dual-branch structure and the fusion of attention mechanisms, can more fully extract deep semantic features and detailed texture information from SAR ship images. It effectively overcomes the limitations of traditional CNNs in SAR image clutter suppression, target feature discrimination, and other aspects, and its overall classification performance reaches the current advanced level. The following significant advantages can be observed from the experimental results:

(a)

On the OpenSARShip dataset, although the accuracy of SeDSG (85.89%) is slightly lower than that of DBDN (87.62%), it is significantly superior to classical models such as AlexNet (82.41%) and VGG-16 (82.00%). Furthermore, after achieving class balance through data augmentation, all evaluation metrics are higher than those of DBDN, verifying the effectiveness of the network on low-resolution datasets.

(b)

On the FUSAR-Ship dataset, the accuracy (91.89%) and F1-Score (91.88%) of SeDSG far exceed those of all comparative models, representing a 2.7 percentage point improvement compared to the second-best model VGG-16 (89.19%). Additionally, higher accuracy can be achieved through traditional data augmentation methods, which effectively improves the classification performance on datasets with a small number of samples.

(c)

On the SRSDD dataset, SeDSG achieves the best performance with an accuracy of 97.41% and an F1-Score of 97.43%, which is higher than that of state-of-the-art models such as Wide-ResNet-50 (96.98%), demonstrating its prominent advantages in high-resolution SAR ship image classification tasks.

To further validate the positive contribution of simulated images’ auxiliary role for the main branch to the classification task, comparative experiments are performed in this paper under the constraint that the total number of simulated and measured images input to SeDSG equals the number of SAR images input to a single branch. The results are presented in

Table 11. Comparison With Single Branch.

Dataset	Single-Branch(ResNet50+CBAM)				Dual-Branch(SeDSG)
	P (%)	R (%)	F1 (%)	Acc (%)	P (%)	R (%)	F1 (%)	Acc (%)
OpenSARShip	84.89	84.66	84.70	84.66	86.05	85.89	85.91	85.89
OpenSARShip Enhanced	86.01	86.00	85.84	86.00	87.61	87.67	87.57	87.67
FUSAR-Ship	84.94	86.49	84.98	86.49	92.10	91.89	91.88	91.89
FUSAR-Ship Enhanced	97.74	97.67	97.67	97.67	98.37	98.33	98.33	98.33

.

Experimental results demonstrate that on the original datasets, the SeDSG model achieves an accuracy of 85.89% on the OpenSARShip dataset. This represents a 1.23 percentage point improvement compared with the single-branch model. On the FUSAR-Ship dataset, the model’s accuracy reaches 91.89%, marking a significant increase of 5.4 percentage points over the single-branch model. After data augmentation, the performance advantage of the dual-branch structure is further highlighted. Specifically, the accuracy increases by 1.67 percentage points on the augmented OpenSARShip dataset and by 0.66 percentage points on the augmented FUSAR-Ship dataset. These results verify the effectiveness of the auxiliary branch in ship classification tasks, particularly for datasets with insufficient sample sizes. Meanwhile, as an independent module, the auxiliary branch exhibits excellent compatibility with other networks. This provides broad prospects for the optimization and improvement of subsequent network structures.

4.5. Validation of Model Pretraining Capability

To validate the compatibility and inference efficiency of the proposed model with ship recognition networks in practical application scenarios, this paper systematically explores the influence of pretraining the model on the FUSAR-Ship and OpenSARShip datasets, respectively, on the classification performance of the SRSDD dataset. When adapting the pretrained model to the SRSDD dataset during fine-tuning, the entire network was kept trainable, with no layers frozen during parameter updates. A comparative analysis is performed using the classification results of different training epochs as the baseline, with the corresponding results summarized in

Table 12. Ship Classification Performance on SRSDD with Pretrain.

Pretrain Dataset	SRSDD				SRSDD Enhanced
	P (%)	R (%)	F1 (%)	Acc (%)	P (%)	R (%)	F1 (%)	Acc (%)
OpenSARShip	96.45	96.55	96.45	96.55	97.72	97.67	97.67	97.67
OpenSARShip Enhanced	96.29	96.12	96.19	96.12	98.69	98.67	98.67	98.67
FUSAR-Ship	97.16	96.98	97.02	96.98	99.01	99.00	99.00	99.00
FUSAR-Ship Enhanced	96.07	96.12	96.09	96.12	98.38	98.33	98.33	98.33
No pretrain (epoch = 20)	95.59	95.69	95.59	95.69	98.04	98.00	98.00	98.00
No pretrain (epoch = 50)	97.49	97.41	97.43	97.41	99.03	99.00	99.00	99.00

.

Pretraining experimental results demonstrate that the model pretrained on the augmented FUSAR-Ship dataset achieves the optimal performance on the SRSDD dataset. Its classification performance is significantly superior to that of the non-pretrained model trained for 20 epochs and substantially comparable to the 50-epoch non-pretrained counterpart. This finding confirms that high-quality pretraining data can provide the model with effective prior knowledge, which not only accelerates model convergence but also remarkably improves the model’s generalization capability.

4.6. Ablation Study

To investigate the working mechanism of each core module in the SeDSG, this paper designs ablation experiments for the CBAM, PPNet, and fusion attention module to verify their effectiveness, with the relevant results presented in

Table 13. Ablation study results of CBAM, PPNet and fusion attention module.

Model Variant			OpenSARShip				FUSAR-Ship
CBAM	PPNet	Fusion Attention	P (%)	R (%)	F1 (%)	Acc (%)	P (%)	R (%)	F1 (%)	Acc (%)
	√	√	84.84	84.66	84.66	84.66	81.04	81.08	80.97	81.08
√		√	85.38	85.07	85.06	85.07	87.68	86.49	86.62	86.49
√	√		83.18	83.03	83.05	83.03	90.27	89.19	89.55	89.19
√	√	√	86.05	85.89	85.91	85.89	92.10	91.89	91.88	91.89

.

Experimental results indicate that the model performance degrades to varying degrees after removing any single module, fully confirming the indispensability of each module. Detailed analyses are as follows:

(a)

When the CBAM module is exclusively removed, the classification accuracy of the OpenSARShip dataset drops to 84.66%, while that of the FUSAR-Ship dataset decreases to 81.08% with a reduction of more than 10% compared to the SeDSG model. This result demonstrates that for datasets with high image resolution but scarce samples, the CBAM module plays a crucial role in improving classification performance by focusing on feature enhancement in the channel dimension.

(b)

Upon exclusive removal of the PPNet, the classification accuracies of the two datasets are 85.07% and 86.49%, respectively, both lower than the performance level of the SeDSG. This illustrates that the PPNet module optimizes the feature extraction process in the spatial dimension through multi-scale feature fusion, enabling it to simultaneously capture detailed features and global features, thereby achieving superior feature representation.

(c)

Following the exclusive removal of the fusion attention module and with the weights of the main branch and auxiliary branch fixed at 0.7 and 0.3, the accuracies of the two datasets are 83.03% and 89.19%, respectively. This confirms that the fusion attention module, by dynamically adjusting branch weights and realizing cross-dimensional feature interaction, can prompt the main branch to more efficiently enhance its feature extraction capability, deeply mine the category-shared features in images, and ultimately achieve a significant improvement in classification performance.

5. Discussion

From the perspective of model structure, the dual-branch design with simulated image guidance avoids the introduction of redundant deep neural network layers. This balance between accuracy and efficiency enables SeDSG to produce classification results with enhanced inference timeliness, thereby reducing the reliance on GPUs.

To address the issue of insufficient sample sizes, we adopt a hybrid strategy that combines traditional data augmentation methods with the simulated image auxiliary method proposed in this paper. This approach significantly enhances the classification performance and generalization capability of the model. Furthermore, the number of simulated images employed in the experiment was dynamically configured to be less than that of SAR images in their corresponding categories. This not only ensures that simulated images perform an effective auxiliary function but also guarantees the reliability of the experimental results.

Moreover, as the SRSDD classification dataset is constructed by cropping based on the detection boxes of the ship recognition network and partitioning according to sample labels, the aforementioned experimental results further validate the excellent compatibility between the proposed model and the ship recognition network, facilitating its integration with subsequent methods.

In future research, this dual-branch network can be further extended to multi-polarization SAR ship classification tasks and integrated with polarization features, thereby further enhancing the model’s applicability to complex real-world scenarios.

6. Conclusions

In order to address the challenges in SAR image datasets, this paper innovatively introduces the concept of BNM and generates simulated images of ship models across different categories under diverse parameter configurations, which enhances electromagnetic scattering characteristics, thus extending the effective feature domain built upon traditional features. Furthermore, accounting for the domain discrepancy between simulated data and SAR images, this paper innovatively devises an auxiliary branch and proposes a dual-branch network assisted by simulated images for ship classification tasks. This branch independently processes simulated data and demonstrates broad compatibility with various classification networks.

Experimental results illustrate that, in comparison to conventional single-branch networks, the proposed dual-branch framework achieves consistent and significant accuracy improvements across datasets with different resolutions and sample sizes. It concurrently mitigates the challenges of class imbalance and insufficient sample sizes. Pretraining experiments further confirm that the model can extract effective prior knowledge from high-quality data, accelerating training convergence and improving generalization performance.

In summary, by leveraging enhanced electromagnetic scattering characteristics, the method proposed in this paper not only effectively expands data diversity but also achieves efficient fusion of real and simulated data features. Moreover, it demonstrates robust compatibility with existing ship recognition networks, providing a practical and reliable solution for target classification tasks utilizing SAR images within diverse practical application scenarios.