SatGS: Remote Sensing Novel View Synthesis Using Multi- Temporal Satellite Images with Appearance-Adaptive 3DGS
Abstract
1. Introduction
- We propose SatGS, a 3D Gaussian Splatting-based framework with a novel appearance-adaptive adjustment strategy, which facilitates both global and local seasonal variation adjustments, while accurately describing the shape and tone of shadow regions;
- We design a specific uncertainty optimization scheme that enables robust removal of transient objects from a trained scene;
- Experimental results demonstrate that SatGS not only outperforms several State-of-the-Art NeRF-based methods in terms of rendering quality but also surpasses them in rendering speed and training time efficiency.
2. Related Work
2.1. 3D Representation for Novel View Synthesis
2.2. Novel View Synthesis for Unstructured Photo Collections
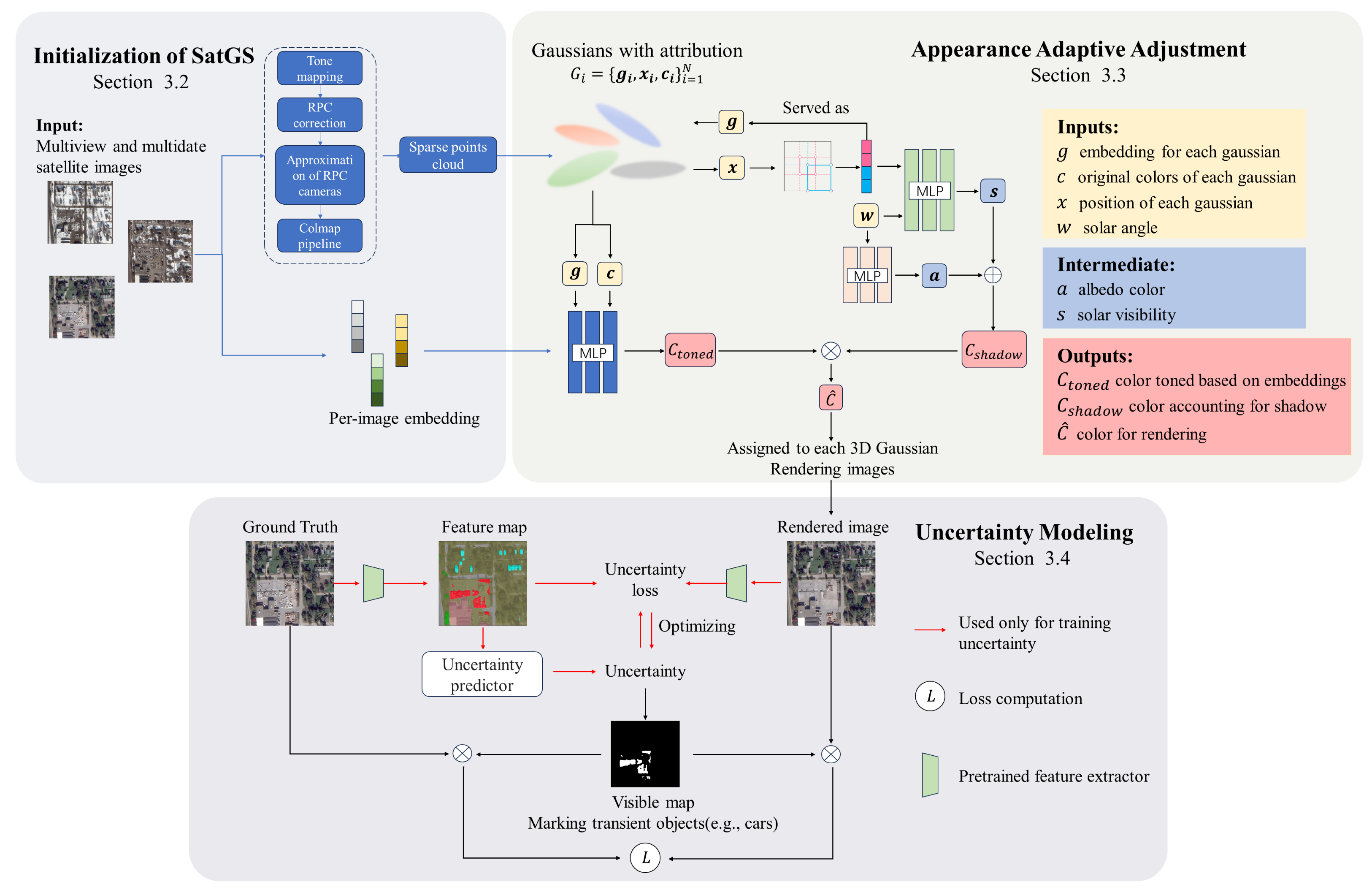
3. Method
3.1. Preliminaries
3.2. Initialization of SatGS
3.3. Appearance Adaptive Adjustment
3.3.1. Appearance Modeling
3.3.2. Shadow Modeling
3.3.3. Additional Loss Terms
3.4. Uncertainty Modeling
3.5. Loss Function
4. Experiments
4.1. Experimental Setup
4.1.1. Dataset
4.1.2. Implementation Details
4.1.3. Evaluation Metrics
4.2. Evaluation Scheme
| Algorithm 1 Test-time Optimization | |
| I: Set of test images | |
| : Pretrained SatGS model (parameters fixed) | |
| : Learnable image embeddings | |
| : Solar angles | |
| Initialize | ▹ Random initialization |
| for epoch to do | |
| for image do | |
| ▹ Only and affect output | |
| ▹ Equation (5) | |
| ▹ Only update current embedding | |
| end for | |
| end for | |
| return | |
4.3. Comparison to State-of-the-Art Methods
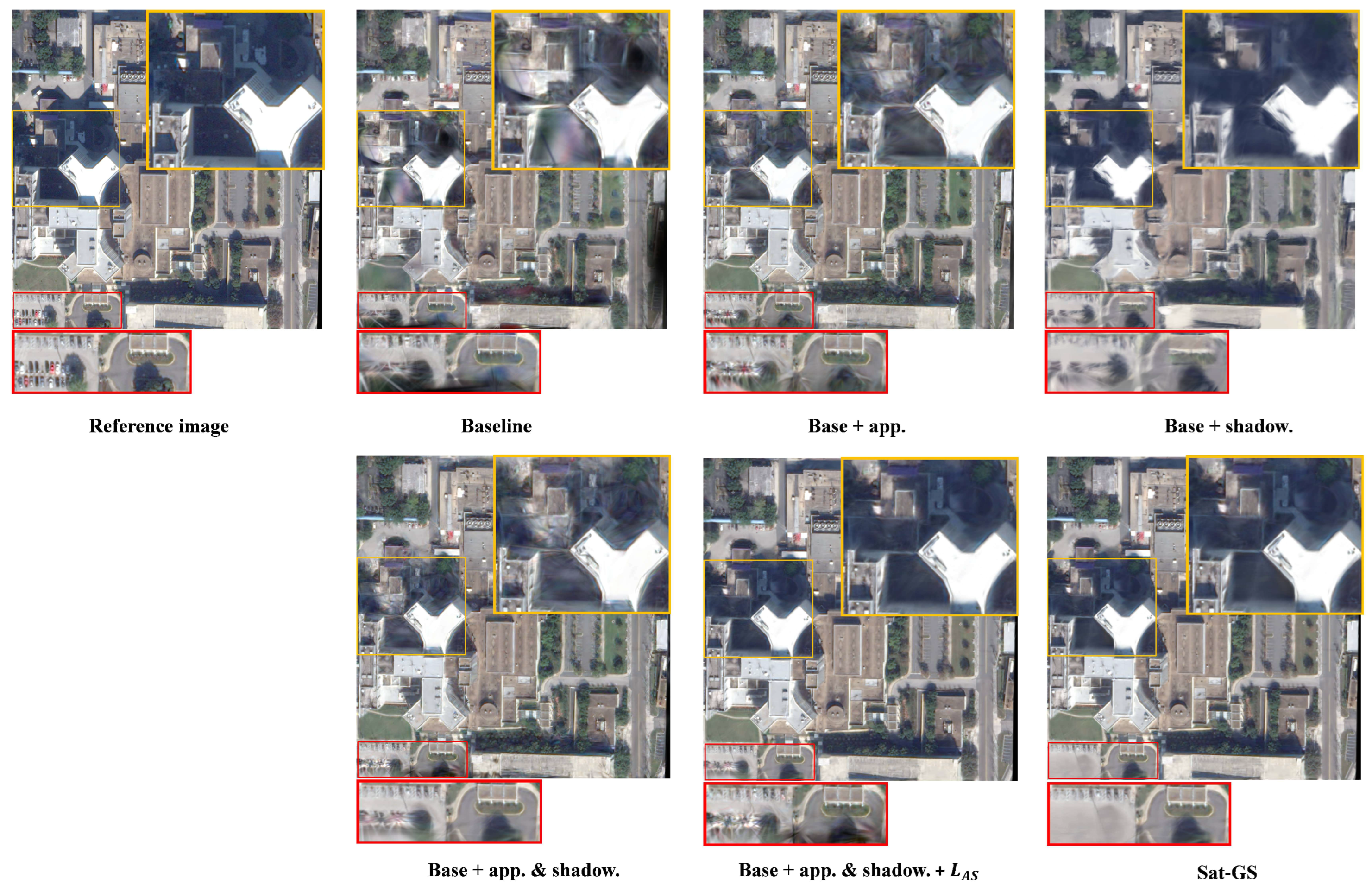
4.4. Ablation Study
4.5. High Resolution Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Y.; Zou, Z.; Shi, Z. Remote sensing novel view synthesis with implicit multiplane representations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5627613. [Google Scholar] [CrossRef]
- Li, Z.; Li, Z.; Cui, Z.; Qin, R.; Pollefeys, M.; Oswald, M.R. Sat2vid: Street-view panoramic video synthesis from a single satellite image. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 12436–12445. [Google Scholar]
- Marí, R.; Facciolo, G.; Ehret, T. Multi-date earth observation NeRF: The detail is in the shadows. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 2035–2045. [Google Scholar]
- Derksen, D.; Izzo, D. Shadow neural radiance fields for multi-view satellite photogrammetry. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 1152–1161. [Google Scholar]
- Marí, R.; Facciolo, G.; Ehret, T. Sat-nerf: Learning multi-view satellite photogrammetry with transient objects and shadow modeling using rpc cameras. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1311–1321. [Google Scholar]
- Zhang, L.; Rupnik, E. Sparsesat-NeRF: Dense depth supervised neural radiance fields for sparse satellite images. arXiv 2023, arXiv:2309.00277. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Lin, D.; Cao, Z.; Li, B.; Liu, J. SatelliteRF: Accelerating 3D Reconstruction in Multi-View Satellite Images with Efficient Neural Radiance Fields. Appl. Sci. 2024, 14, 2729. [Google Scholar] [CrossRef]
- Gableman, M.; Kak, A. Incorporating season and solar specificity into renderings made by a NeRF architecture using satellite images. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4348–4365. [Google Scholar] [CrossRef]
- Kerbl, B.; Kopanas, G.; Leimkühler, T.; Drettakis, G. 3D Gaussian Splatting for Real-Time Radiance Field Rendering. ACM Trans. Graph. 2023, 42, 139. [Google Scholar] [CrossRef]
- Lin, J.; Li, Z.; Tang, X.; Liu, J.; Liu, S.; Liu, J.; Lu, Y.; Wu, X.; Xu, S.; Yan, Y.; et al. Vastgaussian: Vast 3d gaussians for large scene reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 5166–5175. [Google Scholar]
- Liu, Y.; Luo, C.; Fan, L.; Wang, N.; Peng, J.; Zhang, Z. Citygaussian: Real-time high-quality large-scale scene rendering with gaussians. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 265–282. [Google Scholar]
- Liu, Y.; Luo, C.; Mao, Z.; Peng, J.; Zhang, Z. CityGaussianV2: Efficient and Geometrically Accurate Reconstruction for Large-Scale Scenes. arXiv 2024, arXiv:2411.00771. [Google Scholar]
- Wang, Y.; Tang, X.; Ma, J.; Zhang, X.; Zhu, C.; Liu, F.; Jiao, L. Pseudo-Viewpoint Regularized 3D Gaussian Splatting For Remote Sensing Few-Shot Novel View Synthesis. In Proceedings of the IGARSS 2024-2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 8660–8663. [Google Scholar]
- Lian, H.; Liu, K.; Cao, R.; Fei, Z.; Wen, X.; Chen, L. Integration of 3D Gaussian Splatting and Neural Radiance Fields in Virtual Reality Fire Fighting. Remote Sens. 2024, 16, 2448. [Google Scholar] [CrossRef]
- Kulhanek, J.; Peng, S.; Kukelova, Z.; Pollefeys, M.; Sattler, T. WildGaussians: 3D Gaussian Splatting in the Wild. arXiv 2024, arXiv:2407.08447. [Google Scholar]
- Zhang, D.; Wang, C.; Wang, W.; Li, P.; Qin, M.; Wang, H. Gaussian in the Wild: 3D Gaussian Splatting for Unconstrained Image Collections. arXiv 2024, arXiv:2403.15704. [Google Scholar]
- Li, Y.; Lv, C.; Yang, H.; Huang, D. Micro-macro Wavelet-based Gaussian Splatting for 3D Reconstruction from Unconstrained Images. arXiv 2025, arXiv:2501.14231. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Yan, S.; Cui, Z.; Xiao, H.; Liu, Y.; Zhang, M. ThermalGS: Dynamic 3D Thermal Reconstruction with Gaussian Splatting. Remote Sens. 2025, 17, 335. [Google Scholar] [CrossRef]
- Oquab, M.; Darcet, T.; Moutakanni, T.; Vo, H.; Szafraniec, M.; Khalidov, V.; Fernandez, P.; Haziza, D.; Massa, F.; El-Nouby, A.; et al. Dinov2: Learning robust visual features without supervision. arXiv 2023, arXiv:2304.07193. [Google Scholar]
- Trevithick, A.; Yang, B. Grf: Learning a general radiance field for 3d representation and rendering. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 15182–15192. [Google Scholar]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. Nerf: Representing scenes as neural radiance fields for view synthesis. Commun. ACM 2021, 65, 99–106. [Google Scholar] [CrossRef]
- Chibane, J.; Bansal, A.; Lazova, V.; Pons-Moll, G. Stereo radiance fields (srf): Learning view synthesis for sparse views of novel scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 7911–7920. [Google Scholar]
- Mescheder, L.; Oechsle, M.; Niemeyer, M.; Nowozin, S.; Geiger, A. Occupancy networks: Learning 3d reconstruction in function space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4460–4470. [Google Scholar]
- Yariv, L.; Kasten, Y.; Moran, D.; Galun, M.; Atzmon, M.; Ronen, B.; Lipman, Y. Multiview neural surface reconstruction by disentangling geometry and appearance. Adv. Neural Inf. Process. Syst. 2020, 33, 2492–2502. [Google Scholar]
- De Franchis, C.; Meinhardt-Llopis, E.; Michel, J.; Morel, J.M.; Facciolo, G. An automatic and modular stereo pipeline for pushbroom images. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Riva del Garda, Italy, 23–25 June 2014. [Google Scholar]
- Bosch, M.; Leichtman, A.; Chilcott, D.; Goldberg, H.; Brown, M. Metric evaluation pipeline for 3d modeling of urban scenes. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 239–246. [Google Scholar] [CrossRef]
- Bosch, M.; Kurtz, Z.; Hagstrom, S.; Brown, M. A multiple view stereo benchmark for satellite imagery. In Proceedings of the 2016 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 18–20 October 2016; pp. 1–9. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Chen, W.; Chen, H.; Yang, S. 3D Point Cloud Fusion Method Based on EMD Auto-Evolution and Local Parametric Network. Remote Sens. 2024, 16, 4219. [Google Scholar] [CrossRef]
- Schwarz, K.; Sauer, A.; Niemeyer, M.; Liao, Y.; Geiger, A. Voxgraf: Fast 3d-aware image synthesis with sparse voxel grids. Adv. Neural Inf. Process. Syst. 2022, 35, 33999–34011. [Google Scholar]
- Yu, Z.; Chen, A.; Huang, B.; Sattler, T.; Geiger, A. Mip-splatting: Alias-free 3d gaussian splatting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 19447–19456. [Google Scholar]
- Yu, Z.; Sattler, T.; Geiger, A. Gaussian opacity fields: Efficient adaptive surface reconstruction in unbounded scenes. ACM Trans. Graph. (TOG) 2024, 43, 271. [Google Scholar] [CrossRef]
- Charatan, D.; Li, S.L.; Tagliasacchi, A.; Sitzmann, V. pixelsplat: 3d gaussian splats from image pairs for scalable generalizable 3d reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 19457–19467. [Google Scholar]
- Zou, Z.X.; Yu, Z.; Guo, Y.C.; Li, Y.; Liang, D.; Cao, Y.P.; Zhang, S.H. Triplane meets gaussian splatting: Fast and generalizable single-view 3d reconstruction with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 10324–10335. [Google Scholar]
- Yang, Z.; Gao, X.; Sun, Y.; Huang, Y.; Lyu, X.; Zhou, W.; Jiao, S.; Qi, X.; Jin, X. Spec-gaussian: Anisotropic view-dependent appearance for 3d gaussian splatting. arXiv 2024, arXiv:2402.15870. [Google Scholar]
- Do, T.L.P.; Choi, J.; Le, V.Q.; Gentet, P.; Hwang, L.; Lee, S. HoloGaussian Digital Twin: Reconstructing 3D Scenes with Gaussian Splatting for Tabletop Hologram Visualization of Real Environments. Remote Sens. 2024, 16, 4591. [Google Scholar] [CrossRef]
- Shaheen, B.; Zane, M.D.; Bui, B.T.; Shubham; Huang, T.; Merello, M.; Scheelk, B.; Crooks, S.; Wu, M. ForestSplat: Proof-of-Concept for a Scalable and High-Fidelity Forestry Mapping Tool Using 3D Gaussian Splatting. Remote Sens. 2025, 17, 993. [Google Scholar] [CrossRef]
- Le Saux, B.; Yokoya, N.; Hansch, R.; Brown, M.; Hager, G. 2019 data fusion contest [technical committees]. IEEE Geosci. Remote Sens. Mag. 2019, 7, 103–105. [Google Scholar] [CrossRef]
- Ren, W.; Zhu, Z.; Sun, B.; Chen, J.; Pollefeys, M.; Peng, S. NeRF On-the-go: Exploiting Uncertainty for Distractor-free NeRFs in the Wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 8931–8940. [Google Scholar]
- Martin-Brualla, R.; Radwan, N.; Sajjadi, M.S.; Barron, J.T.; Dosovitskiy, A.; Duckworth, D. Nerf in the wild: Neural radiance fields for unconstrained photo collections. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 7210–7219. [Google Scholar]
- Chen, X.; Zhang, Q.; Li, X.; Chen, Y.; Feng, Y.; Wang, X.; Wang, J. Hallucinated neural radiance fields in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12943–12952. [Google Scholar]
- Tancik, M.; Casser, V.; Yan, X.; Pradhan, S.; Mildenhall, B.; Srinivasan, P.P.; Barron, J.T.; Kretzschmar, H. Block-nerf: Scalable large scene neural view synthesis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8248–8258. [Google Scholar]
- Turki, H.; Ramanan, D.; Satyanarayanan, M. Mega-nerf: Scalable construction of large-scale nerfs for virtual fly-throughs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12922–12931. [Google Scholar]
- Dahmani, H.; Bennehar, M.; Piasco, N.; Roldao, L.; Tsishkou, D. SWAG: Splatting in the Wild images with Appearance-conditioned Gaussians. arXiv 2024, arXiv:2403.10427. [Google Scholar]
- Schonberger, J.L.; Frahm, J.M. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Huang, B.; Yu, Z.; Chen, A.; Geiger, A.; Gao, S. 2d gaussian splatting for geometrically accurate radiance fields. In Proceedings of the ACM SIGGRAPH 2024 Conference Papers, Denver, CO, USA, 28 July–1 August 2024; pp. 1–11. [Google Scholar]
- Facciolo, G.; De Franchis, C.; Meinhardt-Llopis, E. Automatic 3D reconstruction from multi-date satellite images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 57–66. [Google Scholar]
- Zhang, K.; Snavely, N.; Sun, J. Leveraging vision reconstruction pipelines for satellite imagery. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27–28 October 2019. [Google Scholar]
- Marí, R.; de Franchis, C.; Meinhardt-Llopis, E.; Anger, J.; Facciolo, G. A Generic Bundle Adjustment Methodology for Indirect RPC Model Refinement of Satellite Imagery. Image Process. OnLine 2021, 11, 344–373. [Google Scholar] [CrossRef]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant neural graphics primitives with a multiresolution hash encoding. ACM Trans. Graph. (TOG) 2022, 41, 102. [Google Scholar] [CrossRef]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 4015–4026. [Google Scholar]
- Dosovitskiy, A. An image is worth 16×16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]
- Ye, Z.; Li, W.; Liu, S.; Qiao, P.; Dou, Y. Absgs: Recovering fine details in 3d gaussian splatting. In Proceedings of the ACM Multimedia 2024, Melbourne, VIC, Australia, 28 October–1 November 2024. [Google Scholar]
- Diederik, P.K. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sun, Y.; Wang, X.; Liu, Z.; Miller, J.; Efros, A.; Hardt, M. Test-time training with self-supervision for generalization under distribution shifts. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 9229–9248. [Google Scholar]




| Area Index | JAX 004 | JAX 068 | JAX 214 | JAX 260 |
|---|---|---|---|---|
| training/test | 9/2 | 17/2 | 21/3 | 15/2 |
| Area Index | OMA 163 | OMA 203 | OMA 212 | OMA 281 |
|---|---|---|---|---|
| training/test | 40/5 | 43/6 | 38/6 | 41/6 |
| PSNR↑ | SSIM↑ | LPIPS↓ | GPU hrs./ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 004 | 068 | 214 | 260 | 004 | 068 | 214 | 260 | 004 | 068 | 214 | 260 | FPS (Mean) | |
| S-NeRF (2021) | 25.87 | 24.2 | 24.51 | 21.52 | 0.864 | 0.901 | 0.939 | 0.829 | 0.262 | 0.130 | 0.251 | 0.326 | 6.2/0.11 |
| Sat-NeRF (2022) | 26.15 | 25.27 | 25.51 | 21.90 | 0.877 | 0.913 | 0.951 | 0.840 | 0.270 | 0.141 | 0.260 | 0.342 | 8.0/0.13 |
| Season-NeRF (2024) | 24.06 | 22.63 | 23.69 | 21.48 | 0.659 | 0.710 | 0.785 | 0.612 | 0.328 | 0.349 | 0.331 | 0.336 | 3.5/0.002 |
| 3DGS (2023) | 17.41 | 16.48 | 16.31 | 16.00 | 0.420 | 0.565 | 0.645 | 0.442 | 0.494 | 0.334 | 0.349 | 0.501 | 1.2/113 |
| Mip-Splatting (2024) | 20.16 | 17.20 | 18.87 | 18.51 | 0.570 | 0.588 | 0.645 | 0.542 | 0.398 | 0.318 | 0.414 | 0.486 | 1.8/108 |
| VastGaussian (2024) | 22.08 | 21.41 | 22.74 | 20.18 | 0.672 | 0.747 | 0.735 | 0.651 | 0.316 | 0.223 | 0.256 | 0.364 | 2.8/56 |
| Sat-GS (Ours) | 30.57 | 26.41 | 26.43 | 25.82 | 0.880 | 0.928 | 0.925 | 0.864 | 0.193 | 0.129 | 0.142 | 0.218 | 2.5/81 |
| PSNR↑ | SSIM↑ | LPIPS↓ | GPU hrs./ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 163 | 203 | 212 | 281 | 163 | 203 | 212 | 281 | 163 | 203 | 212 | 281 | FPS (Mean) | |
| S-NeRF (2021) | 19.23 | 20.00 | 20.35 | 18.50 | 0.539 | 0.629 | 0.672 | 0.551 | 0.514 | 0.452 | 0.379 | 0.594 | 6.5/0.11 |
| Sat-NeRF (2022) | 19.26 | 20.49 | 19.71 | 19.02 | 0.566 | 0.658 | 0.679 | 0.582 | 0.512 | 0.434 | 0.359 | 0.565 | 7.2/0.118 |
| Season-NeRF (2024) | 19.82 | 21.44 | 20.26 | 20.99 | 0.591 | 0.660 | 0.640 | 0.642 | 0.457 | 0.372 | 0.328 | 0.331 | 4.8/0.03 |
| 3DGS (2023) | 13.47 | 14.21 | 12.60 | 13.95 | 0.495 | 0.559 | 0.536 | 0.443 | 0.575 | 0.432 | 0.487 | 0.696 | 1.5/86 |
| Mip-Splatting (2024) | 15.51 | 16.84 | 14.20 | 16.21 | 0.460 | 0.570 | 0.510 | 0.477 | 0.451 | 0.416 | 0.536 | 0.301 | 2.2/71 |
| VastGaussian (2024) | 15.76 | 17.60 | 13.71 | 16.17 | 0.480 | 0.603 | 0.510 | 0.504 | 0.460 | 0.404 | 0.549 | 0.298 | 2.1/63 |
| Sat-GS (Ours) | 22.09 | 23.10 | 22.62 | 21.39 | 0.730 | 0.779 | 0.753 | 0.664 | 0.291 | 0.299 | 0.306 | 0.290 | 2.5/77 |
| PSNR↑ | SSIM↑ | LPIPS↓ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 004 | 068 | 214 | 260 | 004 | 068 | 214 | 260 | 004 | 068 | 214 | 260 | |
| baseline | 20.16 | 17.20 | 18.87 | 18.51 | 0.570 | 0.588 | 0.645 | 0.542 | 0.398 | 0.318 | 0.414 | 0.486 |
| + shadow. | 26.03 | 23.63 | 22.63 | 23.85 | 0.801 | 0.844 | 0.809 | 0.751 | 0.252 | 0.156 | 0.210 | 0.326 |
| + app. | 26.40 | 23.51 | 21.12 | 22.20 | 0.833 | 0.844 | 0.775 | 0.733 | 0.213 | 0.167 | 0.225 | 0.334 |
| + shadow. & app. | 17.66 | 21.87 | 23.05 | 16.80 | 0.424 | 0.815 | 0.830 | 0.455 | 0.471 | 0.187 | 0.174 | 0.479 |
| + . | 30.37 | 26.01 | 26.18 | 25.17 | 0.838 | 0.902 | 0.901 | 0.840 | 0.202 | 0.158 | 0.140 | 0.245 |
| + uncert. (Sat-GS) | 30.57 | 26.41 | 26.43 | 25.82 | 0.880 | 0.928 | 0.925 | 0.864 | 0.193 | 0.129 | 0.142 | 0.218 |
| PSNR↑ | SSIM↑ | LPIPS↓ | GPU hrs./ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 004 | 068 | 214 | 260 | 004 | 068 | 214 | 260 | 004 | 068 | 214 | 260 | FPS (Mean) | |
| Season-NeRF (2024) | 24.02 | 22.14 | 20.67 | 21.73 | 0.725 | 0.740 | 0.675 | 0.705 | 0.712 | 0.587 | 0.553 | 0.454 | 4.5/0.004 |
| 3DGS (2023) | 18.96 | 17.31 | 17.67 | 16.21 | 0.525 | 0.506 | 0.635 | 0.505 | 0.412 | 0.369 | 0.469 | 0.548 | 1.6/11.6 |
| Sat-GS (Ours) | 26.78 | 25.07 | 23.97 | 24.20 | 0.789 | 0.793 | 0.810 | 0.720 | 0.308 | 0.259 | 0.304 | 0.407 | 3.2/5.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, N.; Yang, A.; Chen, H.; Du, C. SatGS: Remote Sensing Novel View Synthesis Using Multi- Temporal Satellite Images with Appearance-Adaptive 3DGS. Remote Sens. 2025, 17, 1609. https://doi.org/10.3390/rs17091609
Bai N, Yang A, Chen H, Du C. SatGS: Remote Sensing Novel View Synthesis Using Multi- Temporal Satellite Images with Appearance-Adaptive 3DGS. Remote Sensing. 2025; 17(9):1609. https://doi.org/10.3390/rs17091609
Chicago/Turabian StyleBai, Nan, Anran Yang, Hao Chen, and Chun Du. 2025. "SatGS: Remote Sensing Novel View Synthesis Using Multi- Temporal Satellite Images with Appearance-Adaptive 3DGS" Remote Sensing 17, no. 9: 1609. https://doi.org/10.3390/rs17091609
APA StyleBai, N., Yang, A., Chen, H., & Du, C. (2025). SatGS: Remote Sensing Novel View Synthesis Using Multi- Temporal Satellite Images with Appearance-Adaptive 3DGS. Remote Sensing, 17(9), 1609. https://doi.org/10.3390/rs17091609






