Waveform Optimization for Enhancing the Performance of a Scanning Imaging Radar Utilizing a Terahertz Metamaterial Antenna
Abstract
1. Introduction
- (1)
- The super-resolution imaging capability of a scanning radar is studied by using an electronically controlled TMPA antenna for the first time.
- (2)
- The proposed waveform optimization method enhances both the range and the azimuth resolution by employing RHF and amplitude modulation simultaneously, thereby improving the imaging performance of the scanning radar.
- (3)
- In contrast to conventional waveform optimization techniques, the proposed method utilizes the minimization of residuals between real and reconstructed echoes as its criterion, eliminating the need to assume that the target scattering characteristics follow a Gaussian distribution, which leads to a wider applicability.
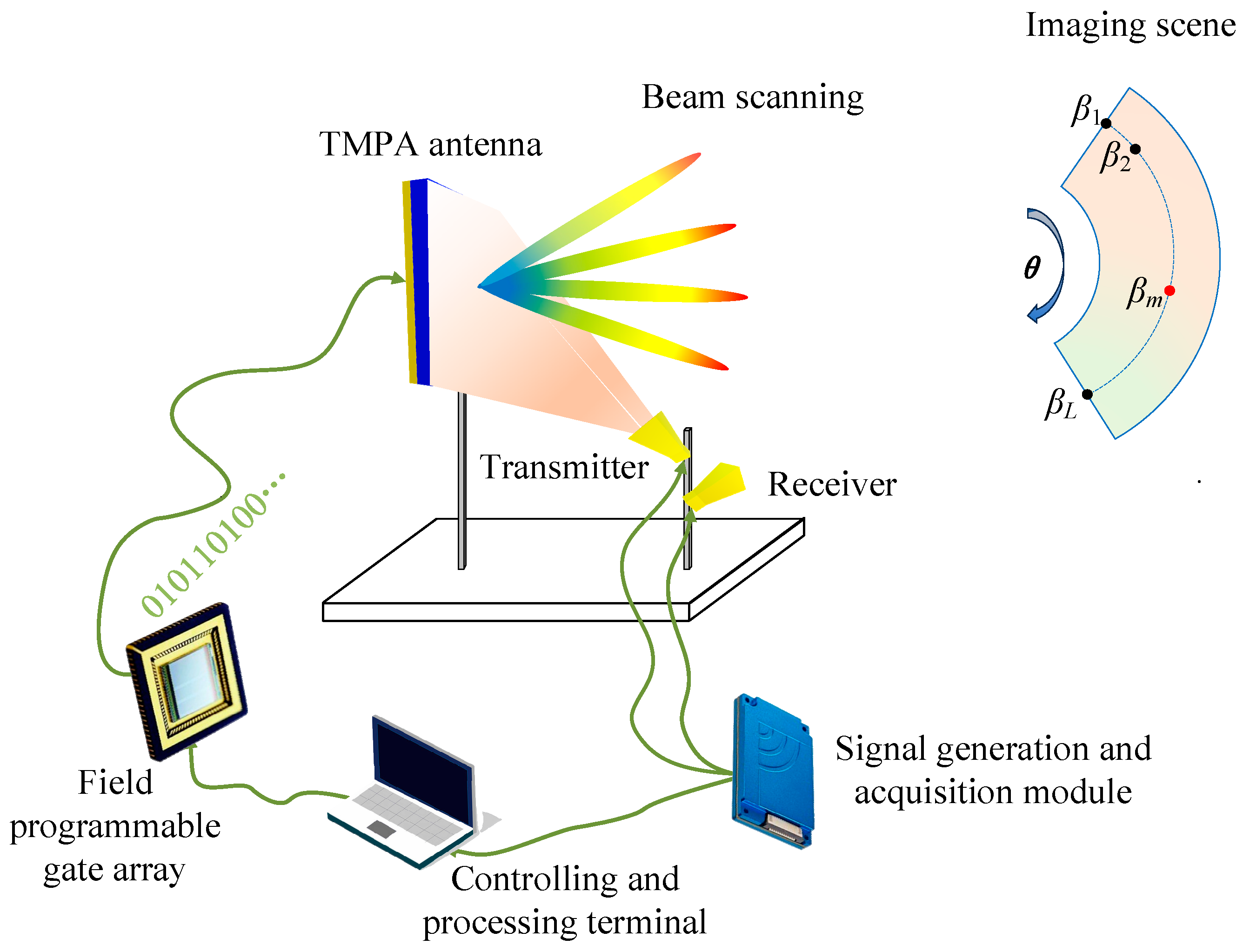
2. System Architecture of the TMPA Scanning Imaging Radar
3. Waveform Optimization Method
| Algorithm 1. Algorithm of waveform optimization for enhancing the range resolution. |
|---|
| Step 1: Initialize the frequency set; Step 2: Calculate the range ambiguity function according to Equation (7); Step 3: Calculate the value of the objective function (the lowest sidelobe); Step 4: Determine whether the terminational condition is met; Step 5: If the conditions are not satisfied, update the frequency set via crossover, mutation, and so on; Repeat step 2 to step 5 until the termination condition is met; Output: The frequency set. |
| Algorithm 2. Algorithm of waveform optimization for enhancing the azimuth resolution. |
| Step 1: Initialize a diagonal matrix α; Step 2: Update the matrix xe by solving Equation (10) with the CS algorithm; Step 3: Calculate the value of the objective function according to (11); Step 4: Determine whether the termination condition is met; Step 5: If the conditions are not satisfied, update α via crossover, mutation and so on; Repeat step 2 to step 5 until the termination condition is met; Output: The optimal matrix α. |
4. Simulations and Experimental Results
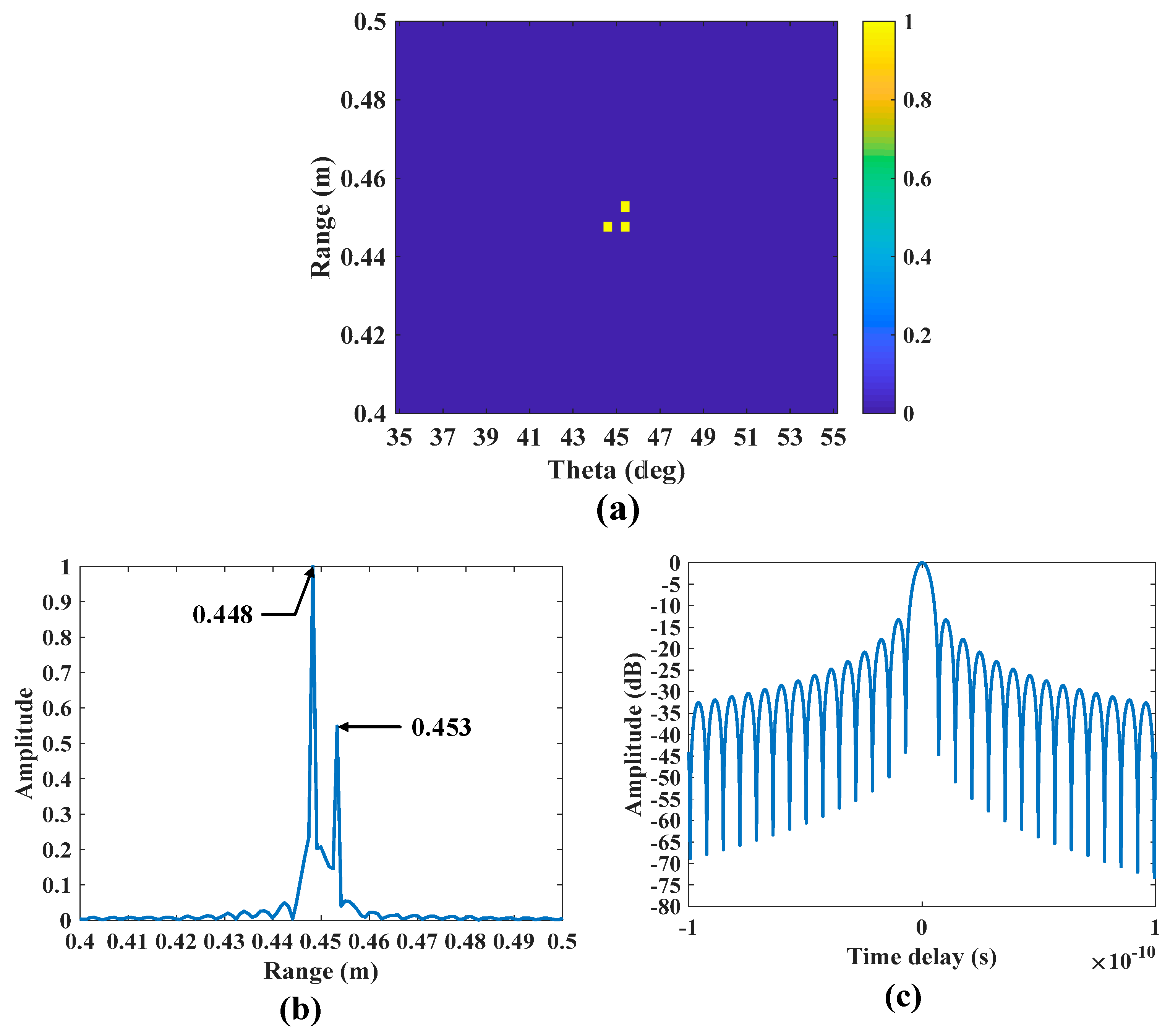
4.1. Simulation Results of Waveform Optimization
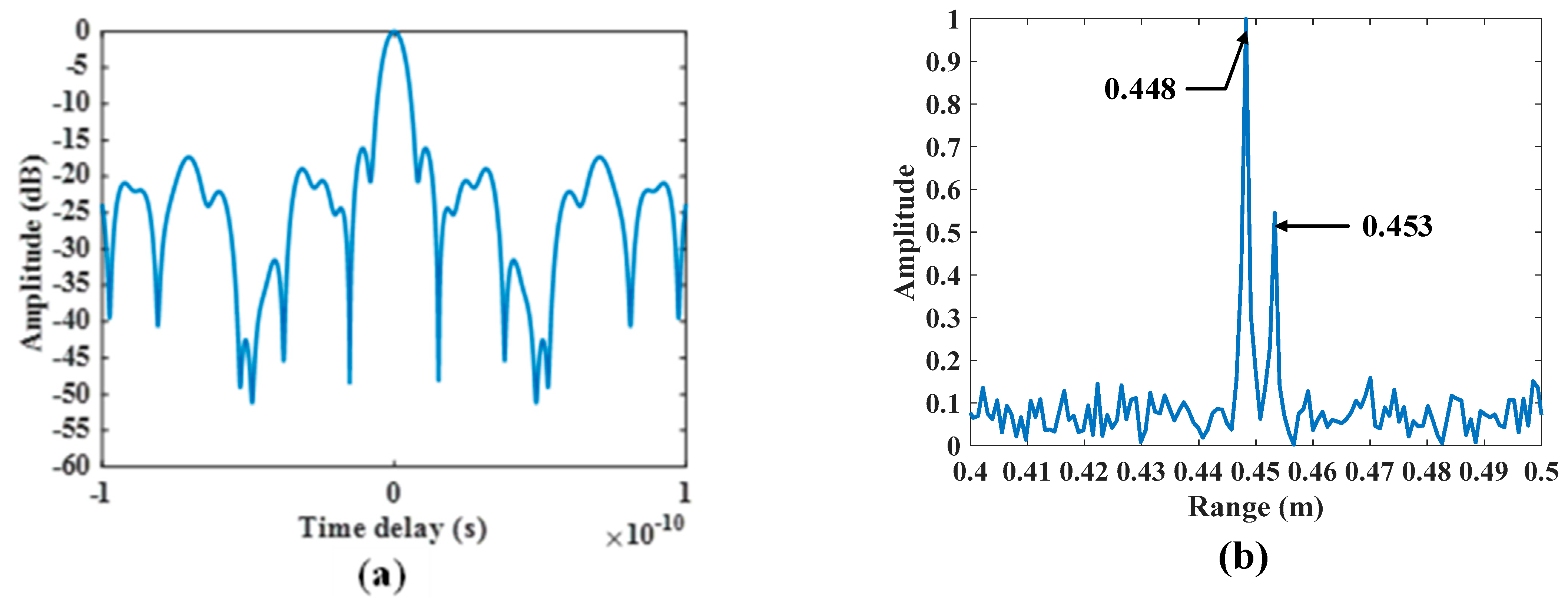
4.2. Experimental Results of Waveform Optimization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ferguson, B.; Zhang, X.C. Materials for terahertz science and technology. Nat. Mater. 2002, 1, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; You, P.; Tomasino, A.; Yurtsever, A.; Morandotti, R. Single-shot ultrafast terahertz photography. Nat. Commun. 2023, 14, 1704. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Wang, H.; Yang, Q.; Deng, B. High-Quality Airborne Terahertz Video SAR Imaging Based on Echo-Driven Robust Motion Compensation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 2001817. [Google Scholar] [CrossRef]
- Siegel, P.H. Terahertz technology. IEEE Trans. Microw. Theory Techn. 2002, 50, 910–928. [Google Scholar] [CrossRef]
- Matsumoto, H.; Watanabe, I.; Kasamatsu, A.; Monnai, Y. Integrated terahertz radar based on leaky-wave coherence tomography. Nat. Electron. 2020, 3, 122–129. [Google Scholar] [CrossRef]
- Yang, X.; Pi, Y.; Liu, T.; Wang, H. Three-dimensional imaging of space debris with space-based terahertz radar. IEEE Sens. J. 2018, 18, 1063–1072. [Google Scholar] [CrossRef]
- Jasteh, D.; Hoare, E.; Cherniakov, M.; Gashinova, M. Experimental Low-Terahertz Radar Image Analysis for Automotive Terrain Sensing. IEEE Geosci. Remote Sens. Lett. 2016, 13, 490–494. [Google Scholar] [CrossRef]
- Jamshed, M.A.; Nauman, A.; Abbasi, M.A.B.; Kim, S.W. Antenna selection and designing for THz applications: Suitability and performance evaluation: A survey. IEEE Access 2020, 8, 113246–113261. [Google Scholar] [CrossRef]
- Gishkori, S.; Daniel, L.; Gashinova, M.; Mulgrew, B. Imaging for a forward scanning automotive synthetic aperture radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 1420–1434. [Google Scholar] [CrossRef]
- Rasheed, I.; Hu, F. Intelligent super-fast vehicle-to-everything 5G communications with predictive switching between mmWave and THz links. Veh. Commun. 2021, 27, 100303. [Google Scholar] [CrossRef]
- Li, W.; Niu, M.; Zhang, Y.; Huang, Y.; Yang, J. Forward-looking scanning radar superresolution imaging based on second-order accelerated iterative shrinkage-thresholding algorithm. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 620–631. [Google Scholar] [CrossRef]
- Tuo, X.; Zhang, Y.; Huang, Y.; Yang, J. Fast sparse-TSVD superresolution method of real aperture radar forward-looking imaging. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6609–6620. [Google Scholar] [CrossRef]
- Li, W.; Yang, Y.; Huang, J.; Kong, J.; Wu, L. An improved Radon-transform-based scheme of Doppler centroid estimation for bistatic forward-looking SAR. IEEE Geosci. Remote Sens. Lett. 2011, 8, 379–383. [Google Scholar] [CrossRef]
- Pu, W.; Li, W.; Wu, J.; Huang, Y.; Yang, J.; Yang, H. An azimuth-variant autofocus scheme of bistatic forward-looking synthetic aperture radar. IEEE Geosci. Remote Sens. Lett. 2017, 14, 689–693. [Google Scholar] [CrossRef]
- Pu, W.; Wu, J.; Wang, X.; Huang, Y.; Zha, Y.; Yang, J. Joint sparsity-based imaging and motion error estimation for BFSAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1393–1408. [Google Scholar] [CrossRef]
- Yuan, Y.; Chen, S.; Zhang, S.; Zhao, H. A chirp scaling algorithm for forward-looking linear-array SAR with constant acceleration. IEEE Geosci. Remote Sens. Lett. 2018, 15, 88–91. [Google Scholar] [CrossRef]
- Liu, R.; Ji, C.; Zhao, Z.; Zhou, T. Metamaterials: Reshape and rethink. Engineering 2015, 1, 179–184. [Google Scholar] [CrossRef]
- Taghvaee, H.; Cabellos-Aparicio, A.; Georgiou, J.; Abadal, S. Error analysis of programmable metasurfaces for beam steering. IEEE J. Emerg. Sel. Top. Circuits Syst. 2020, 10, 62–74. [Google Scholar] [CrossRef]
- Lin, M.; Xu, M.; Wan, X.; Liu, H.; Wu, Z.; Liu, J.; Deng, B.; Guan, D.; Zha, S. Single sensor to estimate DOA with programmable metasurface. IEEE Internet Things J. 2021, 8, 10187–10197. [Google Scholar] [CrossRef]
- Tezsezen, E.; Yigci, D.; Ahmadpour, A.; Tasoglu, S. AI-based metamaterial design. ACS Appl. Mater. Interfaces 2024, 16, 29547–29569. [Google Scholar]
- Wang, S.R.; Chen, M.Z.; Ke, J.C.; Cheng, Q.; Cui, T.J. Asynchronous Space-Time-Coding Digital Metasurface. Adv. Sci. 2022, 9, 2200106. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Cui, T.J.; Ji, W.; Liu, S.; Ding, J.; Wan, X.; Li, Y.B.; Jiang, M.; Qiu, C.W.; Zhang, S. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 2017, 8, 197. [Google Scholar] [CrossRef]
- Zeng, H.; Lan, F.; Zhang, Y.; Liang, S.; Wang, L.; Yin, J.; Song, T.; Wang, L.; Zhang, T.; Shi, Z.; et al. Broadband terahertz reconfigurable metasurface based on 1-bit asymmetric coding metamaterial. Opt. Commun. 2020, 458, 124770. [Google Scholar] [CrossRef]
- Xu, J.S.; Liu, W.W.; Song, Z.Y. Terahertz dynamic beam steering based on graphene coding metasurfaces. IEEE Photon. J. 2021, 13, 4600409. [Google Scholar] [CrossRef]
- Lynch, J.J.; Herrault, F.; Kona, K.; Virbila, G.; McGuire, C.; Wetzel, M.; Fung, H.; Prophet, E. Coded aperture subreflector array for high resolution radar imaging. Proc. SPIE 2019, 1099405, 18. [Google Scholar]
- Venkatesh, S.; Lu, X.; Saeidi, H.; Sengupta, K. A high-speed programmable and scalable terahertz holographic metasurface based on tiled CMOS chips. Nat. Electron. 2020, 3, 785–793. [Google Scholar] [CrossRef]
- Jalili, H.; Momeni, O. A 436-to-467 GHz Lens-Integrated Reconfigurable Radiating Source with Continuous 2D Steering and Multi-Beam Operations in 65nm CMOS. In Proceedings of the 2021 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 13–22 February 2021; Volume 64, pp. 326–328. [Google Scholar]
- Monroe, N.M.; Dogiamis, G.C.; Stingel, R.; Myers, P.; Chen, X.; Han, R. Electronic THz Pencil Beam Forming and 2D Steering for High Angular-Resolution Operation: A 98×98-Unit 265GHz CMOS Reflectarray with In-Unit Digital Beam Shaping and Squint Correction. In Proceedings of the 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 20–26 February 2022; Volume 65, pp. 1–3. [Google Scholar]
- Lan, F.; Wang, L.; Zeng, H.; Liang, S.; Song, T.; Liu, W.; Mazumder, P.; Yang, Z.; Zhang, Y.; Mittleman, D.M. Real-time programmable metasurface for terahertz multifunctional wave front engineering. Light Sci. Appl. 2023, 12, 191. [Google Scholar] [CrossRef]
- Migliaccio, M.; Gambardella, A. Microwave radiometer spatial resolution enhancement. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1159–1169. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Li, W.; Huang, Y.; Yang, J. Super-resolution surface mapping for scanning radar: Inverse filtering based on the fast iterative adaptive approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 127–144. [Google Scholar] [CrossRef]
- Huo, W.; Tuo, X.; Zhang, Y.; Zhang, Y.; Huang, Y. Balanced Tikhonov and total variation deconvolution approach for radar forward-looking super-resolution imaging. IEEE Geosci. Remote Sens. Lett. 2021, 19, 3505805. [Google Scholar] [CrossRef]
- Yang, H.; Yang, F.; Xu, S.; Li, M.; Cao, X.; Gao, J.; Zheng, Y. A study of phase quantization effects for reconfigurable reflectarray antennas. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 302–305. [Google Scholar] [CrossRef]
- Nayeri, P.; Yang, F.; Elsherbeni, A.Z. Reflectarray Antennas: Theory, Designs, and Applications; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Huang, T.; Liu, Y.; Meng, H.; Wang, X. Cognitive random stepped frequency radar with sparse recovery. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 858–870. [Google Scholar] [CrossRef]
- Dai, F.; Zhang, S.; Li, L.; Liu, H. Enhancement of metasurface aperture microwave imaging via information-theoretic waveform optimization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5109512. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Sarker, R.A.; Elsayed, S.M.; Ray, T. Differential evolution with dynamic parameters selection for optimization problems. IEEE Trans. Evol. Comput. 2014, 18, 689–707. [Google Scholar] [CrossRef]

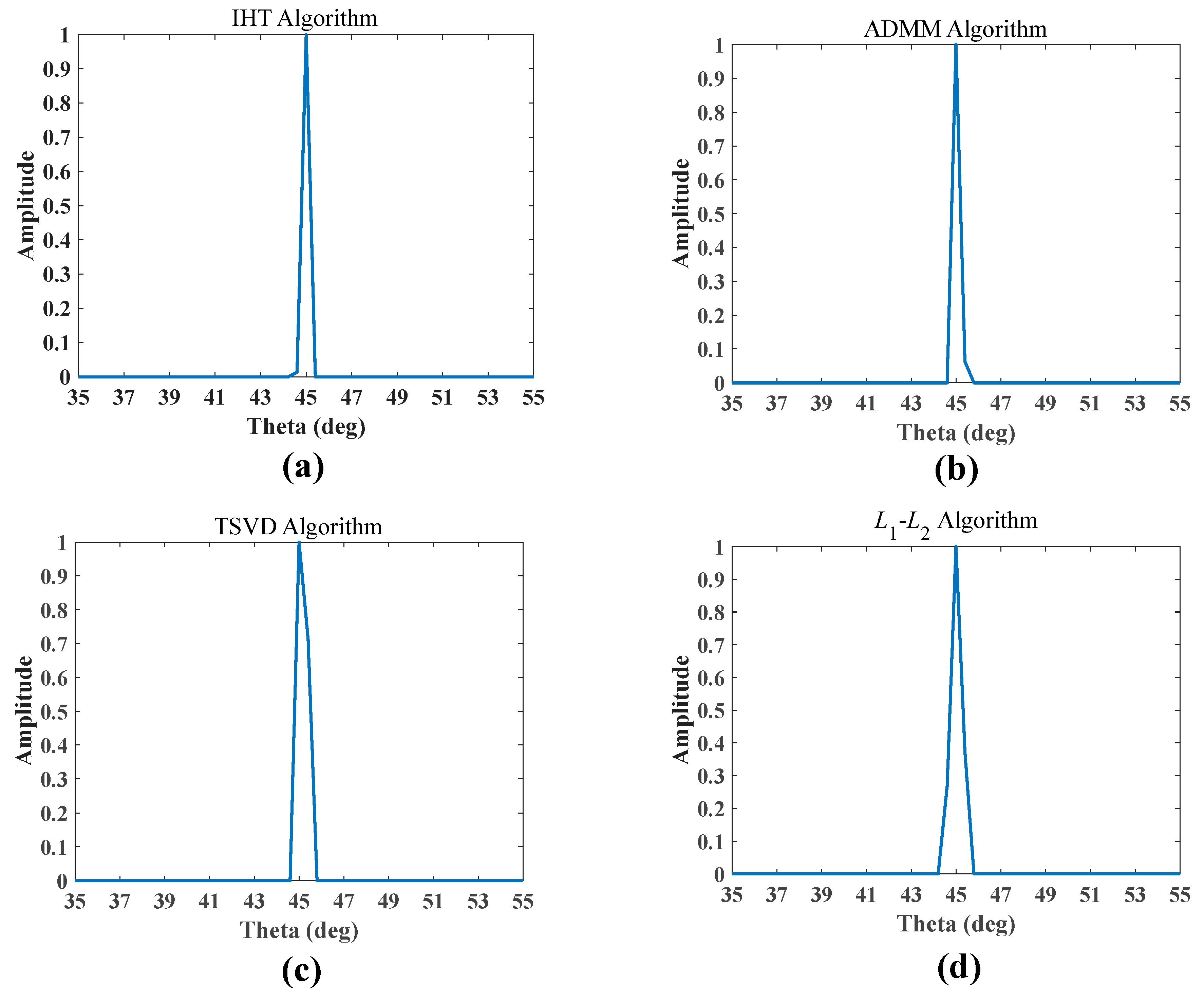



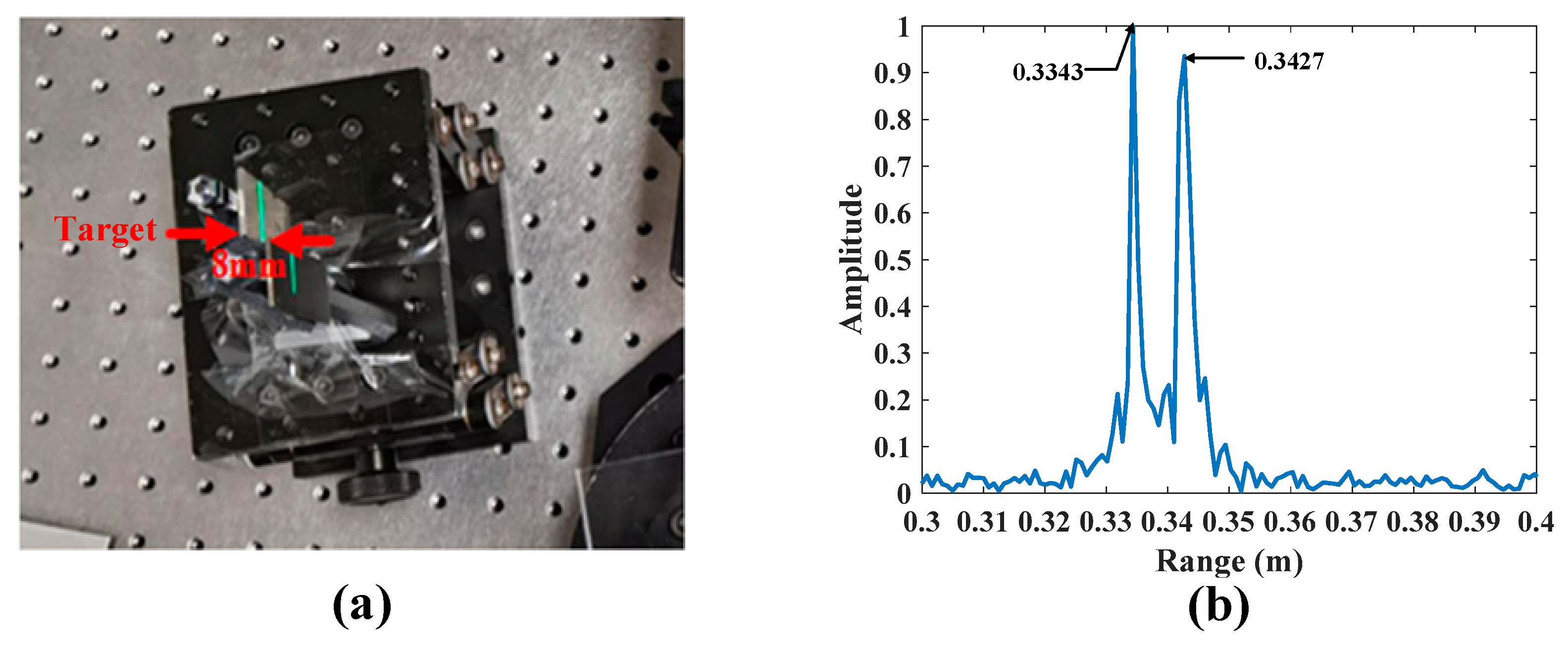
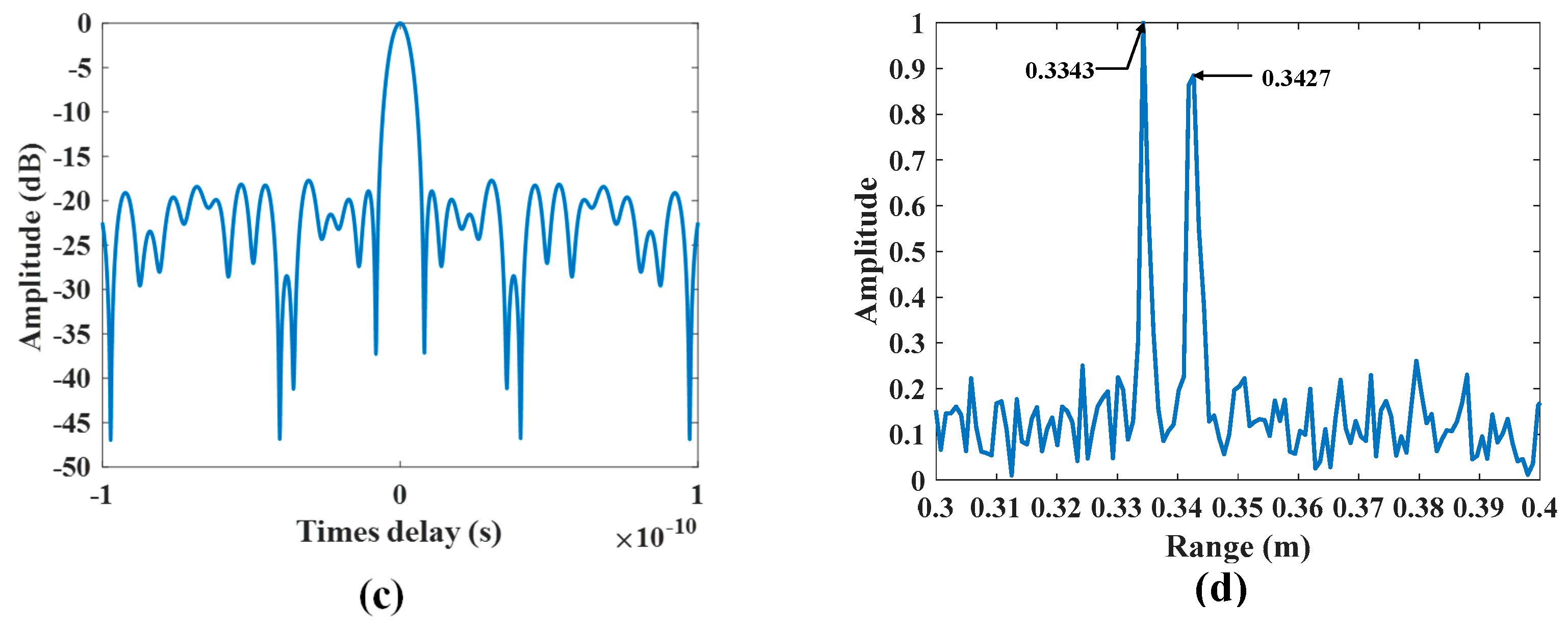

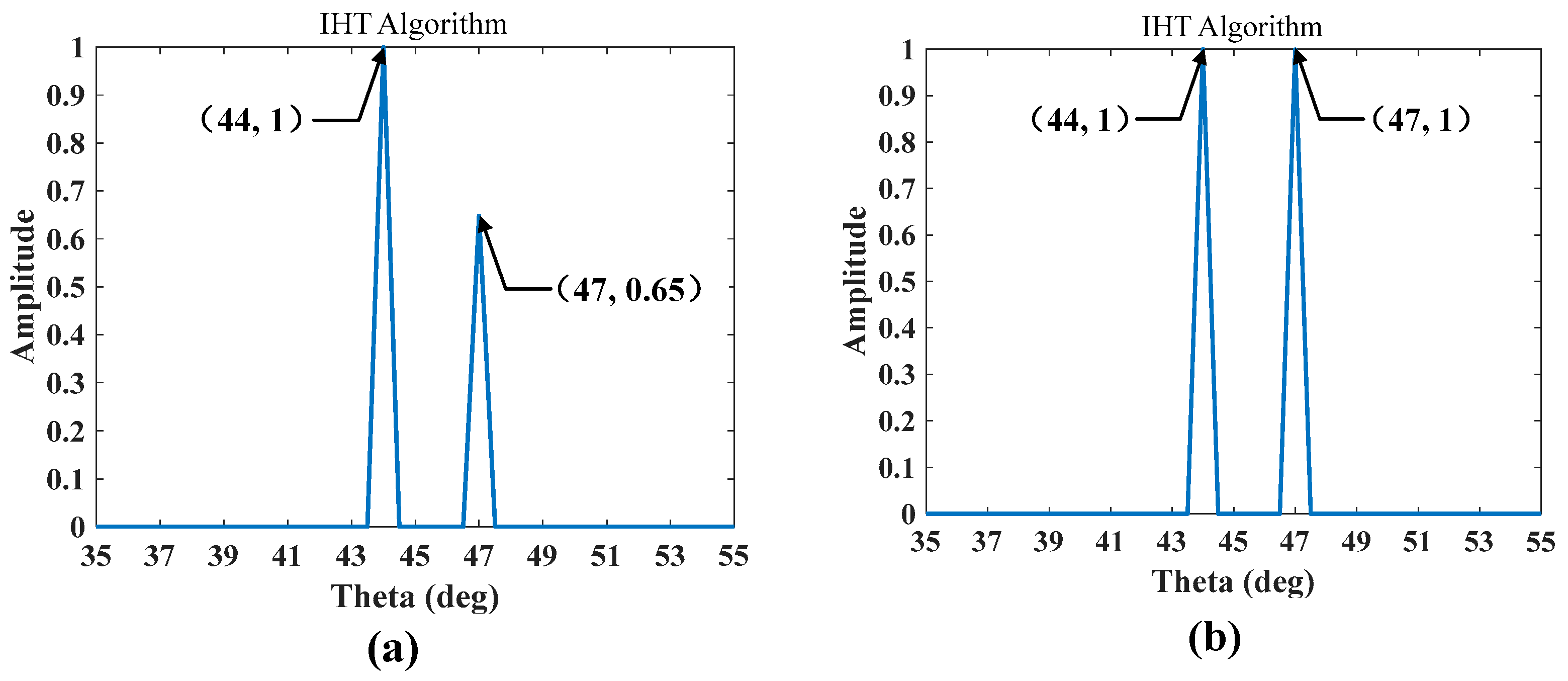


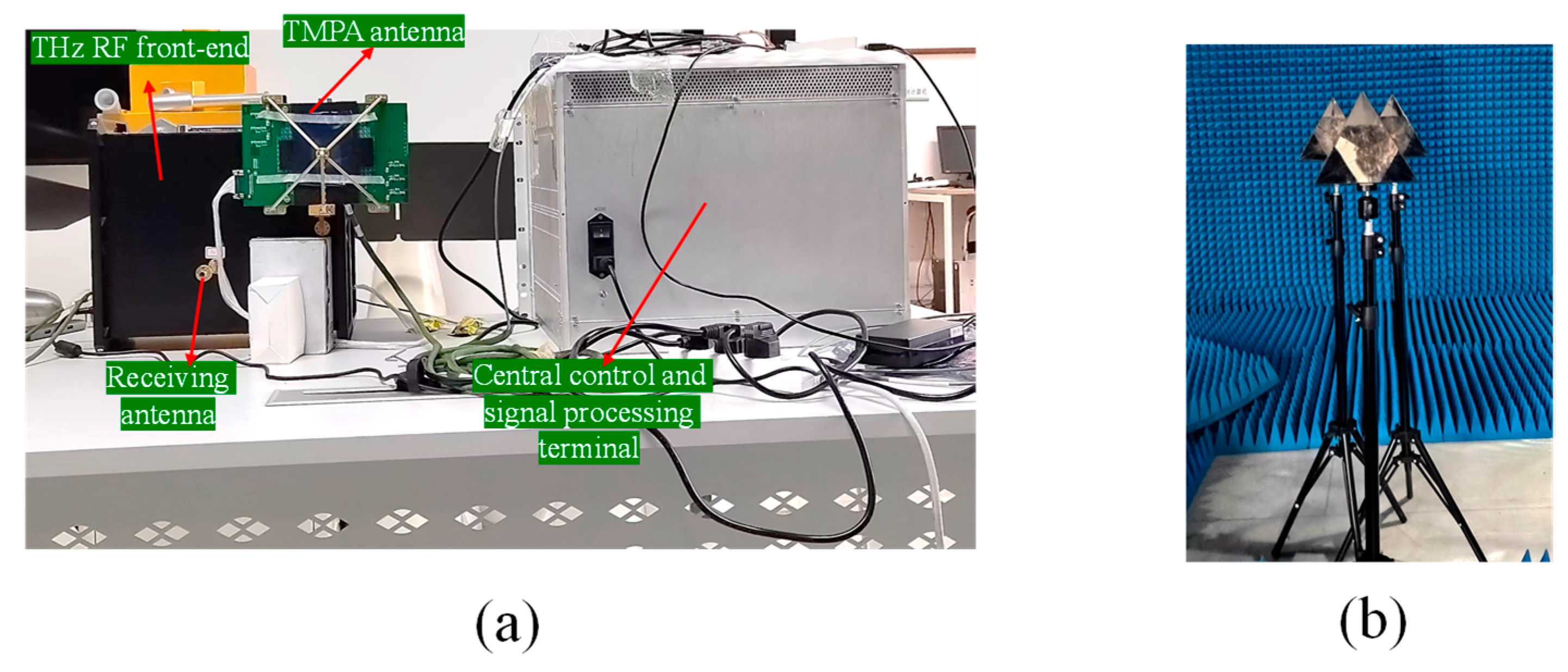

| Parameters | Value |
|---|---|
| Element number | 32 × 32 |
| Scanning area | 35~55° |
| Scanning step | 0.5° |
| Center frequency | 330 GHz |
| Bandwidth | 140 GHz |
| Frequency interval | 0.175 GHz |
| Amplitude modulation range | 0.4~2 |
| Parameters | Value |
|---|---|
| Element number | 48 × 48 |
| Scanning area | −5~2° |
| Scanning step | 0.2° |
| Center frequency | 216 GHz |
| Bandwidth | 900 MHz |
| Signal timewidth | 20 μs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, H.; Luo, C.; Liang, C.; Lan, F. Waveform Optimization for Enhancing the Performance of a Scanning Imaging Radar Utilizing a Terahertz Metamaterial Antenna. Remote Sens. 2025, 17, 1595. https://doi.org/10.3390/rs17091595
Zhang H, Wang H, Luo C, Liang C, Lan F. Waveform Optimization for Enhancing the Performance of a Scanning Imaging Radar Utilizing a Terahertz Metamaterial Antenna. Remote Sensing. 2025; 17(9):1595. https://doi.org/10.3390/rs17091595
Chicago/Turabian StyleZhang, Heng, Hongqiang Wang, Chenggao Luo, Chuanying Liang, and Feng Lan. 2025. "Waveform Optimization for Enhancing the Performance of a Scanning Imaging Radar Utilizing a Terahertz Metamaterial Antenna" Remote Sensing 17, no. 9: 1595. https://doi.org/10.3390/rs17091595
APA StyleZhang, H., Wang, H., Luo, C., Liang, C., & Lan, F. (2025). Waveform Optimization for Enhancing the Performance of a Scanning Imaging Radar Utilizing a Terahertz Metamaterial Antenna. Remote Sensing, 17(9), 1595. https://doi.org/10.3390/rs17091595






