A Stereo Disparity Map Refinement Method Without Training Based on Monocular Segmentation and Surface Normal
Abstract
1. Introduction
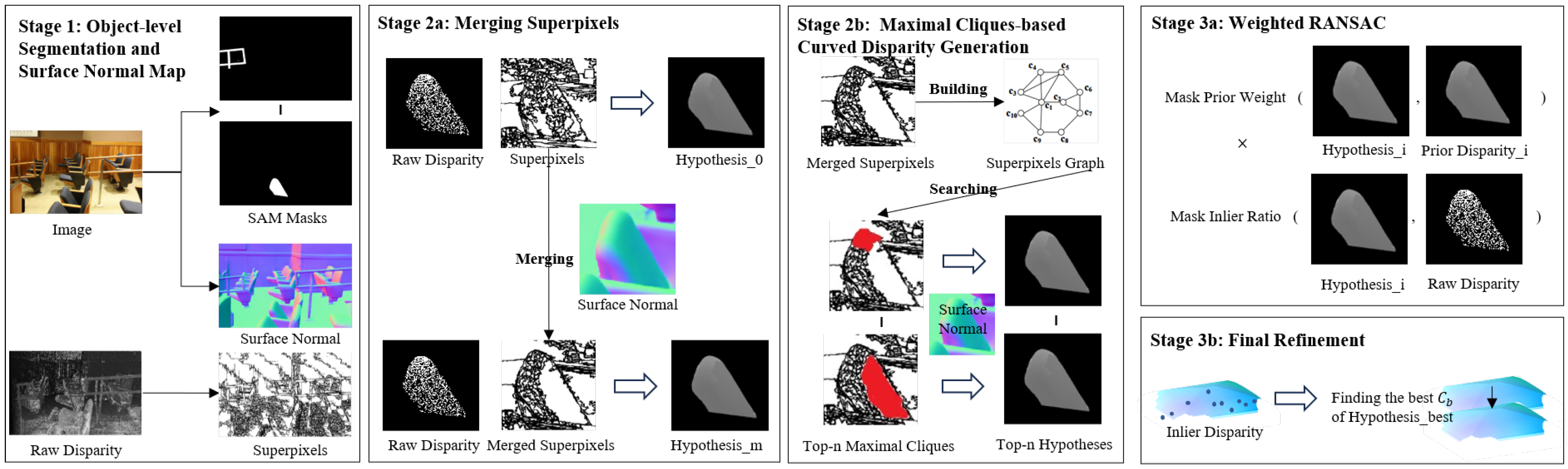
- We refine a stereo matching pipeline with monocular vision models (zero-shot monocular surface normal prediction and SAM). The method can directly enhance the traditional disparity refinement methods and achieve state-of-the-art performance.
- We build a new object-level weighted RANSAC framework based on SAM segmentation masks, which can balance disparity fitting and geometry structure similarity to prior geometry structure (monocular surface normal prediction).
- We utilize the SAM segmentations and surface normal prediction to obtain a better superpixel segmentation with large planes.
- We use maximum cliques search to obtain superpixels with the correct disparity in SAM masks and build possible curved disparity hypotheses.
2. Related Works
2.1. Disparity Refinement in Traditional Stereo Pipelines
2.2. Disparity Refinement in End-to-End Neural Networks
2.3. Normal Assisted Depth (Disparity) Estimation
3. Rethinking Ransac-Based Disparity Refinement
3.1. Former Methods
3.2. Proposed Disparity Map Model and Optimization Equation
4. Disparity Fitting Based on SAM and Surface Normal
| Algorithm 1 Weighted RANSAC-based disparity estimation. |
|
4.1. Object-Level Segmentation and Surface Normal Map
4.2. Two-Step Hypothesis Generation
4.2.1. Merging Superpixels
4.2.2. Surface Normal Transformation
4.2.3. Maximal Cliques-Based Curved Disparity Generation
4.3. Weighted RANSAC and Final Refinement
5. Experiments
5.1. Experiment Setup
5.2. Experiments on US3D Benchmark
5.3. Experiments on Middlebury Benchmark
5.3.1. Comparison with Disparity Refinement Methods
5.3.2. Comparison with Cost Volume-Based Hand-Crafted Methods
5.3.3. Comparison with Cross-Domain Stereo Networks
5.3.4. Hand-Crafted Initial Disparity Maps
5.4. Ablation Experiment
5.5. Generalization Test on More Unseen Dataset
5.6. Efficiency
6. Discusion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seitz, S.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 1, pp. 519–528. [Google Scholar] [CrossRef]
- Zhang, X.; Cao, X.; Yu, A.; Yu, W.; Li, Z.; Quan, Y. UAVStereo: A Multiple Resolution Dataset for Stereo Matching in UAV Scenarios. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2942–2953. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar] [CrossRef]
- Park, J.H.; Park, H.W. Fast view interpolation of stereo images using image gradient and disparity triangulation. Signal Process. Image Commun. 2003, 18, 401–416. [Google Scholar] [CrossRef]
- Zhang, T.; Zhuang, Y.; Chen, H.; Wang, G.; Ge, L.; Chen, L.; Dong, H.; Li, L. Posterior Instance Injection Detector for Arbitrary-Oriented Object Detection from Optical Remote Sensing Imagery. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 5623918. [Google Scholar] [CrossRef]
- Zhuang, Y.; Liu, Y.; Zhang, T.; Chen, L.; Chen, H.; Li, L. Heterogeneous Prototype Distillation with Support-Query Correlative Guidance for Few-Shot Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 5627918. [Google Scholar] [CrossRef]
- Wang, G.; Zhuang, Y.; Chen, H.; Liu, X.; Zhang, T.; Li, L.; Dong, S.; Sang, Q. FSoD-Net: Full-scale object detection from optical remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5602918. [Google Scholar] [CrossRef]
- Zhuang, Y.; Liu, Y.; Zhang, T.; Chen, H. Contour modeling arbitrary-oriented ship detection from very high-resolution optical remote sensing imagery. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6000805. [Google Scholar] [CrossRef]
- Hirschmuller, H. Stereo Processing by Semiglobal Matching and Mutual Information. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef]
- Michael Bleyer, C.R.; Rother, C. PatchMatch Stereo—Stereo Matching with Slanted Support Windows. In Proceedings of the British Machine Vision Conference, Dundee, UK, 29 August–2 September 2011; pp. 14.1–14.11. [Google Scholar] [CrossRef]
- Taniai, T.; Matsushita, Y.; Sato, Y.; Naemura, T. Continuous 3D Label Stereo Matching Using Local Expansion Moves. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2725–2739. [Google Scholar] [CrossRef]
- Yan, T.; Yang, X.; Yang, G.; Zhao, Q. Hierarchical Belief Propagation on Image Segmentation Pyramid. IEEE Trans. Image Process. 2023, 32, 4432–4442. [Google Scholar] [CrossRef]
- Žbontar, J.; Lecun, Y. Stereo matching by training a convolutional neural network to compare image patches. J. Mach. Learn. Res. 2016, 17, 1–32. [Google Scholar]
- Song, X.; Yang, G.; Zhu, X.; Zhou, H.; Wang, Z.; Shi, J. AdaStereo: A Simple and Efficient Approach for Adaptive Stereo Matching. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 10323–10332. [Google Scholar] [CrossRef]
- Weinzaepfel, P.; Lucas, T.; Leroy, V.; Cabon, Y.; Arora, V.; Brégier, R.; Csurka, G.; Antsfeld, L.; Chidlovskii, B.; Revaud, J. CroCo v2: Improved Cross-view Completion Pre-training for Stereo Matching and Optical Flow. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 17969–17980. [Google Scholar]
- Jiang, L.; Wang, F.; Zhang, W.; Li, P.; You, H.; Xiang, Y. Rethinking the Key Factors for the Generalization of Remote Sensing Stereo Matching Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 4936–4948. [Google Scholar] [CrossRef]
- Bae, G.; Budvytis, I.; Cipolla, R. IronDepth: Iterative Refinement of Single-View Depth using Surface Normal and its Uncertainty. In Proceedings of the 33rd British Machine Vision Conference 2022, BMVC 2022, London, UK, 21–24 November 2022. [Google Scholar]
- Qi, X.; Liao, R.; Liu, Z.; Urtasun, R.; Jia, J. GeoNet: Geometric Neural Network for Joint Depth and Surface Normal Estimation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 283–291. [Google Scholar] [CrossRef]
- Rossi, M.; Gheche, M.E.; Kuhn, A.; Frossard, P. Joint Graph-Based Depth Refinement and Normal Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Yan, T.; Gan, Y.; Xia, Z.; Zhao, Q. Segment-Based Disparity Refinement with Occlusion Handling for Stereo Matching. IEEE Trans. Image Process. 2019, 28, 3885–3897. [Google Scholar] [CrossRef] [PubMed]
- Tankovich, V.; Hane, C.; Zhang, Y.; Kowdle, A.; Fanello, S.; Bouaziz, S. HITNet: Hierarchical Iterative Tile Refinement Network for Real-time Stereo Matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 14362–14372. [Google Scholar]
- Lipson, L.; Teed, Z.; Deng, J. RAFT-Stereo: Multilevel Recurrent Field Transforms for Stereo Matching. In Proceedings of the 2021 International Conference on 3D Vision (3DV), Virtual, 1–3 December 2021; pp. 218–227. [Google Scholar] [CrossRef]
- Cheng, H.K.; Oh, S.W.; Price, B.; Schwing, A.; Lee, J.Y. Tracking Anything with Decoupled Video Segmentation. In Proceedings of the ICCV, Paris, France, 2–3 October 2023. [Google Scholar]
- Yu, T.; Feng, R.; Feng, R.; Liu, J.; Jin, X.; Zeng, W.; Chen, Z. Inpaint Anything: Segment Anything Meets Image Inpainting. arXiv 2023, arXiv:2304.06790. [Google Scholar]
- Gao, S.; Lin, Z.; Xie, X.; Zhou, P.; Cheng, M.M.; Yan, S. EditAnything: Empowering Unparalleled Flexibility in Image Editing and Generation. In Proceedings of the 31st ACM International Conference on Multimedia, Demo Track, Ottawa, ON, Canada, 29 October–3 November 2023. [Google Scholar]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment Anything. arXiv 2023, arXiv:2304.02643. [Google Scholar]
- Aleotti, F.; Tosi, F.; Zama Ramirez, P.; Poggi, M.; Salti, S.; Di Stefano, L.; Mattoccia, S. Neural Disparity Refinement for Arbitrary Resolution Stereo. In Proceedings of the International Conference on 3D Vision, Virtual, 1–3 December 2021. [Google Scholar]
- Favaro, P. Recovering thin structures via nonlocal-means regularization with application to depth from defocus. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1133–1140. [Google Scholar] [CrossRef]
- Zhang, S.; Xie, W.; Zhang, G.; Bao, H.; Kaess, M. Robust stereo matching with surface normal prediction. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2540–2547. [Google Scholar] [CrossRef]
- Barron, J.T.; Poole, B. The Fast Bilateral Solver. In Proceedings of the Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 1–14 October 2016; pp. 617–632. [Google Scholar]
- Wang, X.; Jiang, L.; Wang, F.; You, H.; Xiang, Y. Disparity Refinement for Stereo Matching of High-Resolution Remote Sensing Images Based on GIS Data. Remote Sens. 2024, 16, 487. [Google Scholar] [CrossRef]
- Xu, G.; Wang, X.; Ding, X.; Yang, X. Iterative Geometry Encoding Volume for Stereo Matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 21919–21928. [Google Scholar]
- Shen, Z.; Dai, Y.; Song, X.; Rao, Z.; Zhou, D.; Zhang, L. PCW-Net: Pyramid Combination and Warping Cost Volume for Stereo Matching. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 280–297. [Google Scholar]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Nießner, M. ScanNet: Richly-annotated 3D Reconstructions of Indoor Scenes. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Dharmasiri, T.; Spek, A.; Drummond, T. Joint prediction of depths, normals and surface curvature from RGB images using CNNs. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1505–1512. [Google Scholar]
- Yin, W.; Liu, Y.; Shen, C. Virtual Normal: Enforcing Geometric Constraints for Accurate and Robust Depth Prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 7282–7295. [Google Scholar] [CrossRef]
- Scharstein, D.; Taniai, T.; Sinha, S.N. Semi-global Stereo Matching with Surface Orientation Priors. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 215–224. [Google Scholar] [CrossRef]
- Felzenszwalb, P.F.; Huttenlocher, D.P. Efficient graph-based image segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]
- Eppstein, D.; Löffler, M.; Strash, D. Listing All Maximal Cliques in Sparse Graphs in Near-Optimal Time. In Algorithms and Computation; Cheong, O., Chwa, K.Y., Park, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 403–414. [Google Scholar]
- Eftekhar, A.; Sax, A.; Malik, J.; Zamir, A. Omnidata: A Scalable Pipeline for Making Multi-Task Mid-Level Vision Datasets From 3D Scans. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10786–10796. [Google Scholar]
- Atienza, R. Fast disparity estimation using dense networks. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 12–25 May 2018; pp. 3207–3212. [Google Scholar]
- He, S.; Li, S.; Jiang, S.; Jiang, W. HMSM-Net: Hierarchical multi-scale matching network for disparity estimation of high-resolution satellite stereo images. ISPRS J. Photogramm. Remote Sens. 2022, 188, 314–330. [Google Scholar] [CrossRef]
- Scharstein, D.; Hirschmüller, H.; Kitajima, Y.; Krathwohl, G.; Nešić, N.; Wang, X.; Westling, P. High-Resolution Stereo Datasets with Subpixel-Accurate Ground Truth. In Pattern Recognition; Jiang, X., Hornegger, J., Koch, R., Eds.; Springer: Cham, Switzerland, 2014; pp. 31–42. [Google Scholar]
- Li, A.; Chen, D.; Liu, Y.; Yuan, Z. Coordinating Multiple Disparity Proposals for Stereo Computation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4022–4030. [Google Scholar] [CrossRef]
- Li, L.; Zhang, S.; Yu, X.; Zhang, L. PMSC: PatchMatch-Based Superpixel Cut for Accurate Stereo Matching. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 679–692. [Google Scholar] [CrossRef]
- Cheng, X.; Zhao, Y.; Yang, W.; Hu, Z.; Yu, X.; Sang, H.; Zhang, G. LESC: Superpixel cut-based local expansion for accurate stereo matching. IET Image Process. 2022, 16, 470–484. [Google Scholar] [CrossRef]
- Guo, W.; Li, Z.; Yang, Y.; Wang, Z.; Taylor, R.H.; Unberath, M.; Yuille, A.; Li, Y. Context-Enhanced Stereo Transformer. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer: Cham, Switzerland, 2022; pp. 263–279. [Google Scholar]
- Keselman, L.; Iselin Woodfill, J.; Grunnet-Jepsen, A.; Bhowmik, A. Intel RealSense Stereoscopic Depth Cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Menze, M.; Geiger, A. Object Scene Flow for Autonomous Vehicles. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Wang, Q.; Wu, D.; Liu, W.; Lou, M.; Jiang, H.; Ying, Y.; Zhou, M. PlantStereo: A High Quality Stereo Matching Dataset for Plant Reconstruction. Agriculture 2023, 13, 330. [Google Scholar] [CrossRef]




| Method | EPE (Pixel) | D1-Error (%) |
|---|---|---|
| SGM [9] | ||
| DenseMapNet [41] | 2.030 | |
| SGM + SDR [20] | ||
| SGM + ours | 15.48 |
| Types | Methods | Bad 1.0 | Bad 2.0 | Bad 4.0 | Avgerr | Rms | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Noc | All | Noc | All | Noc | All | Noc | All | Noc | All | ||
| Surface Normal- based Methods | SNP-RSM [29] | ||||||||||
| MC-CNN+ours | |||||||||||
| Refinement-based Methods | SGM [9] | ||||||||||
| SGM+MDP [44] | |||||||||||
| MC-CNN-acrt [13] | |||||||||||
| MC-CNN+RBS [30] | |||||||||||
| MC-CNN+SDR [20] | |||||||||||
| HITNet [21] | |||||||||||
| MC-CNN+ours | |||||||||||
| Hand-crafted SOTA Methods | PMSC [45] | ||||||||||
| LocalExp [11] | |||||||||||
| LESC [46] | |||||||||||
| HBP-ISP [12] | |||||||||||
| MC-CNN+ours | |||||||||||
| Cross-domain Stereo Networks | MSTR [47] | ||||||||||
| AdaStereo [14] | |||||||||||
| CroCo-Stereo [15] | |||||||||||
| MC-CNN+ours | |||||||||||
| Methods | Bad 1.0 | Bad 2.0 | Bad 4.0 | Avgerr | Rms | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Noc | All | Noc | All | Noc | All | Noc | All | Noc | All | |
| SGBM | ||||||||||
| SGBM+SDR | ||||||||||
| SGBM+ours | ||||||||||
| R200 [48] | ||||||||||
| R200+SDR | ||||||||||
| R200+ours [48] | ||||||||||
| Methods | Bad 1.0 | Bad 2.0 | Bad 4.0 | Avgerr | Rms | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Noc | All | Noc | All | Noc | All | Noc | All | Noc | All | |
| R200 | ||||||||||
| R200+SDR | ||||||||||
| R200+SDR (m) | ||||||||||
| R200+P | ||||||||||
| R200+P+M (0.3,5) | ||||||||||
| R200+P+M (1.0,5)+R | ||||||||||
| R200+P+M (0.3,10)+R | ||||||||||
| R200+P+M (0.3,5)+R | ||||||||||
| Methods | Bad 1.0 | Bad 2.0 | Bad 4.0 | Avgerr | Rms | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Noc | All | Noc | All | Noc | All | Noc | All | Noc | All | |
| R200 | ||||||||||
| R200+SDR | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Wang, T. A Stereo Disparity Map Refinement Method Without Training Based on Monocular Segmentation and Surface Normal. Remote Sens. 2025, 17, 1587. https://doi.org/10.3390/rs17091587
Sun H, Wang T. A Stereo Disparity Map Refinement Method Without Training Based on Monocular Segmentation and Surface Normal. Remote Sensing. 2025; 17(9):1587. https://doi.org/10.3390/rs17091587
Chicago/Turabian StyleSun, Haoxuan, and Taoyang Wang. 2025. "A Stereo Disparity Map Refinement Method Without Training Based on Monocular Segmentation and Surface Normal" Remote Sensing 17, no. 9: 1587. https://doi.org/10.3390/rs17091587
APA StyleSun, H., & Wang, T. (2025). A Stereo Disparity Map Refinement Method Without Training Based on Monocular Segmentation and Surface Normal. Remote Sensing, 17(9), 1587. https://doi.org/10.3390/rs17091587






