A Subimage Autofocus Bistatic Ground Cartesian Back-Projection Algorithm for Passive Bistatic SAR Based on GEO Satellites
Abstract
1. Introduction
- For the GEO-satellite-based PBSAR, we analyze the wavenumber spectrum and enhance the traditional GCBP to develop BGCBP, extending its applicability to PBSAR.
- To address the limitations of traditional AF algorithms, we integrate the image-sharpness-based SIAF with the proposed BGCBP, improving efficiency and parallelism.
- We propose distinct AF strategies for different scenarios, enhancing the focusing accuracy while maintaining the processing speed.
2. Materials and Methods
2.1. Model
2.1.1. Signal Model
2.1.2. Analysis of the Signal Model
2.2. Bistatic Ground Cartesian Back-Projection Algorithm
2.2.1. The Derivation of the Original GCBP
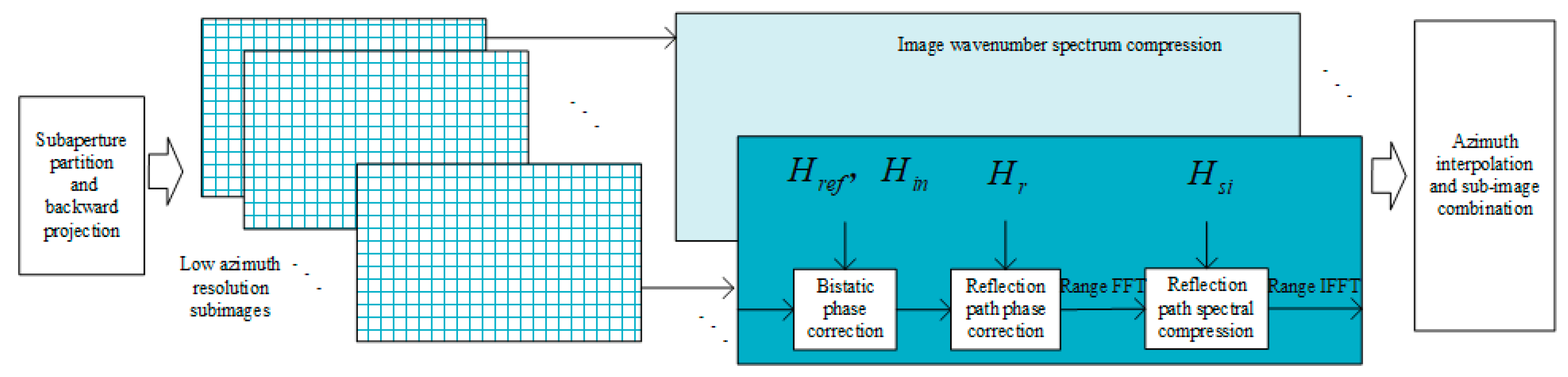
2.2.2. BGCBP for PBSAR Based on the GEO Satellite
2.2.3. Analysis of Spectral Compression
2.2.4. Analysis and Discussion of BGCBP
2.3. Proposed Fast Autofocus Back-Projection Algorithm
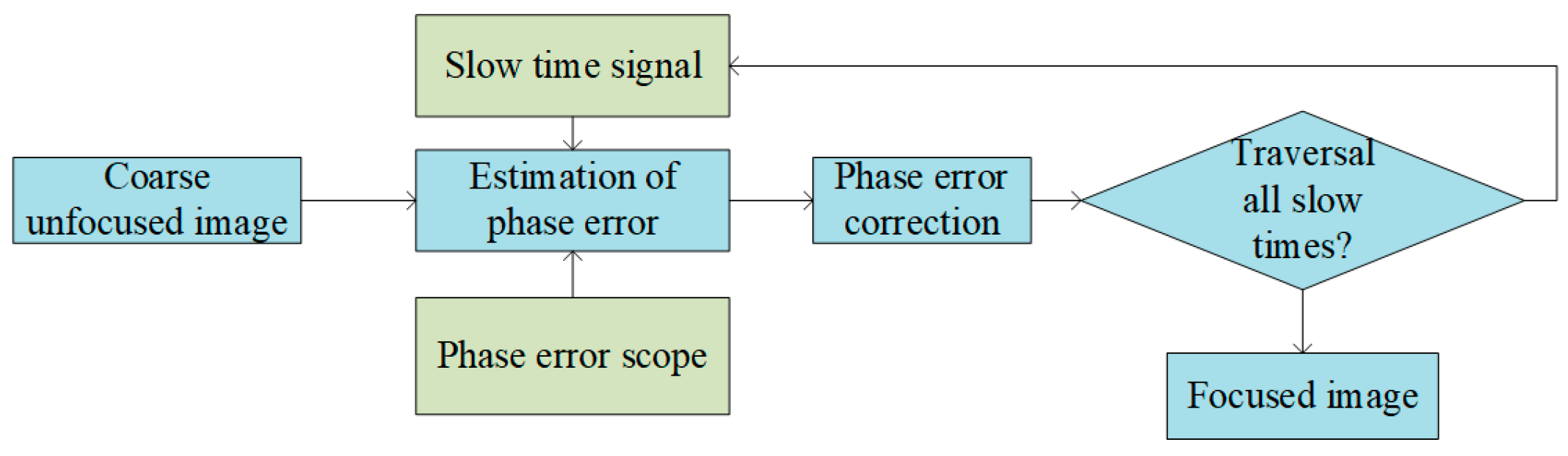
2.3.1. Conventional AFBP Algorithm Based on Sharpness
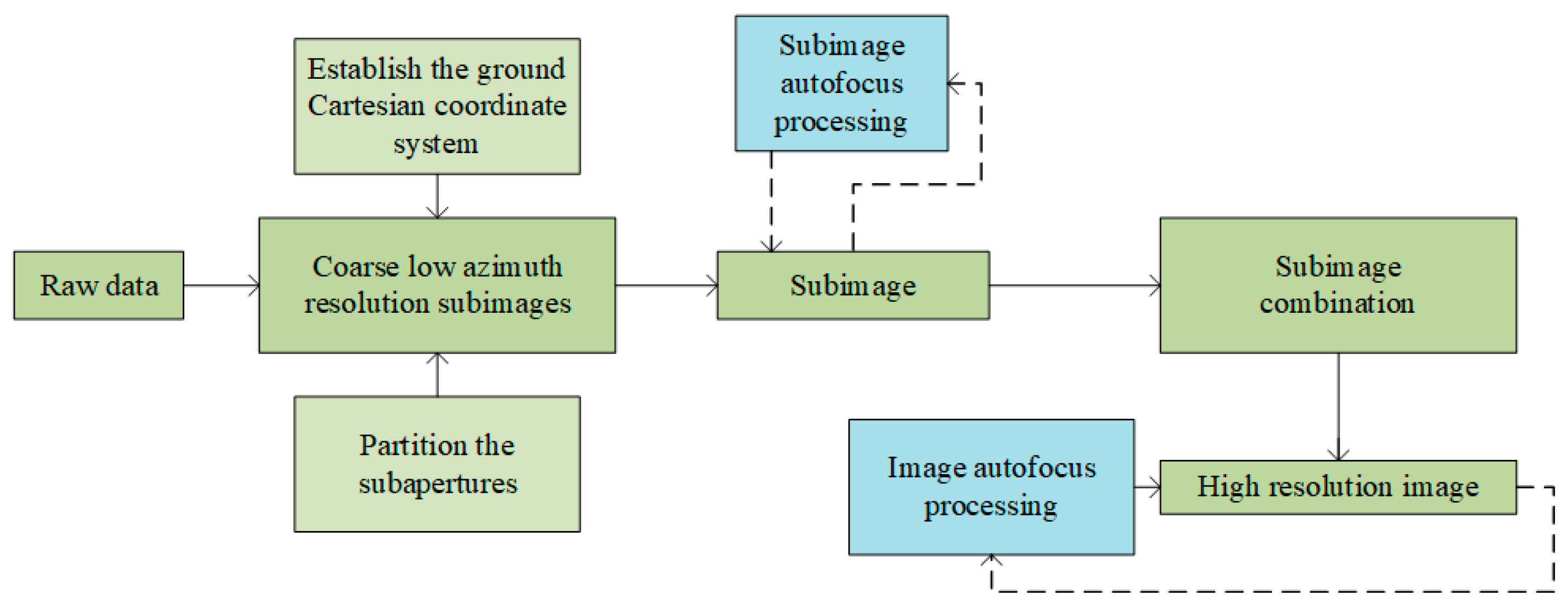
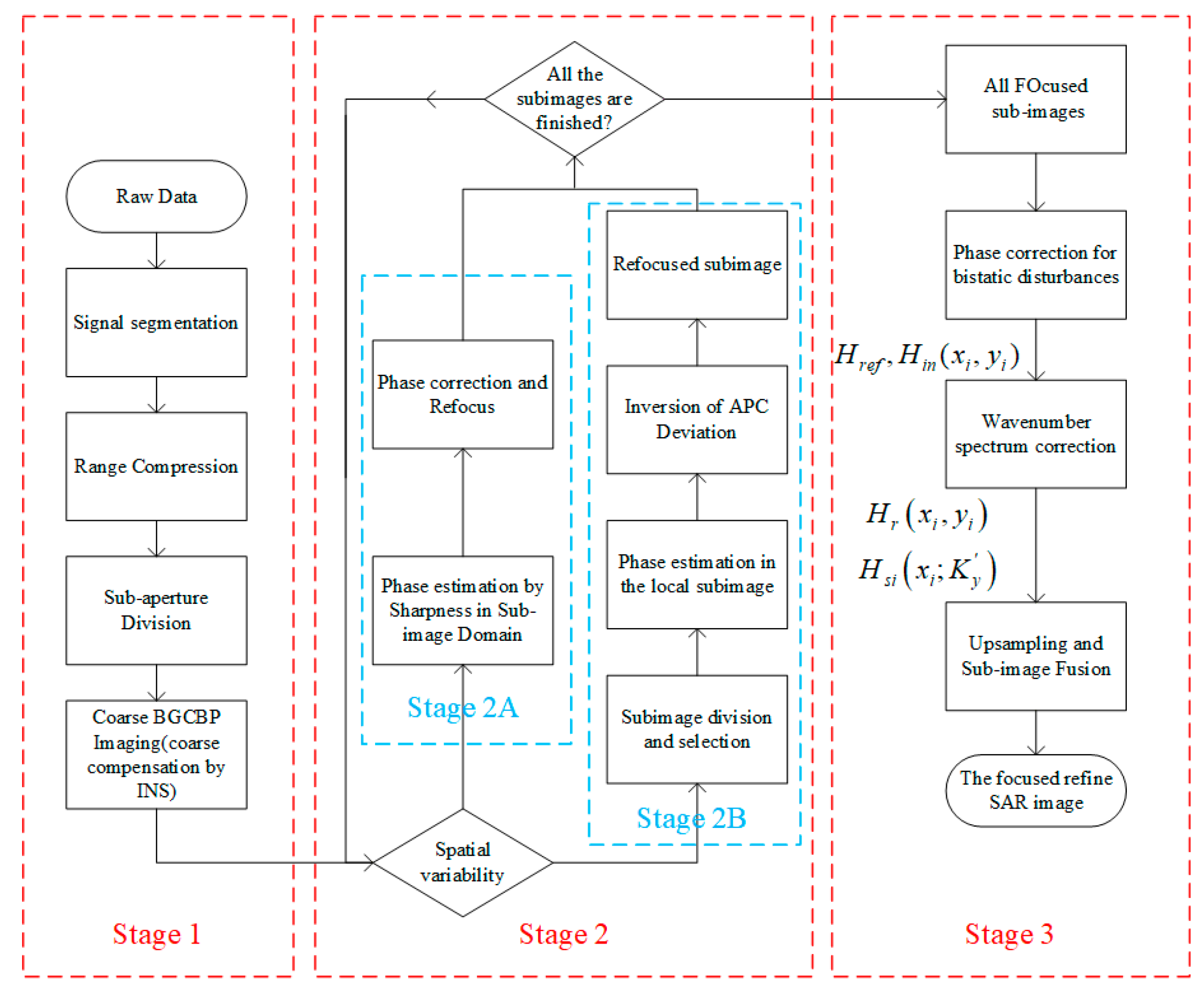
2.3.2. Subimage Autofocus Bistatic Ground Cartesian Back-Projection Algorithm
2.3.3. Analysis and Discussion of the Proposed SIAF-BGCBP
3. Results
3.1. BGCBP Simulation Experiments
3.2. SIAF-BGCBP Simulation Experiments
3.3. Real-Environment Experiments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maslikowski, L.; Samczynski, P.; Baczyk, M.; Krysik, P.; Kulpa, K. Passive Bistatic SAR Imaging—Challenges and Limitations. IEEE Aerosp. Electron. Syst. Mag. 2014, 29, 23–29. [Google Scholar] [CrossRef]
- Colone, F.; Filippini, F.; Pastina, D. Passive Radar: Past, Present, and Future Challenges. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 54–69. [Google Scholar] [CrossRef]
- Chen, X.; Dong, Z.; Zhang, Z.; Tu, C.; Yi, T.; He, Z. Very High Resolution Synthetic Aperture Radar Systems and Imaging: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 7104–7123. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Yu, H.; Liang, B.; Peng, J.; Sun, G.-C. Motion Compensation/Autofocus in Airborne Synthetic Aperture Radar: A Review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 185–206. [Google Scholar] [CrossRef]
- Wu, J.; Li, Z.; Huang, Y.; Yang, J.; Liu, Q.H. An Omega-K Algorithm for Translational Invariant Bistatic SAR Based on Generalized Loffeld’s Bistatic Formula. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6699–6714. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, J.; Zhang, X. Nonlinear RCMC Method for Spaceborne/Airborne Forward-Looking Bistatic SAR. J. Syst. Eng. Electron. 2012, 23, 201–207. [Google Scholar] [CrossRef]
- Luo, Y.; Zhao, F.; Li, N.; Zhang, H. An Autofocus Cartesian Factorized Backprojection Algorithm for Spotlight Synthetic Aperture Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1244–1248. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, Z.; Song, Y.; Li, L.; Bi, H. Backprojection Operator-Based One-Stationary Bistatic SAR Sparse Imaging. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4012405. [Google Scholar] [CrossRef]
- Xu, G.; Zhou, S.; Yang, L.; Deng, S.; Wang, Y.; Xing, M. Efficient Fast Time-Domain Processing Framework for Airborne Bistatic SAR Continuous Imaging Integrated with Data-Driven Motion Compensation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5208915. [Google Scholar] [CrossRef]
- Yegulalp, A.F. Fast Backprojection Algorithm for Synthetic Aperture Radar. In Proceedings of the 1999 IEEE Radar Conference, Radar into the Next Millennium (Cat. No.99CH36249), Waltham, MA, USA, 20–22 April 1999; IEEE: Piscataway, NJ, USA, 1999; pp. 60–65. [Google Scholar]
- Ulander, L.M.H.; Hellsten, H.; Stenstrom, G. Synthetic-Aperture Radar Processing Using Fast Factorized Back-Projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef]
- Lou, Y.; Lin, H.; Li, N.; Xing, M.; Wang, J.; Wu, Z. A Prior 2-D Autofocus Algorithm with Ground Cartesian BP Imaging for Curved Trajectory SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 2422–2436. [Google Scholar] [CrossRef]
- Liang, Y.; Li, G.; Wen, J.; Zhang, G.; Dang, Y.; Xing, M. A Fast Time-Domain SAR Imaging and Corresponding Autofocus Method Based on Hybrid Coordinate System. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8627–8640. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.; Qiao, Z.; Xing, M.; Bao, Z. Integrating Autofocus Techniques with Fast Factorized Back-Projection for High-Resolution Spotlight SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1394–1398. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.L.; Qiao, Z.J.; Xu, Z.W. A Fast BP Algorithm with Wavenumber Spectrum Fusion for High-Resolution Spotlight SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1460–1464. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, W.; Sun, G.-C.; Chen, X.; Han, L.; Xing, M. A Fast Cartesian Back-Projection Algorithm Based on Ground Surface Grid for GEO SAR Focusing. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5217114. [Google Scholar] [CrossRef]
- Bie, B.; Xing, M.; Xia, X.-G.; Sun, G.-C.; Liang, Y.; Jing, G.; Wei, T.; Yu, Y. A Frequency Domain Backprojection Algorithm Based on Local Cartesian Coordinate and Subregion Range Migration Correction for High-Squint SAR Mounted on Maneuvering Platforms. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7086–7101. [Google Scholar] [CrossRef]
- Liang, D.; Zhang, H.; Fang, T.; Lin, H.; Liu, D.; Jia, X. A Modified Cartesian Factorized Backprojection Algorithm Integrating with Non-Start-Stop Model for High Resolution SAR Imaging. Remote Sens. 2020, 12, 3807. [Google Scholar] [CrossRef]
- Li, Y.; Xu, G.; Zhou, S.; Xing, M.; Song, X. A Novel CFFBP Algorithm with Noninterpolation Image Merging for Bistatic Forward-Looking SAR Focusing. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5225916. [Google Scholar] [CrossRef]
- Lou, Y.; Liu, W.; Xing, M.; Lin, H.; Chen, X.; Sun, G.-C. A Novel Motion Compensation Method Applicable to Ground Cartesian Back-Projection Algorithm for Airborne Circular SAR. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5208917. [Google Scholar] [CrossRef]
- Dong, Q.; Sun, G.-C.; Yang, Z.; Guo, L.; Xing, M. Cartesian Factorized Backprojection Algorithm for High-Resolution Spotlight SAR Imaging. IEEE Sens. J. 2018, 18, 1160–1168. [Google Scholar] [CrossRef]
- Chen, X.; Sun, G.-C.; Xing, M.; Li, B.; Yang, J.; Bao, Z. Ground Cartesian Back-Projection Algorithm for High Squint Diving TOPS SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5812–5827. [Google Scholar] [CrossRef]
- Shi, T.; Mao, X.; Jakobsson, A.; Liu, Y. Parametric Model-Based 2-D Autofocus Approach for General BiSAR Filtered Backprojection Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5233414. [Google Scholar] [CrossRef]
- Ran, L.; Liu, Z.; Li, T.; Xie, R.; Zhang, L. Extension of Map-Drift Algorithm for Highly Squinted SAR Autofocus. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4032–4044. [Google Scholar] [CrossRef]
- Evers, A.; Jackson, J.A. A Generalized Phase Gradient Autofocus Algorithm. IEEE Trans. Comput. Imaging 2019, 5, 606–619. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Y.; Ding, Y. Geometric Configuration Design and Fast Imaging for Multistatic Forward-Looking SAR Based on Wavenumber Spectrum Formation Approach. Remote Sens. 2023, 15, 2783. [Google Scholar] [CrossRef]
- Torgrimsson, J.; Dammert, P.; Hellsten, H.; Ulander, L.M.H. Factorized Geometrical Autofocus for Synthetic Aperture Radar Processing. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6674–6687. [Google Scholar] [CrossRef]
- Summerfield, J.; Harcke, L.; Conder, B.; Kasilingam, D. Maximizing the Radar Generalized Image Quality Equation for Bistatic SAR Using Waveform Frequency Agility. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5218918. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Q.; Yang, J. Extended PGA Processing of High Resolution Airborne SAR Imagery Reconstructed via Backprojection Algorithm. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–3. [Google Scholar]
- Li, H.; Suo, Z.; Zheng, C.; Li, Z.; Zhao, B. A Modified Factorized Geometrical Autofocus Method for Wide Angle SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1458–1468. [Google Scholar] [CrossRef]
- Koh, B.; Choi, S.; Chun, J. SAR Autofocus Technique with MUSIC and Golden Section Search for Range Bins with Multiple Point Scatterers. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1600–1604. [Google Scholar] [CrossRef]
- Zhang, T.; Liao, G.; Li, Y.; Gu, T.; Zhang, T.; Liu, Y. A Two-Stage Time-Domain Autofocus Method Based on Generalized Sharpness Metrics and AFBP. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Ash, J.N. An Autofocus Method for Backprojection Imagery in Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2012, 9, 104–108. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, X.; He, S.; Zhao, H.; Shi, J. A Less-Memory and High-Efficiency Autofocus Back Projection Algorithm for SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 890–894. [Google Scholar] [CrossRef]
- Chen, L.; An, D.; Huang, X. Extended Autofocus Backprojection Algorithm for Low-Frequency SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1323–1327. [Google Scholar] [CrossRef]
- Cai, J.; Martorella, M.; Chang, S.; Liu, Q.; Ding, Z.; Long, T. Efficient Nonparametric ISAR Autofocus Algorithm Based on Contrast Maximization and Newton’s Method. IEEE Sens. J. 2021, 21, 4474–4487. [Google Scholar] [CrossRef]
- Sommer, A.; Ostermann, J. Backprojection Subimage Autofocus of Moving Ships for Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8383–8393. [Google Scholar] [CrossRef]
- Pu, W.; Wu, J.; Huang, Y.; Yang, J.; Yang, H. Fast Factorized Backprojection Imaging Algorithm Integrated with Motion Trajectory Estimation for Bistatic Forward-Looking SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3949–3965. [Google Scholar] [CrossRef]
- Wang, P.; Zhou, X.; Fang, Y.; Zeng, H.; Chen, J. GNSS-Based Passive Inverse SAR Imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 508–521. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, J.; Song, Y.; Yang, J.; Li, Z.; Huang, Y. Bistatic-Range-Doppler-Aperture Wavenumber Algorithm for Forward-Looking Spotlight SAR With Stationary Transmitter and Maneuvering Receiver. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2080–2094. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, L.; Zhao, L.; Wang, Y.; Zhou, H.; Chen, L.; Xing, M. A New Fast Factorized Back Projection Algorithm for Bistatic Forward-Looking SAR Imaging Based on Orthogonal Elliptical Polar Coordinate. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1508–1520. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Wu, J.; Sun, Z.; Sun, H.; Yang, J. An Estimation and Compensation Method for Motion Trajectory Error in Bistatic SAR. Remote Sens. 2022, 14, 5522. [Google Scholar] [CrossRef]
- Zhang, T.; Liao, G.; Li, Y.; Gu, T.; Zhang, T.; Liu, Y. An Improved Time-Domain Autofocus Method Based on 3-D Motion Errors Estimation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5223816. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Sun, Z.; Wu, J.; Li, Z.; Yang, J. An Autofocus Scheme of Bistatic SAR Considering Cross-Cell Residual Range Migration. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4507905. [Google Scholar] [CrossRef]


















| Parameters Symbols | Meaning |
|---|---|
| The number of grids in the range direction for the final image | |
| The number of grids in the azimuth direction for the final image | |
| The number of sampling points in the fast-time dimension | |
| The number of sampling points in the slow-time dimension | |
| The number of sub-apertures | |
| Upsampling coefficients in the fast-time dimension |
| Parameter | Setting |
|---|---|
| Longitude of the GEO satellite | 92.2°E |
| Form of signal | Random communication signals |
| Bandwidth of the signal | 20 MHz |
| Frequency band of the signal | 11.7 GHz (Ku) |
| Motion direction of the receiving antenna | From east to west |
| Algorithm | PSLR (dB) | ISLR (dB) | Res-A (m) | Res-R (m) | Computation Time (s) |
|---|---|---|---|---|---|
| Original BP | −13.2703 | −7.7576 | 10 | 16.9073 | 0.231897 |
| SI by BGCBP | −13.2475 | −8.6026 | 40 | 16.9073 | 0.021860 |
| BGCBP | −12.8762 | −8.6971 | 10.0334 | 16.9073 | 0.099937 |
| Algorithm | PSLR (dB) | ISLR (dB) | Res-A (m) | Computation Time (s) |
|---|---|---|---|---|
| Proposed SIAF-BGCBP | −14.1513 | −8.4672 | 45.2261 | 11.400817 |
| AFBP based on entropy | −11.6278 | −7.7834 | 44.2010 | 46.851729 |
| AFBP based on sharpness | −15.3531 | −8.9971 | 45.2261 | 33.374198 |
| Algorithm | Experiment 1 (Eastern Scene) | Experiment 2 (Southern Scene) | ||
|---|---|---|---|---|
| Contrast | Computation Time (s) | Contrast | Computation Time (s) | |
| Original BP | 1.3457 | 0.125261 | 1.2442 | 0.151804 |
| Proposed BGCBP | 1.3593 | 0.036964 | 1.2433 | 0.047015 |
| Proposed SIAF-BGCBP based on GI | 1.3894 | 4.381363 | 1.2761 | 9.268560 |
| AFBP based on entropy | 1.3815 | 36.110968 | 1.2736 | 28.961385 |
| AFBP based on sharpness | 1.3849 | 23.739568 | 1.2717 | 26.717829 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Wang, J.; Cheng, Z.; Huang, Z.; Song, X. A Subimage Autofocus Bistatic Ground Cartesian Back-Projection Algorithm for Passive Bistatic SAR Based on GEO Satellites. Remote Sens. 2025, 17, 1576. https://doi.org/10.3390/rs17091576
Zhao T, Wang J, Cheng Z, Huang Z, Song X. A Subimage Autofocus Bistatic Ground Cartesian Back-Projection Algorithm for Passive Bistatic SAR Based on GEO Satellites. Remote Sensing. 2025; 17(9):1576. https://doi.org/10.3390/rs17091576
Chicago/Turabian StyleZhao, Te, Jun Wang, Zuhan Cheng, Ziqian Huang, and Xueming Song. 2025. "A Subimage Autofocus Bistatic Ground Cartesian Back-Projection Algorithm for Passive Bistatic SAR Based on GEO Satellites" Remote Sensing 17, no. 9: 1576. https://doi.org/10.3390/rs17091576
APA StyleZhao, T., Wang, J., Cheng, Z., Huang, Z., & Song, X. (2025). A Subimage Autofocus Bistatic Ground Cartesian Back-Projection Algorithm for Passive Bistatic SAR Based on GEO Satellites. Remote Sensing, 17(9), 1576. https://doi.org/10.3390/rs17091576








