Real-Time Regional Ionospheric Total Electron Content Modeling Using the Extended Kalman Filter
Abstract
1. Introduction
2. Methodology
2.1. Kalman Filtering Algorithm
2.2. Extended Kalman Filtering Algorithm
3. Data Sources and Modeling
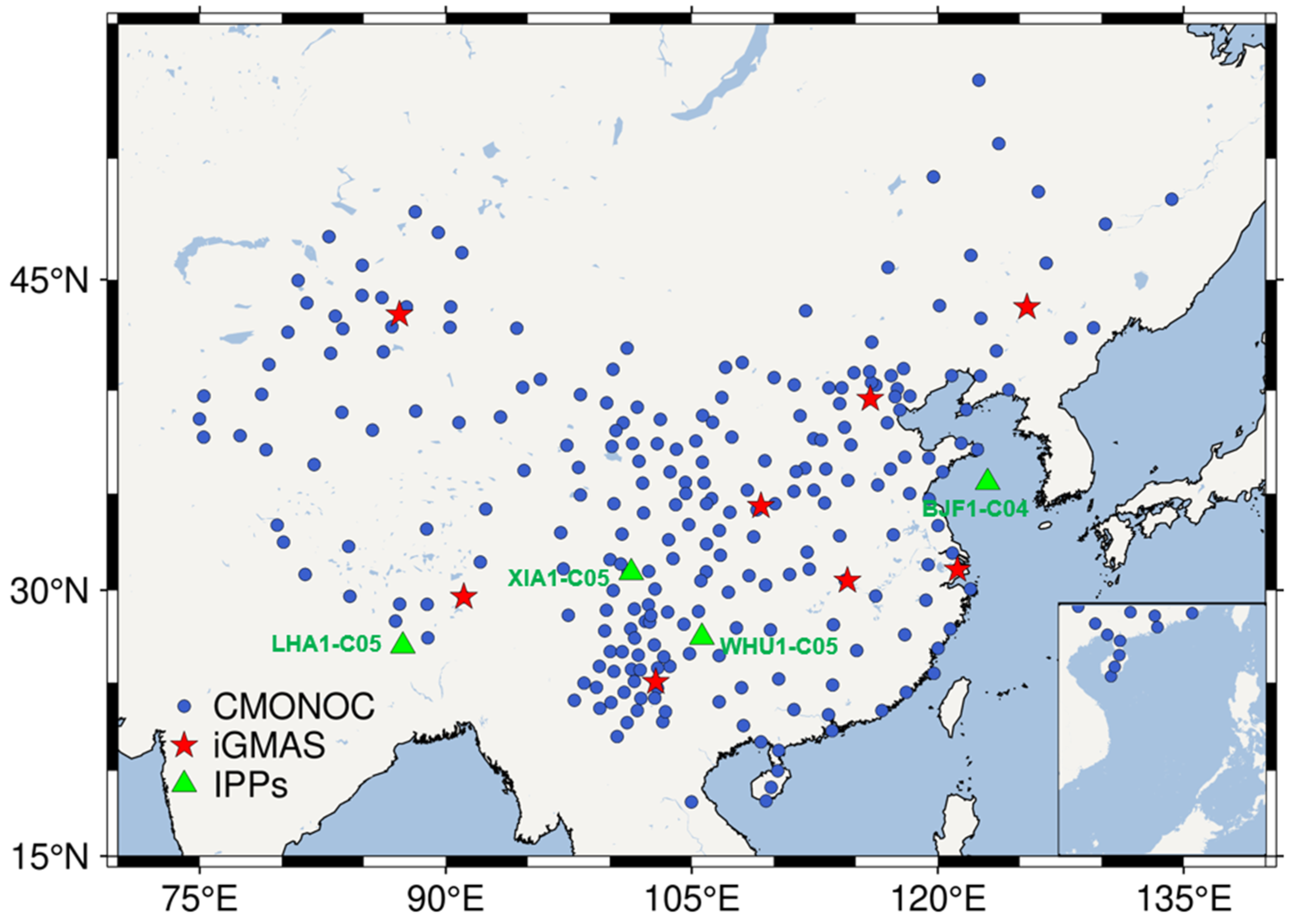
3.1. Data Sources and Station Distribution
3.2. Geomagnetic Storm Classification and Experimental Dates Selection
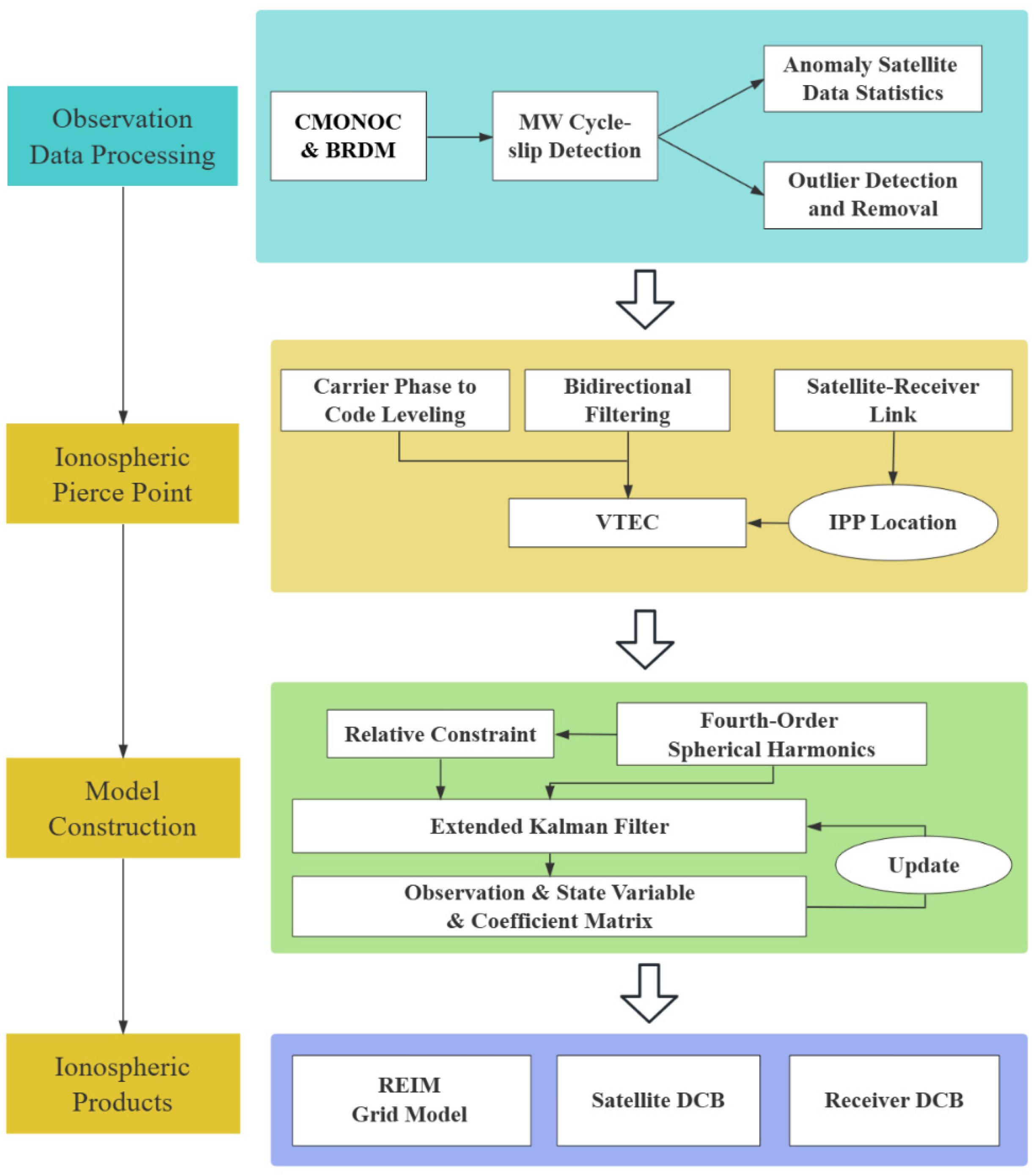
3.3. Modeling Strategies and Processing Workflow
4. Experimental Analyses
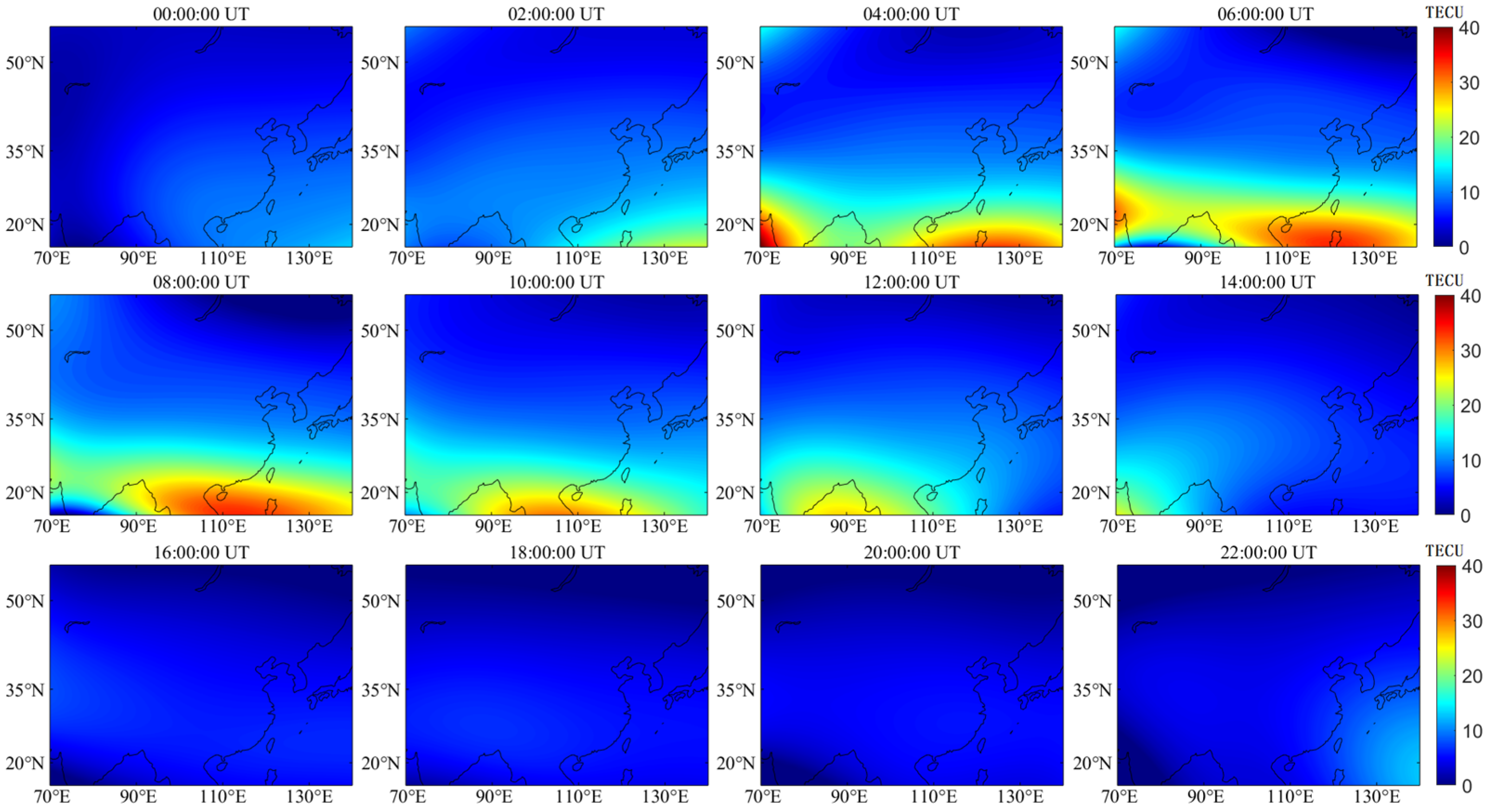
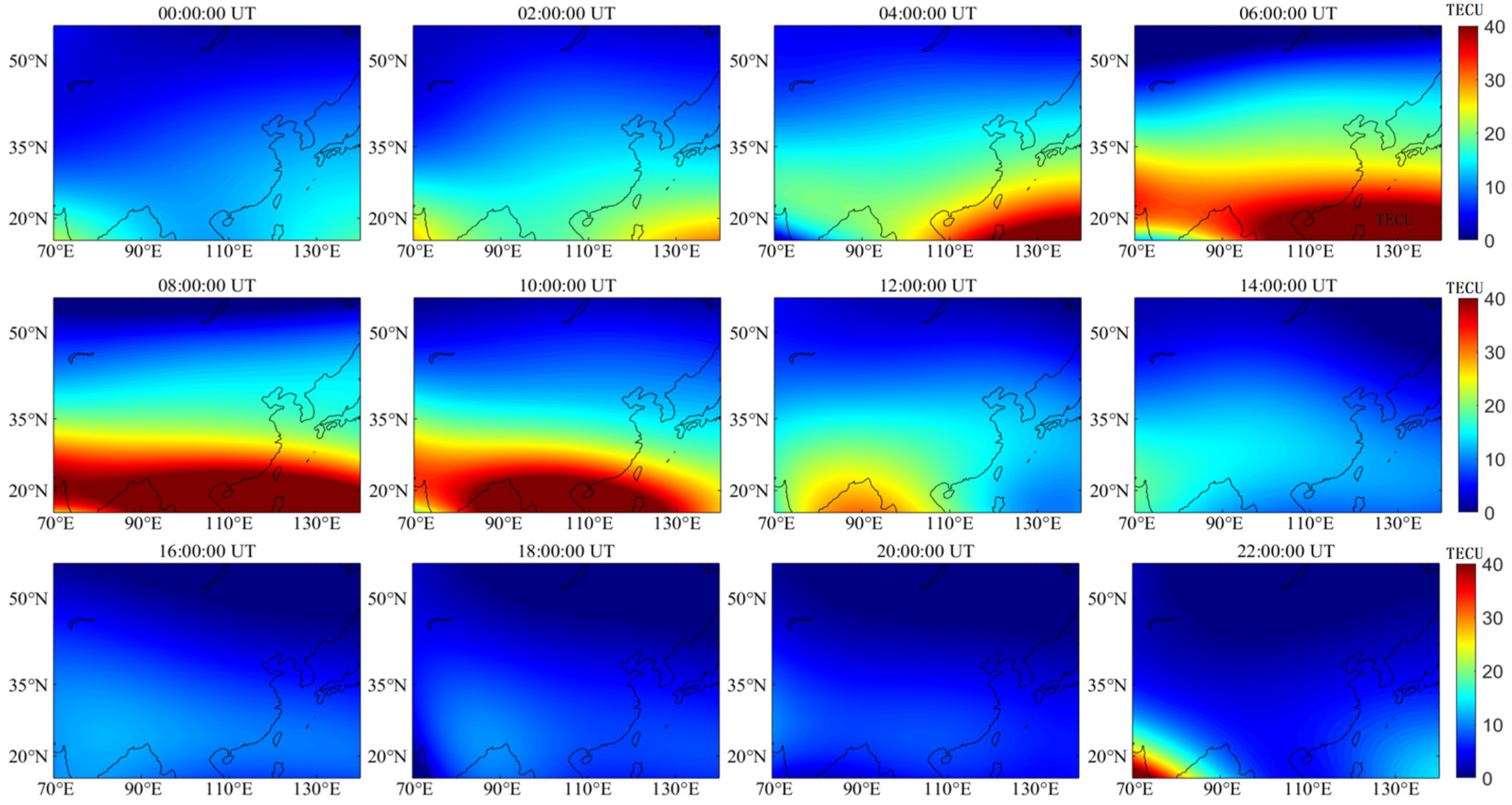
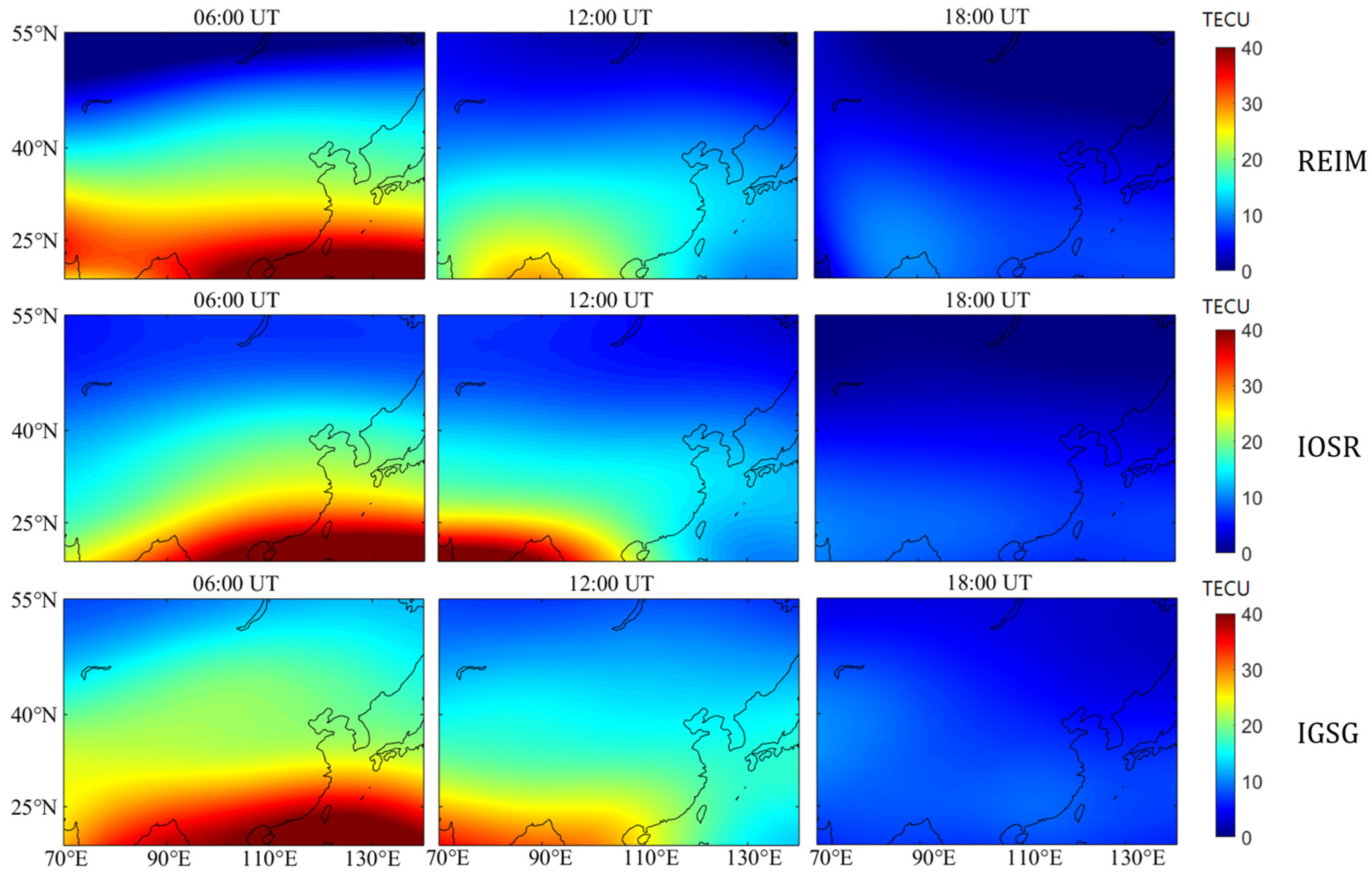
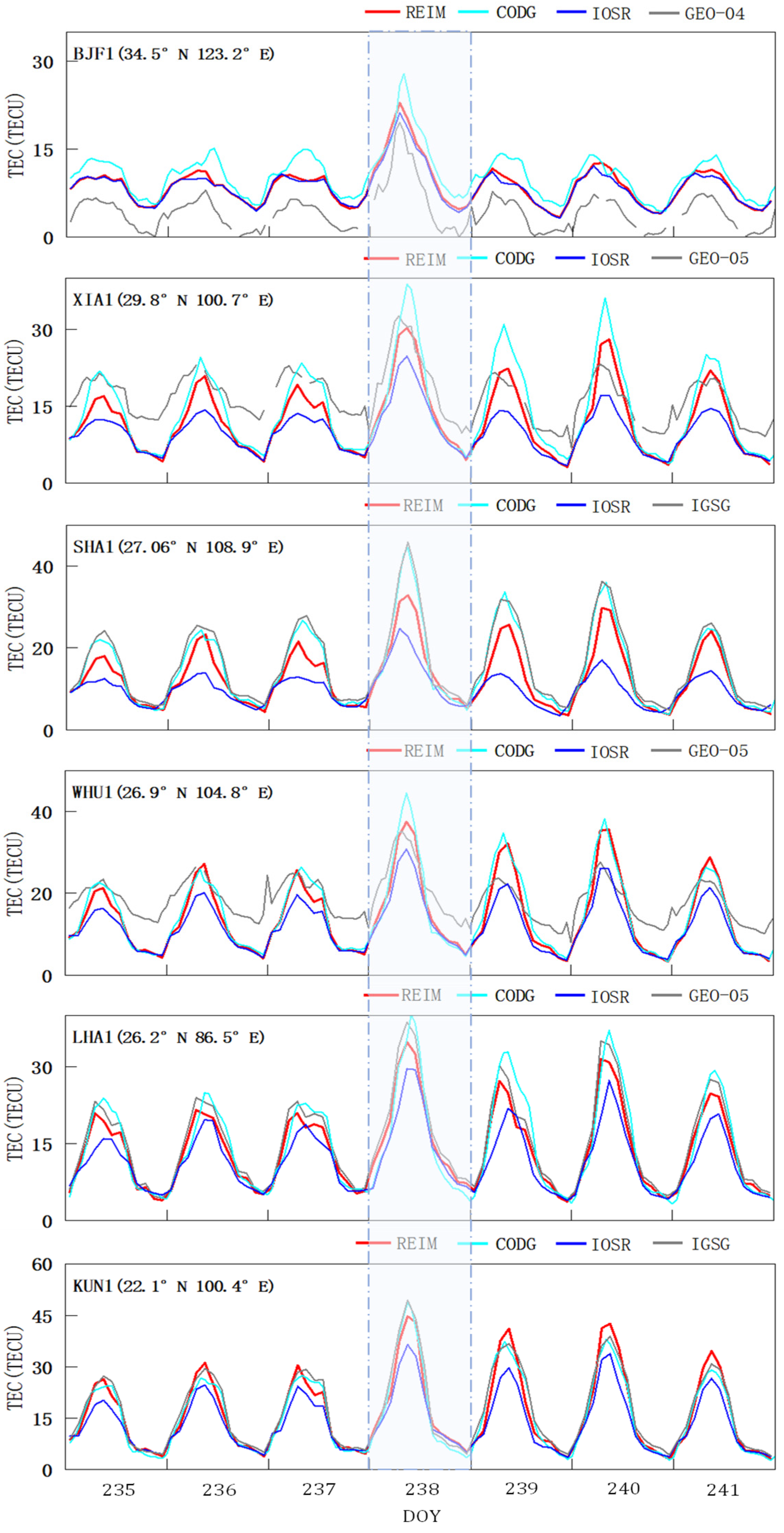
4.1. Spatial and Temporal Variations of VTEC
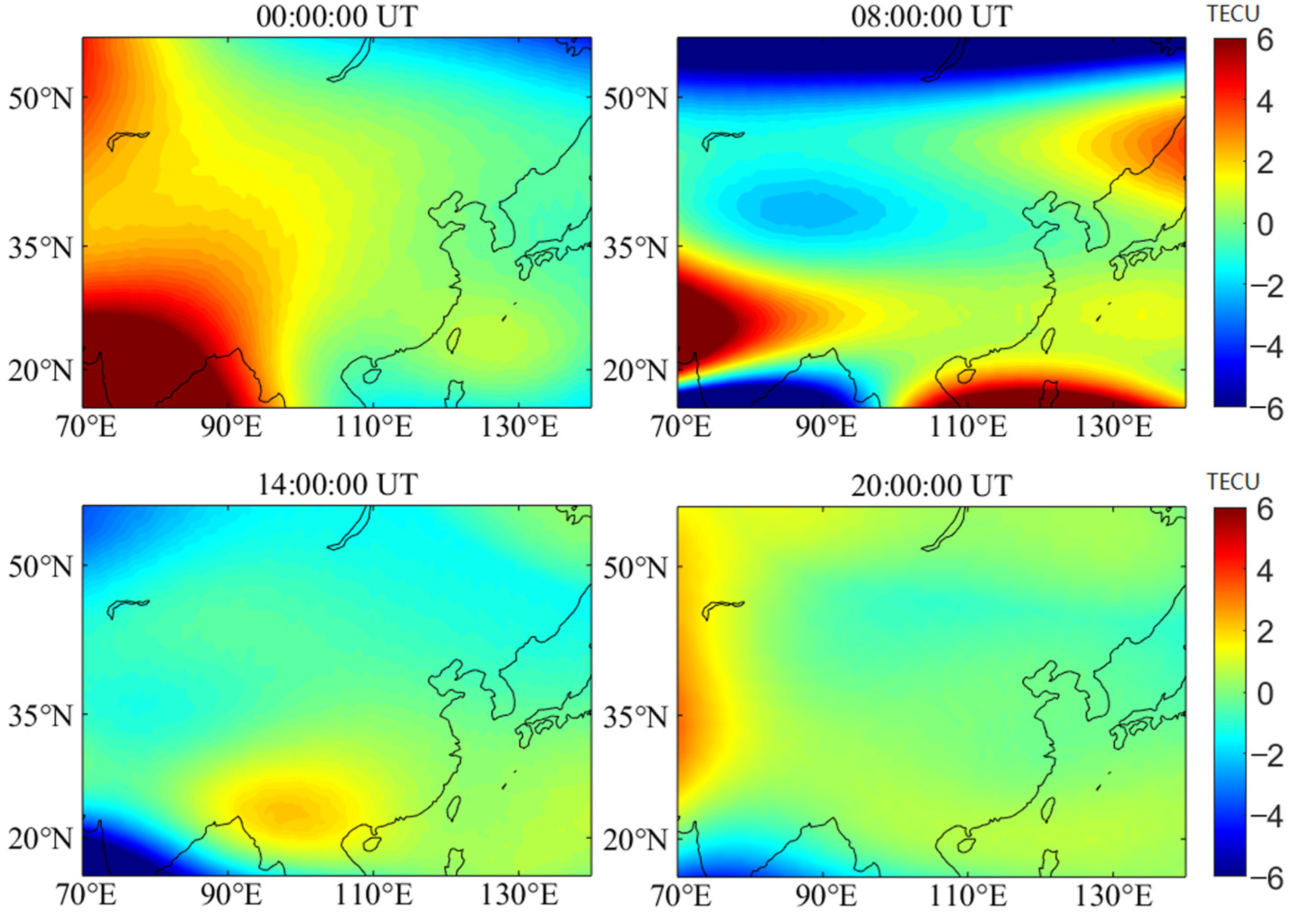
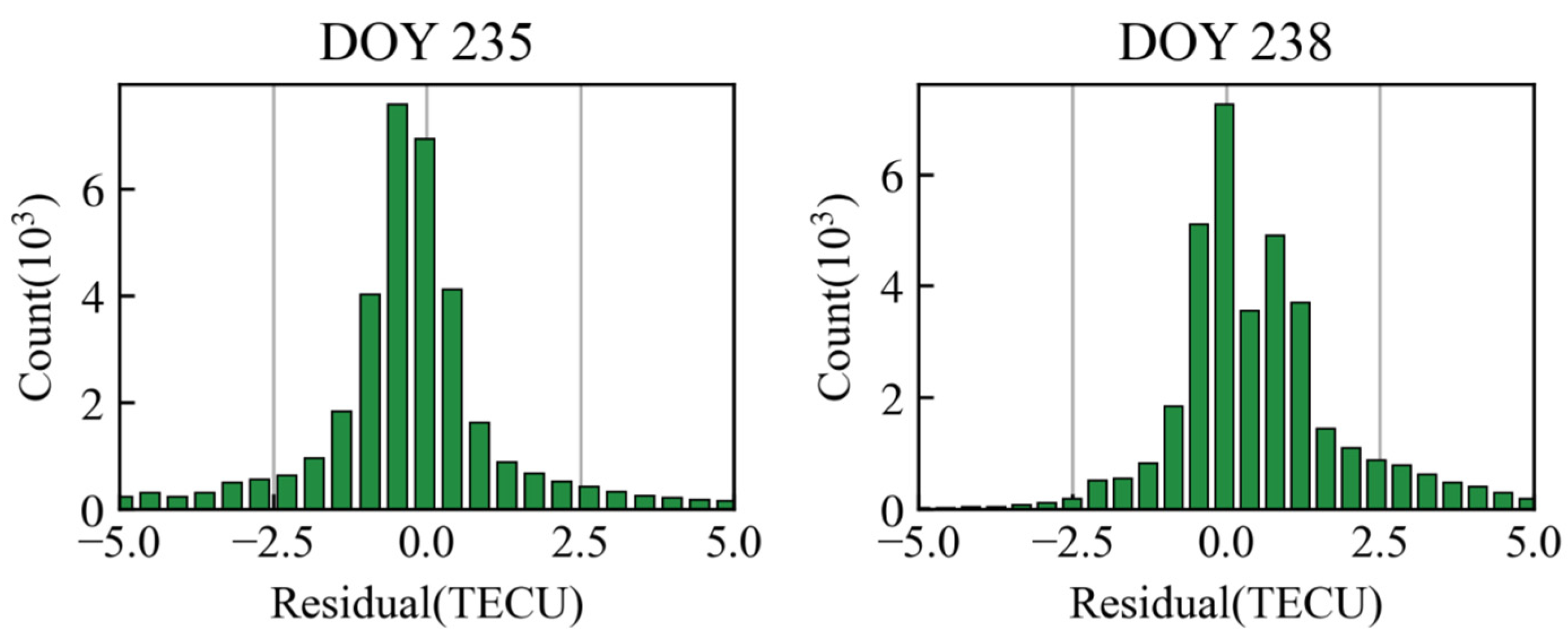
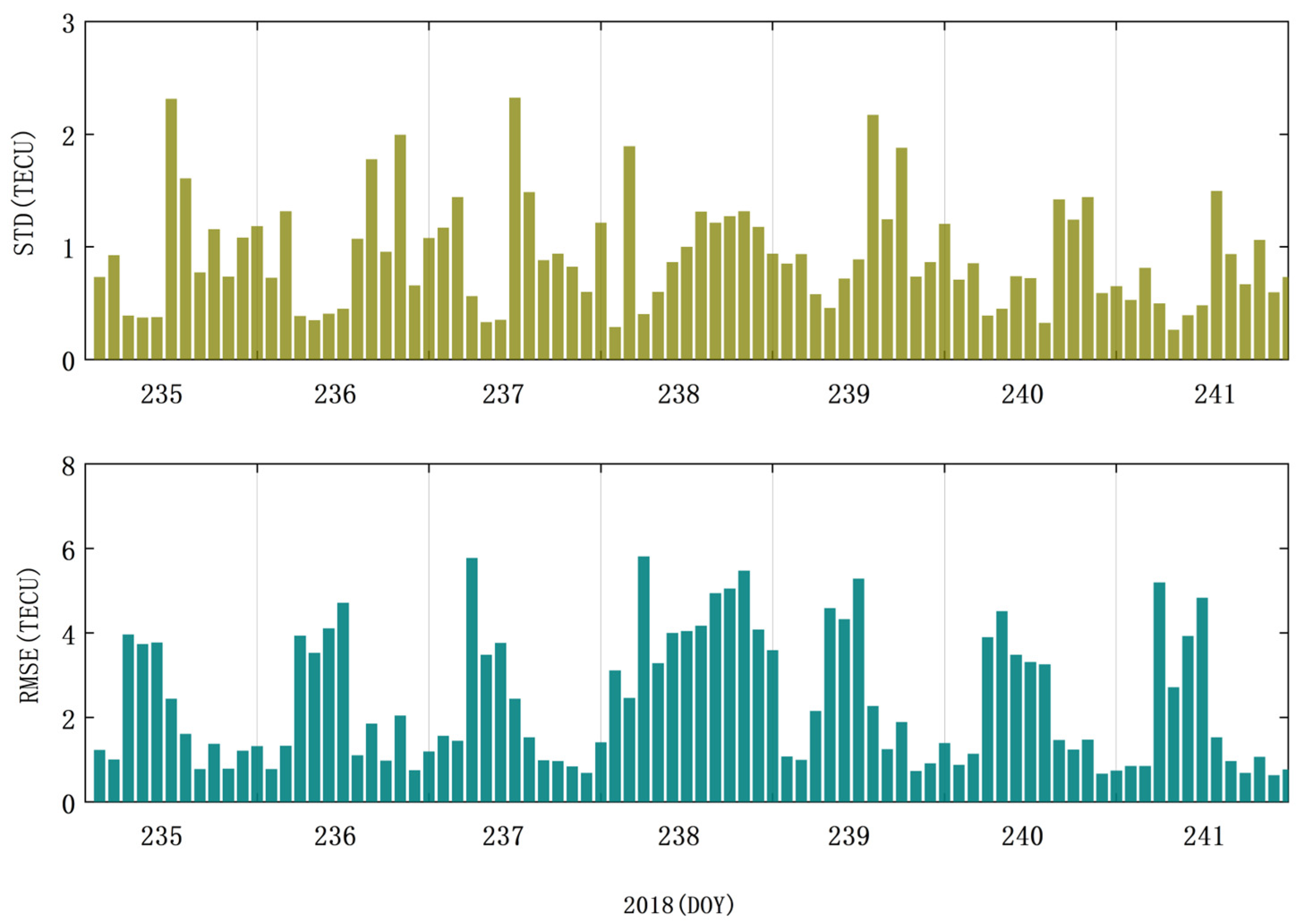
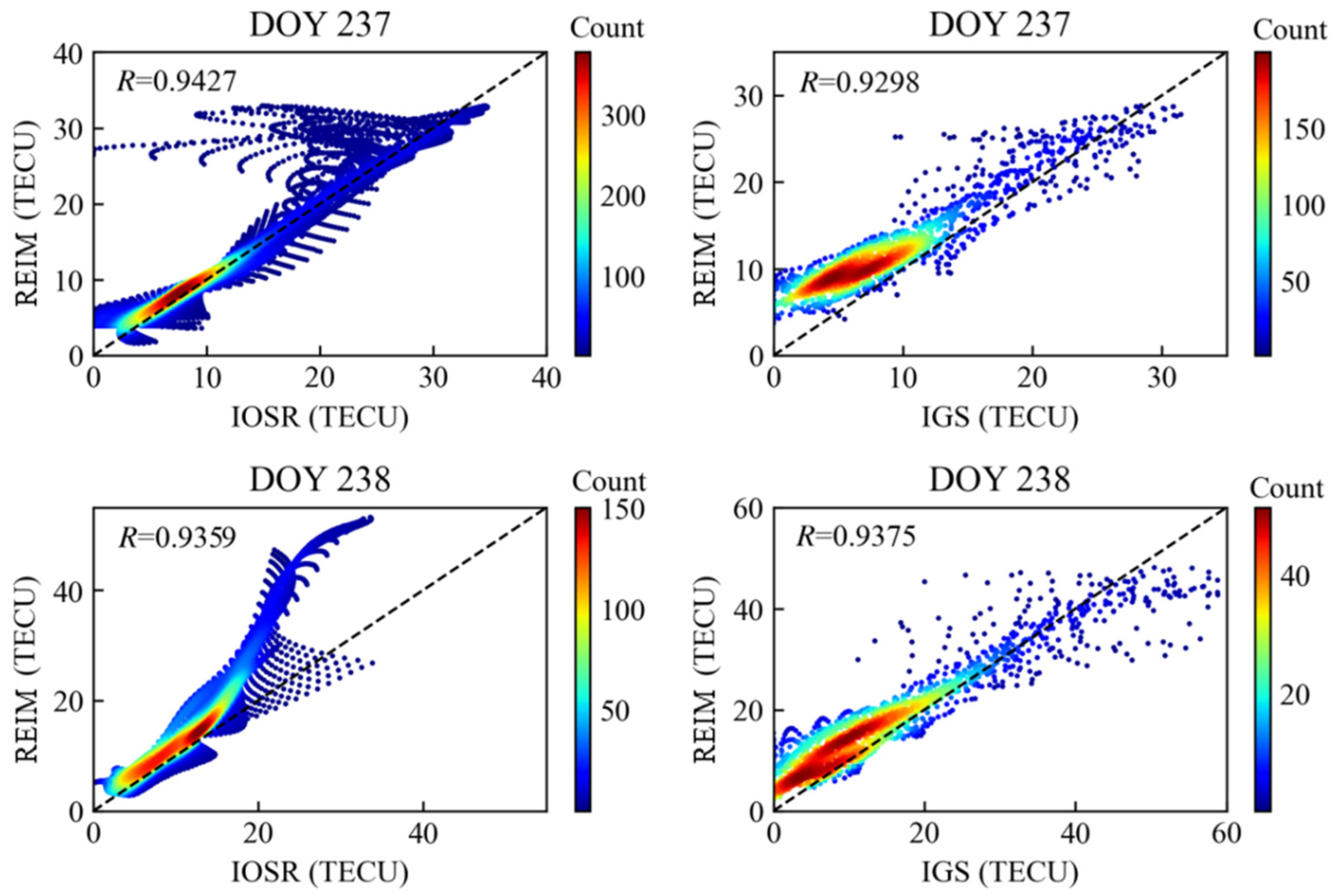
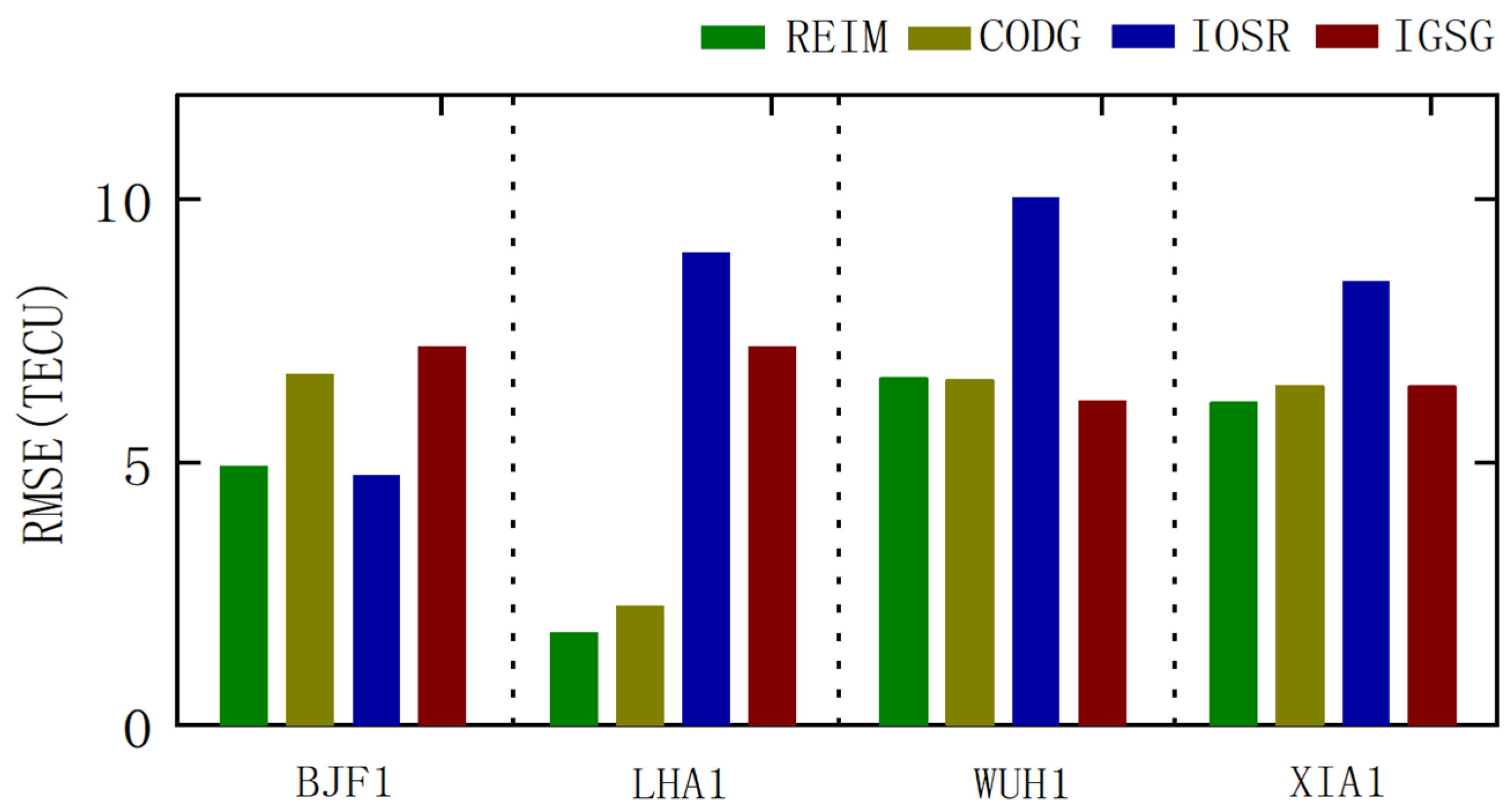
4.2. Consistency Analysis with Post-Processing Models
4.3. Consistency Analysis with BDS GEO Satellites
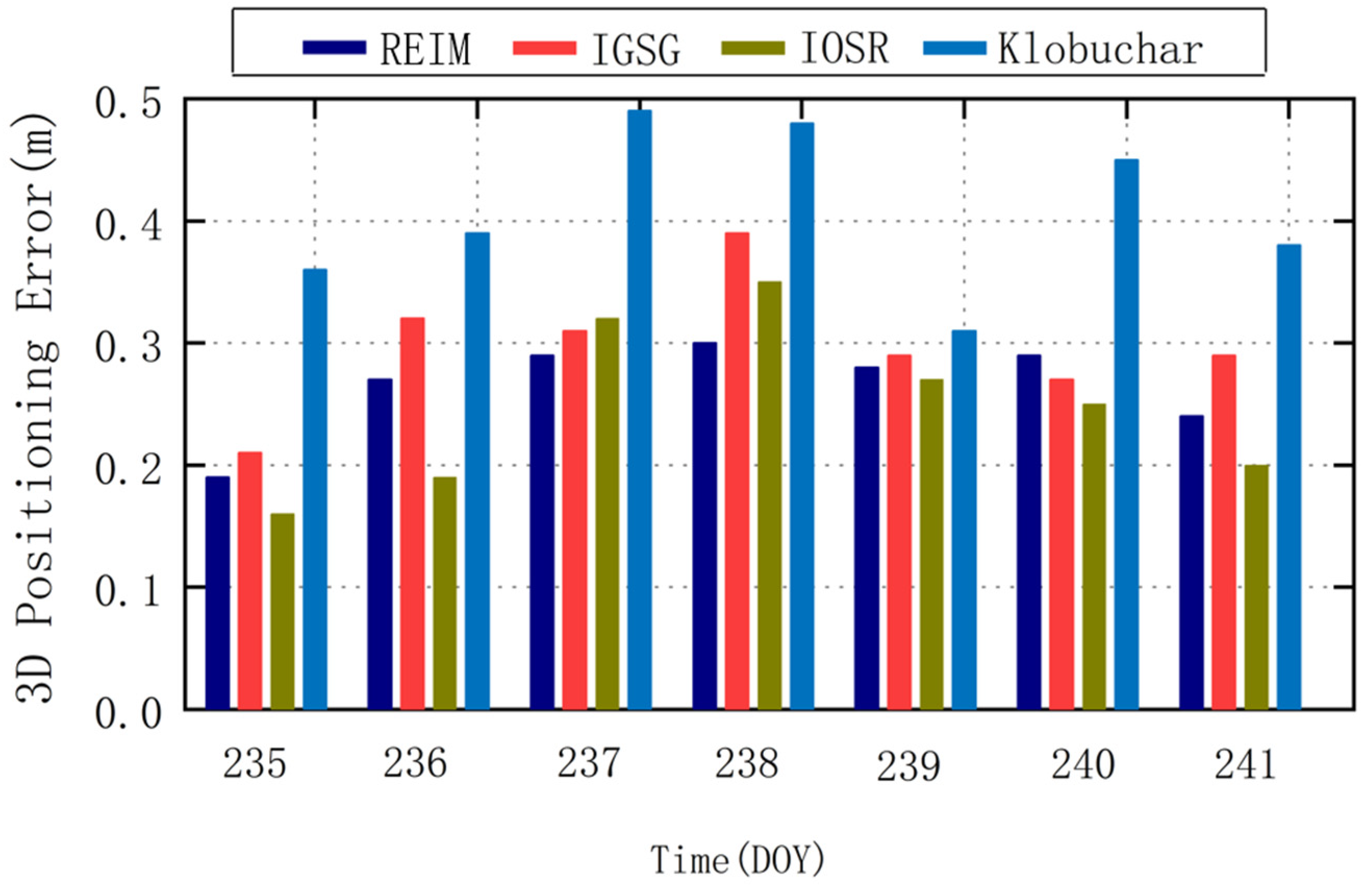
4.4. Assessment in RT-SF-PPP
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Wang, N.; Wang, L.; Liu, A.; Yuan, H.; Zhang, K. Regional ionospheric TEC modeling based on a two-layer spherical harmonic approximation for real-time single-frequency PPP. J. Geod. 2019, 93, 1659–1671. [Google Scholar] [CrossRef]
- Macalalad, E.P.; Tsai, L.-C.; Wu, J.; Liu, C.-H. Application of the Taiwan Ionospheric Model to single-frequency ionospheric delay corrections for GPS positioning. GPS Solut. 2012, 17, 337–346. [Google Scholar] [CrossRef]
- Jin, X.; Song, S. Near real-time global ionospheric total electron content modeling and nowcasting based on GNSS observations. J. Geod. 2023, 97, 27. [Google Scholar] [CrossRef]
- Feltens, J. Development of a new three-dimensional mathematical ionosphere model at European Space Agency/European Space Operations Centre. Space Weather 2007, 5, 12002. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Wang, N.; Hernandez-Pajares, M.; Huo, X. SHPTS: Towards a new method for generating precise global ionospheric TEC map based on spherical harmonic and generalized trigonometric series functions. J. Geod. 2014, 89, 331–345. [Google Scholar] [CrossRef]
- Schaer, S.; Gurtner, W.; Feltens, J. IONEX: The ionosphere map exchange format version 1. In Proceedings of the IGS AC Workshop, Darmstadt, Germany, 25 February 1998; pp. 225–232. [Google Scholar]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J. High resolution TEC monitoring method using permanent ground GPS receivers. Geophys. Res. Lett. 1997, 24, 1643–1646. [Google Scholar] [CrossRef]
- Li, Z.; Wang, N.; Hernández-Pajares, M.; Yuan, Y.; Krankowski, A.; Liu, A.; Zha, J.; García-Rigo, A.; Roma-Dollase, D.; Yang, H. IGS real-time service for global ionospheric total electron content modeling. J. Geod. 2020, 94, 32. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Zhu, F.; Yang, J.; Qing, Y.; Li, X. Assessment and analysis of the global ionosphere maps over China based on CMONOC GNSS data. Front. Earth Sci. 2023, 11, 1095754. [Google Scholar] [CrossRef]
- Fuller-Rowell, T.; Araujo-Pradere, E.; Minter, C.; Codrescu, M.; Spencer, P.; Robertson, D.; Jacobson, A.R. US-TEC: A new data assimilation product from the Space Environment Center characterizing the ionospheric total electron content using real-time GPS data. Radio Sci. 2006, 41, 1–8. [Google Scholar] [CrossRef]
- Wübbena, G.; Schmitz, M.; Bagge, A. Real-Time GNSS Data Transmission Standard RTCM 3.0. In Proceedings of the Geo++® GmbH IGS Workshop, Darmstadt, Germany, 8–12 May 2006. [Google Scholar]
- Chen, P.; Liu, H.; Schmidt, M.; Yao, Y.; Yao, W. Near real-time global ionospheric modeling based on an adaptive Kalman filter state error covariance matrix determination method. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5800812. [Google Scholar] [CrossRef]
- Erdogan, E.; Schmidt, M.; Seitz, F.; Durmaz, M. Near real-time estimation of ionosphere vertical total electron content from GNSS satellites using B-splines in a Kalman filter. Ann. Geophys. 2017, 35, 263–277. [Google Scholar] [CrossRef]
- Bilitza, D.; McKinnell, L.-A.; Reinisch, B.; Fuller-Rowell, T. The international reference ionosphere today and in the future. J. Geod. 2011, 85, 909–920. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric time-delay algorithm for single-frequency GPS users. IEEE Trans. Aerosp. Electron. Syst. 1987, 23, 325–331. [Google Scholar] [CrossRef]
- Chen, J.; Xiong, P.; Wu, H.; Zhang, X.; Feng, J.; Zhang, T. A Multi-Parameter Empirical Fusion Model for Ionospheric TEC in China’s Region. Remote Sens. 2023, 15, 5445. [Google Scholar] [CrossRef]
- He, R.; Li, M.; Zhang, Q.; Zhao, Q. A Comparison of a GNSS-GIM and the IRI-2020 Model Over China Under Different Ionospheric Conditions. Space Weather 2023, 21, e2023SW003646. [Google Scholar] [CrossRef]
- Srivani, I.; Prasad, G.S.V.; Ratnam, D.V. A deep learning-based approach to forecast ionospheric delays for GPS signals. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1180–1184. [Google Scholar] [CrossRef]
- Pan, Y.; Jin, M.; Zhang, S.; Deng, Y. TEC Map Completion Using DCGAN and Poisson Blending. Space Weather 2020, 18, e2019SW002390. [Google Scholar] [CrossRef]
- Ruwali, A.; Kumar, A.J.S.; Prakash, K.B.; Sivavaraprasad, G.; Ratnam, D.V. Implementation of Hybrid Deep Learning Model (LSTM-CNN) for Ionospheric TEC Forecasting Using GPS Data. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1004–1008. [Google Scholar] [CrossRef]
- Guo, D.; Wang, X.; Chen, R. New sequential Monte Carlo methods for nonlinear dynamic systems. Stat. Comput. 2005, 15, 135–147. [Google Scholar] [CrossRef]
- Loewe, C.A.; Prölss, G.W. Classification and mean behavior of magnetic storms. J. Geophys. Res.-Space 1997, 102, 14209–14213. [Google Scholar] [CrossRef]


| Storm Class: | Kp | Dst/nT |
|---|---|---|
| Weak | 40 | −50 < Dst ≤ −30 |
| Moderate | 50 | −100 < Dst ≤ −50 |
| Strong | 7− | −200 < Dst ≤ −100 |
| Severe | 8+ | −350 < Dst ≤ −200 |
| Great | 9− | Dst ≤ −350 |
| Model Products | TEC Extraction Methods | Modeling Methods | Temporal Resolution | Spatial Resolution | Range | Types |
|---|---|---|---|---|---|---|
| IGSG | Weighting of products from various analysis centers | 2 h | 2.5° × 5° | Global | Post-processing | |
| CODG | Carrier phase to code leveling (CCL) | SH | 1 h/2 h | 2.5° × 5° | Global | Post-processing |
| IOSR | CCL | SH | 1 h | 1° × 1° | Regional | Post-processing |
| REIM | CCL | SH | 1 h | 1° × 1° | Regional | Real-time |
| Items | Settings |
|---|---|
| Satellite systems | BDS, GPS, GLONASS |
| Data pre-processing | Cycle-slip detection, CCL |
| Elevation mask | 10° |
| Sampling rate | 30 s |
| Ephemeris type | Broadcast |
| Ionospheric modeling method | Fourth-order SH |
| Models | Stations | ||||
|---|---|---|---|---|---|
| BJF1 | LHA1 | WUH1 | XIA1 | Mean | |
| REIM | 4.32 | 2.79 | 4.93 | 4.58 | 4.15 |
| CODG | 5.57 | 2.88 | 5.23 | 5.06 | 4.68 |
| IOSR | 4.41 | 6.74 | 7.45 | 6.51 | 6.27 |
| IGSG | 6.23 | 6.21 | 5.09 | 5.14 | 5.67 |
| Models | Directions | ||
|---|---|---|---|
| East | North | Up | |
| REIM | 0.086 | 0.116 | 0.301 |
| IGSG | 0.095 | 0.129 | 0.322 |
| IOSR | 0.053 | 0.091 | 0.290 |
| Klobuchar | 0.098 | 0.129 | 0.582 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Gao, Y.; Liu, H.; Hu, M.; Xu, C.; Zhang, L. Real-Time Regional Ionospheric Total Electron Content Modeling Using the Extended Kalman Filter. Remote Sens. 2025, 17, 1568. https://doi.org/10.3390/rs17091568
Tang J, Gao Y, Liu H, Hu M, Xu C, Zhang L. Real-Time Regional Ionospheric Total Electron Content Modeling Using the Extended Kalman Filter. Remote Sensing. 2025; 17(9):1568. https://doi.org/10.3390/rs17091568
Chicago/Turabian StyleTang, Jun, Yuhan Gao, Heng Liu, Mingxian Hu, Chaoqian Xu, and Liang Zhang. 2025. "Real-Time Regional Ionospheric Total Electron Content Modeling Using the Extended Kalman Filter" Remote Sensing 17, no. 9: 1568. https://doi.org/10.3390/rs17091568
APA StyleTang, J., Gao, Y., Liu, H., Hu, M., Xu, C., & Zhang, L. (2025). Real-Time Regional Ionospheric Total Electron Content Modeling Using the Extended Kalman Filter. Remote Sensing, 17(9), 1568. https://doi.org/10.3390/rs17091568








