Bayesian Time-Domain Ringing Suppression Approach in Impulse Ultrawideband Synthetic Aperture Radar
Abstract
1. Introduction
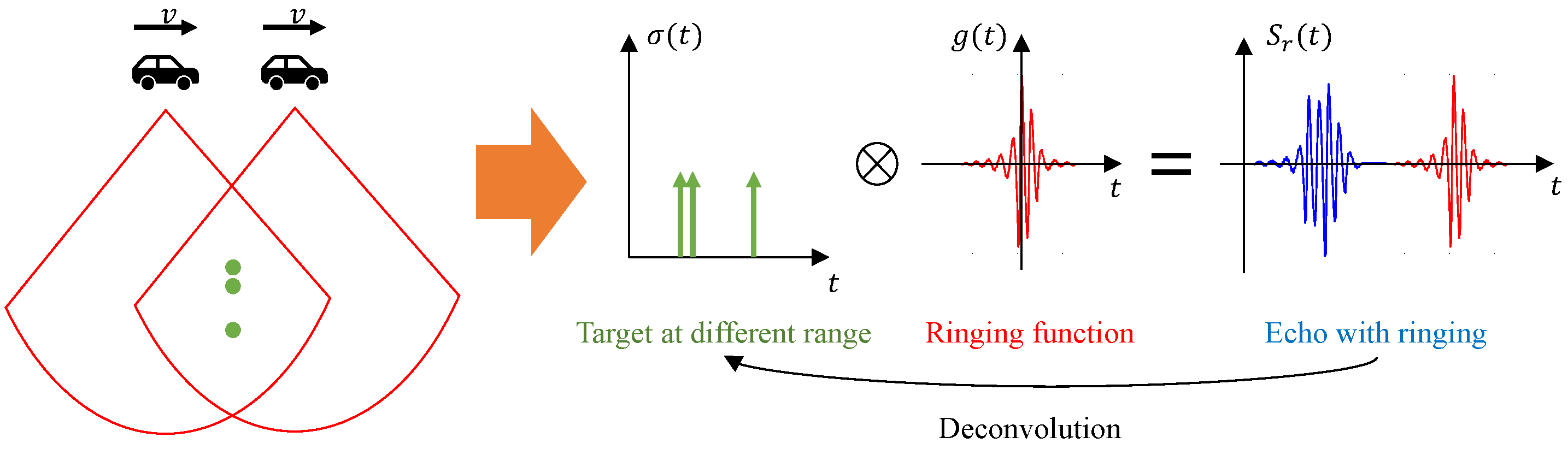
2. Signal Ringing Model
3. Ringing Suppression Algorithm
4. Experiments
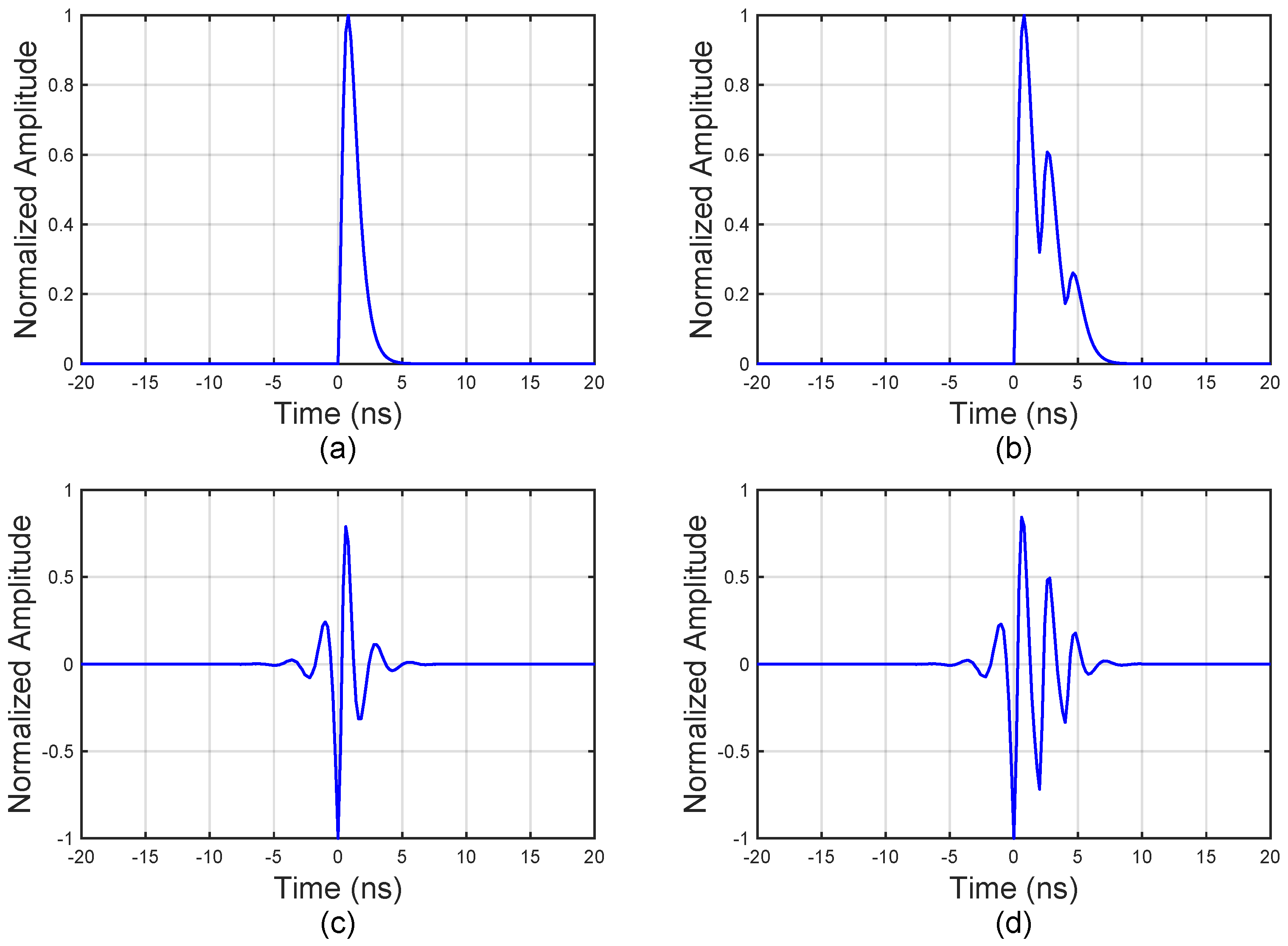
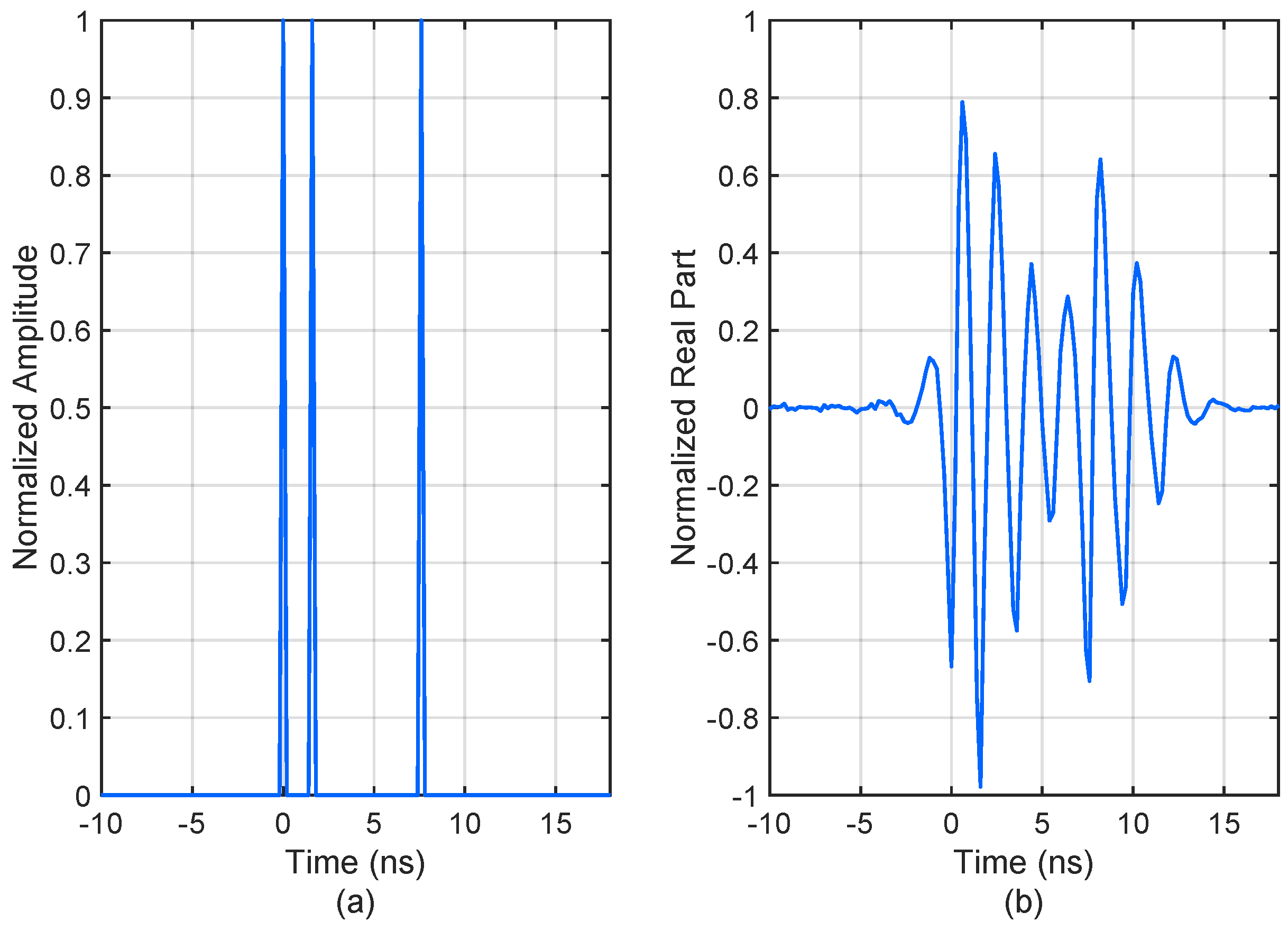
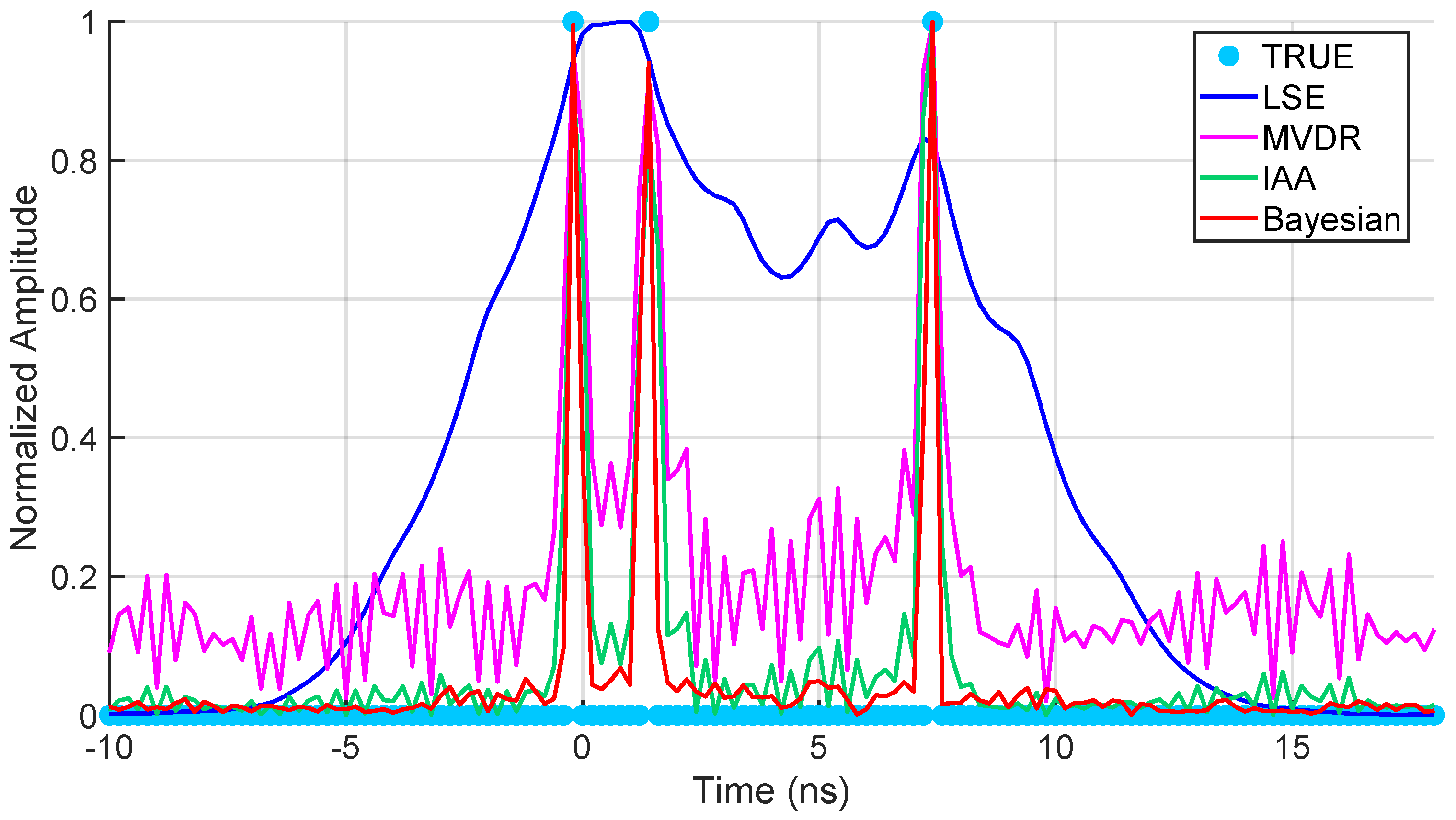
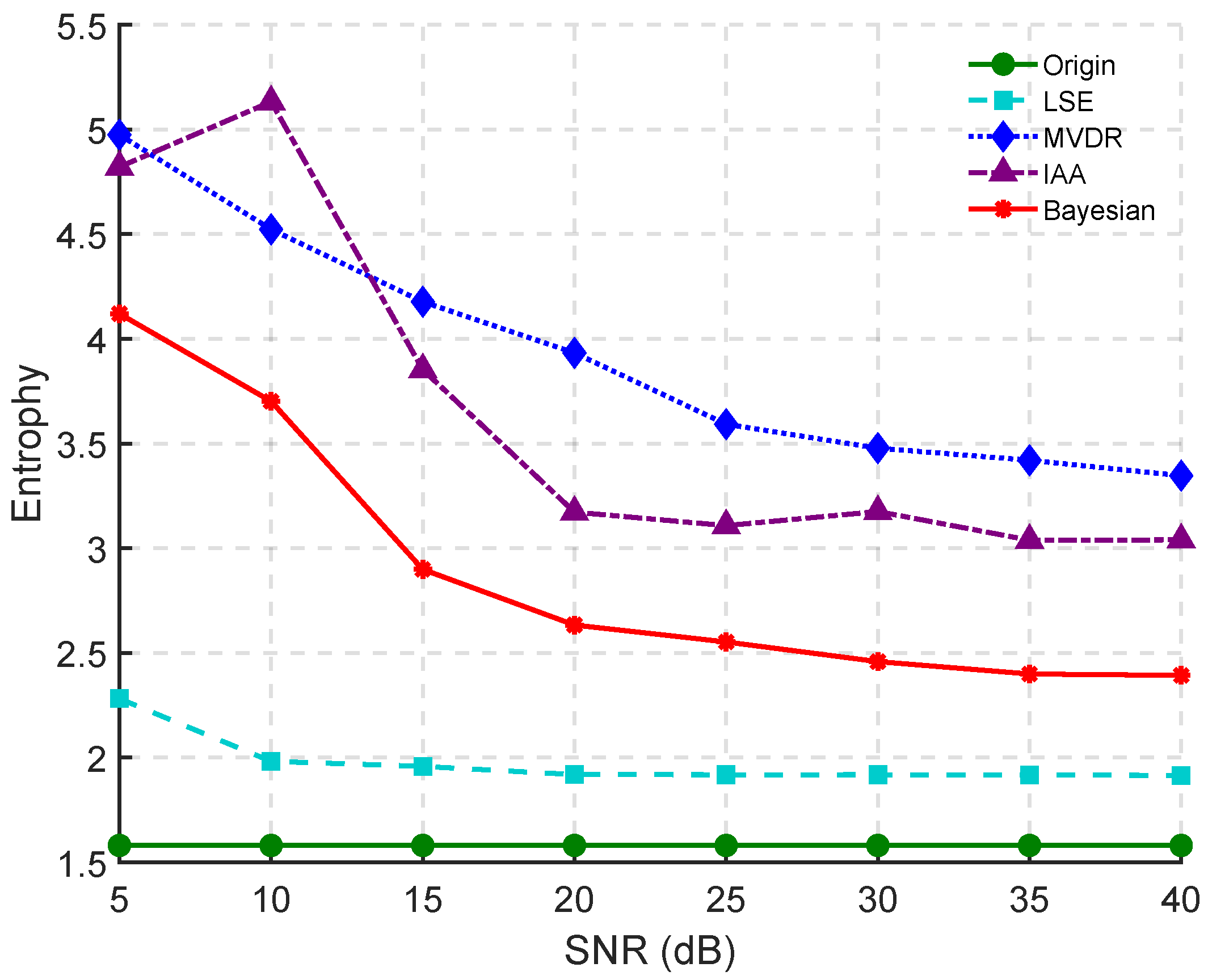
4.1. Point Targets Simulation
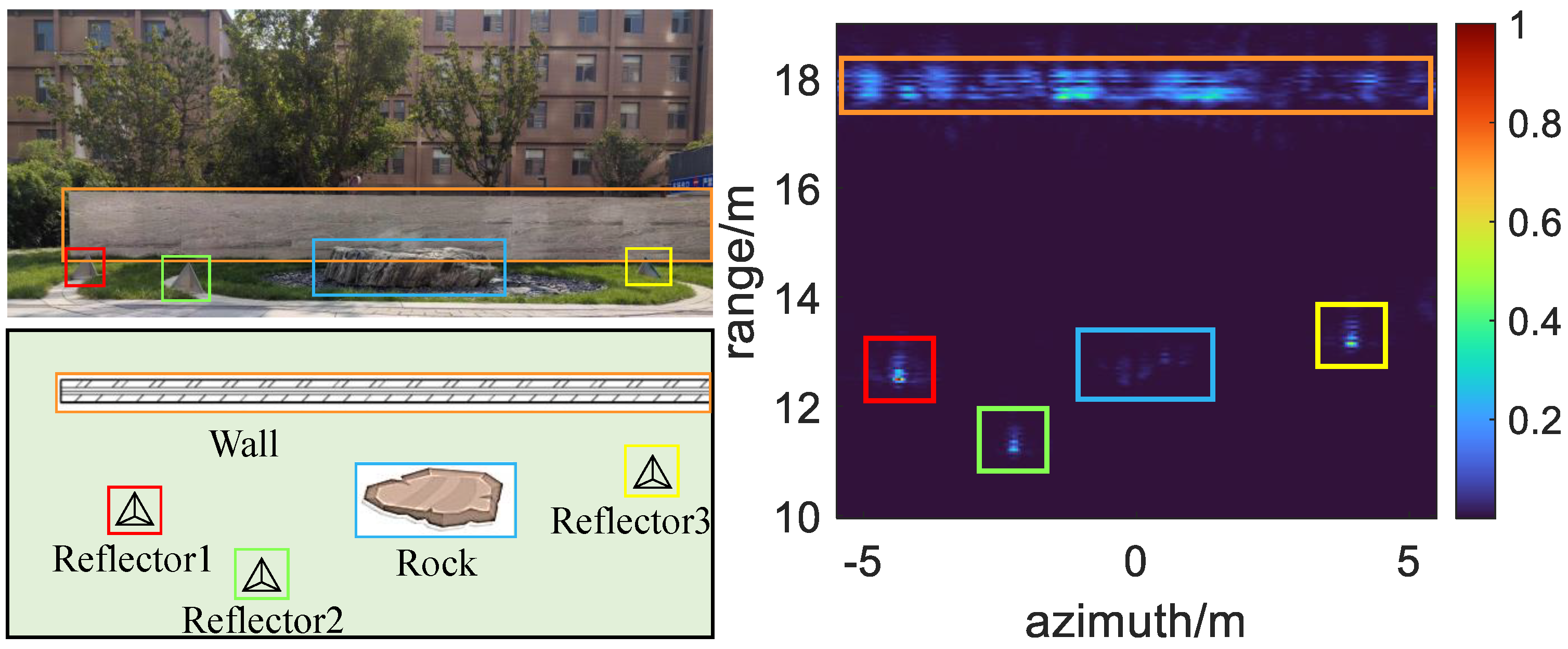
4.2. Real Scene Experiments
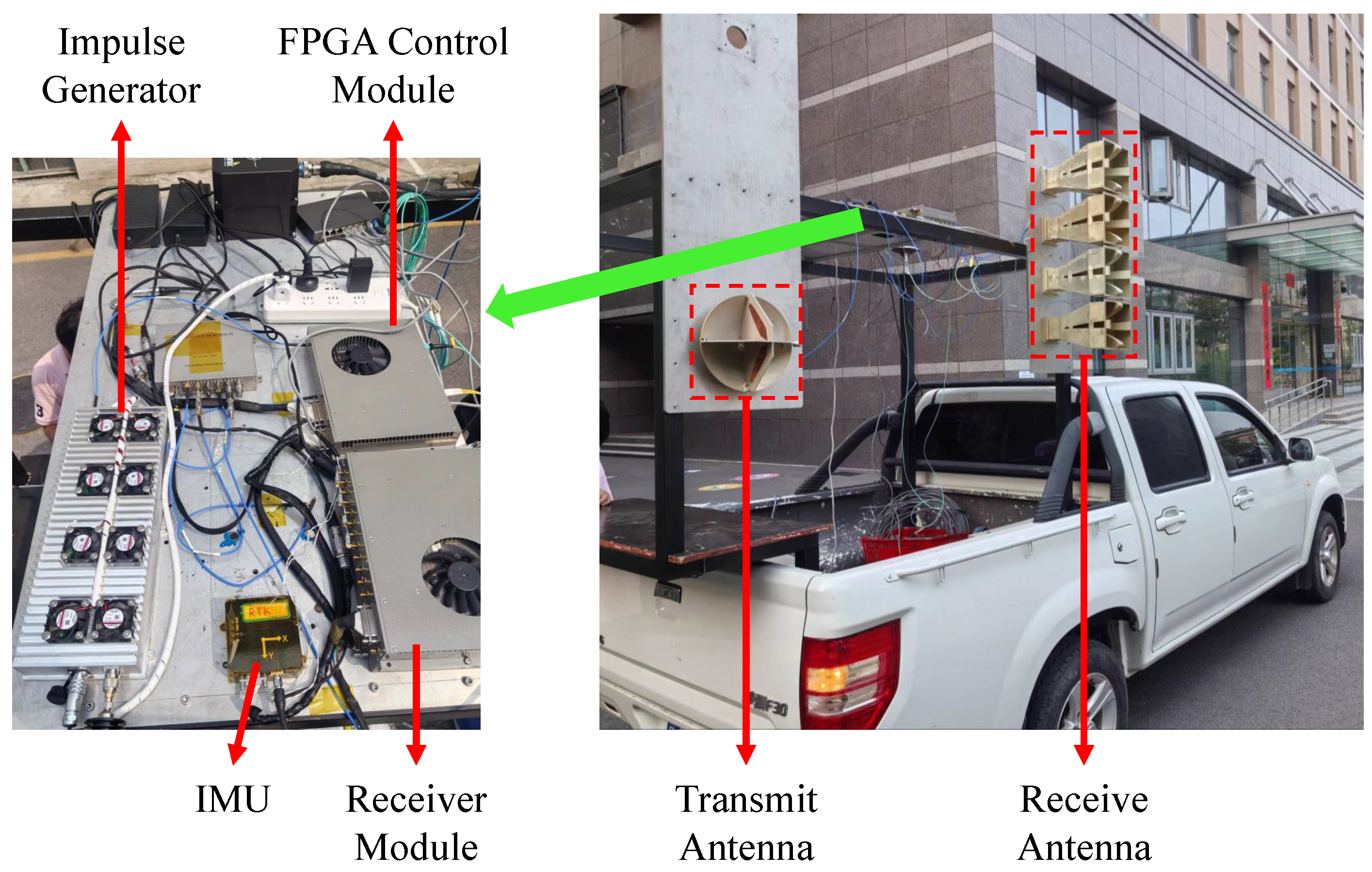
4.2.1. Experimental Setup and Radar System Introduction
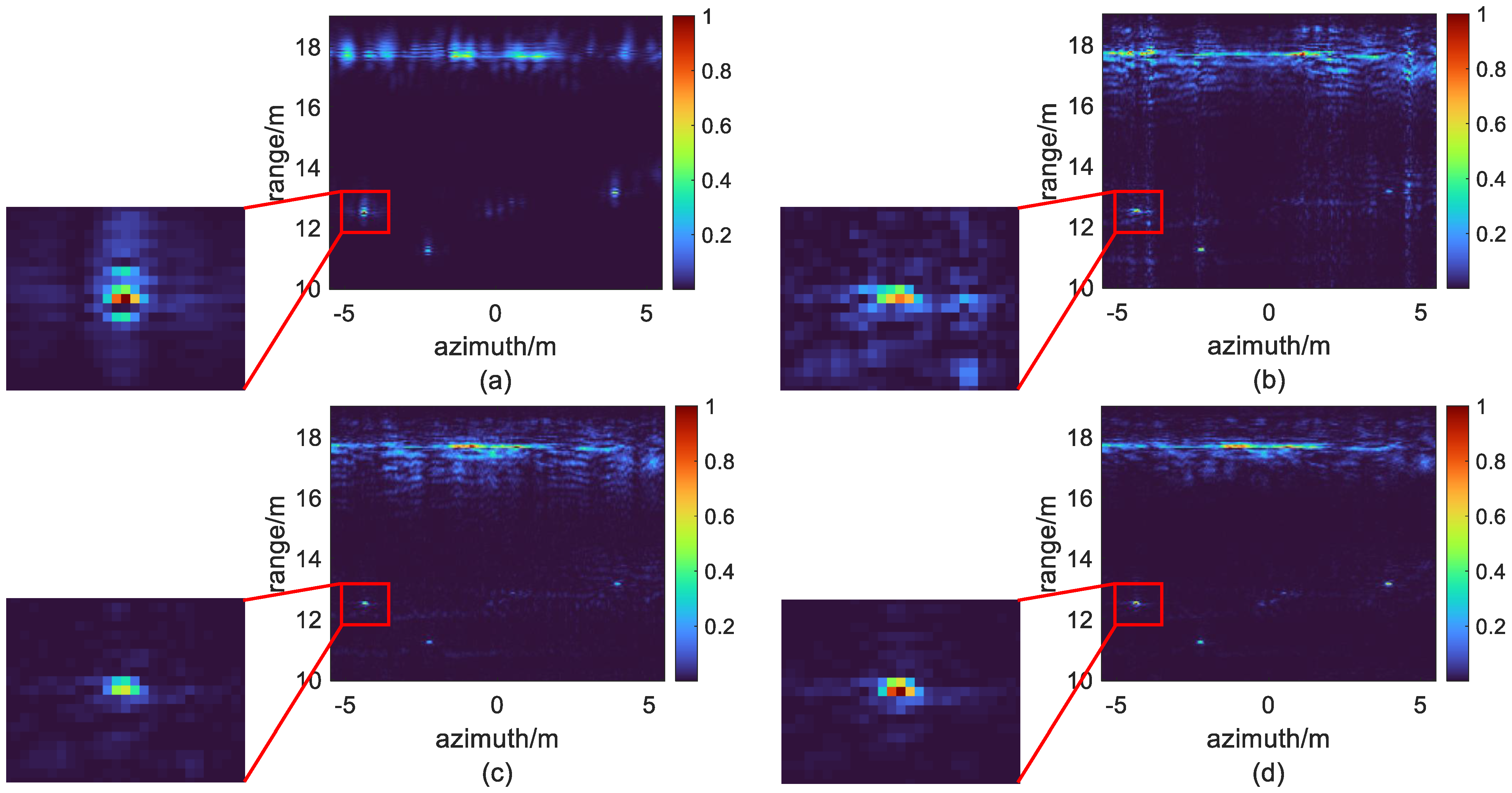
4.2.2. Ringing Suppression Results
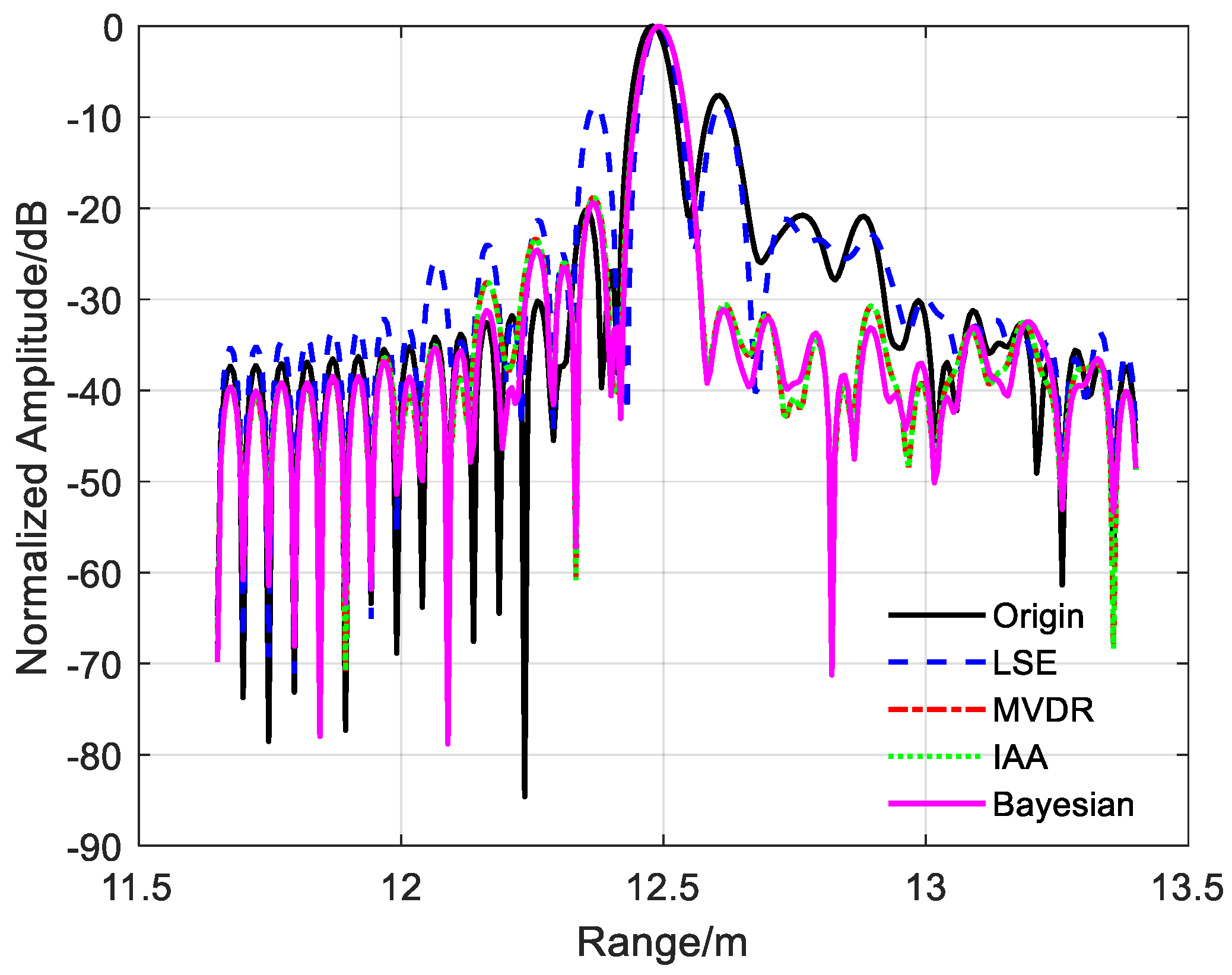
4.2.3. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UWB | ultrawideband |
| SAR | synthetic aperture radar |
| TDR | time-domain ringing |
| SNR | signal-to-noise ratio |
| LSE | least squares estimation |
| MVDR | minimum variance distortionless response |
| IAA | iterative adaptive approach |
| LFM | linear-frequency-modulated |
| PSF | point spread function |
| MAP | maximum a posteriori |
| LNAs | low-noise amplifiers |
| ADCs | analog-to-digital converters |
| IMU | inertial measuring unit |
| PRT | pulse repetition time |
| PSLR | peak sidelobe ratio |
| ISLR | integrated sidelobe ratio |
References
- Debes, C.; Amin, M.G.; Zoubir, A.M. Target Detection in Single- and Multiple-View Through-the-Wall Radar Imaging. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1349–1361. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, G.; Jin, T.; Zhou, Z. Adaptive Through-Wall Indication of Human Target with Different Motions. IEEE Geosci. Remote Sens. Lett. 2014, 11, 911–915. [Google Scholar] [CrossRef]
- Hu, J.; Song, Y.; Jin, T.; Lu, B.; Zhu, G.; Zhou, Z. Shadow Effect Mitigation in Indication of Moving Human Behind Wall via MIMO TWIR. IEEE Geosci. Remote Sens. Lett. 2015, 12, 453–457. [Google Scholar] [CrossRef]
- Li, J.; Zeng, Z.; Sun, J.; Liu, F. Through-Wall Detection of Human Being’s Movement by UWB Radar. IEEE Geosci. Remote Sens. Lett. 2012, 9, 1079–1083. [Google Scholar] [CrossRef]
- Amin, M.G.; Ahmad, F. Change Detection Analysis of Humans Moving Behind Walls. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1410–1425. [Google Scholar] [CrossRef]
- Wang, K.; Zeng, Z.; Sun, J. Through-Wall Detection of the Moving Paths and Vital Signs of Human Beings. IEEE Geosci. Remote Sens. Lett. 2019, 16, 717–721. [Google Scholar] [CrossRef]
- Debes, C.; Riedler, J.; Zoubir, A.M.; Amin, M.G. Adaptive Target Detection With Application to Through-the-Wall Radar Imaging. IEEE Trans. Signal Process. 2010, 58, 5572–5583. [Google Scholar] [CrossRef]
- Ali, J.; Abdullah, N.; Yusof, M.; Mohd, E.; Shah, S.M. Ultrawideband Antenna Design for GPR Applications: A Review. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 392–400. [Google Scholar]
- Schantz, H.G. The Art and Science of Ultrawideband Antennas; Artech House: Boston, MA, USA, 2015. [Google Scholar]
- Rahman, M.; Haider, A.; Naghshvarianjahromi, M. A Systematic Methodology for the Time-Domain Ringing Reduction in UWB Band-Notched Antennas. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 482–486. [Google Scholar] [CrossRef]
- Jafari, H.M.; Deen, M.J.; Hranilovic, S.; Nikolova, N.K. A Study of Ultrawideband Antennas for Near-Field Imaging. IEEE Trans. Antennas Propag. 2007, 55, 1184–1188. [Google Scholar] [CrossRef]
- Lotfi, P.; Azarmanesh, M.; Soltani, S. Rotatable Dual Band-Notched UWB/Triple-Band WLAN Reconfigurable Antenna. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 104–107. [Google Scholar] [CrossRef]
- Liang, J.; Chiau, C.; Chen, X.; Parini, C. Study of a printed circular disc monopole antenna for UWB systems. IEEE Trans. Antennas Propag. 2005, 53, 3500–3504. [Google Scholar] [CrossRef]
- Kim, K.; Scott, W. Design of a resistively loaded vee dipole for ultrawide-band ground-penetrating Radar applications. IEEE Trans. Antennas Propag. 2005, 53, 2525–2532. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, J.; Liang, B.; Yang, D.; Xing, M.; Liu, L. First Demonstration of Using Signal Processing Approach to Suppress Signal Ringing in Impulse UWB Through-Wall Radar. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Lacoss, R.T. Data adaptive spectral analysis methods. Geophysics 1971, 36, 661–675. [Google Scholar] [CrossRef]
- Stoica, P.; Li, J.; He, H. Spectral Analysis of Nonuniformly Sampled Data: A New Approach Versus the Periodogram. IEEE Trans. Signal Process. 2009, 57, 843–858. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Huang, Y.; Li, W.; Yang, J. Angular Superresolution for Scanning Radar with Improved Regularized Iterative Adaptive Approach. IEEE Geosci. Remote Sens. Lett. 2016, 13, 846–850. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Jiang, X.; Huang, X. Angular Superresol for Signal Model in Coherent Scanning Radars. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3103–3116. [Google Scholar] [CrossRef]
- Zhang, Y.; Jakobsson, A.; Zhang, Y.; Huang, Y.; Yang, J. Wideband Sparse Reconstruction for Scanning Radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6055–6068. [Google Scholar] [CrossRef]
- Pan, C. Gibbs phenomenon removal and digital filtering directly through the fast Fourier transform. IEEE Trans. Signal Process. 2001, 49, 444–448. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef] [PubMed]
- Block, K.T.; Uecker, M.; Frahm, J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn. Reson. Med. 2007, 57, 1086–1098. [Google Scholar] [CrossRef]
- Amin, M.G. Through-the-Wall Radar Imaging; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Guru, B.S.; Hiziroglu, H.R. Electromagnetic Field Theory Fundamentals; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kannadhasan, S.; Nagarajan, R. Performance Improvement of Slot Antenna Using Various Parameters and Band Pass Filter. In Proceedings of the 2018 International Conference on Circuits and Systems in Digital Enterprise Technology (ICCSDET), Kottayam, India, 21–22 December 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Wu, C.H.; Wang, C.H.; Chen, S.Y.; Chen, C.H. Balanced-to-Unbalanced Bandpass Filters and the Antenna Application. IEEE Trans. Microw. Theory Tech. 2008, 56, 2474–2482. [Google Scholar] [CrossRef]
- Zhou, X.P.; Wei, G.H.; Wu, S.L.; Liu, Y. Overview of imaging algorithm based on impulse radar. Xi Tong Gong Cheng Yu Dian Zi Ji Shu/Syst. Eng. Electron. 2014, 36, 1081–1087. [Google Scholar]
- Lv, T.g.; Lu, Z.l. The analysis of the azimuth resolution of impulse signal SAR. ACTA Electron. Sin. 2000, 28, 40–43. [Google Scholar]
- Zhang, Y.; Tuo, X.; Huang, Y.; Yang, J. A TV Forward-Looking Super-Resolution Imaging Method Based on TSVD Strategy for Scanning Radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4517–4528. [Google Scholar] [CrossRef]
- Cetin, M.; Karl, W. Feature-enhanced synthetic aperture radar image formation based on nonquadratic regularization. IEEE Trans. Image Process. 2001, 10, 623–631. [Google Scholar] [CrossRef]
- Xu, G.; Xing, M.D.; Xia, X.G.; Zhang, L.; Liu, Y.Y.; Bao, Z. Sparse Regularization of Interferometric Phase and Amplitude for InSAR Image Formation Based on Bayesian Representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2123–2136. [Google Scholar] [CrossRef]
- Wu, K.C. Bringing Order to Disorder: Is Image Entropy the Answer? JACC Cardiovasc. Imaging 2019, 12, 1185–1187. [Google Scholar] [CrossRef]
- Bai, Z.; Liu, Z.; He, P. SAR image target segmentation based on entropy maximization and morphology. J. Syst. Eng. Electron. 2004, 15, 484–487. [Google Scholar]
- Nobre, R.H.; Rodrigues, F.A.; Marques, R.C.; Nobre, J.S.; Neto, J.F.; Medeiros, F.N. SAR image segmentation with Renyi’s entropy. IEEE Signal Process. Lett. 2016, 23, 1551–1555. [Google Scholar] [CrossRef]

| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Raise time | 0.4 ns | Decay time | 0.5 ns |
| Sampling rate | 5 GHz | Duration T | 20 ns |
| Time delay | 1 ns | Number of reflection K | 2 |
| Reflection coefficient1 | 0.5 | Reflection coefficient2 | 0.2 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Platform velocity | 4 m/s | Azimuth beam | 40° |
| Sampling rate | 5 GHz | Effective pulse width | 0.25 ns |
| Pulse repetition time | 200 s | Working frequency | 0.4−2.4 GHz |
| Origin | LSE | MVDR | IAA | Bayesian | |
|---|---|---|---|---|---|
| PSLR (dB) | −7.6145 | −8.5419 | −18.7809 | −18.6574 | −19.3318 |
| ISLR (dB) | −6.8603 | −5.7687 | −18.3457 | −18.7191 | −19.0273 |
| LSE | MVDR | IAA | Bayesian | |
|---|---|---|---|---|
| Simulation data | 0.0127 s | 0.0799 s | 0.2385 s | 0.1947 s |
| Real scene data | 0.0331 s | 1.2754 s | 4.1803 s | 2.6297 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Li, W.; Tang, H.; Chen, L.; Zhang, C.; Jiang, T.; Liu, J.; Liang, X. Bayesian Time-Domain Ringing Suppression Approach in Impulse Ultrawideband Synthetic Aperture Radar. Remote Sens. 2025, 17, 1455. https://doi.org/10.3390/rs17081455
Xu X, Li W, Tang H, Chen L, Zhang C, Jiang T, Liu J, Liang X. Bayesian Time-Domain Ringing Suppression Approach in Impulse Ultrawideband Synthetic Aperture Radar. Remote Sensing. 2025; 17(8):1455. https://doi.org/10.3390/rs17081455
Chicago/Turabian StyleXu, Xinhao, Wenjie Li, Haibo Tang, Longyong Chen, Chengwei Zhang, Tao Jiang, Jie Liu, and Xingdong Liang. 2025. "Bayesian Time-Domain Ringing Suppression Approach in Impulse Ultrawideband Synthetic Aperture Radar" Remote Sensing 17, no. 8: 1455. https://doi.org/10.3390/rs17081455
APA StyleXu, X., Li, W., Tang, H., Chen, L., Zhang, C., Jiang, T., Liu, J., & Liang, X. (2025). Bayesian Time-Domain Ringing Suppression Approach in Impulse Ultrawideband Synthetic Aperture Radar. Remote Sensing, 17(8), 1455. https://doi.org/10.3390/rs17081455







