Evaluation of Different Methods for Retrieving Temperature and Humidity Profiles in the Lower Atmosphere Using the Atmospheric Sounder Spectrometer by Infrared Spectral Technology
Abstract
:1. Introduction
2. Data Sources
2.1. ASSIST
2.2. Radiosonde
3. Methodologies
3.1. Regularization Methods
3.1.1. FR
3.1.2. LC
3.1.3. GCV
3.1.4. MLE
3.1.5. IRGN
3.2. Damped Least Squares Method
3.3. Accuracy Assessment
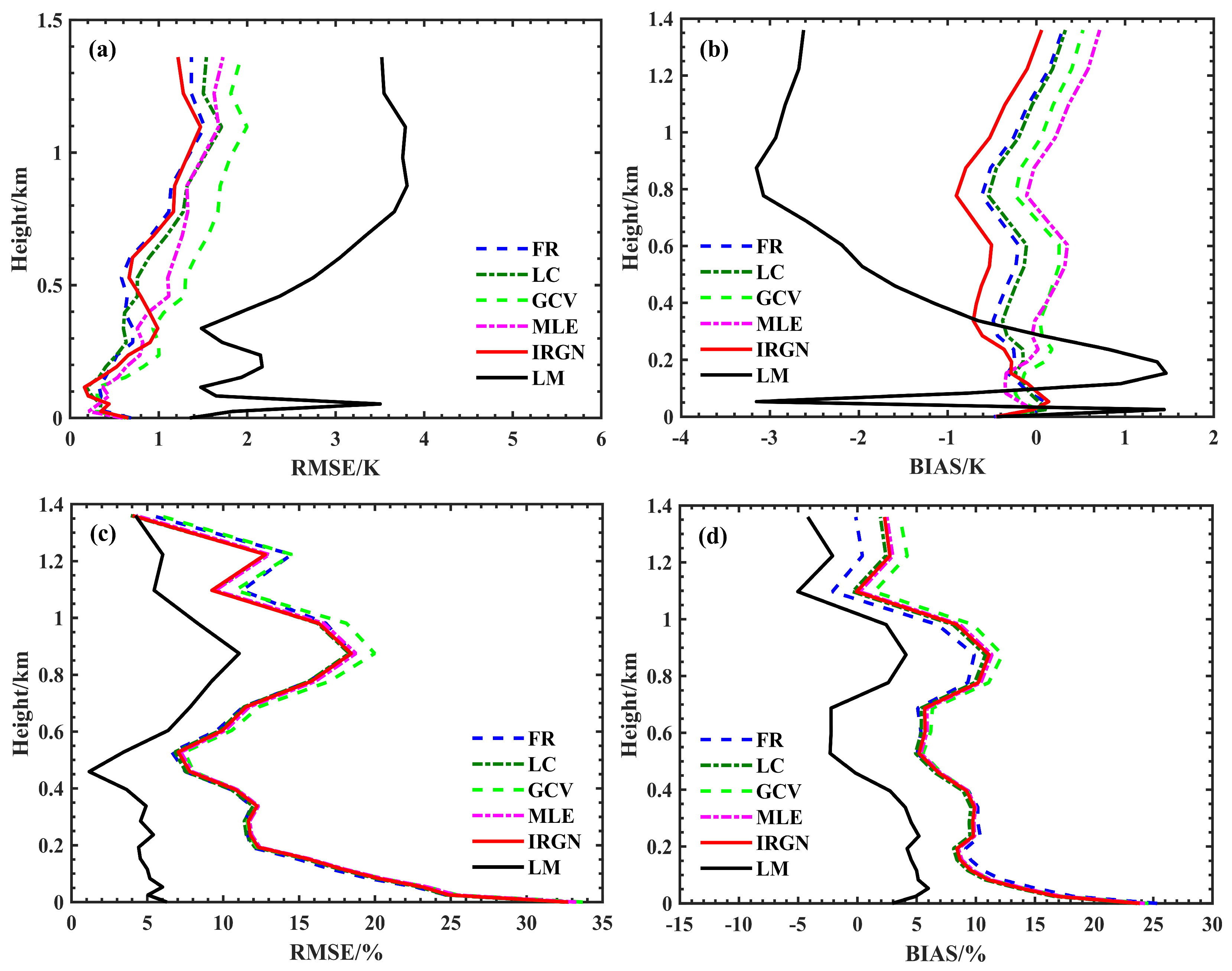
4. Results and Analysis
4.1. Sensitivity Test
4.2. Performance of Different Regularization Methods: Case Study
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, W.; Liu, L.; Yang, B.; Hu, S.; Yang, W.; Li, Z.; Li, W.; Yang, X. Retrieval of temperature and humidity profiles from ground-based high-resolution infrared observations using an adaptive fast iterative algorithm. Atmos. Meas. Tech. 2023, 16, 4101–4114. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Han, H.; Li, J.; Zheng, J. On the assimilation of satellite sounder data in cloudy skies in numerical weather prediction models. J. Meteorol. Res. 2016, 30, 169–182. [Google Scholar] [CrossRef]
- Wulfmeyer, V.; Hardesty, R.M.; Turner, D.D.; Behrendt, A.; Cadeddu, M.P.; Di Girolamo, P.; Schlüssel, P.; Van Baelen, J.; Zus, F. A review of the remote sensing of lower tropospheric thermodynamic profiles and its indispensable role for the understanding and the simulation of water and energy cycles. Rev. Geophys. 2015, 53, 819–895. [Google Scholar] [CrossRef]
- Romine, G.S.; Schwartz, C.S.; Snyder, C.; Anderson, J.L.; Weisman, M.L. Model bias in a continuously cycled assimilation system and its influence on convection-permitting forecasts. Mon. Weather Rev. 2013, 141, 1263–1284. [Google Scholar] [CrossRef]
- Yang, W.; Liu, L.; Deng, W.; Huang, W.; Ye, J.; Hu, S. Deep retrieval architecture of temperature and humidity profiles from ground-based infrared hyperspectral spectrometer. Remote Sens. 2023, 15, 2320. [Google Scholar] [CrossRef]
- Gonzalez, L.; Kos, L.; Lavas, S.; Douglas, M. A new possible plan for a more cost-effective adaptive radiosonde observing strategy for the United States. J. Atmos. Ocean. Technol. 2012, 29, 1–25. [Google Scholar]
- Chu, Y.; Wang, Z.; Xue, L.; Deng, M.; Lin, G.; Xie, H.; Shin, H.H.; Li, W.; Firl, G.; D’Amico, D.F. Characterizing warm atmospheric boundary layer over land by combining Raman and Doppler lidar measurements. Opt. Express 2022, 30, 11892–11911. [Google Scholar] [CrossRef]
- Mao, J.; Abshire, J.B.; Kawa, S.R.; Sun, X.; Riris, H. Airborne lidar measurements of atmospheric CO2 column concentrations to cloud tops made during the 2017 ASCENDS/ABoVE campaign. Atmos. Meas. Tech. 2023, 17, 1–26. [Google Scholar] [CrossRef]
- Yang, F.; Gao, F.; Zhang, C.; Li, X.; Gao, X.; Hua, D.; Wang, L.; Xin, W.; Stanič, S. Lateral scanning Raman scattering lidar for accurate measurement of atmospheric temperature and water vapor from ground to height of interest. Opt. Lett. 2023, 48, 2595–2598. [Google Scholar] [CrossRef]
- Liu, F.; Wang, R.; Yi, F.; Huang, W.; Ban, C.; Pan, W.; Wang, Z.; Hu, H. Pure rotational Raman lidar for full-day troposphere temperature measurement at Zhongshan Station (69.37° S, 76.37° E), Antarctica. Opt. Express 2021, 29, 10059–10076. [Google Scholar] [CrossRef]
- Schneider, M.; Hase, F.; Blumenstock, T. Water vapour profiles by ground-based FTIR spectroscopy: Study for an optimised retrieval and its validation. Atmos. Chem. Phys. 2006, 6, 811–830. [Google Scholar] [CrossRef]
- Angelbratt, J.; Mellqvist, J.; Blumenstock, T.; Borsdorff, T.; Brohede, S.; Duchatelet, P.; Forster, F.; Hase, F.; Mahieu, E.; Murtagh, D. A new method to detect long-term trends of methane (CH4) and nitrous oxide (N2O) total columns measured within the NDACC ground-based high-resolution solar FTIR network. Atmos. Chem. Phys. 2011, 11, 6167–6183. [Google Scholar] [CrossRef]
- De Mazière, M.; Thompson, A.M.; Kurylo, M.J.; Wild, J.D.; Bernhard, G.; Blumenstock, T.; Braathen, G.O.; Hannigan, J.W.; Lambert, J.C.; Leblanc, T. The Network for the Detection of Atmospheric Composition Change (NDACC): History, status and perspectives. Atmos. Chem. Phys. 2018, 18, 4935–4964. [Google Scholar] [CrossRef]
- Knuteson, R.; Revercomb, H.; Best, F.; Ciganovich, N.; Dedecker, R.; Dirkx, T.; Ellington, S.; Feltz, W.; Garcia, R.; Howell, H. Atmospheric emitted radiance interferometer. Part I: Instrument design. J. Atmos. Ocean. Technol. 2004, 21, 1763–1776. [Google Scholar] [CrossRef]
- Rochette, L.; Smith, W.L.; Howard, M.; Bratcher, T. In ASSIST, Atmospheric Sounder Spectrometer for Infrared Spectral Technology: Latest development and improvement in the atmospheric sounding technology. In Imaging Spectrometry XIV; SPIE: Bellingham, WA, USA, 2009; pp. 9–17. [Google Scholar]
- Michaud-Belleau, V.; Gaudreau, M.; Lacoursière, J.; Boisvert, É.; Ravelomanantsoa, L.; Turner, D.D.; Rochette, L. The Atmospheric Sounder Spectrometer by Infrared Spectral Technology (ASSIST): Instrument design and signal processing. EGUsphere 2025, 2025, 1–39. [Google Scholar]
- Schneider, M.; Hase, F. Ground-based FTIR water vapour profile analyses. Atmos. Meas. Tech. 2009, 2, 609–619. [Google Scholar] [CrossRef]
- Barthlott, S.; Schneider, M.; Hase, F.; Blumenstock, T.; Kiel, M.; Dubravica, D.; García, O.E.; Sepúlveda, E.; Mengistu Tsidu, G.; Takele Kenea, S. Tropospheric water vapour isotopologue data (H216O, H218O, and HD16O) as obtained from NDACC/FTIR solar absorption spectra. Earth Syst. Sci. Data 2017, 9, 15–29. [Google Scholar] [CrossRef]
- Turner, D.; Löhnert, U. Information content and uncertainties in thermodynamic profiles and liquid cloud properties retrieved from the ground-based Atmospheric Emitted Radiance Interferometer (AERI). J. Appl. Meteorol. Climatol. 2014, 53, 752–771. [Google Scholar] [CrossRef]
- Yurganov, L.; McMillan, W.; Wilson, C.; Fischer, M.; Biraud, S.; Sweeney, C. Carbon monoxide mixing ratios over Oklahoma between 2002 and 2009 retrieved from Atmospheric Emitted Radiance Interferometer spectra. Atmos. Meas. Tech. 2010, 3, 1319–1331. [Google Scholar] [CrossRef]
- Seo, J.; Choi, H.; Oh, Y. Potential of AOD retrieval using atmospheric emitted radiance interferometer (AERI). Remote Sens. 2022, 14, 407. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, H.; Shi, H.; Wang, X.; Li, C.; Sun, E.; An, Y.; Wu, S.; Xiong, W. Channel selection method for the CH4 profile retrieval using the Atmospheric Sounder Spectrometer by Infrared Spectral Technology. J. Quant. Spectrosc. Radiat. Transf. 2024, 326, 109118. [Google Scholar] [CrossRef]
- Yang, J.; Min, Q. Retrieval of atmospheric profiles in the New York State Mesonet using one-dimensional variational algorithm. J. Geophys. Res. Atmos. 2018, 123, 7563–7575. [Google Scholar] [CrossRef]
- Milstein, A.B.; Santanello, J.A.; Blackwell, W.J. Detail enhancement of AIRS/AMSU temperature and moisture profiles using a 3D deep neural network. Artif. Intell. Earth Syst. 2023, 2, 1–31. [Google Scholar] [CrossRef]
- Bouillon, M.; Safieddine, S.; Whitburn, S.; Clarisse, L.; Aires, F.; Pellet, V.; Lezeaux, O.; Scott, N.A.; Doutriaux-Boucher, M.; Clerbaux, C. Time evolution of temperature profiles retrieved from 13 years of infrared atmospheric sounding interferometer (IASI) data using an artificial neural network. Atmos. Meas. Tech. 2022, 15, 1779–1793. [Google Scholar] [CrossRef]
- Luo, Y.; Wu, H.; Gu, T.; Wang, Z.; Yue, H.; Wu, G.; Zhu, L.; Pu, D.; Tang, P.; Jiang, M. Machine learning model-based retrieval of temperature and relative humidity profiles measured by microwave radiometer. Remote Sens. 2023, 15, 3838. [Google Scholar] [CrossRef]
- Zanetta, F.; Nerini, D.; Beucler, T.; Liniger, M.A. Physics-constrained deep learning postprocessing of temperature and humidity. Artif. Intell. Earth Syst. 2023, 2, e220089. [Google Scholar] [CrossRef]
- Liu, Q.; Liang, X. Physics-constrained deep learning-based radiative transfer model. Opt. Express 2023, 31, 28596–28610. [Google Scholar] [CrossRef]
- Xu, J.; Schreier, F.; Doicu, A.; Trautmann, T. Assessment of Tikhonov-type regularization methods for solving atmospheric inverse problems. J. Quant. Spectrosc. Radiat. Transf. 2016, 184, 274–286. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.L. Retrieval of atmospheric profiles from satellite sounder measurements by use of the discrepancy principle. Appl. Opt. 1999, 38, 916–923. [Google Scholar] [CrossRef]
- Turner, D.D.; Blumberg, W.G. Improvements to the AERIoe thermodynamic profile retrieval algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 1339–1354. [Google Scholar] [CrossRef]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Fuhry, M.; Reichel, L. A new Tikhonov regularization method. Numer. Algorithms 2012, 59, 433–445. [Google Scholar] [CrossRef]
- Wahba, G. Practical approximate solutions to linear operator equations when the data are noisy. SIAM J. Numer. Anal. 1977, 14, 651–667. [Google Scholar] [CrossRef]
- Demoment, G. Image reconstruction and restoration: Overview of common estimation structures and problems. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 2024–2036. [Google Scholar] [CrossRef]
- Hansen, P.C. The L-curve and its use in the numerical treatment of inverse problems. Comput. Inverse Probl. Electrocardiol. 2001, 4, 119–142. [Google Scholar]
- Eriksson, P. Analysis and comparison of two linear regularization methods for passive atmospheric observations. J. Geophys. Res. Atmos. 2000, 105, 18157–18167. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000; p. 238. [Google Scholar]
- Liu, X.; Zhou, D.K.; Larar, A.M.; Smith, W.L.; Schluessel, P.; Newman, S.M.; Taylor, J.P.; Wu, W. Retrieval of atmospheric profiles and cloud properties from IASI spectra using super-channels. Atmos. Chem. Phys. 2009, 9, 9121–9142. [Google Scholar] [CrossRef]
- Gamage, S.M.; Sica, R.J.; Martucci, G.; Haefele, A. A 1D Var retrieval of relative humidity using the ERA5 dataset for the assimilation of Raman lidar measurements. J. Atmos. Ocean. Technol. 2020, 37, 2051–2064. [Google Scholar] [CrossRef]
- Panditharatne, S.; Brindley, H.; Cox, C.; Siddans, R.; Murray, J.; Warwick, L.; Fox, S. Retrievals of water vapour and temperature exploiting the far-infrared: Application to aircraft observations in preparation for the FORUM mission. Atmos. Meas. Tech. 2025, 18, 717–735. [Google Scholar] [CrossRef]
- Peter, D.; Heinz, W.E.; Otmar, S. A convergence analysis of iterative methods for the solution of nonlinear ill-posed problems under affinely invariant conditions. Inverse Probl. 1998, 14, 1081. [Google Scholar]
- Doicu, A.; Schreier, F.; Hess, M. Iteratively regularized Gauss–Newton method for atmospheric remote sensing. Comput. Phys. Commun. 2002, 148, 214–226. [Google Scholar] [CrossRef]
- Doicu, A.; Schreier, F.; Hess, M. Iterative regularization methods for atmospheric remote sensing. J. Quant. Spectrosc. Radiat. Transf. 2004, 83, 47–61. [Google Scholar] [CrossRef]
- Smith, W.L., Sr.; Weisz, E.; Kireev, S.V.; Zhou, D.K.; Li, Z.; Borbas, E.E. Dual-regression retrieval algorithm for real-time processing of satellite ultraspectral radiances. J. Appl. Meteorol. Climatol. 2012, 51, 1455–1476. [Google Scholar] [CrossRef]
- Durre, I.; Yin, X.; Vose, R.S.; Applequist, S.; Arnfield, J. Enhancing the data coverage in the Integrated Global Radiosonde Archive. J. Atmos. Ocean. Technol. 2018, 35, 1753–1770. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, J.; Yang, X. Introduction of IGRA dataset and analysis of its data quality. J. Meteorol. Environ. 2013, 29, 106–111. [Google Scholar]
- Twomey, S. On the Numerical Solution of Fredholm Integral Equations of the First Kind by the Inversion of the Linear System Produced by Quadrature. J. ACM 1963, 10, 97–101. [Google Scholar] [CrossRef]
- Choudhury, D.; Ji, F.; Nishant, N.; Di Virgilio, G. Evaluation of ERA5-simulated temperature and its extremes for Australia. Atmosphere 2023, 14, 913. [Google Scholar] [CrossRef]
- Mustafa, F.; Wang, H.; Bu, L.; Wang, Q.; Shahzaman, M.; Bilal, M.; Zhou, M.; Iqbal, R.; Aslam, R.W.; Ali, M.A. Validation of GOSAT and OCO-2 against in situ aircraft measurements and comparison with carbontracker and GEOS-CHEM over Qinhuangdao, China. Remote Sens. 2021, 13, 899. [Google Scholar] [CrossRef]
- Garcia, R.R.; López-Puertas, M.; Funke, B.; Marsh, D.R.; Kinnison, D.E.; Smith, A.K.; González-Galindo, F. On the distribution of CO2 and CO in the mesosphere and lower thermosphere. J. Geophys. Res. Atmos. 2014, 119, 5700–5718. [Google Scholar] [CrossRef]
- Eguchi, N.; Saito, R.; Saeki, T.; Nakatsuka, Y.; Belikov, D.; Maksyutov, S. A priori covariance estimation for CO2 and CH4 retrievals. J. Geophys. Res. Atmos. 2010, 115, D10215. [Google Scholar] [CrossRef]


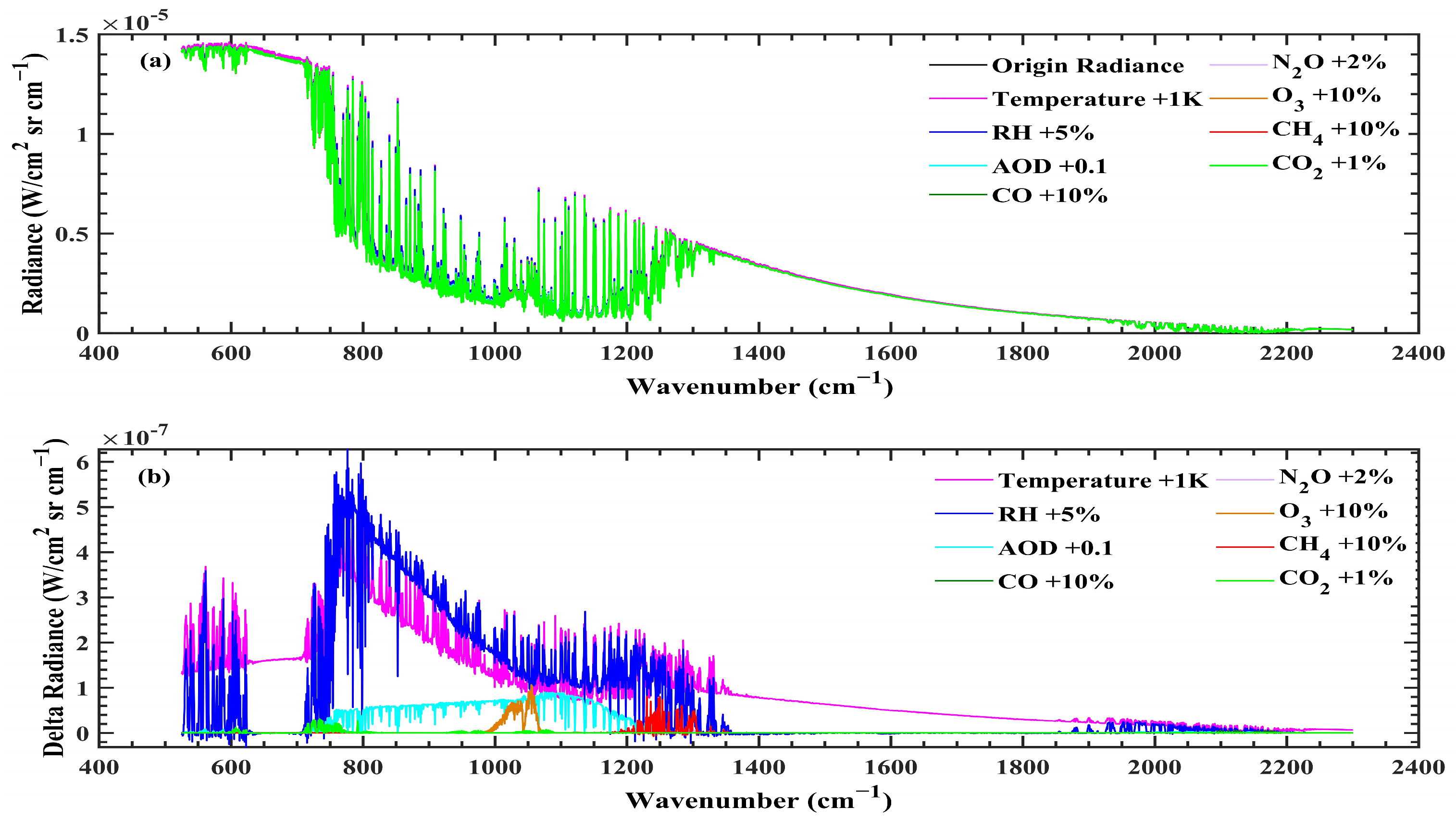
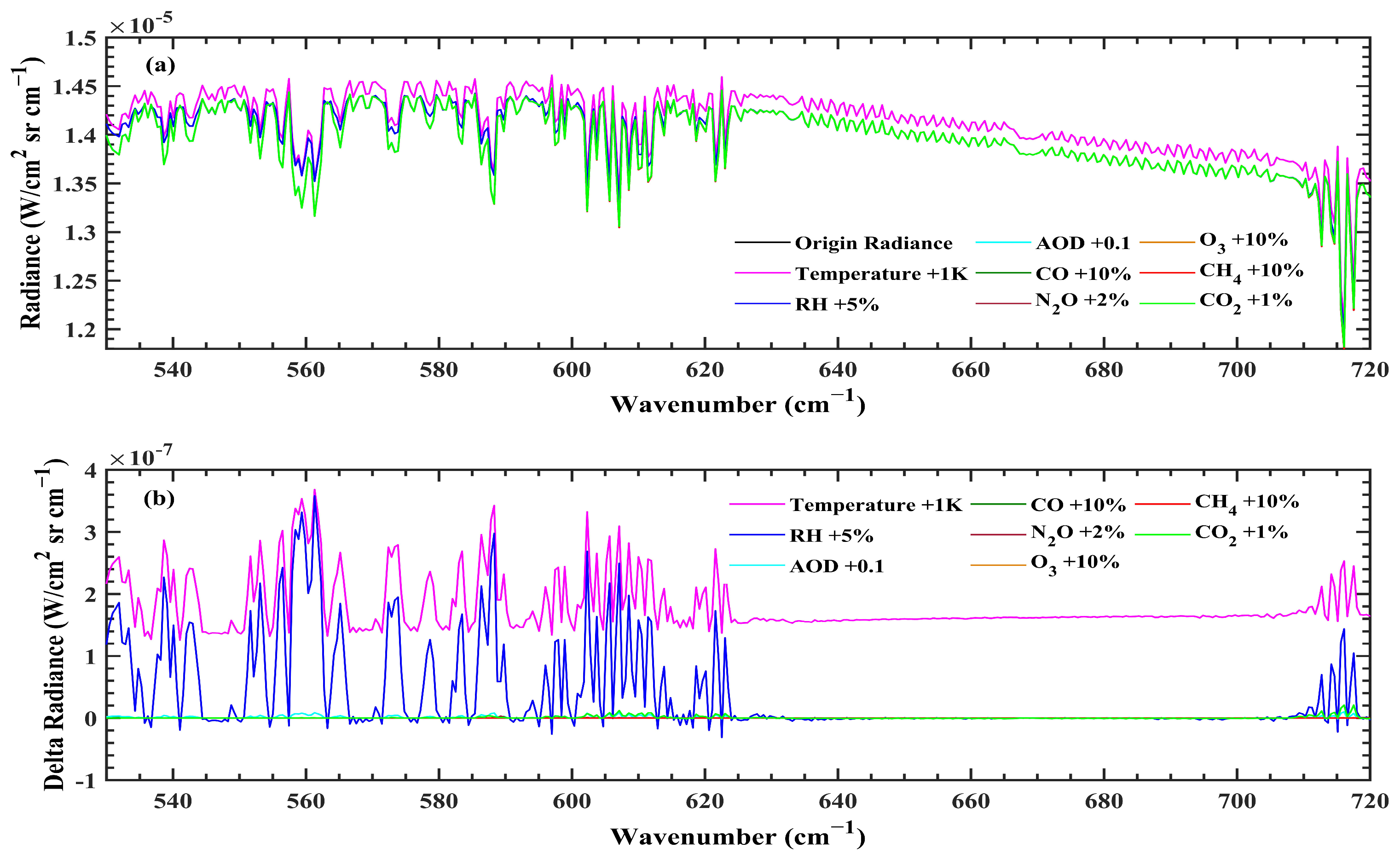

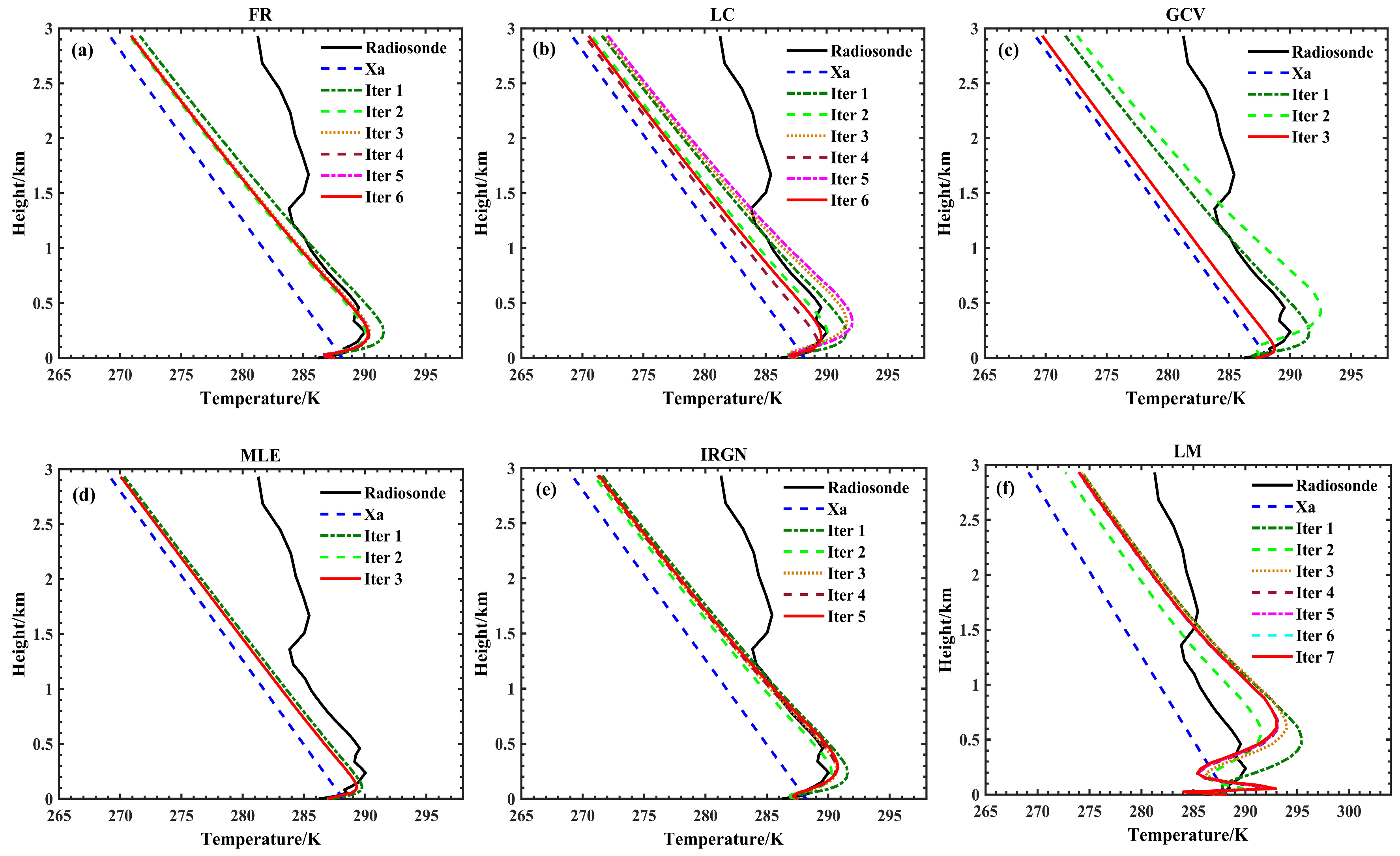
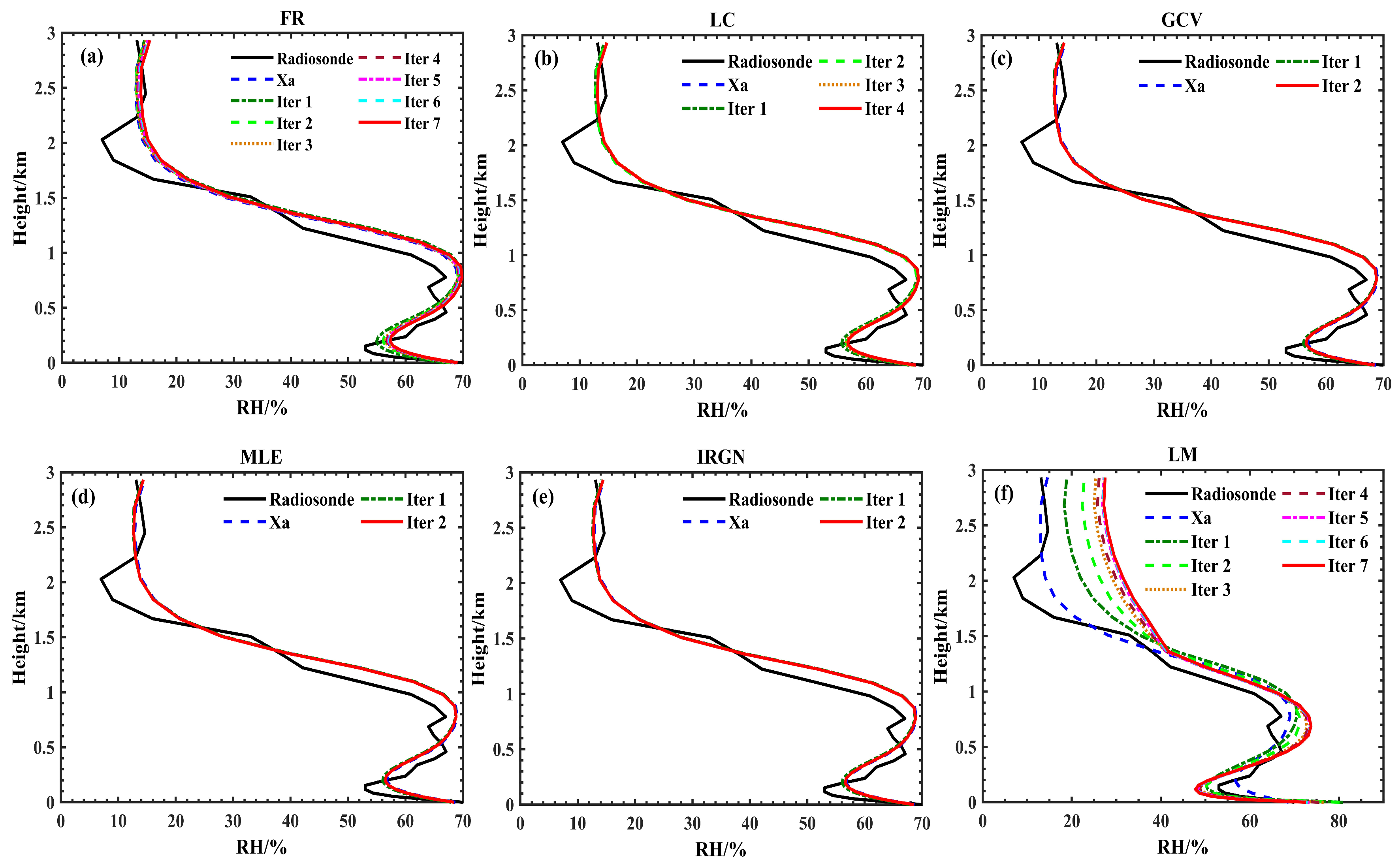

| Parameter | Description |
|---|---|
| Detectors | Mid-wave infrared (InSb) and Long-wave infrared (MCT) |
| Spectrometer type | Interferometric type |
| Observation zenith angle | 0 |
| Field of view angle | |
| Maximum optical path difference | |
| Instrument line shape | Boxcar |
| Spectral resolution | |
| Temporal resolution | |
| The uncertainty of blackbody radiation |
| Parameter | Configuration |
|---|---|
| Observation zenith angle | 0 |
| Atmospheric emissivity | 0.8 |
| Observation altitude | 0 |
| Number of atmospheric layers | 29 |
| Aerosol | Rural aerosol, AOD = 0.1 |
| Temperature profile | ERA5 |
| RH profile | ERA5 |
| CO2 profile | Carbon Tracker |
| Other gas profiles | WACCM |
| Temperature | RH |
|---|---|
| 612–618 | 533–588 |
| 624–660 | |
| 674–703 |
| Date | Method | Feature | Regularization Factor |
Residual | DFS |
|---|---|---|---|---|---|
| 19:15 Beijing time on 2 November 2024 | FR | Temperature | 2.97 | ||
| RH | 1.43 | ||||
| LC | Temperature | 2.97 | |||
| RH | 1.20 | ||||
| GCV | Temperature | 2.18 | |||
| RH | 1.11 | ||||
| MLE | Temperature | 2.18 | |||
| RH | 1.11 | ||||
| IRGN | Temperature | 3.04 | |||
| RH | 1.13 | ||||
| LM | Temperature | 3.74 | |||
| RH | 1.93 |
| Date | Method | Feature | Regularization Factor |
Residual | DFS |
|---|---|---|---|---|---|
| 07:15 Beijing time on 3 November 2024 | FR | Temperature | 3.00 | ||
| RH | 1.51 | ||||
| LC | Temperature | 3.00 | |||
| RH | 1.51 | ||||
| GCV | Temperature | 2.18 | |||
| RH | 2.73 | ||||
| MLE | Temperature | 2.18 | |||
| RH | 1.21 | ||||
| IRGN | Temperature | 3.34 | |||
| RH | 1.25 | ||||
| LM | Temperature | 2.18 | |||
| RH | 2.73 |
| Method | Feature | Mean BIAS | Mean RMSE | Mean Residual | Mean DFS |
|---|---|---|---|---|---|
| FR | Temperature | 0.29 | 0.77 | 3.14 | |
| RH | 9.10 | 14.57 | 1.47 | ||
| LC | Temperature | 0.23 | 0.82 | 3.27 | |
| RH | 8.74 | 14.40 | 1.36 | ||
| GCV | Temperature | 0.19 | 1.13 | 2.64 | |
| RH | 9.53 | 15.23 | 1.92 | ||
| MLE | Temperature | 0.24 | 0.96 | 2.35 | |
| RH | 9.20 | 14.80 | 1.16 | ||
| IRGN | Temperature | 0.42 | 0.80 | 3.37 | |
| RH | 9.01 | 14.58 | 1.19 | ||
| LM | Temperature | 1.80 | 2.60 | 2.93 | |
| RH | 3.65 | 5.62 | 2.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xiong, W.; Ye, H.; Shi, H.; Wang, X.; Li, C.; Wu, S.; Cheng, C. Evaluation of Different Methods for Retrieving Temperature and Humidity Profiles in the Lower Atmosphere Using the Atmospheric Sounder Spectrometer by Infrared Spectral Technology. Remote Sens. 2025, 17, 1440. https://doi.org/10.3390/rs17081440
Wang Y, Xiong W, Ye H, Shi H, Wang X, Li C, Wu S, Cheng C. Evaluation of Different Methods for Retrieving Temperature and Humidity Profiles in the Lower Atmosphere Using the Atmospheric Sounder Spectrometer by Infrared Spectral Technology. Remote Sensing. 2025; 17(8):1440. https://doi.org/10.3390/rs17081440
Chicago/Turabian StyleWang, Yue, Wei Xiong, Hanhan Ye, Hailiang Shi, Xianhua Wang, Chao Li, Shichao Wu, and Chen Cheng. 2025. "Evaluation of Different Methods for Retrieving Temperature and Humidity Profiles in the Lower Atmosphere Using the Atmospheric Sounder Spectrometer by Infrared Spectral Technology" Remote Sensing 17, no. 8: 1440. https://doi.org/10.3390/rs17081440
APA StyleWang, Y., Xiong, W., Ye, H., Shi, H., Wang, X., Li, C., Wu, S., & Cheng, C. (2025). Evaluation of Different Methods for Retrieving Temperature and Humidity Profiles in the Lower Atmosphere Using the Atmospheric Sounder Spectrometer by Infrared Spectral Technology. Remote Sensing, 17(8), 1440. https://doi.org/10.3390/rs17081440







