Multi-Object Feature Extraction in Resonance Region Based on Short-Time Matrix Pencil Method

Abstract

As an intrinsic characteristic of the target, the pole characteristic of the resonant region is solely determined by the target itself and remains invariant with respect to external factors such as the incident direction and polarization of electromagnetic waves. Consequently, it serves as a critical foundation for target identification. The Matrix Pencil Method (MPM) is currently a widely adopted technique for extracting target poles; however, it typically processes single targets. When multiple targets produce time-domain echoes in the echo signal, the MPM fails to distinguish between individual targets, leading to extracted pole information that does not adequately represent the relevant characteristics of each target. In this paper, we propose a Short-Time Matrix Pencil Method (STMPM), which introduces sliding time windows to differentiate multiple targets in time-domain echoes. By analyzing the variations in poles across each sliding time window, the STMPM can accurately extract the poles corresponding to each target.

1. Introduction

The pole property of the target is a critical characteristic that is frequently utilized for target identification [1,2,3]. When a target is irradiated as a scatterer by a short-pulse signal, if the wavelength of the incident electromagnetic wave is comparable to the dimensions of the target, it enters the resonance region. The electromagnetic echo signal reflected from the target comprises two components: one being the specular reflection, referred to as the early response, and the other being the resonance component generated by the induced currents within the target due to the incident electromagnetic wave. This latter component, known as the late-time response, allows for the extraction of the target’s pole characteristics.

Based on the singularity expansion method (SEM) [4,5,6], the late-time response of the target can be decomposed into the form of multiple exponential functions. In order to solve the corresponding exponential function and various parameters, the Prony method and Matrix Pencil Method (MPM) have been proposed to extract the pole information from the late-time response of the target, among which the Matrix Pencil Method is the most commonly used method at present, and it has a good effect in dealing with noise interference [7,8,9,10]. However, the MPM also has certain limitations, including the need to predict late-time moments and sensitivity to higher-order poles. First of all, the MPM cannot distinguish the early-time response from the late-time response, so it is necessary to preprocess the time domain signal to obtain a better estimate of the start time of the late-time response. Secondly, because the attenuation factor of the higher-order poles is large, the MPM often produces obvious deviation when extracting the higher-order poles. In addition, the MPM is often used to extract the pole information in the echo signal of a single target. However, when there are multiple targets in the echo signal, it cannot distinguish each target from the echo signal, nor can it extract the pole information of each target.

In order to solve the problem that the MPM cannot extract the pole information in the echo signal containing multiple targets, a Short-Time Matrix Pencil Method (STMPM) based on a sliding window is proposed to distinguish the target in the echo signal and extract the corresponding target pole information. In Section 2, the corresponding scenario and the basic information of the MPM and STMPM is introduced. In Section 3, the simulation experiment of the STMPM used in target distinction and pole information extraction in multiple target echo information is introduced to verify the effectiveness of the STMPM in extracting pole information when there are multiple targets.

2. Scenario and Method Description

In this section, we describe the scenarios under consideration [11,12] and illustrate the method used to extract relevant feature information from the scenarios.

2.1. Scattering Echo Characteristic

2.1.1. Single Target

In general, when a short-pulse wideband transmitted signal $s_i\left(t\right)$ illuminates the target, the resultant scattered echo of the target $s_r\left(t\right)$ can be categorized into two parts [13,14], the early-time response $h_E\left(t\right)$ and the late-time response $h_L\left(t\right)$, as shown in Formula (1).

$$\begin{array}{ll}{s}_r\left(t\right)& =s_i\left(t\right)\ast h_1\left(t\right)+s_i\left(t\right)\ast h_2\left(t\right)\\ & =h_E\left(t\right)+h_L\left(t\right)\end{array};$$

(1)

where $h_1\left(t\right)$ denotes the modulation of the transmitted signal due to specular reflection, and its duration is $0<t\le 2D/c=T_L$, which is determined by the maximum size $D$ of the target. Under normal circumstances, the early-time response $h_E\left(t\right)$can be represented as a weighted sum of the derivatives of the transmitted signal, and it can be derived from the transmitted signal through simple differentiation, with an additional phase or amplitude change. However, since the early-time response corresponds to the specular reflection of strong scatterers on the target surface, it varies with external factors such as the incident direction and polarization of the electromagnetic wave. Consequently, it requires more data compared to the intrinsic attribute pole information present in the late-time response. In the Formula (1), the modulation $h_2\left(t\right)$ caused by the induced current excited by the transmitted signal on the target surface, and the late-time response can be expressed as the sum of a series of decaying exponential functions, as illustrated in Equation (2).

$$h_L\left(t\right)={\displaystyle \sum _{i=1}^M{R}_i{e}^{s_{i}t}};$$

(2)

where $s_i={\sigma }_i+j{w}_i$ is the $i^{th}$ $i\text{-}\mathrm{th}$ pole of the signal, ${\sigma }_i$ is the attenuation factor associated with this pole, $w_i=2\pi f_i$ is the resonant angular frequency corresponding to this pole, and $R_i$ is the residue associated with this pole. $M$ denotes the total number of poles in the signal. The relationship can be expressed as a transfer function in the complex frequency domain using the Laplace transform, as shown in Equation (3).

$$H\left(s\right)={\displaystyle \sum _{i=1}^M\frac{R_i}{s-s_i}};$$

(3)

As illustrated in Figure 1, when a sphere is irradiated by a uniform plane wave propagating along the X-axis, the electromagnetic wave component incident on the sphere between points A and B on its right side will be directly reflected back toward the source, which is shown by the solid blue line. This reflection constitutes the early-time response of the time-domain echo. The wave component incident at point A diffracts along the spherical surface, contributing to the late-time response of the time-domain echo. After completing one full diffraction cycle, it returns to point A and interferes constructively with the incident signal, which is shown by the solid red line. If the wavelength corresponding to the frequency of the incident wave matches the diffraction path length such that the phase of the diffracted wave after one cycle coincides with the phase of the incident wave at point A, constructive interference occurs, producing the first peak in the frequency domain. This mechanism also explains the formation of peaks in other resonance regions [15,16,17].

2.1.2. Multiple Targets

The scattered-echo characteristics of a single target are described in the last section; in this study, we consider the simple multi-objective model, examining the late-time-domain echo characteristics of dual-target scenarios [18,19,20].

Assume that the transmitted signal is denoted as s(t) and the total ideal echo signal received is denoted as $s_r\left(t\right)$.

When the distance between two objects along the direction of the transmitted signal is denoted as $R$, with the first object located at a distance $R_1$ from the transmitting source, the time-domain expression of the received echo signal can be represented as shown in Equation (4).

$$\begin{array}{ll}{s}_r\left(t\right)& =s_1\left(t\right)+s_2\left(t\right)\\ & {=\mathrm{u}}_1\left(t\right)\ast s\left(t-{\displaystyle \frac{2R_1}{c}}\right)+u_2\left(t\right)\ast s\left(t-2{\displaystyle \frac{R_1+R}{c}}\right)\end{array};$$

(4)

where $s_1\left(t\right)$ and $s_2\left(t\right)$ denote the time-domain echo signals from the first and second objects, respectively, while $u_1\left(t\right)$ and $u_2\left(t\right)$ represent the modulation effects of the transmitted signal $s_i\left(t\right)$ by the first and second objects, respectively.

When the distances of two objects from the transmitting source are the same, that is, when the two objects are at a distance of zero in the direction of transmitting the signal, Equation (5) can be expressed as

$$s_r\left(t\right)=\left({\mathrm{u}}_1\left(t\right)+u_2\left(t\right)\right)\ast s\left(t-{\displaystyle \frac{2R_1}{c}}\right);$$

(5)

It can be observed from the formula that this phenomenon is equivalent to the modulation $u_1\left(t\right)+u_2\left(t\right)$ of the transmitted signal by a new object, so that leads to the misidentification of two goals as a single objective and we could not distinguish either of the targets. Consequently, it is unable to distinguish between targets and extract the corresponding target poles. In order to solve this problem, the direction of the transmitted signal can be changed so that there is a distance difference between the two targets in the direction of transmitted signal. Only when there is a distance difference in the direction of the radar line of sight between the two objects can we differentiate the objects. In such a scenario, the frequency domain representation of the echo signals from the two objects could be expressed as

$$\begin{array}{ll}{S}_r\left(w\right)& =U_1\left(w\right)\times \left[S\left(w\right)e^{-jw{\displaystyle \frac{2R_1}{c}}}\right]+U_2\left(w\right)\times \left[S\left(w\right)e^{-jw{\displaystyle \frac{2\left(R_1+R\right)}{c}}}\right]\\ & =e^{-jw{\displaystyle \frac{2R_1}{c}}}\left[\mathrm{S}\left(w\right)\times U_1\left(w\right)+S\left(w\right)\times U_2\left(w\right)\right]\left(1+e^{-jw{\displaystyle \frac{2R}{c}}}\right)\end{array};$$

(6)

where the first two terms pertain to the propagation distance of the transmitted signal, while the third term is associated with the separation distance between the two objects along the direction of transmission, thereby reflecting the spatial relationship between them. By examining only the amplitude of the third term, the relationship can be expressed as Equation (7), which represents the envelope of the signal.

$$m\left(t\right)=\left|1+e^{-jw{\displaystyle \frac{2R}{c}}}\right|=2\left|\cos {\displaystyle \frac{wR}{c}}\right|=2\left|\cos {\displaystyle \frac{2\pi fR}{c}}\right|;$$

(7)

2.2. The Method to Extract the Pole Information

2.2.1. Matrix Pencil Method for Single Target

Performing time-domain sampling on the time-domain transient late-time response of a single target as shown in Equation (2) with a sampling interval of $T_s$, the sampled signal $y\left(n{T}_s\right)$ is as shown in Equation (8).

$$y\left(n{T}_s\right)={\displaystyle \sum _{i=1}^M{R}_i{z}_i^n,n=0,1,\cdots N-1};$$

(8)

where $N$ represents the total number of samples, $Z_i=e^{s_i{T}_s}=e^{\left({\sigma }_i+j{w}_i\right)T_s},i=\mathrm{1,2},\cdots M$.

The expression (8) can be represented in matrix form as shown in Equation (9).

$$Ax=b;$$

(9)

$$A={\left[\begin{array}{cccc}1& 1& \cdots & 1\\ z_1& z_2& \cdots & z_M\\ \cdots & \cdots & \cdots & \cdots \\ z_1^{N-1}& z_2^{N-1}& \cdots & z_M^{N-1}\end{array}\right]}_{N\times M};$$

(10)

$$x={\left[R_1,R_2,\cdots ,R_M\right]}^T;$$

(11)

$$b={\left[y\left(0\right),y\left(1\right),\cdots y\left(N-1\right)\right]}^T;$$

(12)

Here, using the Matrix Pencil Method, the pole data for three spheres with different radii can be obtained as shown in Figure 2.

Here, we select the first four poles [21] of each sphere as the main poles and present them in

Table 1. The poles of three spheres with different radii (m) $\left(10^9{\mathrm{s}}^{-1},\mathrm{G}\mathrm{H}\mathrm{z}\right)$.

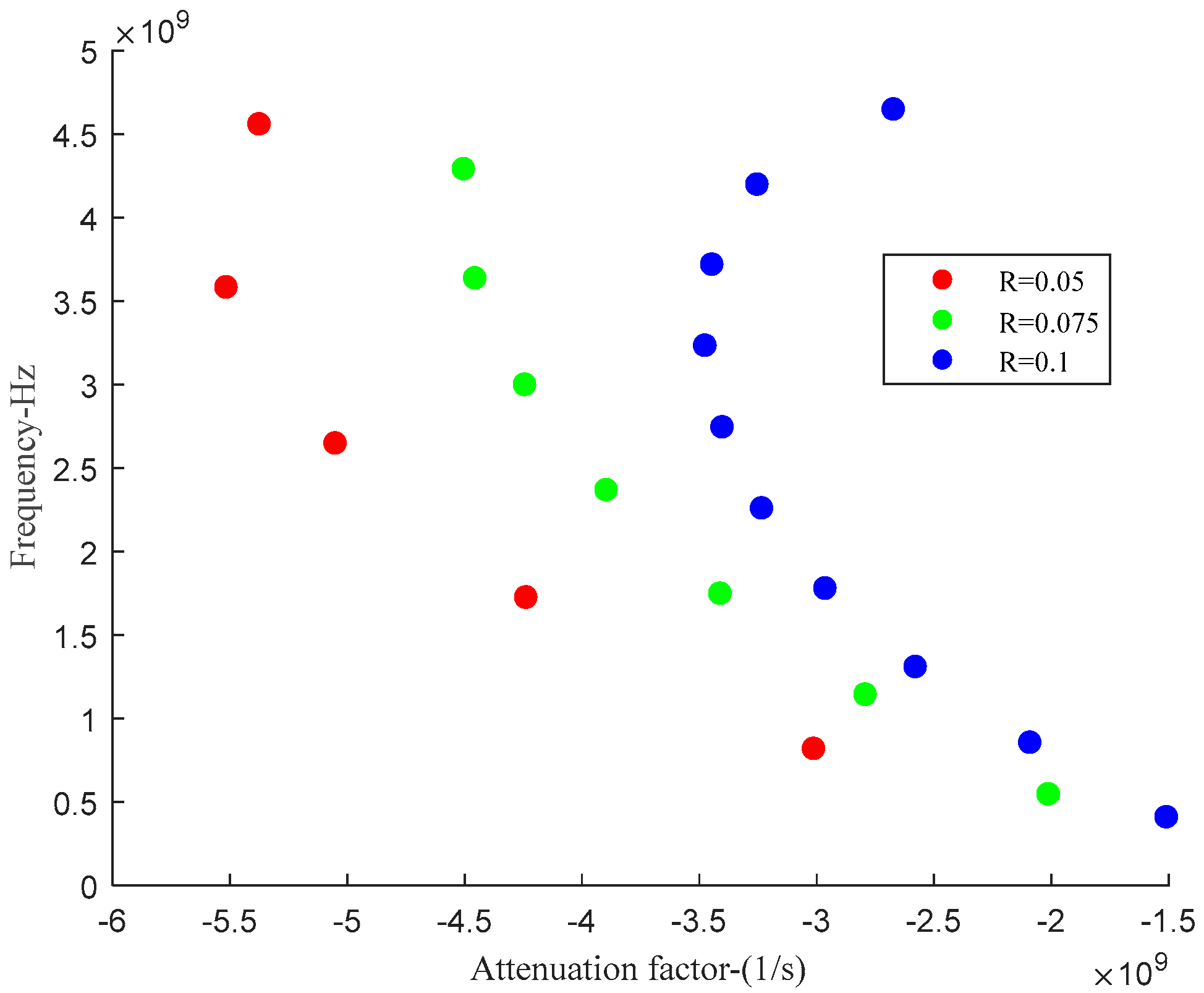
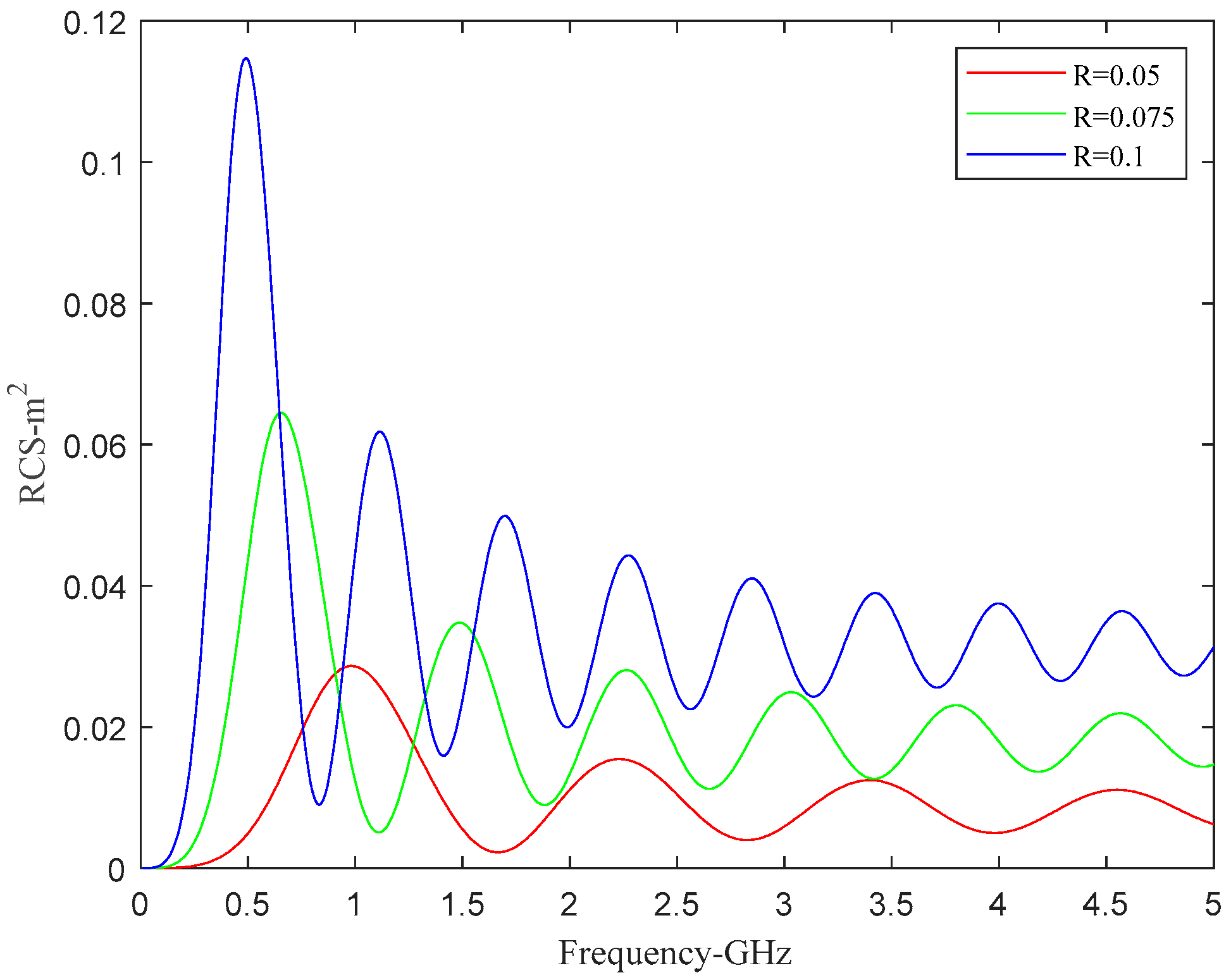
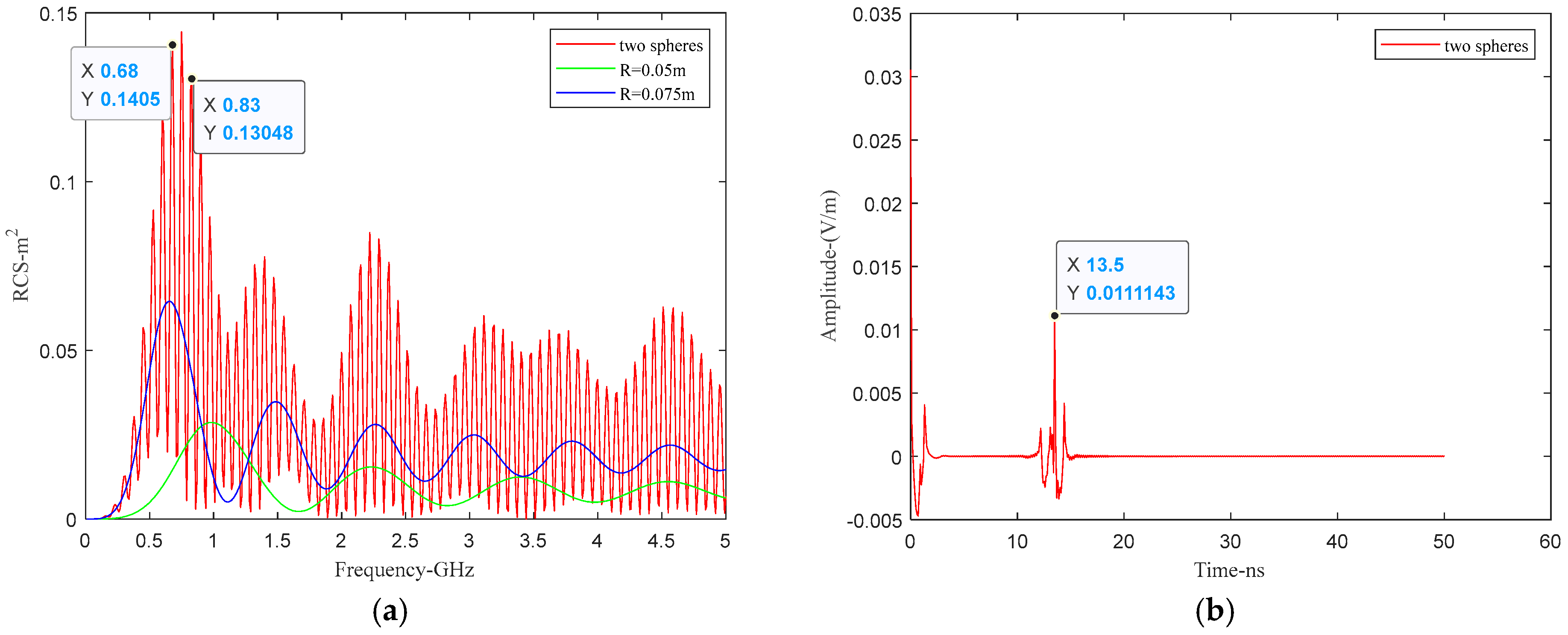
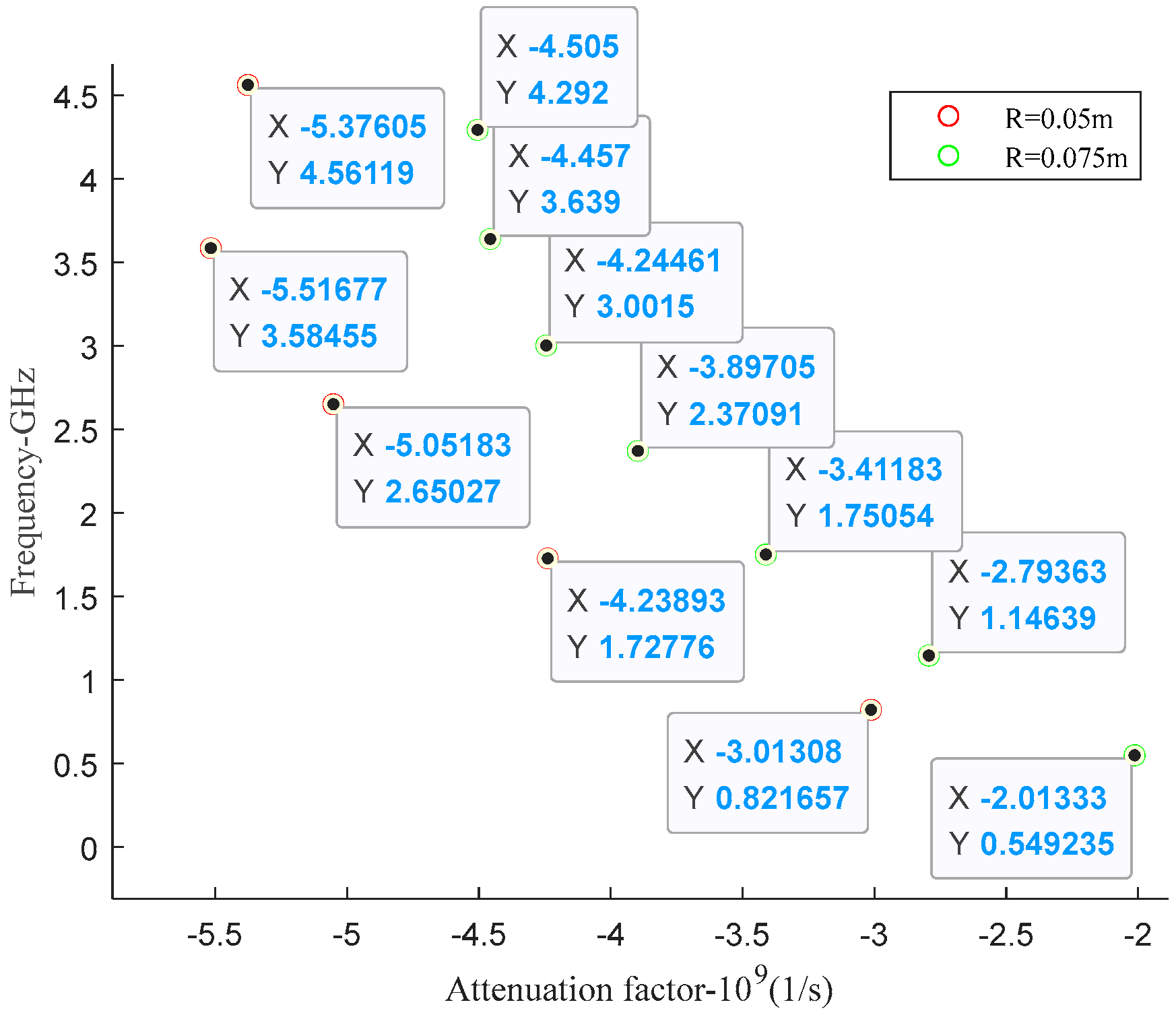
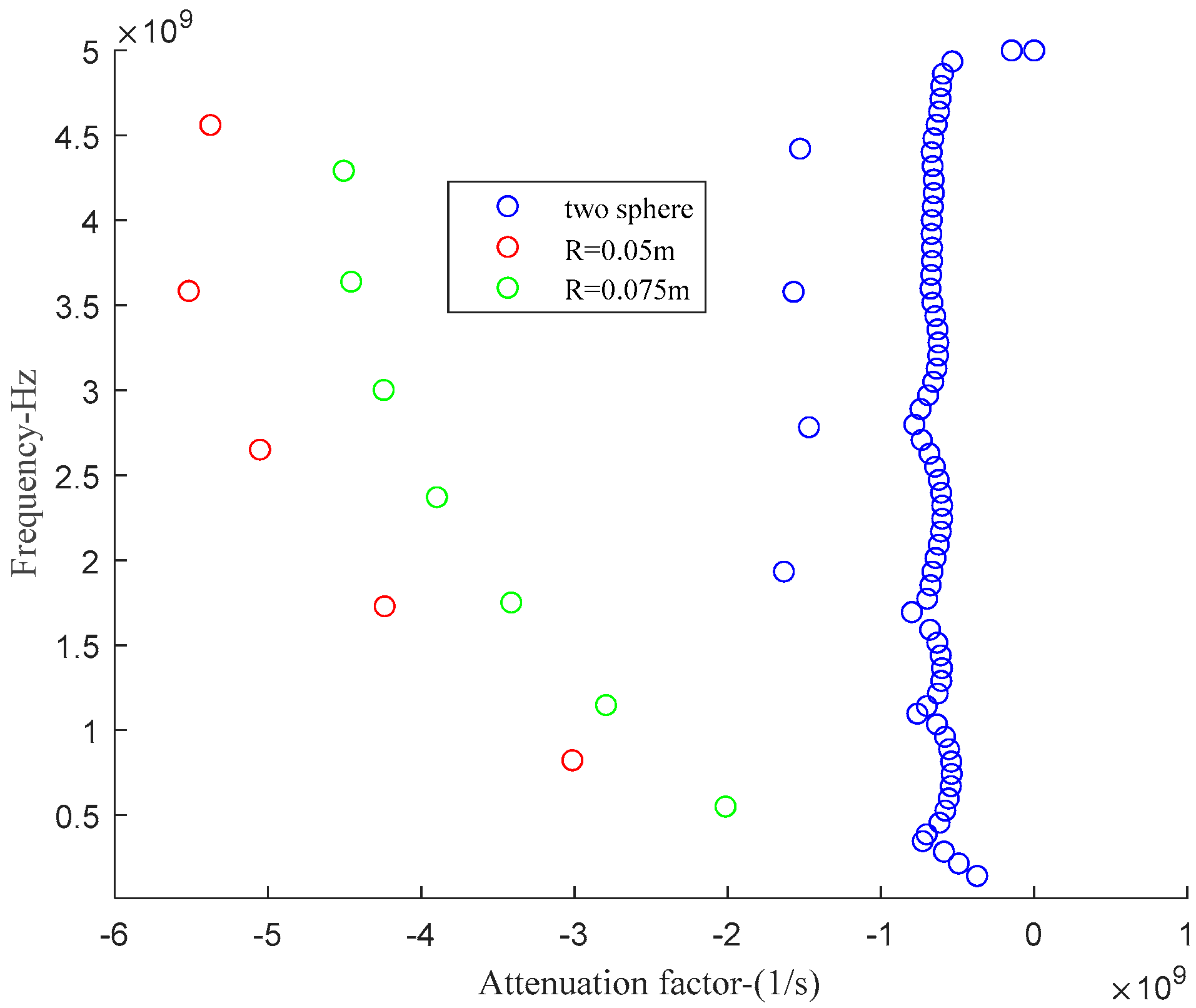
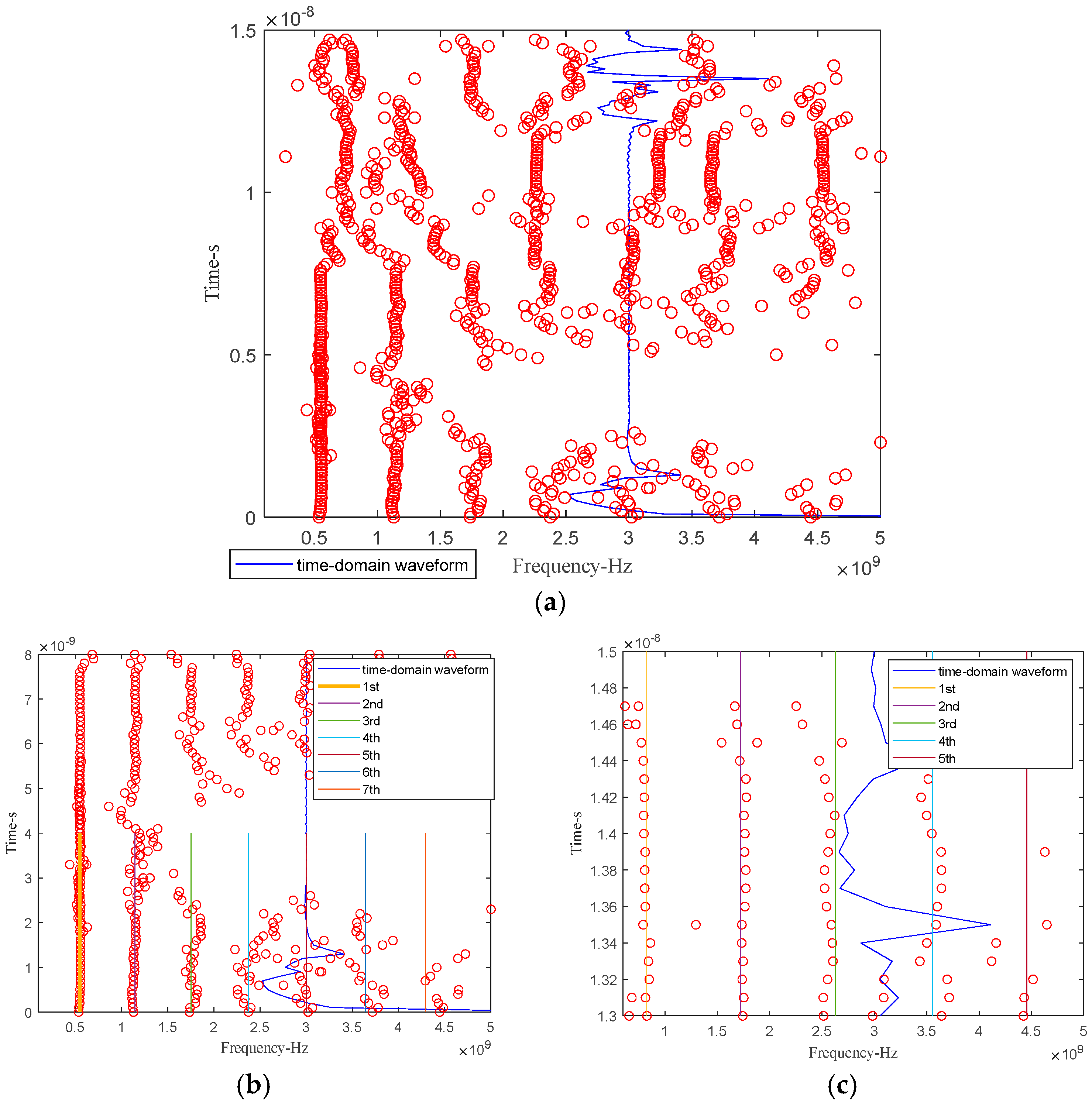
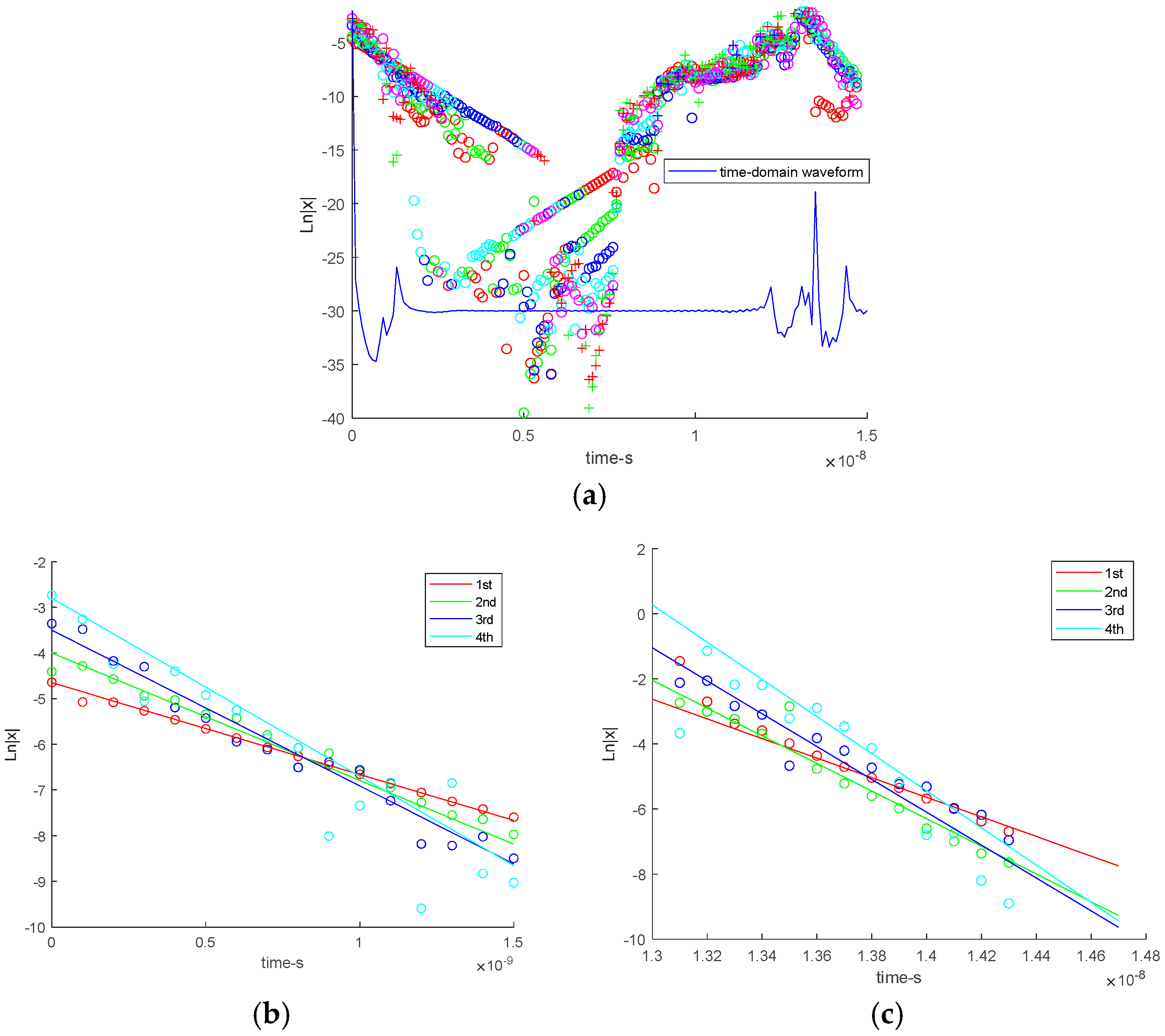
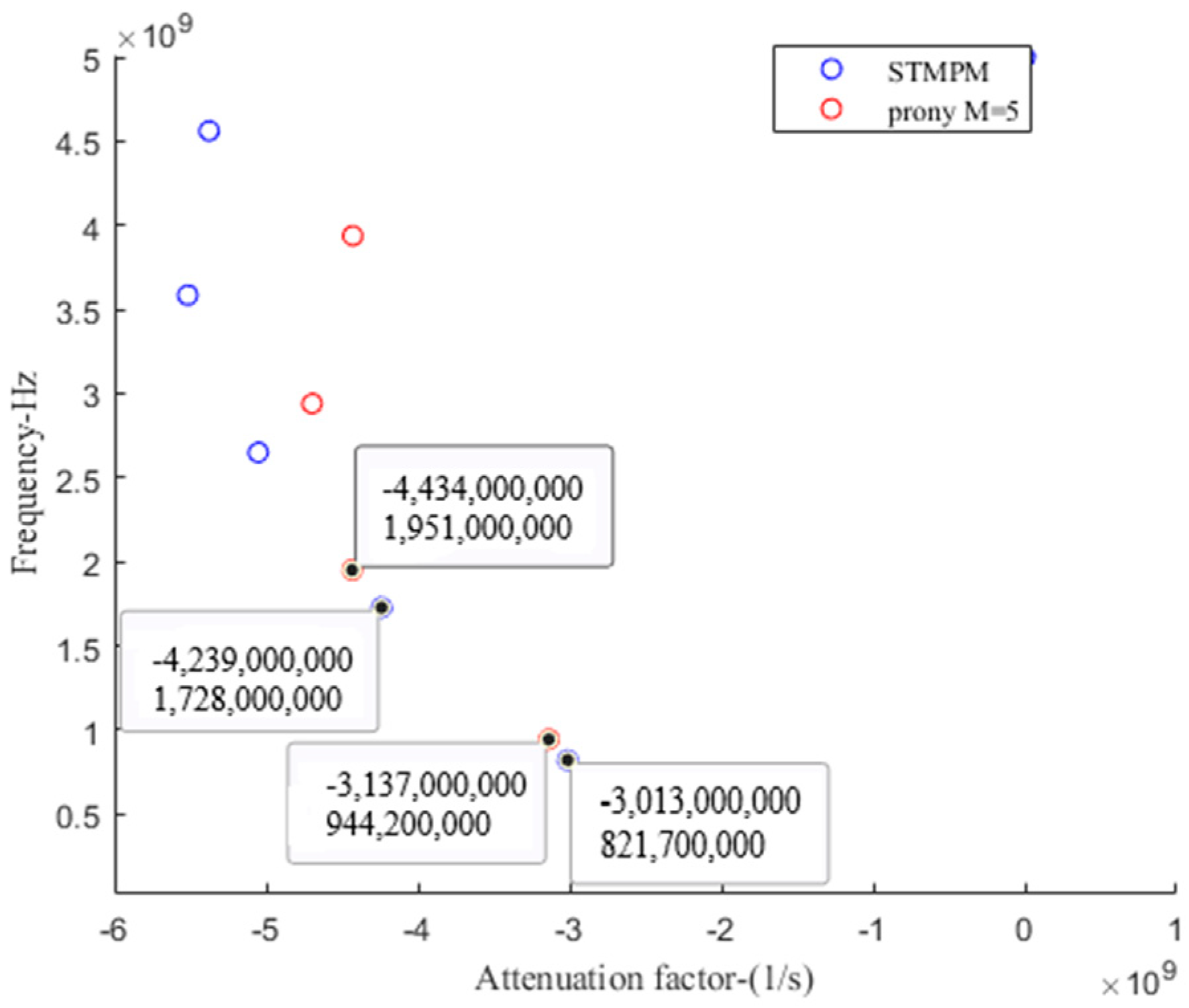
Radii	R = 0.05	R = 0.075	R = 0.1
1st	(−3.01, 0.82)	(−2.01, 0.55)	(−1.51, 0.41)
2nd	(−4.24, 1.73)	(−2.79, 1.15)	(−2.09, 0.86)
3rd	(−5.05, 2.65)	(−3.41, 1.75)	(−2.58, 1.31)
4th	(−5.52, 3.59)	(−3.90, 2.37)	(−2.96, 1.78)

.

2.2.2. Short-Time Matrix Pencil Method for Multiple Targets

The Matrix Pencil Method can yield more accurate pole extraction results for single-target scenarios. However, in the presence of multiple targets within the time-domain echo, this method fails to effectively extract poles.

We first define the matrix $Y$ as presented in Equation (13). Subsequently, we conduct a singular value decomposition of this matrix as illustrated in Equation (14).

$$Y={\left[\begin{array}{cccc}y\left(0\right)& y\left(1\right)& \cdots & y\left(L\right)\\ y\left(1\right)& y\left(2\right)& \cdots & y\left(L+1\right)\\ y\left(2\right)& y\left(3\right)& \cdots & y\left(L+2\right)\\ \cdots & \cdots & \cdots & ⋮\\ y\left(N-L-1\right)& y\left(N-L\right)& \cdots & y\left(N-1\right)\end{array}\right]}_{\left(N-L\right)\times \left(L+1\right)};$$

(13)

$$Y=U\Sigma V^H;$$

(14)

In the formula, $U$ and $V$ are unitary matrices obtained through decomposition, and $\mathsf{\Sigma }$ is the diagonal matrix obtained through decomposition.

In an ideal noise-free environment, the $Y$ matrix can yield $M$ non-zero singular values through singular value decomposition, where both the number and magnitude of these singular values are dictated by the intrinsic properties of the target. However, in the presence of noise within the signal, the originally zero singular values become non-zero due to the influence of noise. If we continue to apply this method, these newly non-zero singular values will be extracted alongside the significant poles. To mitigate the adverse effects of noise, a low-rank matrix approximation method is employed, and the resultant matrix is constructed as per Equation (15).

$$\left\{\begin{array}{c}U’=U\left(:,1:M\right)\\ V’=V\left(:,1:M\right)\\ \Sigma ’=\Sigma \left(1:M,1:M\right)\\ Y’=U’\Sigma ’V{’}^H\end{array}\right.;$$

(15)

Define matrices $Y_1$ and $Y_2$, where the relationship between these matrices $Y,Y_1,Y_2$ is expressed as $Y=\left[y_1,Y_2\right]=\left[Y_1,y_{L+1}\right]$, as presented in Equation (16).

$$\left\{\begin{array}{c}{Y}_1^{’}=U’\Sigma ’V_1^{’H}\\ Y_2^{’}=U’\Sigma ’V_2^{’H}\end{array}\right.;$$

(16)

In the formula, $V_1^{\prime }$ and $V_2^{\prime }$ are obtained by removing the last row and the first row from $V^{\prime },$ respectively. The poles of the target can be obtained by solving the eigenvalues of $Y_1^{\prime +}{Y}_2^{\prime }$.

After obtaining the pole information, the residue corresponding to the pole can be solved by the least squares method, as shown in Equation (17).

$$x={\left(A^{T}A\right)}^{-1}{A}^{T}b;$$

(17)

In an actual multiple target scenario, the late-time response of the first target can interfere with the late-time response of the second target. Specifically, because the electromagnetic wave irradiates the first target before irradiating the second target, there is a coupling signal of two targets in the time-domain echo signal of the second target, and the signal amplitude of the late-time response of the second target is significantly weaker than that of the first target, so it is difficult to use the MPM to extract pole information. Firstly, the late-time responses of both targets in the time domain cannot be accurately represented as a series of decaying exponentials. Consequently, the poles can only be extracted by selecting an appropriate time window using the Matrix Pencil Method. Secondly, the amplitude of the late transient response for the second target is considerably smaller and decays rapidly, resulting in a very short corresponding time window. Therefore, it is necessary to synthesize multiple distinct time windows to reasonably select pole information. In the proposed method, a sliding time window is introduced, and the Matrix Pencil Method (MPM) is utilized to extract poles and residuals from each time interval covered by this sliding window.

The Short-Time Matrix Pencil Method (STMPM) [22,23,24] initially requires the determination of an appropriate time window duration $T_w$ and an optimal time step $T$ (the minimum time step can be set as the sampling interval in the time domain). For an exponential decay function, at least five peak points in the time-domain signal are required to precisely determine the attenuation factor, so at least five cycles of each pole are required to successfully estimate the poles. Correspondingly, the minimum distance between the two objects could also be decided. Based on the cause of the resonance frequency-domain peak generation, this value is 2.5 times the maximum circumferential length of the target. The smaller the step size, the more detailed the description of the change of the pole with the time window, the easier it is to find the position of the target corresponding pole in the time-frequency space. In the case of multiple targets, because a time window that is too long may introduce multi-target coupling interference, combined with the impact on the step length, it is necessary to comprehensively consider the length of the time window and the step length setting.

The time window is then slid across the entire time-domain signal at this specified interval, and the late-time response within the window can be mathematically expressed as

$$y_T\left(t\right)=\mathrm{Re}\left({\displaystyle \sum _{i=1}^M{R}_i^T{e}^{-s_i\left(t-T\right)}}\right);$$

(18)

The residual $R_i^T$, which varies as the time window shifts, can be formally expressed as (19). So, on a logarithmic scale it can be expressed as (20)

$$R_i^T=R_i{e}^{-s_{i}T}=R_i{e}^{-\left({\alpha }_i+j{w}_i\right)T};$$

(19)

$$Ln\left(\left|R_i^T\right|\right)=Ln\left(\left|R_i\right|\right)-{\alpha }_{i}T;$$

(20)

Because the STMPM needs to perform repeated matrix operations in the sliding window, the time complexity of one calculation, which is proportional to the number of poles, is $O\left(n\right)$, while the STMPM needs to perform multiple calculations of poles, so the time complexity of the STMPM is $O\left(n^2\right)$.

By applying the Short-Time Matrix Pencil Method, multiple sets of poles and residuals are extracted. Each set of poles and residuals, along with their corresponding time indices of the time window, forms a time/frequency space. When the imaginary part of the pole in the frequency space converges to a stable value, it may correspond to target information, which needs to be determined by concrete analysis. In the previous chapter, it was mentioned that the real part of the higher-order pole is less stable than the imaginary part, and the residual decreases logarithmically relative to the time index and its slope corresponds to the real part of the complex natural resonance, so the real part of the pole is obtained by using the residual information.

3. Results

The foundation of feature extraction lies in the analysis of the target’s electromagnetic scattering characteristics, which necessitates a solid understanding of the theory and computational methods associated with Radar Cross-Section (RCS). Typically, electromagnetic scattering data for the target are acquired through electromagnetic simulation software; here, the moment of method can be employed to obtain the RCS data. By performing inverse Fourier transform on the RCS data, the time-domain data can be obtained. This study analyzes multi-target feature extraction from the perspective of resonance-region scattering mechanisms. Spherical targets, as canonical structures for resonance analysis, were selected for their representative significance.

3.1. Electromagnetic Scattering Echo Data Analysis

The frequency range was set from 0.01 GHz to 5 GHz, with 500 discrete frequency points at intervals of 10 MHz. The incidence angle of the electromagnetic wave was configured as θ = 90° and ϕ = 0°. Figure 1b illustrates the simulation model, while Figure 3 presents the RCS diagrams for spheres with three distinct radii.

Based on the three different radius sphere models mentioned earlier, considering the multiple-target scenario presented, two distinct spherical models are alternately positioned. The radius of the foremost sphere is 0.075 m, while that of the rear sphere is 0.05 m. The distance separating these two spheres is 2 m, as illustrated in Figure 4.

Figure 5a illustrates the RCS data of two spheres with radii of 0.075 m and 0.05 m, respectively, when they are 2 m apart from each other in the direction of the transmitted signal. When the two objects are positioned two meters apart along the direction of the transmitted signal, the frequency period described by Equation (7) is 75 MHz and is corroborated by the RCS data presented in Figure 5a. This value remains constant as long as the relative positions of the two objects do not change. Figure 5b displays the corresponding time-domain waveform of this RCS data. The red portion of the figure represents the time-domain echo from the two targets, exhibiting a significant peak at 0 ns, which gradually diminishes to zero. While there are multiple peaks before and after 13.5 ns, some of these peaks result from the induced current of the second target, while others are due to the time-domain trailing effect of the first target. Notably, the peak at 13.5 ns is smaller than the initial peak at 0 ns, highlighting the two issues addressed in Section 2.2.2.

3.2. Extracting the Pole Information

After obtaining the echo data in Section 3.1, corresponding methods are used to extract the pole data in two scenarios. The MPM is used to extract the pole information of the single target, and Figure 6 presents the pole data for spheres with radii of 0.05 m and 0.075 m. However, the MPM failed to extract the poles of the target in the case of multiple targets.

The Matrix Pencil Method was employed to extract pole information from the time-domain data presented in Figure 5b. However, since Figure 5b contains time-domain data for two targets that are coupled with each other, directly applying this method results in disordered pole information, preventing accurate extraction of pole information corresponding to each target; just as in Figure 7, the blue data are from the pole extracted from the time-domain echoes of multiple targets, and the others are the poles in Figure 6. Therefore, it is necessary to segment the data of Figure 5b before applying the Matrix Pencil Method.

Now, the length of the time window is set to 60 times the sampling interval, the moving step size of the time window is set to the time-domain sampling interval, the beginning time of each time window is taken as the time index, and the Short-Time Matrix Pencil Method is used to extract the pole information. The obtained multiple sets of pole data and residual data are connected with the time index to construct time/frequency space.

Figure 8a is the time/frequency space formed by the virtual component of the poles (representing the natural resonance) and the time index. In this figure, the X-axis is the frequency, and the Y-axis is the time index. The blue line in the figure represents the time-domain waveform. Here, only its shape is shown, without any practical significance. The vertical coordinate of each red circles in the graph represents the beginning of the time window, and the horizontal coordinate represents the imaginary part of the pole extracted on that time window. The figure can be segmented into four distinct regions. The first region corresponding to the time index of the window ranging from 0 ns to 6 ns corresponds to the time-domain response of the initial target. Initially, the imaginary part of the poles exhibits convergence, which subsequently transitions to divergence as the time index progresses. Additionally, the imaginary components of certain higher-order poles vanish as the time index increases. This phenomenon occurs due to the significant attenuation of higher-order poles, leading to their instability and eventual exclusion from the analysis owing to their minimal contribution. In the second region, the time index ranges from 6 ns to 8 ns, and the time window includes the previous peak (except for the highest peaks) part of the second time-domain fluctuation and part of the time-domain flatness. The imaginary part of the pole of the first object begins to converge again because of the coupling phenomenon between the two targets, resulting in the re-emergence of the late-time response of the first target. In the third one, the time index ranges from 8 ns to 13 ns, and the time window includes part of the time-domain flatness, the previous peak part of the second time-domain fluctuation, and the highest peak part of the second target. Although the pole converges, it does not converge to the theoretical pole because the time window includes all the peak of the second time-domain fluctuation. It was previously speculated that the previous peak was caused by the first object and after the highest peak was caused by the second object; that is, the time-domain waveforms of both objects were included simultaneously, which led to the pole not converging to the theoretical pole. After 13 ns, corresponding to the fourth one, only the time-domain response of the second object is included, and the pole converges to the vertical line again, but it was a short period of time which was shorter than the first one, and therefore, in order to extract the pole information of the second target, the choice of time window is very demanding. By using this time/frequency spatial information and the time-domain waveform, we can know that region 1 and region 4 correspond to the pole information of the two spherical targets. In these two regions, the imaginary parts of the poles converge to the constant values in a long period of time, and the constant value is approximately the imaginary part of the pole of the corresponding targets, as shown in Figure 6. In order to more clearly describe the pole data of the two targets extracted from the figure, Figure 8a is divided into two parts, (b) and (c).

Figure 8b is the first region in Figure 8a, where the information extracted from the first region is the virtual part of information of the pole of the first target, and the vertical line in the figure is the virtual part information of the pole of the 0.075 m sphere mentioned in Figure 9 and Table 1. It can be seen that the virtual part information of the first four poles can be extracted on multiple time windows, while the other poles diverge quickly. The reasons are indicated in the previous description, while Figure 8c is the fourth region, corresponding the second target’s information. Here, we chose the first four poles of these two spheres as the main poles to verify the simulation results, and a high degree of consistency was achieved in both figures.

Figure 9a illustrates the relationship between the pole residual values and the time index. In this figure, the X-axis is the time index, and the Y-axis is the logarithm of the residual amplitude. The blue line in the figure represents the time-domain waveform. Here, only its shape is shown, without any practical significance. The horizontal coordinate of each circle in the figure represents the starting point of the time window, and the vertical coordinate represents the logarithm value of the amplitude of the residue of the poles extracted on the time window. In order to better describe the convergence trend, circles with different colors represent different poles. Based on the aforementioned analytical approach, the data are segmented into four segments, with particular attention given to the first and last segments. Figure 9b shows the information of the initial segment corresponds to a conducting sphere with a radius of 0.075 m, while Figure 9c shows the final segment pertains to a conducting sphere with a radius of 0.05 m. In each graph, there are four lines whose slopes are the real parts of the poles of the corresponding sphere. The data shown in each figure indicate a satisfactory fitting performance.

In short, in the two time/frequency spaces, the information of the first four poles of the corresponding sphere can be obtained more accurately through the four straight lines formed in region 1 and region 4.

The Prony method requires prior knowledge of the number of poles. For the situation expanding to the multi-target scenario, according to the simulation results shown in Figure 8, the number of poles obtained for different time windows is not necessarily the same, thereby significantly increasing the computational complexity. Additionally, noise embedded in the signal may generate spurious poles, further degrading the Prony method’s performance in real-world applications. As demonstrated in Figure 10, a comparative study was conducted to extract the poles of the second sphere in Figure 4.

With input pole count equal to five (Figure 10), comparison with the STMPM results (

Table 2. The poles of second sphere with different method $(10^9{\mathrm{s}}^{-1},\mathrm{G}\mathrm{H}\mathrm{z})$.

Poles	STMPM	Prony (M = 5)	Deviation
1st	(−3.01, 0.82)	(−3.14, 0.94)	0.3%
2nd	(−4.24, 1.73)	(−4.43, 1.95)	0.4%
3rd	(−5.05, 2.65)	(−4.70, 2.94)	0.6%
4th	(−5.52, 3.59)	(−4.43, 3.94)	2%

) reveals good consistency only for the first three poles (with a deviation lower than 1%).

We constructed a dual-target configuration comprising two identical rods (1 m length, 5 m separation) as a supplement. The frequency range was set from 4 MHz to 1.5 GHz, with 375 discrete frequency points. The other condition is the same as the model of the two spheres. Figure 11a presents the RCS curves, while Figure 11b displays the pole diagram of a single rod.

This study focuses exclusively on regions 1 and 4. Figure 12 illustrates the time/frequency space. Notably, all extracted poles show the same properties as the two spheres.

4. Discussion

This paper examines a scenario where there is a time signal which covers a group of targets’ responses, focusing on how to accurately extract the pole information of each target from the signals. Specifically, this study discusses the case of two spherical targets with differing radii. Spherical targets are highly symmetrical, yielding nearly uniform echo data across all directions and can be distinguished based on distance. Therefore, the scenario presented in this paper is relatively straightforward. However, if the two targets differ not in the range dimension, the time-domain signals containing the two targets will fully overlap, and the number of targets cannot be discerned from the time-domain signal. Figure 13 shows two spheres arranged in three distinct spatial configurations. Figure 13d presents RCS curves for both the three dual-sphere configurations and a single sphere. Notably, the RCS curve of configuration (a) exhibits striking morphological similarity to that of the single sphere, while the RCS curves of configurations (b) and (c) exhibit identical variation patterns. This implies that when two targets lack resolvable separation in the range dimension, this method fails.

Furthermore, in actual complex environments, group targets often consist of more intricate shapes whose echo data exhibit varying characteristics depending on direction. Further research is required to address the challenge of processing echo data containing multiple complex targets simultaneously in both distance and azimuth.

5. Conclusions

This paper examines the time-domain echo signals that contain responses from multiple targets and elucidates the limitations of the Matrix Pencil Method in extracting corresponding target pole information in such scenarios. Consequently, this study proposes a Short-Time Matrix Pencil Method which is capable of distinguishing between targets and extracting poles from time-domain echo signals with multiple targets. The proposed method’s efficacy in differentiating targets and extracting corresponding poles from time-domain echo signals containing two distinct targets has been validated through experimental simulations.