Next Article in Journal
Mapping and Analyzing Winter Wheat Yields in the Huang-Huai-Hai Plain: A Climate-Independent Perspective
Previous Article in Journal
Rapid Mapping of Rainfall-Induced Landslide Using Multi-Temporal Satellite Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 17
Issue 8
10.3390/rs17081408
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modeling Worldwide Tree Biodiversity Using Canopy Structure Metrics from Global Ecosystem Dynamics Investigation Data

by
Jin Xu
1,*,
Kjirsten Coleman
1,
Volker C. Radeloff
2,
Melissa Songer
1 and
Qiongyu Huang
1
1
Smithsonian Conservation Biology Institute, National Zoological Park, Front Royal, VA 22630, USA
2
Forest and Wildlife Ecology Department, University of Wisconsin-Madison, 1630 Linden Drive, Madison, WI 53706, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2025, 17(8), 1408; https://doi.org/10.3390/rs17081408
Submission received: 27 January 2025 / Revised: 26 March 2025 / Accepted: 9 April 2025 / Published: 16 April 2025
Browse Figures
Versions Notes

Abstract

:
Accurately quantifying global tree biodiversity is critical for enhancing forest ecosystem management and forest biodiversity conservation. With the launch of NASA’s Global Ecosystem Dynamics Investigation (GEDI), we evaluated the efficacy of space-borne lidar metrics in predicting tree species richness globally and explored whether integrating spectral vegetation metrics with space-borne lidar data could improve model performances. Using Forest Global Earth Observatory (ForestGEO) data, we developed three models using the random forest algorithm to predict global tree species richness across climate zones, including a dynamic habitat index (DHI)-only model, a GEDI-only model, and a combined GEDI-DHI model. We also developed four new canopy indices for our model and determined the optimal extent for aggregating GEDI metrics. Applying the optimal pixel size (5600 m), we found that the GEDI-only model predicted tree species richness across climate zones well (R2 = 0.55). One of our new GEDI metrics, representing canopy structure complexity, was among the top five most important features. The GEDI-DHI model performed similarly to the GEDI-only model using the ForestGEO dataset (R2 = 0.55). Our study provides an efficient and innovative method for using GEDI data to predict global tree species richness. However, the integration of GEDI metrics with DHIs did not significantly improve the model’s performance compared to the GEDI-only model. Considering the substantial variation in tree species richness across different climate zones, we recommend modeling tree species richness for each climate zone rather than using a global model. Additionally, incorporating open-source ground-measured tree species richness data can improve predictions and inform decision-making in forest conservation management.

1. Introduction

Forest ecosystems provide many essential goods and ecosystem services [1,2]. The biodiversity of tree species within forest systems affects productivity, ecosystem resilience, and function [3]. Higher biodiversity increases litter production, decomposition rates, and enhances resilience against extreme climate events, such as droughts or floods [4,5,6]. Moreover, habitat heterogeneity is considered a key characteristic in determining biodiversity patterns, which can be assessed using species richness [7]. Thus, tree species richness can be used as a good proxy for the overall biodiversity within forest ecosystems, especially at a global scale [3,8].
Analyses of field tree species richness datasets show that the global tree species richness pattern varies across latitude and continental regions [9,10]. The number of tree species increases with a decrease in absolute north or south distance from the equator [9], which is related to climate conditions. South America has the highest number of tree species, followed by Eurasia, Africa, and North America [10]. North America has fewer tree species than eastern Asia, and Europe has even fewer [9]. However, global biodiversity distribution is a dynamic process. The rate of species extinction and the loss of biological diversity continue at an unprecedented rate [11,12]. Therefore, assessing the spatial distribution of tree species richness is important to understanding the complexity of forest ecosystems and optimizing conservation planning and management at broad scales. However, ground-based forestry surveys of tree species richness are time-consuming, labor-intensive, and thus challenging to frequently conduct at a global scale [13].
Environmental heterogeneity, including the diversity of vegetation structure and spectral reflectance, is an effective proxy of species biodiversity [14,15]. Since spectral reflectance captures vegetation attributes associated with plant diversity, different plant species presumably display themselves differently in remotely sensed data, leading to higher spectral variability or diversity in a diverse plant community [16]. Vegetation’s vertical structure represents a critical heterogeneity, which fosters niche specialization [17,18]. Consequently, remote sensing can effectively complement or even provide an alternative to ground-based surveys for predicting tree species richness. In this study, we focused on exploring the capacity of forests’ and tree species’ unique spectral and structural characteristics to predict tree species richness [19,20]. A wide range of metrics have been derived from passive and active remote sensing data sources for this purpose. For example, the normalized difference vegetation index (NDVI), the most popular spectral metric from passive remote sensing data sources [21], has demonstrated the ability to predict tropical tree species richness using moderate-resolution imaging spectroradiometer (MODIS) data in New Caledonia (R2 = 0.46 [22]), and to predict temperate tree species richness using Landsat data in the Gönen dam watershed area of Turkey (R2 = 0.36 [23]). Active remote sensing data, especially three-dimensional forest structure information extracted from light detection and ranging (lidar) instruments, have been used for modeling tree species richness [3]. Previous studies have indicated that canopy height is a key driver for determining tree species richness [14]. Canopy structural complexity derived from terrestrial lidar data correlates positively with vegetation biodiversity, with R2 ranging from 0.14 to 0.72 [24].
The metrics derived from passive remote sensing data are based on surface reflectance, whereas metrics from active remote sensing can measure vertical structures [25]. Furthermore, the saturation issues of some optical vegetation indices (VIs) tend to capture less spatial heterogeneity in areas with high tree species richness levels [26]. Therefore, integrating different data sources of spectral and structural information can potentially improve the prediction of tree species richness [27]. For example, a previous study showed that the integration of NDVI with lidar and synthetic aperture radar (SAR)-based woody canopy cover models improves model performance compared to NDVI-only models [28]. However, tree species predictions are typically limited to small areas, and there is a need for global predictions of tree species richness [29,30]. The deficiency in such global assessments is due to a lack of lidar data with global coverage to detect canopy structures.
The launch of NASA’s Global Ecosystem Dynamics Investigation (GEDI) in December 2018 provided new possibilities for exploring tree species richness at a global scale. GEDI is a full-waveform lidar system and the first space-borne sensor specifically designed to measure vegetation [31]. The mission aimed to sample approximately 4% of Earth’s land surface, spanning latitudes between 51.6°N and S, over its initial two-year operational phase (2019–2020). The mission has since extended its data collection operations through 2021 and 2022, and there exists the possibility for GEDI to continue data acquisition until 2030. It has provided over 10 billion cloud-free shots and high-quality measurements of vertical forest structure in temperate and tropical forests with 25 m diameter footprints [31]. Among the different GEDI products, the GEDI L2B products derived from L1 provide canopy cover and vertical profile metrics, capturing the global vertical canopy structure [32]. To date, few studies have applied GEDI data to predict tree species richness. A simulated GEDI-TanDEM-X fusion height product was used for mapping the tree species richness of tropical forests in Gabon (R2 = 0.44; [33]). Additionally, the total plant area index (PAI) and vertical canopy profile from simulated GEDI data using discrete return airborne lidar and Land Vegetation and Ice Sensor (LVIS) data were linked to tree species richness across Central Africa. In South America, R2 ranged from 0.44 to 0.56, and 39% of the variation in pan-tropical tree species richness across four continents was explained [34]. A successive study predicted tree species richness in natural forests by integrating environmental variables and GEDI metrics, including canopy height, PAI, and ground elevation. They concluded that the selected GEDI metrics explained up to 66% of the variation in tree species richness in natural forests, though adding GEDI metrics to environmental variables did not enhance model performance [35]. However, the efficacy of other available GEDI structural metrics in predicting tree species richness has not been tested in different climate zones at the global scale. It is still uncertain whether integrating GEDI data with spectral vegetation metrics can enhance model performance for tree species richness estimation.
To address this gap, we propose a hypothesis that integrating spectral vegetation metrics with GEDI structural metrics will improve the predictive performance of tree species richness models. Accordingly, this study addresses the following three research questions: (1) What is the efficacy of space-borne lidar metrics in predicting global tree species richness? (2) What is the predictive capacity of the GEDI-based model for tree species richness in different climate zones? (3) To what extent does the integration of GEDI and spectral vegetation metrics improve a tree species richness model based on GEDI metrics alone?

2. Materials and Methods

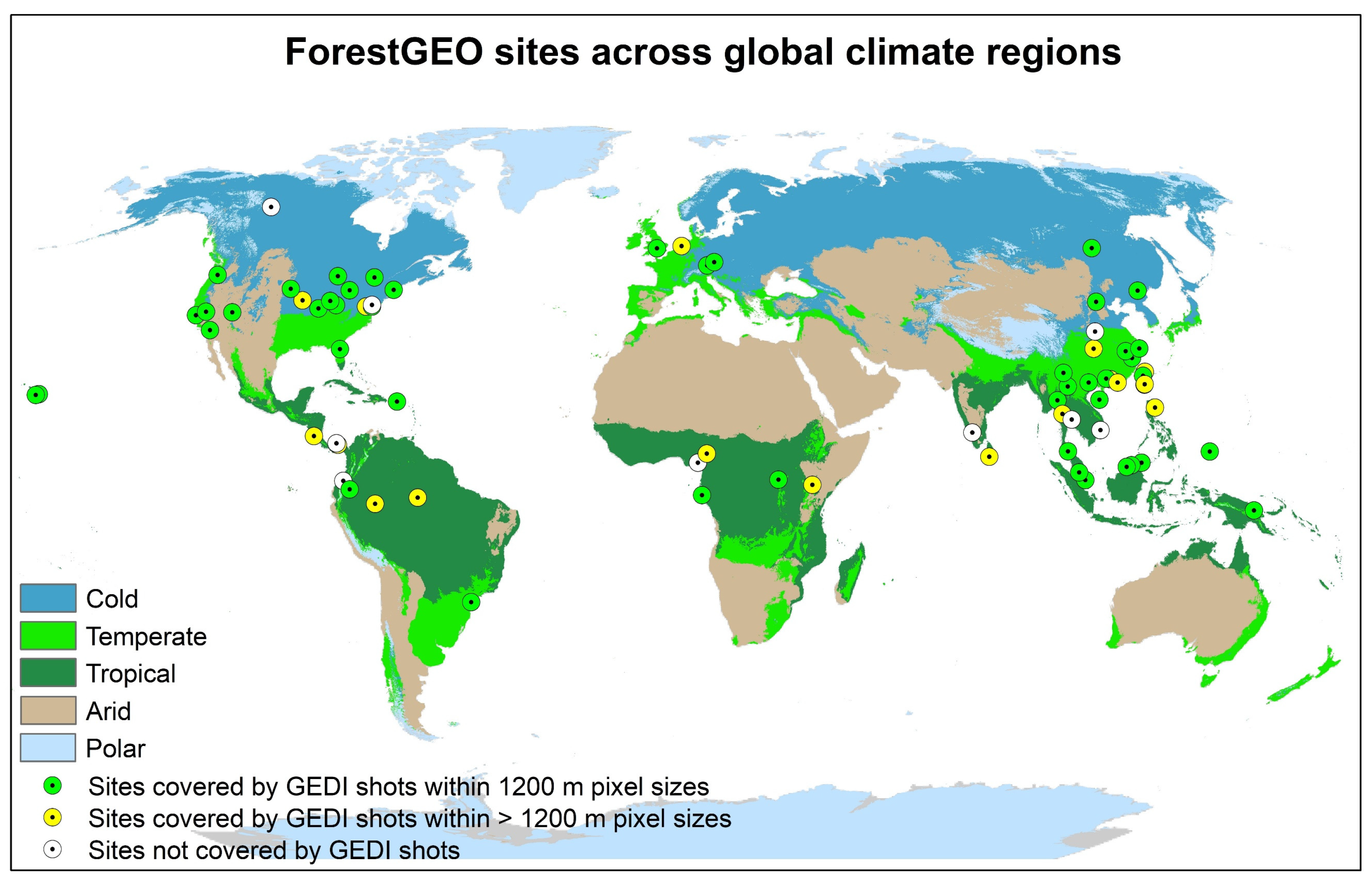
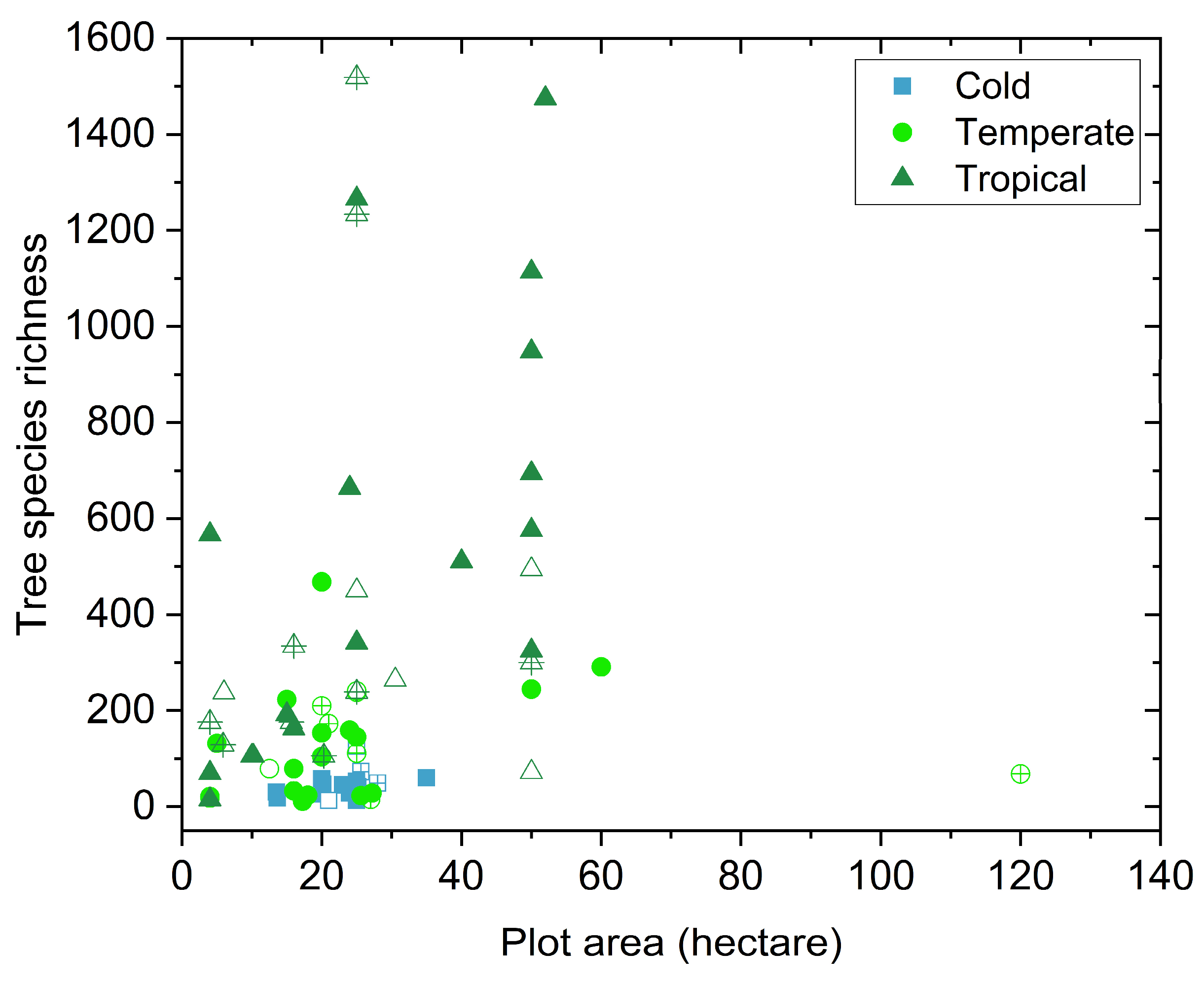
2.1. ForestGEO Data

The Forest Global Earth Observatory (ForestGEO) is a global network of scientists and long-term forest plots spread across major forests. The aim of the ForestGEO network is to understand and explore forest diversity and dynamics [36]. To date, ForestGEO has collected standardized data from 74 sites globally across three of the five Köppen-Geiger climate zones (https://www.gloh2o.org/koppen/; accessed on 1 January 2022; [37]) and 27 countries in the northern hemisphere or near the equator (Figure 1, Supplementary Materials). At each site, one forest plot is surveyed using a standard method where all woody stems with a diameter of 1 cm or greater at 1.3 m above the ground (known as diameter at breast height) are identified relative to their respective species [36]. However, plot sizes vary from 4 to 120 hectares across sites (Figure 2) and a single plot per site is often insufficient for detecting species–area relationships [33,38], which impedes the mapping of tree diversity. Accurate mapping of tree diversity requires the collection of extensive tree species richness across various scales. Moreover, failing to consider the plot size could introduce a bias, with larger plots likely to contain more species [39]. Before amassing sufficient field data across varying scales, it is essential to engage in the mapping of tree diversity. Therefore, similarly to the method used by Marselis, Keil, Chase, and Dubayah [35], we utilized the plot size as a variable in predicting tree species richness from the ForestGEO dataset.

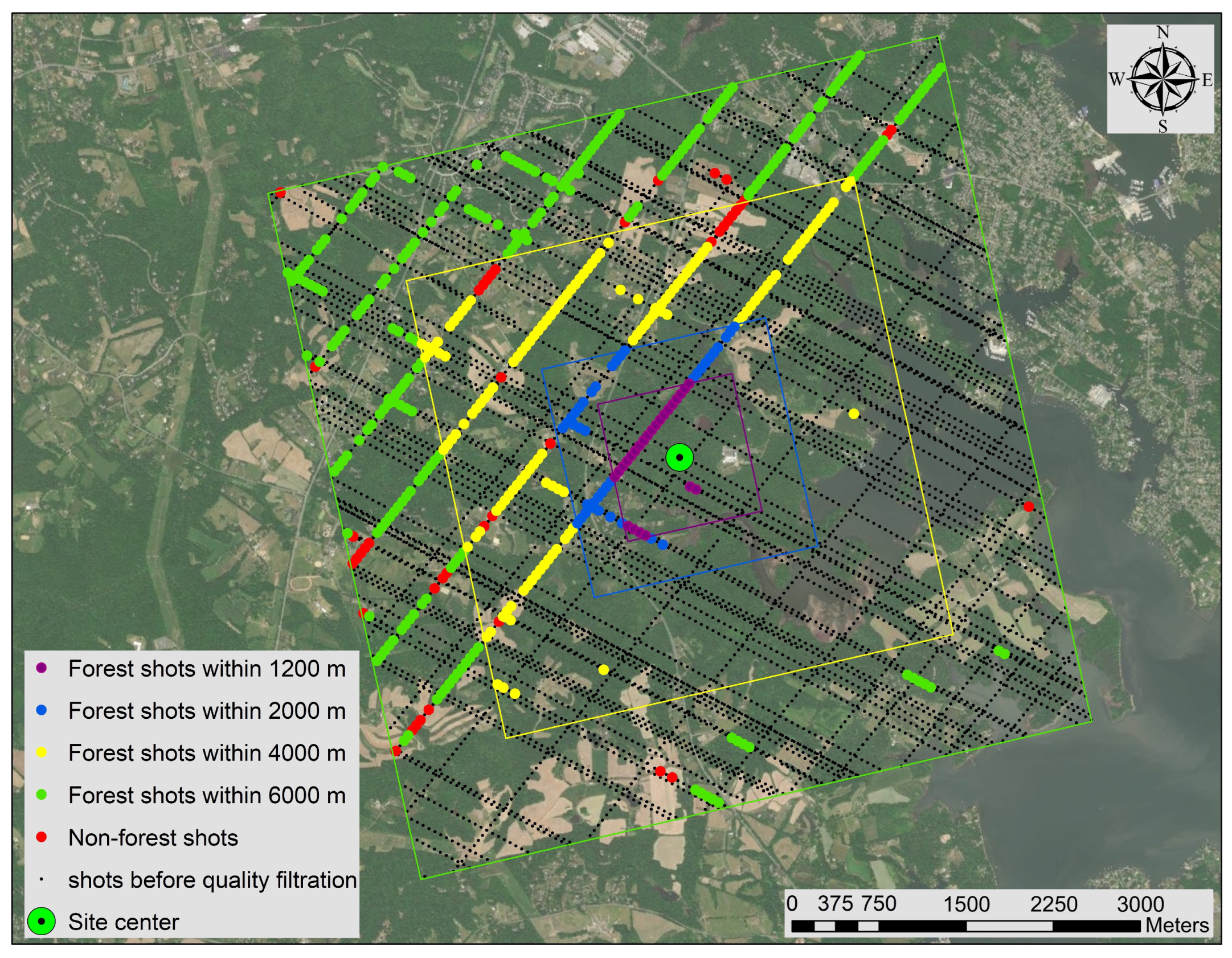
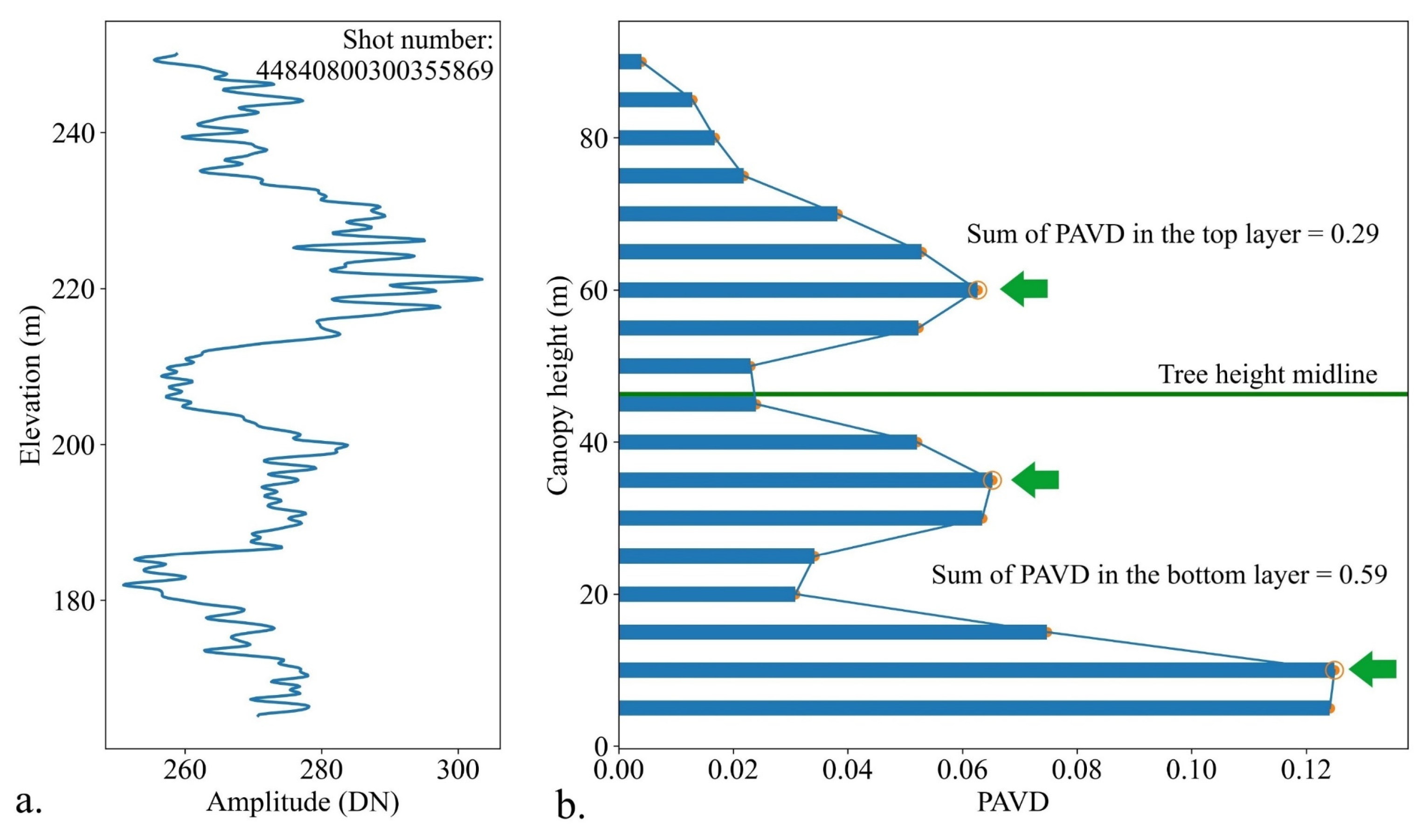
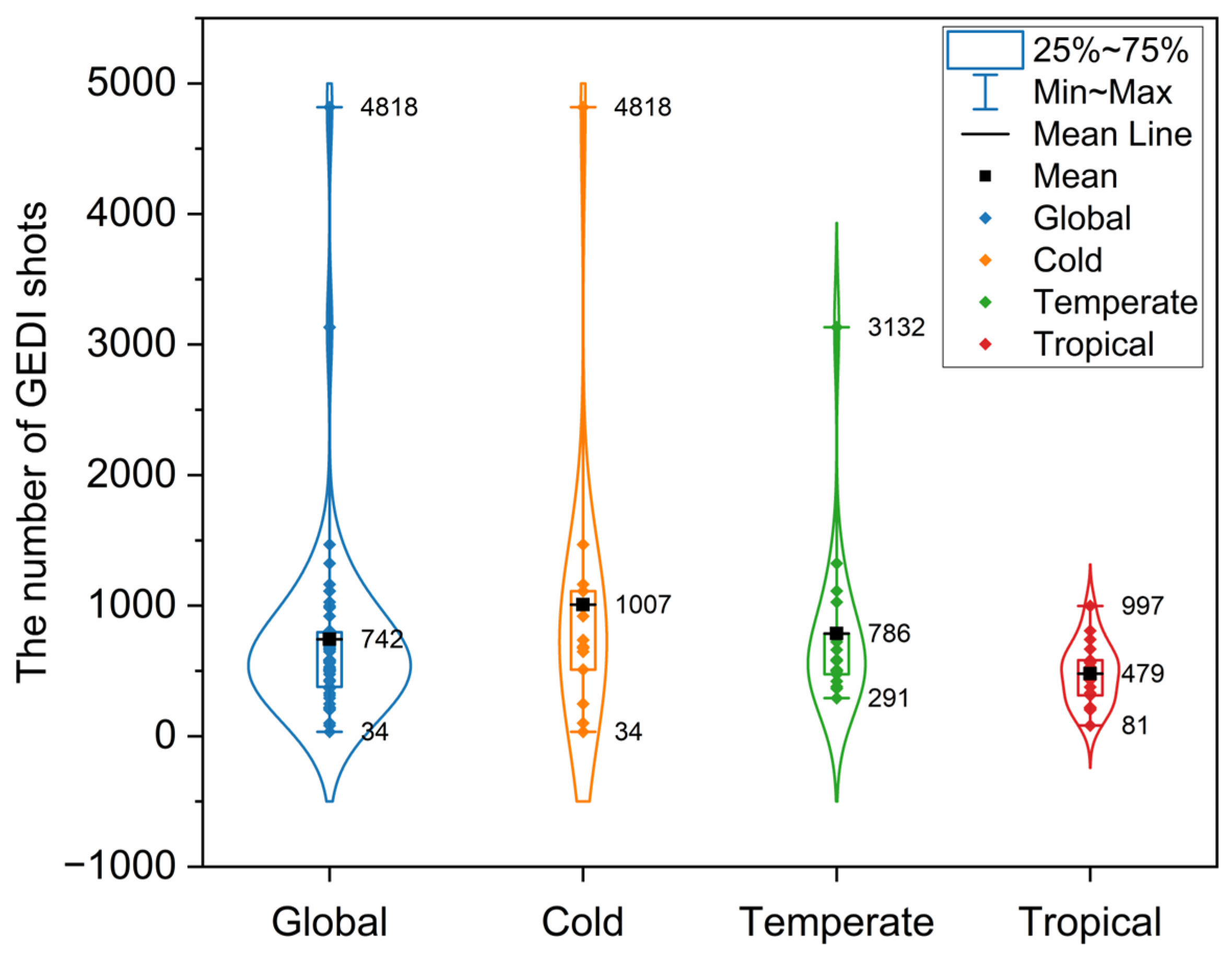
2.2. GEDI Data

Based on the distribution of the ForestGEO plots, we selected GEDI L2A and L2B products (Table 1) collected during the growing season of May to September in 2019, 2020, and 2021. We filtered for high-quality GEDI shots, excluding all shots flagged as “quality flag = 0”, “degrade flag > 1”, and “sensitivity > 0.95”, following the criteria set by Tang and Armston [32]. To ensure that the extracted GEDI shots corresponded to forested areas, we applied a mask using the 2019 forest cover product [40] from Copernicus, the European Union’s Earth Observation Program [41]. This product integrates spectral, temporal, and spatial data derived from a 100 m resolution time series captured by the instrument onboard the PROBA satellite [42].
We summarized GEDI shots within 19 pixel sizes (400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000, 2400, 2800, 3200, 3600, 4000, 4400, 4800, 5200, 5600, and 6000 m resolution) relative to each ForestGEO plot center. The pixel size could affect tree species richness models derived using GEDI data due to the trade-off of obtaining more GEDI shots within plots for more extensive areas but retaining less plot-specific information (Figure 3 [35]). Therefore, we aimed to identify the optimal spatial extent within which GEDI shots should be aggregated for modeling richness. We combined GEDI shots from 2019, 2020, and 2021, however not all ForestGEO sites have overlapping GEDI shots. Even for the largest pixel size, 6000 m, only 65 ForestGEO sites (cold: 15; temperate: 24; tropical: 26) had at least one GEDI shot across 19 pixel sizes (Figure 1 and Figure 4a). While the number of GEDI shots increased as the pixel size increased across climate zones (ordered by increasing latitude; Figure 4a), the number of ForestGEO sites overlapped by GEDI shots also increased as pixel sizes increased (Figure 4b).
In this study, we used one L2A metric, relative height (RH98), i.e., canopy height, and seven L2B metrics as model predictors: PAI, total canopy cover (cover), foliage height diversity (FHD), and four metrics derived from vertical cover, PAI, and plant area volume density (PAVD) profiles (Table 1). FHD, derived from foliage height, characterizes the vertical heterogeneity of the foliage profile [32]. We also derived four new canopy metrics to describe the shape of the vertical foliage distribution: the number of canopy layers and three vertical—PAVD, PAI, and cover—ratios [43]. We considered the number of canopy layers metric as an indicator of canopy vertical structural complexity. The metric was calculated by identifying the number of local maxima in the PAVD vertical profile, excluding the lowest strata (0–5 m) to eliminate the noise from the ground signal (Figure 5 [44]). The vertical PAVD ratio was calculated by dividing the vertical profile into the top and bottom layers using one-half of the top height (RH98) as the threshold value. We then computed the ratio as the sum of the PAVD values in the top layer to the sum of the PAVD values in the bottom layers. The ratio value indicates the vegetation volume difference between the overstory and the understory (Figure 5). The PAI and cover ratio calculation is identical to the PAVD ratio, except that the cumulative PAI and cover are converted to discrete PAI and cover values in vertical profiles, respectively.
We calculated the aggregated means and standard deviations for our GEDI L2A and L2B metrics within each pixel centered on each of the 65 ForestGEO plots. To facilitate the potential to generate a global tree species richness product with wall-to-wall coverage, we chose to use the square pixel aggregation method to model tree species richness. The number of available ForestGEO sites overlapping with GEDI shots shown in Figure 4b, the varying numbers of ForestGEO sites across different pixel sizes are expected to influence the model’s performance. To evaluate scale effects and mitigate the impact of the site count variation, we standardized the number of ForestGEO sites used in all models for pixel sizes ≥ 1200 m to match that of the 1200 m pixel size, i.e., N = 48 (cold: n = 14; temperate: n = 17; tropical: n = 17). Therefore, we have 15 pixel sizes for scale effect analysis. Specifically, we did not include more ForestGEO sites, although more sites overlapped with GEDI shots as pixel size increased. To assess data distribution and variability, we conducted statistical analyses and used violin plots to examine the tree species richness distribution across 48 available ForestGEO sites.

2.3. Spectral Vegetation Metrics

We incorporated three dynamic habitat index (DHI) metrics alongside GEDI structural metrics as they are closely related to the well-established ecological hypotheses of biodiversity. These metrics can effectively predict species richness and hold promise for applications in biodiversity science and conservation [45]. The DHI metrics were derived from MODIS NDVI products at a 1 km resolution (Table 1). These MODIS-based NDVI DHIs were a set of three composite indices summarizing three key vegetative productivity measurements: annual cumulative productivity, minimum productivity throughout the year, and the annual coefficient of variation in productivity [45]. We extracted one DHI-NDVI value at the center of each ForestGEO plot from the three composite DHI images.

2.4. Feature Selection

We calculated the correlation matrix using all 20 metrics for the 15 pixel sizes derived from the ForestGEO dataset to reduce model multicollinearity and eliminate redundant variables. The averaged Pearson correlation coefficient (r) across the 15 pixel sizes was utilized in the final correlation matrix [46]. For feature pairs with an absolute r value above 0.8, we removed the feature with the larger mean absolute r value [47,48].

2.5. Tree Species Richness Model Using the ForestGEO Dataset Across Spatial Scales

Random forest (RF) has been found to be robust for training models with small sample sizes. Therefore, all models were established using the RF algorithm [49,50]. RF models were implemented using the scikit-learn package, an open-source package in Python 3.10 [51]. Based on previous studies, we tuned three hyperparameters: n_estimators, max_depth, and max_features [52]. We assigned some hyperparameters specific discrete values (Table A1) and set other hyperparameters to default values. Discrete RF hyperparameter values were tuned on individual models for each pixel size and each climate zone. This tuning process led to a large number of iterations and was therefore computed on the high-performance computing cluster Hydra [53]. Optimized hyperparameters were determined by comparing the model’s predictive performance, which was evaluated by the pseudo-coefficient of determination (hereafter referred to as R2), root mean square error (RMSE), and normalized RMSE (NRMSE, a proportion of the overall range that the model resolves) from out-of-bag samples, which account for about 36.8% of all samples [54,55].
Based on the feature selection results, which identified 13 model predictors. We built three models to explore the efficacy of GEDI metrics for predicting tree richness (Table 2), all utilizing 15 pixel sizes. The first model assessed the efficacy of spectral vegetation metrics alone, while the second examined the efficacy of GEDI metrics alone and the third evaluated the efficacy of the integrated model using both GEDI and spectral metrics. These models will be referred to as the DHI-only, GEDI-only, and GEDI-DHI models, respectively. Although the spectral vegetation metrics were available for all ForestGEO plots, we retained a consistent number of samples across all pixel sizes in each of the three models to enable comparative performance analysis. The three models (i.e., DHI-only, GEDI-only, and GEDI-DHI models) were developed using the global ForestGEO dataset across various climate zones for each pixel size.
We optimized the universal hyperparameters for DHI-only, GEDI-only, and GEDI-DHI models (Figure 6; Table 2) by conducting a hyperparameter optimization process (Figure A1). The best-averaged model performance across 15 pixel sizes for each climate zone guided the determination of four sets of optimized local hyperparameters (all, cold, temperate, and tropical) for the DHI-only, GEDI-only, and GEDI-DHI models. Among these sets, the one that yielded the highest average model performance across climate zones was selected as the optimized universal hyperparameters for the DHI-only, GEDI-only, and GEDI-DHI models.
We also explored the effects of the pixel sizes on model performance based on the optimized universal hyperparameters of DHI-only, GEDI-only, and GEDI-DHI models. We calculated model performance across 15 pixel sizes for all three models to assess how different pixel sizes affect performance. Given the significant differences in the number of predictors between the DHI-only models and the GEDI-only and GEDI-DHI models, we averaged the performances of the GEDI-only and GEDI-DHI models across these pixel sizes. The pixel size corresponding to the highest mean model performance determined the optimal pixel size. Additionally, given that the number of GEDI shots increases with both pixel size and latitude across climate zones (Figure 4a), we determined whether the total number of GEDI shots across 15 pixel sizes indirectly drove model performance variations. Subsequently, using the optimal pixel size, we conducted statistical analyses and employed violin plots to examine the data distribution and variability of GEDI shots for 48 ForestGEO sites. Furthermore, we predicted tree species richness for these sites and compared the performance of DHI-only, GEDI-only, and GEDI-DHI models. To assess the relative importance of GEDI metrics, we calculated the feature importance of the GEDI-only model under the optimized universal hyperparameters at the optimal pixel size for each climate zone.

3. Results

3.1. Feature Correlation and Selection

The correlation matrix, averaged across 15 pixel sizes, indicated no feature pairs with an r value above 0.8 across three categories. However, within the GEDI metrics (Table 1), several pairs of FHDmean and RH98mean, PAImean and Covermean, PAVD_ratiomean and PAVD_ratiostd, PAI_ratiomean and Cover_ratiomean, and PAI_ratiostd and Cover_ratiostd had an r value larger than 0.8. Following the rule outlined in Section 2.4, RH98mean, PAImean, PAVD_ratiomean, Cover_ratiomean, and Cover_ratiostd were removed. In the spectral vegetation metrics category, only NDVIcum was retained (Table 1).

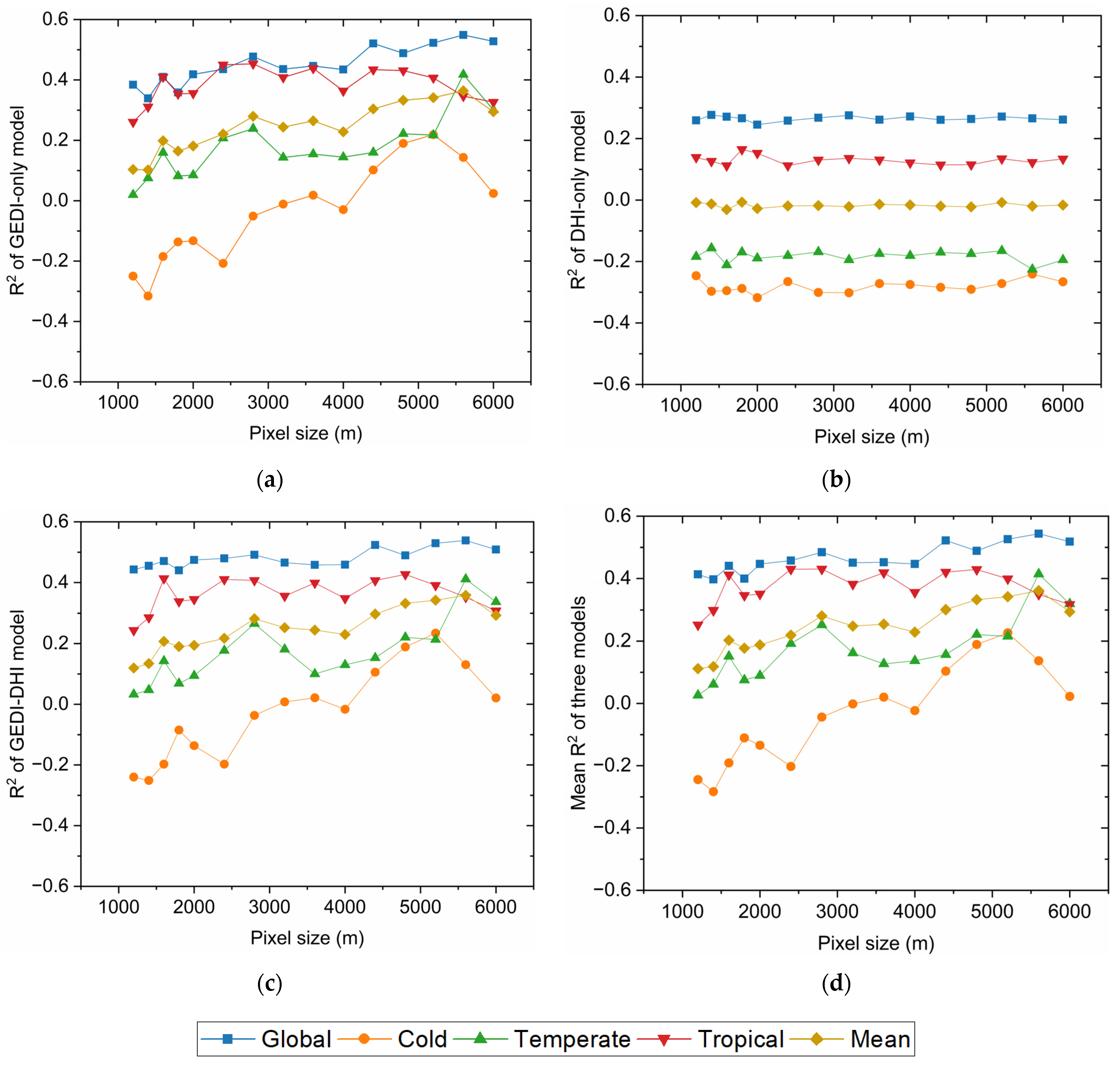
3.2. Optimized Universal Hyperparameter and Pixel Size Determination

The averaged model performance across 15 pixel sizes and climate zones determined the optimized universal hyperparameters for three models (Table 3). Using the optimized universal hyperparameters, we calculated the performance of the GEDI-only, DHI-only, and GEDI-DHI models, as well as the average performance of the GEDI-only and GEDI-DHI models across climate zones for each pixel size (Figure 7). The model built from the global ForestGEO dataset had the highest average model performance (R2 = 0.47; RMSE = 251.91) across 15 pixel sizes (Figure 7d), followed by the tropical zone (R2 = 0.37; RMSE = 341.25), the temperate zone (R2 = 0.17; RMSE = 109.58), and the cold zone (R2 = −0.04; RMSE = 14.75). It is important to note that the R2 value is negative for cold forests, indicating poor performance and less accurate predictions than those provided by simply using the mean of the observed values as the prediction [56].
Model performances vary across the 15 pixel sizes and climate zones (Figure 7d). Considering different climate zones, the optimal pixel sizes are determined as follows: 5200 m for cold regions (R2 = 0.23), 5600 m for temperate regions (R2 = 0.42), 4800 m for tropical regions (R2 = 0.43), and 5600 m for the global scale (R2 = 0.54). Given that the 5600 m pixel size yielded the best-averaged model performance for both the GEDI-only and GEDI-DHI models across the 15 pixel sizes, it has been identified as the optimal pixel size. Following this determination, a statistical analysis for the GEDI shots at the 5600 m pixel size indicated that the shot density within each plot was highly uneven. The number of GEDI shots in cold forests exhibited the largest range and mean, followed by those in temperate and tropical forests (Figure 8).

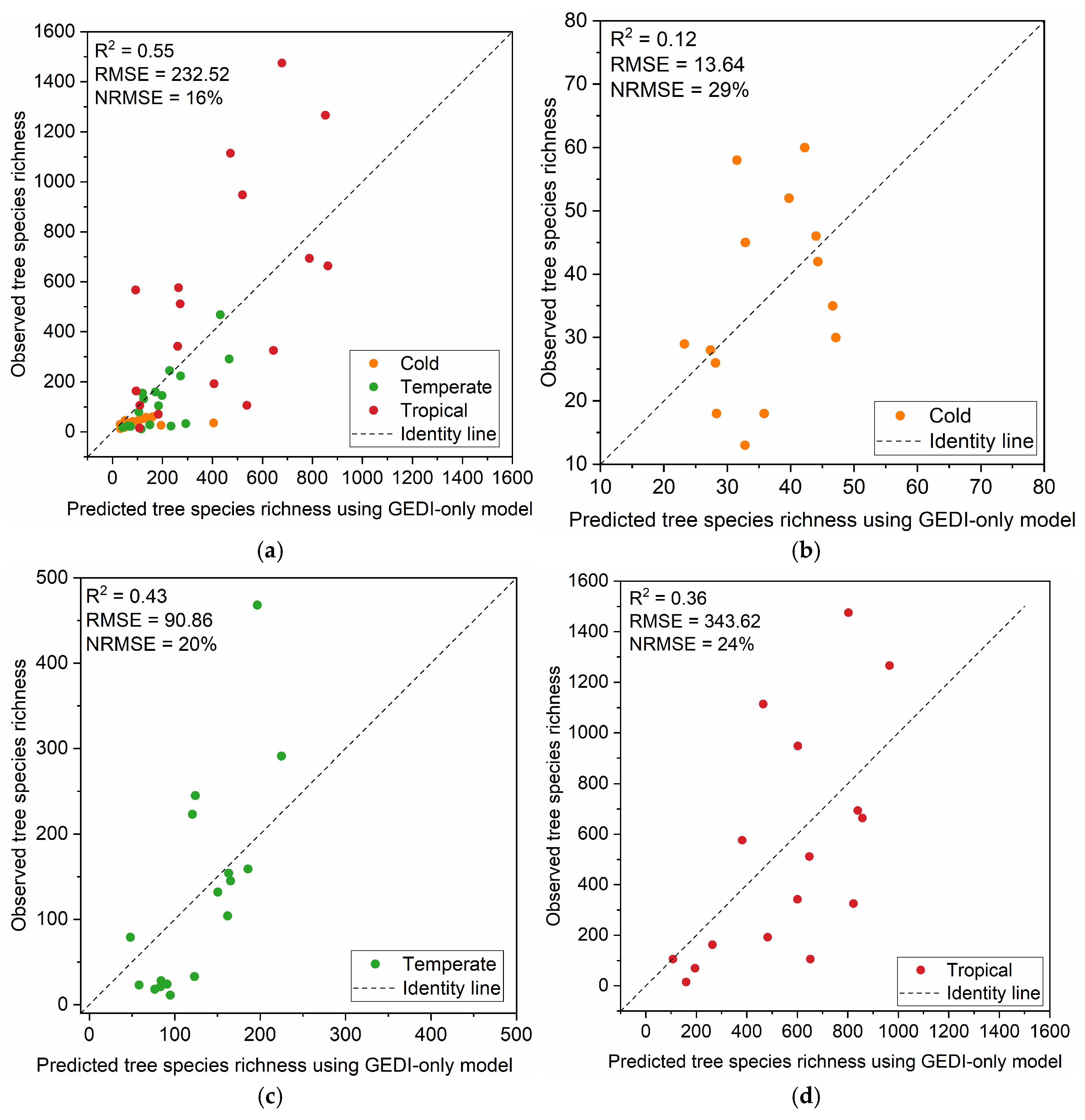
3.3. Model Performance and Comparison

Using the optimal pixel size (5600 m), the statistics for the tree species richness distribution of available ForestGEO sites showed a large variation among climate zones (Figure 9; global: n = 48; cold: n = 14; temperate: n = 17; tropical: n = 17). Tropical forests exhibited the highest tree species richness, followed by temperate forests and cold forests. Based on the optimized universal hyperparameters (Table 3), we compared the model performance of the GEDI-only and GEDI-DHI models across 48 ForestGEO plots in three climate zones (Table 4). Generally, the GEDI-DHI models performed similarly to the GEDI-only models, suggesting that the inclusion of DHI metrics did not significantly improve model performances in this study.
Since the global ForestGEO dataset included variations from all climate zones, the results demonstrated that the global dataset using the GEDI-only model performed well, achieving an R2 of 0.55. The GEDI-only model yielded R2 of 0.43 for temperate forest, 0.36 for tropical forests, and 0.12 for cold forests (Figure 10). Specifically, predictions for cold forests showed considerable deviations from the trendline (Figure 10b) and there were severe underestimations for tropical forests, particularly those with extremely high tree species richness (>800).
The feature importance analysis for the GEDI-only models in global forests revealed that the top five features, namely Coverstd (20%), Covermean (17%), N_layerstd (13%), and FHDstd (10%), and plot size (9%), contributed more to the models than other features combined (Figure 11). Among 12 features, Covermean notably influenced model performance across all climate zones, contributing over 10% in global, cold, temperate, and tropical forests. The N_layerstd metric, a new metric developed from the vertical strata of PAVD distribution, was the third largest contributor, accounting for 13% of tree species richness prediction in global forests and 10% in tropical forests. In temperate forests, PAI_ratiostd, Covermean, and PAIstd each contributed more than 10% to model performance. For tropical forests, the top contributors exceeding 10% were PAI_ratiomean, Coverstd, and N_layerstd, while in cold forests, FHDmean, Covermean, and FHDstd were the most important three features.

4. Discussion

4.1. Model Performance

Similar to previous studies [35,57], our findings demonstrate that the pixel sizes present a general forest structure instead of a plot-level forest structure. We observed that the pixel size could affect the relationship between structural metrics and ground-measured tree species richness. Therefore, identifying the optimal pixel size is an essential and challenging step for modeling tree species richness using GEDI and other space-borne lidar data with point sampling formats. The results suggest that the GEDI shot distribution within a pixel size affects the model performance for tree species richness prediction, a trend echoed in previous studies [58,59]. As the number of GEDI shots increases, model performance tended to reach a saturation level.
Model performance varies across the 15 pixel sizes and climate zones. GEDI data aggregated at the 5600m pixel size provided the best-averaged model performance and was thus considered the optimal pixel size in our study using the ForestGEO dataset. Based on the optimized universal hyperparameters and optimal pixel size selection, our global-scale models performed well within the range of predictions. Models built from the ForestGEO dataset demonstrated the efficacies of GEDI metrics. The model performance indicated that there were fairly strong over-predictions for low richness and underpredictions for high richness (Figure 10).
Regarding cold forests, models built from the ForestGEO dataset consistently performed worse than other climate zones but were similar to a previous study (R2 = 0.18; [60]). The number of tree species within a single plot at a 5600 m pixel size ranged from 13 to 60 for the ForestGEO dataset. Compared to the temperate and tropical climate zones, the narrower range of species richness in the cold climate zone may partly account for the model’s lower performance. The relationship between the observed and predicted tree species richness shows that the model prediction lacks variability when the tree species richness is near the extreme low and high ends of the distribution (Figure 10b), which could further contribute to the poor model performance in ForestGEO cold forests. Additionally, the limited number of available cold forest plots (n = 14) in the ForestGEO dataset may have limited the model’s ability to generalize.
For temperate forests, the model’s performance was generally better than that for cold and tropical forests. In previous studies, tree species richness was estimated with an NRMSE of 22% for sub-Mediterranean temperate forests [18] and an R2 of 0.5 for a Mediterranean Oak forest [61]. However, the ForestGEO dataset as a global network does contain one rare temperate forest site with an exceptionally high richness that was severely underestimated by our model (Figure 10c). This poor performance may be due to the lack of high-richness sampling in temperate forests for training models. Given that we only had one site with high tree species richness, more field surveys with high species richness within global temperate forests are needed. Expanding the ground-based dataset would be beneficial for exploring the cause of poor model performances and providing training data to improve model performance further.
Finally, for tropical forests, previous studies such as Madonsela, Cho, Ramoelo, Mutanga, and Naidoo [28] mapped tree species diversity in the savannah of South Africa (R2 = 0.33), and Pouteau, Gillespie, and Birnbaum [22] predicted tree species richness in New Caledonia (R2 = 0.46). Additionally, simulated GEDI metrics have also been used for mapping pan-tropical tree species richness with R2 = 0.39 [34]. Using the ForestGEO dataset, our study presented higher model performances than previous studies (R2 = 0.55), specifically with the optimal pixel size identified as 4800 m for tropical forests. However, the model for predicting tree species richness from ForestGEO data appeared to saturate beyond the 4800 m level in tropical forests, 5200 m in cold forests, and 5600 m in temperate and global forests. This suggests that at these pixel sizes, the model captures habitat heterogeneity the best, but beyond these pixel sizes, the quantification of habitats becomes less effective in characterizing species richness at the plot center within the ForestGEO plot size.
Meanwhile, the distribution of GEDI shots varying over ForestGEO (Figure 8, Supplementary Materials) resulted in different GEDI shot densities. By comparing the tree species richness prediction for each plot and the corresponding number of GEDI shots, we did not have enough evidence to demonstrate that more GEDI shots would lead to a high R2 and low RMSE. However, different GEDI shot densities may still cause different model performances across climate zones.
While the models built using the global ForestGEO dataset showed better performances than those for the individual climate zones, the predicted tree species richness for cold and temperate forests consistently overestimated forest richness. Considering the limited ground data range and the large variation in tree species richness among three climate zones (Figure 9), we suggest calibrating tree species richness models for each climate zone rather than one model using the global ForestGEO dataset.
As the availability of open-source ground-measured tree species data increases, there arises an opportunity to not only refine these models but also to drive innovation in ecological modeling is presented. Specifically, future models should incorporate machine learning algorithms that can dynamically adjust to the unique ecological characteristics of different regions, potentially enhancing the accuracy of global tree species richness predictions. This approach would enable more sophisticated handling of variations across climate zones and continents [9,10], and facilitate the integration of spatial autocorrelation effects, which are critical for understanding the complex patterns of tree diversity worldwide.

4.2. Data Source

Since GEDI is a relatively new data source, few previous studies have mapped tree species richness using GEDI metrics [31]. In addition, the DHI-NDVI data are also new spectral vegetation metrics produced for biodiversity modeling [45]. Unlike prior studies that integrated nine GEDI metrics with environment variables to predict tree species richness from forest plots in tropical and temperate regions around the globe [35], we developed a workflow to integrate 11 GEDI and spectral vegetation metrics, testing an expanded set of GEDI metrics. We demonstrated the efficacy of GEDI metrics and the integration of GEDI and DHI-NDVI for predicting tree species richness across climate zones at a global scale.
In terms of GEDI metric predictors, we used both the GEDI L2B products and four new metrics that we developed. Our feature importance analysis of the best-performing model reveals that the most significant predictors are the forest cover metrics, which alone account for approximately 37% of the predictive power among all variables. This finding suggests that incorporating forest cover metrics, derived from optical remote sensing data, may significantly enhance model performance. Metrics that describe the vertical forest structure are also vital. In particular, N_layerstd, the aggregated standard deviation of the number of canopy layers across available GEDI shots, which quantifies canopy structure complexity, was the third most influential feature. Consequently, metrics that capture both the horizontal and vertical canopy structure are vital for accurate predictions of tree species richness. A key contribution of our work is demonstrating the effectiveness of direct canopy structure measurements obtained from GEDI data in modeling tree species richness, highlighting the predominance of cover metrics in influencing these predictions.
Our study indicates that the GEDI-only and GEDI-DHI models yield similar results, suggesting that the inclusion of spectral metrics did not substantially enhance model performance. This may be attributed to the spatial resolution of the spectral data, which, at a pixel size of 5600 m, likely led to signal homogenization or saturation by averaging heterogeneous landscape features within each pixel.
Notably, with the exception of the cold climate zone, the optimal pixel sizes for all DHI-only models were below 2000 m. This discrepancy suggests that horizontal heterogeneity, as captured by spectral metrics, may reach a threshold of similarity or spatial autocorrelation beyond 2000 m, resulting in diminishing returns for predicting tree species richness. In contrast, vertical structural heterogeneity, as captured by GEDI, continues to contribute meaningful information at broader spatial scales. This implies the complexity of forest ecosystems and highlights the distinct roles that horizontal and vertical heterogeneities play in shaping our understanding of biodiversity patterns. Therefore, future work could incorporate additional high-resolution optical remote sensing data, such as metrics derived from Sentinel-2 and Landsat datasets, which have a similar spatial resolution as GEDI footprints, in enhancing model accuracy.
In terms of the field tree species richness, ForestGEO is a popularly used dataset for exploring long-term forest characteristics [36]. However, sampling strategies and plot sizes vary among sites. This makes it difficult to validate the model built from the ForestGEO dataset using other ground datasets. Furthermore, due to the limited number of field surveys measuring tree species richness, applying more GEDI metrics for predicting tree species richness around the globe is challenging. Therefore, the availability of globally standardized open-source ground-measured tree species richness data would allow for the validation of models with additional field data and produce more precise global tree species richness outputs in future efforts.

4.3. Future Work

GEDI is not a wall-to-wall product [31]. Therefore, the limited ground-measured plots that overlap with both GEDI data and tree species richness data have led to the underutilization of the ForestGEO dataset. Considering the optimal pixel size (5600 m), only 48 of the 74 ForestGEO plots had at least one GEDI shot. Therefore, with the increasing coverage of global GEDI data, there is potential to improve model performances. Meanwhile, with the increasing availability of GEDI data, expanding the field data range with normal distributions is critical for developing high-accuracy forest richness models.
In terms of the data source, the DHI-NDVI metric products from Landsat and Sentinel-2, with higher spatial resolutions, remain to be untested. These high spatial resolution datasets also support mapping tree species richness at a finer scale [62]. In addition, models that use higher spectral resolution, such as those from hyperspectral images with numerous narrow bands, could be used [63]. Finally, metrics derived from radio detection and ranging (radar) data could also be considered for predicting tree species richness [27].

5. Conclusions

This study demonstrated the use of GEDI data for predicting global tree species diversity. We developed a framework to optimize point sample space-borne lidar data and explored the efficacy of space-borne lidar metrics in predicting global tree species richness using the ForestGEO dataset. The results indicated that both GEDI-only and GEDI-DHI models using the ForestGEO dataset performed well in predicting tree species richness. However, the addition of DHI metrics in the GEDI-DHI model did not significantly enhance the prediction accuracy compared to the GEDI-only model. Our analysis revealed that climate zones play a critical role in modeling tree species richness, with model performance varying significantly across different zones. Specifically, the model utilizing the global ForestGEO dataset exhibited the highest average performance, followed by models for tropical and temperate zones, while the cold zone models showed the lowest performance. We also identified that the 5600 m pixel size is optimal for aggregating GEDI metrics in predicting tree species richness, suggesting its potential utility in future studies. Notably, among all GEDI metrics applied, the number of canopy layers (N_layerstd), a new metric developed in this study, played an important role. The method and findings presented in this paper provide a new avenue for incorporating additional metrics related to tree species richness across climate zones in future research and for informing forest conservation management.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/rs17081408/s1.

Author Contributions

Conceptualization, J.X., Q.H. and V.C.R.; methodology, J.X., Q.H. and V.C.R.; validation, J.X.; formal analysis, J.X.; investigation, J.X.; data curation, J.X.; writing—original draft preparation, J.X.; writing—review and editing, J.X., K.C., V.C.R., M.S. and Q.H.; visualization, J.X.; supervision, Q.H.; project administration, Q.H.; funding acquisition, Q.H. and V.C.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Aeronautics and Space Administration (NASA) Early Career Investigator Program in Earth Science (ECIP-ES; 80NSSC21K0936), the NASA Ecological Conservation Program (80NSSC23K1536), and the Life on a Sustainable Planet Pool Funds of Smithsonian Institution (000-2023-010024).

Data Availability Statement

This study’s field data are freely available online. The original ForestGEO data are downloaded from the website: https://forestgeo.si.edu/sites-all (accessed on 1 January 2022).

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Table A1. Hyperparameters and assigned values for RF models.
Table A1. Hyperparameters and assigned values for RF models.
ParameterDescriptionAssigned Values
n_estimatorsThe number of trees in the forest.10, 50, 100, 300, 500, 700, 900, 1100, 1300, 1500, 1700, 1900, 2100
max_depthThe maximum depth of the tree. If None, then split until nodes cannot expand further and until all leaves contain less than min_samples_split samples.2, 4, 6, 8, 10, 20, None
max_featuresThe number of features to consider when looking for the best split.“sqrt”, “log2”, “auto”
Remotesensing 17 01408 g0a1
Figure A1. Workflow for determining the universal and optimal hyperparameters for DHI-only, GEDI-only, and GEDI-DHI models. For each DHI-only, GEDI-only, and GEDI-DHI model, we averaged all model performances across 15 pixel sizes for modelGlobal, modelCold, modelTemperate, and modelTropical. The four hyper-combos (hyper-comboGlobal, hyper-comboCold, hyper-comboTemperate, and hyper-comboTropical) corresponding to the best-averaged model performances (RMSEbest_Global, RMSEbest_Cold, RMSEbest_Temperate, and RMSEbest_Tropical) informed the optimized local hyper-combos. Based on four optimized local hyper-combos, the hyper-combo providing the best-averaged model performance across modelGlobal, modelCold, modelTemperate, and modelTropical was the optimized universal hyperparameters.
Figure A1. Workflow for determining the universal and optimal hyperparameters for DHI-only, GEDI-only, and GEDI-DHI models. For each DHI-only, GEDI-only, and GEDI-DHI model, we averaged all model performances across 15 pixel sizes for modelGlobal, modelCold, modelTemperate, and modelTropical. The four hyper-combos (hyper-comboGlobal, hyper-comboCold, hyper-comboTemperate, and hyper-comboTropical) corresponding to the best-averaged model performances (RMSEbest_Global, RMSEbest_Cold, RMSEbest_Temperate, and RMSEbest_Tropical) informed the optimized local hyper-combos. Based on four optimized local hyper-combos, the hyper-combo providing the best-averaged model performance across modelGlobal, modelCold, modelTemperate, and modelTropical was the optimized universal hyperparameters.
Remotesensing 17 01408 g0a1

References

  1. Marín, A.I.; Abdul Malak, D.; Bastrup-Birk, A.; Chirici, G.; Barbati, A.; Kleeschulte, S. Mapping forest condition in Europe: Methodological developments in support to forest biodiversity assessments. Ecol. Indic. 2021, 128, 107839. [Google Scholar] [CrossRef]
  2. Taye, F.A.; Folkersen, M.V.; Fleming, C.M.; Buckwell, A.; Mackey, B.; Diwakar, K.C.; Le, D.; Hasan, S.; Ange, C.S. The economic values of global forest ecosystem services: A meta-analysis. Ecol. Econ. 2021, 189, 107145. [Google Scholar] [CrossRef]
  3. Wang, R.; Gamon, J.A. Remote sensing of terrestrial plant biodiversity. Remote Sens. Environ. 2019, 231, 111218. [Google Scholar] [CrossRef]
  4. Isbell, F.; Craven, D.; Connolly, J.; Loreau, M.; Schmid, B.; Beierkuhnlein, C.; Bezemer, T.M.; Bonin, C.; Bruelheide, H.; de Luca, E.; et al. Biodiversity increases the resistance of ecosystem productivity to climate extremes. Nature 2015, 526, 574–577. [Google Scholar] [CrossRef]
  5. Schnabel, F.; Liu, X.; Kunz, M.; Barry, K.E.; Bongers, F.J.; Bruelheide, H.; Fichtner, A.; Härdtle, W.; Li, S.; Pfaff, C.-T.; et al. Species richness stabilizes productivity via asynchrony and drought-tolerance diversity in a large-scale tree biodiversity experiment. Sci. Adv. 2021, 7, eabk1643. [Google Scholar] [CrossRef]
  6. Scherer-Lorenzen, M.; Luis Bonilla, J.; Potvin, C. Tree species richness affects litter production and decomposition rates in a tropical biodiversity experiment. Oikos 2007, 116, 2108–2124. [Google Scholar] [CrossRef]
  7. Tuanmu, M.N.; Jetz, W. A global, remote sensing-based characterization of terrestrial habitat heterogeneity for biodiversity and ecosystem modelling. Glob. Ecol. Biogeogr. 2015, 24, 1329–1339. [Google Scholar] [CrossRef]
  8. Gotelli, N.J.; Colwell, R.K. Quantifying biodiversity: Procedures and pitfalls in the measurement and comparison of species richness. Ecol. Lett. 2001, 4, 379–391. [Google Scholar] [CrossRef]
  9. Ricklefs, R.E.; He, F. Region effects influence local tree species diversity. Proc. Natl. Acad. Sci. USA 2016, 113, 674–679. [Google Scholar] [CrossRef]
  10. Cazzolla Gatti, R.; Reich, P.B.; Gamarra, J.G.; Crowther, T.; Hui, C.; Morera, A.; Bastin, J.-F.; De-Miguel, S.; Nabuurs, G.-J.; Svenning, J.-C. The number of tree species on Earth. Proc. Natl. Acad. Sci. USA 2022, 119, e2115329119. [Google Scholar] [CrossRef]
  11. Secretariat of the Convention on Biological Diversity. Global Biodiversity Outlook 5; Convention on Biological Diversity: Montreal, QC, Canada, 2020. [Google Scholar]
  12. Xu, H.; Cao, Y.; Yu, D.; Cao, M.; He, Y.; Gill, M.; Pereira, H.M. Ensuring effective implementation of the post-2020 global biodiversity targets. Nat. Ecol. Evol. 2021, 5, 411–418. [Google Scholar] [CrossRef]
  13. Steane, D.A.; Potts, B.M.; McLean, E.; Prober, S.M.; Stock, W.D.; Vaillancourt, R.E.; Byrne, M. Genome-wide scans detect adaptation to aridity in a widespread forest tree species. Mol. Ecol. 2014, 23, 2500–2513. [Google Scholar] [CrossRef]
  14. Meyer, L.; Diniz-Filho, J.A.F.; Lohmann, L.G.; Hortal, J.; Barreto, E.; Rangel, T.; Kissling, W.D. Canopy height explains species richness in the largest clade of Neotropical lianas. Glob. Ecol. Biogeogr. 2020, 29, 26–37. [Google Scholar] [CrossRef]
  15. Stein, A.; Gerstner, K.; Kreft, H. Environmental heterogeneity as a universal driver of species richness across taxa, biomes and spatial scales. Ecol. Lett. 2014, 17, 866–880. [Google Scholar] [CrossRef]
  16. Ollinger, S.V. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef]
  17. Bergen, K.; Goetz, S.; Dubayah, R.; Henebry, G.; Hunsaker, C.; Imhoff, M.; Nelson, R.; Parker, G.; Radeloff, V. Remote sensing of vegetation 3-D structure for biodiversity and habitat: Review and implications for lidar and radar spaceborne missions. J. Geophys. Res. Biogeosciences 2009, 114, G00E06. [Google Scholar] [CrossRef]
  18. Lopatin, J.; Dolos, K.; Hernández, H.; Galleguillos, M.; Fassnacht, F. Comparing generalized linear models and random forest to model vascular plant species richness using LiDAR data in a natural forest in central Chile. Remote Sens. Environ. 2016, 173, 200–210. [Google Scholar] [CrossRef]
  19. Hill, S.L.L.; Arnell, A.; Maney, C.; Butchart, S.H.M.; Hilton-Taylor, C.; Ciciarelli, C.; Davis, C.; Dinerstein, E.; Purvis, A.; Burgess, N.D. Measuring Forest Biodiversity Status and Changes Globally. Front. For. Glob. Change 2019, 2, 70. [Google Scholar] [CrossRef]
  20. Schiefer, F.; Kattenborn, T.; Frick, A.; Frey, J.; Schall, P.; Koch, B.; Schmidtlein, S. Mapping forest tree species in high resolution UAV-based RGB-imagery by means of convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2020, 170, 205–215. [Google Scholar] [CrossRef]
  21. Huang, S.; Tang, L.; Hupy, J.P.; Wang, Y.; Shao, G. A commentary review on the use of normalized difference vegetation index (NDVI) in the era of popular remote sensing. J. For. Res. 2021, 32, 1–6. [Google Scholar] [CrossRef]
  22. Pouteau, R.; Gillespie, T.W.; Birnbaum, P. Predicting Tropical Tree Species Richness from Normalized Difference Vegetation Index Time Series: The Devil Is Perhaps Not in the Detail. Remote Sens. 2018, 10, 698. [Google Scholar] [CrossRef]
  23. Arekhi, M.; Yılmaz, O.Y.; Yılmaz, H.; Akyüz, Y.F. Can tree species diversity be assessed with Landsat data in a temperate forest? Environ. Monit. Assess. 2017, 189, 586. [Google Scholar] [CrossRef]
  24. Walter, J.A.; Stovall, A.E.L.; Atkins, J.W. Vegetation structural complexity and biodiversity in the Great Smoky Mountains. Ecosphere 2021, 12, e03390. [Google Scholar] [CrossRef]
  25. Vogeler, J.C.; Cohen, W.B. A review of the role of active remote sensing and data fusion for characterizing forest in wildlife habitat models. Rev. De Teledetección 2016, 45, 1–14. [Google Scholar] [CrossRef]
  26. Almeida, D.R.A.d.; Broadbent, E.N.; Ferreira, M.P.; Meli, P.; Zambrano, A.M.A.; Gorgens, E.B.; Resende, A.F.; de Almeida, C.T.; do Amaral, C.H.; Corte, A.P.D.; et al. Monitoring restored tropical forest diversity and structure through UAV-borne hyperspectral and lidar fusion. Remote Sens. Environ. 2021, 264, 112582. [Google Scholar] [CrossRef]
  27. Fagua, J.C.; Jantz, P.; Burns, P.; Massey, R.; Buitrago, J.Y.; Saatchi, S.; Hakkenberg, C.; Goetz, S.J. Mapping tree diversity in the tropical forest region of Chocó-Colombia. Environ. Res. Lett. 2021, 16, 054024. [Google Scholar] [CrossRef]
  28. Madonsela, S.; Cho, M.A.; Ramoelo, A.; Mutanga, O.; Naidoo, L. Estimating tree species diversity in the savannah using NDVI and woody canopy cover. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 106–115. [Google Scholar] [CrossRef]
  29. Schmidt-Traub, G. National climate and biodiversity strategies are hamstrung by a lack of maps. Nat. Ecol. Evol. 2021, 5, 1325–1327. [Google Scholar] [CrossRef]
  30. Keil, P.; Chase, J.M. Global patterns and drivers of tree diversity integrated across a continuum of spatial grains. Nat. Ecol. Evol. 2019, 3, 390–399. [Google Scholar] [CrossRef]
  31. Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
  32. Tang, H.; Armston, J. Algorithm Theoretical Basis Document (ATBD) for GEDI L2B Footprint Canopy Cover and Vertical Profile Metrics; Goddard Space Flight Center: Greenbelt, MD, USA, 2019. [Google Scholar]
  33. Marselis, S.M.; Tang, H.; Armston, J.; Abernethy, K.; Alonso, A.; Barbier, N.; Bissiengou, P.; Jeffery, K.; Kenfack, D.; Labrière, N.; et al. Exploring the relation between remotely sensed vertical canopy structure and tree species diversity in Gabon. Environ. Res. Lett. 2019, 14, 094013. [Google Scholar] [CrossRef]
  34. Marselis, S.M.; Abernethy, K.; Alonso, A.; Armston, J.; Baker, T.R.; Bastin, J.-F.; Bogaert, J.; Boyd, D.S.; Boeckx, P.; Burslem, D.F.R.P.; et al. Evaluating the potential of full-waveform lidar for mapping pan-tropical tree species richness. Glob. Ecol. Biogeogr. 2020, 29, 1799–1816. [Google Scholar] [CrossRef]
  35. Marselis, S.M.; Keil, P.; Chase, J.M.; Dubayah, R. The use of GEDI canopy structure for explaining variation in tree species richness in natural forests. Environ. Res. Lett. 2022, 17, 045003. [Google Scholar] [CrossRef]
  36. Davies, S.J.; Abiem, I.; Abu Salim, K.; Aguilar, S.; Allen, D.; Alonso, A.; Anderson-Teixeira, K.; Andrade, A.; Arellano, G.; Ashton, P.S.; et al. ForestGEO: Understanding forest diversity and dynamics through a global observatory network. Biol. Conserv. 2021, 253, 108907. [Google Scholar] [CrossRef]
  37. Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
  38. Jantz, S.M.; Barker, B.; Brooks, T.M.; Chini, L.P.; Huang, Q.; Moore, R.M.; Noel, J.; Hurtt, G.C. Future habitat loss and extinctions driven by land-use change in biodiversity hotspots under four scenarios of climate-change mitigation. Conserv. Biol. 2015, 29, 1122–1131. [Google Scholar] [CrossRef]
  39. Lomolino, M.V. The species-area relationship: New challenges for an old pattern. Prog. Phys. Geogr. Earth Environ. 2001, 25, 1–21. [Google Scholar] [CrossRef]
  40. Buchhorn, M.; Smets, B.; Bertels, L.; De Roo, B.; Lesiv, M.; Tsendbazar, N.E.; Tarko, A.J. Copernicus Global Land Service: Land Cover 100m: Version 3 Globe 2015-2019: Product User Manual (Dataset v3.0, doc issue 3.4). Zenodo. [CrossRef]
  41. Jutz, S.; Milagro-Pérez, M. Copernicus: The European Earth Observation programme. Rev. De Teledetección 2020, 56, V–XI. [Google Scholar] [CrossRef]
  42. Buchhorn, M.; Lesiv, M.; Tsendbazar, N.-E.; Herold, M.; Bertels, L.; Smets, B. Copernicus Global Land Cover Layers—Collection 2. Remote Sens. 2020, 12, 1044. [Google Scholar] [CrossRef]
  43. Xu, J.; Farwell, L.; Radeloff, V.C.; Luther, D.; Songer, M.; Cooper, W.J.; Huang, Q. Avian diversity across guilds in North America versus vegetation structure as measured by the Global Ecosystem Dynamics Investigation (GEDI). Remote Sens. Environ. 2024, 315, 114446. [Google Scholar] [CrossRef]
  44. Whitehurst, A.S.; Swatantran, A.; Blair, J.B.; Hofton, M.A.; Dubayah, R. Characterization of Canopy Layering in Forested Ecosystems Using Full Waveform Lidar. Remote Sens. 2013, 5, 2014–2036. [Google Scholar] [CrossRef]
  45. Radeloff, V.C.; Dubinin, M.; Coops, N.C.; Allen, A.M.; Brooks, T.M.; Clayton, M.K.; Costa, G.C.; Graham, C.H.; Helmers, D.P.; Ives, A.R.; et al. The Dynamic Habitat Indices (DHIs) from MODIS and global biodiversity. Remote Sens. Environ. 2019, 222, 204–214. [Google Scholar] [CrossRef]
  46. Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
  47. Schulz, D.; Yin, H.; Tischbein, B.; Verleysdonk, S.; Adamou, R.; Kumar, N. Land use mapping using Sentinel-1 and Sentinel-2 time series in a heterogeneous landscape in Niger, Sahel. ISPRS J. Photogramm. Remote Sens. 2021, 178, 97–111. [Google Scholar] [CrossRef]
  48. Jin, Z.; Azzari, G.; You, C.; Di Tommaso, S.; Aston, S.; Burke, M.; Lobell, D.B. Smallholder maize area and yield mapping at national scales with Google Earth Engine. Remote Sens. Environ. 2019, 228, 115–128. [Google Scholar] [CrossRef]
  49. Segal, M.R. Machine Learning Benchmarks and Random Forest Regression; UCSF Center for Bioinformatics and Molecular Biostatistics: San Francisco, CA, USA, 2004. [Google Scholar]
  50. Qi, Y. Random forest for bioinformatics. In Ensemble Machine Learning; Springer: Berlin/Heidelberg, Germany, 2012; pp. 307–323. [Google Scholar]
  51. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  52. Xu, J.; Quackenbush, L.J.; Volk, T.A.; Im, J. Estimation of shrub willow biophysical parameters across time and space from Sentinel-2 and unmanned aerial system (UAS) data. Field Crops Res. 2022, 287, 108655. [Google Scholar] [CrossRef]
  53. Smithsonian Institution. Smithsonian Institution High Performance Computing Cluster; Smithsonian Institution: Washington, DC, USA, 2020. [Google Scholar]
  54. Probst, P.; Wright, M.N.; Boulesteix, A.-L. Hyperparameters and tuning strategies for random forest. WIREs Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
  55. Chernick, M.R.; LaBudde, R.A. An Introduction to Bootstrap Methods with Applications to R; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
  56. Nakagawa, S.; Schielzeth, H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 2013, 4, 133–142. [Google Scholar] [CrossRef]
  57. Fricker, G.A.; Wolf, J.A.; Saatchi, S.S.; Gillespie, T.W. Predicting spatial variations of tree species richness in tropical forests from high-resolution remote sensing. Ecol. Appl. 2015, 25, 1776–1789. [Google Scholar] [CrossRef] [PubMed]
  58. Chu, H.-J.; Wang, C.-K.; Huang, M.-L.; Lee, C.-C.; Liu, C.-Y.; Lin, C.-C. Effect of point density and interpolation of LiDAR-derived high-resolution DEMs on landscape scarp identification. GIScience Remote Sens. 2014, 51, 731–747. [Google Scholar] [CrossRef]
  59. LaRue, E.A.; Fahey, R.; Fuson, T.L.; Foster, J.R.; Matthes, J.H.; Krause, K.; Hardiman, B.S. Evaluating the sensitivity of forest structural diversity characterization to LiDAR point density. Ecosphere 2022, 13, e4209. [Google Scholar] [CrossRef]
  60. Yeboah, D.; Chen, H.Y.; Kingston, S. Tree species richness decreases while species evenness increases with disturbance frequency in a natural boreal forest landscape. Ecol. Evol. 2016, 6, 842–850. [Google Scholar] [CrossRef]
  61. Simonson, W.D.; Allen, H.D.; Coomes, D.A. Use of an airborne lidar system to model plant species composition and diversity of Mediterranean oak forests. Conserv. Biol. 2012, 26, 840–850. [Google Scholar] [CrossRef]
  62. Reddy, C.S. Remote sensing of biodiversity: What to measure and monitor from space to species? Biodivers. Conserv. 2021, 30, 2617–2631. [Google Scholar] [CrossRef]
  63. Skidmore, A.K.; Coops, N.C.; Neinavaz, E.; Ali, A.; Schaepman, M.E.; Paganini, M.; Kissling, W.D.; Vihervaara, P.; Darvishzadeh, R.; Feilhauer, H. Priority list of biodiversity metrics to observe from space. Nat. Ecol. Evol. 2021, 5, 896–906. [Google Scholar] [CrossRef]
Remotesensing 17 01408 g001
Figure 1. Distribution map of the 74 ForestGEO sites across climate zones and global regions: Lighter green circles denote plots that have GEDI shots within 1200 m pixel sizes (N = 48; cold: n = 14; temperate: n = 17; tropical: n = 17). Yellow circles denote plots that have GEDI shots within >1200 m pixel sizes (N = 17; cold: n = 1; temperate: n = 7; tropical: n = 9), and white circles denote plots that do not have GEDI shots (N = 9; cold: n = 2; temperate: n = 2; tropical: n = 5).
Figure 1. Distribution map of the 74 ForestGEO sites across climate zones and global regions: Lighter green circles denote plots that have GEDI shots within 1200 m pixel sizes (N = 48; cold: n = 14; temperate: n = 17; tropical: n = 17). Yellow circles denote plots that have GEDI shots within >1200 m pixel sizes (N = 17; cold: n = 1; temperate: n = 7; tropical: n = 9), and white circles denote plots that do not have GEDI shots (N = 9; cold: n = 2; temperate: n = 2; tropical: n = 5).
Remotesensing 17 01408 g001
Remotesensing 17 01408 g002
Figure 2. ForestGEO Site Plot Area vs. the corresponding Number of Species: Filled shapes represent sites within 1200 m pixel sizes overlapped by GEDI shots; hollowed shapes with a cross indicate plots overlapped by GEDI shots within pixel sizes greater then 1200 m; hollowed shapes denote plots not overlapped by GEDI shots.
Figure 2. ForestGEO Site Plot Area vs. the corresponding Number of Species: Filled shapes represent sites within 1200 m pixel sizes overlapped by GEDI shots; hollowed shapes with a cross indicate plots overlapped by GEDI shots within pixel sizes greater then 1200 m; hollowed shapes denote plots not overlapped by GEDI shots.
Remotesensing 17 01408 g002
Remotesensing 17 01408 g003
Figure 3. Example ForestGEO plot (400 m × 400 m; as we lack the specific shape outline of all ForestGEO plots, only the plot size is provided) located at Smithsonian Environmental Research Center (Edgewater, MD) with 1200 m (purple), 2000 m (blue), 4000 m (yellow), and 6000 m (green) pixel sizes. GEDI shots have been filtered for quality and masked according to landcover type. Filtered GEDI shots are represented as points in the color corresponding to the associated pixel size.
Figure 3. Example ForestGEO plot (400 m × 400 m; as we lack the specific shape outline of all ForestGEO plots, only the plot size is provided) located at Smithsonian Environmental Research Center (Edgewater, MD) with 1200 m (purple), 2000 m (blue), 4000 m (yellow), and 6000 m (green) pixel sizes. GEDI shots have been filtered for quality and masked according to landcover type. Filtered GEDI shots are represented as points in the color corresponding to the associated pixel size.
Remotesensing 17 01408 g003
Remotesensing 17 01408 g004
Figure 4. (a) The minimum, maximum, and mean of the number of ForestGEO plots overlapped by GEDI shots across 19 pixel sizes and climate zones (different colors represent different climate zones), indicating that the global value represents the highest number of shots among the cold, temperate, and tropical zones. (b) The total number of ForestGEO plots overlapped by GEDI shots across 19 pixel sizes.
Figure 4. (a) The minimum, maximum, and mean of the number of ForestGEO plots overlapped by GEDI shots across 19 pixel sizes and climate zones (different colors represent different climate zones), indicating that the global value represents the highest number of shots among the cold, temperate, and tropical zones. (b) The total number of ForestGEO plots overlapped by GEDI shots across 19 pixel sizes.
Remotesensing 17 01408 g004
Remotesensing 17 01408 g005
Figure 5. An example from the plot located at the Smithsonian Environmental Research Center (Edgewater, MD) demonstrates the application of the number of canopy layers and plant area volume density (PAVD) ratio metrics. Using GEDI Level 1B full waveform data for a single shot (a) and the associated vertical profile of PAVD (b), we can identify four canopy layers from the PAVD vertical profile in this example, as indicated by three green arrows. It is important to note that the canopy height corresponds to RH98. A vertical PAVD ratio of 0.49 is calculated by dividing the sum of the PAVD value in the top layer (0.29) by the sum of the PAVD value in the bottom layer (0.59).
Figure 5. An example from the plot located at the Smithsonian Environmental Research Center (Edgewater, MD) demonstrates the application of the number of canopy layers and plant area volume density (PAVD) ratio metrics. Using GEDI Level 1B full waveform data for a single shot (a) and the associated vertical profile of PAVD (b), we can identify four canopy layers from the PAVD vertical profile in this example, as indicated by three green arrows. It is important to note that the canopy height corresponds to RH98. A vertical PAVD ratio of 0.49 is calculated by dividing the sum of the PAVD value in the top layer (0.29) by the sum of the PAVD value in the bottom layer (0.59).
Remotesensing 17 01408 g005
Remotesensing 17 01408 g006
Figure 6. The study workflow: A workflow demonstrating the analysis based on the ForestGEO dataset and GEDI metrics. The analyses included feature extraction and selection for model building, hyperparameter optimization, and the optimal pixel size selection.
Figure 6. The study workflow: A workflow demonstrating the analysis based on the ForestGEO dataset and GEDI metrics. The analyses included feature extraction and selection for model building, hyperparameter optimization, and the optimal pixel size selection.
Remotesensing 17 01408 g006
Remotesensing 17 01408 g007
Figure 7. Model performance of the following models is detailed: (a) DHI-only, (b) GEDI-only, and (c) GEDI-DHI models. Additionally, (d) presents the average model performance of the GEDI-only and GEDI-DHI models across each climate zone and pixel size, starting from 1200 m, based on optimized universal hyperparameters.
Figure 7. Model performance of the following models is detailed: (a) DHI-only, (b) GEDI-only, and (c) GEDI-DHI models. Additionally, (d) presents the average model performance of the GEDI-only and GEDI-DHI models across each climate zone and pixel size, starting from 1200 m, based on optimized universal hyperparameters.
Remotesensing 17 01408 g007
Remotesensing 17 01408 g008
Figure 8. Violin plot presenting probability density and the statistics of the number of GEDI shots of ForestGEO plots within a 5600 m pixel size across climate zones.
Figure 8. Violin plot presenting probability density and the statistics of the number of GEDI shots of ForestGEO plots within a 5600 m pixel size across climate zones.
Remotesensing 17 01408 g008
Remotesensing 17 01408 g009
Figure 9. Violin plot presenting probability density and the statistics of the observed species richness of ForestGEO plots across climate zones.
Figure 9. Violin plot presenting probability density and the statistics of the observed species richness of ForestGEO plots across climate zones.
Remotesensing 17 01408 g009
Remotesensing 17 01408 g010
Figure 10. The relationship between observed and predicted tree species richness from (a) global ForestGEO plots (n = 48), (b) cold climate zones (n = 14), (c) temperate climate zones (n = 17), and (d) tropical climate zones (n = 17) using the GEDI-only model.
Figure 10. The relationship between observed and predicted tree species richness from (a) global ForestGEO plots (n = 48), (b) cold climate zones (n = 14), (c) temperate climate zones (n = 17), and (d) tropical climate zones (n = 17) using the GEDI-only model.
Remotesensing 17 01408 g010
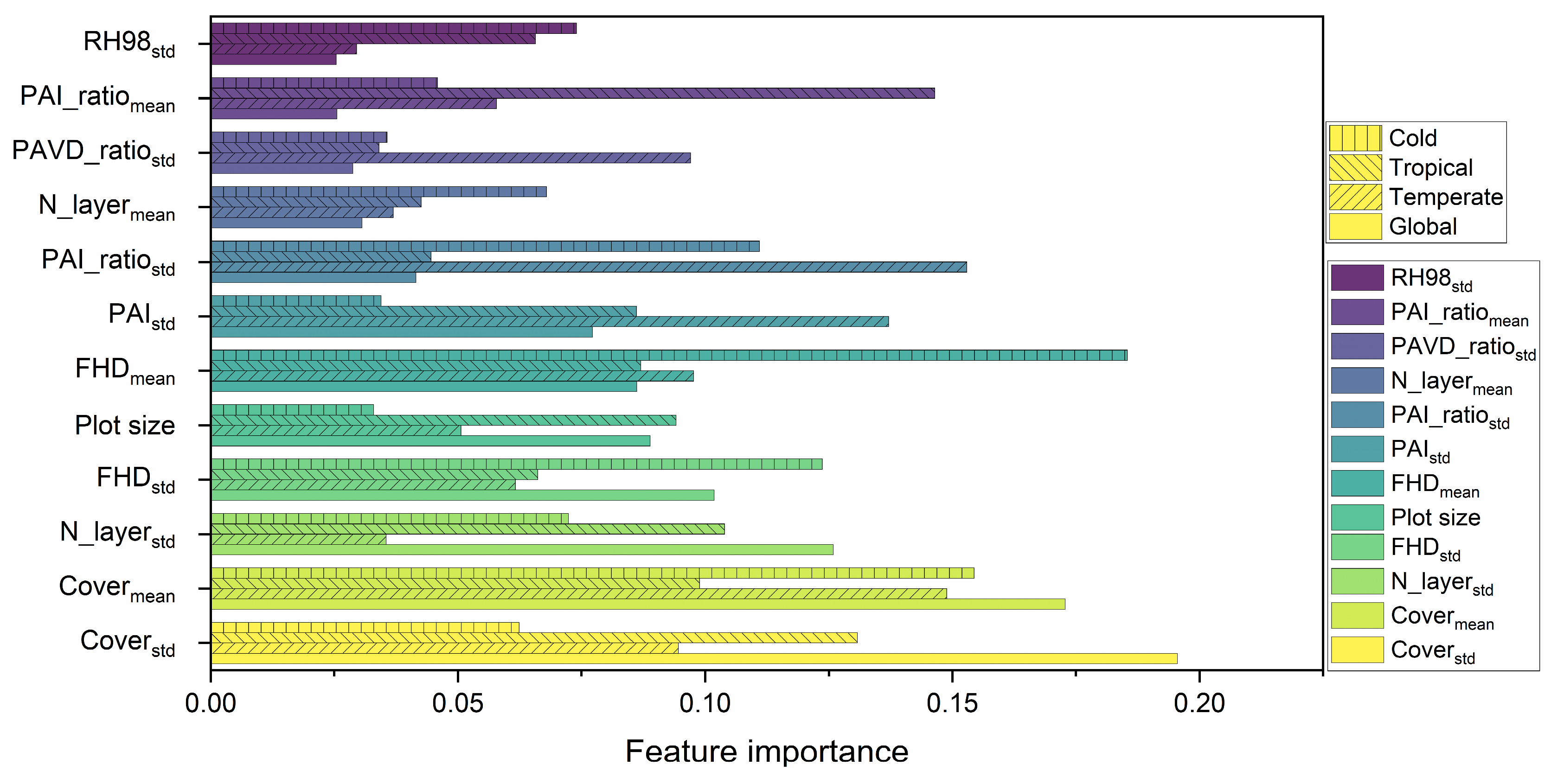
Remotesensing 17 01408 g011
Figure 11. Feature importance from the GEDI-only model across different climate zones and global forests. Metric names are defined as follows: the number of canopy layers (N_layer), relative height (RH98), plant area index (PAI), plant area volume density (PAVD), foliage height diversity (FHD), standard deviation (std).
Figure 11. Feature importance from the GEDI-only model across different climate zones and global forests. Metric names are defined as follows: the number of canopy layers (N_layer), relative height (RH98), plant area index (PAI), plant area volume density (PAVD), foliage height diversity (FHD), standard deviation (std).
Remotesensing 17 01408 g011
Table 1. List of metrics used in this study. In addition to the predictor of plot size, all metrics were divided into GEDI structural and spectral vegetation metric categories. The number of metrics within each category was also annotated in parentheses.
Table 1. List of metrics used in this study. In addition to the predictor of plot size, all metrics were divided into GEDI structural and spectral vegetation metric categories. The number of metrics within each category was also annotated in parentheses.
Metric CategoriesMetric Name *
Plot metrics (1)Plot Size (ha)
GEDI metrics (16)RH98mean, RH98std,
PAImean, PAIstd,
Covermean, Coverstd,
FHDmean, FHDstd,
N_layermean, N_layerstd,
PAVD_ratiomean, PAVD_ratiostd,
PAI_ratiomean, PAI_ratiostd,
Cover_ratiomean, Cover_ratiostd
Spectral vegetation metrics (3)DHIs-NDVIcum, DHIs-NDVImin, DHIs-NDVIvar
* Reference for metric names: standard deviation (std), relative height (RH98), plant area index (PAI), total canopy cover (cover), foliage height diversity (FHD), the number of canopy layers (N_layer), a vertical plant area volume density ratio (PAVD_ratio), a vertical PAI ratio (PAI_ratio), a vertical cover ratio (Cover_ratio), dynamic habitat indices (DHIs), normalized difference vegetation index (NDVI), cumulative (cum), minimum (min), and variation (var). The metrics in bold were retained after feature selection.
Table 2. Models for predicting tree species richness using the ForestGEO dataset. All metrics used in these models were derived based on feature selection results.
Table 2. Models for predicting tree species richness using the ForestGEO dataset. All metrics used in these models were derived based on feature selection results.
Response VariableModelsPredictors
ForestGEO tree species richnessDHI-onlyPlot size + spectral vegetation metrics
GEDI-onlyPlot size + GEDI metrics
GEDI-DHIPlot size + GEDI metrics + spectral vegetation metrics
Table 3. Universal hyperparameters for DHI-only, GEDI-only, and GEDI-DHI models.
Table 3. Universal hyperparameters for DHI-only, GEDI-only, and GEDI-DHI models.
Modelsn_estimatorsmax_depth max_features
DHI only3002‘log2’
GEDI only50020‘log2
GEDI-DHIs7008‘log2’
Table 4. Model performance of a 5600 m pixel for DHI-only, GEDI-only, and GEDI-DHI models across climate zones (global: n = 48; cold: n = 14; temperate: n =17; tropical: n =17).
Table 4. Model performance of a 5600 m pixel for DHI-only, GEDI-only, and GEDI-DHI models across climate zones (global: n = 48; cold: n = 14; temperate: n =17; tropical: n =17).
Model
Performance		GEDI-Only DHI-Only GEDI-DHIs
R2RMSENRMSER2RMSENRMSER2RMSENRMSE
Global0.55232.5216%0.27295.6620%0.54234.3016%
Cold0.1213.6429%−0.2416.1934%0.1313.5929%
Temperate0.4390.8620%−0.23133.6829%0.4291.9120%
Tropical0.36343.6224%0.12403.8928%0.34349.5224%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Xu, J.; Coleman, K.; Radeloff, V.C.; Songer, M.; Huang, Q. Modeling Worldwide Tree Biodiversity Using Canopy Structure Metrics from Global Ecosystem Dynamics Investigation Data. Remote Sens. 2025, 17, 1408. https://doi.org/10.3390/rs17081408

AMA Style

Xu J, Coleman K, Radeloff VC, Songer M, Huang Q. Modeling Worldwide Tree Biodiversity Using Canopy Structure Metrics from Global Ecosystem Dynamics Investigation Data. Remote Sensing. 2025; 17(8):1408. https://doi.org/10.3390/rs17081408

Chicago/Turabian Style

Xu, Jin, Kjirsten Coleman, Volker C. Radeloff, Melissa Songer, and Qiongyu Huang. 2025. "Modeling Worldwide Tree Biodiversity Using Canopy Structure Metrics from Global Ecosystem Dynamics Investigation Data" Remote Sensing 17, no. 8: 1408. https://doi.org/10.3390/rs17081408

APA Style

Xu, J., Coleman, K., Radeloff, V. C., Songer, M., & Huang, Q. (2025). Modeling Worldwide Tree Biodiversity Using Canopy Structure Metrics from Global Ecosystem Dynamics Investigation Data. Remote Sensing, 17(8), 1408. https://doi.org/10.3390/rs17081408

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop