Abstract
SAR target detection and signal detection are critical tasks in electromagnetic signal processing, with wide-ranging applications in remote sensing and communication monitoring. However, these tasks are challenged by complex backgrounds, multi-scale target variations, and the limited integration of domain-specific priors into existing deep learning models. To address these challenges, we propose Refined Deformable-DETR, a novel Transformer-based method designed to enhance detection performance in SAR and signal processing scenarios. Our approach integrates three key components, including the half-window filter (HWF) to leverage SAR and signal priors, the multi-scale adapter to ensure robust multi-level feature representation, and auxiliary feature extractors to enhance feature learning. Together, these innovations significantly enhance detection precision and robustness. The Refined Deformable-DETR achieves a mAP of 0.682 on the HRSID dataset and 0.540 on the spectrograms dataset, demonstrating remarkable performance compared to other methods.
1. Introduction
Radar, particularly Synthetic Aperture Radar (SAR), is a tool that detects the distance, velocity, and altitude of objects by emitting electromagnetic waves, offering advantages over traditional optical sensors [1,2]. In recent years, with the advancement of SAR imaging technology and the improvement of image resolution, SAR target detection has become a hot topic, being part of SAR image post-processing. The goal of SAR target detection is to extract the orientation and location of targets from complex scenes quickly and effectively. This is crucial for Synthetic Aperture Radar automatic target recognition, where the accuracy of detection determines the success of subsequent tasks. This study is applicable to not only SAR target detection but also signal detection, aiming to enhance the ability to identify signals and targets in complex electromagnetic environments through deep learning techniques. Signal detection and recognition in dynamic electromagnetic environments is a critical field of study within electronic engineering, driven by the exponential growth of wireless technology usage across sectors. In a wireless monitoring system, signal detection is fundamental and important, serving as the basis for signal recognition, direction, and spectral analysis. However, the electromagnetic environment is complex, presenting significant challenges to detection. Signal detection can be divided into time and frequency domain detection. Additionally, deep learning has demonstrated superior performance in signal detection, enabling automatic feature extraction, improving detection accuracy. Wireless radio signal classification and modulation recognition are crucial issues in intelligent signal processing, holding significance for managing electromagnetic spectrum resources and ensuring reliability and security of communication systems. Researchers have proposed various methods for wireless radio signal identification to improve classification and modulation recognition accuracy.
In recent years, deep learning has been extensively applied across various industries, demonstrating superior performance relative to traditional methods. Many researchers globally have incorporated deep learning techniques into signal detection. O’Shea pioneered using convolutional neural networks (CNN) [3] and deep neural networks (DNN) in radio communications for feature learning and signal recognition [4]. Deep learning-based signal recognition methods typically utilize the spectro-temporal image obtained after short-time Fourier transformation (STFT) [5] as input and output the spectro-temporal information. Prasad et al. [5] used a reduced version of Faster-RCNN [6] for radio signal detection to reduce network size. Another study [7] applied YOLO object detectors to spectrum images to discover signals including Zigbee, Bluetooth, and Wi-Fi from the Internet of Things (IoT). Rahman et al. proposes a Bi-LSTM-based channel estimation and signal detection method, demonstrating its effectiveness in RIS-supported multi-user SISO OFDM systems [8]. Compared to traditional detection algorithms requiring manual feature extraction, deep learning methods leverage convolutional neural networks with superior feature extraction capabilities, enabling richer feature collection.
Despite the remarkable performance of Transformer-based models in the field of image processing and the potential they exhibit in SAR target detection and electromagnetic signal detection, they have not yet incorporated prior knowledge from signal processing. In this study, we introduce the latest deep learning models to enhance the accuracy and efficiency of signal modulation identification. These new models not only demonstrate superior performance in image processing and object recognition, particularly outperforming traditional methods in terms of processing speed and accuracy, but also overcome the high misclassification rates and slow response times of traditional models in specific scenarios through innovative algorithm optimization. Our key innovations are as follows.
- Half-window filtering technology: By proposing the half-window filter (HWF), which leverages prior knowledge from SAR signal processing, the feature extraction process is enhanced, significantly improving the recognition performance for targets of different scales. While Transformer-based models have demonstrated strong performance in image processing, SAR target detection and electromagnetic signal detection, they have not yet fully integrated SAR signal processing priors, which this approach addresses.
- Auxiliary feature extractors: During training, auxiliary feature extractors are introduced to provide additional supervision signals, enhancing the model’s encoding and decoding capabilities. Traditional object detection algorithms have shown poor performance on SAR target detection tasks. The introduction of auxiliary feature extractors significantly improves this by providing more robust feature learning and enhancing overall recognition accuracy.
- Multi-scale adapter: The multi-scale adapter dynamically constructs feature pyramids through upsampling and downsampling operations, enhancing multi-scale feature alignment and significantly improving detection accuracy for targets of varying sizes and scales.
2. Related Work
2.1. Detection Transformer
Following the success of convolutional neural networks (CNNs) and deep neural networks (DNNs), the Transformer architecture [9] has garnered widespread attention for its exceptional sequence modeling capabilities. It has been successfully applied to various visual tasks, including object detection. Transformer-based models, such as DETR [10] and its variants, not only offer new perspectives and approaches for object detection but also demonstrate great potential in signal detection and recognition. Despite these advances, existing detection models still face challenges, such as detection accuracy, model convergence speed, and the recognition of small or partially occluded objects in complex scenarios.
The primary objective of this study is to introduce improved attention mechanisms and propose a novel object detection model aimed at enhancing performance in dynamic and complex environments. Specifically, the model seeks to improve detection of small or partially occluded objects or signals. Detailed technical analyses and comparisons will be provided in subsequent sections to establish a solid theoretical and technical foundation for this work.
Detection Transformer (DETR) [10] treats object detection as a direct set prediction problem. By leveraging the Transformer encoder–decoder architecture and a global loss function, DETR infers object relationships and global image context through a set of learned object queries. This approach avoids many hand-designed components, offering a more end-to-end solution. On the COCO object detection dataset, DETR achieves accuracy and runtime performance comparable to Faster R-CNN [11].
Originally designed for natural language processing (NLP) tasks, the Transformer’s unique self-attention mechanism is well-suited to handling sequential data such as images and sound signals. In signal detection tasks, Transformers excel at capturing global characteristics of signals, enabling more accurate feature extraction and classification. DETR brings the Transformer’s self-attention mechanism to object detection, simplifying the traditional detection pipeline by directly predicting both object category and location, thus eliminating the need for non-maximum suppression (NMS) [12].
Further advancements, such as Deformable-DETR [13], optimize this architecture with a variable attention mechanism, improving adaptability to diverse object sizes and shapes. Conditional DETR [14] accelerates convergence and enhances detection efficiency through conditioned decoding. Additionally, DAB-DETR (Deformable Attention-Based DETR) [15] increases flexibility and accuracy in handling complex scenes by introducing deformable attention modules. This is especially valuable in complex electromagnetic environments, where such advancements significantly improve signal classification and recognition performance.
2.2. SAR Target Detection
In the field of SAR (Synthetic Aperture Radar) target detection, researchers have been striving to overcome challenges posed by environmental noise, sensor errors, and variations in target scale and shape. Early SAR target detection methods primarily relied on feature-based techniques, such as the extraction of texture, edge, and shape features. These methods were often combined with traditional machine learning classifiers, such as support vector machines (SVM) and random forests, for target recognition [16]. However, these approaches often required complex feature engineering and were limited in handling complex backgrounds and varying targets.
In recent years, the rise of deep learning has significantly improved the effectiveness of SAR target detection. Convolutional neural networks (CNNs) have become the most commonly used tool because they can automatically learn effective spatial features from raw SAR images, eliminating the need for manual feature extraction required by traditional methods [17]. Advanced object detection algorithms, such as Faster R-CNN and YOLO, have been successfully applied to SAR images, showing higher detection accuracy and speed [18,19]. Additionally, generative adversarial metworks (GANs) have been applied in SAR target detection for data augmentation and noise reduction, thereby improving the robustness and generalization ability of the models [20].
Despite the significant progress made by deep learning methods in SAR target detection, there are still many challenges. In particular, improving model performance with limited data remains a crucial issue. Many methods perform poorly in few-shot learning and when labeled data is scarce. As a result, effective data augmentation and the use of unsupervised learning methods have become hot topics in current research [21]. Furthermore, the environmental variability and diversity of targets in SAR images require detection models to have greater adaptability, and techniques such as transfer learning and domain adaptation are progressively being applied [22].
2.3. Filtering Technology
Filtering technology has widespread applications in image processing [23]. Traditional filtering methods like Gaussian [24], mean [25], and median filtering reduce image noise through local processing, but lack adaptability. Modern filter techniques incorporate deep learning methods like the one proposed in the literature, using fast discrete filters based on Gaussian curvature, mean curvature, and total variation (TV) [26] regularization to reduce variational energy. These methods effectively reduce noise and preserve features via pixel-level filters. In deep learning, ResNet [27] has achieved significant success in tasks like image classification and feature extraction through its residual module. Research combining filter technology and deep learning suggests adaptive filter layers can enhance feature extraction, improving model performance.
2.4. Auxiliary Supervision
Auxiliary supervision enhances model training by introducing extra supervisory signals, which improve feature learning and overall detection and recognition performance. In self-supervised learning, auxiliary supervision combined with self-supervised tasks enhances feature learning efficiency [28]; in generative adversarial networks, auxiliary supervision improves image generation quality through conditional generation [29]; in reinforcement learning, auxiliary tasks accelerate policy learning and model convergence [30,31]. For instance, Zong et al. [32] used auxiliary supervision signals through collaborative hybrid assignments training (CHAT) to improve the DETR model’s detection efficiency and accuracy. Zhang, Junbo and Tian [33] introduced the SUGAR algorithm, using two complementary heterogeneous networks and additional supervision signals during training to strengthen feature learning. The auxiliary feature extractor generates extra classification and regression losses, optimizing the feature learning process and improving the encoding and decoding capabilities of the model, thus enhancing recognition performance.
3. Method
As shown in Figure 1, our model processes input images to produce final outputs. The image is initially processed by the main network and Transformer encoder, generating feature maps. These feature maps are then processed by the multi-scale adapter to create multi-scale features. Further processing by auxiliary feature extractors generates classification and regression predictions. By comparing these predictions with real labels, we calculate classification and regression losses. The total loss optimizes model parameters, enhancing feature learning and improving performance.
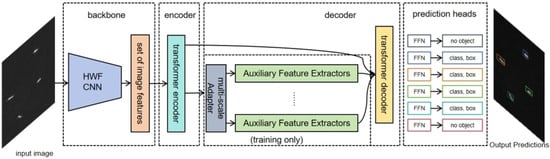
Figure 1.
Overview of the proposed Refined Deformable-DETR model architecture for SAR target detection and radio signal detection. The model processes input SAR image and spectrograms through HWF and a Transformer encoder, followed by multi-scale feature adaptation and auxiliary feature extraction to generate final classification and regression predictions.
3.1. Half-Window Filter
The half-window filter (HWF) is a learnable operator that dynamically adapts to SAR image characteristics through end-to-end training. Unlike traditional fixed convolution kernels, its projection weights are optimized via backpropagation to balance edge preservation and noise suppression. HWF is designed to reduce the variational energy while maintaining image edges. Its basic concept is to use the pixel local solutions of the regularization operator as the projection operation, and to reduce the regularization energy by approximating the image as a constant, minimum or expandable surface within a local window.
Given the input image I, after passing through the and , we obtain the feature map F.
As shown in Equation (1), after passing the input image I through the and , we obtain the feature map F.
The HWF works through two main steps. First, in the neighborhood of each pixel, the image is approximated locally as a constant, minimal surface, or developable surface through local regression. Second, among all possible local approximations, the one that results in the smallest change in the central pixel intensity is selected, thereby minimizing the increase in data fitting energy.
The following equations describe the implementation of the projection operator used in the HWF. Let represent the value of the input function at the pixel (or index) . The surrounding values can be defined as follows: .
The projection operator is applied as follows. The coefficients in (2)–(5) are derived based on a local regression approach within a window, aiming to approximate the image as a constant, minimal, or developable surface. The weighting factors are chosen to minimize the local variation energy while preserving edge structures. The computed differences correspond to directional variations, and the smallest one () is used to adjust the central pixel value, ensuring minimal distortion while effectively suppressing noise.
where , , , and represent the computed differences based on the surrounding values of , and is the minimum absolute difference. The final result, , is obtained by adding to the original value , which adjusts the value based on the neighboring pixel differences.
In our model, the HWF serves as a layer within the CNN and is trained via backpropagation using standard error. This method harnesses deep learning techniques for image processing and feature extraction while significantly reducing variational energy, thereby enhancing model performance and training efficiency. This approach effectively supplants traditional convolution kernels, utilizing deep learning methodologies to achieve superior image processing and feature extraction.
3.2. Multi-Scale Adapter
In object detection tasks, the multi-scale adapter, a specialized tool, is strategically utilized to transform single-scale or multi-scale features. These features are meticulously processed and output by the encoder into a multi-scale feature pyramid. The adapter’s functionality significantly enhances the ability of auxiliary feature extractors to meet their specific needs. This process results in a more effective and efficient object detection system.
As shown in Figure 2, For the single-scale encoder output, the feature pyramid is first constructed through bilinear interpolation and convolution operations. Let the feature map output by the encoder be F. We construct the feature pyramid through the following steps.
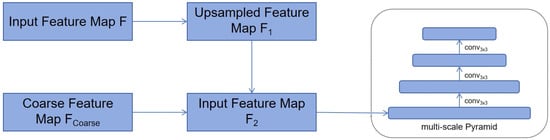
Figure 2.
Multi-scale adapter workflow for feature pyramid construction.
In the process of upsampling the feature map, bilinear interpolation is applied. For each feature map , the upsampling operation can be expressed as Equation (8).
After upsampling, the feature map is further processed with a convolution. The convolution operation is defined as Equation (9).
As shown in Equation (8), the feature map is upsampled using bilinear interpolation. Then, as described in Equation (9), the upsampled feature map undergoes a convolution operation.
For the multi-scale encoder, we only downsample the coarsest feature in the multi-scale encoder features to build the feature pyramid. For the multi-scale encoder output, assuming the coarsest feature map is , we construct the feature pyramid through downsampling operations:
Start with the coarsest feature map . The initial feature map is given.
Next, apply a convolution with stride 2 to the feature map to downsample it. This downsampling operation can be expressed.
Repeat this downsampling step as necessary to construct the feature pyramid.
As shown in Equation (10), we start with the coarsest feature map . Then, as described in Equation (11), a downsampling operation is applied to the feature map.
The multi-scale adapter is crucial for object detection tasks, as it transforms single-scale or multi-scale features into a multi-scale feature pyramid. This enhances the ability of auxiliary feature extractors to meet their needs, improving the effectiveness and efficiency of the object detection system. The adapter achieves this through bilinear interpolation and convolution operations or downsampling the coarsest feature map, constructing multi-level feature representations. In summary, the multi-scale adapter greatly facilitates performance optimization and training convergence of object detection models.
3.3. Auxiliary Feature Extractor
In modern object detection frameworks, feature extraction and accurate prediction play crucial roles in achieving high performance. Auxiliary feature extractors are introduced to provide additional supervision signals during the training phase, thereby enhancing the learning of features. This section explains the process and significance of using auxiliary feature extractors in our model.
Given the input image I, after passing through the Backbone (including the HWF and convolutional neural network (CNN)) and the Transformer encoder, we obtain the feature map F.
Multi-scale adapter processes the feature map F, generating multi-scale features .
Each auxiliary feature extractor processes the multi-scale features, generating classification predictions and regression predictions .
where k denotes the k-th auxiliary feature extractor.
The use of auxiliary feature extractors enhances feature learning by providing additional supervision signals during training. Unlike traditional data augmentation, which increases data diversity through geometric and color transformations, auxiliary feature extractors generate extra labels and features to improve the model’s encoding and decoding abilities. This method enhances feature-level diversity and information content, leading to improved model performance and generalization.
We use three different auxiliary feature extractors in our experiments: ATSS, YOLOv3 and Faster-RCNN. ATSS (Adaptive Training Sample Selection) [34] bridges the gap between anchor-based and anchor-free detection methods, offering adaptability and robustness in various scenarios. YOLOv3 [35] is a single-stage detector that predicts multiple object bounding boxes and categories in a single forward pass, excelling in computational efficiency. Faster-RCNN [11] is a region-based convolutional neural network that combines a region proposal network (RPN) with a Fast R-CNN detector. It provides higher detection accuracy but requires more computational resources.
The selection of ATSS, YOLOv3, and Faster-RCNN as auxiliary feature extractors is driven by their complementary methodological frameworks in object detection research. ATSS represents state-of-the-art anchor-free detection with adaptive training sample selection, YOLOv3 exemplifies efficient single-stage detection through its real-time optimization paradigm, while Faster-RCNN stands as the seminal two-stage detector with precise region proposal mechanisms. This combination ensures comprehensive feature supervision by spanning: global semantic modeling (ATSS) versus local discriminative analysis (Faster-RCNN), and computational efficiency (YOLOv3) versus high-precision localization capabilities. Their synergistic integration addresses the intrinsic challenges of SAR targets, which demand both context-aware interpretation and multi-scale sensitivity.
3.4. Loss Function and Optimization
In deep learning, the loss function and optimization are central to the training process. The loss function quantifies the discrepancy between the model’s predictions and the ground truth, while optimization methods are used to adjust the model parameters to minimize this discrepancy. In this section, we discuss the loss functions used in our model, the total loss function, and the optimization process.
The loss function in our model consists of two main components: classification loss and regression loss. These losses are calculated separately for each auxiliary feature extractor. The classification loss measures the difference between the predicted class probabilities and the true class labels, while the regression loss measures the difference between the predicted bounding box coordinates and the ground-truth coordinates.
In object detection, the classification loss measures the difference between the predicted class and the ground truth class label, typically calculated using cross-entropy loss. The formula is as Equation (15).
where is the predicted class output from the k-th auxiliary feature extractor, and is the ground truth class label.
The regression loss measures the difference between the predicted bounding box and the ground truth bounding box, typically computed using smooth L1 loss. The formula is as Equation (16).
where is the regression output (e.g., bounding box coordinates) from the k-th auxiliary feature extractor, is the ground truth bounding box coordinates, and is an indicator function that checks whether the predicted and ground truth boxes are matched.
Similarly, the regression loss is computed as Equation (18).
where and are the predicted class and bounding box coordinates, and and are the ground truth class labels and bounding box coordinates.
The total loss function is the weighted sum of the classification and regression losses from all auxiliary feature extractors. It is formulated as Equation (19).
Here, and are the weighting coefficients, which balance the contributions of the classification and regression losses. The coefficients and are empirically set to 0.8 and 0.2, respectively, prioritizing localization stability while maintaining classification accuracy.
To minimize the total loss function , we use an optimization algorithm to update the model parameters during training. We employ the Adam optimizer, which combines the benefits of both adaptive learning rates and momentum, making it effective for training deep networks. The optimization process aims to minimize the total loss function by adjusting the model’s parameters iteratively.
The design of the loss function significantly impacts the optimization process. By balancing the classification and regression losses appropriately, we ensure that the model is not biased toward one task over the other. The loss function guides the optimization process toward finding the best model parameters that minimize the prediction errors for both classification and bounding box regression tasks. Furthermore, the auxiliary feature extractors help regularize the model by providing additional supervision signals, which enhances the optimization process and prevents overfitting.
In summary, the loss function and optimization play a crucial role in training our model, ensuring that it effectively learns to perform both classification and regression tasks while generalizing well to unseen data.
4. Results
4.1. Dataset and Experimental Settings
In this study, we utilized the HRSiD (high-resolution Synthetic Aperture Radar ship detection) [36] dataset, which is specifically designed for ship detection tasks using high-resolution Synthetic Aperture Radar (SAR) images. The HRSiD dataset contains a large number of high-resolution SAR images captured under various environmental conditions, aimed at evaluating the performance of ship detection algorithms in complex backgrounds. The dataset includes data from multiple voyages, covering a range of weather conditions, sea states, and different types of ships. Each image is meticulously annotated with detailed information, such as ship categories and locations, providing comprehensive support for model training and performance evaluation. In this research, we used the HRSiD dataset for both model training and testing, with the goal of validating the effectiveness and robustness of our proposed method in ship detection tasks.
To better illustrate the characteristics of the HRSiD dataset, we present two example images. Figure 3a shows a high-resolution SAR image of a ship under calm sea conditions, while Figure 3b depicts a ship in a more complex maritime environment with rough sea states. These images highlight the challenges of ship detection in SAR imagery, including varying ship types, sea states, and environmental conditions. The HRSID dataset contains 120 high-resolution SAR images (1 m spatial resolution, HH polarization) with diverse maritime scenarios, including open oceans, coastal areas, and harbor regions. Each image captures varying ship densities (5–32 vessels) and clutter interference levels (calm seas to stormy conditions), reflecting real-world operational challenges in SAR-based maritime surveillance.

Figure 3.
Example SAR images from the HRSiD dataset illustrating ship detection in different sea states.
Our experiments also use two-dimensional spectrograms generated from radio waves through a short-time Fourier transform (STFT). These serve as primary input for our model, with the horizontal axis representing signal frequency and the vertical axis denoting time. The signal is visually depicted as a rectangular block within the spectrogram for clarity. We also utilize the spectral color mapping scheme to enhance diagram efficacy. Specific parameter settings tailored for our dataset are as shown in Table 1.

Table 1.
Dataset parameters.
In our experiments, the 10 modulation modes are considered separately. The signal can be divided into two types: unaliased and aliased, as shown in Figure 4a. Figure 4a is a simple pattern of radio with no time and frequency aliasing, while Figure 4b is a complex pattern with time or frequency aliasing.
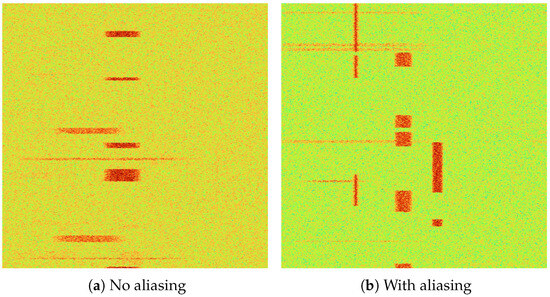
Figure 4.
Visualization of spectrograms of radio signal.
We conducted extensive trials to compare our model with other successful detectors. All experiments were carried out on a GeForce RTX 3070 GPU. We trained all detectors using the SGD optimizer, with a momentum of 0.937 and a weight decay of 0.00001. In our experiments, we adopted ATSS [34] as auxiliary feature extractors. We set the number of learnable object queries to 300 and the hyperparameters to the default values of .
4.2. Comparative Results on HRSiD Dataset
Table 2 presents the results of the comparative experiments conducted on the HRSiD dataset, evaluating different methods using and mAP (). The results demonstrate that our proposed method achieves a mAP of 0.682, surpassing all other methods, including the previous state-of-the-art Net (0.660). Additionally, our method achieves competitive performance in terms of , reaching 0.902, which is comparable to Net (0.912) and Yue et al. [37] (0.911).

Table 2.
Comparison experiments on HRSID.
4.3. Comparative Results on Spectrogram Dataset
As shown in Table 3, the proposed Refined Deformable-DETR outperforms a range of DETR-based detectors and other popular object detection frameworks on the spectrogram dataset. It achieves the best performance across all evaluation metrics: AP = 0.540, AP50 = 0.804, and AP75 = 0.586.

Table 3.
Comparison of different methods on spectrograms dataset.
To further analyze the model’s performance across different modulation schemes, we present the confusion matrix in Figure 5. From the confusion matrix, we observe that the model performs exceptionally well on certain classes, such as GMSK and 64QAM, with classification accuracies of 66% and 89%, respectively. This indicates that these modulation schemes have distinct characteristics, making them easier for the model to classify correctly.
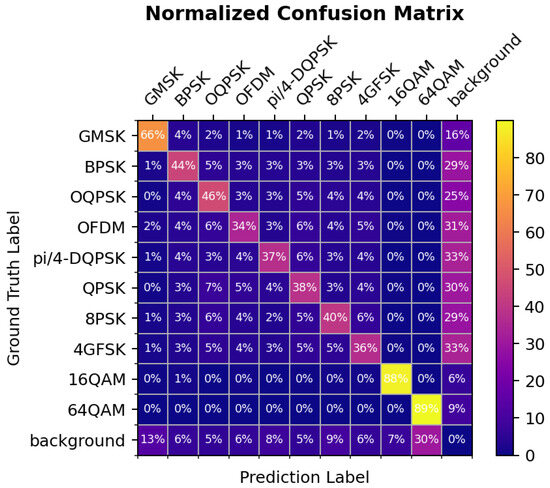
Figure 5.
Normalized confusion matrix showing the classification performance of the model for each modulation type. The diagonal values represent correct classifications, while the off-diagonal values represent misclassifications.
4.4. Ablation Study
To assess the contribution of the HWF module and auxiliary feature extractors, we conducted ablation experiments on both the HRSiD and spectrogram datasets. As shown in Table 4, enabling HWF consistently improves performance. For instance, with YOLOv3 as the extractor, AP improves from 0.619 to 0.682 and from 0.887 to 0.902.

Table 4.
Comparison of auxiliary extractors on HRSID.
Similarly, results on the spectrogram dataset (Table 5) show consistent improvements when HWF is enabled. Notably, ATSS achieves the best performance with AP = 0.533 and = 0.771 when using HWF.

Table 5.
Comparison of auxiliary extractors on spectrograms dataset.
The inference time analysis shows that while enabling HWF introduces a slight computational overhead (e.g., 5–7 ms increase), the performance gains are substantial. This highlights the utility of HWF in precision-critical tasks.
5. Discussion
The extensive experimental results confirm the superior performance and practical potential of the proposed Refined Deformable-DETR model. This section elaborates on the comparative advantages, robustness analysis, ablation insights, and remaining challenges, based on both quantitative metrics and qualitative observations.
5.1. Performance Comparison with State-of-the-Art
Across both SAR (HRSiD) and spectrogram-based detection tasks, our method achieves the best overall mAP scores (0.682 on HRSiD and 0.540 on spectrograms), outperforming not only classical detectors (e.g., Faster R-CNN, YOLO variants) but also Transformer-based baselines (DETR, Deformable-DETR, DAB-DETR, Conditional-DETR). In particular, although Net and Yue et al. [37,42] report high values, their mAP (under stricter IoU thresholds) falls short, indicating that our model achieves better localization precision under challenging conditions.
5.2. Robustness and Generalization
The results indicate that Refined Deformable-DETR generalizes well across domains—from maritime SAR scenes to complex signal spectrograms. Its resilience to spatial deviations, as demonstrated by the strong high-IoU performance and confusion matrix analysis, makes it particularly suitable for scenarios requiring accurate region localization, such as ship detection in cluttered sea conditions or fine-grained signal demodulation in spectrum monitoring.
5.3. Effectiveness of the HWF Module
The ablation studies (Table 4 and Table 5) clearly demonstrate the contribution of the proposed Half-Window Filtering (HWF) module. Across all backbone extractors (YOLOv3, ATSS, Faster R-CNN), HWF leads to consistent improvements in both AP and , at the cost of only minor increases in inference time. These results suggest that HWF effectively enhances temporal-spectral attention and can be considered a lightweight yet powerful plug-in module.
5.4. Remaining Limitations and Future Work
Despite strong results, challenges remain. As revealed in the confusion matrix (Figure 5), certain modulation types—especially those with overlapping spectral patterns—remain difficult to classify. Future work may involve leveraging more expressive feature hierarchies, integrating contrastive learning signals, or applying cross-modal regularization. Moreover, deploying the system in real-time or edge settings will require further model compression and latency optimization.
6. Conclusions
We proposed Refined Deformable-DETR for SAR target detection and signal modulation recognition. Experimental results demonstrate the outstanding performance of Refined Deformable-DETR. By proposing the half-window filtering technique and the auxiliary feature extractor, Refined Deformable-DETR enhances detection performance, particularly for small, medium, and large targets. In the context of SAR target detection, the model effectively handles complex background environments, improving detection accuracy in cluttered or noisy scenarios. Moreover, the model shows robust performance in signal modulation recognition, further validating its effectiveness in electromagnetic environments. Future work will focus on optimizing the training process to enhance efficiency and exploring additional application scenarios to achieve more efficient and accurate signal detection and recognition, particularly in SAR-based tasks.
Author Contributions
Z.L. was responsible for methodology, software development, formal analysis, and drafting the original manuscript. X.Z. contributed to the conceptualization, investigation, resource acquisition, and reviewing and editing of the manuscript. Both authors collaborated on the design and implementation of the research and approved the final version of the manuscript for submission. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are openly available at https://gitcode.com/gh_mirrors/hr/HRSID (accessed on 12 January 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, C.; He, C.; Hu, C.; Pei, H.; Jiao, L. MSARN: A Deep Neural Network Based on an Adaptive Recalibration Mechanism for Multiscale and Arbitrary-Oriented SAR Ship Detection. IEEE Access 2019, 7, 159262–159283. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Zhang, H. Ship Classification in High-Resolution SAR Images Using Deep Learning of Small Datasets. Sensors 2018, 18, 2929. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.Q.; Zheng, P.; Xu, S.T.; Wu, X. Object Detection with Deep Learning: A Review. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3212–3232. [Google Scholar] [CrossRef] [PubMed]
- O’Shea, T.J.; Corgan, J.; Clancy, T.C. Convolutional Radio Modulation Recognition Networks. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Aberdeen, UK, 2–5 September 2016; pp. 213–226. [Google Scholar]
- Sturmel, N.; Daudet, L. Signal Reconstruction from STFT Magnitude: A State of the Art. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Paris, France, 19–23 September 2011; pp. 375–386. [Google Scholar]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar] [CrossRef]
- Krasner, N. Optimal Detection of Digitally Modulated Signals. IEEE Trans. Commun. 1982, 30, 885–895. [Google Scholar] [CrossRef]
- Rahman, M.H.; Sejan, M.A.S.; Aziz, M.A.; Baik, J.I.; Kim, D.S.; Song, H.K. Deep Learning Based Improved Cascaded Channel Estimation and Signal Detection for Reconfigurable Intelligent Surfaces-Assisted MU-MISO Systems. IEEE Trans. Green Commun. Netw. 2023, 7, 1515–1527. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-End Object Detection with Transformers. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 213–229. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar] [CrossRef]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable detr: Deformable transformers for end-to-end object detection. arXiv 2020, arXiv:2010.04159. [Google Scholar]
- Meng, D.; Chen, X.; Fan, Z.; Zeng, G.; Li, H.; Yuan, Y.; Sun, L.; Wang, J. Conditional detr for fast training convergence. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 3651–3660. [Google Scholar]
- Liu, S.; Li, F.; Zhang, H.; Yang, X.; Qi, X.; Su, H.; Zhu, J.; Zhang, L. Dab-detr: Dynamic anchor boxes are better queries for detr. arXiv 2022, arXiv:2201.12329. [Google Scholar]
- Ding, S.G.; Nie, X.L.; Qiao, H.; Zhang, B. Online classification for SAR target recognition based on SVM and approximate convex hull vertices selection. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 1473–1478. [Google Scholar]
- Yu, G.; Ying, X. Architecture design of deep convolutional neural network for SAR target recognition. J. Image Graph. 2018, 23, 928–936. [Google Scholar]
- Kang, M.; Leng, X.; Lin, Z.; Ji, K. A modified faster R-CNN based on CFAR algorithm for SAR ship detection. In Proceedings of the 2017 International Workshop on Remote Sensing with Intelligent Processing (RSIP), Shanghai, China, 18–21 May 2017. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Oh, J.; Kim, M. PeaceGAN: A GAN-Based Multi-Task Learning Method for SAR Target Image Generation with a Pose Estimator and an Auxiliary Classifier. Remote Sens. 2021, 13, 3939. [Google Scholar] [CrossRef]
- Lu, D.; Cao, L.; Liu, H. Few-Shot Learning Neural Network for SAR Target Recognition. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Zhu, X.; Mori, H. Data augmentation using style transfer in SAR automatic target classification. In Proceedings of the Artificial Intelligence and Machine Learning in Defense Applications III, Online, 13–17 September 2021; p. 12. [Google Scholar] [CrossRef]
- Gong, Y.; Sbalzarini, I.F. Curvature Filters Efficiently Reduce Certain Variational Energies. IEEE Trans. Image Process. 2017, 26, 1786–1798. [Google Scholar] [CrossRef]
- Ibrahim, M.; Chen, K.; Brito-Loeza, C. A novel variational model for image registration using Gaussian curvature. Geom. Imaging Comput. 2014, 1, 417–446. [Google Scholar] [CrossRef]
- Zhu, H.; Shu, H.; Zhou, J.; Bao, X.; Luo, L. Bayesian algorithms for PET image reconstruction with mean curvature and Gauss curvature diffusion regularizations. Comput. Biol. Med. 2007, 37, 793–804. [Google Scholar] [CrossRef] [PubMed]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Caruana, R. Multitask Learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Radford, A.; Kim, J.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Amanda, A.; Mishkin, P.; Clark, J.; et al. Learning Transferable Visual Models From Natural Language Supervision. In Proceedings of the 38th International Conference on Machine Learning, PMLR 139, Virtual, 18–24 July 2021. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Jaderberg, M.; Mnih, V.; Czarnecki, W.; Schaul, T.; Leibo, J.; Silver, D.; Kavukcuoglu, K. Reinforcement Learning with Unsupervised Auxiliary Tasks. arXiv 2016, arXiv:1611.05397. [Google Scholar]
- Zong, Z.; Song, G.; Liu, Y. DETRs with Collaborative Hybrid Assignments Training. arXiv 2022, arXiv:2211.12860. [Google Scholar]
- Zhang, J.; Tian, G.; Mu, Y.; Fan, W. Supervised deep learning with auxiliary networks. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014. [Google Scholar] [CrossRef]
- Zhang, S.; Chi, C.; Yao, Y.; Lei, Z.; Li, S.Z. Bridging the Gap Between Anchor-based and Anchor-free Detection via Adaptive Training Sample Selection. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. In Proceedings of the Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Wei, S.; Zeng, X.; Qu, Q.; Wang, M.; Su, H.; Shi, J. HRSID: A High-Resolution SAR Images Dataset for Ship Detection and Instance Segmentation. IEEE Access 2020, 8, 120234–120254. [Google Scholar] [CrossRef]
- Yue, T.; Zhang, Y.; Liu, P.; Xu, Y.; Yu, C. A Generating-Anchor Network for Small Ship Detection in SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7665–7676. [Google Scholar] [CrossRef]
- Gao, F.; Cai, C.; Tang, W.; He, Y. A compact and high-efficiency anchor-free network based on contour key points for SAR ship detection. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4002705. [Google Scholar] [CrossRef]
- Bai, L.; Yao, C.; Ye, Z.; Xue, D.; Lin, X.; Hui, M. Feature Enhancement Pyramid and Shallow Feature Reconstruction Network for SAR Ship Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1042–1056. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Liu, C.; Shi, J.; Wei, S.; Ahmad, I.; Zhan, X.; Zhou, Y.; Pan, D.; Li, J.; et al. Balance learning for ship detection from synthetic aperture radar remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2021, 182, 190–207. [Google Scholar] [CrossRef]
- Bai, L.; Yao, C.; Ye, Z.; Xue, D.; Lin, X.; Hui, M. A Novel Anchor-Free Detector Using Global Context-Guide Feature Balance Pyramid and United Attention for SAR Ship Detection. IEEE Geosci. Remote Sens. Lett. 2023, 20, 4003005. [Google Scholar] [CrossRef]
- Chen, C.; Zeng, W.; Zhang, X.; Zhou, Y. CS n Net: A Remote Sensing Detection Network Breaking the Second-Order Limitation of Transformers with Recursive Convolutions. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4207315. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).