Soil Organic Carbon Prediction and Mapping in Morocco Using PRISMA Hyperspectral Imagery and Meta-Learner Model
Abstract
1. Introduction
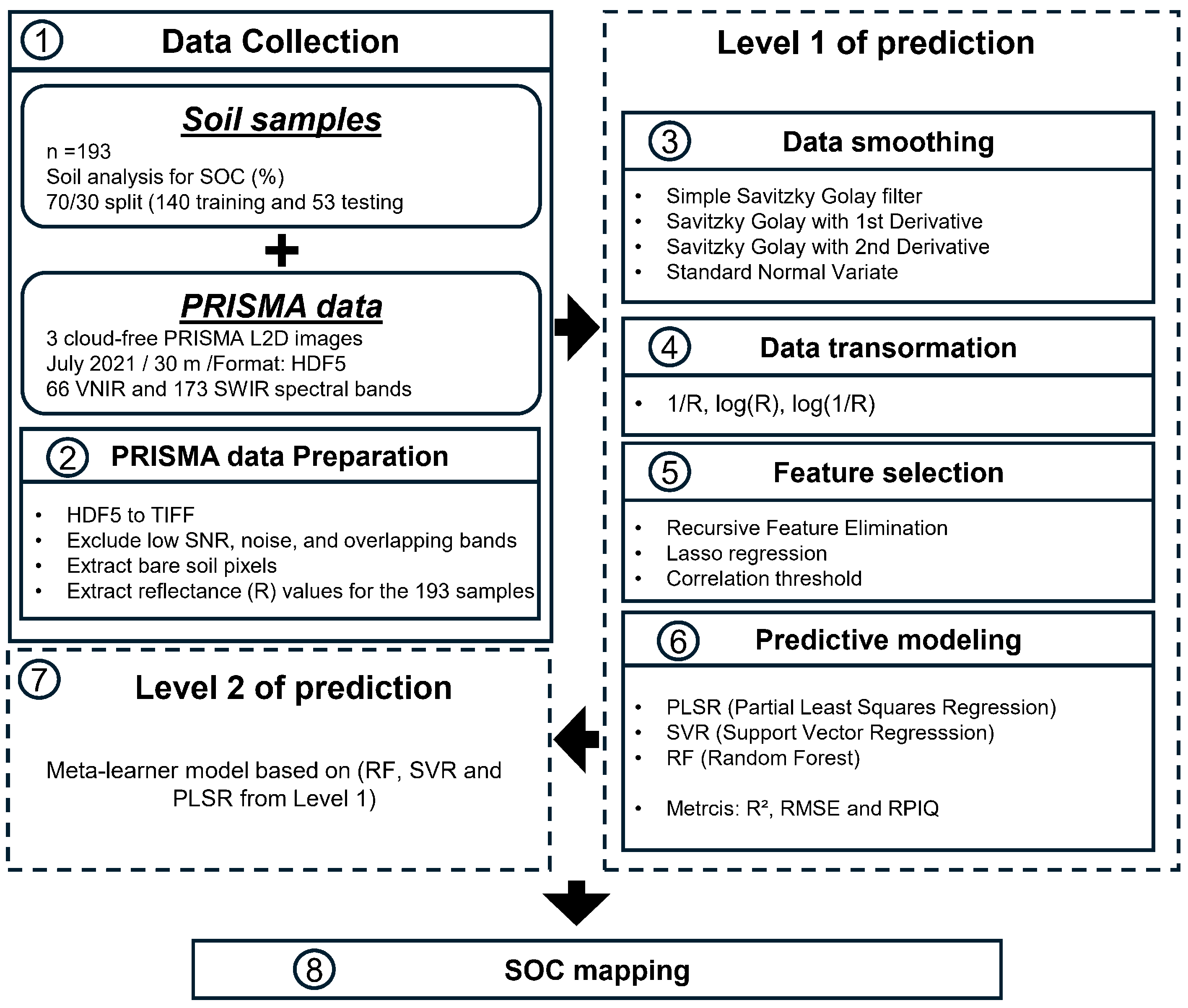
2. Materials and Methods
2.1. Study Area and Data Collection
2.2. PRISMA Hyperspectral Imagery and Pre-Processing
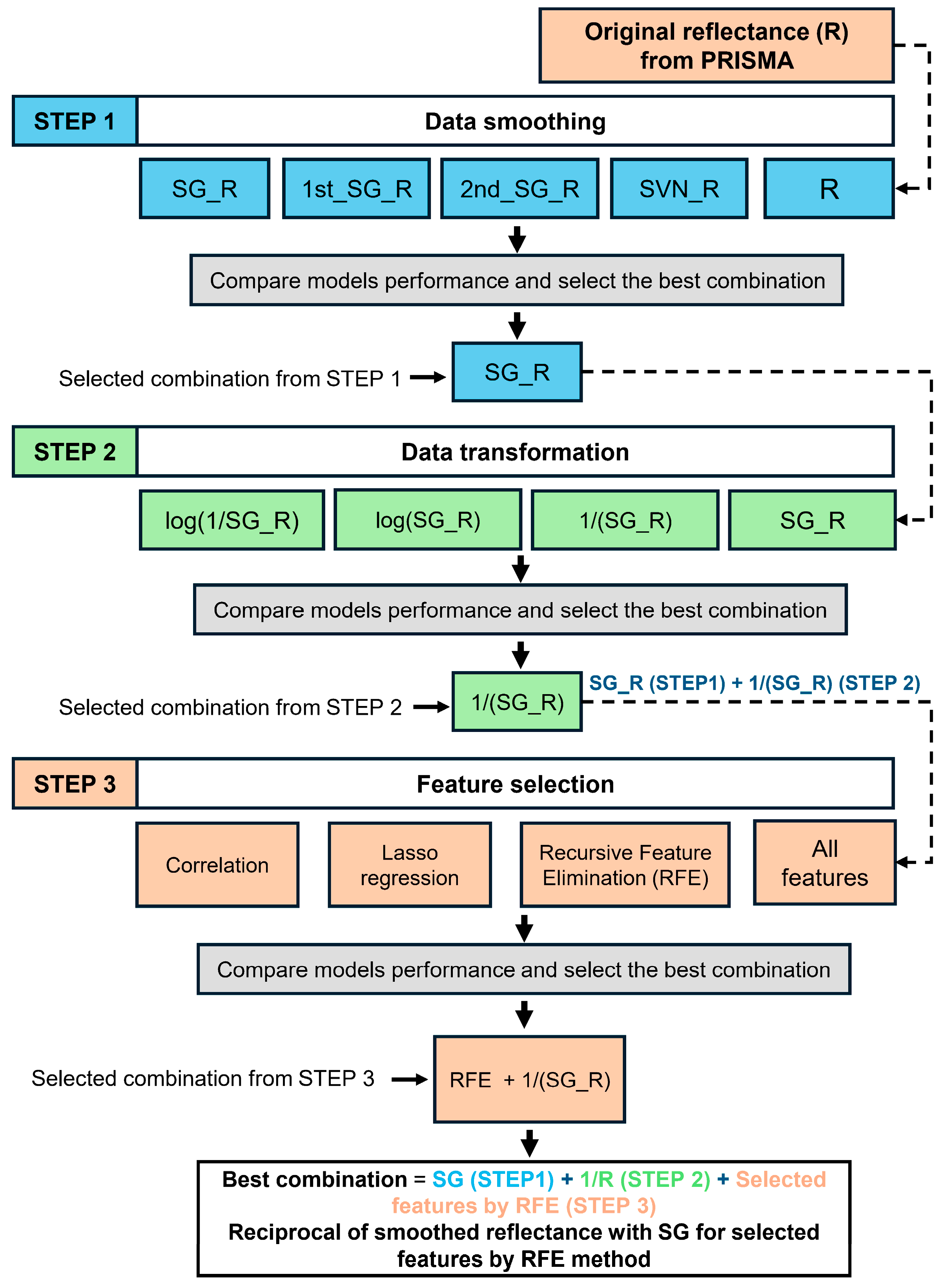
2.3. Data Processing: Smoothing, Transformation, and Feature Selection
2.4. First Layer—Base Models
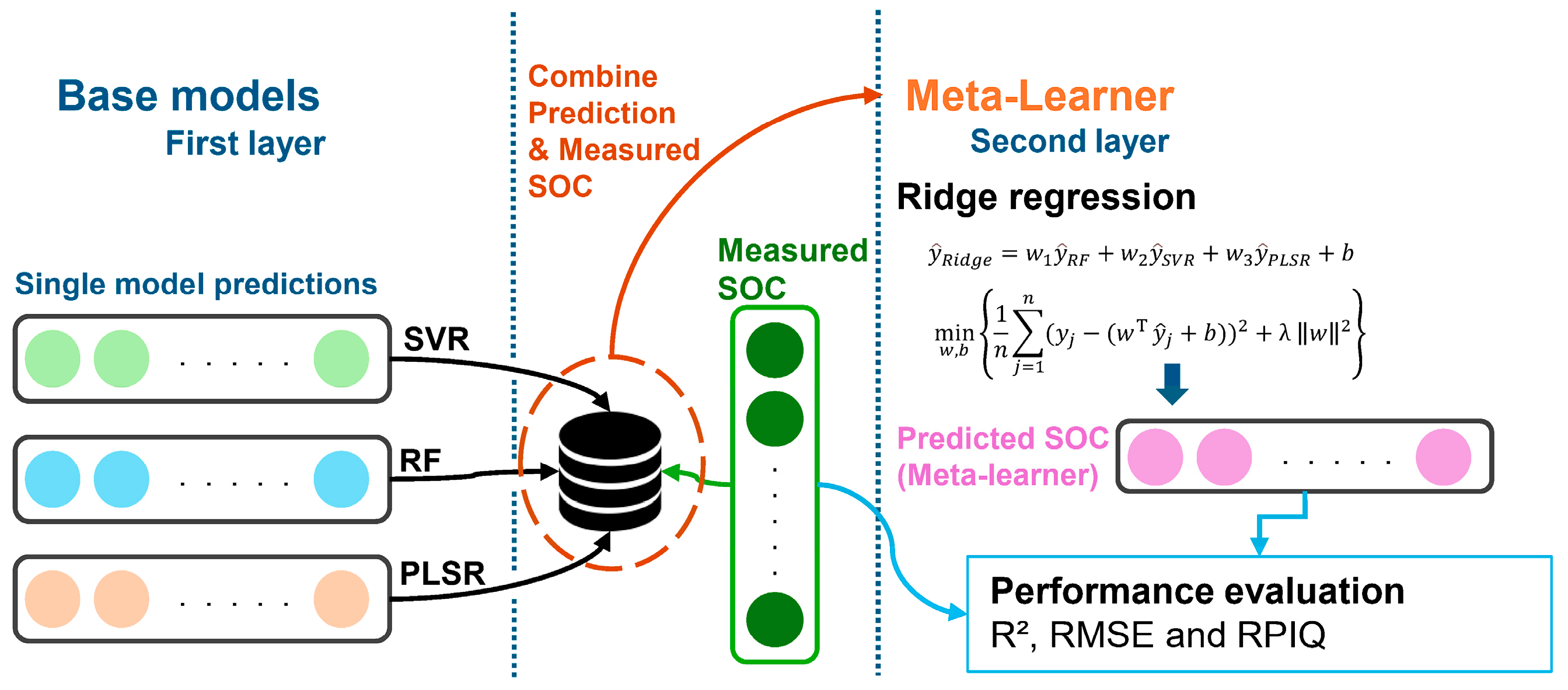
2.5. Second Layer—Ridge Regression as a Meta-Learner
2.6. Model Validation
- Coefficient of Determination (R2): This metric quantifies how well the predicted values approximate the actual data points. It represents the proportion of the variance in the observed data that is captured by the predictions. A value close to 1 indicates strong predictive accuracy, while a value near 0 suggests weak predictive performance.
- Root Mean Square Error (RMSE): This offers insight into the model’s prediction accuracy by gauging the magnitude of the residual errors. A lower RMSE signifies a better fit, though its interpretation is more meaningful when compared with the range of the dependent variable.
- Residual Prediction Inter-Quartile (RPIQ): is a model performance metric that measures the model’s predictive ability. It is calculated by dividing the interquartile range (IQR) of the observed values by the model’s RMSE. A higher RPIQ value indicates better model performance.
2.7. Spatial Prediction of SOC
3. Results
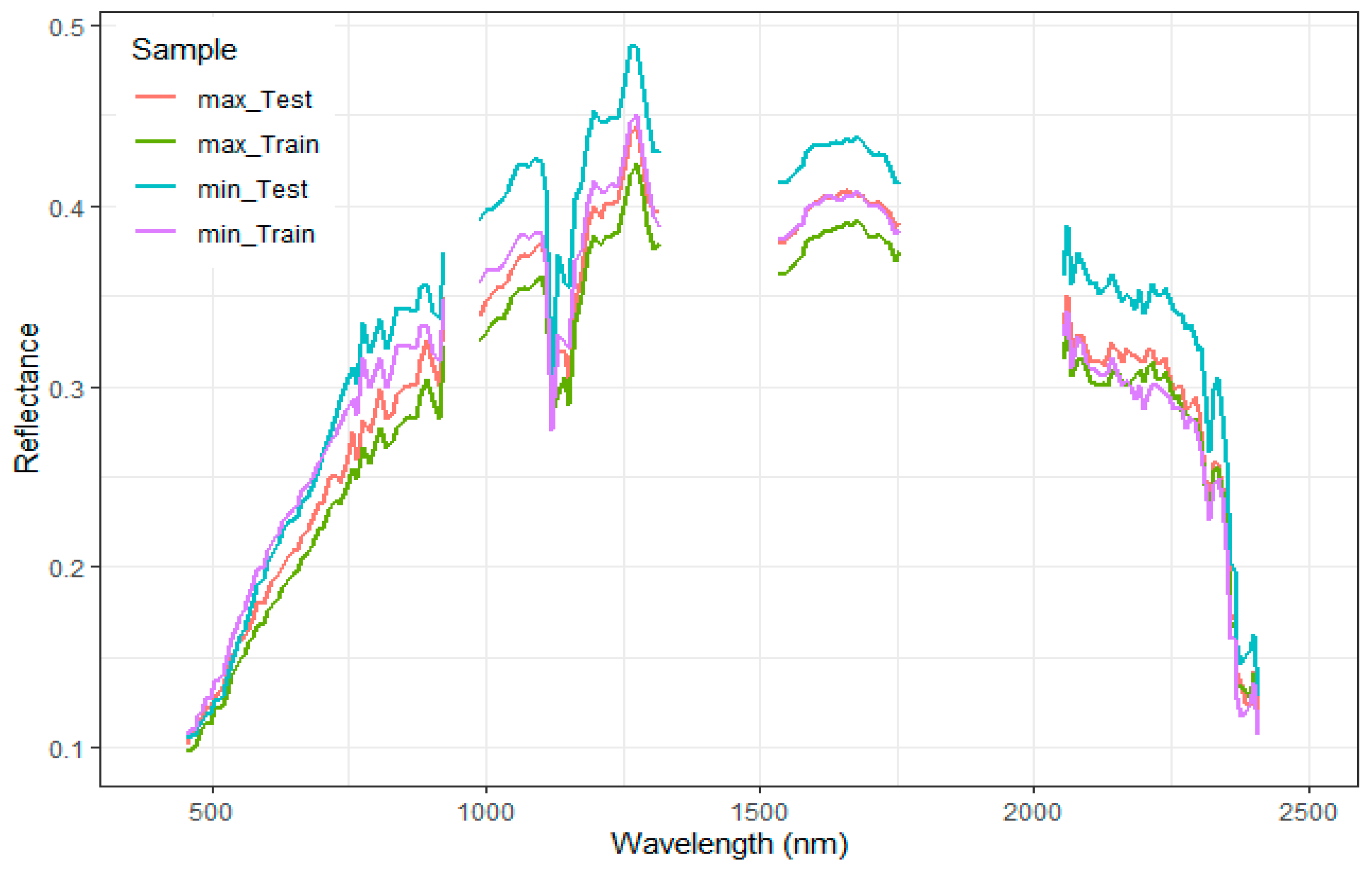
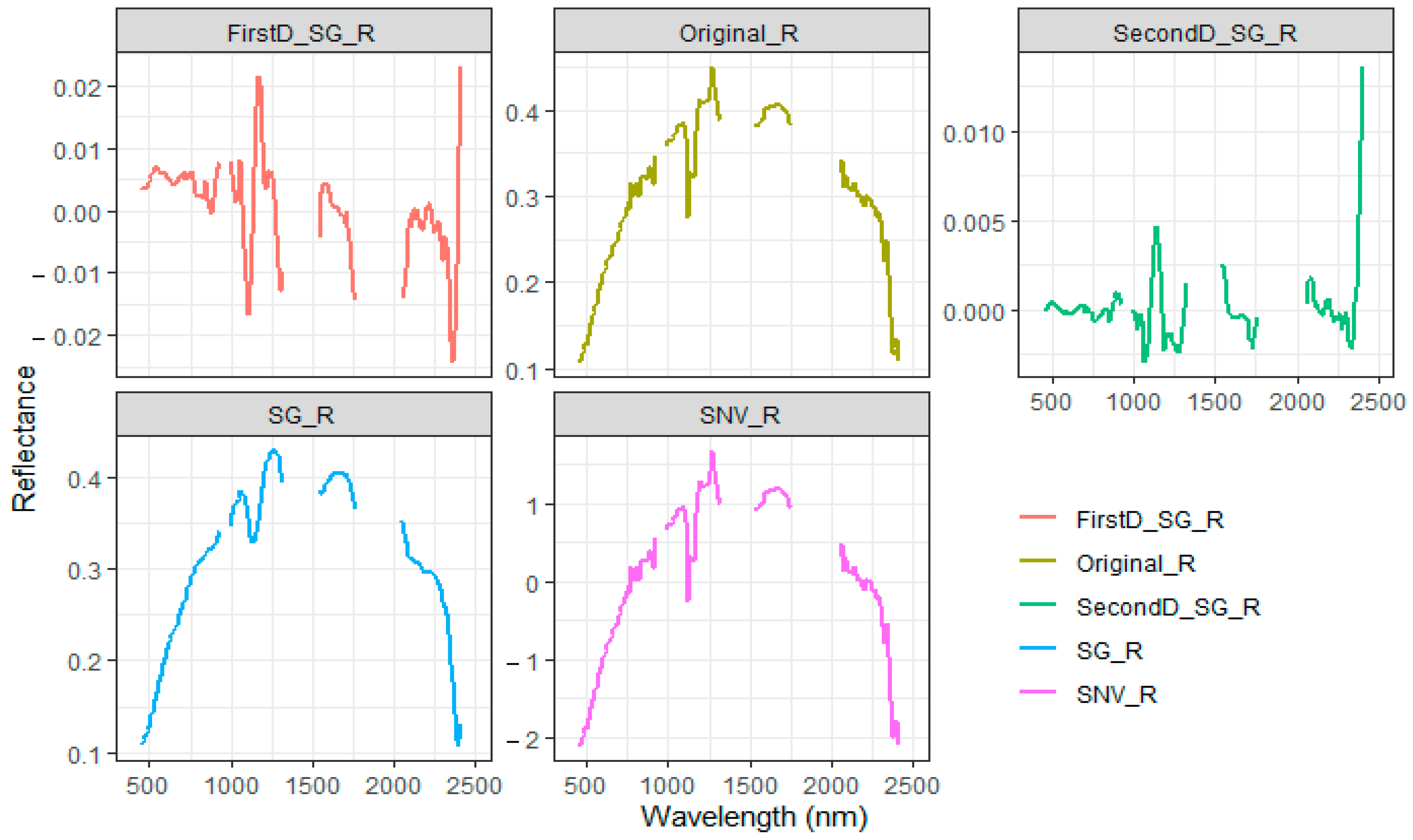
3.1. Statistical Analysis and Spectral Characteristics
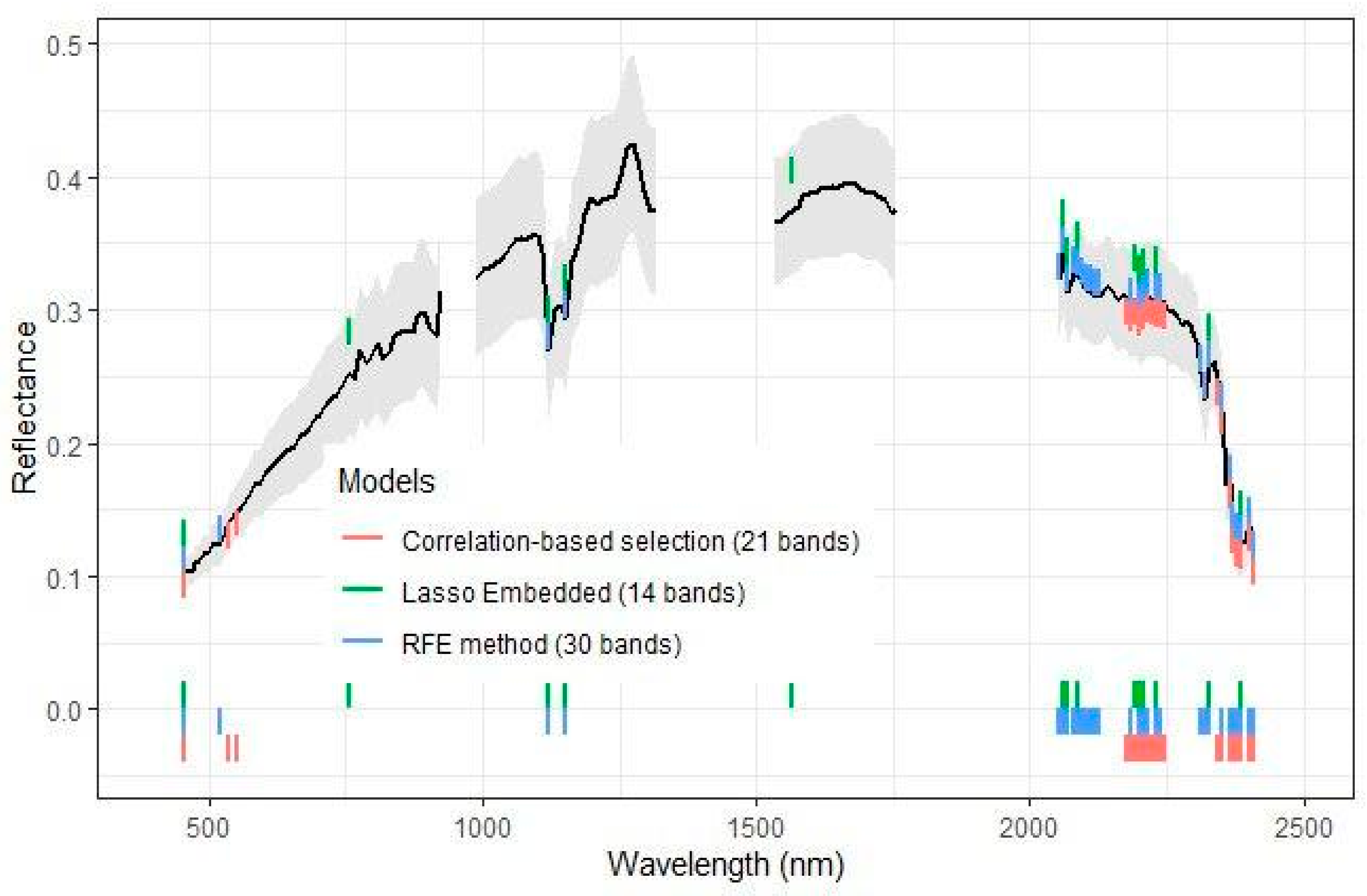
3.2. Feature Selection
3.3. Performance Evaluation of ML Models
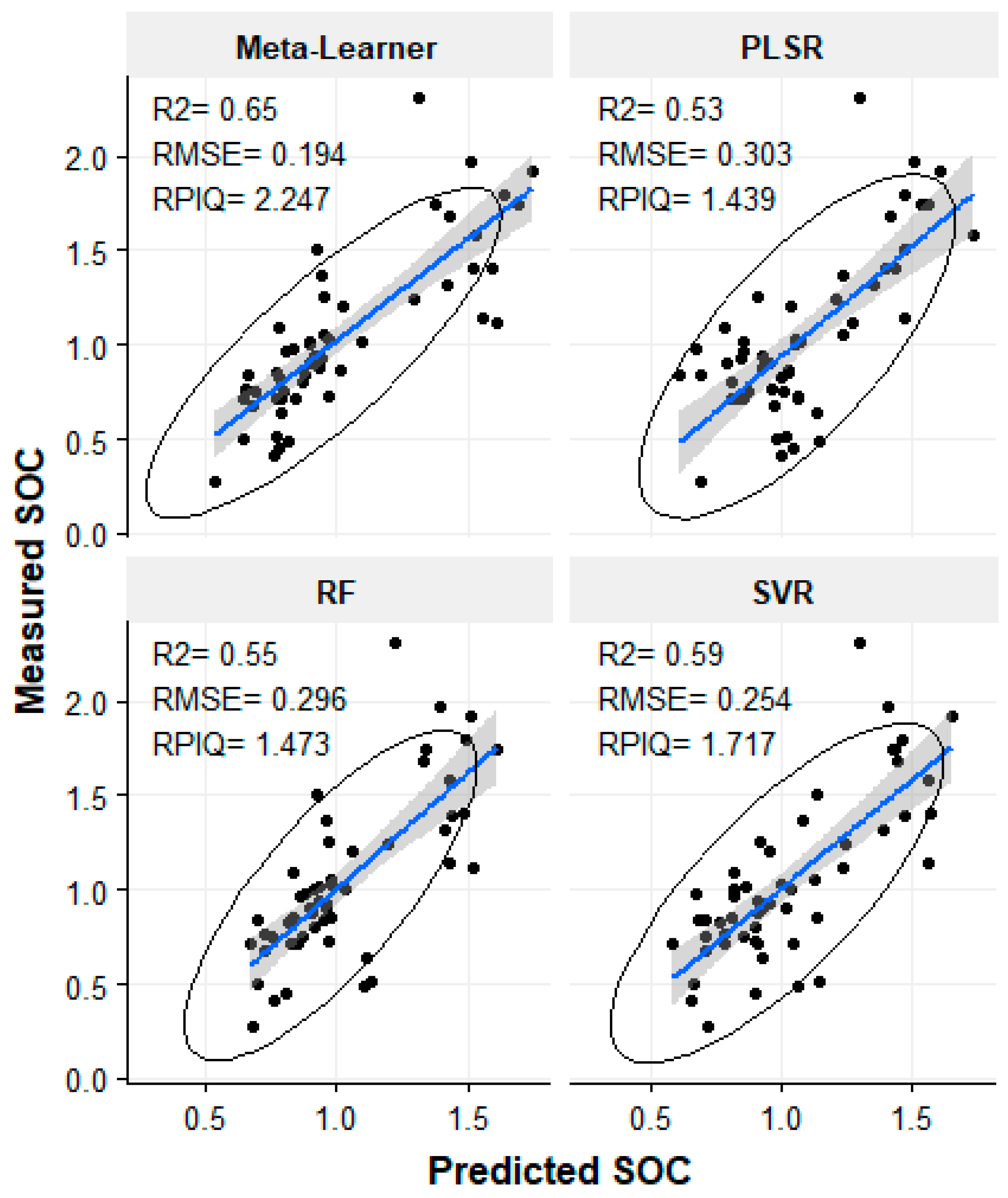
3.4. Meta-Learner Results
4. Discussion
4.1. Importance of Wavelength Selection for SOC Prediction
4.2. Analysis of the Effect of Base and Meta-Learner Models
4.3. SOC Distribution in Relation to Intrinsic and Extrinsic Soil Factors
4.4. Potentials, Limitations, and Recommendations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, T.; Cui, L.; Wu, Y.; McLaren, T.I.; Xia, A.; Pandey, R.; Dang, Y.P. Soil organic carbon estimation via remote sensing and machine learning techniques: Global topic modeling and research trend exploration. Remote Sens. 2024, 16, 3168. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Urbanski, L.; Hobley, E.; Lang, B.; von Lützow, M.; Marin-Spiotta, E.; van Wesemael, B.; Rabot, E.; Ließ, M.; Garcia-Franco, N.; et al. Soil organic carbon storage as a key function of soils-A review of drivers and indicators at various scales. Geoderma 2019, 333, 149–162. [Google Scholar] [CrossRef]
- Evangelista, S.J.; Field, D.J.; McBratney, A.B.; Minasny, B.; Ng, W.; Padarian, J.; Dobarco, M.R.; Wadoux, A.M.C. Soil security—Strategizing a sustainable future for soil. Adv. Agron. 2024, 183, 1–70. [Google Scholar]
- Das, B.S.; Wani, S.P.; Benbi, D.K.; Muddu, S.; Bhattacharyya, T.; Mandal, B.; Santra, P.; Chakraborty, D.; Bhattacharyya, R.; Basak Reddy, N.N. Soil health and its relationship with food security and human health to meet the sustainable development goals in India. Soil Secur. 2022, 8, 100071. [Google Scholar] [CrossRef]
- Uddin, M.J.; Hooda, P.S.; Mohiuddin, A.S.M.; Haque, M.E.; Smith, M.; Waller, M.; Biswas, J.K. Soil organic carbon dynamics in the agricultural soils of Bangladesh following more than 20 years of land use intensification. J. Environ. Manag. 2022, 305, 114427. [Google Scholar] [CrossRef]
- El Mouridi, Z.; Ziri, R.; Douaik, A.; Bennani, S.; Lembaid, I.; Bouharou, L.; Moussadek, R. Comparison between Walkley-Black and loss on ignition methods for organic matter estimation in different Moroccan soils. Ecol. Eng. Environ. Technol. 2023, 24, 253–259. [Google Scholar] [CrossRef]
- Dahhani, S.; Raji, M.; Bouslihim, Y. Synergistic Use of Multi-Temporal Radar and Optical Remote Sensing for Soil Organic Carbon Prediction. Remote Sens. 2024, 16, 1871. [Google Scholar] [CrossRef]
- Nawar, S.; Delbecque, N.; Declercq, Y.; De Smedt, P.; Finke, P.; Verdoodt, A.; Mouazen, A.M. Can spectral analyses improve measurement of key soil fertility parameters with X-ray fluorescence spectrometry? Geoderma 2019, 350, 29–39. [Google Scholar] [CrossRef]
- Benedet, L.; Acuña-Guzman, S.F.; Missina Faria, W.; Silva, S.H.G.; Mancini, M.; Teixeira, A.; Pierangeli, L.M.P.; Acerbi Júnior, F.W.; Gomide, L.R.; Júnior, A.L.P.; et al. Rapid soil fertility prediction using X-ray fluorescence data and machine learning algorithms. Catena 2021, 197, 105003. [Google Scholar] [CrossRef]
- Dharumarajan, S.; Gomez, C.; Lalitha, M.; Kalaiselvi, B.; Vasundhara, R.; Hegde, R. Soil order knowledge as a driver in soil properties estimation from Vis-NIR spectral data–Case study from northern Karnataka (India). Geoderma Reg. 2023, 32, e00596. [Google Scholar] [CrossRef]
- Francos, N.; Gedulter, N.; Ben-Dor, E. Estimation of Iron Content Using Reflectance Spectroscopy in a Complex Soil System After a Loss-on-Ignition Pre-treatment. J. Soil Sci. Plant Nutr. 2023, 23, 6866–6873. [Google Scholar] [CrossRef]
- Ng, W.; Minasny, B.; Mendes, W.D.S.; Demattê, J.A.M. The influence of training sample size on the accuracy of deep learning models for the prediction of soil properties with near-infrared spectroscopy data. Soil 2020, 6, 565–578. [Google Scholar] [CrossRef]
- Bouasria, A.; Bouslihim, Y.; Mrabet, R.; Devkota, K. National baseline high-resolution mapping of soil organic carbon in Moroccan cropland areas. Geoderma Reg. 2025, 40, e00941. [Google Scholar] [CrossRef]
- Bouslihim, Y.; Rochdi, A.; Aboutayeb, R.; El Amrani-Paaza, N.; Miftah, A.; Hssaini, L. Soil aggregate stability mapping using remote sensing and GIS-based machine learning technique. Front. Earth Sci. 2021, 9, 748859. [Google Scholar] [CrossRef]
- Zhao, L.; Tan, K.; Wang, X.; Ding, J.; Liu, Z.; Ma, H.; Han, B. Hyperspectral feature selection for SOM prediction using deep reinforcement learning and multiple subset evaluation strategies. Remote Sens. 2022, 15, 127. [Google Scholar] [CrossRef]
- Nenkam, A.M.; Wadoux, A.M.C.; Minasny, B.; Silatsa, F.B.; Yemefack, M.; Ugbaje, S.U.; McBratney, A.B. Applications and challenges of digital soil mapping in Africa. Geoderma 2024, 449, 117007. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Borůvka, L.; Saberioon, M.; Vašát, R. Visible, near-infrared, and mid-infrared spectroscopy applications for soil assessment with emphasis on soil organic matter content and quality: State-of-the-art and key issues. Appl. Spectrosc. 2013, 67, 1349–1362. [Google Scholar] [CrossRef]
- Chabrillat, S.; Ben-Dor, E.; Cierniewski, J.; Gomez, C.; Schmid, T.; van Wesemael, B. Imaging spectroscopy for soil mapping and monitoring. Surv. Geophys. 2019, 40, 361–399. [Google Scholar] [CrossRef]
- Villas-Boas, P.R.; Franco, M.A.; Martin-Neto, L.; Gollany, H.T.; Milori, D.M. Applications of laser-induced breakdown spectroscopy for soil analysis, part I: Review of fundamentals and chemical and physical properties. Eur. J. Soil Sci. 2020, 71, 789–804. [Google Scholar] [CrossRef]
- Ng, W.; Minasny, B.; Jeon, S.H.; McBratney, A. Mid-infrared spectroscopy for accurate measurement of an extensive set of soil properties for assessing soil functions. Soil Secur. 2022, 6, 100043. [Google Scholar] [CrossRef]
- Angelopoulou, T.; Tziolas, N.; Balafoutis, A.; Zalidis, G.; Bochtis, D. Remote sensing techniques for soil organic carbon estimation: A review. Remote Sens. 2019, 11, 676. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Patkin, K.; Banin, A.; Karnieli, A. Mapping of several soil properties using DAIS-7915 hyperspectral scanner data—A case study over clayey soils in Israel. Int. J. Remote Sens. 2002, 23, 1043–1062. [Google Scholar] [CrossRef]
- Montanarella, L.; Panagos, P. The relevance of sustainable soil management within the European Green Deal. Land Use Policy 2021, 100, 104950. [Google Scholar] [CrossRef]
- Castaldi, F. Sentinel-2 and landsat-8 multi-temporal series to estimate topsoil properties on croplands. Remote Sens. 2021, 13, 3345. [Google Scholar] [CrossRef]
- Sun, W.; Liu, S.; Zhang, X.; Li, Y. Estimation of soil organic matter content using selected spectral subset of hyperspectral data. Geoderma 2022, 409, 115653. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, J.; Song, X.; Qin, Z.; Wu, L.; Wang, H.; Tang, J. Hyperspectral band selection and modeling of soil organic matter content in a forest using the Ranger algorithm. PLoS ONE 2021, 16, e0253385. [Google Scholar] [CrossRef]
- Polley, E.C.; van der Laan, M.J. Super Learner in Prediction. In U.C. Berkeley Division of Biostatistics Working Paper Series; The Berkeley Electronic Press: Berkeley, CA, USA, 2010; p. 266. Available online: https://biostats.bepress.com/ucbbiostat/paper266 (accessed on 14 July 2024).
- Zhao, D.; Wang, J.; Zhao, X.; Triantafilis, J. Clay content mapping and uncertainty estimation using weighted model averaging. Catena 2022, 209, 105791. [Google Scholar] [CrossRef]
- Chen, S.; Mulder, V.L.; Heuvelink, G.B.; Poggio, L.; Caubet, M.; Dobarco, M.R.; Walter, C.; Arrouays, D. Model averaging for mapping topsoil organic carbon in France. Geoderma 2020, 366, 114237. [Google Scholar] [CrossRef]
- Hengl, T.; Miller, M.A.; Križan, J.; Shepherd, K.D.; Sila, A.; Kilibarda, M.; Crouch, J. African soil properties and nutrients mapped at 30 m spatial resolution using two-scale ensemble machine learning. Sci. Rep. 2021, 11, 6130. [Google Scholar] [CrossRef]
- Tajik, S.; Ayoubi, S.; Zeraatpisheh, M. Digital mapping of soil organic carbon using ensemble learning model in Mollisols of Hyrcanian forests, northern Iran. Geoderma Reg. 2020, 20, e00256. [Google Scholar] [CrossRef]
- Zhou, Y.; Xue, J.; Chen, S.; Zhou, Y.; Liang, Z.; Wang, N.; Shi, Z. Fine-resolution mapping of soil total nitrogen across China based on weighted model averaging. Remote Sens. 2019, 12, 85. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Schmidt, K.; Amirian-Chakan, A.; Rentschler, T.; Zeraatpisheh, M.; Sarmadian, F.; Valvi, R.; Davatgar, N.; Behrens, T.; Scholten, T. Improving the spatial prediction of soil organic carbon content in two contrasting climatic regions by stacking machine learning models and rescanning covariate space. Remote Sens. 2020, 12, 1095. [Google Scholar] [CrossRef]
- Wu, M.; Dou, S.; Lin, N.; Jiang, R.; Zhu, B. Estimation and Mapping of Soil Organic Matter Content Using a Stacking Ensemble Learning Model Based on Hyperspectral Images. Remote Sens. 2023, 15, 4713. [Google Scholar] [CrossRef]
- Castaldi, F.; Palombo, A.; Santini, F.; Pascucci, S.; Pignatti, S.; Casa, R. Evaluation of the potential of the current and forthcoming multispectral and hyperspectral imagers to estimate soil texture and organic carbon. Remote Sens. Environ. 2016, 179, 54–65. [Google Scholar] [CrossRef]
- Angelopoulou, T.; Chabrillat, S.; Pignatti, S.; Milewski, R.; Karyotis, K.; Brell, M.; Ruhtz, T.; Bochtis, D.; Zalidis, G. Evaluation of airborne hyspex and spaceborne PRISMA hyperspectral remote sensing data for soil organic matter and carbonates estimation. Remote Sens. 2023, 15, 1106. [Google Scholar] [CrossRef]
- Mzid, N.; Castaldi, F.; Tolomio, M.; Pascucci, S.; Casa, R.; Pignatti, S. Evaluation of agricultural bare soil properties retrieval from landsat 8, sentinel-2 and PRISMA satellite data. Remote Sens. 2022, 14, 714. [Google Scholar] [CrossRef]
- Gasmi, A.; Gomez, C.; Chehbouni, A.; Dhiba, D.; El Gharous, M. Using PRISMA hyperspectral satellite imagery and GIS approaches for soil fertility mapping (FertiMap) in northern Morocco. Remote Sens. 2022, 14, 4080. [Google Scholar] [CrossRef]
- Bouasria, A.; Ibno Namr, K.; Rahimi, A.; Ettachfini, E.M.; Rerhou, B. Evaluation of Landsat 8 image pansharpening in estimating soil organic matter using multiple linear regression and artificial neural networks. Geo-Spat. Inf. Sci. 2022, 25, 353–364. [Google Scholar] [CrossRef]
- FAO. Standard Operating Procedure for Soil Organic Carbon Walkley-Black Method Titration and Colorimetric Method; Food & Agriculture Org: Rome, Italy, 2019. [Google Scholar]
- Tripathi, P.; Garg, R.D. First impressions from the PRISMA hyperspectral mission. Curr. Sci. 2020, 119, 1267–1281. [Google Scholar] [CrossRef]
- Pellegrino, A.; Fabbretto, A.; Bresciani, M.; de Lima, T.M.A.; Braga, F.; Pahlevan, N.; Giardino, C. Assessing the Accuracy of PRISMA Standard Reflectance Products in Globally Distributed Aquatic Sites. Remote Sens. 2023, 15, 2163. [Google Scholar] [CrossRef]
- Braga, F.; Fabbretto, A.; Vanhellemont, Q.; Bresciani, M.; Giardino, C.; Scarpa, G.M.; Manf`e, G.; Concha, J.A.; Brando, V.E. Assessment of PRISMA water reflectance using autonomous hyperspectral radiometry. ISPRS J. Photogramm. Remote Sens. 2022, 192, 99–114. [Google Scholar] [CrossRef]
- Busetto, L.; Ranghetti, L. prismaread: A Tool for Facilitating Access and Analysis of PRISMA L1/L2 Hyperspectral Imagery. v1.0.0. 2020. Available online: https://irea-cnr-mi.github.io/prismaread/ (accessed on 22 April 2024).
- Demattê, J.A.M.; Paiva, A.F.d.S.; Poppiel, R.R.; Rosin, N.A.; Ruiz, L.F.C.; Mello, F.A.d.O.; Minasny, B.; Grunwald, S.; Ge, Y.; Ben Dor, E.; et al. The Brazilian Soil Spectral Service (BraSpecS): A User-Friendly System for Global Soil Spectra Communication. Remote Sens. 2022, 14, 740. [Google Scholar] [CrossRef]
- Demattê, J.A.; Safanelli, J.L.; Poppiel, R.R.; Rizzo, R.; Silvero, N.E.Q.; Mendes, W.D.S.; Bonfatti, B.R.; Dotto, A.C.; Salazar, D.F.U.; Mello, F.A.D.O. Bare earth’s surface spectra as a proxy for soil resource monitoring. Sci. Rep. 2020, 10, 4461. [Google Scholar] [CrossRef]
- Diek, S.; Schaepman, M.E.; De Jong, R. Creating multi-temporal composites of airborne imaging spectroscopy data in support of digital soil mapping. Remote Sens. 2016, 8, 906. [Google Scholar] [CrossRef]
- Ward, K.J.; Chabrillat, S.; Brell, M.; Castaldi, F.; Spengler, D.; Foerster, S. Mapping soil organic carbon for airborne and simulated EnMAP imagery using the LUCAS soil database and a local PLSR. Remote Sens. 2020, 12, 3451. [Google Scholar] [CrossRef]
- Schafer, R.W. What is a Savitzky-Golay filter? IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- Vaiphasa, C. Consideration of smoothing techniques for hyperspectral remote sensing. ISPRS J. Photogramm. Remote Sens. 2006, 60, 91–99. [Google Scholar] [CrossRef]
- Guo, Q.; Wu, W.; Massart, D.L. The robust normal variate transform for pattern recognition with near-infrared data. Anal. Chim. Acta 1999, 382, 87–103. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 1996; Volume 9. [Google Scholar]
- Schaepman, M.E. Spectrodirectional remote sensing: From pixels to processes. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 204–223. [Google Scholar] [CrossRef]
- Rinnan, Å.; Van Den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Asgari, N.; Ayoubi, S.; Demattê, J.A.M.; Dotto, A.C. Carbonates and organic matter in soils characterized by reflected energy from 350–25000 nm wavelength. J. Mt. Sci. 2020, 17, 1636–1651. [Google Scholar] [CrossRef]
- Ding, J.; Yang, A.; Wang, J.; Sagan, V.; Yu, D. Machine-learning-based quantitative estimation of soil organic carbon content by VIS/NIR spectroscopy. PeerJ 2018, 6, e5714. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, Y.; Yu, L.; Liu, Y.; Liu, Y.; Zhang, Y.; Liu, Y.; Cheng, H. Combining fractional order derivative and spectral variable selection for organic matter estimation of homogeneous soil samples by VIS–NIR spectroscopy. Remote Sens. 2018, 10, 479. [Google Scholar] [CrossRef]
- Stenberg, B.; Rossel, R.A.V.; Mouazen, A.M.; Wetterlind, J. Visible and near infrared spectroscopy in soil science. Adv. Agron. 2010, 107, 163–215. [Google Scholar]
- Xu, L.; Hong, Y.; Wei, Y.; Guo, L.; Shi, T.; Liu, Y.; Jiang, Q.; Fei, T.; Liu, Y.; Mouazen, A.; et al. Estimation of organic carbon in anthropogenic soil by VIS-NIR spectroscopy: Effect of variable selection. Remote Sens. 2020, 12, 3394. [Google Scholar] [CrossRef]
- Wang, S.; Guan, K.; Zhang, C.; Lee, D.; Margenot, A.J.; Ge, Y.; Peng, J.; Zhou, W.; Zhou, Q.; Huang, Y. Using soil library hyperspectral reflectance and machine learning to predict soil organic carbon: Assessing potential of airborne and spaceborne optical soil sensing. Remote Sens. Environ. 2022, 271, 112914. [Google Scholar] [CrossRef]
- Miloš, B.; Bensa, A. Prediction of soil organic carbon using VIS-NIR spectroscopy: Application to Red Mediterranean soils from Croatia. Eurasian J. Soil Sci. 2017, 6, 365–373. [Google Scholar] [CrossRef]
- Al-Abbas, A.H.; Swain, P.H.; Baumgardner, M.F. Relating organic matter and clay content to the multispectral radiance of soils. Soil Sci. 1972, 114, 477–485. [Google Scholar] [CrossRef]
- Xu, S.; Shi, X.; Wang, M.; Zhao, Y. Effects of subsetting by parent materials on prediction of soil organic matter content in a hilly area using Vis–NIR spectroscopy. PLoS ONE 2016, 11, e0151536. [Google Scholar] [CrossRef]
- Heller Pearlshtien, D.; Ben-Dor, E. Effect of organic matter content on the spectral signature of iron oxides across the VIS–NIR spectral region in artificial mixtures: An example from a red soil from Israel. Remote Sens. 2020, 12, 1960. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Inbar, Y.; Chen, Y. The reflectance spectra of organic matter in the visible near-infrared and short wave infrared region (400–2500 nm) during a controlled decomposition process. Remote Sens. Environ. 1997, 61, 1–15. [Google Scholar] [CrossRef]
- Ladoni, M.; Bahrami, H.A.; Alavipanah, S.K.; Norouzi, A.A. Estimating soil organic carbon from soil reflectance: A review. Precis. Agric. 2010, 11, 82–99. [Google Scholar] [CrossRef]
- Guo, P.T.; Li, M.F.; Luo, W.; Tang, Q.F.; Liu, Z.W.; Lin, Z.M. Digital mapping of soil organic matter for rubber plantation at regional scale: An application of random forest plus residuals kriging approach. Geoderma 2015, 237, 49–59. [Google Scholar] [CrossRef]
- Su, H.; Shen, W.; Wang, J.; Ali, A.; Li, M. Machine learning and geostatistical approaches for estimating aboveground biomass in Chinese subtropical forests. For. Ecosyst. 2020, 7, 64. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Pouladi, N.; Møller, A.B.; Tabatabai, S.; Greve, M.H. Mapping soil organic matter contents at field level with Cubist, Random Forest and kriging. Geoderma 2019, 342, 85–92. [Google Scholar] [CrossRef]
- Gomez, C.; Rossel, R.A.V.; McBratney, A.B. Soil organic carbon prediction by hyperspectral remote sensing and field vis-NIR spectroscopy: An Australian case study. Geoderma 2008, 146, 403–411. [Google Scholar] [CrossRef]
- Zhang, T.; Li, L.; Zheng, B. Estimation of agricultural soil properties with imaging and laboratory spectroscopy. J. Appl. Remote Sens. 2013, 7, 073587. [Google Scholar] [CrossRef]
- Beguin, J.; Fuglstad, G.A.; Mansuy, N.; Paré, D. Predicting soil properties in the Canadian boreal forest with limited data: Comparison of spatial and non-spatial statistical approaches. Geoderma 2017, 306, 195–205. [Google Scholar] [CrossRef]
- Geoffroy, J.-L. Carte Pédologique: Plaine des Doukkala; Ministère Agriculture et Réforme Agraire: Rabat, Morocco, 1978. [Google Scholar]
- Bouasria, A.; Ibno Namr, K.; Rahimi, A.; Ettachfini, E.M. Geospatial Assessment of Soil Organic Matter Variability at Sidi Bennour District in Doukkala Plain in Morocco. J. Ecol. Eng. 2021, 22, 120–130. [Google Scholar] [CrossRef]
- Hassink, J. Effects of Soil Texture and Structure on Carbon and Nitrogen Mineralization in Grassland Soils. Biol. Fertil. Soils 1992, 14, 126–134. [Google Scholar] [CrossRef]
- Hassink, J. Effects of Soil Texture and Grassland Management on Soil Organic C and N and Rates of C and N Mineralization. Soil Biol. Biochem. 1994, 26, 1221–1231. [Google Scholar] [CrossRef]
- Naman, F.; Soudi, B.; Chiang, C.N. Humic Balance of Soils under Intensive Farming: The Case of Soils Irrigated Perimeter of Doukkala in Morocco. J. Mater. Environ. Sci. 2015, 6, 3574–3581. [Google Scholar]
- Rerhou, B.; Mosseddaq, F.; Moughli, L.; Ezzahiri, B.; Mokrini, F.; Bel Lahbib, S.; Ibno Namr, K. Effect of Crop Residues Management on Soil Fertility and Sugar Beet Productivity in Western Morocco. Ecol. Eng. Environ. Technol. 2022, 23, 256–271. [Google Scholar] [CrossRef]
- Mzid, N.; Pignatti, S.; Huang, W.; Casa, R. An analysis of bare soil occurrence in arable croplands for re-mote sensing topsoil applications. Remote Sens. 2021, 13, 474. [Google Scholar] [CrossRef]
- Broeg, T.; Don, A.; Gocht, A.; Scholten, T.; Taghizadeh-Mehrjardi, R.; Erasmi, S. Using local ensemble models and Landsat bare soil composites for large-scale soil organic carbon maps in cropland. Geoderma 2024, 444, 116850. [Google Scholar] [CrossRef]
- Dvorakova, K.; Heiden, U.; Pepers, K.; Staats, G.; van Os, G.; van Wesemael, B. Improving soil organic car-bon predictions from a Sentinel–2 soil composite by assessing surface conditions and uncertainties. Geoderma 2023, 429, 116128. [Google Scholar] [CrossRef]
- Heiden, U.; d’Angelo, P.; Schwind, P.; Karlshöfer, P.; Müller, R.; Zepp, S.; Reinartz, P. Soil reflectance composites—Improved thresholding and performance evaluation. Remote Sens. 2022, 14, 4526. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B.; McBratney, A.B. Transfer learning to localise a continental soil vis-NIR calibration model. Geoderma 2019, 340, 279–288. [Google Scholar] [CrossRef]
- Broeg, T.; Blaschek, M.; Seitz, S.; Taghizadeh-Mehrjardi, R.; Zepp, S.; Scholten, T. Transferability of covariates to predict soil organic carbon in cropland soils. Remote Sens. 2023, 15, 876. [Google Scholar] [CrossRef]
- Fernandes, K.; Júnior, J.M.; Ribon, A.A.; de Almeida, G.M.; Moitinho, M.R.; de Lima Dias Delarica, D.; da Silva Oliveira, D.M. Characterization and detailed mapping of C by spectral sensor for soils of the Western Plateau of São Paulo. Sci. Rep. 2024, 14, 17311. [Google Scholar] [CrossRef]
- Sui, Y.; Jiang, R.; Lin, N.; Yu, H.; Zhang, X. Improving the Spatiotemporal Transferability of Hyperspectral Remote Sensing for Estimating Soil Organic Matter by Minimizing the Coupling Effect of Soil Physical Properties on the Spectrum: A Case Study in Northeast China. Agronomy 2024, 14, 1067. [Google Scholar] [CrossRef]
- Bai, Z.; Chen, S.; Hong, Y.; Hu, B.; Luo, D.; Peng, J.; Shi, Z. Estimation of soil inorganic carbon with visible near-infrared spectroscopy coupling of variable selection and deep learning in arid region of China. Geoderma 2023, 437, 116589. [Google Scholar] [CrossRef]
- Aydın, Y.; Işıkdağ, Ü.; Bekdaş, G.; Nigdeli, S.M.; Geem, Z.W. Use of machine learning techniques in soil classification. Sustainability 2023, 15, 2374. [Google Scholar] [CrossRef]
- Guo, L.; Sun, X.; Fu, P.; Shi, T.; Dang, L.; Chen, Y.; Linderman, M.; Zhang, G.; Zhang, Y.; Jiang, Q.; et al. Mapping soil organic carbon stock by hyperspectral and time-series multispectral remote sensing images in low-relief agricultural areas. Geoderma 2021, 398, 115118. [Google Scholar] [CrossRef]
- Musacchio, M.; Silvestri, M.; Romaniello, V.; Casu, M.; Buongiorno, M.F.; Melis, M.T. Comparison of ASI-PRISMA Data, DLR-EnMAP Data, and Field Spectrometer Measurements on “Sale ‘e Porcus”, a Salty Pond (Sardinia, Italy). Remote Sens. 2024, 16, 1092. [Google Scholar] [CrossRef]
- Sharififar, A.; Minasny, B.; Arrouays, D.; Boulonne, L.; Chevallier, T.; van Deventer, P.; Field, D.J.; Gomez, C.; Jang, H.J.; Jeon, S.H.; et al. Soil inorganic carbon, the other and equally important soil carbon pool: Distribution, controlling factors, and the impact of climate change. Adv. Agron. 2023, 178, 165–231. [Google Scholar]
- Marcinkowska-Ochtyra, A.; Gryguc, K.; Ochtyra, A..; Kopeć, D.; Jarocińska, A.; Sławik, Ł. Multitemporal hyperspectral data fusion with topographic indices—Improving classification of natura 2000 grassland habitats. Remote Sens. 2019, 11, 2264. [Google Scholar] [CrossRef]
- Minasny, B.; Bandai, T.; Ghezzehei, T.A.; Huang, Y.C.; Ma, Y.; McBratney, A.B.; Ng, W.; Norouzi, S.; Padarian, J.; Sharififar, A.; et al. Soil Science-Informed Machine Learning. Geoderma 2024, 452, 117094. [Google Scholar] [CrossRef]




| Vis-NIR | SWIR | |
|---|---|---|
| Spectral range Spectral resolution/bands Spatial resolution | 400–1010 nm 12 nm/66 band 30 m | 920–2500 nm 12 nm/171 band 30 m |
| Signal-to-Noise Ratio | >200:1 on 400–1000 nm >600:1 @ 650 nm | >400:1 @ 1550 nm >200:1 @ 2100 nm |
| Dataset | Min | Max | Mean | Median | Stdv | CV | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|
| Training (140 samples) | 0.226 | 2.355 | 1.048 | 0.940 | 0.457 | 43.59 | 1.023 | 0.591 |
| Test (53 samples) | 0.273 | 2.309 | 1.041 | 0.945 | 0.436 | 41.88 | 0.846 | 0.441 |
| Data | RF | SVR | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE (%) | RPIQ | R2 | RMSE (%) | RPIQ | |
| STEP 1: Data smoothing | ||||||
| Original_R | 0.49 | 0.316 | 1.38 | 0.55 | 0.291 | 1.498 |
| SG_R | 0.44 | 0.326 | 1.337 | 0.5 | 0.31 | 1.406 |
| 1st_SG_R | 0.45 | 0.323 | 1.35 | 0.45 | 0.322 | 1.354 |
| 2nd_SG_R | 0.42 | 0.336 | 1.298 | 0.38 | 0.34 | 1.282 |
| SNV_R | 0.26 | 0.37 | 1.178 | 0.26 | 0.38 | 1.147 |
| STEP 2: Data transformation | ||||||
| Original_R | 0.49 | 0.316 | 1.38 | 0.55 | 0.291 | 1.498 |
| 1/R | 0.47 | 0.319 | 1.367 | 0.54 | 0.292 | 1.493 |
| log(R) | 0.46 | 0.324 | 1.346 | 0.55 | 0.29 | 1.503 |
| log(1/R) | 0.44 | 0.332 | 1.313 | 0.55 | 0.29 | 1.503 |
| STEP 3: Feature selection | ||||||
| All Original_R | 0.49 | 0.316 | 1.38 | 0.55 | 0.291 | 1.498 |
| Correlation-based selection | 0.47 | 0.329 | 1.325 | 0.16 | 0.402 | 1.085 |
| RFE | 0.55 | 0.296 | 1.473 | 0.59 | 0.254 | 1.717 |
| Lasso | 0.5 | 0.314 | 1.389 | 0.46 | 0.32 | 1.363 |
| Best model | RF + Original_R + RFE | SVR + Original_R + RFE | ||||
| Data | PLSR | ||
|---|---|---|---|
| R2 | RMSE (%) | RPIQ | |
| STEP 1: Data smoothing | |||
| Original_R | 0.43 | 0.32 | 1.363 |
| SG_R | 0.53 | 0.303 | 1.439 |
| 1st_SG_R | 0.34 | 0.352 | 1.239 |
| 2nd_SG_R | 0.22 | 0.383 | 1.138 |
| SNV_R | 0.29 | 0.373 | 1.169 |
| STEP 2: Data transformation | |||
| SG_R | 0.53 | 0.303 | 1.439 |
| 1/SG_R | 0.44 | 0.323 | 1.35 |
| log (SG_R) | 0.49 | 0.31 | 1.406 |
| log (1/SG_R) | 0.49 | 0.31 | 1.406 |
| STEP 3: Feature selection | |||
| All SG_R data | 0.53 | 0.303 | 1.439 |
| Correlation-based selection | 0.35 | 0.351 | 1.242 |
| RFE | 0.33 | 0.359 | 1.214 |
| Lasso | 0.46 | 0.319 | 1.367 |
| Best model | PLSR + SG_R | ||
| Model | R2 | RMSE (%) | RPIQ |
|---|---|---|---|
| RF (Original_R + RFE) | 0.55 | 0.296 | 1.473 |
| SVR (Original_R + RFE) | 0.59 | 0.254 | 1.717 |
| PLSR (Original_R + RFE) | 0.48 | 0.316 | 1.379 |
| Meta-learner (ridge regression) | 0.65 | 0.194 | 2.247 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouslihim, Y.; Bouasria, A.; Minasny, B.; Castaldi, F.; Nenkam, A.M.; El Battay, A.; Chehbouni, A. Soil Organic Carbon Prediction and Mapping in Morocco Using PRISMA Hyperspectral Imagery and Meta-Learner Model. Remote Sens. 2025, 17, 1363. https://doi.org/10.3390/rs17081363
Bouslihim Y, Bouasria A, Minasny B, Castaldi F, Nenkam AM, El Battay A, Chehbouni A. Soil Organic Carbon Prediction and Mapping in Morocco Using PRISMA Hyperspectral Imagery and Meta-Learner Model. Remote Sensing. 2025; 17(8):1363. https://doi.org/10.3390/rs17081363
Chicago/Turabian StyleBouslihim, Yassine, Abdelkrim Bouasria, Budiman Minasny, Fabio Castaldi, Andree Mentho Nenkam, Ali El Battay, and Abdelghani Chehbouni. 2025. "Soil Organic Carbon Prediction and Mapping in Morocco Using PRISMA Hyperspectral Imagery and Meta-Learner Model" Remote Sensing 17, no. 8: 1363. https://doi.org/10.3390/rs17081363
APA StyleBouslihim, Y., Bouasria, A., Minasny, B., Castaldi, F., Nenkam, A. M., El Battay, A., & Chehbouni, A. (2025). Soil Organic Carbon Prediction and Mapping in Morocco Using PRISMA Hyperspectral Imagery and Meta-Learner Model. Remote Sensing, 17(8), 1363. https://doi.org/10.3390/rs17081363










