Abstract
The recent rapid deployment of low-Earth-orbit (LEO) broadband constellations has positioned these systems as expected emerging navigation sources, thereby driving research interest in integrated navigation and communication (INAC) technologies. Existing INAC waveforms face various challenges in LEO environments, including limited ranging accuracy due to high mutual interference (MI) between signal components, a heavy signal processing burden for navigation users, or degraded data transmission reliability. We propose an INAC waveform named delay–Doppler block division multiplexing (DDBDM) in this work. MI is effectively reduced by modulating pseudo-random noise (PRN) codes and data separately on orthogonal delay–Doppler (DD) blocks. Navigation and communication signals in DDBDM can be separated in the frequency band, which allows the user to receive only the bandwidth occupied by the navigation subcarriers, reducing the signal processing overhead. Moreover, data transmission in the DD domain exhibits a low bit error rate in high-mobility channels, which enables fast and reliable navigation augmentation information for users. Simulation results demonstrate that DDBDM offers superior navigation performance and data transmission reliability compared to existing INAC schemes. The proposed waveform enhances the performance of the LEO INAC system and effectively extends the position, navigation, and timing (PNT) service capability.
1. Introduction
Recent advancements in satellite technology, along with decreased launch costs and the commercialization of low-Earth-orbit (LEO) constellations, have emerged as key driving forces behind the development of mega-constellations. There is a growing trend in the building of LEO constellations worldwide to deliver global broadband Internet services [1,2]. LEO satellites provide signals with high temporal resolution, extending their applications to the fields of position, navigation, and timing (PNT) and remote sensing. Many studies have demonstrated the potential of LEO satellites as promising and reliable sources for navigation [3,4]. The advantages of LEO satellite navigation include strong signal strength, favorable dilution of precision (DOP) factors, fast geometric changes that enhance precise point positioning (PPP) performance, and easy collaboration with the global navigation satellite system (GNSS) [5,6]. These advantages compensate for the limitations of GNSS signals in environments characterized by deep attenuation and interference, fostering the development of integrated navigation and communication (INAC) technology based on broadband modulation. An INAC system can effectively reduce the costs associated with constellation construction; thus, the implementation of navigation based on broadband modulation has become an important research area [7].
Orthogonal frequency division multiplexing (OFDM) offers high spectral efficiency, effective multipath mitigation, and a large mean square bandwidth [8,9], making it widely used in wireless communication and INAC systems. The long-term evolution (LTE) system independently performs positioning using a positioning reference signal (PRS) based on OFDM, which is located in the positioning subframes, and the new radio (NR) further optimizes the PRS for better positioning performance [10,11]. However, there are severe near–far effects between the positioning signals from different base stations, which make the signals from far base stations more difficult to receive, resulting in a positioning accuracy of a few tens of meters. This is not enough for the high-precision positioning of future applications [12,13]. To mitigate the near–far effects, Yin proposed a multi-scale non-orthogonal multiple access (MS-NOMA) scheme [14]. In this scheme, the navigation signal is modulated using OFDM, and employs different pseudo-random noise (PRN) code sequences across various subcarriers to allocate resources to multiple positioning users. However, it imposes a limitation on the number of positioning users. Deng proposed a time code division-OFDM (TC-OFDM) signal [15,16]. TC-OFDM integrates OFDM for communication with binary phase shift keying (BPSK) modulation for navigation, both of which share the same frequency band. However, the spectral fluctuations and high out-of-band (OOB) emissions associated with the BPSK signal lead to interference with the OFDM demodulation, adversely affecting signals in adjacent frequency bands. For the LEO satellite INAC system, Wang proposed a Zadoff–Chu NOMA (ZC-NOMA) scheme [17]. ZC-NOMA superimposes low-power ZC sequences onto the communication subcarriers of OFDM to mitigate the Doppler effect on time-of-arriving (TOA) estimation. However, there is also MI between the communication symbols and the ZC sequences, which limits performance in massive LEO satellite positioning scenarios. Furthermore, the communication reliability of OFDM-based signals is compromised in high-mobility channels due to Doppler spread, which induces inter-carrier interference (ICI) and results in an increased bit error rate (BER).
Orthogonal time–frequency space (OTFS) modulation is specifically designed for reliable communication in high-mobility channels. It multiplexes information symbols over two-dimensional orthogonal basis functions in the delay–Doppler (DD) domain [18], converting a fast time-varying multipath channel into a sparse and slow time-varying channel, thereby facilitating low-complexity detection and channel estimation [19]. Consequently, OTFS is regarded as a candidate waveform for 6G, and has been utilized in the design of INAC schemes [20]. In recent years, research on OTFS has focused on communication areas such as waveform design [21], channel estimation [22,23], detection [24], and diversity [25,26] techniques. Refs. [27,28,29] studied the random access, spatial correlation, and downlink outage probability of OTFS in LEO satellite communication systems. Ref. [30] designed a realizable DD orthogonal pulse and proposed orthogonal delay–Doppler division multiplexing modulation (ODDM), achieving lower OOB emission and BER in practical systems. In addition, integrated sensing and communication (ISAC) based on OTFS has also received attention [31,32,33,34]. The main purpose of these works was to enable localization, velocimetry, imaging, detection, etc., of the environment or targets, rather than acquiring time and space information about the users themselves. Specifically, the ISAC scheme for the Internet of Things (IoT) in [32] achieves low-complexity, high-precision target parameter estimation under the assumption of perfect delay and frequency synchronization. In contrast, navigation receivers do not transmit signals, but synchronize and localize themselves by passively receiving line-of-sight (LOS) signals from satellites [35]. For the same reason, the schemes in [33,34] for target detection and tracking in multi-antenna radar receivers are not suitable as PNT solutions for single-antenna navigation receivers. In [31], a random-padded OTFS (RP-OTFSM) is proposed to improve radar sensing performance by replacing the impulse pilot surrounded by zero guard zone by random-value pilot with a cyclic prefix, but it is not designed to provide continuous and accurate PNT services with dedicated broadcast signals. In terms of research on OTFS-based INAC, Ref. [36] utilizes the distance and velocity information estimated from the delay–Doppler channel matrix of the OTFS system for positioning. However, the signal does not incorporate a dedicated navigation component, resulting in a limited number of navigation users. Ref. [37] superimposes the alternating binary offset carrier (AltBOC) modulated navigation message with the quadrature amplitude-modulated communication data to enhance the reliability of data transmission. Additionally, a time-domain PRN sequence for channel estimation and positioning is inserted before the OTFS frame, and we refer to this scheme as PN-OTFS later. However, due to the successive interference cancelation (SIC) employed to separate navigation messages from communication data, the computational burden on the receiver to process multi-satellite signals is substantial. Furthermore, the proposed signals in [36,37] must process the entire bandwidth to demodulate the data used for navigation, which undoubtedly increases the processing burden on the navigation receiver.
In summary, the existing INAC waveforms still face the following challenges: (1) A high-power communication signal impacts the correlation function of the navigation signal in waveforms that share frequency bands, thereby limiting ranging accuracy. (2) The complexity of receiving navigation signals is quite high. Navigation receivers typically process signals from dozens of satellites [38], while broadband LEO satellites usually operate in the Ka, Ku, and C frequency bands, with signal bandwidths exceeding hundreds of megahertz, imposing a significant burden on signal processing. (3) Data transmission reliability is poor in high-mobility channels. OFDM-based signals experience severe ICI in high-mobility channels, leading to a significant increase in BER.
We focus on the design of an INAC waveform based on OTFS to address these three issues, inspiring LEO PNT applications while ensuring communication reliability in high-mobility channels. Specifically, the contributions of this paper include the following four aspects:
- A delay–Doppler block division multiplexing (DDBDM) waveform is proposed. The navigation PRN codes and communication data are modulated on two-dimensional orthogonal basis functions in the DD domain, and this orthogonality limits MI, making it easier to improve ranging accuracy. Meanwhile, data transmission in the DD domain ensures reliability of communication.
- By independently transforming navigation and communication signals across different DD blocks, they are separated in the frequency domain. This allows users to receive the navigation signal independently, without the loss of useful power, thereby reducing the signal processing overhead. Additionally, the dedicated broadcast signal enables continuous and passive positioning, facilitating easier collaboration with the GNSS.
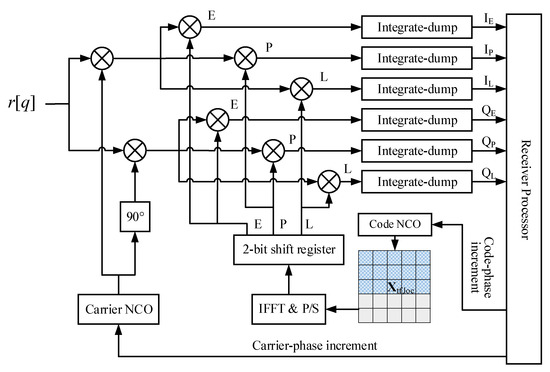
- We propose a navigation receiver architecture for DDBDM that extracts continuous and accurate measurements. The proposed acquisition and tracking structure is compatible with traditional navigation receivers, facilitating the simplification of receiver design and reducing the development costs for user equipment (UE). Furthermore, we implement a software-defined radio (SDR) prototype of the INAC system to validate the design of the proposed architecture.
- Simulation results indicate that the proposed waveform exhibits superior comprehensive performance compared to existing schemes. The ranging accuracy of DDBDM is higher than that of ZC-NOMA, PN-OTFS, and RP-OTFSM, with the same bandwidth. Even with an 80% reduction in the signal bandwidth of DDBDM, the ranging accuracy remains higher than that of PN-OTFS and RP-OTFSM, and it also surpasses that of ZC-NOMA when the signal-to-noise ratio (SNR) is greater than 10 dB and the communication-to-navigation power ratio (CNPR) is 30 dB. In LEO high-mobility multipath channels, DDBDM has a lower BER compared to the other schemes, thus providing reliable communication. It also aids in the transmission of broadcast messages to reduce the time to first fix (TTFF) for navigation receivers and to provide information augmentation services.
The remainder of this paper is organized as follows. Section 2 introduces the system model and elucidates the problem of the original OTFS. Section 3 introduces the proposed waveform and elaborates on the steps of signal generation. Section 4 proposes the navigation signal processing method. Section 5 evaluates the navigation and communication performance and implements the prototype of the INAC system. Finally, the paper is summarized in Section 6.
2. System Model and Problem Formulation
2.1. System Model
The INAC system utilizing LEO satellites is depicted in Figure 1, where the satellites simultaneously provide broadband communication and navigation services to ground users. Communication users need only to establish a bidirectional data transmission link with a single satellite, whereas navigation users must receive broadcast signals from four or more satellites for passive positioning. INAC users are equipped with the capabilities for both communication and navigation. This differs from a multiple-access communication system [39]. As a waveform that is compatible with OFDM, OTFS provides a reliable communication solution for LEO satellites [40].
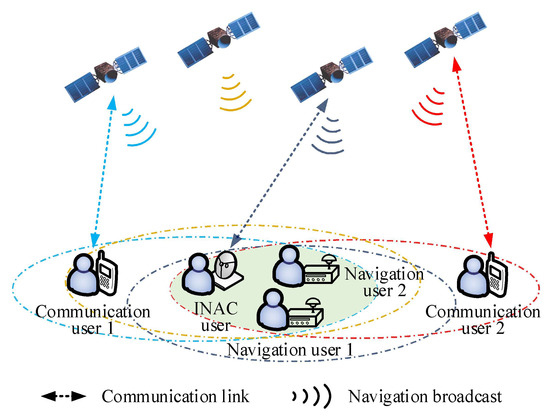
Figure 1.
The INAC system based on LEO satellites. Communication users transmit data to a satellite via uplink and downlink signals, while navigation users receive downlink broadcast signals from a minimum of four satellites for positioning. INAC users possess both functionalities.
OTFS transmits symbols in the DD domain, and the modulated data matrix is denoted as , where M is the delay bins and N is the Doppler bins. Figure 2 (left) shows an OTFS signal with a bandwidth and a frame duration of NT; the delay resolution and Doppler resolution of the DD grid are and , respectively, where and T are the subcarrier spacing and the symbol period, respectively, and .
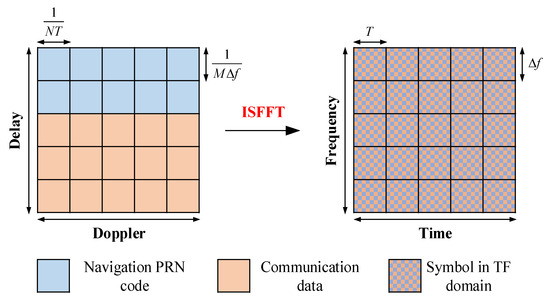
Figure 2.
The ISFFT of the original OTFS modulation; each symbol in the TF grid is derived from all the navigation PRN codes and communication symbols in the DD grid.
The transmitter first converts the DD matrix to the time–frequency (TF) matrix by the inverse symplectic fast Fourier transform (ISFFT):
where m and n are the delay index and the Doppler index, is the subcarrier index, and is the symbol index.
Next, the OFDM modulator uses the Heisenberg transform to convert the TF matrix to a continuous-time waveform:
where is the frequency of the k-th subcarrier. is a rectangular pulse defined as follows:
The original OTFS system does not incorporate a dedicated navigation component, which limits the ranging performance and the number of navigation users. Therefore, it is necessary to insert continuous broadcast signals to meet the requirements of the PNT applications. Additionally, the navigation and communication components in the new scheme should be orthogonal to maintain low MI.
2.2. Problem Formulation
Inspired by the orthogonal TF resource blocks allocated in OFDM, a similar approach is to deploy navigation PRN codes and communication symbols in the DD grid. In this case, the data modulated in the DD grid is written as follows:
where is the delay bins occupied by the navigation signal. The navigation PRN code matrix is as follows:
where , converts a sequence into an size matrix. is a PRN code sequence. is the communication symbol matrix; the symbols are mapped from the transmitted serial data stream. In this case, the communication and navigation signals are orthogonal, and PRN codes with good correlation can be utilized as navigation downlink broadcast signals.
Substituting (4) into the original ISFFT defined in (1) yields the INAC signal expression in the TF domain. Figure 2 provides a graphical representation of this process, from which it can be observed that each symbol in the TF domain of the INAC signal is derived from all the navigation PRN codes and communication symbols in the DD domain. This indicates that the navigation and communication signals are spread across the entire bandwidth.
The positioning of the navigation receiver with TOA estimations, by correlating the received signal with a local replica, requires four or more satellites. A common solution to reduce the signal processing burden is to use a front-end filter with a bandwidth smaller than the main frequency band of the signal to process a portion of the bandwidth; this is a method that is widely employed in navigation signal processing [41]. However, this may lead to degradation in navigation performance. The autocorrelation function (ACF) corresponding to the time-domain signal in (2) is expressed as follows [42]:
where is the power of the navigation PRN code. Since the ISFFT does not alter the power and orthogonality of the signal [19], we have . Without loss of generality, we assume that the front-end filter is ideal, and that the bandwidth of the received signal is (corresponding to the delay bins occupied in the DD domain). In this case, the ACF is given by the following:
The value of the ACF is maximized if . Therefore, the ratio of the peak values of the ACFs in (6) and (7) is as follows:
Typically, Mn < M, which implies that . This indicates that when receiving a portion of the bandwidth, the peak value of the ACF decreases, resulting in a loss of navigation signal power. This occurs because the PRN codes are spread across the entire bandwidth, and the receiver is unable to separate the navigation signal in the frequency domain, as illustrated in Figure 2.
From the analyses in this section, it can be seen that directly splitting the DD grid into two halves for communication and navigation, respectively, suffers from the problem of overburdening the navigation signal processing, while reducing the navigation signal reception bandwidth will result in an obvious loss of navigation performance. Therefore, it is necessary to develop a more flexible INAC scheme that mitigates the signal processing burden on navigation users while ensuring navigation performance. Furthermore, we hope to minimize modifications to the communication transmitter to make it easier to integrate navigation and satellite communication systems.
3. The Proposed Delay–Doppler Block Division Multiplexing
This section proposes a waveform named delay–Doppler block division multiplexing (DDBDM). We first introduce the signal generation process of the DDBDM, and then explain how it addresses the issues present in existing INAC waveforms for PNT applications.
3.1. Signal Generation
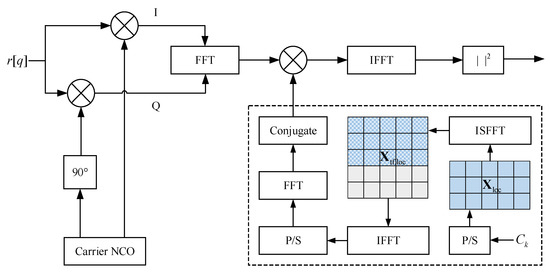
The block diagram of the DDBDM signal generation is shown in Figure 3. The generation of the transmitted signal includes the following steps.

Figure 3.
The block diagram of the DDBDM signal generation.
(1) Navigation message mapping. The navigation message is spread by the PRN code and placed in the DD matrix. The in (5) is rewritten as follows:
where , converts a one-dimensional sequence into an size matrix . is the number of subcarriers (delay bins) occupied by the navigation signal. is a PRN code sequence, and the code division multiple access (CDMA) could be utilized for limiting MI between different satellite signals [43]. is the transmitted navigation message that remains constant within a PRN code chips matrix duration. To provide the integrity of navigation services, navigation messages are still transmitted on the navigation subcarriers after being spread by PRN codes, because the amount of data required for positioning is not large.
(2) Communication symbol mapping. The communication information symbols are taken from the quadrature amplitude modulation (QAM) alphabet of size Q and placed in the DD matrix , where is the number of subcarriers/delay bins occupied by the communication signal.
(3) Block-wise ISFFT. The modulated navigation and communication data and are transformed to matrices and in the TF domain, respectively, by the ISFFT:
where , , and are the normalized DFT matrices with different sizes, and is the Hermitian of the matrix. The above equation is the matrix form of the ISFFT.
(4) Zero subcarrier padding. Having zero-padded subcarriers between the navigation and communication subcarriers creates a guard band for the front-end filter. This reserves a transition bandwidth for the receiving part of the signal, while mitigating possible MI between the navigation and communication blocks in high-mobility channels. Then, the TF matrix becomes the following:
where is the number of zero-padding subcarriers, and satisfies . Here, we assume that the power of navigation and communication signals is normalized.
(5) Subcarrier power allocation. Let P denote the total signal power; denotes the k-th subcarrier power, where at least one out of the navigation subcarrier power and the communication subcarrier power is zero for a specific k. The subcarrier power and total power satisfy . The power allocation of the communication and navigation signals determines the overall performance of the signal; the relationship between power allocation and performance will be discussed in detail in Section 5.
(6) IFFT modulation. The discrete-time transmitted DDBDM samples modulated by the inverse fast Fourier transform (IFFT) are expressed as follows:
where , . Subsequently, is converted into a discrete-time sample vector s[q] by parallel-to-serial (P/S) conversion:
where , denotes the vectorization operator.
(7) Add CP and convert to analog signal. To combat the effects of multipath on the transmitted symbols, the last LCP samples of s[q] are typically added to the beginning of the frame as a cyclic prefix (CP):
The duration of the CP is greater than the maximum delay spread of the multipath channel. Finally, the discrete-time transmitted samples are converted into a continuous-time baseband signal s(t) through a digital-to-analog converter (DAC):
where Ts is the sampling interval. Steps (6) and (7) are essentially regarded as the Heisenberg transform.
Similarly to the power spectral density (PSD) expression for OFDM [44,45], the PSD of the DDBDM signal can be written as follows:
It is composed of communication subcarriers and navigation subcarriers, each allocated a different power.
3.2. Property Analysis
In the remainder of this section, we briefly analyze how DDBDM addresses the issues present in existing INAC waveforms for LEO PNT.
First, the orthogonality between the navigation and communication components keeps the MI between them low. Similarly to the orthogonality between subcarriers in OFDM, the two-dimensional basis functions in the DD domain are also orthogonal, and this orthogonality remains unchanged in the time domain and TF domain [19,46]. However, due to high mobility and time-varying Doppler shifts, interference may still exist between navigation PRN codes and communication data [47,48]. The MI between different signal components can be measured using the spectral separation coefficient (SSC) [49]. The MI becomes lower with a decreasing SSC value; its expression is as follows:
where is the front-end bandwidth, is the normalized PSD of the signal, and is the normalized PSD of the interference. Table 1 gives the results of the theoretical analysis of MI between navigation and communication signals under different channel conditions. The number of navigation and communication subcarriers is 500 for both, the number of zero-padded subcarriers is zero, and the other signal parameters are consistent with Section 5.1. The Doppler shift and its rate are zero for the static channel and 0.91 ppm and 0.09 ppm/s for the LEO channel, respectively, in agreement with Section 5. Meanwhile, we give a case where the navigation and communication bands overlap for comparison. This both represents the case of a shared-band waveform, and can be considered as a worst-case scenario for the navigation and communication components of the OTFS modulation in Figure 2 that is affected by Doppler spread. From the table, we can observe that the MI between the navigation and communication signals is lowest in the static channel, and the SSC is only 0.04 dB higher than the former in the LEO channel, which indicates that the MI is limited. In contrast, when the navigation and communication signal bands overlap, the SSC value is 28.4 dB higher than that of the static channel, which leads to severe MI. As a result, the strong communication signal of DDBDM has less of an impact on the ACF of the navigation signal, its MI is much lower than that of the shared-band INAC waveform, and it also avoids the potential MI of the original OTFS.

Table 1.
SSC values under different conditions.
In addition, DDBDM allows for the independent reception of navigation subcarriers, thereby reducing the signal processing overhead without incurring a loss of navigation signal power. The navigation PRN codes and communication data are placed on different DD blocks to separate the two components in the TF domain, as shown in Figure 3. Consequently, the navigation receiver utilizes a front-end filter with a bandwidth smaller than that of the INAC signal to receive and process only the navigation signal component. In this case, the ACF can be rewritten as follows:
Comparing (7) and (18), it can be found that the difference between and lies only in the denominator of the first term in the ACF, because the navigation signal of the former occupies all M subcarriers, while the latter occupies only Mn subcarriers. The second and fourth terms, on the other hand, depend on the received navigation signal bandwidth , which is the same for both. Therefore, whenever the received signal bandwidth is less than the main lobe of the signal, and . This means that there is a peak value loss of the ACF for OTFS, but not for DDBDM. Figure 4 compares the ACFs of OTFS and DDBDM when receiving half of the bandwidth, with the blue solid line representing the ACF of OTFS, using the total bandwidth as the baseline. It can be observed that the main lobe of the ACF of the half-bandwidth OTFS experiences significant attenuation and becomes flattened, which is detrimental to accurate TOA estimation. In contrast, although the main lobe of DDBDM is also widened, it does not experience attenuation, allowing users to process signals with a smaller bandwidth, and thereby reduce the signal processing burden.
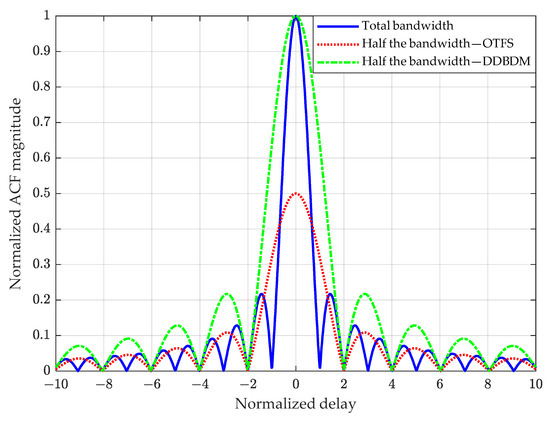
Figure 4.
A comparison of the ACFs of the original OTFS and DDBDM when receiving half the signal bandwidth.
Third, DDBDM eliminates the limitation on the number of navigation users, while retaining the reliability advantages of data transmission. Public PRN codes with good correlation can be used as downlink broadcast signals to provide wide-area passive positioning services, removing the limitation on the number of positioning users present in the OTFS communication system. Meanwhile, DDBDM divides the orthogonal resource blocks in the DD domain along the delay direction, ensuring that the navigation signals can be continuously tracked in the time domain, which allows for higher measurement accuracy than burst pilot/preamble in communication systems. Additionally, since DDBDM still transmits data in the DD domain, the demodulation process remains consistent with the original OTFS [18]. It is anticipated that DDBDM will keep the BER low in the LEO high-mobility channel. For INAC users, the high-speed data transmission of the communication component can be used to assist in broadcasting the necessary data for navigation, thereby reducing the receiver’s TTFF. Additionally, the DDBDM can also be used to transmit the error correction parameters required for high-precision applications, so as to provide better PNT services.
5. Performance Evaluation
This section evaluates the navigation and communication performance of DDBDM, while comparing it with ZC-NOMA [17], PN-OTFS [37], and TFBDM (time–frequency block division multiplexing). The first two are INAC schemes designed for LEO satellites, while TFBDM uses an OFDM-based TF block structure similar to DDBDM. Moreover, to compare the performance of DDBDM more generally, we also use RP-OTFSM in the ISAC system as a benchmark [31], since it uses known random pilot, and thus may be used as the signal for LEO satellites. Finally, an INAC system prototype, based on SDR, is implemented, and it is used to verify the proposed waveform and navigation receiver architecture.
5.1. Parameter Setup
The system simulation parameters were selected from the LEO-based non-terrestrial networks (NTN) scenario (C2&D2), specified by the third-generation partnership project (3GPP) [53,54]. The parameters are summarized in Table 2, where the subcarrier spacing is Δf = 120 kHz, the total number of subcarriers (delay bins) is M = 1024, and the number of time slots (Doppler bins) is N = 16. The number of zero-padding subcarriers is Mp = 24, and the number of subcarriers that can be allocated to navigation and communication is Mn + Mc = 1000. The signal frame duration is NT = 0.133 ms. The duration of the CP should be greater than the maximum delay spread of the multipath channel given in Table 3, set to TCP = 1.482 μs. The navigation message and communication data mapping are BPSK and 4QAM, respectively. The satellite communication channel adopts the tapped delay line (TDL) model. The signal strength in the multiple satellites scenario is based on the actual OneWeb constellation at an orbital altitude of 1200 km, with a user longitude of 112.99° and latitude of 28.22°.

Table 2.
System simulation parameters.

Table 3.
Channel parameters of TDL-C.
The power allocation of the navigation and communication signals has a significant impact on the performance of the INAC signal. In this paper, we define the communication-to-navigation power ratio (CNPR) as the indicator of power allocation:
For ease of analysis, the power of the navigation and communication subcarriers is equally distributed separately. The larger the CNPR, the higher the power allocated to the communication subcarriers. To fairly compare the performance between DDBDM, ZC-NOMA, and PN-OTFS, we evaluate their performance with the same SNR of the received INAC signal.
5.2. Ranging Accuracy
In this section, we first evaluate the ranging accuracy of DDBDM under different conditions, based on the theoretical expressions, and then verify the consistency between the theoretical and simulation results by Monte Carlo simulation. The ranging accuracy of DDBDM can be assessed based on the code tracking accuracy of the DLL, using the NELP discriminator [55]:
where is the equivalent noise bandwidth, is the coherent integration time, is the front-end bandwidth of the receiver, and d is the early–late spacing of the correlator. is the received power of the navigation signal, where is the channel coefficient, is the PSD of the environmental noise, is the normalized PSD of the navigation signal, and and are the power and normalized PSD of the interference signal, respectively. The ranging accuracy of ZC-NOMA is also fairly compared using the above equation, as it has a continuous navigation signal. PN-OTFS and RP-OTFSM use a discontinuous PRN preamble or pilot for positioning, so their ranging accuracy is assessed based on the code tracking accuracy of the open-loop estimator using the NELP discriminator [55,56]. We discuss an SNR range from −6 dB to 30 dB. The carrier power-to-noise density ratio (C/N0) of the navigation signal is 44.8 dB∙Hz at SNR = −6 dB and CNPR = 30 dB, which is equivalent to the power level of GNSS signals. Due to the low orbital altitude of LEO satellites, it is easier to increase the SNR of the received signal.
Firstly, we analyze the effect of the number of visible satellites V on the ranging accuracy. In this case, V is set to 4, 8, and 12, respectively, and CNPR = 30 dB. The navigation signal bandwidth is 24 MHz for both DDBDM and TFBDM, and 120 MHz for ZC-NOMA, PN-OTFS, and RP-OTFSM. The tracking loop parameters are BL = 0.2 Hz, Tcoh = 0.133 ms, and d = 0.5 chip. Figure 7 shows the curves of ranging accuracy for the five INAC schemes as a function of the SNR. It can be seen that the ranging accuracies of ZC-NOMA, PN-OTFS, and RP-OTFSM all decrease with the number of visible satellites, and do not improve significantly with the increase in SNR. This is because the navigation signals of the three schemes are subject to interference from communication signals from other satellites in a multi-satellite scenario, and ZC-NOMA, in particular, additionally receives interference with the communication signal from the same satellite. Therefore, the more visible satellites there are, the stronger the power of the interference signals, and the increase in SNR also raises the power of the communication signals acting as interference, which limits the improvement in ranging accuracy. In contrast, the ranging accuracy of DDBDM and TFBDM is almost independent of the number of visible satellites, thanks to the separation of the navigation and communication subcarriers and the employment of CDMA between the navigation signals from different satellites. For the sake of clarity of the Figure, we no longer distinguish their ranging accuracies at different numbers of visible satellites. The navigation signals of DDBDM and TFDBM have similar PSDs, so their ranging accuracies are the same, and are always higher than those of PN-OTFS and RP-OTFSM. The ranging accuracy of DDBDM surpasses that of the ZC-NOMA, with a larger bandwidth if the SNR exceeds 10 dB. This indicates that DDBDM has low MI, making it easier to improve the ranging accuracy.
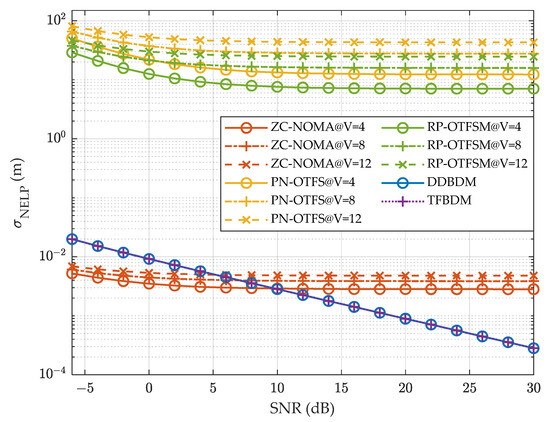
Figure 7.
Ranging accuracy vs. SNR for various numbers of visible satellites. CNPR = 30 dB; bandwidth is 24 MHz for both DDBDM and TFBDM, and 120 MHz for ZC-NOMA, PN-OTFS, and RP-OTFSM.
Secondly, we evaluate the ranging accuracy of the five schemes with different received navigation signal bandwidths. The number of navigation subcarriers Mn is set to 200, 600, and 1000, with the corresponding navigation signal bandwidth determined based on Br = MnΔf. V = 8, CNPR = 30 dB, and the other parameters remain unchanged. Figure 8 shows the curves of ranging accuracy as a function of the SNR under different navigation signal bandwidths. The results indicate that DDBDM and TFBDM have the highest ranging accuracy with the same bandwidth. Even when Mn = 200, the ranging accuracy of DDBDM is still significantly higher than that of PN-OTFS and RP-OTFSM with Mn = 1000, and it also exceeds that of ZC-NOMA when the SNR is greater than 7 dB, a condition that is easily met in LEO scenarios. The results imply that to achieve the same or higher ranging accuracy, the navigation signal bandwidth of DDBDM can be reduced by 80% compared to ZC-NOMA, PN-OTFS, and RP-OTFSM, mitigating the signal processing burden on the navigation receiver. This is supported by the fact that DDBDM has both a dedicated broadcast signal, allowing continuous tracking of the signal, and a very low MI. In addition, the ranging accuracy of RP-OTFSM is slightly higher than that of PN-OTFS, thanks to the fact that the pilot used for ranging in RP-OTFSM has a larger mean square bandwidth than that of the time-domain PN preamble [8,42]. Since PN-OTFS and RP-OTFSM do not have a dedicated broadcast signal component, the ranging accuracy of their open-loop estimators is significantly lower than that of DDBDM, TFBDM, and ZC-NOMA.
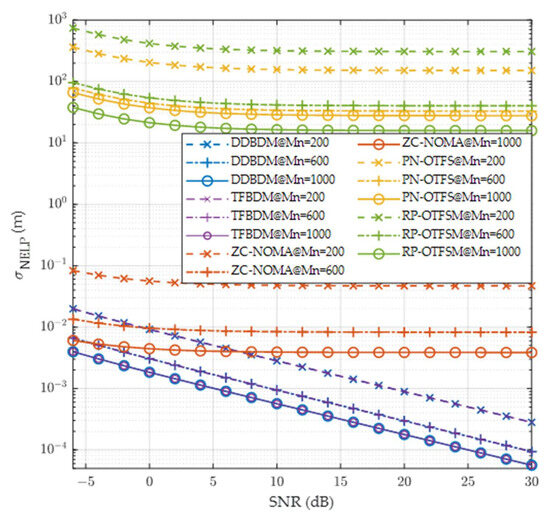
Figure 8.
Ranging accuracy vs. SNR for various navigation signal bandwidths. CNPR = 30 dB, V = 8.
Subsequently, we discuss the impact of different power allocations on ranging accuracy. With V = 8 and SNR = 20 dB, the remaining parameters are consistent with those in Figure 7. Figure 9 illustrates that as the CNPR increases, the ranging accuracy of all signals decreases, because the power is used more for communication rather than for navigation. Under the condition of a fixed SNR, the ranging accuracy curves for the five schemes do not intersect. DDBDM and TFBDM always have the highest ranging accuracy, while RP-OTFSM and PN-OTFS are worse because they are unable to perform continuous tracking. This is consistent with the previous results.
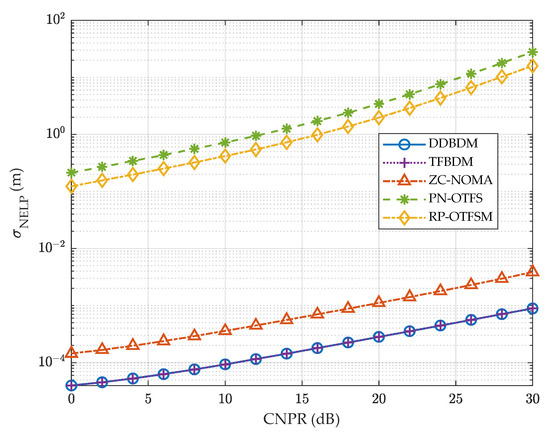
Figure 9.
Ranging accuracy vs. CNPR. SNR = 20 dB, V = 8.
Finally, we verify the consistency of the theoretical analysis with the simulation. The Monte Carlo simulation uses the tracking loop given in Figure 6, with the loop parameters BL = 0.2 Hz, Tcoh = 0.133 ms, and d = 0.5 chip. The tracking loop conforms to the generalized structure specified in [55], and thus allows for evaluation with the theoretical results given in (30). The number of navigation subcarriers of DDBDM is set to 200 and 600, the CNPR is set to 20 and 30, and each point corresponds to 104 periods of signal processing. The ranging accuracy is statistically derived as shown in Figure 10. THE and SIM in the Figure represent the theoretical and simulation results for the given conditions, respectively. It can be observed that under different navigation signal bandwidths and power allocation conditions, the ranging accuracy of the simulation agrees well with the theoretical results in general, which suggests that the assessment of the ranging accuracy using (30) is justified.
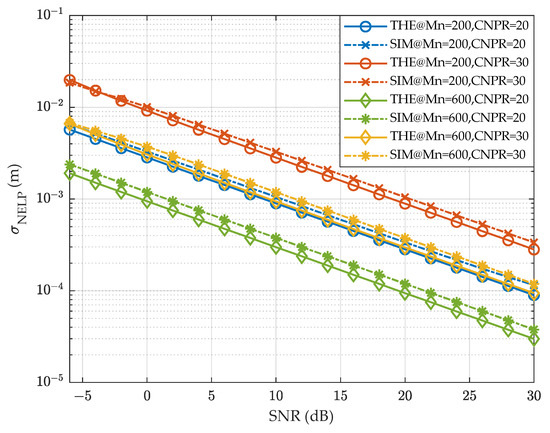
Figure 10.
Comparison of theoretical and simulation results of DDBDM.
From the above discussion, DDBDM offers excellent navigation performance in the scenario of the massive LEO satellites. The low MI of DDBDM ensures that its ranging accuracy effectively improves as the SNR of the INAC signal increases, and its block structure makes it virtually unaffected by communication signals from other satellites. Additionally, the separation of the navigation and communication subcarriers of DDBDM makes the signal processing overhead of the navigation receiver much lower than that of other schemes, making it easier to collaborate with the GNSS to enhance PNT service.
5.3. Data Transmission Reliability
The reliability of data transmission not only affects the quality of service for broadband communication, but is also crucial for quickly receiving navigation messages and high-precision correction parameters in PNT applications. It is usually evaluated by the BER. Therefore, we compare the BER performance of different signals under the same received SNR and the amount of transmitted data. The BER performance depends on the SNR with the determined modulation and coding scheme. The actual SNR of the communication signal of satellite i is calculated as follows:
where denotes the channel coefficient on the k-th subcarrier from satellite i to the UE link, including antenna gain, free space propagation loss, shadow fading, and other effects.
Channel estimation and signal detection algorithms are not the focus of this work, so ideal channel estimation is used here, and a linear minimum mean square error (LMMSE) detector is employed [57]. Meanwhile, the number of visible satellites discussed here is V = 1, as the communication receivers could mitigate the impact of signals from other satellites using SIC. Due to the Doppler frequency of the Ka-band signal caused by the dynamic of the satellite far exceeding the subcarrier spacing, the satellite side compensated Doppler frequency shift scenario recommended by 3GPP is adopted, with a residual Doppler frequency of 0.91 ppm [54]. The parameters of the TDL-C channel model used in the simulation are provided in Table 3. For each SNR and subcarrier point, the BER simulation exceeds 104 frames.
Figure 11 shows the BER curves for the five schemes as a function of the SNR. It can be observed that DDBDM has the lowest BER for the same CNPR, which is attributed to the good orthogonality maintained by the DD basis functions in high-mobility multipath channels. ZC-NOMA has the highest BER, followed by TFBDM, as the OFDM-based design introduces ICI in high-mobility scenarios, adversely affecting data demodulation. Additionally, the navigation signal from ZC-NOMA interferes with the communication signal, resulting in a higher BER than that of TFBDM, which is also based on OFDM. The difference in BER performance between the two becomes especially more significant as the CNPR decreases. The BER of RP-OTFSM is slightly higher than that of DDBDM, due to its larger noise bandwidth. The BER performance of PN-OTFS falls between that of RP-OTFSM and TFBDM. Although it employs OTFS modulation for data transmission, the overlay of navigation messages on the communication data constellation increases the BER during the demodulation process. This effect is especially noticeable under low-CNPR conditions, leading to a special case where its BER is even higher than that of OFDM-based TFBDM, at CNPR = 0 dB.
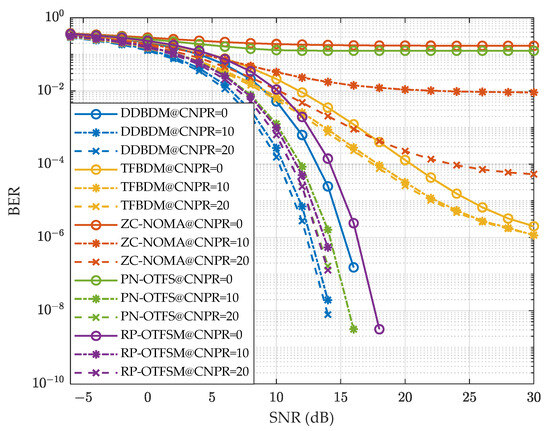
Figure 11.
BER vs. SNR with different CNPRs.
Figure 12 shows the BER curves varying with different numbers of communication subcarriers Mc, where SNR = 10 dB and CNPR = 20 dB. It can be seen that the BER performance of DDBDM and TFBDM deteriorates as the bandwidth of the communication signal increases. This is because an increase in the noise bandwidth leads to a decrease in the effective SNR defined in (31), while the power of the communication signal remains constant. However, DDBDM still has the lowest BER compared to all other schemes. Moreover, the BER performance of PN-OTFS is almost the same as that of RP-OTFSM in this case, since the former allocates little power to the navigational message, and has little effect on the communication constellation diagram.
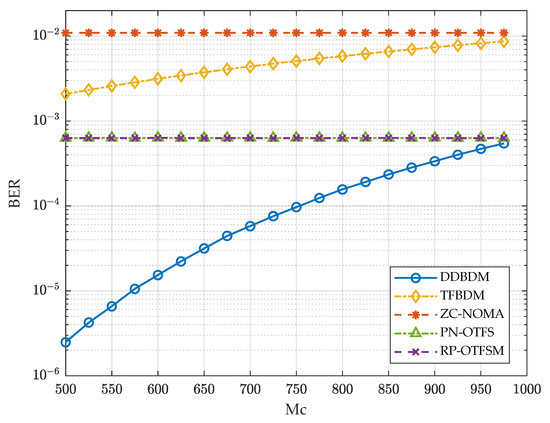
Figure 12.
BER vs. Mc, with SNR = 10 dB and CNPR = 20 dB.
Finally, we summarize the performance of DDBDM signals under different CNPR and bandwidth (subcarriers) conditions. The primary function of LEO constellations is to provide broadband communication services, which typically means that the power and bandwidth allocated for navigation are less than those for communication. To ensure communication capacity when allocating bandwidth, it is necessary to allocate most subcarriers to communication signals. Based on the above results, it is appropriate to allocate 200 and 800 subcarriers for navigation and communication signals, respectively. In contrast to ZC-NOMA and PN-OTFS, we can allocate more power to the navigation signals of DDBDM to further improve the navigation performance, as the BER performance of DDBDM does not significantly degrade with a decrease in CNPR. Therefore, DDBDM not only achieves the lowest BER in broadband communication, but also provides fast and reliable augmentation information for PNT applications.
5.4. Prototype Implementation
The comparison of ranging accuracy and data transmission reliability has been simulated in the previous subsections, and here, we focus on the validation of the feasibility of the proposed navigation receiver architecture in a practical system. We implement a prototype of the INAC system for DDBDM based on the SDR, and develop a software receiver utilizing the architecture proposed in Section 4. The hardware system based on the SDR is shown in Figure 13. The system includes two universal software radio peripherals (USRPs), transmitting and receiving terminals (Tx and Rx computers), a radio frequency (RF) attenuator, and a low-noise amplifier (LNA). The transmitting terminal generates the DDBDM discrete-time baseband signal file. The USRP hardware driver (UHD) program transmits the signal to the USRP via a network cable, and conducts digital-to-analog conversion. Another USRP down-converts and samples the analog signal, which passes through an RF attenuator and LNA. Subsequently, the UHD transmits the signal to the receiving terminal and saves it as a signal file. Finally, the software receiver processes the signal file to verify the feasibility of using DDBDM for navigation. The RF attenuator and LNA in the RF link jointly form an AWGN channel, where the RF attenuator can be adjusted to obtain the desired SNR. The effects of the high-mobility channel (maximum Doppler shift and Doppler rate of 0.91 ppm and 0.09 ppm/s, respectively) are considered in the INAC signal generation. As the navigation receiver processes LOS signals, it is justified for the validation of the navigation function in this channel.

Figure 13.
A photograph of the INAC system prototype.
The Ka-band exceeds the carrier frequency of most commercial SDRs, and the RF is reduced from 20 GHz to 2 GHz. The maximum Doppler shift and Doppler rate are still set to 0.91 ppm and 0.09 ppm/s, respectively [54]. The master clock rate of USRP N210 is 100 MHz, and the sampling rate supported is limited to dividing the master clock rate by an integer factor. Therefore, the sampling rate of the transmitted signal is set to fs = 20 MHz, the subcarrier spacing is Δf =100 kHz, and the numbers of total subcarriers, navigation subcarriers, and zero-padding subcarriers are M = 188, Mn = 88, and Mp = 12, respectively. The sampling frequency for the navigation signal receiver is set to 10 MHz, and the RF center frequency should be offset by half of the navigation signal bandwidth, i.e., 1.995 GHz, based on 2 GHz. The SNR is 5 dB, and the CNPR is 23 dB, so the C/N0 of the navigation signal is 55 dB∙Hz. The coherent integration time Tcoh = 0.16 ms (a signal frame duration), the noncoherent integration time is 1.6 ms, and the Doppler frequency search step of the PCS method is set to 6.25 kHz. The equivalent noise bandwidth of DLL is 0.2 Hz, the early–late spacing of the correlator is 0.5 chip, the PLL bandwidth is 60 Hz, and the other parameters are consistent with Table 2.
Figure 14 shows the acquisition result of the DDBDM signal. The code phase (delay) is at the 2863rd sample. The peak of the correlation values is located at −12.5 kHz and the fine Doppler frequency is calculated as −12.6 kHz. This result is used to initialize the tracking loop. Figure 15 shows the corresponding tracking results. The navigation message demodulation constellation and message bits are located on the top-left and top-right of the panel, respectively. The result indicates that even if the transmitted navigation message is spread by the PRN code mapping in the DD domain, the UE still measures the pseudo-range and demodulates the navigation message in the time domain. The bottom-left of the panel shows the Doppler frequency output by the PLL through the loop filter, which is consistent with the dynamic of 1.8 kHz/s (0.09 ppm/s × 20 GHz). The bottom-right of the panel shows the magnitude of the correlation function output from the DLL. The magnitude of the prompt branch is the highest, so the code tracking is successful. This indicates that the proposed receiver architecture is capable of independently receiving the DDBDM navigation signals and outputting accurate measurements of delay and frequency.
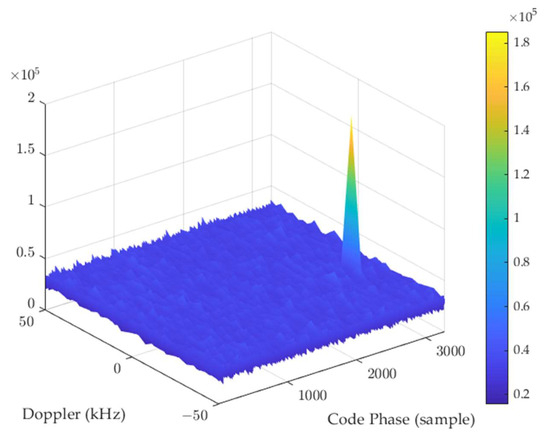
Figure 14.
Acquisition result of DDBDM signal.
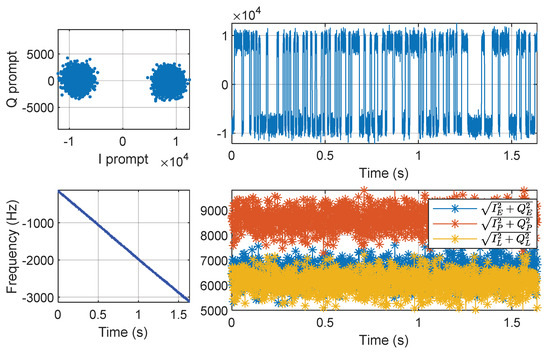
Figure 15.
Tracking results of DDBDM signal: discrete-time scatter plot (top-left), bits of navigation message (top-right), filtered PLL discriminator (bottom-left), and correlation results (bottom-right).
The experimental results verify the feasibility of the proposed waveform and navigation receiver architecture, indicating that DDBDM has the advantages of flexible reception and a low processing bandwidth. Furthermore, since the rectangular pulse in the TF domain is difficult to satisfy the bi-orthogonal robust property in practical applications [30], an interesting direction in the future is to design INAC waveforms directly based on the DD plane orthogonal pulse to improve their performance in practical systems, instead of converting them to the TF domain.
6. Conclusions
This work proposes an INAC waveform named DDBDM. By modulating navigation PRN codes and communication data on orthogonal DD blocks, MI between the two signal components is limited, which helps to improve ranging accuracy in scenarios with a large number of LEO satellites. The independent transformation of DD blocks allows users to receive only the navigation signals within the frequency band, thereby mitigating the signal processing burden. In addition, the reliable data transmission capability of DDBDM in LEO high-mobility channels helps to shorten the TTFF and provide information augmentation services for navigation receivers. Finally, we propose a navigation receiver architecture for DDBDM to achieve accurate delay and Doppler measurements. Evaluation results indicate that the ranging accuracy of DDBDM is higher than that of ZC-NOMA, PN-OTFS, and RP-OTFSM under the same bandwidth condition. Even with an 80% reduction in bandwidth, the ranging accuracy of DDBDM remains higher than that of PN-OTFS and RP-OTFSM, and it also surpasses that of ZC-NOMA when SNR > 10 dB and CNPR = 30 dB. This condition becomes easier to achieve with an increasing number of visible satellites and by allocating more power to the navigation signals. Meanwhile, DDBDM exhibits the lowest BER level, and the decrease in CNPR does not lead to a significant degradation in BER. It significantly improves the reliability of data transmission, although it has a similar ranging accuracy to TFBDM. Compared to existing INAC waveforms, DDBDM offers superior comprehensive performance, enhancing the PNT service capabilities of LEO constellations.
Author Contributions
Conceptualization, D.F., G.O. and Y.M.; methodology, D.F. and H.L.; software, D.F. and S.W.; validation, J.P. and G.O.; formal analysis, D.F. and H.L.; investigation, D.F. and S.W.; resources, H.L.; data curation, D.F.; writing—original draft preparation, D.F. and H.L.; writing—review and editing, J.P. and G.O.; visualization, D.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China, grant number 2023YFC2205400, and the National Natural Science Foundation of China, grant number U20A20193.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Curzi, G.; Modenini, D.; Tortora, P. Large Constellations of Small Satellites: A Survey of Near Future Challenges and Missions. Aerospace 2020, 7, 133. [Google Scholar] [CrossRef]
- Kassas, Z.M.; Khairallah, N.; Kozhaya, S. Ad Astra: Simultaneous Tracking and Navigation with Megaconstellation LEO Satellites. IEEE Aerosp. Electron. Syst. Mag. 2024, 39, 46–71. [Google Scholar] [CrossRef]
- Reid, T.G.R.; Walter, T.; Enge, P.K.; Lawrence, D.; Cobb, H.S.; Gutt, G.; O’Connor, M.; Whelan, D. Navigation from Low Earth Orbit: Part 1: Concept, Current Capability, and Future Promise. In Position, Navigation, and Timing Technologies in the 21st Century; Morton, Y.T.J., Diggelen, F., Spilker, J.J., Parkinson, B.W., Lo, S., Gao, G., Eds.; Wiley: Hoboken, NJ, USA, 2020; pp. 1359–1379. ISBN 978-1-119-45849-4. [Google Scholar]
- Kassas, Z.M. Navigation from Low-Earth Orbit: Part 2: Models, Implementation, and Performance. In Position, Navigation, and Timing Technologies in the 21st Century; Wiley: Hoboken, NJ, USA, 2020; pp. 1381–1412. ISBN 978-1-119-45849-4. [Google Scholar]
- Joerger, M.; Gratton, L.; Pervan, B.; Cohen, C.E. Analysis of Iridium-Augmented GPS for Floating Carrier Phase Positioning. Navig. J. Inst. Navig. 2010, 57, 137–160. [Google Scholar] [CrossRef]
- Reid, T.; Gunning, K.; Perkins, A.; Lo, S.; Walter, T. Going Back for the Future: Large/Mega LEO Constellations for Navigation. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation, Miami, FL, USA, 16–20 September 2019; pp. 2452–2468. [Google Scholar]
- Deng, L.; Yang, Y.; Ma, J.; Feng, Y.; Ye, L.; Li, H. OFDM-BOC: A Broadband Multicarrier Navigation Modulation-Based BOC for Future GNSS. IEEE Trans. Veh. Technol. 2024, 73, 3964–3979. [Google Scholar] [CrossRef]
- Wang, D.; Michel, F. OFDM Transmission for Time-Based Range Estimation. IEEE Signal Process. Lett. 2010, 17, 571–574. [Google Scholar] [CrossRef]
- Liu, X.; Liang, M.; Morton, Y.; Closas, P.; Zhang, T.; Hong, Z. Performance Evaluation of MSK and OFDM Modulations for Future GNSS Signals. GPS Solut. 2014, 18, 163–175. [Google Scholar] [CrossRef]
- Del Peral-Rosado, J.A.; L’opez-Salcedo, J.A.; Seco-Granados, G. Analysis of Positioning Capabilities of 3GPP LTE. In Proceedings of the 25th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012. [Google Scholar]
- Fischer, S. 5G NR Positioning. In 5G and Beyond; Lin, X., Lee, N., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 429–483. ISBN 978-3-030-58196-1. [Google Scholar]
- Shamaei, Z.M.; Khalife, K.; Kassas, J. Exploiting LTE Signals for Navigation: Theory to Implementation. IEEE Trans. Wirel. Commun. 2018, 17, 2173–2189. [Google Scholar]
- Kassas, K.S.M. Receiver Design and Time of Arrival Estimation for Opportunistic Localization with 5G Signals. IEEE Trans. Wirel. Commun. 2021, 20, 4716–4731. [Google Scholar]
- Yin, L.; Cao, J.; Lin, K.; Deng, Z.; Ni, Q. A Novel Positioning-Communication Integrated Signal in Wireless Communication Systems. IEEE Wirel. Commun. Lett. 2019, 8, 1353–1356. [Google Scholar] [CrossRef]
- Zhongliang, D.; Yanpei, Y.; Xie, Y.; Neng, W.; Lei, Y. Situation and Development Tendency of Indoor Positioning. China Commun. 2013, 10, 42–55. [Google Scholar]
- Han, K.; Yin, J.; Deng, Z.; Dong, J.; Tang, S.; Ma, Z. The Base Stations’ Networking Scheme and Spreading Code Optimization Strategy of TC-OFDM. In China Satellite Navigation Conference (CSNC) 2020 Proceedings: Volume I; Springer Nature: Cambridge, UK, 2020. [Google Scholar]
- Wang, M.; Liu, G.; Ma, R.; Zhao, W.; Kang, W. A Novel Navigation-Communication Integrated Waveform for LEO Network. In Proceedings of the GLOBECOM 2022-2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4 December 2022; IEEE: New York, NY, USA, 2022; pp. 747–752. [Google Scholar]
- Hadani, R.; Rakib, S.; Tsatsanis, M.; Monk, A.; Goldsmith, A.J.; Molisch, A.F.; Calderbank, R. Orthogonal Time Frequency Space Modulation. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Hong, Y.; Thaj, T.; Viterbo, E. Delay-Doppler Communications: Principles and Applications; Academic Press: London, UK, 2022; ISBN 978-0-323-85028-5. [Google Scholar]
- Prasad, R.; Das, S.S. Orthogonal Time Frequency Space Modulation: OTFS a Waveform for 6G, 1st ed.; River Publishers: New York, NY, USA, 2022; ISBN 978-1-00-333902-1. [Google Scholar]
- Raviteja, P.; Hong, Y.; Viterbo, E.; Biglieri, E. Practical Pulse-Shaping Waveforms for Reduced-Cyclic-Prefix OTFS. IEEE Trans. Veh. Technol. 2019, 68, 957–961. [Google Scholar] [CrossRef]
- Raviteja, P.; Phan, K.T.; Hong, Y. Embedded Pilot-Aided Channel Estimation for OTFS in Delay–Doppler Channels. IEEE Trans. Veh. Technol. 2019, 68, 4906–4917. [Google Scholar] [CrossRef]
- Sanoopkumar, P.S.; Farhang, A. A Practical Pilot for Channel Estimation of OTFS. In Proceedings of the ICC 2023-IEEE International Conference on Communications, Rome, Italy, 28 May 2023; IEEE: New York, NY, USA, 2023; pp. 1319–1325. [Google Scholar]
- Raviteja, P.; Phan, K.T.; Hong, Y.; Viterbo, E. Interference Cancellation and Iterative Detection for Orthogonal Time Frequency Space Modulation. IEEE Trans. Wirel. Commun. 2018, 17, 6501–6515. [Google Scholar] [CrossRef]
- Raviteja, P.; Hong, Y.; Viterbo, E.; Biglieri, E. Effective Diversity of OTFS Modulation. IEEE Wirel. Commun. Lett. 2020, 9, 249–253. [Google Scholar] [CrossRef]
- Surabhi, G.D.; Augustine, R.M.; Chockalingam, A. On the Diversity of Uncoded OTFS Modulation in Doubly-Dispersive Channels. IEEE Trans. Wirel. Commun. 2019, 18, 3049–3063. [Google Scholar] [CrossRef]
- Shen, B.; Wu, Y.; An, J.; Xing, C.; Zhao, L.; Zhang, W. Random Access with Massive MIMO-OTFS in LEO Satellite Communications. IEEE J. Select. Areas Commun. 2022, 40, 2865–2881. [Google Scholar] [CrossRef]
- Bora, A.S.; Phan, K.T.; Hong, Y. Spatially Correlated MIMO-OTFS for LEO Satellite Communication Systems. In Proceedings of the 2022 IEEE International Conference on Communications Workshops (ICC Workshops), Seoul, Republic of Korea, 16 May 2022; IEEE: New York, NY, USA, 2022; pp. 723–728. [Google Scholar]
- Shi, J.; Hu, J.; Yue, Y.; Xue, X.; Liang, W.; Li, Z. Outage Probability for OTFS Based Downlink LEO Satellite Communication. IEEE Trans. Veh. Technol. 2022, 71, 3355–3360. [Google Scholar] [CrossRef]
- Lin, H.; Yuan, J. Orthogonal Delay-Doppler Division Multiplexing Modulation. IEEE Trans. Wirel. Commun. 2022, 21, 11024–11037. [Google Scholar] [CrossRef]
- Karpovich, P.; Zielinski, T.P. Random-Padded OTFS Modulation for Joint Communication and Radar/Sensing Systems. In Proceedings of the 2022 23rd International Radar Symposium (IRS), Gdansk, Poland, 12 September 2022; IEEE: New York, NY, USA, 2022; pp. 104–109. [Google Scholar]
- Wu, K.; Zhang, J.A.; Huang, X.; Guo, Y.J. OTFS-Based Joint Communication and Sensing for Future Industrial IoT. IEEE Internet Things J. 2023, 10, 1973–1989. [Google Scholar] [CrossRef]
- Keskin, M.F.; Marcus, C.; Eriksson, O.; Alvarado, A.; Widmer, J.; Wymeersch, H. Integrated Sensing and Communications With MIMO-OTFS: ISI/ICI Exploitation and Delay-Doppler Multiplexing. IEEE Trans. Wirel. Commun. 2024, 23, 10229–10246. [Google Scholar] [CrossRef]
- Lin, L.; Tong, J.; Lin, H.; Zheng, H.; Shi, Z. Joint Target Localization and Channel Estimation for ODDM-ISAC Systems. IEEE Signal Process. Lett. 2025, 1–5. [Google Scholar] [CrossRef]
- Kozhaya, S.; Kassas, Z.M. On the Fundamental Tracking Performance and Design Considerations of Radio Navigation. IEEE J. Select. Areas Commun. 2024, 42, 2395–2409. [Google Scholar] [CrossRef]
- Hou, X.; Yang, H.; Jing, X.; Mu, J. Waveform Design of Integrated Communication and Navigation Based on Orthogonal Time Frequency Space. In Proceedings of the 2023 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Beijing, China, 14 June 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar]
- Li, Y.; Zhang, G.; Yu, J.; Li, G.; Li, Y. OTFS-Based Communication and Navigation Integrated Signal Transmission for LEO Satellites. In Proceedings of the 2022 IEEE 22nd International Conference on Communication Technology (ICCT), Nanjing, China, 11 November 2022; IEEE: New York, NY, USA, 2022; pp. 451–457. [Google Scholar]
- Reid, T.G.R.; Neish, A.M.; Walter, T.; Enge, P.K. Broadband LEO Constellations for Navigation: Broadband LEOs for Navigation. J. Inst. Navig. 2018, 65, 205–220. [Google Scholar] [CrossRef]
- Khammammetti, V.; Mohammed, S.K. OTFS-Based Multiple-Access in High Doppler and Delay Spread Wireless Channels. IEEE Wirel. Commun. Lett. 2019, 8, 528–531. [Google Scholar] [CrossRef]
- Shi, J.; Li, Z.; Hu, J.; Tie, Z.; Li, S.; Liang, W.; Ding, Z. OTFS Enabled LEO Satellite Communications: A Promising Solution to Severe Doppler Effects. IEEE Netw. 2024, 38, 203–209. [Google Scholar] [CrossRef]
- Li, Y.; Shivaramaiah, N.C.; Akos, D.M. Design and Implementation of an Open-Source BDS-3 B1C/B2a SDR Receiver. GPS Solut. 2019, 23, 60. [Google Scholar] [CrossRef]
- Fu, D.; Lin, H.; Ma, M.; Yuan, M.; Ou, G. Pulsed Orthogonal Time Frequency Space: A Fast Acquisition and High-Precision Measurement Signal for Low Earth Orbit Position, Navigation, and Timing. Remote Sens. 2024, 16, 4432. [Google Scholar] [CrossRef]
- Foucras, M.; Leclère, J.; Botteron, C.; Julien, O.; Macabiau, C.; Farine, P.-A.; Ekambi, B. Study on the Cross-Correlation of GNSS Signals and Typical Approximations. GPS Solut. 2017, 21, 293–306. [Google Scholar] [CrossRef]
- Talbot, S.L.; Farhang-Boroujeny, B. Spectral Method of Blind Carrier Tracking for OFDM. IEEE Trans. Signal Process. 2008, 56, 2706–2717. [Google Scholar] [CrossRef]
- Liu, C.; Li, F. On Spectrum Modeling of OFDM Signals for Digital Broadcasting. In Proceedings of the 7th International Conference on Signal Processing, ICSP’04, Beijing, China, 31 August–4 September 2004; IEEE: San Marcos, CA, USA, 2004; Volume 3, pp. 1886–1889. [Google Scholar]
- Cho, Y.S. MIMO-OFDM Wireless Communications with MATLAB; Wiley: Chichester, UK, 2010; ISBN 978-0-470-82563-1. [Google Scholar]
- Liu, H.; Liu, Y.; Yang, M.; Zhang, Q. On the Characterizations of OTFS Modulation Over Multipath Rapid Fading Channel. IEEE Trans. Wirel. Commun. 2023, 22, 2008–2021. [Google Scholar] [CrossRef]
- Bora, A.S.; Phan, K.T.; Hong, Y. Diversity Analysis of OTFS Over Block Time-Varying Channels. IEEE Trans. Veh. Technol. 2024, 73, 14062–14067. [Google Scholar] [CrossRef]
- Betz, J.W.; Kolodziejski, K.R. Generalized Theory of Code Tracking with an Early-Late Discriminator Part I: Lower Bound and Coherent Processing. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1538–1556. [Google Scholar] [CrossRef]
- Elliott, D.; Kaplan, E.D.K. Understanding GPS: Principles and Applications, 2nd ed.; Artech House: New York, NY, USA, 2005. [Google Scholar]
- Rife, D.; Boorstyn, R. Single Tone Parameter Estimation from Discrete-Time Observations. IEEE Trans. Inform. Theory 1974, 20, 591–598. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Y.; Deng, L.; Ye, L.; Li, Z.; Xiao, Y.; Dong, W. Design and Performance Analysis of Navigation Signal Based on OFDM. Appl. Sci. 2022, 12, 9486. [Google Scholar] [CrossRef]
- 3GPP. Study on New Radio (NR) to Support Non-Terrestrial Networks; 3GPP: Sophia Antipolis, France, 2020; pp. 88–95. [Google Scholar]
- 3GPP. Solutions for NR to Support Non-Terrestrial Networks (NTN); 3GPP: Sophia Antipolis, France, 2023; pp. 34–58. [Google Scholar]
- Betz, J.W.; Kolodziejski, K.R. Generalized Theory of Code Tracking with an Early-Late Discriminator Part II: Noncoherent Processing and Numerical Results. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1557–1564. [Google Scholar] [CrossRef]
- Ruan, H.; Li, J.; Zhang, L.; Long, T. Adaptive Correlation Space Adjusted Open-Loop Tracking Approach for Vehicle Positioning with Global Navigation Satellite System in Urban Areas. Sensors 2015, 15, 21581–21612. [Google Scholar] [CrossRef]
- Tiwari, S.; Das, S.S.; Rangamgari, V. Low Complexity LMMSE Receiver for OTFS. IEEE Commun. Lett. 2019, 23, 2205–2209. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).