Advanced Building Detection with Faster R-CNN Using Elliptical Bounding Boxes for Displacement Handling
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Research Objectives
2. Related Work
2.1. Challenges in Building Detection and the Role of Bounding Box Design
2.2. Limitations of Building Detection Based on Nadir Imagery
2.3. Object Detection in Off-Nadir Imagery
2.4. Rotated and Non-Rectangular Bounding Boxes in Remote Sensing
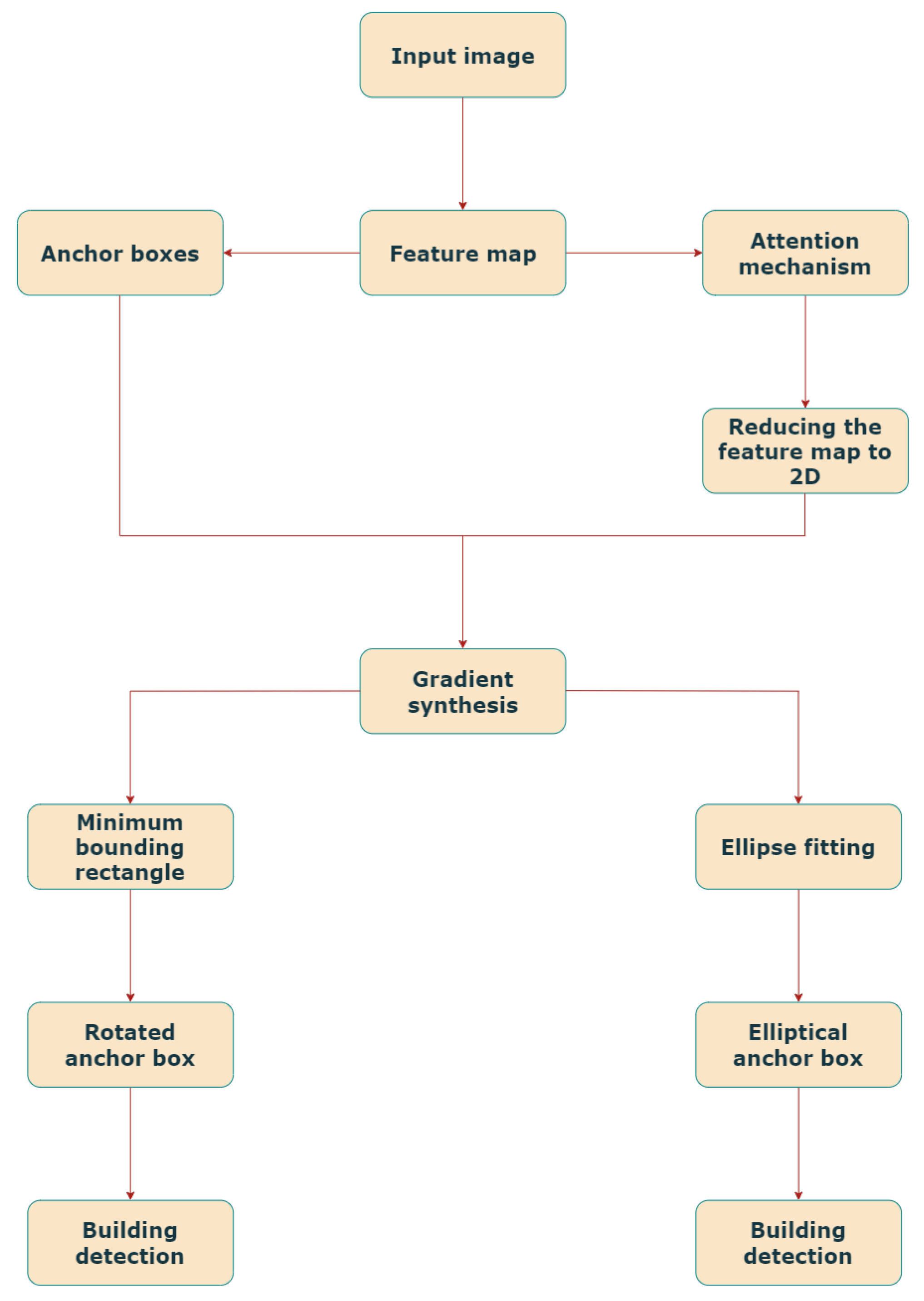
3. Methodology
- Feature extraction using ResNet-50-FPN to capture multi-scale building representations.
- Region proposal using elliptical bounding boxes to improve adaptability to complex shapes.
- Final detection and classification via a Faster R-CNN framework optimized for off-nadir building detection.
- Regular buildings, with aspect ratios close to 1 and minimal rotation angles.
- Irregular buildings, with extreme aspect ratios or significant rotation angles.
3.1. Faster R-CNN
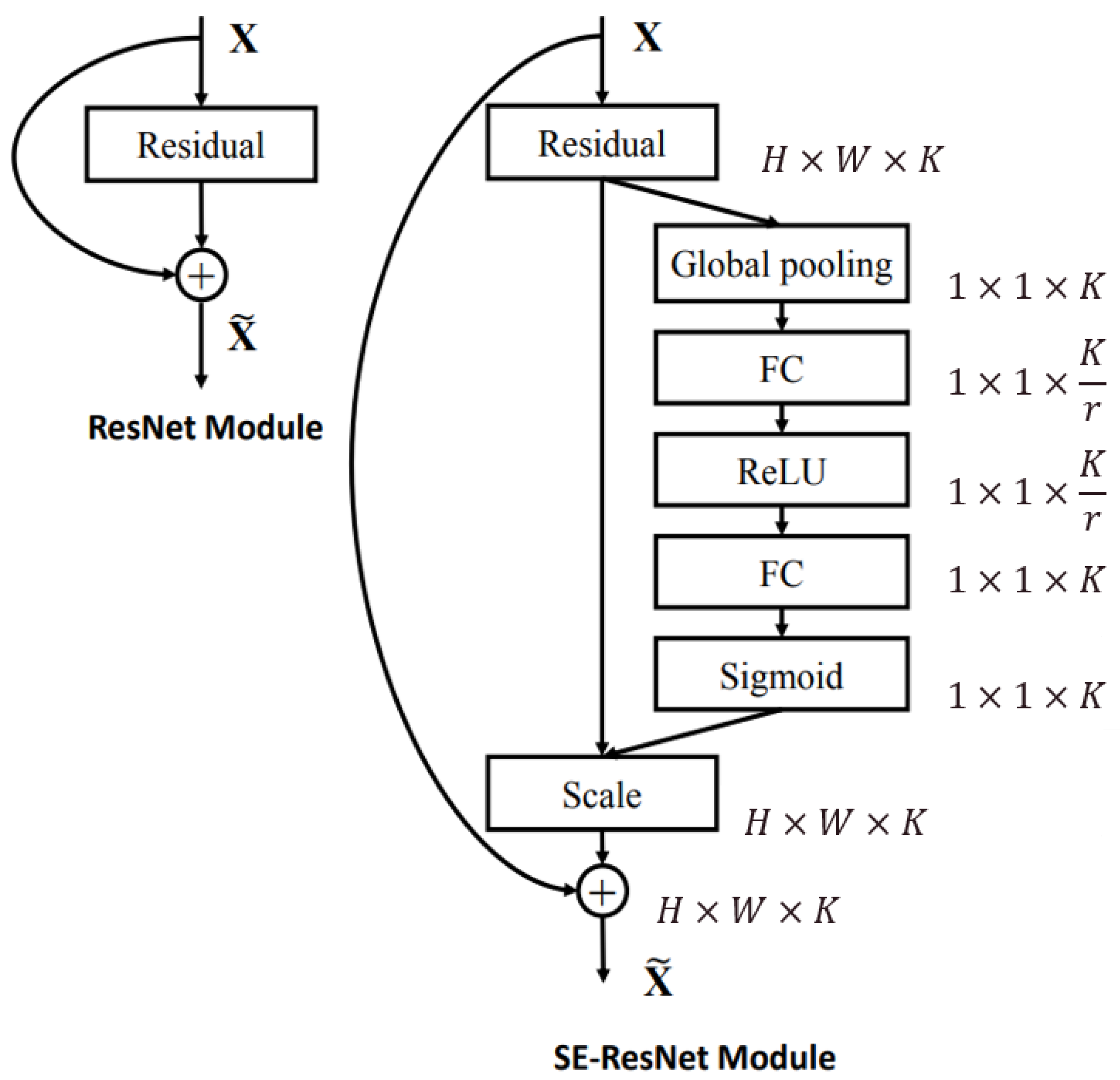
- Feature Enhancement via Channel Attention Mechanism: An SE algorithm is applied within the anchor boxes to prioritize critical features. This mechanism enhances boundary extraction by amplifying important feature channels, leading to more precise detection of building orientation and edges.
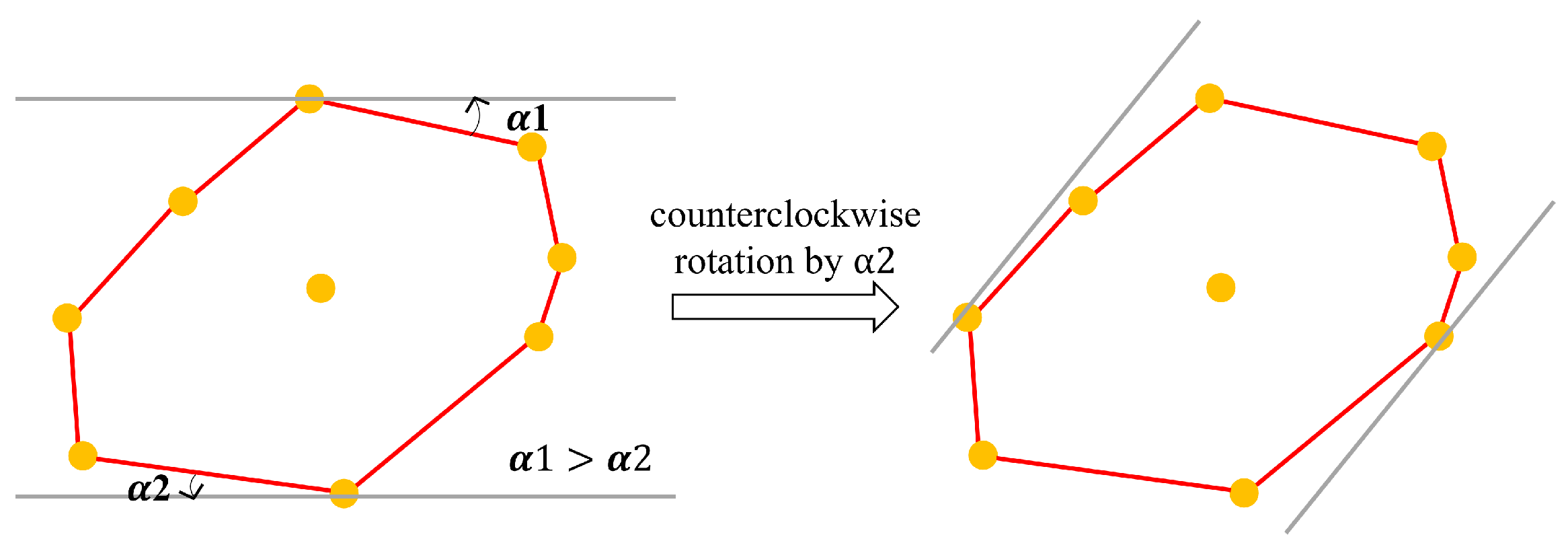
- Rotation-based Transformation for Rotated Bounding Boxes: The initial axis-aligned anchor boxes are adjusted by applying a minimum bounding rectangle (MBR) algorithm, ensuring the smallest enclosing rectangle around the detected object. The rotation angle is calculated withwhere () and () are the coordinates of two adjacent points on the object’s convex hull.
- Elliptical Bounding Box Fitting: To better capture curved and irregular building contours, an ellipse is fitted to the extracted boundary points utilizing the least squares fitting method [50]. The general ellipse equation is as follows:where x and y denote the coordinates of a point, while are constants that determine the ellipse’s position and shape.
3.2. Pre-Processing for Rotating and Elliptical Bounding Boxes
- Optimal feature map selection
- Two-dimensional reduction via channel attention mechanism
- Finding object’s outer contour within anchor box
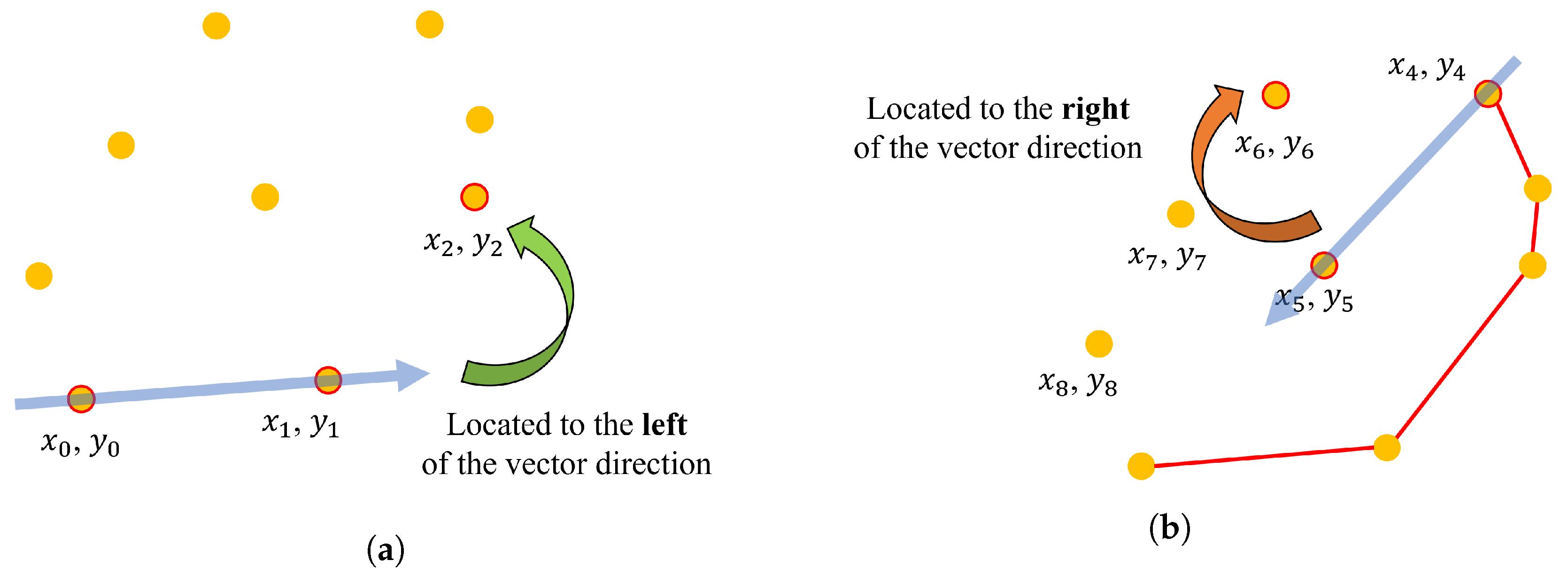
- Convex hull calculation
- : indicates a counterclockwise (left turn) orientation.
- : indicates a clockwise (right turn) orientation.
- : indicates that the points are collinear.
- If it is a left turn, the new point is included in the convex hull.
- If it is a right turn, the last added point is removed, and the orientation is recalculated.
- If the points are collinear, only the farthest point is kept.
3.3. Rotated Bounding Box Approach
- Convex Hull Initialization: Define the convex hull to be enclosed by the MBR.
- Rotation Angle Calculation: For each edge of the convex hull, calculate the angle between that edge and the x-axis (Equation (18)).
- Area Calculation: Utilizing these boundary values, calculate the width, height, and area of the rectangle (Equation (20)).
- Minimum Area Selection: Repeat this process for each edge, and select the rectangle with the smallest area.
- Return the Final Rectangle: Output the rectangle with the minimum area as the final MBR.
3.3.1. Loss Function for Rotated Bounding Boxes
3.3.2. NMS for Rotated Bounding Boxes
3.4. Elliptical Bounding Box Approach
- Ellipse fitting
- Center coordinates of the ellipse :
- Lengths of the major and minor axes :
- Rotation angle of the ellipse :
- Deriving Elliptical Bounding Box
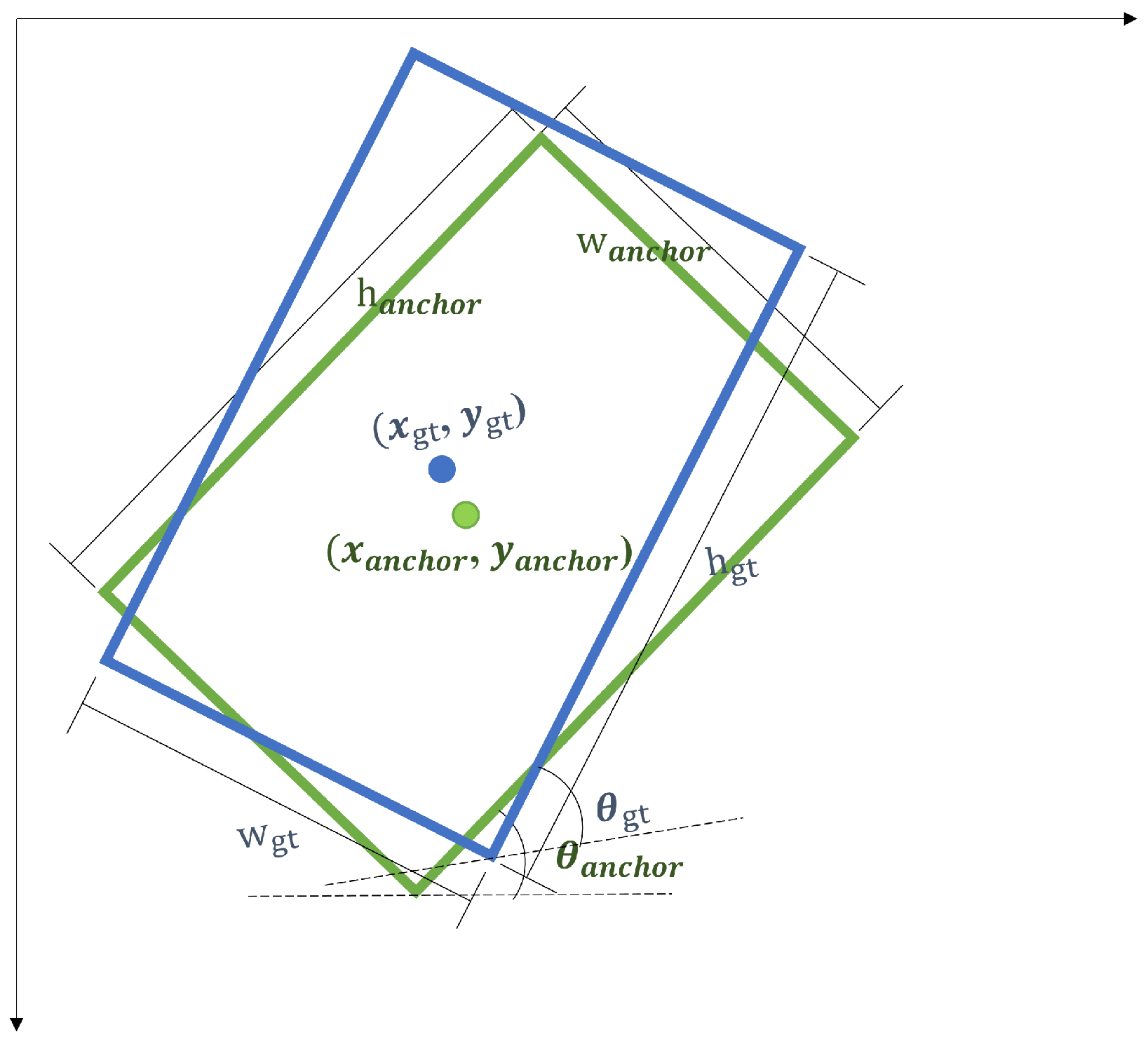
3.4.1. Loss Function for Elliptical Bounding Boxes
- Center Coordinates (): Define the center of the ellipse.
- Major Axis Length (a): Represents the length of the ellipse’s longest axis.
- Minor Axis Length (b): Represents the length of the ellipse’s shortest axis.
- Rotation Angle (): Denotes the orientation of the ellipse.
- Center Transformation: Describes the shift in the ellipse’s center from the anchor box.
- Axis Length Transformation: Models the relative scaling of the major and minor axes.
- Rotation Transformation: Captures the angular difference between the ellipse and anchor box.
- Center Loss: Evaluates the Euclidean distance between the predicted and actual ellipse centers.
- Axis Length Loss: Measures the absolute error between predicted and actual lengths of the major and minor axes.
- Rotation Angle Loss: Computes the absolute angular difference between the predicted and actual rotation angles.
- IoU Loss: Quantifies the overlap between the predicted and actual ellipses utilizing IoU.
3.4.2. NMS for Elliptical Bounding Boxes
- Intersection Area: The area of overlap between the boundaries of two ellipses. Determining the intersection area is mathematically significant and typically involves numerical methods.
- Union Area: The union area is determined by summing the areas of the two ellipses and subtracting the intersection area:where represents the area of an individual ellipse, computed asHere, a and b are the lengths of the major and minor axes of the ellipse, respectively.
- IoU: The IoU is then calculated as
- Select Highest Confidence Box: The bounding box with the highest confidence score is selected.
- Suppress Overlapping Boxes: Other bounding boxes with IoU values above the threshold are suppressed.
- Repeat: The process is repeated until no bounding boxes remain for evaluation.
4. Experimental Setup
4.1. Dataset Description
- BONAI dataset
- Annotation
- Implementation Details
- Dataset Preprocessing: The BONAI dataset images were cropped to for training to balance computational efficiency and feature preservation. This resolution preserves essential building details while minimizing memory and computational demands, enabling the model to efficiently process images during training.
- Backbone Selection (ResNet-50-FPN): ResNet-50-FPN was chosen as the backbone network because of its ability to generate multi-resolution feature maps through a feature pyramid network (FPN) [51]. Compared to other backbones such as VGG-16 or ResNet-101, ResNet-50-FPN provides a balance between computational efficiency and accuracy, enabling robust detection of buildings with varying sizes and shapes. This architecture effectively captures both the fine details of small structures and the high-level features of large buildings, making it particularly well-suited for the BONAI dataset, which encompasses diverse urban environments. Its ability to detect irregular and tilted buildings outperforms simpler architectures like VGG-16, making it a preferred choice despite the potential for slightly higher accuracy in models like ResNet-101, which come with significantly greater computational demands.
- Environment: The training was conducted on Google Colab Pro+ with an NVIDIA GeForce RTX 3060 Ti GPU, 52 GB RAM, and 170 GB disk space (Santa Clara, CA, USA). The use of a GPU significantly accelerated the training process, allowing efficient handling of the computational demands posed by the BONAI dataset.
- Training Configuration: The model was trained with Stochastic Gradient Descent with a learning rate of 0.02, momentum of 0.9, and a weight decay of . Training was performed over 12 epochs with a batch size of 16. These hyperparameters were fine-tuned to optimize convergence and detection performance.
4.2. Performance Metrics and Analysis
5. Results and Discussion
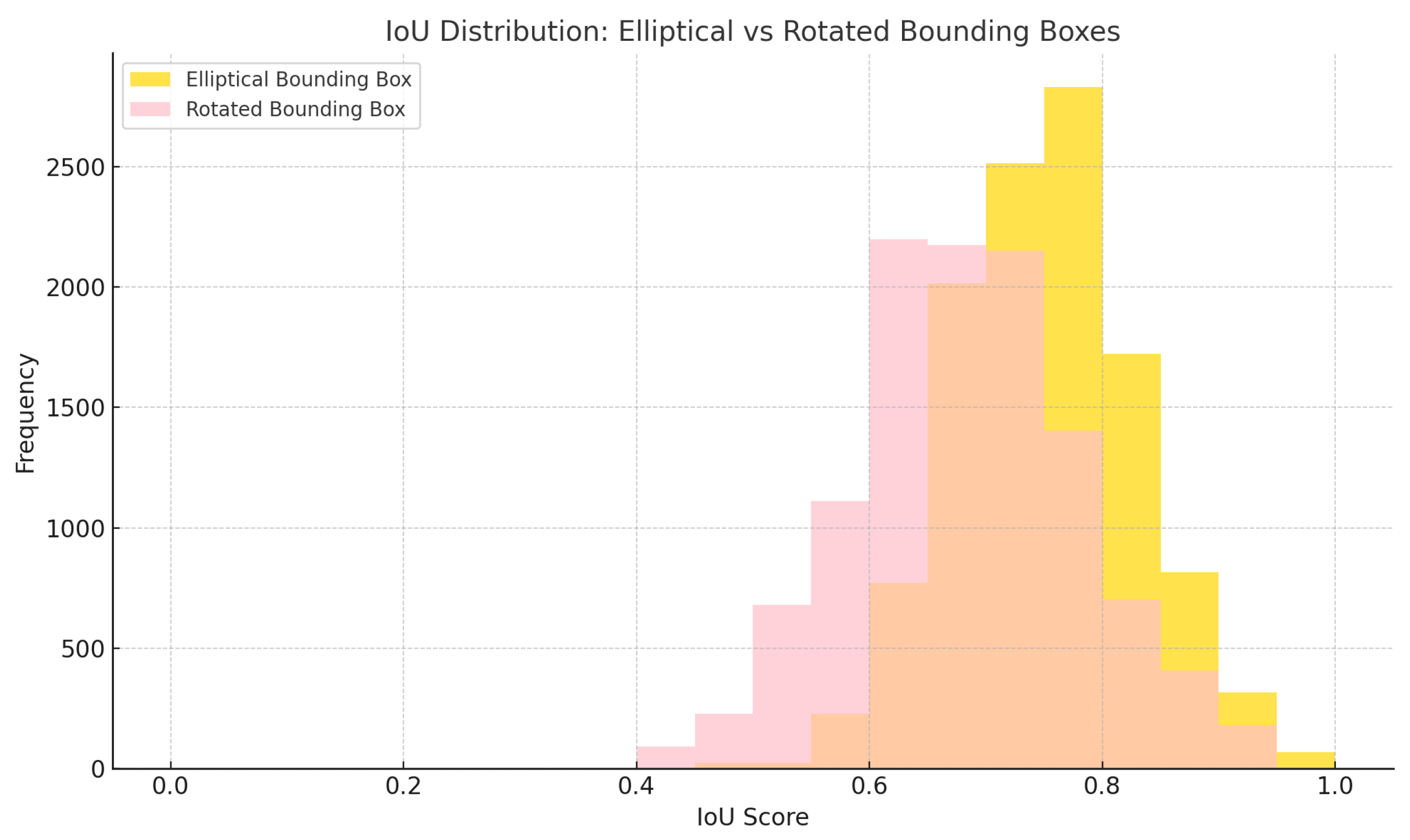
5.1. Results
5.2. Discussion
5.2.1. Overall Detection Performance
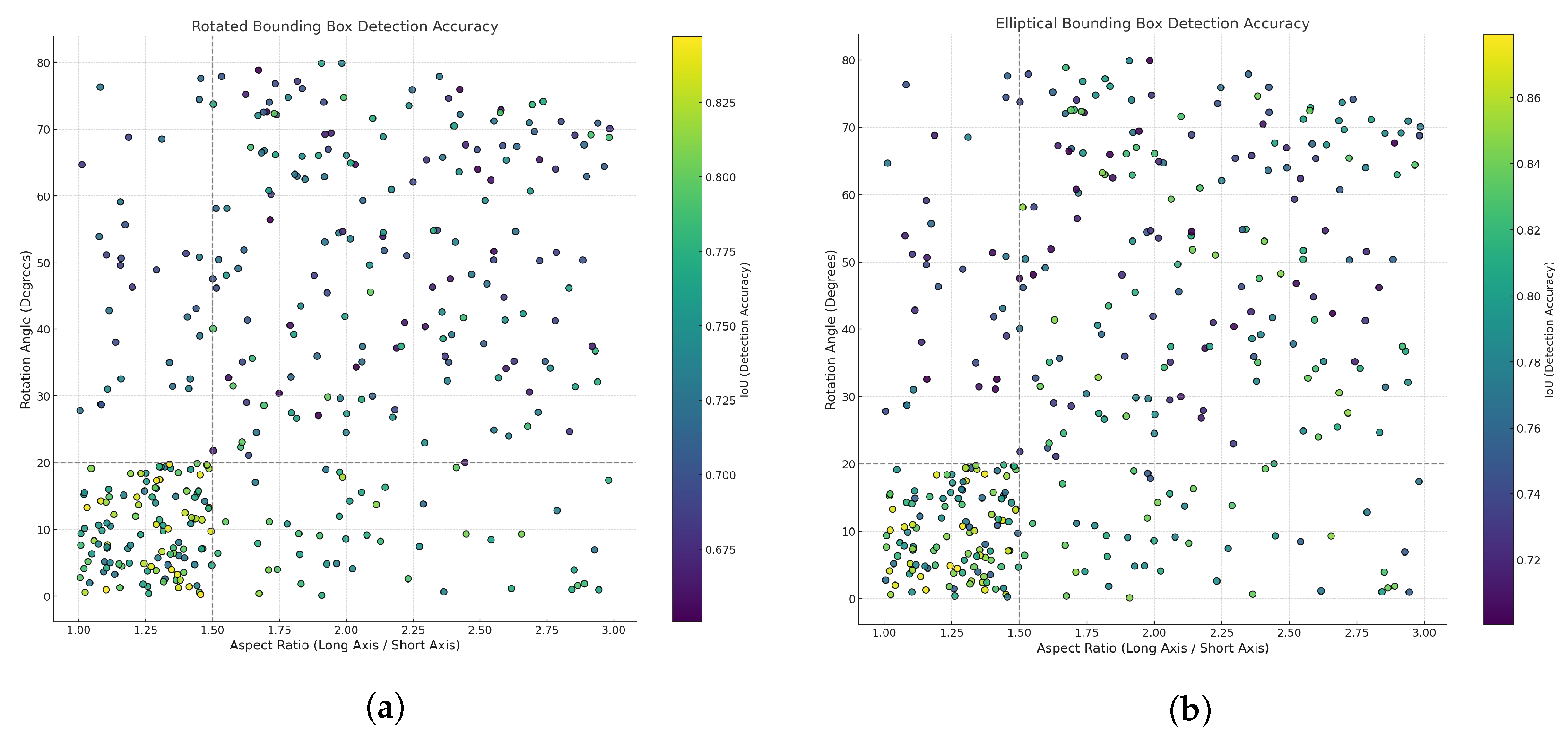
5.2.2. Categorical Analysis: Regular vs. Irregular Buildings
- IoU Distribution Analysis for Irregular Buildings
- Detection and False Detection Rate Analysis
5.2.3. Error Analysis
- Error Patterns in Rotated and Elliptical Bounding Boxes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krayenhoff, E.S.; Moustaoui, M.; Broadbent, A.M.; Gupta, V.; Georgescu, M. Diurnal interaction between urban expansion, climate change and adaptation in US cities. Nat. Clim. Change 2018, 8, 1097–1103. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y. Investigating the effects of 3D urban morphology on the surface urban heat island effect in urban functional zones by using high-resolution remote sensing data: A case study of Wuhan, Central China. ISPRS J. Photogramm. Remote Sens. 2019, 152, 119–131. [Google Scholar]
- Wang, C.; Zhang, Y.; Chen, X.; Jiang, H.; Mukherjee, M.; Wang, S. Automatic building detection from high-resolution remote sensing images based on joint optimization and decision fusion of morphological attribute profiles. Remote Sens. 2021, 13, 357. [Google Scholar] [CrossRef]
- Yang, M.; Yu, K.; Zhang, C.; Li, Z.; Yang, K. Denseaspp for semantic segmentation in street scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3684–3692. [Google Scholar]
- Zhou, Q.; Yu, C. Point rcnn: An angle-free framework for rotated object detection. Remote Sens. 2022, 14, 2605. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Z.; Li, B.; Li, C. Multiscale rotated bounding box-based deep learning method for detecting ship targets in remote sensing images. Sensors 2018, 18, 2702. [Google Scholar] [CrossRef]
- Ni, L.; Huo, C.; Zhang, X.; Wang, P.; Zhang, L.; Guo, K.; Zhou, Z. NaGAN: Nadir-like generative adversarial network for off-nadir object detection of multi-view remote sensing imagery. Remote Sens. 2022, 14, 975. [Google Scholar] [CrossRef]
- Hao, H.; Baireddy, S.; LaTourette, K.; Konz, L.; Chan, M.; Comer, M.L.; Delp, E.J. Improving building segmentation for off-nadir satellite imagery. arXiv 2021, arXiv:2109.03961. [Google Scholar]
- Pang, C.; Wu, J.; Ding, J.; Song, C.; Xia, G.S. Detecting building changes with off-nadir aerial images. Sci. China Inf. Sci. 2023, 66, 140306. [Google Scholar]
- McNally, S.; Nielsen, A.; Barrieau, A.; Jabari, S. Improving Off-Nadir Deep Learning-Based Change and Damage Detection through Radiometric Enhancement. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, 48, 33–39. [Google Scholar]
- Xia, G.S.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; Zhang, L. DOTA: A large-scale dataset for object detection in aerial images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3974–3983. [Google Scholar]
- Ding, J.; Xue, N.; Long, Y.; Xia, G.S.; Lu, Q. Learning RoI transformer for oriented object detection in aerial images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2849–2858. [Google Scholar]
- Follmann, P.; König, R. Oriented boxes for accurate instance segmentation. arXiv 2019, arXiv:1911.07732. [Google Scholar]
- He, X.; Ma, S.; He, L.; Ru, L.; Wang, C. Learning rotated inscribed ellipse for oriented object detection in remote sensing images. Remote Sens. 2021, 13, 3622. [Google Scholar] [CrossRef]
- Dong, R.; Yin, S.; Jiao, L.; An, J.; Wu, W. ASIPNet: Orientation-Aware Learning Object Detection for Remote Sensing Images. Remote Sens. 2024, 16, 2992. [Google Scholar] [CrossRef]
- Wang, J.; Meng, L.; Li, W.; Yang, W.; Yu, L.; Xia, G.S. Learning to extract building footprints from off-nadir aerial images. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 1294–1301. [Google Scholar]
- Chen, J.; Jiang, Y.; Luo, L.; Gong, W. ASF-Net: Adaptive screening feature network for building footprint extraction from remote-sensing images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4706413. [Google Scholar]
- Zhang, H.; Xu, C.; Fan, Z.; Li, W.; Sun, K.; Li, D. Detection and Classification of Buildings by Height from Single Urban High-Resolution Remote Sensing Images. Appl. Sci. 2023, 13, 10729. [Google Scholar] [CrossRef]
- Ali, M.M.; Moon, K.S. Advances in structural systems for tall buildings: Emerging developments for contemporary urban giants. Buildings 2018, 8, 104. [Google Scholar] [CrossRef]
- Anand, A.; Deb, C. The potential of remote sensing and GIS in urban building energy modelling. Energy Built Environ. 2024, 5, 957–969. [Google Scholar]
- Biljecki, F.; Chow, Y.S. Global building morphology indicators. Comput. Environ. Urban Syst. 2022, 95, 101809. [Google Scholar]
- Lian, W.; Sen, W. Building Structural Design Innovation and Code Development. Int. J. Archit. Arts Appl. 2024, 10, 9–19. [Google Scholar] [CrossRef]
- Zand, M.; Etemad, A.; Greenspan, M. Oriented bounding boxes for small and freely rotated objects. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4701715. [Google Scholar]
- Huang, X.; Zhang, L. A multidirectional and multiscale morphological index for automatic building extraction from multispectral GeoEye-1 imagery. Photogramm. Eng. Remote Sens. 2011, 77, 721–732. [Google Scholar] [CrossRef]
- Swan, B.; Laverdiere, M.; Yang, H.L.; Rose, A. Iterative self-organizing SCEne-LEvel sampling (ISOSCELES) for large-scale building extraction. GIScience Remote Sens. 2022, 59, 1–16. [Google Scholar] [CrossRef]
- Sirmacek, B.; Unsalan, C. Building detection from aerial images using invariant color features and shadow information. In Proceedings of the 2008 23rd International Symposium on Computer and Information Sciences, Istanbul, Turkey, 27–29 October 2008; pp. 1–5. [Google Scholar]
- Mnih, V.; Hinton, G.E. Learning to detect roads in high-resolution aerial images. In Computer Vision–ECCV 2010, Proceedings of the 11th European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; Proceedings, Part VI 11; Springer: Berlin/Heidelberg, Germany, 2010; pp. 210–223. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, Proceedings of the 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Lei, J.; Liu, X.; Yang, H.; Zeng, Z.; Feng, J. Dual Hybrid Attention Mechanism-Based U-Net for Building Segmentation in Remote Sensing Images. Appl. Sci. 2024, 14, 1293. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Momeni, M. Object-based rule sets and its transferability for building extraction from high resolution satellite imagery. J. Indian Soc. Remote Sens. 2018, 46, 169–178. [Google Scholar] [CrossRef]
- Ngo, T.T.; Mazet, V.; Collet, C.; De Fraipont, P. Shape-based building detection in visible band images using shadow information. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 920–932. [Google Scholar] [CrossRef]
- Cheng, G.; Zhou, P.; Han, J. Learning rotation-invariant convolutional neural networks for object detection in VHR optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7405–7415. [Google Scholar] [CrossRef]
- Jung, S.; Lee, W.H.; Han, Y. Change detection of building objects in high-resolution single-sensor and multi-sensor imagery considering the sun and sensor’s elevation and azimuth angles. Remote Sens. 2021, 13, 3660. [Google Scholar] [CrossRef]
- Dosovitskiy, A. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Abdollahi, A.; Pradhan, B.; Gite, S.; Alamri, A. Building footprint extraction from high resolution aerial images using generative adversarial network (GAN) architecture. IEEE Access 2020, 8, 209517–209527. [Google Scholar] [CrossRef]
- Pang, S.; Hu, X.; Wang, Z.; Lu, Y. Object-based analysis of airborne LiDAR data for building change detection. Remote Sens. 2014, 6, 10733–10749. [Google Scholar] [CrossRef]
- Hamaguchi, R.; Hikosaka, S. Building detection from satellite imagery using ensemble of size-specific detectors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–23 June 2018; pp. 187–191. [Google Scholar]
- Tu, Y.H.; Johansen, K.; Aragon, B.; Stutsel, B.M.; Ángel, Y.; Camargo, O.A.L.; Al-Mashharawi, S.K.; Jiang, J.; Ziliani, M.G.; McCabe, M.F. Combining nadir, oblique, and façade imagery enhances reconstruction of rock formations using unmanned aerial vehicles. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9987–9999. [Google Scholar]
- Ji, S.; Wei, S.; Lu, M. Fully convolutional networks for multisource building extraction from an open aerial and satellite imagery data set. IEEE Trans. Geosci. Remote Sens. 2018, 57, 574–586. [Google Scholar]
- Jang, H.; Kim, S.; Yoo, S.; Han, S.; Sohn, H.G. Feature matching combining radiometric and geometric characteristics of images, applied to oblique-and nadir-looking visible and TIR sensors of UAV imagery. Sensors 2021, 21, 4587. [Google Scholar] [CrossRef]
- Fatty, A.; Li, A.J.; Yao, C.Y. Instance segmentation based building extraction in a dense urban area using multispectral aerial imagery data. Multimed. Tools Appl. 2024, 83, 61913–61928. [Google Scholar]
- Ye, S.; Nedzved, A.; Chen, C.; Chen, H.; Leunikau, A.; Belotserkovsky, A. Shadow detection on urban satellite images based on building texture. Pattern Recognit. Image Anal. 2022, 32, 332–339. [Google Scholar]
- Wang, J.; Sun, K.; Cheng, T.; Jiang, B.; Deng, C.; Zhao, Y.; Liu, D.; Mu, Y.; Tan, M.; Wang, X.; et al. Deep high-resolution representation learning for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3349–3364. [Google Scholar]
- Wu, J.; Su, L.; Lin, Z.; Chen, Y.; Ji, J.; Li, T. Object Detection of Flexible Objects with Arbitrary Orientation Based on Rotation-Adaptive YOLOv5. Sensors 2023, 23, 4925. [Google Scholar] [CrossRef]
- Qu, H.; Tong, C.; Liu, W. Image shadow removal algorithm guided by progressive attention mechanism. Signal Image Video Process. 2023, 17, 2565–2571. [Google Scholar]
- Yang, X.; Yang, J.; Yan, J.; Zhang, Y.; Zhang, T.; Guo, Z.; Sun, X.; Fu, K. Scrdet: Towards more robust detection for small, cluttered and rotated objects. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8232–8241. [Google Scholar]
- Zhou, K.; Zhang, M.; Zhao, H.; Tang, R.; Lin, S.; Cheng, X.; Wang, H. Arbitrary-oriented ellipse detector for ship detection in remote sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 7151–7162. [Google Scholar]
- Acuna, D.; Ling, H.; Kar, A.; Fidler, S. Efficient interactive annotation of segmentation datasets with polygon-rnn++. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 859–868. [Google Scholar]
- Ahn, S.J.; Rauh, W.; Warnecke, H.J. Least-squares orthogonal distances fitting of circle, sphere, ellipse, hyperbola, and parabola. Pattern Recognit. 2001, 34, 2283–2303. [Google Scholar] [CrossRef]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]









| BONAI Dataset | City | # of Imagery | # of Instances |
|---|---|---|---|
| Training set | Shanghai | 1656 | 167,595 |
| Beijing | 684 | 36,932 | |
| Chengdu | 72 | 4448 | |
| Harbin | 288 | 16,480 | |
| Validation set | Shanghai | 228 | 16,747 |
| Jinan | 72 | 6147 | |
| Test set | Shanghai | 200 | 15,100 |
| Xi’an | 100 | 5489 | |
| Total | - | 3300 | 268,958 |
| Bounding Box Type | IoU | P | R | F1 Score |
|---|---|---|---|---|
| Aligned | 0.58 | 0.77 | 0.69 | 0.73 |
| Rotated | 0.72 | 0.90 | 0.81 | 0.85 |
| Elliptical | 0.88 | 0.93 | 0.91 | 0.92 |
| Bounding Box Type | Detected | Undetected | Detection Rate (%) | Miss Rate (%) |
|---|---|---|---|---|
| Aligned | 13,537 | 7052 | 65.75 | 34.25 |
| Rotated | 17,940 | 2649 | 87.13 | 12.87 |
| Elliptical | 18,933 | 1656 | 91.96 | 8.04 |
| Bounding Box Type | Building Type | IoU | P | R | F1 Score |
|---|---|---|---|---|---|
| Rotated | Regular | 0.88 | 0.94 | 0.91 | 0.94 |
| Irregular | 0.79 | 0.81 | 0.78 | 0.79 | |
| Elliptical | Regular | 0.84 | 0.92 | 0.88 | 0.90 |
| Irregular | 0.81 | 0.82 | 0.80 | 0.82 |
| Bounding Box Type | Detection Rate (%) | Miss Rate (%) | False Detection Rate (%) |
|---|---|---|---|
| Rotated | 84.79 | 15.21 | 5.93 |
| Elliptical | 91.93 | 8.07 | 4.59 |
| Buildings | Rotated FN Rate (%) | Elliptical FN Rate (%) |
|---|---|---|
| Small | 3.8 | 10.4 |
| Distorted | 13.9 | 6.7 |
| High curvature | 24.1 | 4.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, S.; Song, A.; Lee, K.; Lee, W.H. Advanced Building Detection with Faster R-CNN Using Elliptical Bounding Boxes for Displacement Handling. Remote Sens. 2025, 17, 1247. https://doi.org/10.3390/rs17071247
Jung S, Song A, Lee K, Lee WH. Advanced Building Detection with Faster R-CNN Using Elliptical Bounding Boxes for Displacement Handling. Remote Sensing. 2025; 17(7):1247. https://doi.org/10.3390/rs17071247
Chicago/Turabian StyleJung, Sejung, Ahram Song, Kirim Lee, and Won Hee Lee. 2025. "Advanced Building Detection with Faster R-CNN Using Elliptical Bounding Boxes for Displacement Handling" Remote Sensing 17, no. 7: 1247. https://doi.org/10.3390/rs17071247
APA StyleJung, S., Song, A., Lee, K., & Lee, W. H. (2025). Advanced Building Detection with Faster R-CNN Using Elliptical Bounding Boxes for Displacement Handling. Remote Sensing, 17(7), 1247. https://doi.org/10.3390/rs17071247






