Next Article in Journal
Perfect Labelling: A Review and Outlook of Label Optimization Techniques in Dynamic Earth Observation
Previous Article in Journal
An Improved Machine Learning-Based Method for Unsupervised Characterisation for Coral Reef Monitoring in Earth Observation Time-Series Data
Previous Article in Special Issue
Simulation and Prediction of Thermokarst Lake Surface Temperature Changes on the Qinghai–Tibet Plateau
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 17
Issue 7
10.3390/rs17071245
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Predictive Skill of a Remote Sensing-Based Machine Learning Model for Ice Wedge and Visible Ground Ice Identification in Western Arctic Canada

by
Qianyu Chang
1,*,
Simon Zwieback
2 and
Aaron A. Berg
1
1
Department of Geography, Environment & Geomatics, University of Guelph, Guelph, ON N1G 2W1, Canada
2
Geophysical Institute, University of Alaska Fairbanks, Fairbanks, AK 99775, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2025, 17(7), 1245; https://doi.org/10.3390/rs17071245
Submission received: 15 February 2025 / Revised: 28 March 2025 / Accepted: 29 March 2025 / Published: 1 April 2025
(This article belongs to the Special Issue The Applications of Remote Sensing, Machine Learning and Deep Learning in Frozen Ground Regions)
Browse Figures
Versions Notes

Abstract

:
Fine-scale maps of ground ice and related surface features are critical for permafrost-related modelling and management. However, such maps are lacking across almost the entire Arctic. Machine learning provides the potential to automate regional fine-scale ground ice mapping using remote sensing and topographic data. Here, we evaluate the predictive skill of XGBoost models for identifying (1) ice wedge and (2) top-5m visible ground ice in the Tuktoyaktuk Coastlands. We find high predictive skill for ice wedge occurrence (ROC AUC = 0.95, macro F1 = 0.80), with the most important predictors being slope, distance to the coast, and probability of depression. The model accurately predicted regional and local trends in ice wedge occurrence, with an increase in ice wedge polygon (IWP) probability towards the coast and in poorly drained depressions. The model also captured IWP in well-drained uplands of the study area, including locations with poorly visible troughs not contained in the training data. Spatial transferability analyses highlight the regional variability of ice wedge probability, reflecting contrasting climatic and surface conditions. Conversely, the low predictive skill for visible ground ice (ROC AUC = 0.67, macro F1 = 0.53) is attributed to limitations in training data and weak associations with the remotely sensed predictors. The varying predictive accuracy highlights the importance of high-quality reference data and site-specific conditions for improving ground ice studies with data-driven modelling from remote sensing observations.

1. Introduction

Ground ice is of fundamental importance to permafrost stability and functioning [1,2,3]. Ground ice contents, especially excess ice, control the permafrost response to climate warming and disturbances by determining potential thaw subsidence [4,5]. Excess ice occurs as massive ice bodies, including ice wedges and tabular ice of glacial origin, as well as segregated ice [1]. However, fine-scale maps of ground ice at a 10–50 m resolution are lacking across most of the Arctic, which limits planning, prediction, and adaptation capacities in this rapidly changing environment.
The regional mapping of ground ice conditions is difficult. Point-scale data of excess ice and related parameters can be obtained from coring. Although this method is accurate, it is costly and spatially limited. Near-surface geophysical methods can generate local-scale ground ice information but are also spatially limited [6,7,8]. Regional fine-scale mapping of ground ice is generally indirect because ground ice is not directly observable at the surface [9]. Such mapping relies on expert understanding, association with easily observable variables such as vegetation cover and topography, or ground ice-associated landforms [10,11,12]. The reliability of the results depends on the availability of ground truth data and the strength of association between ground ice contents and surface indications, including degradational landforms such as high-centred polygons or thaw slumps, aggradational landforms such as palsas and pingos, and ecotypes with relatively uniform ground ice conditions (e.g., ice-poor bedrock or active floodplains). At local scales, most mapping efforts have hitherto relied on labour-intensive manual expert interpretation or on specific landforms [11,13,14].
Remote sensing data combined with machine learning provides the potential for automated ground ice mapping at the regional scale, but the predictive skill for ground ice parameters based on topographic and remotely sensed surface predictors remains to be quantified. While remote sensing data have shown promise in mapping active layer thickness or permafrost presence [15,16,17,18], quantitative assessments for ground ice prediction in the Arctic are necessary. On the Tibetan Plateau, Zou et al. [19] were able to map the volumetric ice content at a coarse resolution of 1 km using machine learning. Conversely, in Arctic regions and at finer spatial resolution relevant for planning, we cannot answer basic questions such as the achievable accuracy, the most important predictor variables, and the spatial transferability across the landscape for such mapping products. Answering these questions is a necessary step for compiling regional-scale ground ice maps utilizing the wide spatial coverage of remote sensing datasets while incorporating data-driven modelling with expert assessments, paleogeographic approaches, geophysics, and radar interferometry [12,13,20]. Additional opportunities include the gap-filling of deep-learning-based maps of ground-ice-related landforms such as ice wedge polygons (IWPs) [14] and the development or testing of conceptual and process-based models of ground ice dynamics [20,21].
eXtreme Gradient Boosting (XGBoost) is a widely used machine learning algorithm in data-driven modelling in various remote sensing fields, such as drought monitoring, biomass estimation, and permafrost studies [22,23,24]. These studies indicate the suitability of XGBoost for our study due to its competitive prediction accuracy, flexibility, and ability to be trained using low to moderate amounts of training data [23,24,25,26]. The XGBoost classification model generates predictions based on decision tree ensembles, in which sequential trees are built to learn from the previous trees while optimizing the bias–variance tradeoff [27]. Here, we determine the predictive skill of XGBoost models for two ground ice variables in the Tuktoyaktuk Coastal Plain in Northwestern Canada, namely, (1) IWPs and (2) near-surface visible ground ice (0–5 m depth). The principal model predictors are topographic, geographic, optical and radar variables at a 30 m horizontal resolution, such as slope, distance to the coast, Normalized Difference Vegetation Index (NDVI), and radar backscattering coefficients.
Data-driven prediction of ice wedge occurrence based on remote sensing datasets and existing inventories enables gap-filling and refining of those inventories, potentially identifying inconspicuous ice wedge troughs on hillslopes that are not included in the inventory [28,29]. We predicted visible ground ice in the upper 5 m because it is the best proxy for thaw sensitivity at our disposal [8]. The study area’s rich archive of geological information and recent geological history (last glaciated in the Late Pleistocene), which is expected to induce a stronger association between surficial conditions and ground ice than unglaciated environments, make it an optimal area for developing our models [28]. Nevertheless, it is a challenging test case because of the presence of tabular ice of glacial origin, variable Holocene surface modification, heterogeneous surficial geology, and steep climatic gradients [30,31,32]. We thus complement assessments of predictability and variable importance with a spatial transferability analysis, in which we test how well models trained in a subregion apply to a larger area. These analyses establish the data requirements, accuracy, and spatial transferability of remote sensing-based ground ice prediction models.

2. Methods

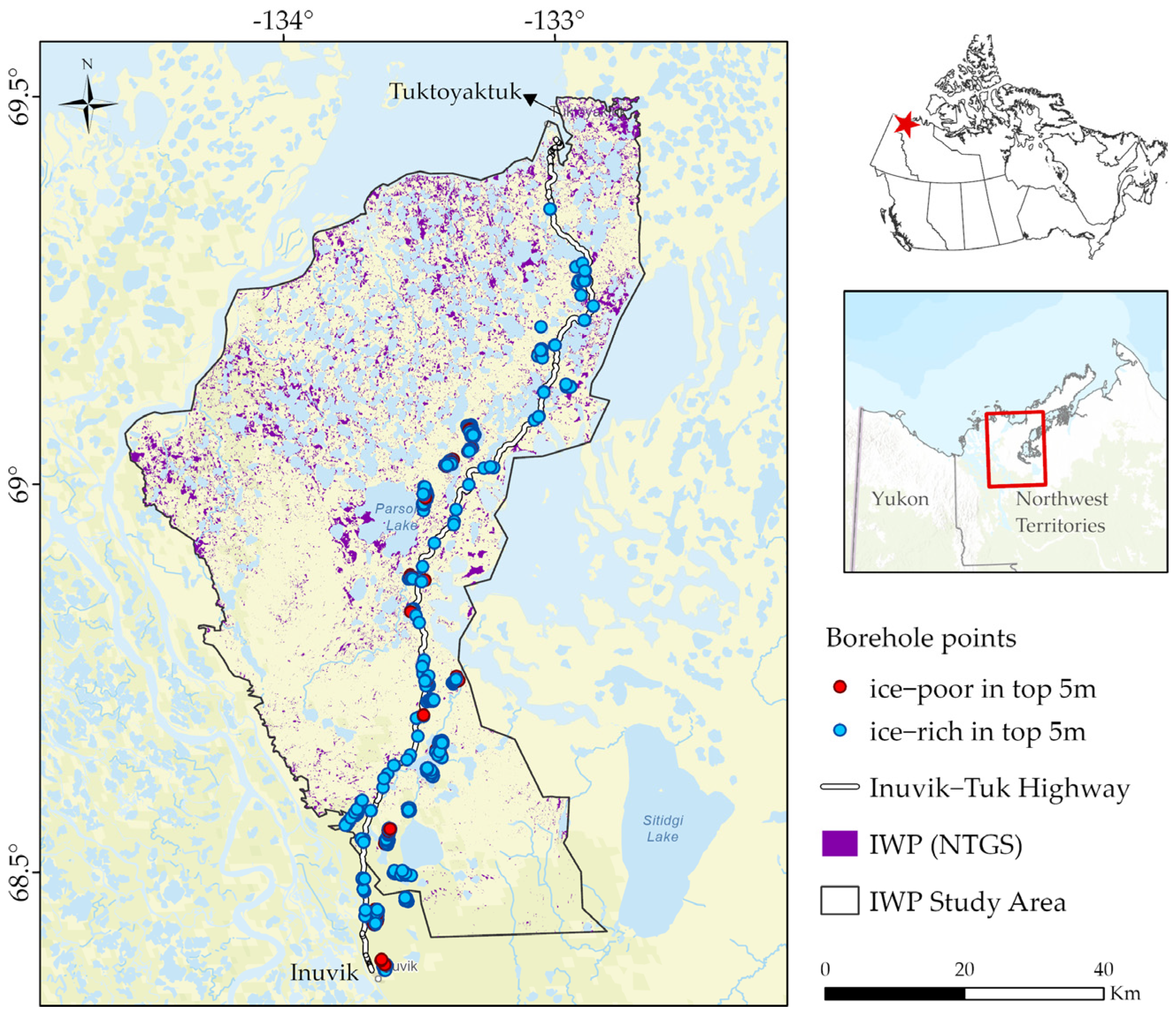
2.1. Study Area

The study area covers 4767 km2 of the Tuktoyuktak Coastal and Anderson Plain between Inuvik and Tuktoyuktak in the Northwest Territories, Canada (Figure 1). This area is underlain by continuous permafrost, with typical temperatures at 10 m depth in undisturbed locations varying from −2 °C near Inuvik to −6 °C near the Beaufort Sea coast [33]. This range reflects a steep climatic gradient. In Inuvik, the mean annual air temperature and precipitation are −7 °C and 250 mm (1991–2020), compared to the colder (−10 °C) and drier (160 mm) climate in Tuktoyaktuk [34]. The climatic gradient is also expressed in the vegetation cover, which varies from open spruce forest in the south, a tall shrub transition zone in the central part, and low shrub tundra near the coast [28].
The study area is characterized by low rolling terrain and lacustrine lowlands underlain by thick, ice-rich permafrost and dotted with numerous small lakes [33]. The topography, soils, and permafrost conditions reflect the region’s Quaternary history near the margin of the Wisconsin ice sheet [36]. According to Dyke and Brooks [37], the area was entirely covered by the northwestern corner of the Laurentide ice sheet ~30 ka BP (before present), which retreated after ~22 ka BP, the area eventually being ice-free after 12 ka BP. Hummocky or rolling moraine of fine-grained and stony tills is dominant in the southern half of the study area, interspersed with lowlands characterized by fine-grained lacustrine deposits [38]. Towards the coast, flat and poorly drained lacustrine lowlands increase in abundance [36]. Glaciofluvial deposits of low to moderate relief that are generally well drained except in depressions occupy approximately one-third of the northern study area [38].
The Quaternary deposits in the study area host various forms of ground ice. Ice wedges are found throughout the study area with an increasing density from south to north (Figure 1) [29,39]. While they occur in poorly drained peatlands across the study area, Kokelj et al. [28] concluded that ice wedge polygons in mineral deposits were largely restricted to the northern half of the study area. The epigenetic and anti-syngenetic ice wedges of Holocene age can exceed 3 m in width in organic deposits in the northern part, while thicknesses of <2 m are typical in mineral deposits and organic deposits further south [28]. More than 90% of the polygonal terrain mapped by Steedman et al. [39] was high-centred, with melt pond area increasing towards the coast and over time (1974–2004). In addition to wedge ice, massive segregated and buried glacial ice is found in Pleistocene deposits, most notably below a mid-Holocene thaw unconformity at 3–5 m depth [33]. Abundant segregated ice is found above and below the unconformity, contributing to a greater fraction of potential thaw subsidence than the massive ice in moraine and lacustrine deposits [8]. Finally, pingos are abundant in drained lake basins near the coast but form an insubstantial contribution to the ice volume on regional scales due to their sparsity [40].
The 137 km long Inuvik–Tuktoyuktak Highway (ITH) transects the study area and extends the Dempster Highway from Inuvik to Tuktoyaktuk. This all-season road opened in 2017 after four years of construction [41]. The ITH’s sensitivity to thaw highlights the need for regional knowledge of ground ice conditions.

2.2. Reference Data

We trained and tested predictive models of ice wedge polygon (IWP) occurrence using the Northwest Territories Geological Survey (NTGS) inventory of polygonal terrain [29]. This dataset outlines polygonal terrain fields greater than 100 m2 in the Tuktoyaktuk Coastlands and the Anderson Plain, manually digitized from 0.5 m—orthomosaics obtained from aerial photographs taken in 2004 [29]. Polygon fields with no or poor surface expression were not included in the inventory as they were not visually detectable. Using the inventory, we generated training and testing data by randomly sampling 60,000 points within the intersection of the inventory and our study area, excluding a 30 m buffer around water bodies and the boundaries of polygonal fields. To reduce spatial autocorrelation, a minimum distance of 120 m was imposed between sample points. We assigned a binary label to each sample based on whether it was inside (IWP) or outside (non-IWP) of a polygonal field. The sampling and classification regime resulted in 4952 (8%) IWP and 55,048 (92%) non-IWP points.
We trained and tested the visible ground ice prediction model based on Castagner et al.’s [8,35] compilation of 564 boreholes (after removing one invalid record). The boreholes were drilled between 2012 and 2017 along the ITH corridor in support of the ITH construction and ranged from 1 to 23 m in depth. Visible ground ice content was assessed in the field at 0.5 m intervals and recompiled by Castagner et al. [35] into the following classes: NA (e.g., unfrozen), no visible ice, low, medium to high, high, and pure ice. While this dataset provides the most extensive training data in the study area, we also note limitations due to the qualitative nature of the classification scheme and the moderate association between visible and excess ice [8]. Based on the visible ground ice profile, we labelled a borehole ice-rich if any visible ice was recorded within 0–5 m in depth and ice-poor otherwise. Of the 564 boreholes, 494 (88%) were ice-rich, and 70 (12%) were ice-poor.

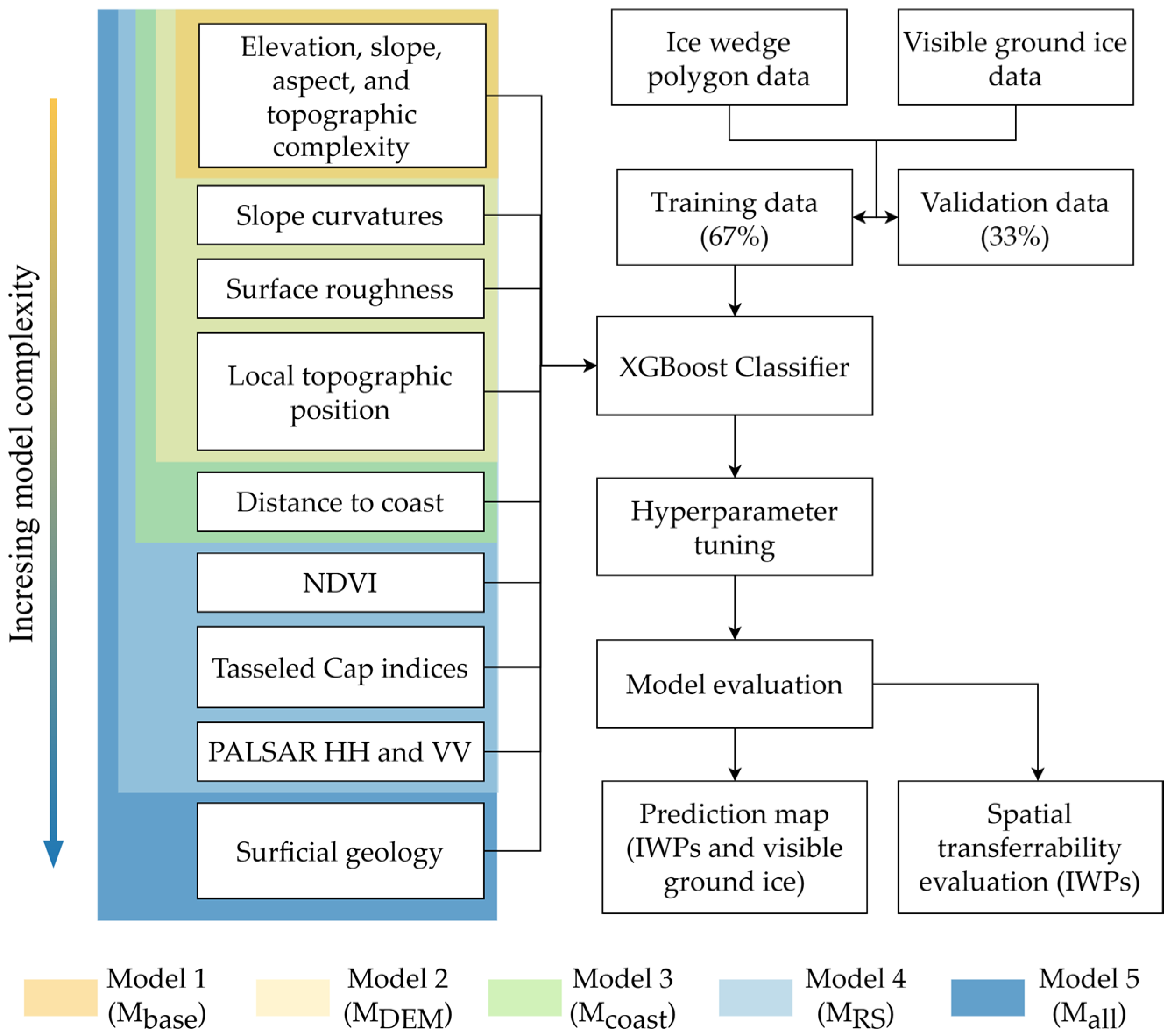
2.3. Predictor Variables

We used the same set of predictor variables for the IWP and visible ground ice prediction models, including a suite of topographic variables, distance to the coast, remotely sensed surface proxies, and surficial geology.
All topographic variables were derived from a 30 m Copernicus digital elevation model (DEM) based on TanDEM-X data acquired during 2011–2015. Basic variables included the elevation, slope, and aspect. In addition, we used the multi-scale elevation percentile (EP) and multi-scale maximum deviation from mean elevation (maxDev) as attributes for local topographic position [42,43]. Topographic roughness and complexity across various spatial scales are considered because of their established value for predicting drainage conditions and peat accumulation [44], thereby helping identify locations susceptible to frost cracking [28]. Specifically, we calculated the average normal vector angular deviation (ANVAD) and the spherical standard deviation of the distribution of surface normal (SSDN), both at micro- (100 m), meso- (500 m), and macro- (1000 m) spatial scales [45,46,47]. To characterize the topographic controls on hillslope hydrology, we calculated three slope curvature variables commonly used in terrain analysis, namely, the mean, median, and profile curvature. These metrics help predict gravity-controlled drainage conditions by identifying areas of flow convergence and deceleration [48]. Since curvature values are often small and of wide dynamic range, we log-transformed all three curvature variables [48,49]. In addition, we also performed a stochastic depression analysis to calculate the probability of each DEM cell belonging to a depression (Pdep) [50].
The remote sensing predictors were derived from Landsat and Phased Array L-band Synthetic Aperture Radar (PALSAR) composites and are an indication of moisture and vegetation characteristics, in turn associated with ground ice [51,52]. We computed common proxies associated with vegetation characteristics (e.g., biomass and moisture content), namely, the median Normalized Difference Vegetation Index (NDVI), Enhanced Vegetation Index (EVI), and Tasseled Cap indices (greenness, brightness, and wetness), from summer cloud-free composite of Landsat 5 during 2007–2012. The five-year window prior to the ITH highway construction was selected to account for annual variability in vegetation cover while avoiding the impact of construction. The availability of PALSAR data during 2007–2012 was limited to annual composites, which we used to calculate the median HH- and HV polarization backscattering coefficients that correspond to surface characteristics such as biomass, soil moisture, and surface water [53,54,55]. The PALSAR images were re-sampled to 30 m to match the resolution of Landsat and Copernicus DEM. Both the DEM and remote sensing products were acquired within 10 years of the reference data. While the temporal discrepancy is small compared to the characteristic time scales of IWP and near-surface ground ice dynamics, and the binary classification system of visible ground ice provides resilience to small changes, localized inconsistencies related to abrupt thaw cannot be excluded.
Regional physiographic variables comprised the distance to the coast and surficial geology. The distance to the coast measures the shortest distance (km) of any given pixel to the Beaufort Sea coastline. It serves as a proxy for past and present climatic conditions [30], such as mid-Holocene annual air temperature, continentality and precipitation, and present-day air temperature, precipitation, and ground temperature exhibit co-variance with distance to the (present-day) coast [36]. We opted for this proxy rather than climatological variables to restrict the number of covariates in light of limited training data and the wide range of relevant climatological variables. However, we caution that the use of this proxy restricts the model configuration to regional scales and limits the interpretability of the model parameters. The surficial geology variable describes the surficial sediment type in eight classes based on existing geological maps, namely, Colluvial, Fluvial, Glaciofluvial, Lacustrine, Moraine, Marine, or Organic [56]. It was included because of its spatial association with wedge ice [28] and visible ice [8], reflecting the dependence of ground ice conditions on the glacial history and edaphic variables such as grain size related to surface geology. The coarse 1:1,000,000 scale of the geological map precludes inclusion of terrain features such as drained lake basins within moraines.

2.4. Training and Evaluation

2.4.1. Prediction Model

We tested the performance of five XGBoost classification models (Mbase, MDEM, Mcoast, MRS, and Mall) on the prediction of both IWP and visible ground ice, each model with an increasing number of predictor variables based on the previous model (Figure 2, XGBoost v1.7.3). These models were determined a priori rather than adaptively in light of the limited training data and literature results. We started with a simple base Model 1(Mbase) with only basic topographic variables (n = 5), namely, elevation, slope, aspect (expressed as eastness and northness), and maxDev as an index for local topographic position. These predictors are expected to be included in most ground ice prediction models because they are easy to compute and capture dominant geomorphic and edaphic controls on ground ice conditions and dynamics; for instance, flat and low-lying areas are conducive to ice wedge formation through process links involving peat accumulation and saturated conditions [28,57].
Model 2 (MDEM) used all topographic variables (n = 19), including those of Mbase, to capture complex multi-scale topographic characteristics. These were included next because of the universal availability of DEMs and their previously documented ability in data-driven prediction of environmental variables closely connected to drainage conditions [58,59]. Model 3 (Mcoast) included all MDEM parameters plus distance to the coast (n = 20). It was based on the expectation that for a given local topographic setting captured by MDEM, the probability of IWP decreases with distance to the coast. If, conversely, the observed increase in IWP can be explained entirely by the greater abundance of topographic conditions conducive to ice wedge formation, Mcoast predictive skill is identical to that of MDEM. Model 4 (MRS) further included remote sensing (RS) information, namely, the Landsat indices and PALSAR backscatter coefficients (n = 25). We included these at a late stage because they are expected to largely represent surface conditions, such as vegetation cover that can change on shorter timescales than that of ground ice. Finally, Model 5 (Mall) is an all-encompassing model using all of the predictor variables, including surficial geology (n = 26). It was included last because of the coarse resolution and the restricted availability of homogeneous surficial geology data across the Arctic.

2.4.2. Model Training

To train the models, we split the IWP and ground ice reference data randomly into 67% training and 33% test samples, following a common splitting strategy with proven robustness and optimal model performance [60,61]. This resulted in 42,000 training and 18,000 test points for the IWP dataset and 395 training and 170 test points for visible ground ice.
For each XGBoost model, several hyperparameters were tuned to optimize the model performance [27], including the number of gradient boosted trees, the subsample ratio for training to prevent overfitting, the subsample ratio of columns for each tree split that controls individual tree’s complexity, and the weight of each class to account for class imbalance [27]. Hyperparameter optimization was achieved for each model using a 5-fold cross-validated grid search to maximize the ROC AUC (Area under the Receiver Operator Characteristic Curve), a measure of the overall classification performance without imposing a threshold probability. It takes on values between 0 and 1, corresponding to a model that gets all predictions wrong and right, respectively, for all probability thresholds [62]. We selected this metric because it is insensitive to class imbalances and non-random sampling, as both training datasets contained imbalanced classes, and the visible ground ice samples were spatially skewed along the ITH.

2.4.3. Model Evaluation

The predictive skill was evaluated based on the ROC AUC and the macro-averaged F1 score on the independent test data. The macro-averaged F1 score is the arithmetic mean of F1 scores for both classes, giving equal weight to each class regardless of its size. It complements the ROC AUC because it depends on the class balance and the probability threshold, accounting for precision (the fraction of positive predictions that are actually true) and recall (the fraction of true instances that were correctly predicted) [62]. The change of the two metrics as more predictors were added is a measure of the additional predictive value of the new predictors.
The permutation importance of predictor variables was calculated for the best-performing model for IWPs. It quantifies each predictor’s relative contribution in predicting ground ice feature occurrence by measuring the degradation in skill when the values of the predictor are randomly perturbed. A probability map of IWP was also generated using the best-performing model, with a 30 m resolution consistent with that of the predictor variables.
We conducted a spatial transferability analysis whereby the model was trained in one subregion and its prediction was evaluated in a different, non-overlapping subregion. Our analysis quantifies how well the model predictions can be extrapolated on scales of ~50 km, as is relevant for, e.g., gap-filling inventories of polygonal terrain. In contrast to the spatially unstructured split for our main evaluations, the spatial transferability exercise involves extrapolation in geographical and, potentially, environmental conditions.
We tested the transferability for two scenarios. First, a latitudinal partition, in which we split the study area into three equal-area sections: North, Middle, and South (Figure 3a). We established this spatial split scheme to test the model’s generalizability in the sense of both geographical and environmental extrapolation, owing to the pronounced North–South gradient in climate and ground ice conditions. We expect the prediction accuracy for Mnorth and Msouth to be worse than that of Mmiddle (Figure 3), as these two models need to extrapolate to more extreme environmental conditions than included in their training data. Second, a longitudinal partition, in which the study area was split into three equal-area sections as West, Centre, and East (Figure 3b). This scenario is intended to test the geographical extrapolation accuracy while limiting extrapolation across environmental gradients. We expect the predictive skill to be less than for the random split but greater than for the latitudinal partition.
For each section within a spatial transferability assessment, we tested the applicability of an XG Boost sub-model that was trained and optimized on the other two sections, keeping the predictors and hyperparameters identical to the full model (MRS) (Figure 3). For instance, the distance to the coast variable was left unchanged so that Mnorth and Msouth extrapolate beyond the distribution of this variable in the training set when making prediction in North and South, respectively. To evaluate the performance difference with respect to the full model, we compared the ROC AUC scores of the sub-model and the full model in the respective test section.

3. Results

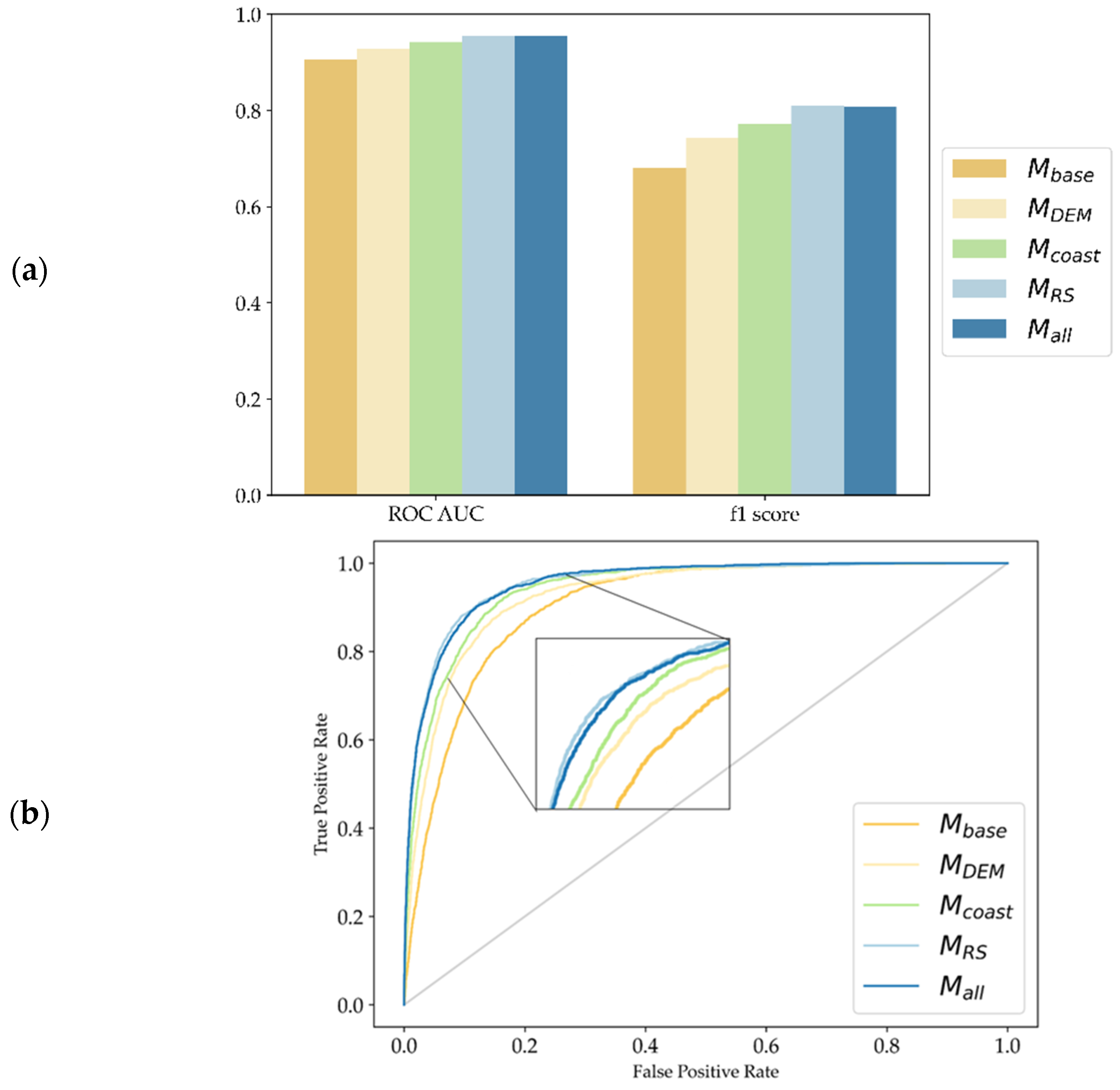
3.1. IWP Model Predictive Skill

The models yielded skillful predictions of ice wedge occurrence, as quantified by ROC AUC scores > 0.90 with respect to the test dataset (Figure 4). The baseline model Mbase achieved a ROC AUC score of 0.91, indicating substantial predictive skill of the five topographic predictors.
Model 2 (MDEM) and Model 3 (Mcoast) showed consistent but comparatively small improvements in performance with the addition of predictors when measured by the ROC AUC and F1 scores (Figure 4). The ROC AUC increased to 0.93 for MDEM upon the addition of multi-scale topographic predictors and further increased to 0.94 for Mcoast (the addition of distance to the coast). The F1 score improved from 0.65 for Mbase to 0.76 for Mcoast.
The inclusion of remotely sensed predictors, such as the NDVI, enabled further improvements in the predictive skill. Model 4 (MRS) increased the ROC and F1 scores to 0.95 and 0.80. But the addition of surficial geology (Mall) led to no noticeable further improvement in model performance, as both ROC AUC and F1 scores remained essentially the same as MRS.
Overall, MRS, which included all predictor variables except surficial geology (n predictors = 25), had the best performance and was selected for mapping IWP probability across the study area.

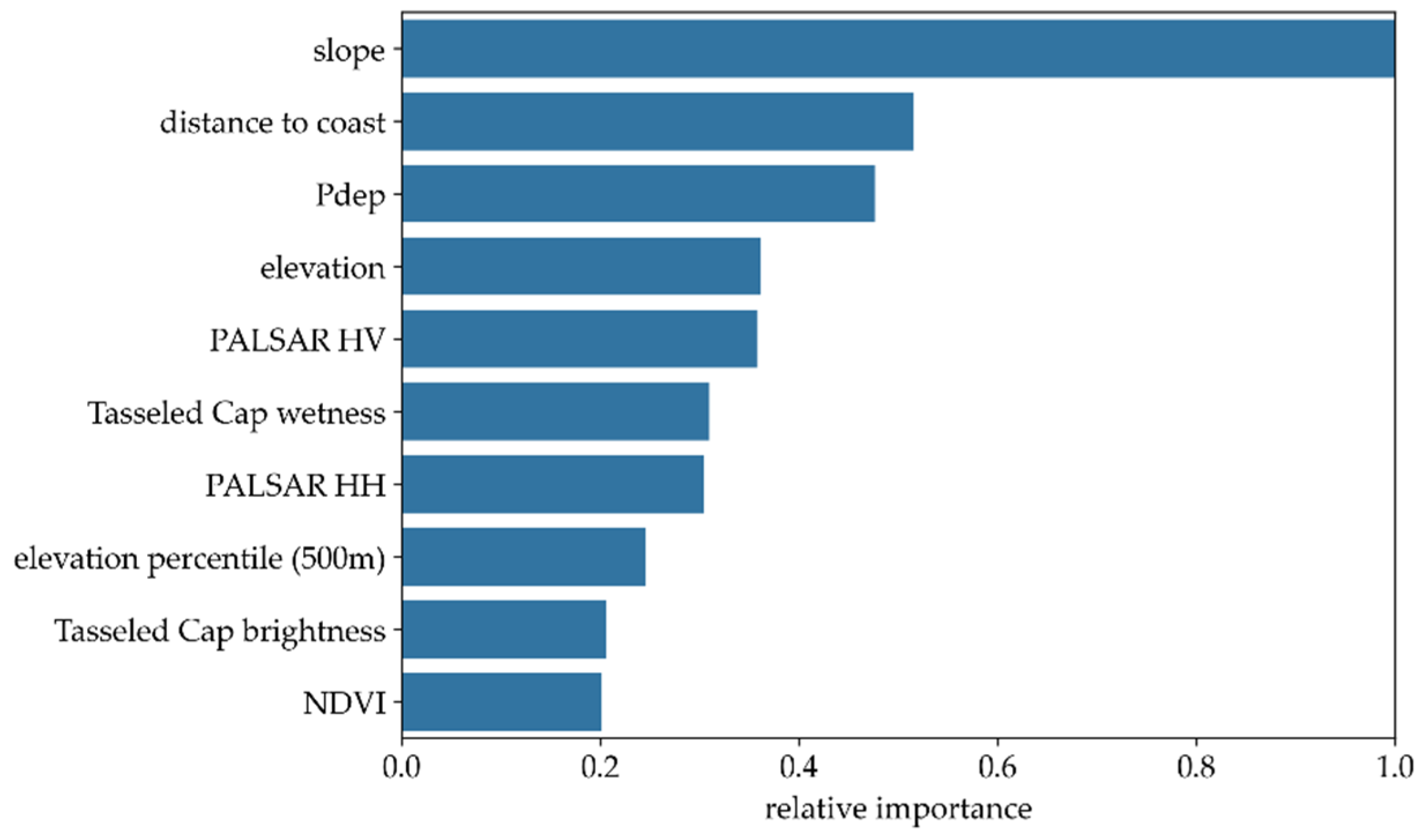
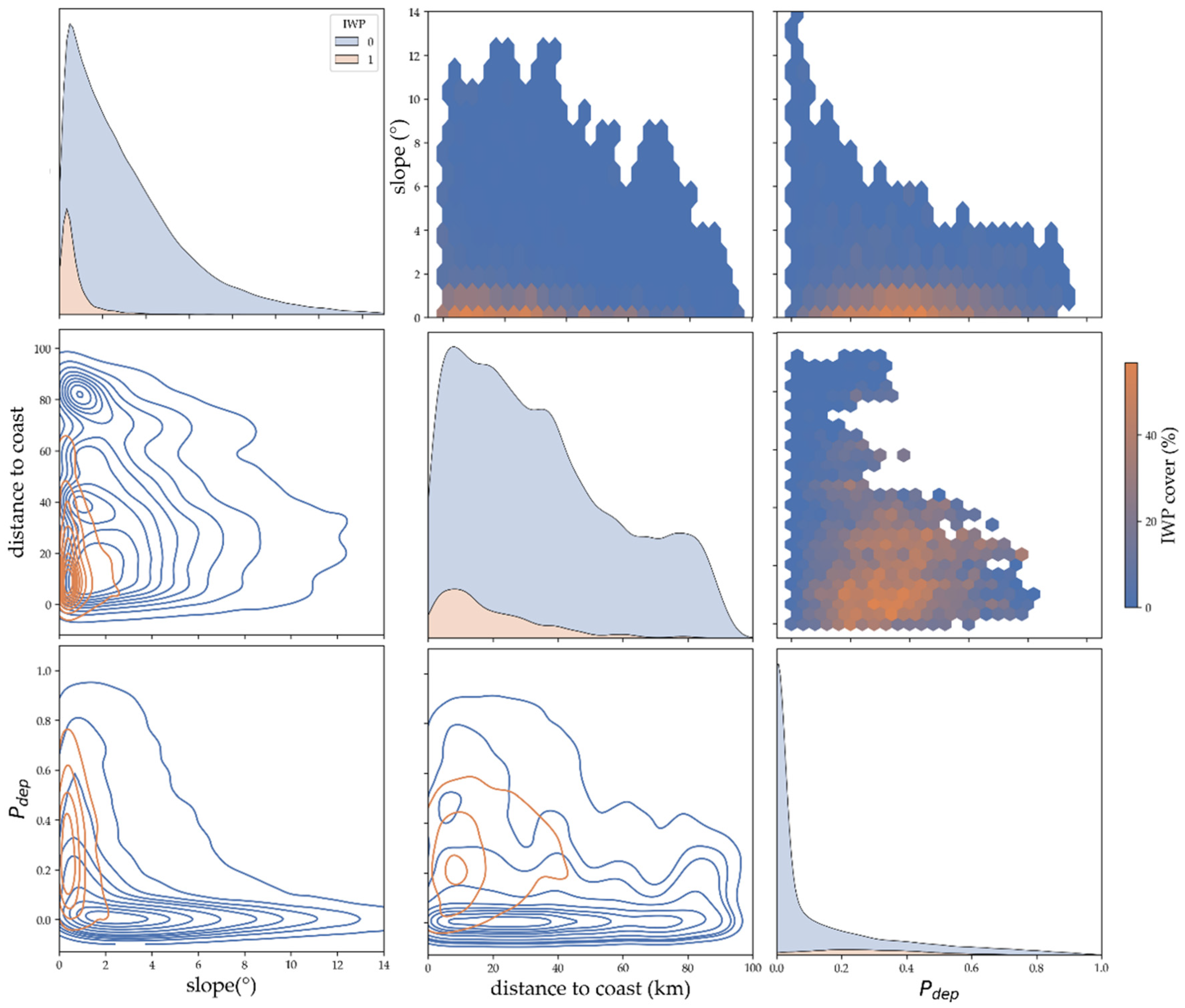
3.2. IWP Variable Importance

Permutation variable importance analysis identified the slope as the most important variable in predicting IWP occurrence, followed by the distance to the coast and the probability of depression (Pdep) (Figure 5). The high importance of these variables, along with that of elevation and Tasseled Cap wetness, suggests a strong control of local topography, in particular depressional areas with poor drainage, on IWP occurrence. The importance of the distance to the coast in predicting IWP occurrence correlates with the observed decreasing density of IWPs from the coastline towards the south. Remotely sensed indices are also among the top 10 variables, including the PALSAR HH- and HV backscattering coefficients, as well as the Tasseled Cap wetness, brightness, and NDVI (Figure 5).
Figure 6 shows the kernel density estimate (KDE) and the hexagonal binned plots of the top 3 most important variables. IWP abundance and cover (conditional probability of ice wedge occurrence) are greatest for gentle slopes in coast-proximal locations. In comparison, the relation to Pdep for IWP and non-IWP areas was less visually distinguished. The Pdep of non-IWP areas varied from 0 to 1, while the Pdep of IWPs varied between 0 and 0.8 (Figure 6).
The partial dependence plots of the three most important predictors (Figure 7) visualize the dependence of IWP prediction on each predictor through repeated sampling. Each blue line (n = 200) indicates the dependence of predicted IWP probability as the respective predictor is varied, fixing all other predictors to the respective sample’s values. The average across all samples is represented by the orange dashed line. Increases in both slope and distance to coast correspond to a decrease in predicted IWP probability, although no pronounced change was observed when the slope is above 2°. Conversely, higher Pdep increases predicted IWP probability, encoding a positive dependence between Pdep and IWP that saturates at Pdep ~0.2. Trends observed in the partial dependence plots complement the kernel density plots (Figure 6) that show higher IWP abundance in low-lying depressions near the coast.

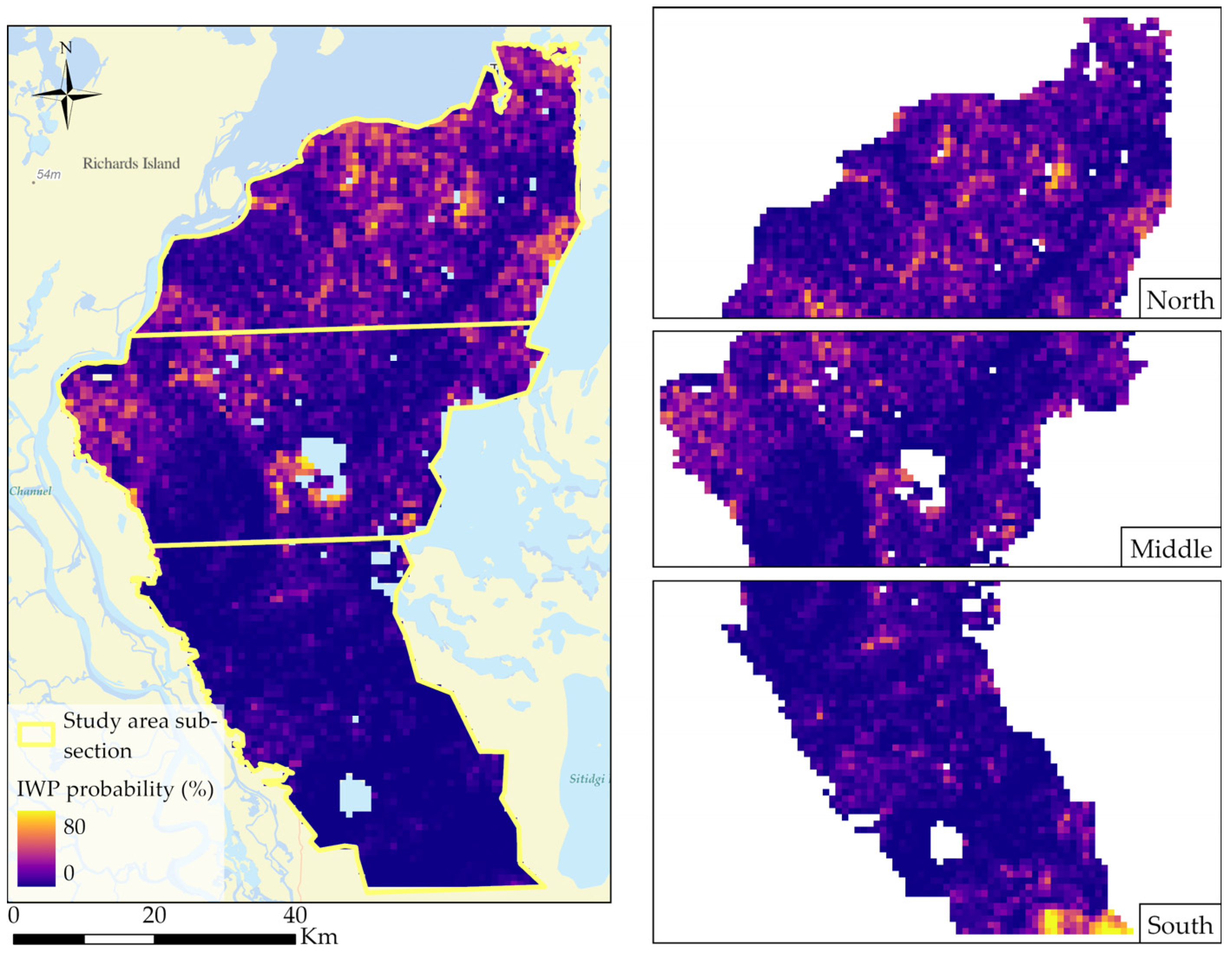
3.3. Map of Predicted IWP Probability

The IWP probability map predicted by the model (MRS) showed a similar regional distribution as the reference inventory, with decreasing densities from the Beaufort coast to the south. Hot spots with dense IWP networks in the northern third of the study area and along the shores of Parsons Lake (central study area) and Husky Lakes (northeast of the study area) were all successfully captured in the probability map (Figure 8b).
The model successfully predicted some IWPs that were not included in the ground reference data, demonstrating its ability in gap-filling and capturing the geophysical process controls on IWP formation (Figure 9). While the model was successful in identifying these IWPs, it also showed some discrepancies with satellite images along the marginal areas. The left column of Figure 9 illustrates one such example, where the area of high IWP probability predicted by the model is larger than the IWP areas that could be identified in the satellite image (see delineation in Figure 9). However, without subsurface ground data, it is unclear if such discrepancies are due to model inaccuracies or subsurface ice wedges lacking surficial expression. The right column of Figure 9 demonstrates a similar example from outside the reference dataset boundary, in which the model predicted a polygonal network on a plateau that features conspicuous troughs in the optical image.
IWPs were identified in both depressional and elevated areas by the reference dataset and the model prediction. Figure 10 demonstrates a zoomed-in example from the northern study area, which is representative of the surrounding landscape that is characterized by numerous small lakes connected by gentle slopes and valleys. IWP networks of varying shapes and sizes surround the Heart Lake in the middle of the map, with clear surficial expressions visible in the satellite image (Figure 10, left map). These IWP networks can be roughly grouped into four clusters, A–D, of which A and D are in low-lying areas immediate to the lake, whereas B and C are in elevated areas further away from the lake (Figure 10, middle). The large and small IWPs in all four groups were successfully predicted by the model, with only minor discrepancies along the margins (Figure 10, right). Overall, these examples demonstrate the model’s accuracy across variable surface positions and polygonal field sizes.
Drained lake basins were a prominent source of prediction errors. While high probabilities of IWP were often predicted by the model, recent basins commonly lack clearly discernible IWPs (see Figure S1).

3.4. Spatial Transferability of IWP Model

While the model predicted IWP probability accurately when trained and tested across the entire study area, the latitudinal transferability analysis revealed insufficiencies in spatial extrapolation. When tested in each subsection of the study area (North, Middle, and South), the full model consistently achieved higher ROC AUC scores than the transferred sub-model (Table 1). The decrease in model performance was more pronounced with sub-models in the North and South, where the ROC AUC scores dropped more than Mmiddle compared to the full model. These decreased accuracies in Mnorth and Msouth can be visualized in the prediction maps of each sub-model (Figure 11). Msouth, in whose training areas IWPs are more abundant, showed a considerable overestimation of IWP probability compared to that of the full model, especially in the southeast corner of the study area. Similarly, Mnorth predicted slightly lower IWP probability than the full model in the north, as it was trained in the southern areas with less prominent IWPs. Such differences between the full model and sub-models indicate the importance of the study area’s geological and climatic settings when adapting the IWP prediction model to different areas.
The loss in predictive skill was observed but smaller for extrapolation across the dominant environmental gradients (longitudinal split) than along this gradient (latitudinal split). For the longitudinal split, the ROC score for Mcentre was 0.01 lower than that of the full model, while Meast and Mwest were reduced by 0.02 (Table 1).

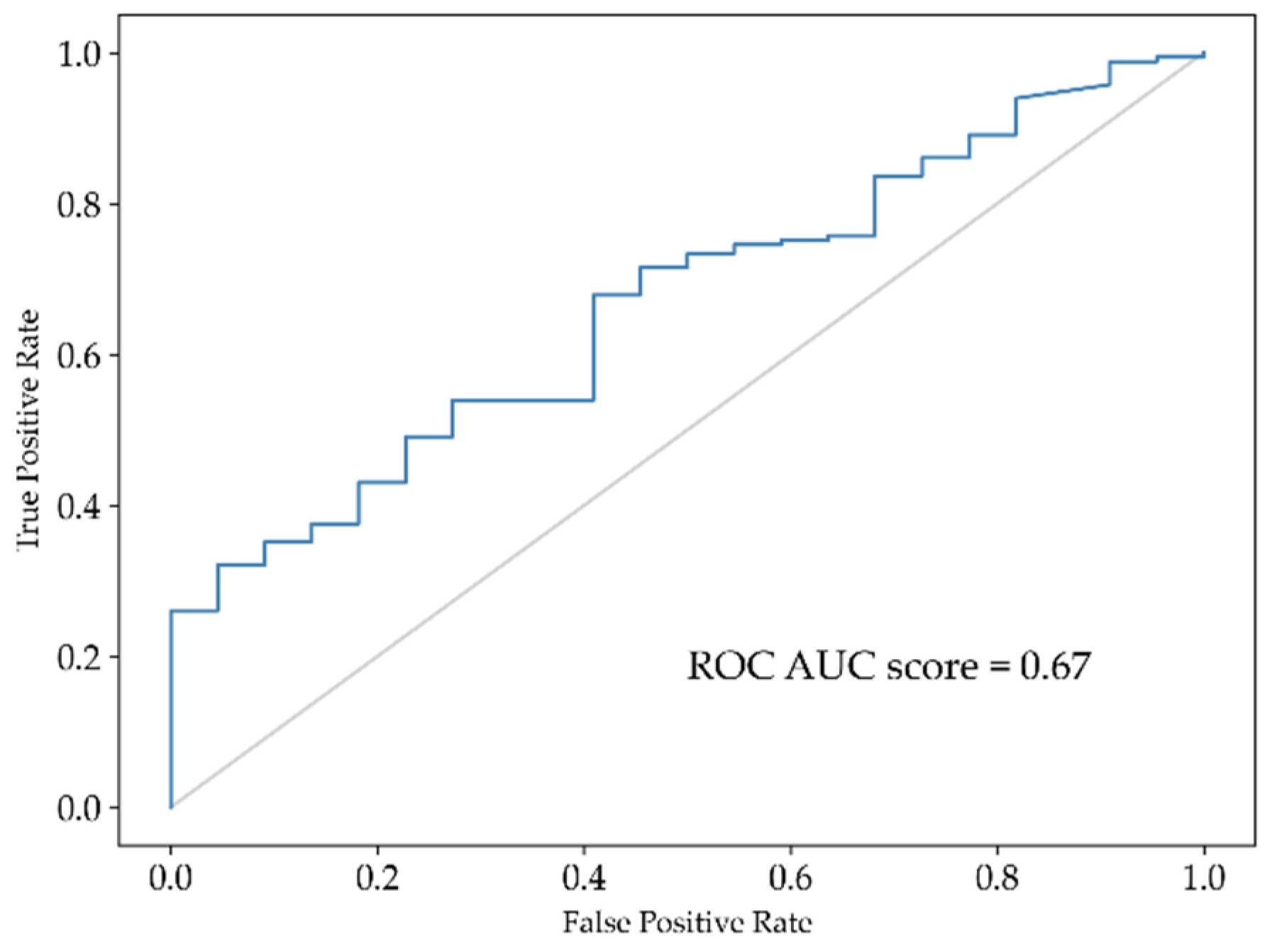
3.5. Visible Ground Ice Model

Predictions of the visible ground ice model were considerably less accurate than the IWP model. ROC AUC of visible ice prediction was 0.67, but with a high false positive rate of 63.6%, thus a low accuracy in identifying ice-poor locations (Figure 12, Table 2). Similarly, the macro F1 score of 0.53 reflects an imbalanced performance for each class, with an F1 score of 0.82 for the ice-rich class but 0.24 for the ice-poor class. With hyperparameter optimization, the highest ROC AUC score was achieved when ice-poor samples were assigned a weight of 10 relative to ice-rich samples to handle the class imbalance. However, even this balanced weight assignment did not provide enough remedy for satisfactory model performance. Due to the model’s low accuracy and apparent misidentification of known ice-poor and ice-rich areas in the prediction map, we only present the visible ground ice probability map in the Supplementary Material (Figure S2).

4. Discussion

4.1. Predictive Skill

We were able to predict IWP occurrence accurately from moderate-resolution remote sensing predictors, while the inferred predictive skill for visible ground ice in the top 5 m was low. We conjecture that the disparity is related to the strength of the association between the ground ice parameter of interest and remote sensing predictors, as well as training data limitations.
The strong associations between IWPs and the 30 m topographic and remote sensing indices contributed to the high accuracy of the IWP prediction model. This strong association is evidenced by the high predictability of IWP from topographic metrics alone, of which slope, Pdep, and elevation were among the most important ones. The high importance of these variables reflects the control of drainage and, in turn, peat thickness on thermal contraction cracking during the Holocene [28]. Part of the prediction inaccuracy resulted from the overestimation of IWPs in recently drained lake basins (e.g., Figure S1), reflecting the strong controls of depressional topography on model-predicted IWP probability. While recently drained lake basins commonly lack well-developed ice wedges, they are susceptible to frost cracking, and ice wedge development can start as early as the first year post-drainage [63]. However, the development of mature IWP may take thousands of years [64]. Given the overall strong association between surface characteristics and IWP occurrence in this geologically recent landscape, it will be interesting to contrast it with regions that remained unglaciated during the Late Pleistocene.
Both radar and optical remote sensing predictors are among the top 10 most important predictors following topographical variables, including the PALSAR HH- and HV backscattering coefficients, the Tasseled Cap wetness and brightness, and the NDVI (Figure 5). As these predictors respond to vegetation, moisture content, surface roughness, and microtopography [53,54,65], their importance reflects the close associations between IWP occurrence and these parameters [28,39,51]. For instance, the varying microtopography and wetness within IWP networks lead to distinctive vegetation assemblages (e.g., wetlands and aquatic species in troughs) that can be identified using moderate-resolution remote sensing [51,66]. The distinctive radar and optical signatures of inundated troughs and polygon centres contribute to successful IWP delineation [29,39].
Visible ground ice in the upper 5 m was not predicted accurately by the remotely sensed predictors. While a quantitative comparison would necessitate comparable training samples, the low prediction accuracy and previous findings suggest a weak association with our topographic and remote sensing covariates. Visible ground ice in the upper 5 m relates to ground ice of variable genesis during the Pleistocene and Holocene periods and also to deeper strata than near-surface ice wedges [67]. For instance, within hummocky moraines with fine-grained materials, ice-rich sediments and tabular ground ice can occur in any topographic position without a necessary association with present-day vegetation covers [36]. While mechanistic interpretations suggest a strong linkage between visible ground ice and surface geology [1], the limited training data and coarse geological maps may have obscured this relationship. Moving forward, the inclusion of additional parameters such as the land surface temperature, snow water equivalent, or species-level vegetation information warrants testing across diverse permafrost landscapes [16,17]. We also hypothesize that very-high-resolution data can enhance the predictive skill in our region by resolving submetre hummocks that indicate segregated ground ice.
The size and sampling characteristics of the training data affected the prediction accuracies for both IWP and visible ground ice. The ice wedge training sample (n = 60,000) was two orders of magnitude larger than that of visible ice (n = 564). Compared to the uniform and random sampling scheme of IWP training data, the borehole locations are clustered along the ITH and likely reflect targeted sampling in areas of concern for highway construction. These differences in sampling are interpreted to partially explain the greater accuracy of the ice wedge prediction. While the size of an adequate training sample will depend on the region, ground ice parameter, and the model, our findings suggest a sample size of ~1000 to be propitious for regional ground ice mapping. The high ROC score of 0.95 for IWP indicates that the model consistently assigns a higher probability of IWP to areas with IWP presence compared to those without, reflecting robust rank-based discrimination. Conversely, the lower macro F1 score of 0.80 highlights a lower performance for the minority IWP class (F1 = 0.63) relative to the majority non-IWP class (F1 = 0.97) at a fixed probability threshold of 0.5. While the IWP and non-IWP training samples each comprise 8% and 92% of the entire training data, the macro F1 score equally weighs each class, magnifying the impact of misclassifications in the rarer IWP class as limited by the class imbalance. A similar pattern is observed in ground ice predictions with a ROC and F1 score of 0.67 and 0.53, respectively, suggesting poorer classification performance compounded by the unrepresentative reference dataset.
Our IWP spatial transferability evaluation suggests that regional prediction needs to account for the spatial variability of the association between ground ice and surface characteristics (Figure 10). Consistently high accuracies for sub-models across longitude suggest high spatial transferability of the model across longitudinal environmental gradients. However, the reduced accuracy of the latitudinal sub-models indicated the importance of interactions between local predictors (e.g., slope) and regional predictors capturing geological and climatic gradients. The regional variability of local controls is illustrated by how the modelled dependence of IWP on slope varies with distance from the coast (Figure 6), as well as the high variable importance of distance to the coast (Figure 5). Its usefulness is comparable to Rudy et al.’s [57] finding that elevation is a valuable proxy of the marine limit for predicting susceptibility to permafrost slope disturbance. Our reliance on the distance proxy is thought to limit the model’s transferability beyond the training area because it does not capture regional factors such as past and present climate directly. We conjecture transferability will be enhanced if such relevant regional factors are distilled successfully into a sufficiently small number of predictors to enable model training with limited data. In summary, our results show that simple, regional variables such as distance to the coast and topography can enhance the regional mapping of ground ice parameters, but the inclusion of variables with a stronger process link to the predicted feature, such as the frequency of temperature conditions conducive to frost cracking throughout the Holocene, may further improve predictive skill.

4.2. Improving Ground Ice Maps and Process Understanding

Ground ice mapping can be enhanced through the synergy of remote sensing-based prediction with process-based modelling and interpretation, field data, and complementary geophysical methods. For ice wedges, which could be accurately predicted from remote sensing features in the Tuktoyaktuk Coastlands, synergies include the refinement and gap-filling of maps derived from high-resolution imagery and the identification of locations susceptible to ice wedge development that currently have no or faint surficial expression (e.g., Figure 9) [29,68]. Where the association between the ground ice parameter and available predictors is weak, remote sensing predictions require and complement field data acquisition, mechanistic modelling, and expert interpretation.
Our findings indicate opportunities and limitations of remote sensing-based modelling for elucidating spatial controls. Local topographic conditions enable skillful predictions (Mbase ROC AUC = 0.91) of IWP occurrence across a substantial gradient in vegetation and past and present climate [28], suggesting strong local controls. For instance, the predicted IWP probability generally decreases with slope, albeit with pronounced variability across the sample (Figure 7). The spatial transferability analyses, the importance of the distance to the coast variable, and the improved predictive skill of Mcoast further align with the relevance of past and present air temperature, precipitation, and vegetation cover identified by Kokelj et al. [28]. The simple distance to the coast proxy obscures these process-based links. These would, however, also be difficult to identify using remote sensing modelling on regional scales due to the strong collinearity between relevant controls across a steep climate gradient, underscoring the importance of detailed process-based studies to enhance understanding. Moving forward, we anticipate the integration of remote sensing and machine learning to allow refining and testing models and data records of ground ice occurrence and dynamics.

5. Conclusions

We predicted ice wedge occurrence and visible ground ice at a 30 m resolution with machine learning models using a suite of topographic and remote sensing predictors. Based on our predictive skill assessments and qualitative interpretation of the results, we draw the following conclusions:
  • We found a high predictability of IWPs from topographic and remote sensing attributes with a ROC AUC and macro F1 score of 0.95 and 0.80 for MRS. The most important predictors were slope, distance to the coast, and probability of depression.
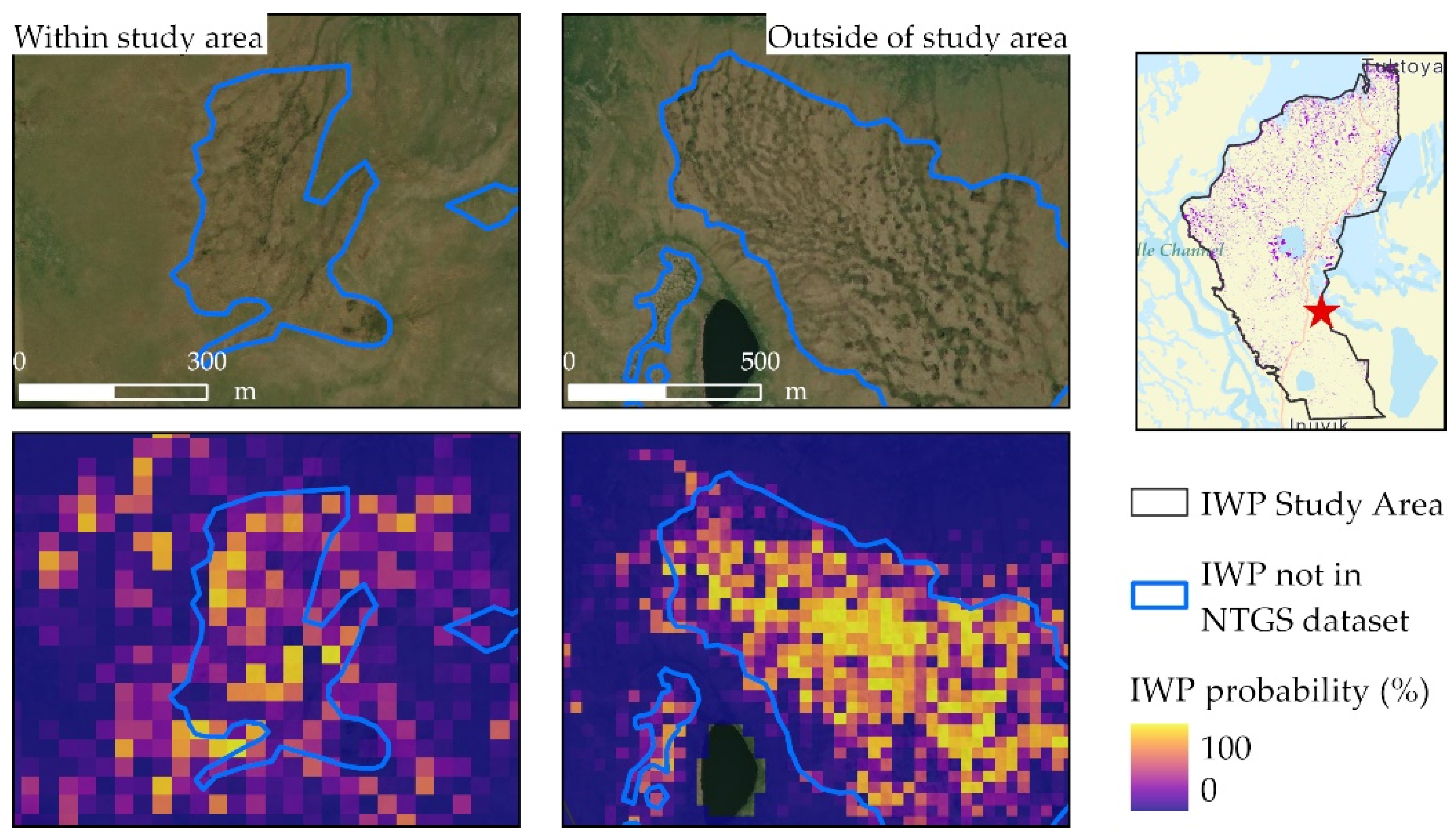
  • The model accurately predicted regional and local trends in ice wedge occurrence, with a decrease in IWP probability moving away from the coast and a greater probability in poorly drained depressions. On local scales, the model accurately predicted IWPs in the southern uplands of the study area, also predicting elevated IWP probability locations with poorly visible troughs not contained in the training data. As the training and test data only refer to ice wedge polygons recognizable at the surface, the model predictions cannot be expected to consistently identify wedge ice where no surface troughs have formed, a key limitation for planning and adaptation.
  • The spatial transferability of the IWP prediction model was relatively limited within the study area. Models trained on subsections of the study area showed underestimation of IWP when they were tested in the north and overestimation when tested in the south. These findings demonstrate the need for a sufficient number and spatial extent of training samples in heterogeneous regions.
  • The prediction of visible ground ice in the upper 5 m did not perform well, with a ROC AUC of 0.67 and macro F1 of 0.53. The poor performance is likely related to the small and spatially skewed training data, as well as the weaker correlation between visible ice and local topography compared to wedge ice.
In summary, our analyses show that machine learning models based on moderate-resolution remote sensing data can support the mapping of ground ice parameters. However, they also highlight the importance of high-quality ground data and process understanding. In conjunction with remote sensing advances such as pan-Arctic automated mapping of ground-ice-related landforms, enhanced modelling capabilities, and process understanding, we anticipate progress in our knowledge and understanding of broad-scale ground ice conditions and dynamics in the coming decade.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs17071245/s1, Table S1: List of predictor variables used in each prediction model; Figure S1: An example of IWP prediction in a drained lake basin in the northeastern study area; Figure S2. Visible ground ice (top 5 m) probability map predicted by the random forest model (Section 3.4) (left) and zoomed-in maps at selected locations (right).

Author Contributions

Conceptualization, Q.C., S.Z. and A.A.B.; methodology, Q.C., S.Z. and A.A.B.; formal analysis, Q.C. and S.Z.; data curation, Q.C.; writing—original draft preparation, Q.C.; writing—review and editing, S.Z. and A.A.B.; visualization, Q.C.; supervision, A.A.B.; project administration, A.A.B.; funding acquisition, A.A.B. All authors have read and agreed to the published version of the manuscript.

Funding

This work is funded by the Natural Sciences and Engineering Research Council (NSERC) Strategic Partnership Grant (SPG), the NSERC Postgraduate Scholarships—Doctoral program (PGS-D), and Northern Water Futures (NWF) (part of Global Water Futures, funded by the Canada First Research Excellence Fund).

Data Availability Statement

Primary research datasets used for this study include “Inventory of polygonal terrain in the Tuktoyaktuk Coastlands, Northwest Territories” (NWT Open Report 2016-022) and “A Cryostratigraphic Synthesis of Inuvik to Tuktoyaktuk Highway Corridor Geotechnical Boreholes (2012–2017)” (NWT Open Report 2022-002; https://doi.org/10.46887/2022-002). Both datasets are published by the Northwest Territories Geological Survey with open access. Other data used include Landsat 5, PALSAR, and Copernicus DEM, accessible through Google Earth Engine.

Acknowledgments

The authors would like to thank John Lindsay for his suggestions on topographic analysis.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
IWPIce wedge polygon.
XGBoosteXtreme Gradient Boosting.
ITHInuvik–Tuktoyuktak Highway.
DEMDigital elevation model.
PALSARPhased Array L-band Synthetic Aperture Radar.
NDVINormalized Difference Vegetation Index.
ROC AUCArea Under the Receiver Operating Characteristic curve.

References

  1. French, H.; Shur, Y. The Principles of Cryostratigraphy. Earth-Sci. Rev. 2010, 101, 190–206. [Google Scholar] [CrossRef]
  2. Kanevskiy, M.; Shur, Y.; Jorgenson, M.T.; Ping, C.-L.; Michaelson, G.J.; Fortier, D.; Stephani, E.; Dillon, M.; Tumskoy, V. Ground Ice in the Upper Permafrost of the Beaufort Sea Coast of Alaska. Cold Reg. Sci. Technol. 2013, 85, 56–70. [Google Scholar] [CrossRef]
  3. Jorgenson, M.T.; Kanevskiy, M.; Shur, Y.; Moskalenko, N.; Brown, D.R.N.; Wickland, K.; Striegl, R.; Koch, J. Role of Ground Ice Dynamics and Ecological Feedbacks in Recent Ice Wedge Degradation and Stabilization. J. Geophys. Res. Earth Surf. 2015, 120, 2280–2297. [Google Scholar] [CrossRef]
  4. Morse, P.D.; Burn, C.R.; Kokelj, S.V. Near-Surface Ground-Ice Distribution, Kendall Island Bird Sanctuary, Western Arctic Coast, Canada. Permafr. Periglac. Process. 2009, 20, 155–171. [Google Scholar] [CrossRef]
  5. Lee, H.; Swenson, S.C.; Slater, A.G.; Lawrence, D.M. Effects of Excess Ground Ice on Projections of Permafrost in a Warming Climate. Environ. Res. Lett. 2014, 9, 124006. [Google Scholar] [CrossRef]
  6. Angelopoulos, M.C.; Pollard, W.H.; Couture, N.J. The Application of CCR and GPR to Characterize Ground Ice Conditions at Parsons Lake, Northwest Territories. Cold Reg. Sci. Technol. 2013, 85, 22–33. [Google Scholar] [CrossRef]
  7. Oldenborger, G.A.; LeBlanc, A.-M. Geophysical Characterization of Permafrost Terrain at Iqaluit International Airport, Nunavut. J. Appl. Geophys. 2015, 123, 36–49. [Google Scholar] [CrossRef]
  8. Castagner, A.; Brenning, A.; Gruber, S.; Kokelj, S. Vertical Distribution of Excess Ice in Icy Sediments and Its Statistical Estimation from Geotechnical Data (Tuktoyaktuk Coastlands and Anderson Plain, Northwest Territories). Arct. Sci. 2022, 9, 483–496. [Google Scholar] [CrossRef]
  9. Heginbottom, J.A. Permafrost Mapping: A Review. Prog. Phys. Geogr. Earth Environ. 2002, 26, 623–642. [Google Scholar] [CrossRef]
  10. Jorgenson, M.T.; Shur, Y.L.; Walker, H.J. Evolution of a Permafrost-Dominated Landscape on the Colville River Delta, Northern Alaska. In Proceedings of the PERMAFROST—Seventh International Conference Proceedings, Yellowknife, NT, Canada, 23–27 June 1998; pp. 523–529. [Google Scholar]
  11. Reger, R.D.; Solie, D.N. Reconnaissance Interpretation of Permafrost, Alaska Highway Corridor, Delta Junction to Dot Lake, Alaska; Alaska Division of Geological & Geophysical Surveys: Fairbanks, AK, USA, 2008; p. PIR 2008-3C. [Google Scholar]
  12. Zwieback, S.; Meyer, F.J. Top-of-Permafrost Ground Ice Indicated by Remotely Sensed Late-Season Subsidence. Cryosphere 2021, 15, 2041–2055. [Google Scholar] [CrossRef]
  13. Allard, M.; L’Hérault, E.; Aubé-Michaud, S.; Carbonneau, A.-S.; Mathon-Dufour, V.; St-Amour, A.B.; Gauthier, S. Facing the Challenge of Permafrost Thaw in Nunavik Communities: Innovative Integrated Methodology, Lessons Learnt, and Recommendations to Stakeholders. Arct. Sci. 2023, 9, 657–677. [Google Scholar] [CrossRef]
  14. Witharana, C.; Bhuiyan, M.A.E.; Liljedahl, A.K.; Kanevskiy, M.; Epstein, H.E.; Jones, B.M.; Daanen, R.; Griffin, C.G.; Kent, K.; Ward Jones, M.K. Understanding the Synergies of Deep Learning and Data Fusion of Multispectral and Panchromatic High Resolution Commercial Satellite Imagery for Automated Ice-Wedge Polygon Detection. ISPRS J. Photogramm. Remote Sens. 2020, 170, 174–191. [Google Scholar] [CrossRef]
  15. Obu, J.; Westermann, S.; Bartsch, A.; Berdnikov, N.; Christiansen, H.H.; Dashtseren, A.; Delaloye, R.; Elberling, B.; Etzelmüller, B.; Kholodov, A.; et al. Northern Hemisphere Permafrost Map Based on TTOP Modelling for 2000–2016 at 1 km2 Scale. Earth-Sci. Rev. 2019, 193, 299–316. [Google Scholar] [CrossRef]
  16. Zhang, C.; Douglas, T.A.; Anderson, J.E. Modeling and Mapping Permafrost Active Layer Thickness Using Field Measurements and Remote Sensing Techniques. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102455. [Google Scholar] [CrossRef]
  17. Thaler, E.A.; Uhleman, S.; Rowland, J.C.; Schwenk, J.; Wang, C.; Dafflon, B.; Bennett, K.E. High-Resolution Maps of Near-Surface Permafrost for Three Watersheds on the Seward Peninsula, Alaska Derived From Machine Learning. Earth Space Sci. 2023, 10, e2023EA003015. [Google Scholar] [CrossRef]
  18. Pastick, N.J.; Jorgenson, M.T.; Wylie, B.K.; Nield, S.J.; Johnson, K.D.; Finley, A.O. Distribution of Near-Surface Permafrost in Alaska: Estimates of Present and Future Conditions. Remote Sens. Environ. 2015, 168, 301–315. [Google Scholar] [CrossRef]
  19. Zou, D.; Pang, Q.; Zhao, L.; Wang, L.; Hu, G.; Du, E.; Liu, G.; Liu, S.; Liu, Y. Estimation of Permafrost Ground Ice to 10 m Depth on the Qinghai-Tibet Plateau. Permafr. Periglac. 2024, 35, 423–434. [Google Scholar] [CrossRef]
  20. O’Neill, H.B.; Wolfe, S.A.; Duchesne, C. New Ground Ice Maps for Canada Using a Paleogeographic Modelling Approach. Cryosphere 2019, 13, 753–773. [Google Scholar] [CrossRef]
  21. Jorgenson, M.; Yoshikawa, K.; Kanevskiy, M.; Shur, Y.; Romanovsky, V.; Marchenko, S.; Jones, B. Permafrost Characteristics of Alaska. In Proceedings of the NICOP, Fairbanks, Alaska, 1 July 2008. [Google Scholar]
  22. Mardian, J.; Champagne, C.; Bonsal, B.; Berg, A. A Machine Learning Framework for Predicting and Understanding the Canadian Drought Monitor. Water Resour. Res. 2023, 59, e2022WR033847. [Google Scholar] [CrossRef]
  23. Li, Y.; Li, M.; Li, C.; Liu, Z. Forest Aboveground Biomass Estimation Using Landsat 8 and Sentinel-1A Data with Machine Learning Algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef]
  24. Liu, W.; Li, R.; Wu, T.; Shi, X.; Wu, X.; Zhao, L.; Hu, G.; Yao, J.; Ma, J.; Wang, S.; et al. Preliminary Simulation of Spatial Distribution Patterns of Soil Thermal Conductivity in Permafrost of the Arctic. Int. J. Digit. Earth 2023, 16, 4512–4532. [Google Scholar] [CrossRef]
  25. Niazkar, M.; Menapace, A.; Brentan, B.; Piraei, R.; Jimenez, D.; Dhawan, P.; Righetti, M. Applications of XGBoost in Water Resources Engineering: A Systematic Literature Review (Dec 2018–May 2023). Environ. Model. Softw. 2024, 174, 105971. [Google Scholar] [CrossRef]
  26. Akosah, S.; Gratchev, I.; Kim, D.-H.; Ohn, S.-Y. Application of Artificial Intelligence and Remote Sensing for Landslide Detection and Prediction: Systematic Review. Remote Sens. 2024, 16, 2947. [Google Scholar] [CrossRef]
  27. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
  28. Kokelj, S.V.; Lantz, T.C.; Wolfe, S.A.; Kanigan, J.C.; Morse, P.D.; Coutts, R.; Molina-Giraldo, N.; Burn, C.R. Distribution and Activity of Ice Wedges across the Forest-Tundra Transition, Western Arctic Canada. J. Geophys. Res. Earth Surf. 2014, 119, 2032–2047. [Google Scholar] [CrossRef]
  29. Lantz, T.C.; Steedman, S.V.; Kokelj, S.V.; Segal, R.A. Inventory of Polygonal Terrain in the Tuktoyaktuk Coastlands, Northwest Territories; Northwest Territories Geological Survey: Yellowknife, NT, Canada, 2017; p. 10. [Google Scholar]
  30. Burn, C.R. Cryostratigraphy, Paleogeography, and Climate Change during the Early Holocene Warm Interval, Western Arctic Coast, Canada. Can. J. Earth Sci. 1997, 34, 912–925. [Google Scholar] [CrossRef]
  31. Murton, J.B.; Whiteman, C.A.; Waller, R.I.; Pollard, W.H.; Clark, I.D.; Dallimore, S.R. Basal Ice Facies and Supraglacial Melt-out till of the Laurentide Ice Sheet, Tuktoyaktuk Coastlands, Western Arctic Canada. Quat. Sci. Rev. 2005, 24, 681–708. [Google Scholar] [CrossRef]
  32. Kokelj, S.V.; Lantz, T.C.; Tunnicliffe, J.; Segal, R.; Lacelle, D. Climate-Driven Thaw of Permafrost Preserved Glacial Landscapes, Northwestern Canada. Geology 2017, 45, 371–374. [Google Scholar] [CrossRef]
  33. Kokelj, S.V.; Palmer, M.J.; Lantz, T.C.; Burn, C.R. Ground Temperatures and Permafrost Warming from Forest to Tundra, Tuktoyaktuk Coastlands and Anderson Plain, NWT, Canada. Permafr. Periglac. Process. 2017, 28, 543–551. [Google Scholar] [CrossRef]
  34. Environment and Climate Change Canada. Canadian Climate Normals. Available online: https://climate.weather.gc.ca/climate_normals/index_e.html (accessed on 8 February 2024).
  35. Castagner, A.; Kokelj, S.V.; Gruber, S. A Cryostratigraphic Synthesis of Inuvik to Tuktoyaktuk Highway Corridor Geotechnical Boreholes (2012–2017); Northwest Territories Geological Survey: Yellowknife, NT, Canada, 2022; p. 12. [Google Scholar]
  36. Burn, C.R.; Kokelj, S.V. The Environment and Permafrost of the Mackenzie Delta Area. Permafr. Periglac. Process. 2009, 20, 83–105. [Google Scholar] [CrossRef]
  37. Dyke, L.D.; Brooks, G.R. The Physical Environment of the Mackenzie Valley, Northwest Territories: A Base Line for the Assessment of Environmental Change; Natural Resources Canada: Ottawa, ON, Canada, 2000; p. 208. [Google Scholar]
  38. Aylsworth, J.M.; Burgess, M.M.; Desrochers, D.T.; Duk-Rodkin, A.; Robertson, T.; Traynor, J.A. Surficial geology, subsurface materials, and thaw sensitivity of sediments. In The Physical Environment of the Mackenzie Valley, Northwest Territories: A Base Line for the Assessment of Environmental Change, Geological Survey of Canada; Dyke, L.D., Brooks, G.R., Eds.; Natural Resources Canada: Ottawa, ON, Canada, 2000; Volume 547, pp. 41–48. [Google Scholar] [CrossRef]
  39. Steedman, A.E.; Lantz, T.C.; Kokelj, S.V. Spatio-Temporal Variation in High-Centre Polygons and Ice-Wedge Melt Ponds, Tuktoyaktuk Coastlands, Northwest Territories: Variation in High-Centre Polygons and Ice-Wedge Melt Ponds, NWT. Permafr. Periglac. Process. 2016, 28, 66–78. [Google Scholar] [CrossRef]
  40. Pollard, W.H.; French, H.M. A First Approximation of the Volume of Ground Ice, Richards Island, Pleistocene Mackenzie Delta, Northwest Territories, Canada. Can. Geotech. J. 1980, 17, 509–516. [Google Scholar] [CrossRef]
  41. De Guzman, E.M.B.; Alfaro, M.C.; Doré, G.; Arenson, L.U.; Piamsalee, A. Performance of Highway Embankments in the Arctic Constructed under Winter Conditions. Can. Geotech. J. 2021, 58, 722–736. [Google Scholar] [CrossRef]
  42. Lindsay, J.B.; Cockburn, J.M.H.; Russell, H.A.J. An Integral Image Approach to Performing Multi-Scale Topographic Position Analysis. Geomorphology 2015, 245, 51–61. [Google Scholar] [CrossRef]
  43. Newman, D.R.; Lindsay, J.B.; Cockburn, J.M.H. Evaluating Metrics of Local Topographic Position for Multiscale Geomorphometric Analysis. Geomorphology 2018, 312, 40–50. [Google Scholar] [CrossRef]
  44. Clare, S.; Creed, I.F. Tracking Wetland Loss to Improve Evidence-Based Wetland Policy Learning and Decision Making. Wetl. Ecol. Manag. 2014, 22, 235–245. [Google Scholar] [CrossRef]
  45. Hodgson, M.E.; Galle, G.L. A Cartographic Modeling Approach for Surface Orientation-Related Applications. Photogramm. Eng. Remote Sens. 1999, 65, 85–95. [Google Scholar]
  46. Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale Analysis of Topographic Surface Roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1200–1213. [Google Scholar] [CrossRef]
  47. Ko, M.; Kang, H.; Kim, J.U.; Lee, Y.; Hwang, J.-E. How to Measure Quality of Affordable 3D Printing: Cultivating Quantitative Index in the User Community. In HCI International 2016—Posters’ Extended Abstracts; Stephanidis, C., Ed.; Communications in Computer and Information Science; Springer International Publishing: Cham, Switzerland, 2016; Volume 617, pp. 116–121. ISBN 978-3-319-40547-6. [Google Scholar]
  48. Florinsky, I.V. An Illustrated Introduction to General Geomorphometry. Prog. Phys.Geogr. Earth Environ. 2017, 41, 723–752. [Google Scholar] [CrossRef]
  49. Lindsay, J.B. WbW documentation—Whitebox Workflows for Python v1.3 User Manual. Available online: https://www.whiteboxgeo.com/manual/wbw-user-manual/book/tool_help.html (accessed on 9 February 2024).
  50. Lindsay, J.B.; Creed, I.F. Sensitivity of Digital Landscapes to Artifact Depressions in Remotely-Sensed DEMs. Photogramm. Eng. Remote Sens. 2005, 71, 1029–1036. [Google Scholar] [CrossRef]
  51. Wolter, J.; Lantuit, H.; Fritz, M.; Macias-Fauria, M.; Myers-Smith, I.; Herzschuh, U. Vegetation Composition and Shrub Extent on the Yukon Coast, Canada, Are Strongly Linked to Ice-Wedge Polygon Degradation. Polar Res. 2016, 35, 27489. [Google Scholar] [CrossRef]
  52. Wang, P.; de Jager, J.; Nauta, A.; van Huissteden, J.; Trofim, M.C.; Limpens, J. Exploring Near-Surface Ground Ice Distribution in Patterned-Ground Tundra: Correlations with Topography, Soil and Vegetation. Plant Soil 2019, 444, 251–265. [Google Scholar] [CrossRef]
  53. Chang, Q.; Zwieback, S.; DeVries, B.; Berg, A. Application of L-Band SAR for Mapping Tundra Shrub Biomass, Leaf Area Index, and Rainfall Interception. Remote Sens. Environ. 2022, 268, 112747. [Google Scholar] [CrossRef]
  54. Zwieback, S.; Berg, A.A. Fine-Scale SAR Soil Moisture Estimation in the Subarctic Tundra. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4898–4912. [Google Scholar] [CrossRef]
  55. Evans, T.L.; Costa, M.; Telmer, K.; Silva, T.S.F. Using ALOS/PALSAR and RADARSAT-2 to Map Land Cover and Seasonal Inundation in the Brazilian Pantanal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 560–575. [Google Scholar] [CrossRef]
  56. Côté, M.M.; Duchesne, C.; Wright, J.F.; Ednie, M. Digital Compilation of the Surficial Sediments of the Mackenzie Valley Corridor, Yukon Coastal Plain, and the Tuktoyaktuk Peninsula; Geological Survey of Canada: Ottawa, ON, Canada, 2013; p. 7289. [Google Scholar]
  57. Rudy, A.C.A.; Lamoureux, S.F.; Treitz, P.; van Ewijk, K.Y. Transferability of Regional Permafrost Disturbance Susceptibility Modelling Using Generalized Linear and Generalized Additive Models. Geomorphology 2016, 264, 95–108. [Google Scholar] [CrossRef]
  58. Lindsay, J.B.; Newman, D.R.; Francioni, A. Scale-Optimized Surface Roughness for Topographic Analysis. Geosciences 2019, 9, 322. [Google Scholar] [CrossRef]
  59. Ließ, M.; Glaser, B.; Huwe, B. Uncertainty in the Spatial Prediction of Soil Texture. Geoderma 2012, 170, 70–79. [Google Scholar] [CrossRef]
  60. Joseph, V.R. Optimal Ratio for Data Splitting. Stat. Anal. DataMin. ASA Data Sci. J. 2022, 15, 531–538. [Google Scholar] [CrossRef]
  61. Dobbin, K.K.; Simon, R.M. Optimally Splitting Cases for Training and Testing High Dimensional Classifiers. BMC Med. Genom. 2011, 4, 31. [Google Scholar] [CrossRef]
  62. Ferri, C.; Hernández-Orallo, J.; Modroiu, R. An Experimental Comparison of Performance Measures for Classification. Pattern Recognit. Lett. 2009, 30, 27–38. [Google Scholar] [CrossRef]
  63. Mackay, J.R. Periglacial Features Developed on the Exposed Lake Bottoms of Seven Lakes That Drained Rapidly after 1950, Tuktoyaktuk Peninsula Area, Western Arctic Coast, Canada. Permafr. Periglac. Process. 1999, 10, 39–63. [Google Scholar] [CrossRef]
  64. Fritz, M.; Wolter, J.; Rudaya, N.; Palagushkina, O.; Nazarova, L.; Obu, J.; Rethemeyer, J.; Lantuit, H.; Wetterich, S. Holocene Ice-Wedge Polygon Development in Northern Yukon Permafrost Peatlands (Canada). Quat. Sci. Rev. 2016, 147, 279–297. [Google Scholar] [CrossRef]
  65. Brooker, A.; Fraser, R.H.; Olthof, I.; Kokelj, S.V.; Lacelle, D. Mapping the Activity and Evolution of Retrogressive Thaw Slumps by Tasselled Cap Trend Analysis of a Landsat Satellite Image Stack. Permafr. Periglac. Process. 2014, 25, 243–256. [Google Scholar] [CrossRef]
  66. Jorgenson, M.T.; Marcot, B.G.; Swanson, D.K.; Jorgenson, J.C.; DeGange, A.R. Projected Changes in Diverse Ecosystems from Climate Warming and Biophysical Drivers in Northwest Alaska. Clim. Change 2015, 130, 131–144. [Google Scholar] [CrossRef]
  67. Kokelj, S.V.; Burn, C.R. Near-Surface Ground Ice in Sediments of the Mackenzie Delta, Northwest Territories, Canada. Permafr. Periglac. Process. 2005, 16, 291–303. [Google Scholar] [CrossRef]
  68. Abolt, C.J.; Young, M.H.; Atchley, A.L.; Wilson, C.J. Brief Communication: Rapid Machine-Learning-Based Extraction and Measurement of Ice Wedge Polygons in High-Resolution Digital Elevation Models. Cryosphere 2019, 13, 237–245. [Google Scholar] [CrossRef]
Remotesensing 17 01245 g001
Figure 1. Map of the study area highlighting the Inuvik–Tuktoyuktak Highway (ITH) and the ground reference datasets—the borehole ground ice records [35] and the ice wedge polygon (IWP) inventory [29], both provided by Northwest Territories Geological Survey (NTGS). Inset maps indicate the location of the study area within Canada (red star in upper-right map) and within Northwest Territories (middle-right map).
Figure 1. Map of the study area highlighting the Inuvik–Tuktoyuktak Highway (ITH) and the ground reference datasets—the borehole ground ice records [35] and the ice wedge polygon (IWP) inventory [29], both provided by Northwest Territories Geological Survey (NTGS). Inset maps indicate the location of the study area within Canada (red star in upper-right map) and within Northwest Territories (middle-right map).
Remotesensing 17 01245 g001
Remotesensing 17 01245 g002
Figure 2. Flowchart of the XGBoost models for predicting ice wedge and visible ground ice occurrence and the predictor variables used for each model.
Figure 2. Flowchart of the XGBoost models for predicting ice wedge and visible ground ice occurrence and the predictor variables used for each model.
Remotesensing 17 01245 g002
Remotesensing 17 01245 g003
Figure 3. Training and test area split of each sub-model under the (a) latitudinal and (b) longitudinal spatial partition scenarios to evaluate the spatial transferability of the IWP prediction model.
Figure 3. Training and test area split of each sub-model under the (a) latitudinal and (b) longitudinal spatial partition scenarios to evaluate the spatial transferability of the IWP prediction model.
Remotesensing 17 01245 g003
Remotesensing 17 01245 g004
Figure 4. (a). The ROC AUC scores and macro-averaged F1 scores and (b). The ROC curves of the five random forest classification models for the prediction of ice wedge polygon probability.
Figure 4. (a). The ROC AUC scores and macro-averaged F1 scores and (b). The ROC curves of the five random forest classification models for the prediction of ice wedge polygon probability.
Remotesensing 17 01245 g004
Remotesensing 17 01245 g005
Figure 5. Relative permutation importance of the top 10 most important variables in predicting ice wedge polygon occurrence.
Figure 5. Relative permutation importance of the top 10 most important variables in predicting ice wedge polygon occurrence.
Remotesensing 17 01245 g005
Remotesensing 17 01245 g006
Figure 6. The kernel density estimate (KDE) (lower-left) and the hexagonal binned plots (upper-right) of the distribution of IWP and non-IWP areas among the top 3 most important variables, namely, the slope (°), Pdep (probability of depression), and distance to coast (km). Diagonal plots show the histograms of IWP and non-IWP for each variable.
Figure 6. The kernel density estimate (KDE) (lower-left) and the hexagonal binned plots (upper-right) of the distribution of IWP and non-IWP areas among the top 3 most important variables, namely, the slope (°), Pdep (probability of depression), and distance to coast (km). Diagonal plots show the histograms of IWP and non-IWP for each variable.
Remotesensing 17 01245 g006
Remotesensing 17 01245 g007
Figure 7. Partial dependence plots of the three most important variables—slope (°), Pdep (probability of depression), and distance to coast (km). The partial dependence of individual samples and their average are represented by the blue and orange lines, respectively. Tick marks on x-axes represent the deciles in the variables.
Figure 7. Partial dependence plots of the three most important variables—slope (°), Pdep (probability of depression), and distance to coast (km). The partial dependence of individual samples and their average are represented by the blue and orange lines, respectively. Tick marks on x-axes represent the deciles in the variables.
Remotesensing 17 01245 g007
Remotesensing 17 01245 g008
Figure 8. Maps of (a) ice wedge polygon (IWP) areal cover (% per unit area) based on the ground reference data [29] and (b) IWP probability (% per unit area) predicted by MRS (Model 4). Both maps are resampled to 900 × 900 m for easier visual comparisons.
Figure 8. Maps of (a) ice wedge polygon (IWP) areal cover (% per unit area) based on the ground reference data [29] and (b) IWP probability (% per unit area) predicted by MRS (Model 4). Both maps are resampled to 900 × 900 m for easier visual comparisons.
Remotesensing 17 01245 g008
Remotesensing 17 01245 g009
Figure 9. Two inland polygonal networks on plateaus that were predicted by the model but were not delineated in the ground reference dataset (left) or immediately outside of the reference data boundary (right). Outlines of the IWP networks were delineated based on Esri World Imagery acquired in 2023. Inset map indicates the two IWP networks’ location within the study area.
Figure 9. Two inland polygonal networks on plateaus that were predicted by the model but were not delineated in the ground reference dataset (left) or immediately outside of the reference data boundary (right). Outlines of the IWP networks were delineated based on Esri World Imagery acquired in 2023. Inset map indicates the two IWP networks’ location within the study area.
Remotesensing 17 01245 g009
Remotesensing 17 01245 g010
Figure 10. Zoomed-in map of polygonal networks surrounding a small heart-shaped lake in the northern study area, showing IWPs identified in the ground reference dataset outlined in purple, underlaid by 2023 Esri World Imagery (left) and elevation (middle), and the model-predicted IWP probability (right). A–D in the middle map denotes groups of ice wedge polygon (IWP) networks discussed in the text. Inset map indicates the location of the lake within the study area.
Figure 10. Zoomed-in map of polygonal networks surrounding a small heart-shaped lake in the northern study area, showing IWPs identified in the ground reference dataset outlined in purple, underlaid by 2023 Esri World Imagery (left) and elevation (middle), and the model-predicted IWP probability (right). A–D in the middle map denotes groups of ice wedge polygon (IWP) networks discussed in the text. Inset map indicates the location of the lake within the study area.
Remotesensing 17 01245 g010
Remotesensing 17 01245 g011
Figure 11. Comparison of the IWP probability maps predicted by the full model across the study area (left) and predicted by each of the sub-spatial models in the corresponding test area (right). All maps share the same scale and a resolution of 900 × 900 m for easier visual comparison.
Figure 11. Comparison of the IWP probability maps predicted by the full model across the study area (left) and predicted by each of the sub-spatial models in the corresponding test area (right). All maps share the same scale and a resolution of 900 × 900 m for easier visual comparison.
Remotesensing 17 01245 g011
Remotesensing 17 01245 g012
Figure 12. ROC AUC curve (blue line) and score of the visible ground ice prediction model with optimized hyperparameters.
Figure 12. ROC AUC curve (blue line) and score of the visible ground ice prediction model with optimized hyperparameters.
Remotesensing 17 01245 g012
Table 1. ROC AUC scores of the full model and sub-spatial models for both latitudinal and longitudinal splits.
Table 1. ROC AUC scores of the full model and sub-spatial models for both latitudinal and longitudinal splits.
Test AreaROC AUC Score
Sub-ModelFull Model
Latitudinal splitNorth0.89 (Mnorth)0.93
Middle0.93 (Mmiddle)0.94
South0.93 (Msouth)0.97
Longitudinal splitEast0.93 (Meast)0.95
Centre0.94 (Mcentre)0.95
West0.94 (Mwest)0.96
Table 2. Confusion matrix of the visible ground ice predictions generated by the model.
Table 2. Confusion matrix of the visible ground ice predictions generated by the model.
Predicted Class
Ice-RichIce-Poor
True ClassIce-rich12540
Ice-poor148
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chang, Q.; Zwieback, S.; Berg, A.A. The Predictive Skill of a Remote Sensing-Based Machine Learning Model for Ice Wedge and Visible Ground Ice Identification in Western Arctic Canada. Remote Sens. 2025, 17, 1245. https://doi.org/10.3390/rs17071245

AMA Style

Chang Q, Zwieback S, Berg AA. The Predictive Skill of a Remote Sensing-Based Machine Learning Model for Ice Wedge and Visible Ground Ice Identification in Western Arctic Canada. Remote Sensing. 2025; 17(7):1245. https://doi.org/10.3390/rs17071245

Chicago/Turabian Style

Chang, Qianyu, Simon Zwieback, and Aaron A. Berg. 2025. "The Predictive Skill of a Remote Sensing-Based Machine Learning Model for Ice Wedge and Visible Ground Ice Identification in Western Arctic Canada" Remote Sensing 17, no. 7: 1245. https://doi.org/10.3390/rs17071245

APA Style

Chang, Q., Zwieback, S., & Berg, A. A. (2025). The Predictive Skill of a Remote Sensing-Based Machine Learning Model for Ice Wedge and Visible Ground Ice Identification in Western Arctic Canada. Remote Sensing, 17(7), 1245. https://doi.org/10.3390/rs17071245

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop