A Fast and Accurate Calculation Method of Water Vapor Transmission: Based on LSTM and Attention Mechanism Model
Abstract
1. Introduction
2. Materials and Methods
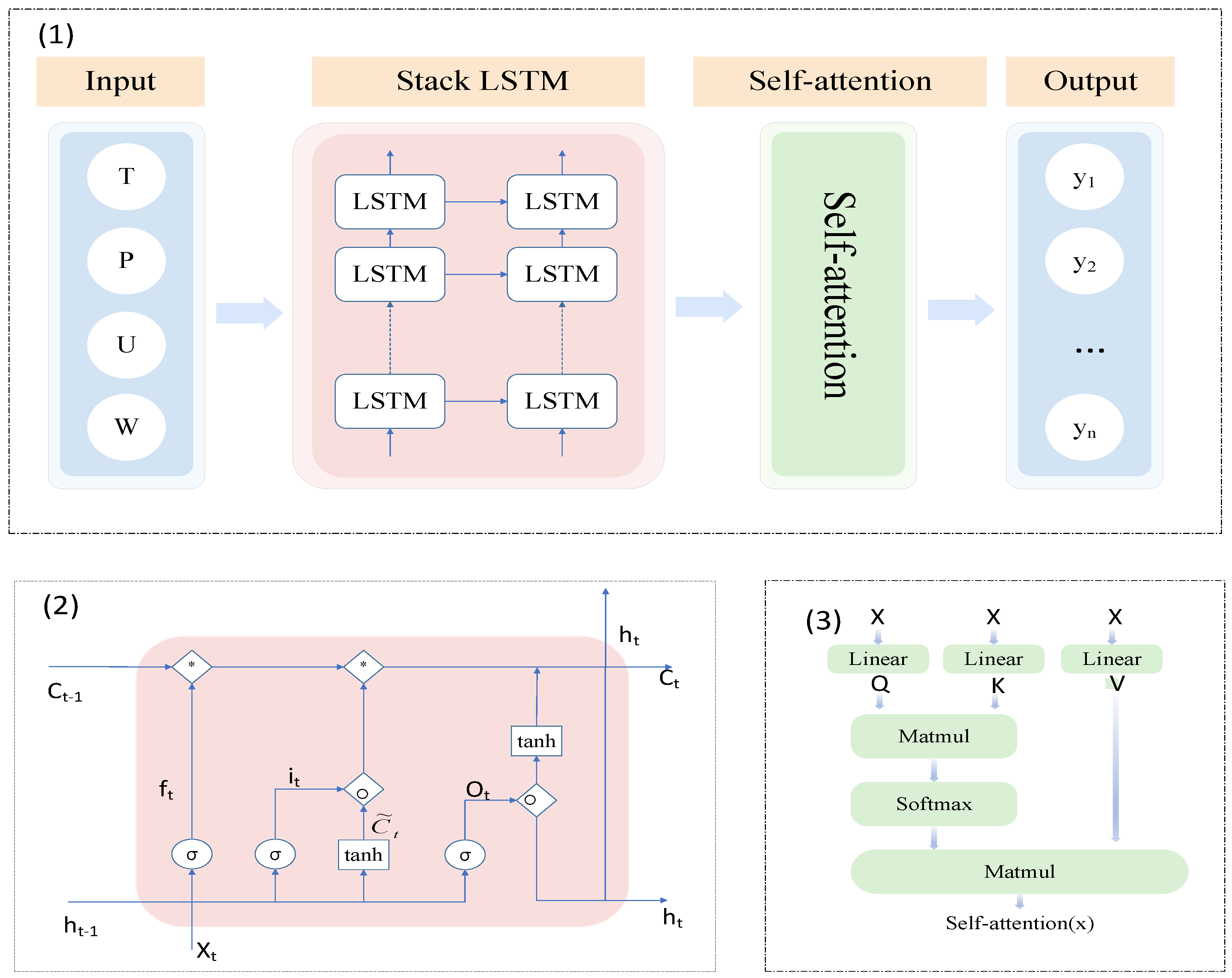
2.1. Stack LSTM-AT Model
2.1.1. Input and Output Module
2.1.2. Stack LSTM Module
2.1.3. Self-Attention Module
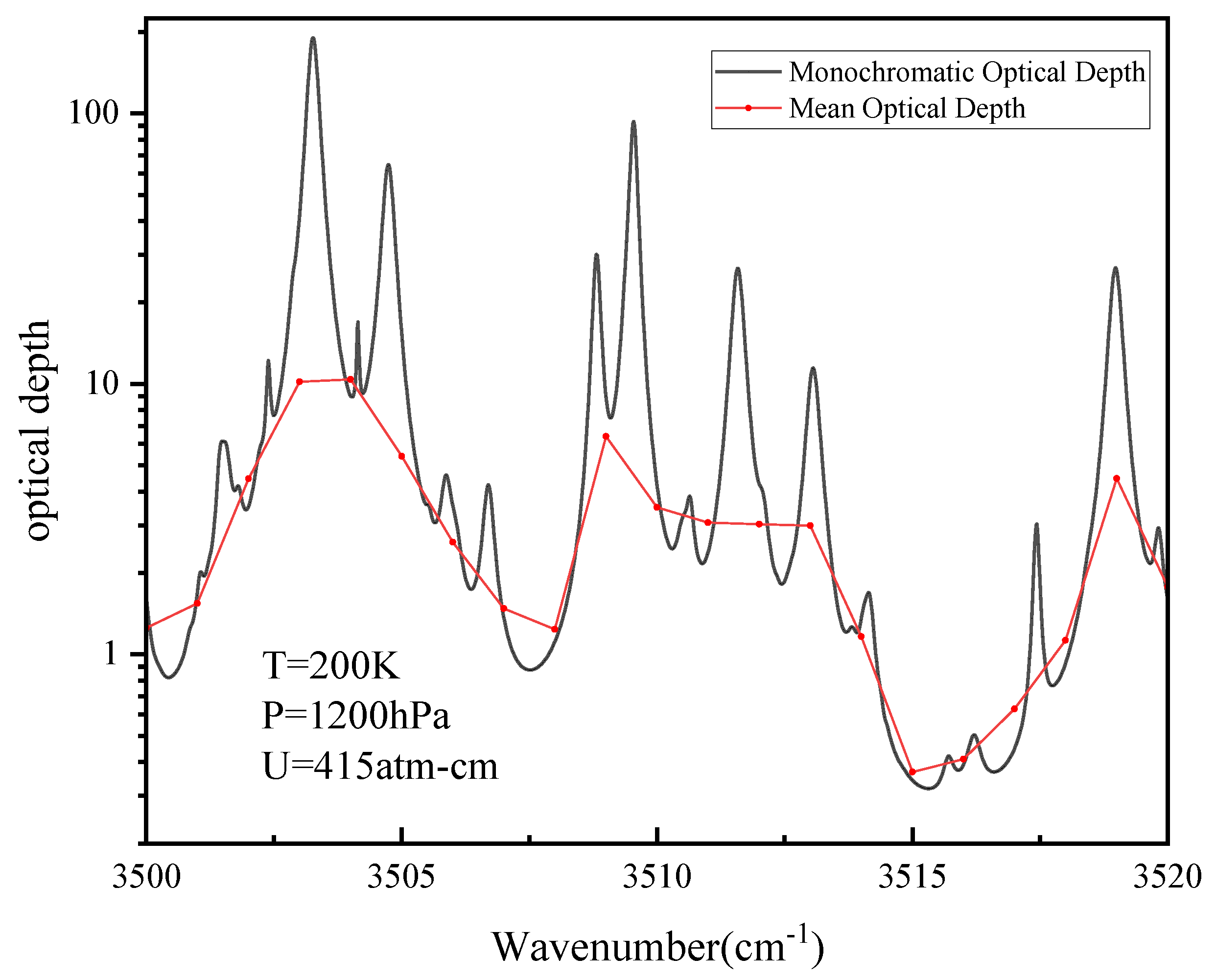
2.2. Evaluation Criteria
3. Results and Analysis
3.1. Ablation Experiments for Stack LSTM-AT
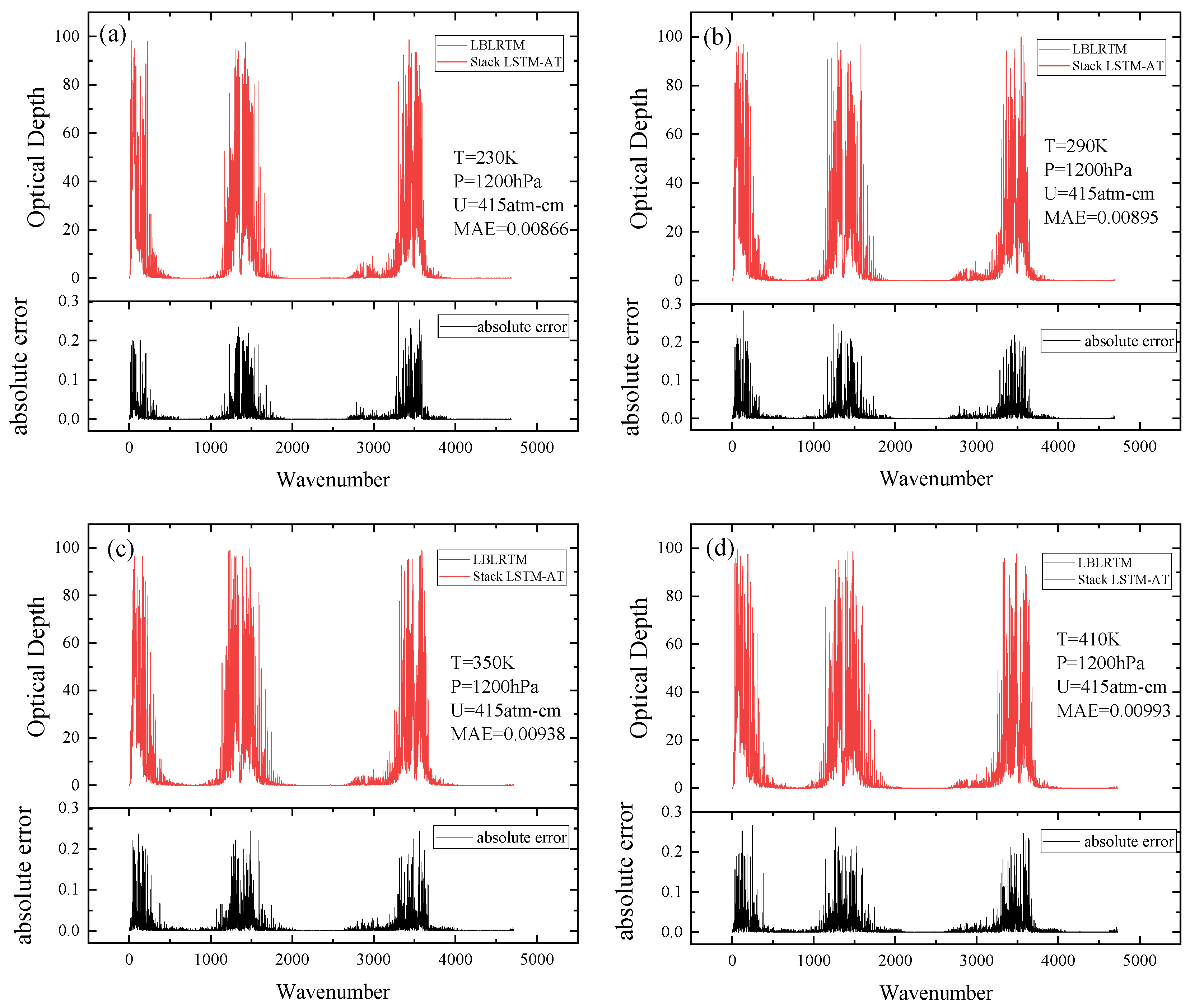
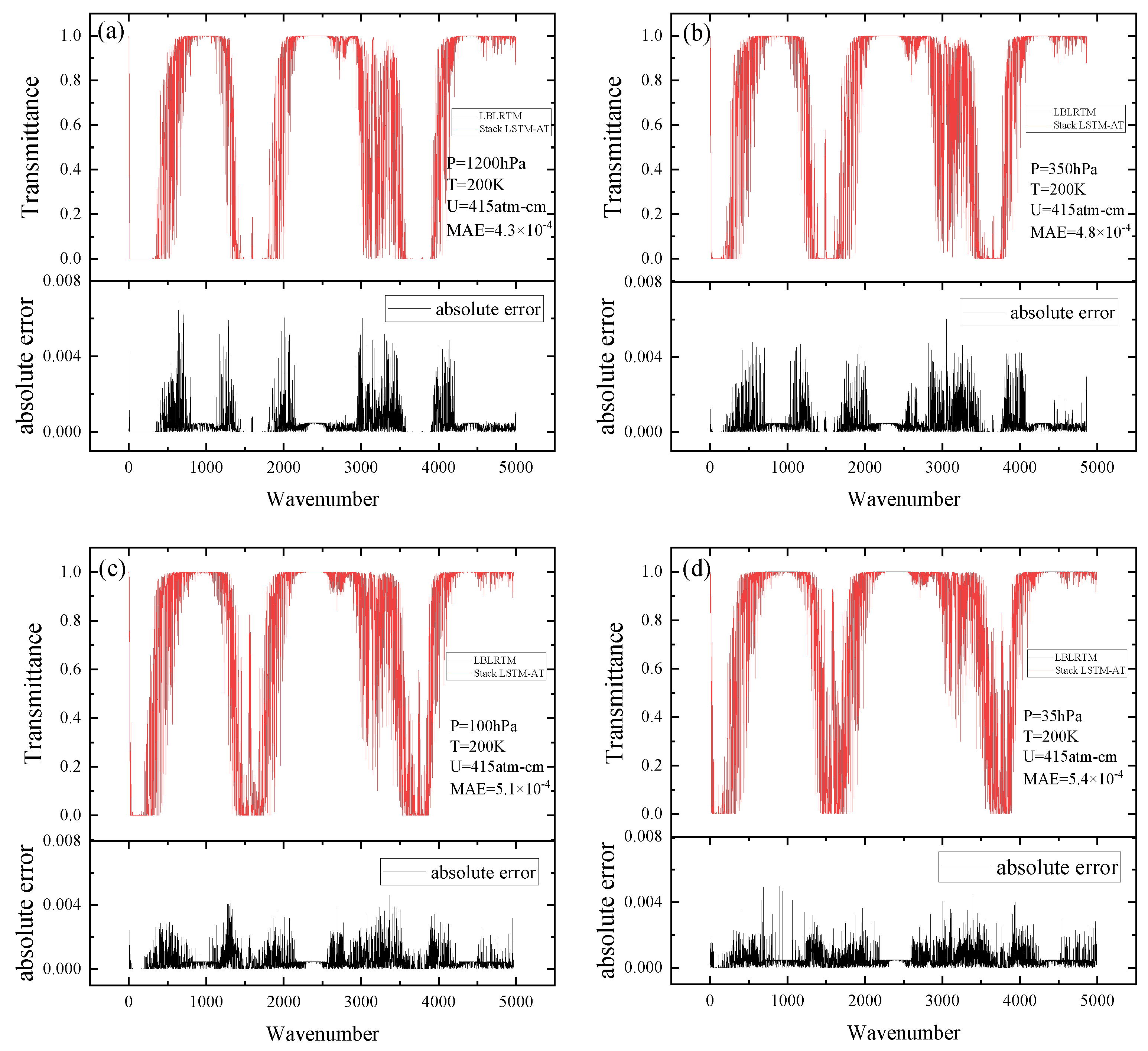
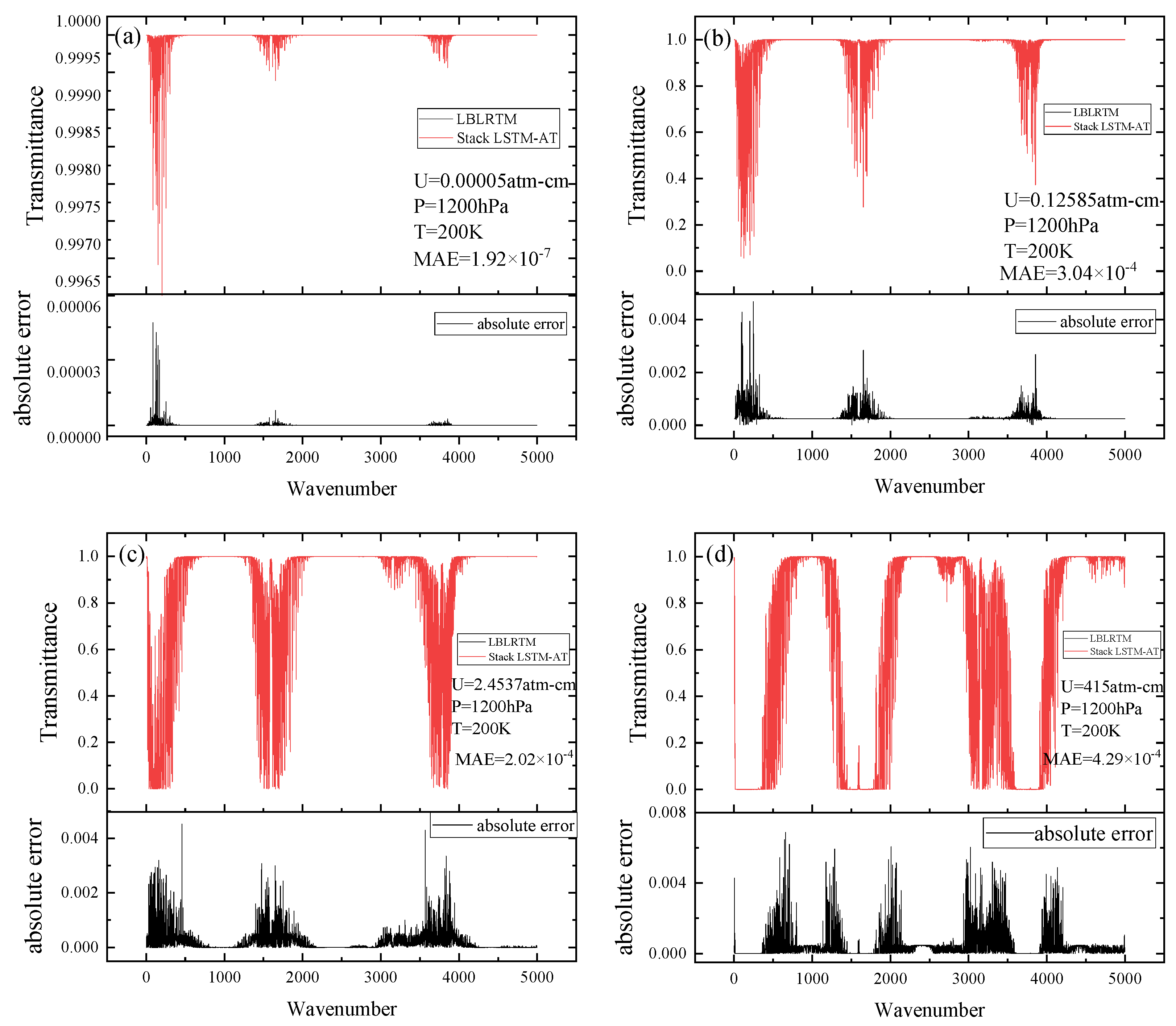
3.2. Comparison with LBLRTM
3.2.1. The Optical Depth
3.2.2. Atmospheric Transmittance
3.2.3. Calculation Time
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soden, B.J.; Held, I.M. An Assessment of Climate Feedbacks in Coupled Ocean–Atmosphere Models. J. Clim. 2006, 19, 3354–3360. [Google Scholar]
- Chen, Y.; Han, Y.; Van Delst, P.; Weng, F. On Water Vapor Jacobian in Fast Radiative Transfer Model. J. Geophys. Res. Atmospheres 2010, 115. [Google Scholar]
- Schneider, T.; O’Gorman, P.A.; Levine, X.J. Water Vapor and the Dynamics of Climate Changes. Rev. Geophys. 2010, 48. [Google Scholar]
- Colman, R. A Comparison of Climate Feedbacks in General Circulation Models. Clim. Dyn. 2003, 20, 865–873. [Google Scholar]
- Vaquero-Martínez, J.; Antón, M.; de Galisteo, J.P.O.; Román, R.; Cachorro, V.E. Water Vapor Radiative Effects on Short-Wave Radiation in Spain. Atmos. Res. 2018, 205, 18–25. [Google Scholar]
- Clough, S.A.; Iacono, M.J.; Moncet, J. Line-by-Line Calculations of Atmospheric Fluxes and Cooling Rates: Application to Water Vapor. J. Geophys. Res. Atmos. 1992, 97, 15761–15785. [Google Scholar]
- Clough, S.; Shephard, M.; Mlawer, E.; Delamere, J.; Iacono, M.; Cady-Pereira, K.; Boukabara, S.; Brown, P. Atmospheric Radiative Transfer Modeling: A Summary of the Aer Codes. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar]
- Li, W.; Zhang, F.; Shi, Y.-N.; Iwabuchi, H.; Zhu, M.; Li, J.; Han, W.; Letu, H.; Ishimoto, H. Efficient Radiative Transfer Model for Thermal Infrared Brightness Temperature Simulation in Cloudy Atmospheres. Opt. Express 2020, 28, 25730–25749. [Google Scholar]
- Morcrette, J.-J.; Mozdzynski, G.; Leutbecher, M. A Reduced Radiation Grid for the Ecmwf Integrated Forecasting System. Mon. Weather Rev. 2008, 136, 4760–4772. [Google Scholar]
- Manners, J.; Thelen, J.C.; Petch, J.; Hill, P.; Edwards, J.M. Two Fast Radiative Transfer Methods to Improve the Temporal Sampling of Clouds in Numerical Weather Prediction and Climate Models. Q. J. R. Meteorol. Soc. J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2009, 135, 457–468. [Google Scholar]
- Isaacs, R.G.; Vogelmann, A.M. Multispectral Sensor Data Simulation Modeling Based on the Multiple Scattering Lowtran Code. Remote Sens. Environ. 1988, 26, 75–99. [Google Scholar]
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.; Robertson, D.; Chetwynd, J.; Adler-Golden, S. Modtran Cloud and Multiple Scattering Upgrades with Application to Aviris. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar]
- Strow, L.L.; Hannon, S.E.; De-Souza Machado, S.; Motteler, H.E.; Tobin, D.C. Validation of the Atmospheric Infrared Sounder Radiative Transfer Algorithm. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar]
- Engelen, R.J.; Stephens, G.L. Infrared Radiative Transfer in the 9.6-Μm Band: Application to TIROS Operational Vertical Sounder Ozone Retrieval. J. Geophys. Res. Atmos. 1997, 102, 6929–6939. [Google Scholar] [CrossRef]
- Buchwitz, M.; Rozanov, V.V.; Burrows, J.P. A Correlated-K Distribution Scheme for Overlapping Gases Suitable for Retrieval of Atmospheric Constituents from Moderate Resolution Radiance Measurements in the Visible/near-Infrared Spectral Region. J. Geophys. Res. Atmos. 2000, 105, 15247–15261. [Google Scholar]
- Stegmann, P.G.; Johnson, B.; Moradi, I.; Karpowicz, B.; McCarty, W. A Deep Learning Approach to Fast Radiative Transfer. J. Quant. Spectrosc. Radiat. Transf. 2022, 280, 108088. [Google Scholar]
- Cotronei, A.; Slawig, T. Single-Precision Arithmetic in ECHAM Radiation Reduces Runtime and Energy Consumption. Geosci. Model Dev. 2020, 13, 2783–2804. [Google Scholar]
- Alizamir, M.; Shiri, J.; Fard, A.F.; Kim, S.; Gorgij, A.D.; Heddam, S.; Singh, V.P. Improving the Accuracy of Daily Solar Radiation Prediction by Climatic Data Using an Efficient Hybrid Deep Learning Model: Long Short-Term Memory (LSTM) Network Coupled with Wavelet Transform. Eng. Appl. Artif. Intell. 2023, 123, 106199. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L.; Zhu, C.; Zou, L.; Zhang, M.; Feng, L.; Cao, Q. Predicting Surface Solar Radiation Using a Hybrid Radiative Transfer–Machine Learning Model. Renew. Sustain. Energy Rev. 2023, 173, 113105. [Google Scholar]
- André, F.; Cornet, C.; Delage, C.; Dubuisson, P.; Galtier, M. On the Use of Recurrent Neural Networks for Fast and Accurate Non-Uniform Gas Radiation Modeling. J. Quant. Spectrosc. Radiat. Transf. 2022, 293, 108371. [Google Scholar] [CrossRef]
- Chevallier, F.; Chéruy, F.; Scott, N.A.; Chédin, A. A Neural Network Approach for a Fast and Accurate Computation of a Longwave Radiative Budget. J. Appl. Meteorol. 1998, 37, 1385–1397. [Google Scholar] [CrossRef]
- Krasnopolsky, V.M.; Fox-Rabinovitz, M.S.; Belochitski, A.A. Decadal Climate Simulations Using Accurate and Fast Neural Network Emulation of Full, Longwave and Shortwave, Radiation. Mon. Weather Rev. 2008, 136, 3683–3695. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [PubMed]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [PubMed]
- Demir, F. Deepcoronet: A Deep LSTM Approach for Automated Detection of COVID-19 Cases from Chest X-Ray Images. Appl. Soft Comput. 2021, 103, 107160. [Google Scholar] [PubMed]
- Mamdouh, M.; Ezzat, M.; Hefny, H. Improving Flight Delays Prediction by Developing Attention-Based Bidirectional LSTM Network. Expert Syst. Appl. 2024, 238, 121747. [Google Scholar]
- Huang, F.; Li, X.; Yuan, C.; Zhang, S.; Zhang, J.; Qiao, S. Attention-Emotion-Enhanced Convolutional LSTM for Sentiment Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 4332–4345. [Google Scholar]
- Chen, Y.; Rao, M.; Feng, K.; Zuo, M.J. Physics-Informed LSTM Hyperparameters Selection for Gearbox Fault Detection. Mech. Syst. Signal Process. 2022, 171, 108907. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y.; Li, G.; Zhang, J.; Zhou, H.; Wu, J. A Novel Solar Irradiance Forecasting Method Based on Multi-Physical Process of Atmosphere Optics and LSTM-Bp Model. Renew. Energy 2024, 226, 120367. [Google Scholar]
- Zhao, X.; Niu, Q.; Chi, Q.; Chen, J.; Liu, C. A New LSTM-Based Model to Determine the Atmospheric Weighted Mean Temperature in Gnss Pwv Retrieval. GPS Solut. 2024, 28, 74. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; Kong, D.; Han, H.; Zhao, Y. Ea-LSTM: Evolutionary Attention-Based LSTM for Time Series Prediction. Knowl. Based Syst. 2019, 181, 104785. [Google Scholar] [CrossRef]
- Cai, S.; Gao, H.; Zhang, J.; Peng, M. A Self-Attention-LSTM Method for Dam Deformation Prediction Based on Ceemdan Optimization. Appl. Soft Comput. 2024, 159, 111615. [Google Scholar] [CrossRef]
- Liu, L.; Xu, X. Self-Attention Mechanism at the Token Level: Gradient Analysis and Algorithm Optimization. Knowl.-Based Syst. 2023, 277, 110784. [Google Scholar]
- Xie, Y.; Liang, R.; Liang, Z.; Huang, C.; Zou, C.; Schuller, B. Speech Emotion Classification Using Attention-Based LSTM. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 1675–1685. [Google Scholar] [CrossRef]
- Pan, S.; Yang, B.; Wang, S.; Guo, Z.; Wang, L.; Liu, J.; Wu, S. Oil Well Production Prediction Based on Cnn-LSTM Model with Self-Attention Mechanism. Energy 2023, 284, 128701. [Google Scholar]
- Zang, H.; Xu, R.; Cheng, L.; Ding, T.; Liu, L.; Wei, Z.; Sun, G. Residential Load Forecasting Based on LSTM Fusing Self-Attention Mechanism with Pooling. Energy 2021, 229, 120682. [Google Scholar]
- Xia, J.; Feng, Y.; Lu, C.; Fei, C.; Xue, X. LSTM-Based Multi-Layer Self-Attention Method for Remaining Useful Life Estimation of Mechanical Systems. Eng. Fail. Anal. 2021, 125, 105385. [Google Scholar]
- Rothman, L.S. History of the Hitran Database. Nat. Rev. Phys. 2021, 3, 302–304. [Google Scholar] [CrossRef]
- Wei, H.; Chen, X.; Rao, R.; Wang, Y.; Yang, P. A Moderate-Spectral-Resolution Transmittance Model Based on Fitting the Line-by-Line Calculation. Opt. Express 2007, 15, 8360–8370. [Google Scholar]
- Turkoglu, M.O.; D’Aronco, S.; Wegner, J.D.; Schindler, K. Gating Revisited: Deep Multi-Layer RNNs That Can Be Trained. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 4081–4092. [Google Scholar]
- Guo, P.; Wang, P. Qhan: Quantum-Inspired Hierarchical Attention Mechanism Network for Question Answering. Int. J. Artif. Intell. Tools 2023, 32, 2360009. [Google Scholar]
- Niu, Z.; Zhong, G.; Yu, H. A Review on the Attention Mechanism of Deep Learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Gülmez, B. Stock Price Prediction with Optimized Deep LSTM Network with Artificial Rabbits Optimization Algorithm. Expert Syst. Appl. 2023, 227, 120346. [Google Scholar] [CrossRef]
- Dai, C.; Wei, H.; Chen, X. Validation of the Precision of Atmospheric Molecular Absorption and Thermal Radiance Calculated by Combined Atmospheric Radiative Transfer(C 10 Art) Code. Infrared Laser Eng. 2013, 42, 174–180. [Google Scholar]
- Cui, J.; Zhang, J.; Dong, C.; Liu, D.; Huang, X. An Ultrafast and High Accuracy Calculation Method for Gas Radiation Characteristics Using Artificial Neural Network. Infrared Phys. Technol. 2020, 108, 103347. [Google Scholar]
- Zhou, J.; Dai, C.; Wu, P.; Wei, H. A Fast Computing Model for the Oxygen a-Band High-Spectral-Resolution Absorption Spectra Based on Artificial Neural Networks. Remote Sens. 2024, 16, 3616. [Google Scholar] [CrossRef]





| Variant | Value |
|---|---|
| T/K | 200:410:30 |
| P/hPa | 1200.0, 350.0, 100.0, 35.0 |
| U/atm-cm | 0.00005:415:0.00005*1.31(i−1) |
| Wavenumber/cm−1 | 1:5000:1 |
| Model | R2 | MAE | RMSE |
|---|---|---|---|
| Single LSTM | 0.99991 | 2.98 × 10−3 | 0.00421 |
| Stack LSTM | 0.99996 | 1.70 × 10−3 | 0.00289 |
| Self-attention | 0.99998 | 2.82 × 10−3 | 0.00338 |
| LSTM-AT | 0.99997 | 1.71 × 10−3 | 0.00241 |
| Stack LSTM-AT | 0.9999964 | 5.56 × 10−4 | 0.00094 |
| Model | Time (s) |
|---|---|
| Single LSTM | 3.567 × 10−2 |
| Stack LSTM | 8.755 × 10−2 |
| Self-attention | 4.91 × 10−2 |
| LSTM-AT | 7.764 × 10−2 |
| Stack LSTM-AT | 9.784 × 10−2 |
| LBLRTM | 284.943 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, X.; Li, Y.; Wei, H.; Liu, J.; Li, W.; Zhao, Y.; Dai, C. A Fast and Accurate Calculation Method of Water Vapor Transmission: Based on LSTM and Attention Mechanism Model. Remote Sens. 2025, 17, 1224. https://doi.org/10.3390/rs17071224
Zhang X, Zhang X, Li Y, Wei H, Liu J, Li W, Zhao Y, Dai C. A Fast and Accurate Calculation Method of Water Vapor Transmission: Based on LSTM and Attention Mechanism Model. Remote Sensing. 2025; 17(7):1224. https://doi.org/10.3390/rs17071224
Chicago/Turabian StyleZhang, Xuehai, Xinhui Zhang, Yao Li, Heli Wei, Jia Liu, Weidong Li, Yanchuang Zhao, and Congming Dai. 2025. "A Fast and Accurate Calculation Method of Water Vapor Transmission: Based on LSTM and Attention Mechanism Model" Remote Sensing 17, no. 7: 1224. https://doi.org/10.3390/rs17071224
APA StyleZhang, X., Zhang, X., Li, Y., Wei, H., Liu, J., Li, W., Zhao, Y., & Dai, C. (2025). A Fast and Accurate Calculation Method of Water Vapor Transmission: Based on LSTM and Attention Mechanism Model. Remote Sensing, 17(7), 1224. https://doi.org/10.3390/rs17071224






