Abstract
This extensive study examines the solar rooftop photovoltaic potential (RTP) over polluted cities in major geographic and economic zones of India. The study examines the climatology of solar radiation attenuation due to aerosol, clouds, architectural effects, etc. The study exploits earth observations from ground, satellite, and radiative transfer modeling (RTM) in conjunction with geographic information systems tools. The study exploits long-term observations of cloud properties from the Meteosat Second Generation (MSG) satellites operated by EUMETSAT and aerosol properties data gathered from ground-based measurements provided by AERONET. The innovation in the study is defined in two steps. Firstly, we estimated the RTP using the current state of the art in the field, which involved using suitability factors and energy output based on the PVGIS simulations and extrapolating these for effective rooftop areas of the cities. Secondly, we advanced beyond the current state of the art by incorporating roof morphological characteristics and various area share factors to assess the RTP in more realistic terms. These two steps were applied under two different scenarios. The study determined that the optimum tilt angle is equal to the cities’ latitude for installing solar PV systems. In addition, the research emphasizes the advantages for the environment while offering energy and economic losses. According to our findings, the RTP in the rural city examined in this study is 31% greater than the urban city of India under both scenarios. The research has found that the metropolitan city, which boasts a maximum rooftop area of approximately 167 km2, could host a significant RTP of around 13,005 ± 1210.71 (6970 ± 751.38) MWh per year under scenario 1 (scenario 2). Overall, solar radiation losses due to aerosol effects dominate radiation losses due to cloud effects on the city scale. Amongst all polluted cities, estimated financial losses due to aerosols, clouds, and shadows are 11,241.70 million, 4439 million, and 1167.65 million rupees, respectively. Our findings emphasize the necessity of accounting for air pollution for accurate solar potential assessments in thoughtful city planning. The creative approach that utilizes publicly available data establishes a strong foundation for penetrating solar photovoltaic (PV) technology into society. This integration could significantly contribute to climate change mitigation and adaptation efforts, promoting environmentally sustainable urban development and prevention strategies.
1. Introduction
Globally, greenhouse gas emissions (GHG) are distributed across various economic sectors—electricity and heat production contribute approximately 29.7%, transportation accounts for 13.7%, manufacturing and construction contribute 12.7%, and buildings themselves account for about 6.6% [1]. Within these, residential buildings represent the largest share of energy sector emissions, contributing 12.5% of global emissions, i.e., from direct emissions (e.g., cooking with gas) and indirect emissions (e.g., home electricity) [2].
The contribution includes emissions from household energy generation and direct fossil fuel use, such as gas for cooking. Thus, the focus of every country worldwide is to shift to clean energy and reduce the dependence on fossil fuels for the energy sectors, especially the concern to residential households and commercial buildings. The rising floor space of the buildings has increased by 4000 square kilometers, sufficient to cover areas like the Netherlands during the last decade in emerging markets and developing economies [3]. The solar PV rooftop system offers one of the most effective ways to maximize space utilization. Over the past decade, their costs have decreased by 50%, eliminating the need for additional space [3]. They require a one-time investment and offer the added benefits of zero transmission losses [3].
India leads the energy demand against the backdrop of all emerging markets and developing countries of the world under the Stated Policies Scenario (STEPS) [3]. STEPS is the scenario that produces the energy sector’s trajectory based on the latest market data, technological costs, and a comprehensive analysis under present policy settings across countries worldwide. The underlying factors of India’s rising demands are the most populous, expanding economy, urbanization, and industrialization. The decarbonization of the energy sector is the goal of India to satiate the net zero carbon emissions by the year 2070 [3], as pledged by the Government of India (GOI) at a Conference of Parties (COP) 26 Glasgow Meeting in 2021 in one of its five nectar elements (Panchamrit), a climate plan. In this direction, the country is targeting the 500 GW of renewable energy production by 2030 [4]. India is endowed with a vast solar energy potential [5]. The annual solar energy incident of the country is ~five quadrillion kWh, with most of this part receiving daily solar energy in the range of 4–7 kWh per square meter [6,7]. The National Institute of Solar Energy projected the country’s solar energy potential to ~748 GW, considering 3% of the wasteland area to be covered by Solar PV modules [8,9]. According to the International Renewable Energy Agency (IRENA)’s renewable energy statistics for 2024, India’s solar power installed capacity will reach ~92.12 GW by October 2024 [10]. That would lead to the country’s total renewable installed capacity surpassing ~200 GW—a key milestone for its 2030 target [11], and thus the country would become fourth in the world regarding maximum renewable installed capacity.
In the recent two years, the government of India has taken groundbreaking decisions and policy frames for solar rooftop PV deployment, such as decentralizing the solar PV rooftop and shifting from the net metering system to the net billing system, which has benefited distribution companies (DISCOMS). Not only that, but the government liberalized the companies to invest with the OPEX model (operating expenditure), which is a system model in which the third party owned and installed the rooftop PV panels at the consumer premises, whilst CPEX (capital expenditure) model-based systems are financed and owned by the consumer itself [12]. These facilities could be set up over the available residential and commercial infrastructure rooftop area. The rooftop PV could offer a win–win situation for households and even low-requirement consumers to sell the electricity after fulfilling their requirements. Many studies have demonstrated that the solar potential of the rooftop has a surplus of residential requirements [13,14,15,16].
The advancement of solar PV technology with a significant reduction in the cost of PV during the past ten years enhances the appeal of rooftop PV. Rooftop PV offers many advantages, such as affordability, savings, scalability, self-reliance on energy, the utilization of free space, and low transmission losses. Rooftop PV is significant for climate resilience, energy sufficiency, and lowering dependency on fossil fuels, thus meeting the future energy demands towards energy justice [17]. Hence, an accurate assessment of the RTP is required to penetrate rooftop PV technology in an optimum, efficient, and sustainable manner.
RTP is generally expressed in terms of geographical, metrological, technical, and economic potential [16]. Metrological potential exploits the favorable climate and environmental conditions for the optimum energy generation and performance of the rooftop PV [18]. The key parameters for the metrological potential are solar radiation, cloud cover, aerosol optical depth (AOD), wind speed, tilt and orientation, etc. Geographical potential includes identifying hot spot locations for solar irradiance with exploitable and suitable rooftop areas. The efficiency of solar PV panels with performance parameters is accounted for in the technical potential, while the cost of installation and maintenance part is emphasized in the economic potential assessment [19].
The recent studies conducted at a global scale published in Nature Communications, utilizing machine learning, it was reported that 200,000 square kilometers (km2) of a rooftop area could generate 27,000 terawatt-hours (TWh) of electricity annually, with generation rates ranging from 40 to 280 megawatt-hours per hour [20]. The study also has reported that India has a huge potential, i.e., RTP ~1815 tera watthours per year (TWh y−1) for effective roof area ~11,731 km2 with a low cost of deployment ~66 $ MWh−1. Moreover, another study has reported a globally exploitable rooftop area of 400 km2, which could be utilized to produce 8300 TWh y−1 [19].
The RTP assessment with accuracy has gained importance, but still, due to the persistent challenge of the absence of high-resolution, building information, solar radiation, and environmental data, there is uncertainty associated with the applied methods [16,21,22].
Previous studies have identified the three primary factors motivating the enhancement and promotion of renewable energy: politics, socio-economic, and geographic factors [23,24]. For example, without providing attractive feed-in tariffs (FIT) and subsidies, the government could not scale up the RES in potential geographical areas such as Maharashtra and Rajasthan, as mentioned in the report [4]. In the current study on rooftop PV installations, we focused on examining the socio-economic benefits for various geographically diverse cities within the framework of current government schemes and applicable FIT rates state-wise.
The approaches for estimating RTP include the bottom-up, top-down, and combined methods [20,25,26]. The bottom-up method exploits the small set of building footprint areas and socio-economic information, thus extrapolating it to a larger area region. On the other hand, the top-down approach uses satellite observations to get information about the building footprints and building heights.
Furthermore, the methods are categorized as low, medium, and high-level techniques based on the spatial resolution [20]. The approach that depends on the larger area and aggregated statistical data also assumes homogenous characteristics over the complete area, which is known as the low-level approach. The medium-level approach utilizes statistical data and spatially resolved data. The high-resolution approach analyzes specific buildings or areas, exploiting rooftop morphology, geographic variability, solar insolation patterns, and panel-specific factors [27].
Rooftop structures exhibit significant spatial variability, figuring diverse tilts, azimuths, superstructures, and solar insolation. Therefore, the accurate identification of roof components and a precise quantification of these areas, including the shading effect, is essential for effective PV installation [28,29].
Many studies utilize the different combinations of the abovementioned methods and databases. Most studies have employed the LIDAR and 3D models for city-specific assessments of building solar potential, which is highly expensive and time-consuming [30]. A newly published study leverages building height data from the Copernicus Urban Atlas, three-dimensional geospatial datasets, and Google Earth in advanced urban ray-tracing-based modeling for the capital of Greece by creating the twin city to estimate the exploitable rooftop area and its RTP [29].
During 2023–24, a ~10 GW energy generation capacity was added, out of which ~7.0 GW is renewable capacity, with 5.5 GW alone added from solar.
The report shows India has a residential rooftop solar capacity of ~637 GW, and more than 60% of the technical potential is concentrated in just seven states: Uttar Pradesh, Maharashtra, West Bengal, Odisha, Rajasthan, Andhra Pradesh, and Tamil Nadu [4]. Moreover, this report has also concluded that the country’s rural areas show more potential than the ones based on the residential rooftop area. Over the Indian region, studies on rooftop estimation are minimal; only a few studies related to academic areas, single states, cities, and solar plants have been conducted [28,31,32]. The study by Kaleshwarwar and Bahadure (2023) explored the solar energy potential of five diverse urban built forms (UBF) using digitized 3D models followed by simulations using the Grasshopper and Ladybug plugin in ArcGIS [32]. The study conducted in Nagpur has considered two scenarios for calculating solar energy potential: PV panel mounting at a 50% roof area availability and a 70% roof area availability. According to the research findings, if the solar panels are mounted at the capacity (50% roof area) [32], we can save 10% on conventional energy use in the dense areas and up to 30% in the lower-density regions [32]. If 70% of the roof area is made available for installing PV panels, only dense areas can generate about 33% surplus from solar energy compared to what it consumes [32]. In the city of Nagpur, in the Maharashtra state, authors have estimated the RTP ~2190 MW over Mumbai (18.98°N, 72.83°E) using the land use data and GIS-based satellite imaginary exploiting the PVSyst simulations [33]. The study conducted by Mishra et al. (2020) has estimated the solar energy potential for PV deployment over the Hill state Uttarakhand using satellite images [34]. The study also has examined that 58% of the area of the state receives solar radiation > 4 kWh/m2/day throughout the year [34].
Atmospheric effects have been studied by estimating the attenuation of solar radiation due to atmospheric aerosols and clouds [15,35,36]. The solar radiation from the sun reaching the Earth’s surface is primarily influenced by aerosols and clouds, which can affect its intensity and distribution both directly and indirectly [37]. Aerosols can scatter and absorb sunlight, while clouds can reflect, absorb, or transmit solar radiation, thereby playing a crucial role in regulating the Earth’s climate and energy balance. The deposing of atmospheric particulate matter results in a decrease in the capacity of solar power generation by the PV panels in the recent study by [38]. Also, there are very few studies assessing the effects of clouds and aerosols on solar energy in the Indian region [28,35,36,39,40]. Urban effects have been studied by assessing the shadow effects, which, up to our knowledge, have been done for the first time over the Indian region using the method used in the recent research [29]. The present study is the first study assessing the RTP under the scenario-based approach, which is, top to bottom, a high-level approach collectively focusing on all major zones in the Indian Region. This research aims to estimate RTP in polluted Indian cities using a robust and realistic approach. The study focuses on assessing the effects of aerosols, clouds, and shadowing on solar radiation in these cities, translating the resulting losses into financial terms, economic savings, and reduced carbon footprint equivalents. Moreover, the energy adequacy of the estimated RTP will be assessed to address optimal energy planning for the cities.
Section 2 deals with the area/cities of interest, data set, and methods used to conduct the study. Further, Section 3 focuses on the results and discussions investigating the effects of aerosols, clouds, and shadows. Section 3 also discussed the potential socio-economic benefits, energy adequacy, and the carbon footprint avoided over the cities. Finally, Section 4 describes the conclusions with key findings from the study.
2. Materials and Methods
Research plans for the study focused on assessing the RTP. Its socio-economic and climate effects involve the following steps: (1) Processing the Aerosols Robotic Network (AERONET) (ground truth) and cloud properties from the MSG satellite, further using these properties simulating long-term solar radiation under different environmental conditions from RTM to assess the cloud and aerosol effects. (2) Determining the building height, building footprint area, and population data from the Global Human Settlement (GHS) data [41,42]. (3) Extracting the areas of polluted Indian cities from the open street maps using the QGIS tool. (4) Estimating the effective rooftop area based on the more accurate roof morphological factors and general suitability factors (5) Extrapolating the solar energy simulation of the PVGIS tool over the cities. (6) Further translating the energy losses into financial losses. (7) Finally, evaluating the energy sufficiency and carbon emission reduction.
2.1. Study Area
We have chosen the polluted Indian cities based on the long-term availability of the ground truth aerosol optical depth (AOD) data covering the different zones of the country [43]. Here, we cover the country’s northern, central, western, and southern zones. Keeping the factors mentioned above into consideration, the selected sites are Amity University Gurugram as representative of Gurugram (~northern zone), Gandhi College, Kanpur (~central zone), Jaipur (~western zone), and Pune Metropolitan (~southern zone). The AOD at 500 nm has been utilized except for Jaipur at 440 nm due to the unavailability of the AOD at 500 nm. Our study utilizes AOD data available from the AERONET site, covering the entire period of availability up to the present date. Thus, the AOD data has been used for the years 2017–2023, 2006–2023, 2001–2023, 2009–2023, and 2004–2022 for the Gurugram (28.32°N, 76.92°E), Gandhi College (25.87°N, 84.12°E) (GC), Kanpur (26.51°N, 80.28°E), Jaipur (25.87°N, 84.12°E), and Pune (18.53°N, 73.80°E), respectively (Figure 1a) [43,44]. Based on characteristics, Gurugram is both a rural and city area. Gurugram, also called Gurgaon, is located within Delhi’s National Capital Region (NCR). It is situated roughly 30 km southwest of New Delhi and functions as one of the famous satellite cities in the NCR. Kanpur is in the central part of Uttar Pradesh (UP) and is recognized as an industrial city transitioning into a smart city. In contrast, Gandhi College is situated in the eastern part of UP, specifically in the Ballia district, which is typically recognized as a rural area. Both cities are geographically located over the central Indo-Gangetic Plains (IGP), the country’s primary economic zone. Jaipur is situated demographically near the Thar desert region in the country. Although the AERONET site is positioned in a rural part of Jaipur, this study independently examines Jaipur’s urban and rural areas for the RTP estimation and solar energy planning analysis, assuming that the aerosol and cloud properties are comparable in both regions [45]. We have done this to get insights into the RTP and energy adequacy for the rural areas and cities of the country. Jaipur is known as a pink city and a tourist place situated in the state of Rajasthan. Lastly, Pune is a metropolitan city focused on transforming smart cities by the government of the Maharashtra state and the Ministry of New and Renewable Energy [46]. In 2024, the government launched a friendly solar rooftop scheme, Pradhan Mantri Surya Ghar: Muft Bijli Yojna (PMSY), and various solar energy-expanding missions [47,48].
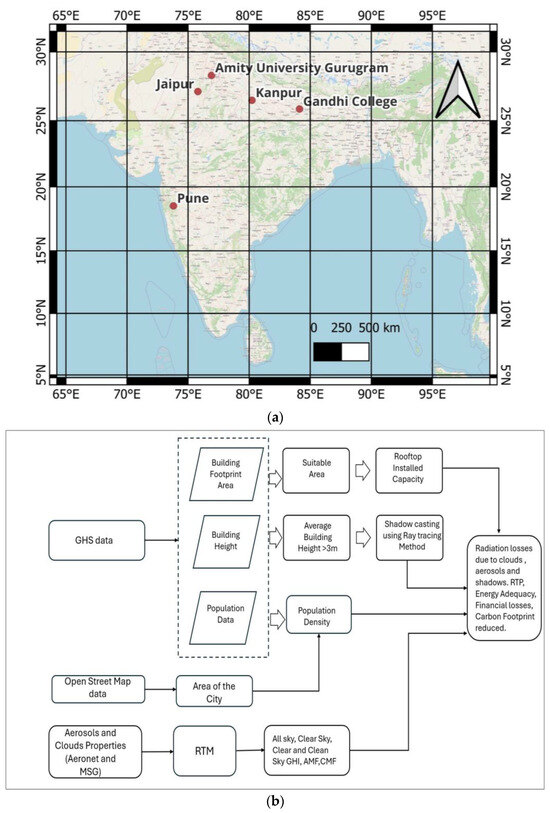
Figure 1.
(a) The AERONET sites Gurugram (28.32°N, 76.92°E), Gandhi College (25.87°N, 84.12°E), Kanpur (26.51°N, 80.28°E), Jaipur (25.87°N, 84.12°E), and Pune (18.53°N, 73.80°E). (b) A flow chart for the methodology used in the present study.
2.2. Aerosol and Clouds Data
In the present study, we have used the possible long-term ground truth measurements available from the AERONET data to understand the aerosol effect. We have downloaded version 3 Level 2 data daily for the period mentioned above for the cities of interest [43]. We have used a dimensionless parameter incorporating the direct effects of solar radiation known as AOD. The version 3 data, level 2 from AERONET, is quality-controlled and assured data, having the uncertainty of a +0.2 bias and one sigma uncertainty of 0.2, spectrally [44].
Cloud properties such as cloud optical thickness (COT) measure how much solar radiation clouds block before reaching the ground surface. It is a key parameter for assessing the impact of cloud cover on solar radiation. The COT data in the study is retrieved as the satellite cloud data products from the Spinning Enhanced Visible and Infrared Imager (SEVIRI) on board the MSG satellite. COT is a near real-time product derived from satellite data, eliminating the need for post-processing. COT is related to the moisture density within the cloud and a cloud reflectance at 0.6 µm in the visible part of the electromagnetic spectrum is used to determine the COT [49]. The MSG is a geostationary satellite that orbits at an altitude of approximately 36,000 km above the equator [35]. The cloud properties data of a spatial resolution of 0.05° with a temporal resolution of 15 min has been used in the present data for the same synchronized period for which the AERONET data were utilized.
As the PV system utilizes direct and diffused solar radiation, it is ideal to use the global horizontal irradiance (GHI) for analysis. As discussed in the subsequent sections, the COT and AOD were used as input for the RTM simulation. The RTM simulations yield solar radiation under different environmental settings.
2.3. GHS Data
The freely available Global Human Settlement (GHS) data was utilized for this study [41]. The population data was sourced from the available product GHS_POP_E2030_GLOBE_R2023A_54009_100_V1_R6_C6, which provides global coverage at a spatial resolution of 100 m, focusing on cities of interest. Additionally, building footprint and height data were obtained from the products GHS-BUILT-S-R2023A and GHS-BUILT-H-R2023A, respectively. The GHS-BUILT-S-R2023A dataset represents the built-up area at a resolution of 10 m, expressed in square meters per grid cell, derived from Sentinel-2 and Landsat imagery across multiple epochs (1975–2030). The GHS-BUILT-H-R2023A dataset provides average building height estimates at a resolution of 100 m, derived from digital elevation models and satellite imagery, which provides global coverage at a spatial resolution of 100 m. All the downloaded datasets are spatially raster files; hence, they are further processed and extracted for the sites of interest in the QGIS. Detailed information about the GHS data products can be found in the documents [41,42]. The GHS dataset is used for its higher spatial resolution of ~10–100 m on built-up areas, building heights, volumes, and the population, with a multitemporal coverage spanning 1975–2030 in 5-year intervals. This enables a detailed analysis of urbanization trends and population dynamics, offering valuable insights for global urban planning, environmental studies, and sustainable development.
2.4. Simulations of Solar Radiation
Estimating the power production from solar radiation requires determining the amount of the solar irradiance incident on the solar PV panels. PV technology takes advantage of global horizontal irradiance (GHI). Under realistic conditions, the aerosols and clouds affected the GHI radiation incident on PV panels. The work utilizes the traditional radiative transfer model, libRadtran 2.0.4 [50,51]. This software package comprises tools for radiative transfer calculations within the Earth’s atmosphere [52]. The primary tool, uvspec, calculates radiance, irradiance, and actinic fluxes across the spectrum’s solar and terrestrial portions [29].
As per those mentioned above, all types of GHI for the studied sites, i.e., GHI00 (clean and clear sky irradiation), GHI0 (clear sky irradiation), and GHI (all-sky irradiation), were simulated from the RTM using the libRadtran 2.0.4, so for GHI00, we specified the solar irradiation under clean (from aerosols) and clear (from clouds) sky conditions. In contrast, for GHI0, we used the aerosol optical properties to calculate the clear sky. The GHI is for all of the sky, so aerosols and clouds are included [29,52]. Thoroughly, the input parameters used in libRadtran for clear-sky conditions included the AOD, solar zenith angle (SZA), Ångström exponent (AE), single scattering albedo (SSA), total ozone column (TOC), and columnar water vapor (CWV). Only the SZA, TOC, and COT were utilized to estimate the GHI under cloudy conditions. The AOD is not included as an input in libRadtran when the COT exceeds one, as the influence of aerosols becomes significantly weaker compared to that of thick clouds (COT > 1). Additional parameters were sourced from various models: the SZA was obtained from an in-house astronomical model and software (NOA) code version 2024, the AE and SSA were derived from the Aerosol Comparisons between Observations and Models (Aerocom) on a monthly average basis [53], the TOC was retrieved daily from the Tropospheric Emission Monitoring Internet Service (TEMIS), [54] and the CWV was obtained from the Copernicus Atmosphere Monitoring Service (CAMS). The RTM simulations are performed under standard atmosphere and default aerosol model conditions, yielding output at a spectral resolution of 1 nm [55]. The solar radiation simulations were obtained for the same duration in line with the span for which the aerosols and cloud properties were fed as input for the cities’ conditions.
To quantify the impact of aerosols and clouds more precisely, we have estimated the AMF and SMF from the GHI00, GHI0, and GHI data generated as an output from the RTM simulations. A similar methodology has been adopted in the recently published article [15]. Mathematically, the AMF and CMF are calculated as the fraction of the depicted Equations (1) and (2) with radiation components. Here, GHI0 represents clear sky radiation, GHI00 represents the clean from aerosols and clear (from clouds) sky, and GHI is the radiation under all clear-sky conditions.
AMF = GHI0/GHI00
CMF = GHI/GHI0
Here, the AMF and CMF can take values from 0 to 1. For instance, an AMF ~ 1 implies atmospheric conditions with no aerosols, i.e., clean and clear-sky conditions. However, AMF < 1 suggests an atmosphere with high pollution or aerosol loading. Moreover, a CMF ~ 1 implies atmospheric conditions with no clouds, i.e., clear-sky conditions. If the CMF < 1, it suggests the atmospheric condition with dense cloud cover that has blocked the majority of the radiations; the moderate CMF values (0.5–0.8) indicate the partial cloud cover with sunlight reaching the surface [35]. The online PVGIS (Photovoltaic Geographic Information System) tool under general settings for specific grid PV systems was used for potential PV energy production over the cities of interest. The general setting involves the database ~PVGIS-SARAH-2, technology for the PV system ~crystalline silicon, installed peak PV power[kWp] = 1, system loss percentage ~14%, and the fixed mounting option = Roof Added and Azimuth = 0 degree/latitude in degree for each city of interest. The PV output monthly variation is simulated for solar irradiation to quantify the aerosol, cloud, and shadow-casting effects [15,56]. The PVGIS energy production output for the AERONET sites was further extrapolated for the entire cities under the hypothesis using estimated useful rooftop areas [15]. The suitable rooftop area is computed in the present research under two scenarios discussed in the subsequent Section 2.4.
2.5. Shadow Casting in Different Environments
Shadowing is one crucial factor for quantifying the urban or architectural effect of shadows formed on PV modules or panels. These shadows might be formed due to the trees, building heights, adjacent PV panels, terrain variations, and other elevated constructions [29]. The formation of shadows due to elevated structures reduces the efficiency of the installed PV systems, mainly rooftops. Studies have reported that shadows lessen the efficiency of PV panels [57,58]. The factor used to quantify the effect of the shadows on the PV panels is the Shadow Modification factor (SMF). Generally, it is the ratio of the direct irradiance with a shadow effect to the irradiance without shadows. Bring the fraction, and have its values vary from 0 to 1. The SMF is 0, implying the PV panel has no shadowing when fully exposed to sunlight. The SMF means the PV panel has complete shadowing with no sunlight. The process of assessing the shadow projection formed by the obstacles over the PV panels due to the sunlight is termed shadow casting. Shadow casting is complex in dense urban areas and metropolitan cities involving diverse components. The SMF depends on both large-scale cloud effects and the small-scale architectural design of rooftops. The methodology uses a ray tracing-based RTM to simulate the GHI under varying atmospheric conditions, including cloud effects, and to determine the diffusion constant R. R is calculated as the diffuse radiation divided by the global radiation, considering the SZA and CMF. Therefore, the diffuse radiation coefficient, R, accounts for the solar radiation diffused by clouds as depicted by Equation (3a). The present research calculates the diffuse radiation coefficient, R, for shadowed areas using the libRadtran package 2.0.4. This coefficient is then used to determine the diffuse radiation using Equation (3a). This is coupled with a geospatial analysis using the Grass GIS library integrated into QGIS, utilizing building height and footprint data from the GHS to construct 3D urban models [59]. These models enable the quantification of shadow-induced radiation attenuation, which is subsequently used to calculate the shadow modulation factor (SMF) through Equation (3b,c). The referenced research literature provides a detailed description of this approach [29].
DHIclouds = GHIclouds × R
GHIdirect,clouds = GHIclouds − DHIclouds
GHIdirect,clouds,shadows = GHIdirect,clouds × SMF
DHI is the diffuse horizontal irradiance, and R is the diffusion coefficient. The SMF in the present study is calculated using the ray tracing method from Equation (3a–c), as mentioned in the recent research article [29].
2.6. The Calculation of the Rooftop Area and Its Potential
Two approaches in the research have been used to calculate the rooftop area. The first approach is based on the roof surface morphology, area share, and correction factors [16,60]. The second approach uses the suitability factor and exploits simulated PV generation at the optimal tilt equal to the site’s latitude, an assumption-based PVGIS tool [15]. The first method in the research we are considering is scenario 1, and the second is scenario 2. Under scenario 1, the building footprint data (Ab) from the global human settlement (GHS) was adjusted using the roof morphology correction factors to the usable rooftop area (RTAu) [33,61]. As the Ab could not be used as the rooftop PV panel could not cover the full space of the roof, we have decreased it to RTAu using the calibration factor fca (Equation (4a)) [62]. Next, the total area share factor cfa is computed using Equation (4b) [16]. The total area correction factor depends on the roof morphological factors such as the area share and area correction factors of the flat and slant roof. The cities-specific values were computed, assuming 0.65 for cfa,flt, 0.93 for cfa,slt, with Sflt,u varying between 0.65 to 0.75, respectively [16]. The relation for the total area correction factor is depicted in Equation (4b) [16]. The total area correction factor (cfa) values vary from 0.71 to 0.75. Finally, the RTP (in MWh yr−1) is estimated using Equation (5). Thus, knowing the PV cell temperature, i.e., Tcell is a solar PV cell temperature (in degrees Celsius) from Equation (6) can be found by substituting the GHI as the mean annual GHI per city (in Wm2) and Tai as the average mean temperature of the city (in °C). Moreover, the three constants µref, β, and are known as the electrical efficiency under standard resting conditions; and the temperature coefficient, reference temperature, and performance ratio (PR) were used in the study with values 023, −0.0029 °C−1, 25, and 0.8, respectively [16]. The first three factors are determined by the specifications provided by the manufacturers of the latest rooftop solar PV module type; here, we are using these specifications from the largest PV manufacturers globally [63]. The value of the radiation correction factor, i.e., cfrad used in the present study, is 1.07, which is also used in recent research and might not vary in the context of the Indian region [16]. Here, in the cell temperature ) equations C1, C2, and C3 are the constants, and their values are −3.75 °C, 1.14, and 0.0175 Cm2 W−1 [16]. Tai is the average temperature (°C) of the city we used in the study. This methodology we adopted is applicable for the modern solar module parameters sensitive to temperature-induced changes in the PV system efficiency, thus reducing the PV output. Additionally, the roof area morphological factors and radiation consider realistic diverse roof types and attributes [16].
cfa = Sflt,u × cfa,flt + (1 − Sflt,u) × cfa,slt
Equation (4b) has been used to calculate the total area correction factor.
The is defined as the solar photovoltaic cell temperature (°C) computed by the below equation.
The errors associated with RTP estimates using Equations (A1a,b) and (A2) are discussed in Appendix A.
2.7. An Estimation of the Energy Adequacy, Financial Losses, and Earnings
The information related to the energy consumption per city has been obtained from the site [64]. The amount of consumption for the cities, taken from the local authorities, and the possible energy produced, is calculated for the installed rooftop capacity using Equation (7). The energy production scheme under scenario 1 is based on incorporating all of the rooftops’ morphological factors, as discussed in the methodology section of the study. The energy production projections under scenario 2 are mainly based on the theoretical potential for utilizing exploitable building rooftops for PV installations. Firstly, the building footprint data for the six cities has been extracted from the QGIS 3.36.1 software for the final energy production. Further processing for the total footprint area and multiplying it by the suitability factor, the exploitable rooftop area is estimated. The exploitable is the effective usable area for the rooftop installation. Additionally, this area has been converted into the rooftop installable capacity using the assumption that the rooftop area of ~20,500 m2 could produce the energy of 1 MWp [15]. Finally, multiplying the installed capacity with the annual PVGIS output under a hypothetical coverage scenario for the particular tilt, i.e., at the latitude of the city, the final energy production is projected using Equation (7). Here, PR is the performance ratio, which is technically the efficiency of the solar PV system taken here as 0.85 [65,66]. Therefore, for each city’s energy consumption and production, we estimated the energy adequacy for the cities of interest using Equation (8). The energy adequacy gives information on the possible energy efficiency after installing the solar PV rooftop. For the calculation of the FL, assuming the hypothesis, we have extrapolated the PVGIS output in KWp over the entire city for accurate PV outputs in KWh. Further, we have calculated the maximum energy produced over each city by dividing the total energy produced with the annual, monthly ten-year mean of the calculated factors, such as incorporating the effects of the aerosols, clouds, and shadows, respectively, i.e., the AMF, CMF, and SMF. The energy losses have been translated into financial losses (FL) in rupees using Equation (9).
Equation (7) is further used for estimating the , i.e., the maximum energy produced under clean and clear-sky conditions excluding the effects of the aerosols (with AOD~0) and clouds (with COT~0), respectively. However, the has been calculated by multiplying the with the annual monthly mean of the studied years of each factor of the CMF, AMF, and MF, respectively. Finally, the difference between the and is multiplied with a state-specific feed-in tariff (FIT) per unit of energy produced in KWh to estimate the FL (Equation (9)) [45]. The FIT is the fixed incentive the government ensures to the solar energy producers, individuals, and business companies for each unit of electricity produced, thus feeding back to the grid in rupees per kilowatt. The incentives vary from one state to another in the country or region based on factors such as the amount of energy produced (EP). The FIT rate used in present studies for Gurugram, GC, Kanpur, Jaipur Rural, and Jaipur City is in the range of 2.48 to 3.10 ( based on the GOI reports with web source [64]. Lastly, we have computed the earnings or savings for the amount of energy produced using Equation (10). We have considered the efficiency of the PV system output energy as 80% with 20% losses, as also assumed in previous studies for the earnings and financial losses (FL) calculations [15,33,34,45].
Energy Adequacy = Energy Produced/Energy consumed
Figure 1b illustrates the overall methodology of the state-of-the-art approach employed in the study. We estimated the building footprint area using downloaded GHS data processed in QGIS 3.36.1 software, following these steps: (1) plotting a Digital Elevation Model (DEM) over the building area, (2) reprojecting the DEM, (3) calculating the slope, (4) reclassifying the slope data, and (5) converting to a vector format and calculating the area with a slope of 0–10 degrees. We considered a building area with a slope equal to zero as for flat roofs. Based on the previously described scenarios, this building footprint area was converted into suitable rooftop areas. Subsequently, the suitable rooftop area was converted into the rooftop installed capacity. Further, the downloaded GHS key parameters products, such as building height and population data, were processed in QGIS for the cities of interest. The building height is filtered to remove elevated structures like trees (with heights more significant than three meters). As mentioned earlier, these extracted key parameters, such as building area, building height, and city area, were then used to estimate the SMF using the ray tracing-based RTM. Finally, modification factors such as the AMF, CMF SMF, and GHI data were used to calculate energy losses due to aerosols, clouds, and shadows, respectively, as discussed above. Finally, the equivalent carbon footprint reduced for all polluted cities is estimated.
3. Results
This entire section is organized into four subsections. Section 3.1 examines the variation of atmospheric effects, while Section 3.2 addresses architectural effects. Section 3.3 investigates the impact of solar radiation on polluted cities in India. Lastly, Section 3.4 estimates the rooftop area and photovoltaic potential.
3.1. The Variation of Aerosol and Clouds Properties
The effect of the aerosols has been depicted in Figure 2 in terms of the average monthly AOD and AMF variation over the polluted AERONET sites in the Indian region. On the one side, Figure 2a depicts the average monthly variation of the AOD and shows the effect of transported aerosols and local emissions over the cities of interest. Amidst all the towns during the summer months (March–April–May), a higher AOD was observed over the Central IGP region sites AU Gurugram, Kanpur, and Jaipur, followed by the southern zone metropolitan Pune. The observed pattern aligns with the fact that aerosol dust transported from the desert region near the Jaipur site gets transported to the IGP plain, thus affecting the air quality and solar radiation over the north and central IGP region [45,67,68,69]. The AOD climatology in Heraklion, the largest city in Crete, exhibits similar monthly variation characteristics observed over central IGP sites, with AOD values reaching approximately 0.28 during the summer months. A recent study indicates that this increase is due to dust transported from North Africa and the Sahara [15,56]. Overall, the AOD values of the largest cities of mainland Greece are about one-third of those found in polluted Indian cities [15].
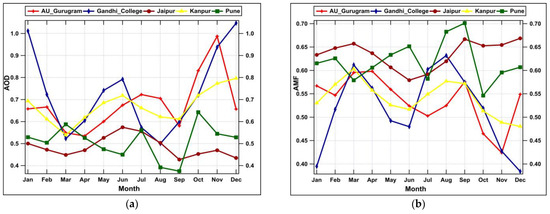
Figure 2.
(a) The monthly average AOD@500 nm in five AERONET sites except for Jaipur (green color) at 440 nm during the study period. (b) The monthly average AMF in five AERONET sites during the study period.
The AOD variation peaks during June, i.e., at the start of the monsoon season. The concentration of the AOD drops during the monsoon season months (June–July–August–September) attributed to the wet deposition of aerosols over all the sites [70]. The monthly increase in the AOD from October to November can be attributed to the local generation of aerosols, primarily driven by biomass burning, fossil fuel combustion, and industrial emissions, particularly over the IGP sites AU Gurugram, Kanpur, and GC, respectively [71,72,73,74,75]. Further, the values rise over Kanpur, AU Gurugram, and GC, respectively, due to the shallow planetary boundary layer height (PBLH), lesser vertical mixing, local coal and wood burning, and the lower ambient temperature during the winter months from December to February [76,77]. Our findings indicate that at the rural site of Gandhi College in Ballia, the AOD increases annually by 1.0 to 1.5%. This aligns with a recent climatological study conducted for the period 2005–2018 using a Moderate Resolution Imaging Spectroradiometer (MODIS) that reported an AOD increase in Indian rural areas of 0.50–0.67% per year [78].
However, the AOD levels over Pune have decreased due to the usual northeastern monsoon rainfall from October to November near coastal sites like Pune [79]. We have observed the mean AOD concentration over GC ~0.73 ± 0.18, AU Gurugram ~0.68 ± 0.12, Kanpur ~0.67 ± 0.08, Pune ~0.51 ± 0.08, and Jaipur ~0.48 ± 0.05, respectively.
On the other hand, Figure 2b shows the average monthly variation of the AMF defined by Equation (1) over the cities of interest. The monthly variation is the mirror image of the average monthly variation of the cities of interest, showing the AOD variation. Figure 2b depicts the drop in the AMF values in the range over GC ~0.49–0.61, Kanpur ~0.52–0.60, Jaipur ~0.60–0.65, Pune ~0.58–0.63, and AU Gurugram, respectively. We observed a significant drop in the AMF during the winter months of December and January over the IGP sites such as AU Gurugram, GC, and Kanpur, respectively. The low AMF values suggest a higher concentration of aerosols, and this higher AOD presence attenuates more solar radiation. However, during the monsoon months from June to September, the substantial increase in AMF values indicates a reduction in aerosol levels, primarily due to wet deposition processes.
During the summer, the AMF in Heraklion, a Greek city affected by dust transport, reached approximately 0.81. In contrast, Gandhi College in Ballia, a rural polluted site representative of the central Indo-Gangetic Plain (IGP), had an AMF of 0.50, nearly 30% lower than the Greek city. On average, the climatological monthly AMF values are lower in Indian cities (0.40–0.70) than in the most significant Greek cities (0.81–0.90), suggesting higher pollution levels in India [15].
Figure 3 portrays the impact of cloud effects on polluted AERONET sites in Indian cities. The effect of clouds is quantified using the dimensionless cloud property known as cloud optical thickness (COT), which measures the amount of light obstructed by the clouds. The monthly COT variation indicates that the clouds were generally thick over Pune, like cumulus, deep convective, or nimbus clouds during the monsoon months (June–July–August–September) [80]. On the other hand, medium-thick clouds such as Stratocumulus and Altostratus were present during the monsoon months. Moreover, fog haze and medium and thick clouds were present during winter. During the summer, cirrus clouds with haze conditions might exist over all the sites. During summer, dust storms frequently led to clouds forming over the IGP sites [45]. Figure 3b illustrates the behavior of the CMF, which gives insights into the effect of clouds on solar radiation. The low CMF values during the monsoon months indicate dense cloud cover over the cities, with notably denser clouds observed over Pune city. However, the cloud cover is less dense during winter (December–February), especially in Pune. During the transition from summer to monsoon (May to July), the CMF decreases, which can be attributed to a reduction in cloud cover over Gurugram, Jaipur, and Kanpur. However, the decrease was more rapid, particularly over Pune, likely due to the early onset of the southwest monsoon, owing to its near location to the Western Ghats (Figure 3a) [81]. The analysis reveals that the temporal variability of clouds is greater than that of aerosols over polluted Indian cities, aligning with their typical behavior due to the inherently variable distribution of clouds [15], while over sites such as Kanpur, GC, and Gurugram, the effect of aerosols is predominant, owing to their location in the polluted IGP region.

Figure 3.
(a) The monthly average COT in five AERONET sites during the study period. (b) The monthly average CMF in five AERONET sites during the study period. (c) The monthly average variation of the SMF over AERONET sites during the study period.
During the monsoon season in India (June to September) and the peak rainy period during the winter season in Greece (December to January), CMF values differ significantly. Greek cities exhibit CMF values ranging from 0.68 to 0.75, while Indian cities show lower values between 0.5 and 0.69 [15]. This lower CMF in Indian cities, particularly the coastal city of Pune, suggests a denser cloud cover than in Greek cities. Unlike India, Greece lacks a defined traditional monsoon season, which may account for the observed difference in cloud cover.
3.2. The Variation of Architecture Effects Parameters
Another crucial factor in evaluating solar radiation potential and planning smart cities is the SMF, whose average monthly variations have been analyzed in major geographic zones of India (Figure 3c). Various factors could contribute to the variation in the SMF, including shadowing from adjacent panels, terrain features, neighboring buildings, trees, and clouds, all of which can cast shadows on the panels [15,29]. Also, there is the impact of self-shading, which dominates whenever there are parallel alignments of solar panels.
The low SMF values in Pune exhibit the least fluctuation, owing to a maximum building density with the highest average height among all the cities of interest (Table 1). Further, the lower SMF values observed in Jaipur city were attributed to the significant building density in conjunction with a high cloud variability due to its proximity to the western ghats. However, Figure 3c portrays the nearly similar variation of the SMF values over the rest of the cities owing to the almost equal building densities and average building heights. The SMF was relatively low during the winter months and varies in the range ~0.88–0.94, attributed to the lower solar elevation levels and reduced sunshine hours [15].

Table 1.
A summary of the key parameters of cities of interest.
Moreover, Pune experiences extremely low SMF values, ~0.84–0.86, during winter, primarily due to reduced sunshine hours combined with cloud cover from the usual northeastern monsoon. Urban architectural effects have been compared between cities with the highest building density and those with the tallest average building height over Indian and Greek cities. The urban effect parameter, SMF, shows more variation in Pune (0.88–0.98) compared to Athens (0.84–0.99), based on monthly mean climatological data. The lower variability observed in Athens can be attributed to its 37% higher building density and an average building height nearly double that of Pune [15,82].
3.3. Aerosol and Cloud Effects on Solar Radiations
The GHI losses due to the aerosols were observed to be maximum over the IGP sites, Gurugram Gandhi College and Kanpur, with a mean of nearly 200.94 ± 52.16 kWh m−2, 213.35 ± 44.79 kWh m−2, and 196.91 ± 43.02 kWh m−2, respectively. The maximum GHI losses due to aerosols at the IGP sites were attributed to anthropogenic activities, dust storms, biomass burning, and metrological factors [83,84,85]. The least GHI attenuation due to aerosols~144.6 ± 45.48 kWh m−2, was observed in Jaipur, situated at the epicenter of frequent dust storms during summer, as most of the naturally generated aerosols are transported away [45,86]. Jaipur has significantly fewer anthropogenic activities than the cities in the IGP region [85]. The southern city of Pune has the lowest mean GHI reduction due to the aerosols being ~162.02 ± 32.09 kWh m−2 per month for the study duration. Although Pune has the maximum incident mean all-sky GHI ~213.3 ± kWh m−2 among all northern, central, and western zones of India, Pune recorded the highest mean all-sky GHI, approximately 213.3 ± 42.16 kWh m−2, among India’s northern, central, and western zones. This observation aligns with the findings reported in recent research on the Indian region [39]. Among all the sites observed, Pune showed the highest average monthly GHI attenuation by clouds, approximately 48.57 ± 48.95 kWh m−2. The high standard deviation is attributed to the temporally variable cloud cover over Pune (Figure 4b). Further, the least GHI losses due to the clouds were observed over Jaipur ~33.7 ± 32.31 kWh m−2, situated against the backdrop of the Thar desert region (Figure 4b). Furthermore, the IGP cites the mean monthly GHI losses vary in the range of 33.7–42.07 kWh m−2 over Gandhi College, Gurugram, and Kanpur, respectively (Figure 4b). The overall GHI loss analysis reveals that the losses due to the aerosols are prominent, especially over the IGP cities, as compared to the clouds at the city scale. Moreover, the aerosol effects dominate the cloud effects over all the cities of interest. The overall GHI loss analysis indicates that aerosol-induced losses are particularly significant over IGP cities compared to cloud-induced losses on the city scale. Moreover, the effects of aerosols surpass that of clouds in all the cities of interest. This could lead to higher pollution levels and microclimates on a city scale. This study’s estimated losses caused by aerosols and clouds align with recent research on the North Indian (NI) region [87]. The research indicates that aerosols and clouds contribute equally to reducing PV potential in the NI region. In contrast, clouds over Southern China (SC) have a more significant impact than aerosols in diminishing PV potential. The dominant effect of clouds over aerosols on PV potential in the SC region is attributed to the frequent presence of low- and mid-level clouds with a high optical depth combined with sulfate aerosols in the area. Conversely, in the NI region, the coexistence of low-level clouds with a low optical depth and dust aerosols results in nearly equal contributions from aerosols and clouds to the PV potential reduction. These findings highlight the comparable influence of aerosols and clouds on PV potential in the NI region at a regional scale. At the city level, aerosols likely have a more significant impact than clouds in reducing the PV potential, particularly in polluted cities of the NI region examined in this study, such as Gurugram, Gandhi College, Ballia, and Kanpur. Global-scale studies have shown that Particulate Matter (PM) reduces PV output by over 50% in polluted and desert regions, with soiling contributing to more than 66% of the total PV generation losses [88]. As far as the error in the GHI simulations is concerned, a study has validated the simulated GHI from the RTM against ground-based measurements collected from six Baseline Surface Radiation Network (BSRN) stations located in Europe and North Africa, using data from the entire year of 2021 (1 January to 31 December) [52]. It reported a maximum percentage difference of 20% and a correlation coefficient of 0.82 between the modeled and observed GHI values [52]. Consequently, the study has revealed that the simulated GHI aligns well with the ground truth observations. The GHI simulations using the RTM exploited in this study have been tested and validated against ground truth measurements from Europe, Africa, and South Asia [28,36,52,89]. It is worth noting that variations in the simulated GHI over the Indian cities would be quite in agreement with the ground truth measurements.

Figure 4.
The monthly average GHI losses (a) due to aerosols and (b) due to clouds over the five AERONET sites during the study period.
The research emphasizes the benefits of panel cleaning in heavily polluted, low-precipitation areas and highlights how air quality improvements could significantly boost solar energy production.
3.4. Rooftop Area and Rooftop Photovoltaic Potential Under Different Scenarios
Under scenario 1, we have considered the rooftop morphological factors, which are more realistic. We have used a two-step process to determine the suitable rooftop area (RAS) in scenario 1. In the first step, the 100% rooftop area is multiplied with calibration factor fca to obtain RTAu (i.e., the useful rooftop area using Equation (4a)) [33]. This factor is multiplied to convert the total building footprint area into realistic terms because, under realistic scenarios, a rooftop cannot utilize the entire roof after its installation. Secondly, the RTAu is converted into an estimated suitable or final rooftop area using the total area share factor cfa using Equation (4b) [16]. The calibration has already been discussed in the above methodology section [16]. In scenario 2, we applied suitability factors ranging from 0.6 to 0.8 for the cities of interest, based on the specific characteristics of each city, as the report suggests using a factor of approximately 0.7 [4]. The rooftop suitable area (RAS) was highest over metropolitan Pune and lowest over Gurugram under both scenarios (Table 2).

Table 2.
The suitable rooftop area (RAS) under different scenarios in the cities of interest. RAS1 assumes the roof morphology for determining an area, and RAS2 assumes a suitability factor.
Figure 5 reveals the estimated rooftop PV potential in MWh/year for the cities of interest using Equation (5). The computation yields the maximum rooftop PV potential of nearly 6970.66 ± 751.38 (13,005.65 ± 1210.71) MWh/year over the Pune metropolitan city and a minimum of ~1723.10 ± 254.14 (4306.34 ± 381.85) MWh/year over Ballia based on scenario 1 (scenario 2). Both scenarios showed a highly significant difference in RTP between Jaipur’s rural and urban areas within the western zone cities; the rural RTP was nearly 31% higher. Here, possible errors in the RTP estimates occur due to the variability of the GHI and Tcell variables in Equation (5). Here, Tcell depends on the city’s average temperature, i.e., Tai. The studies suggest that the standard deviation of the temperature climatologies throughout India typically falls between 0.5 °C and 1.5 °C, varying by the region and the period examined [90]. Therefore, we have considered the average limit, i.e., ~1 °C, that was taken here for the present study. Moreover, the standard deviation associated with the average annual GHI values for the cities is 182.5 to 365.0 kWh/m2/year, as per reports and research articles [89,91,92]. The variation of these variables to overall RTP estimates has been addressed by computing the propagation error using the (A1a,b) mentioned in Appendix A section. The results emphasize the tremendous scope of harnessing energy from rural areas of the country via optimum solar planning. The following important finding is that the Kanpur District has a higher RTP, even though the Gurugram has skyscraper buildings.
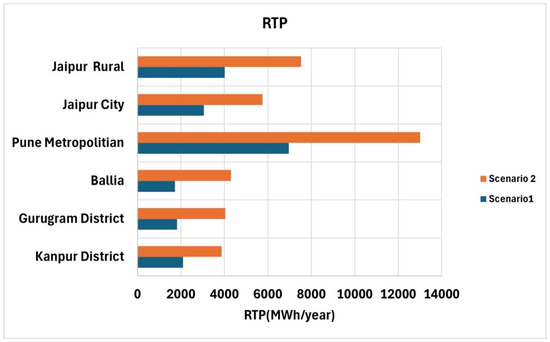
Figure 5.
The estimated annual rooftop PV potential in MWh across polluted Indian cities under various scenarios during the study period.
4. Discussions
The following section consists of four sections; Section 4.1 focuses on and discusses solar energy planning concerning energy adequacy. Section 4.2 is dedicated to the financial analysis of the potential solar energy production, considering atmospheric and architectural effects. Finally, Section 4.3 and Section 4.4 highlight the potential for carbon footprint reduction and the prospects of solar energy in India.
4.1. Solar Energy Planning
This study examines energy sustainability in polluted Indian cities using a realistic and idealized energy scheme. We used a comprehensive and systematic approach to calculate energy production under two scenarios: The first scenario involves energy generation from PV installations based on the estimated rooftop area, incorporating rooftop morphological factors such as area share factors for flat and slanted surfaces. The second scenario uses suitability factors with an assumed PV output based on the PVGIS tool at the tilt angle specific to the studied cities, further extrapolating the PV output for the entire city/region area incorporating the suitable factor for calculating the exploitable rooftop area, which is challenging to apply in realistic conditions.
Figure 6a,b below shows the PVGIS energy output at slope zero and the slope equal to the latitude for the cities. The information relation the energy consumption per city has been obtained from the site [64]. Finally, the summary of the essential parameters has been framed under the two scenarios, 1 and 2, respectively, as demonstrated in Table 3a,b.
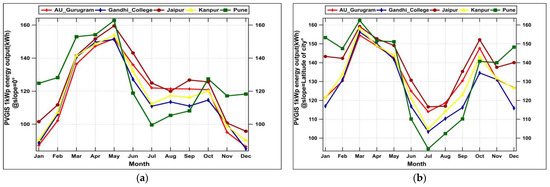
Figure 6.
The monthly variation of energy production per 1 kWp PV system (a) at zero and (b) the optimum latitude slope from PVGIS over polluted Indian cities.

Table 3.
(a) Essential parameters for energy planning under scenario 1 for each city. (b) Essential parameters for energy planning under scenario 2 for each city.
The location of the Indian region is near the equator, which spans the latitude from 8°N to 37°N. Thus, India’s location enables solar altitudes compared to the world’s region. This results in a lesser seasonal variation of sunlight, especially during the winter months at a slope equal to the latitude of the cities. The simulated outputs of the PVGIS tool indicate that the energy production levels are more significant when the PV panels have a tilt equal to the latitude compared to the horizontally tilted panels. The results for the PV output are in line with the findings of the research on an Indian city [31]. Not only that, but worldwide studies have investigated that the energy production at the best tilt angle for long-term optimal performance for PV panels is the same as the latitude of the place [15,93,94]. The next feature we observed in Figure 6a among Indian cities is that Pune depicted higher sunlight than other cities, as Pune has a lower latitude of 18°N compared to other Indian cities.
Thus, the geographic location facilitates Pune city’s harnessing of the solar rooftop for the 0-degree tilt, i.e., by flat panels. However, the IGP cities have a lesser solar harnessing potential via flat rooftops. On the other hand, Figure 6b shows that the optimum amount of solar energy could be harnessed via the tilted rooftop with a slope ~ latitude of the city or place over the Indian cities. The analysis reveals the total RTP from all five cites as 19,689.74 ± 2379.29 (38,504.76 ± 3715.42) MWh/year under scenario 1 (scenario 2) using the high-level approach in the present study (Table 3a,b).
Moreover, we estimated the energy adequacy for the cities as portrayed in Figure 7, computed using Equation (8). The energy adequacy in rural areas, such as Ballia, is the maximum (~58%) compared to all of the cities and Jaipur rural, especially when contrasted with Jaipur City. The reason for the significant high-energy adequacy might be a lesser energy consumption than the possible energy production capacity. However, both the cities, Kanpur and Ballia, are located in a similar geographical zone, Central IGP; Ballia has an energy adequacy nearly three times that of Kanpur. Being industrial, Kanpur has a higher energy consumption and a more significant population density than Ballia. Next to Ballia, we observed a higher energy adequacy of ~40% over Pune metropolitan city. The higher energy adequacy observed in Pune can be attributed to its maximum energy production capacity, which results in the most significant building footprint area compared to the other cities. Gurugram city has an energy adequacy of ~31%, with an RTP of ~4036 MWh/year. Although the city has a multistory building, it is still in the development phase; thus, in the future, the city might have an enormous potential for solar power in North India. While energy adequacies are lower in scenario 2 than in scenario 1, the overall trend remains consistent across all of the cities. This discrepancy may arise because scenario 2 presents a more realistic approach by carefully incorporating rooftop morphological factors, making it more robust than the other scenarios. A detailed energy planning analysis might be used to develop rooftop solar potential maps that focus on the government’s interest in making smart cities. Moreover, the results of the investigation help establish the RTP map and mitigate climate change over the IGP, known as the “food bowl” of the Indian region [95]. The results obtained from the extensive study are pretty helpful for the policymakers and stakeholders, and the better implementation of govt solar rooftop schemes such as Pradhan Mantri Surya Ghar Muft Bijli Yojna (PMSY). The details of this scheme are here, with the link [96].
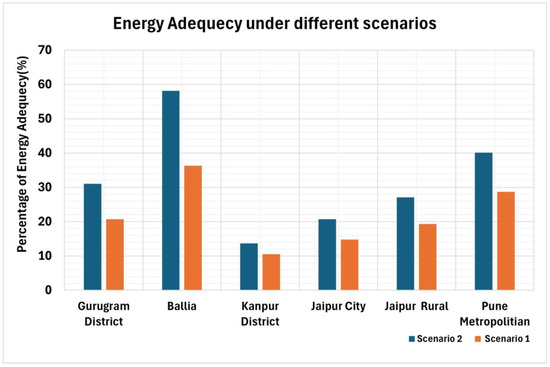
Figure 7.
The energy adequacy percentage that annually, per city, can be potentially produced to meet its daily usage under scenario 1 (i.e., this applies to the PV installations following the rooftop morphology) and scenario 2 (i.e., the optimum installation in terms of panels tilt and orientation with suitability factors which are assumed to be not realistic to apply).
4.2. Financial Analysis
As far as the energy losses were concerned, we discussed them extensively in the above sections. The financial analysis has been conducted by exploiting the rooftop installed capacity. The FL losses were estimated using Equation (9) utilizing the FIT rates discussed in methodology Section 2.6. The previous studies follow the same methods for assessing the FL and earnings [15,35,36,56,67]. Below is the estimation for the FL due to aerosols, clouds, and shadows under the energy planning scenario for each city (Table 4).

Table 4.
Financial losses due to aerosols, clouds, and shadows are under the energy planning scenario for each city. The estimated net profits correspond to the earnings and financial losses.
The FL assessment analysis reveals from Table 4 that the most significant cities, Northern and Central IGP, were too polluted, contributing to the larger FL due to aerosols compared to clouds. However, the potential FL over the southern zone city is larger due to large, simulated PVGIS energy productions, which aligns with all the Maharashtra solar potential in India [4]. The losses due to the aerosols are higher than the clouds at the city level, suggesting strong measures to combat air pollution in the direction of developing smart cities, as seen in Table 4. Secondly, we observed that the losses due to the shadows were significantly lesser, varying from 146.32 to 809.22 million rupees, except in metropolitan Pune. The FL due to shadows being significant over metropolitan Pune might be due to the maximum building density and average building height, i.e., ~36.72% and 5.48 m, respectively. The total FL due to all of the factors over the Ballia is about ~42.3% higher than Kanpur and 29.4% higher than Gurugram, respectively. For overall FL losses due to all of the factors, the maximum losses were observed for Pune and the minimum over Kanpur of nearly 6283.54 and 1958.28 million INR, respectively. The financial analysis of Jaipur’s rural and urban regions reveals a lower FL and higher earnings in rural areas, leading to greater profits than in the city.
The present study results align with agency reports showing a higher RTP in rural areas than urban regions, with a significantly lower FL in Ballia and Jaipur rural compared to cities like Gurugram, Kanpur, and Jaipur, except metropolitan Pune [60,97]. Regarding the potential profits, the maximum profits in a million INR rupees are ~9443.39 over metropolitan Pune. Also, these profits are two to three times that of cities such as Gurugram, Kanpur, and Jaipur (Table 4). The possible financial loss calculation error depends entirely on two factors. The first one is the FIT, as per state and government reports, which may vary from time to time depending on the policies implemented. The second factor is energy production, which we have estimated under a hypothetical coverage for the entire city at the optimum angle equal to the city’s latitude. However, some studies over the city scale have reported that the optimum angle of tilt for the plane of irradiance of the PV panel is equal to the city’s latitude, which might not be accurate for all cities in India [98]. The study of the 25 cities in Europe and North Africa has reported a 0.48% change in the FL estimates for the approximately 0.19% change in energy production [99]. This reported change in the energy production corresponds to a change in the tilt of the plane of irradiance of the PV panel from the latitude of the place to the optimum angle. So, in our study also, the error contributed by the energy production to the estimated FL could fall in this range only.
Here, not merely focusing on the profits but also on the actuality, the earnings of the installer or customer only started after the payback period of the PV installation, known in technical terms as the breakeven point, which is the time required to recover the PV installation cost. The span of getting to this point depends on numerous factors: geographical location, the number of systems installed, and various other factors. Realistically, the profit may vary depending on the local authorities and government policies for solar incentives and electricity prices per kWh. As far as the cost efficiency of the solar PV rooftop is concerned, a study across six Indian cities with varying climates showed that rooftop solar PV systems have a PR of 70% to 80% and can produce 400–500 kWh of energy daily at INR 6–7 per unit [66]. The MNRE has set a benchmark cost of INR 43,140 per kW (excluding GST) for rooftop solar systems of 1–2 kW [4]. The payback period for these systems is approximately 5–6 years, making them economically feasible [4]. However, the payback period varies based on system size, electricity generation and consumption, and subsidies.
The positive aspects of solar rooftop installation involve the decreasing cost of renewable energy system (RES) technology, decarbonizing the energy emissions, improved air quality, reduced greenhouse gas emissions, and profits to local municipals with customers. However, research also shows that the rooftop PV installation might affect the urban heat budget, thus reducing the back-emitted longer wavelength radiations, therefore the sensible heat flux and rooftop cooling capacity [100,101].
In brief, getting the profit due to the factors mentioned above yields the profit in general simple terms, but in realistic terms, various other factors should be taken care of, such as the PV system life, its maintenance cost, changing power rates, the study of its feasibility, and a cost analysis urges guidance from the professional solar energy planning experts and advisors [4].
4.3. The Equivalent Reduction in Carbon Footprints
Solar energy is an eco-friendly, cost-effective solution to curb air pollution and mitigate climate change and GHG emissions using PV technology. Irrespective of the manufacturing and installation cost of the rooftop PV system, the benefit from the amount of carbon emissions significantly for the solar energy produced surpasses the invested cost with their maintenance. Though there are environmental impacts also from solar PV panels, their overall contribution to lower GHG emissions, and thus climate change, is significant [20].
It will be interesting to convert the potential solar energy produced based on the cities’ RTP (MWh/year) based on the two scenarios for the polluted Indian cities.
Quantitively, every kilowatt of non-conventional energy helps reduce carbon emissions. For instance, the 5 kW solar plant could save 15,000 pounds of CO2 emissions per year in the context of solar energy [102]. The CO2 emissions avoided could be significantly vital socio-economically for any country. Also, a minimal amount of CO2 is emitted from the solar panel compared to tons of carbon emissions during natural gas extraction or other energy sources.
For the polluted Indian Cities having long-term ground truth aerosol measurements, we estimated the carbon footprint minimized using the well-known Greenhouse equivalence calculator [15]. This calculator may allow us to convert the RTP or solar energy produced to equivalent CO2 emissions by that source. The calculators also facilitate the estimation of the emissions every year for the energy produced by any power plant, industry, and manufacturing unit. The calculator output helps identify and form the actionable clean air/environment mitigation plan for any production/manufacturing agency or unit. The calculator utilizes the Avoided Emissions and Green Ration Tool (AVERT) to cover the kilowatt of the energy produced by the entity to its equivalent CO2 emission reduced in metric tons as per the equation used in the recent research over European cities [15]. The important thing is that the equation only accounts for the CO2 emissions and incorporates inline losses. The inline transmission and distribution losses are relatively high (~20% in some areas of India), which can affect the accuracy when adjusting for line losses. The tool also assumes that displaced generation comes from marginal fossil units (e.g., gas peakers). Misidentifying the displaced fuel type (e.g., gas vs. coal) introduces a ±15–30% variability in CO2 estimates, according to the AVERT manual [103]. So, the values estimated for the CO2 emissions avoided in Mt reported in the present work had variability in the range of ±15–30%. In the present study, using the AVERT equation, we have estimated the equivalent CO2 emissions avoided in Metric Tons (Mt), thus representing them per capita depending on the population density under scenario 1 and scenario 2 (Figure 8).

Figure 8.
The CO2 emissions avoided per capita under scenario 1 (i.e., this applies to the PV installations following the rooftop morphology) and scenario 2 (i.e., the optimum installation in terms of panels tilt and orientation, which is assumed to be not realistic to apply).
Our estimates for Indian cities in Table 5a,b under different scenarios reveal the importance of rooftop PV installation to reduce carbon emissions, henceforth decentralizing and decarbonizing the energy generation and its mix to mitigate climate change and thereby imposing public-friendly solar schemes such as making the rooftop installation affordable even for smaller energy requirement consumers—a few kilowatts. This could be achieved by increasing the FIT rates for distribution companies (DISCOMs) and facilitating large-scale RES production for highly demanding countries like India. Further, not only will the installation be cheaper, but it will also parallelly increase the awareness of ordinary people by organizing social programs and media in layperson’s terms. As published in the survey, not more than 50% are aware of the solar rooftop scheme [4]. The students and youngsters must be aware of this, especially at the country’s schools, colleges, and universities. The data for electricity consumption on an annual basis has been utilized in the present study [104]. Here, we have assumed Ballia’s annual electric consumption ~800,000 MWh of yearly consumption, which is less comparatively due to its rural nature and the unavailability of data.

Table 5.
(a) Estimates of the carbon footprint minimized based on the energy consumption of the installed rooftop capacity for scenario 1 (i.e., this applies to the PV installations following the rooftop morphology). (b) Estimates of the carbon footprint are minimized based on the installed rooftop capacity for scenario 2 (i.e., the optimum installation in terms of panel tilt and orientation, which is assumed to be not realistic to apply).
The report and published studies further claim that rural areas have shown a higher technical roof potential than urban areas based on the residential rooftop area [4,60].
Our analysis resulted in a maximum per capita CO2 emissions avoided of ~1.26 and ~0.90 in Mt with variability in the range of ±15–30% over the metropolitan city Pune based on both scenarios. Secondly, the critical finding of our research reveals that the rural areas of the countries have a more significant potential for CO2 emissions to be avoided. As Table 5a shows, the per capita CO2 emissions avoided by Jaipur rural has a ~0.20 Mt compared to Jaipur city, ~0.09 Mt, with a variability of ±15–30% (Table 5a). Among the Gurugram, Gandhi College, and Kanpur cities, the central IGP city Kanpur has the lowest per capita of CO2 emissions avoided, which might be due to its high population density (Table 5a). However, the overall estimation for carbon emission reduction per city under both scenarios is shown in Table 5a and 5b, respectively.
4.4. Future Challenges from India’s Perspective
By promoting rooftop solar, consumers can lower their electricity bills and generate surplus energy, creating an additional source of income. These RTP assessment studies provide the government and various stakeholders with quantitative evidence regarding the future of rooftop solar deployment, particularly in rural areas where few studies have quantitatively assessed the high potential. Detailed assessments yield valuable data that can guide government policies and incentives, such as subsidies and tax credits, to encourage rooftop solar adoption. Additionally, increasing the distributed generation through rooftop solar enhances the stability and resilience of the power grid, especially in urban areas prone to outages. This ultimately assists various DISCOMS in managing excess load during peak demand periods, particularly in metropolitan cities, as highlighted in the study. This study will fill the significant gap between energy consumers and energy producers. The work effectively provides insights into economic benefits regarding potential profits and savings. The challenge of raising electricity bills, coupled with political parties’ promises to provide free electricity, has contributed to budget deficits in the state. However, this issue can be effectively addressed. The analysis shows significant potential financial savings for people from their rooftops. Beyond the positive impacts on electricity bills, solar PV provides an option to participate directly in battles against climate change and energy justice. Solar PVs are the entry point for many people on their sustainable journey. The penetration of Solar PV in society will create thousands of purposeful jobs with real meaning. The study demonstrates that solar PV installation can potentially boost the supply chain from manufacturing and installation to maintenance, thus strengthening the Indian economy. Furthermore, rooftop solar PV will enhance the solar energy experts’ and planners’ requirements for optimum solar PV installation. Lastly, enabling participation in the energy transition will not only create jobs but ensure the direct involvement of the people in the Indian journey towards decarbonizing energy and achieving sustainability SDG goals. In the future, countries will require more studies and country-specific solar cadaster for more robust solar PV planning. Although the GOI has taken initiatives to set up semiconductor industries, India must still focus on solar PV manufacturing as we depend on China for our raw materials for solar PV panels and silicon wafers. We further suggest through this study that it is not only the solar potential the country has that is important but also the public, DISCOMS, utilities, and solar company-friendly policy framework that could help in rooftop PV installation on a large scale. There is still a significant need to make the common man aware of the benefits of rooftop PV installation. Although the GOI has initiated various awareness programs and recently approved the Production Linked Incentive (PLI) scheme for promoting solar PV module manufacturing, the country has a long way to go. Regarding the current challenges in India of the solar PV value chain, we must focus primarily on the monocrystalline and polycrystalline silicon production at zero capacity till now. Secondly, we should focus on the monocrystalline to the Ingo and Ingot to the wafer production capacity. Thirdly, although we have some cell production, i.e., from the wafer and module production capacity, a significant production capacity is still required in the coming years. There is still no company in India that recycles solar PV. Otherwise, it will create a tremendous amount of waste for the earth. The market opportunity for solar PV production is there for India as the world not only wants to depend on China’s monopoly, i.e., China plus one, but GOI should reduce the import duties on raw materials from China to enhance module fabrication for self-consumption and exports. A skilled workforce is required in the country for the wafer and cell manufacturing as it is a high-precision engineering job. There are no integrated companies in the Indian solar PV market that can increase the cost advances. Domestic consumers are still not convinced about locally manufactured solar PV products. India should aim to be self-sufficient in solar PV manufacturing as soon as possible. The policymaker should incorporate the significant impact of air pollution/aerosols and clouds in their framework during the solar potential assessment over the Indian region. In the future, we may have solar cadasters over the Indian region in the public domain for less risky PV investments, thus ensuring the optimum penetration of solar PV in society.
5. Conclusions
Our analysis of the carbon footprint emissions avoided gives insights into the capacity to make smart cities such as Pune, Jaipur, Gurugram, and Kanpur, respectively, soon in the future. The reduction in the carbon footprint accelerates India’s net zero emission goal for the energy planning schemes under the scenarios discussed above. The present research study reveals insights that, at the city level, rural areas in India possess a significant solar RTP due to the unrestricted availability of large roof spaces and fewer environmental constraints. From the overall study, we can draw the following key conclusions:
- The present research estimates the maximum total RTP for the southern city of Pune metropolitan to be approximately 6970.66 ± 751.38 MWh/year (13,005.65 ± 1210.71 MWh/year). In the central zone, the total RTP for the cities of Ballia and Kanpur is estimated at 3816.83 ± 541.24 MWh/year (8175.26 ± 818.59 MWh/year) under scenario 1 (scenario 2). The total RTP for the western zone cities, including Jaipur rural and city, is around 7073.38 ± 828.69 MWh/year (13,287.36 ± 1297.87 MWh/year). Conversely, the RTP assessment indicates a lower potential for the northern zone city of Gurugram, estimated at 1822.87 ± 257.99 MWh/year (4036.46 ± 388.25 MWh/year). Thus, it depicted the higher RTP over western zone cities of the country. Moreover, the RTP in the rural city examined in this study is 31% greater than the urban city of India under both scenarios.
- For the polluted Indian cities examined in this current research, we determined that tilting the plane of irradiance PV panels at an angle equivalent to the latitude of the location provides a superior long-term performance compared to a horizontal arrangement.
- We observed the significant effect of aerosols compared to the clouds over all the Indian cities. The climatological trends analysis of the AOD resulted over cities as Gurugram (0.019/month), Kanpur (0.013/month), Gandhi College/Ballia (−0.003/month), Jaipur (0.013/month), and Pune (−0.001/month). The significant aerosol levels resulted in GHI losses over the cities Gurugram (3.77 kW/m2/month), Kanpur (0.68 kW/m2/month), Gandhi College/Ballia (−0.912 kW/m2/month), Jaipur (−2.69 kW/m2/month), and Pune (−1.60 kW/m2/month). We observed significant rising AOD trends over the northern Gurugram and central IGP city of Kanpur, respectively, resulting in maximum GHI losses. Kanpur and Ballia are situated in the central IGP, but Kanpur exhibits higher aerosol trends due to significant industrial emissions, in contrast to the less industrialized Ballia. Conversely, the declining trends of the AOD in Pune metropolitan may be attributed to its coastal location and lower anthropogenic activity levels compared to cities in the IGP region. On the other hand, Jaipur shows a positive trend, likely due to its proximity to the arid areas. Therefore, these results highlight the need to consider aerosol effects in future assessments and planning for rooftop PV potential.
- The climatological trends of cloud effects were assessed using the COT results of Gurugram (0.09/month), Kanpur (0.31/month), Gandhi College/Ballia (−0.31/month), Jaipur (0.31/month), and Pune (1.51/month) over the cities. The presence of the cloud cover resulted in the GHI losses due to clouds over Gurugram (0.59 kW/m2/month), Kanpur (0.94 kW/m2/month), Gandhi College/Ballia (1.33 kW/m2/month), Jaipur (1.24 kW/m2/month), and Pune (3.70 kW/m2/month), respectively. The analysis indicates that AOD values are higher over the coastal city of Pune. This can be attributed to a denser cloud cover occurring twice a year during the monsoon season. Additionally, similar trends are observed in the IGP cities and the western city of Jaipur, primarily due to the influence of the southwest monsoon.
- The total GHI losses due to aerosols, clouds, and shadows have been translated into the total financial losses over the cities, of nearly 11,241.70 million rupees, 4439.49 million rupees, and 1167.65 million rupees, respectively, over all the five polluted cities of the Indian region. Under the scenario, for solar energy produced, we could have total estimated earnings of 45,282.87 million rupees with a total savings of nearly 279,340.3 million rupees. Moreover, the financial analysis reveals a maximum economic potential for generating income from RTP installations in urban metropolitan areas, with a significant economic potential in rural regions.
- According to the statistics [105], the burning of one ton of coal produces 2.07 tons of CO2. Using the conversion factor from scenario 1, deploying solar rooftop PV in cities could save between 153,570.04 to 501,342.02 metric tons of coal. Under scenario 2, the CO2 equivalent emission avoided has been translated to nearly 98,134.23 to 358,101.45 tons of coal burnt for electricity production for the Indian cities. The estimates of coal savings have an uncertainty range of ±7.25% to 14.49% per ton of avoided CO2 emissions under both scenarios. Thus, India could reach the net zero target as early as possible.The core objective and novelty of this study stem from its two-part methodological approach. Firstly, we estimated the RTP using current state-of-the-art methods, which involved assuming suitability factors and energy outputs based on PVGIS simulations and extrapolating these for effective city rooftop areas. Secondly, we advanced beyond the existing approaches by incorporating roof morphology metrics and various area allocation factors to assess RTP in more realistic terms. Both steps were applied under two distinct scenarios to evaluate variability. Moreover, the study concluded the more significant effect of aerosols than clouds over polluted Indian cities. The information in the assessment done in the study could be utilized by the GOI, various stakeholders, policymakers, and DISCOMS to analyze the investment opportunities and risks in implementing solar PV rooftops. The assessments help identify the realistic potential for rooftop solar installations by mapping suitable areas for deployment, allowing the government to plan and achieve its renewable energy targets effectively. In the future, studies that incorporate atmospheric and urban effects must be conducted using advanced machine-learning techniques. Additionally, there is a need to develop a solar cadaster for Indian cities to enable optimal solar PV planning and facilitate a greater penetration into society.
Author Contributions
Conceptualization, P.G.K. and D.S.; methodology, P.G.K. and D.S.; software.; validation, D.S. and P.G.K.; formal analysis, D.S.; investigation, D.S.; resources, D.S.; data curation, D.S.; writing—original draft preparation, D.S.; writing—review and editing, P.G.K.; visualization, D.S.; supervision, P.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Data Availability Statement
Data can be available upon request from the corresponding author.
Acknowledgments
We thank the open-source data providers AERONET, the European Commission, the Joint Research Centre (JRC), and the Publications Office of the European Union. The authors acknowledge the project Thinking Earth, funded under Grant Agreement number 101130544 by the Horizon Europe program topic HORIZON-EUSPA-2022-SPACE-02-55, which promotes the large-scale Copernicus data uptake with AI and HPC.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| AMF | Aerosol modification factor |
| CMF | Cloud modification factor |
| GHI0 | Clear sky radiation (W m−2) |
| GHI00 | Radiation under clean (no aerosols) and clear (no cloud) conditions (W m−2) |
| GHI | Radiation under all clear-sky conditions (W m−2) |
| DHI | Diffuse horizontal irradiance (W m−2) |
| R | Diffusion coefficient |
| RTAu | Usable rooftop Area (km2) |
| Ab | Building footprint Area (km2) |
| fca | Calibration factor |
| cfa | Total area correction factor |
| Sflt,u | Area shares of usable flat roofs |
| cfa,slt | Area correction factor for slanted roof |
| cfa,flt | Area correction factor for flat roof |
| RTP | Rooftop photovoltaic potential (MWh yr−1) |
| µref | Electrical module efficiency at the standard testing conditions |
| cfrad | Radiation correction factor |
| β | Temperature coefficient (°C−1) |
| Tcell | Solar photovoltaic cell temperature (°C) |
| Tref | Reference temperature under standard testing conditions (°C) |
| PR | Performance ratio is the efficiency of the solar PV |
| Tai | Average temperature of the city (°C) |
| FL | Financial losses (Rupees) |
| FIT | Feed in Tariff (INR/KWh) |
| PVGIS | Photovoltaic Geographic Information System |
| EPmax | Maximum energy produced under the clean and clear conditions (KWh) |
| EPactual | Actual energy produced is inclusive of the effect of factors such as clouds/aerosols/shadows (KWh) |
| RES | Renewable energy system |
| GOI | Government of India |
| DISCOM | Distribution companies |
Appendix A
Here below are the Equations (A1a,b) and (A2) used for the error estimates for the estimation of Rooftop photovoltaic potential (MWh yr−1):
The propagated error associated with the is defined as the solar photovoltaic cell temperature (°C) computed by the below equation:
where are the standard deviations between the average yearly temperature and GHI of the cities. Moreover, C2 and C3 are the constants with defined values mentioned above in Section 2.5. The studies indicate that the standard deviation of temperature climatologies across India generally ranges between 0.5 °C and 1.5 °C, depending on the region and period analyzed [90]. We assume that ~1 °C was taken here for the present study. Moreover, the standard deviation associated with the average annual GHI values for the cities is 182.5 to 365.0 kWh/m2/year [89,91,92]. For calculation purposes, we have used the average value of the lower and upper bounds of the range.
References
- Ge, M.; Friedrich, J.; Vigna, L. Where Do Emissions Come From? 4 Charts Explain Greenhouse Gas Emissions by Sector. Available online: https://www.wri.org/insights/4-charts-explain-greenhouse-gas-emissions-countries-and-sectors (accessed on 6 January 2025).
- Cabeza, L.F.; Bai, Q.; Bertoldi, P.; Kihila, J.M.; Lucena, A.F.P.; Mata, É.; Mirasgedis, S.; Novikova, A.; Saheb, Y. Buildings. In Climate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Shukla, P.R., Skea, J., Slade, R., Al Khourdajie, A., van Diemen, R., McCollum, D., Pathak, M., Some, S., Vyas, P., Fradera, R., et al., Eds.; Cambridge University Press (CUP): Cambridge, UK; New York, NY, USA, 2022; pp. 953–1019. [Google Scholar]
- IEA. World Energy Outlook; IEA: Paris, France, 2024. [Google Scholar]
- Zachariah, S.; Tyagi, B.; Kuldeep, N. Mapping India’s Residential Rooftop Solar Potential—A Bottom-Up Assessment Using Primary Data; Report; Council on Energy, Environment and Water: New Delhi, India, 2023. [Google Scholar]
- MNRE. Year End Review 2023 of Ministry of New & Renewable Energy. Available online: https://pib.gov.in/PressReleaseIframePage.aspx?PRID=1992732 (accessed on 6 January 2025).
- Shahrukh Anis, M.; Jamil, B.; Azeem Ansari, M.; Bellos, E. Generalized Models for Estimation of Global Solar Radiation Based on Sunshine Duration and Detailed Comparison with the Existing: A Case Study for India. Sustain. Energy Technol. Assess. 2019, 31, 179–198. [Google Scholar] [CrossRef]
- Kapoor, K.; Pandey, K.K.; Jain, A.K.; Nandan, A. Evolution of Solar Energy in India: A Review. Renew. Sustain. Energy Rev. 2014, 40, 475–487. [Google Scholar] [CrossRef]
- MNRE. Solar Overview, Ministry of New and Renewable Energy (MNRE), Government of India, New Delhi, India. Available online: https://pib.gov.in/PressReleaseIframePage.aspx?PRID=2003561 (accessed on 6 January 2025).
- Corti, P.; Bonomo, P.; Ramachandran, A.M.; Asok, A. Indian BIPV Report 2022: Status and Roadmap; SUPSI-ISAAC, CSIR-NIST: Lugano, Switzerland, 2022. [Google Scholar]
- IRENA. Renewable Energy Statistics 2024; IRENA: Abu Dhabi, United Arab Emirates, 2024. [Google Scholar]
- MNRE. India’s Renewable Energy Capacity Hits New Milestone Renewable Energy Now Constitutes More than 46.3% of Total Capacity. Available online: https://pib.gov.in/PressReleaseIframePage.aspx?PRID=2073038 (accessed on 6 January 2025).
- Bridge To India. India Solar Rooftop Map; Bridge To India: Mumbai, India, 2024. [Google Scholar]
- Md Khairi, N.H.; Akimoto, Y.; Okajima, K. Suitability of Rooftop Solar Photovoltaic at Educational Building towards Energy Sustainability in Malaysia. Sustain. Horiz. 2022, 4, 100032. [Google Scholar] [CrossRef]
- Ranjgar, B.; Niccolai, A. Large-Scale Rooftop Solar Photovoltaic Power Production Potential Assessment: A Case Study for Tehran Metropolitan Area, Iran. Energies 2023, 16, 7111. [Google Scholar] [CrossRef]
- Vigkos, S.; Kosmopoulos, P.G. Photovoltaics Energy Potential in the Largest Greek Cities: Atmospheric and Urban Fabric Effects, Climatic Trends Influences and Socio-Economic Benefits. Energies 2024, 17, 3821. [Google Scholar] [CrossRef]
- Sander, L.; Schindler, D.; Jung, C. Application of Satellite Data for Estimating Rooftop Solar Photovoltaic Potential. Remote Sens. 2024, 16, 2205. [Google Scholar] [CrossRef]
- Galvin, R. Re-Thinking Energy Justice to Achieve a Fair Distribution of Shared Electricity from Rooftop Photovoltaics in a Typical Multi-Apartment Building in Germany: An Interdisciplinary Approach. Energy Res. Soc. Sci. 2024, 112, 103531. [Google Scholar] [CrossRef]
- Fakhraian, E.; Forment, M.A.; Dalmau, F.V.; Nameni, A.; Guerrero, M.J.C. Determination of the Urban Rooftop Photovoltaic Potential: A State of the Art. Energy Rep. 2021, 7, 176–185. [Google Scholar] [CrossRef]
- Gernaat, D.E.H.J.; de Boer, H.S.; Dammeier, L.C.; van Vuuren, D.P. The Role of Residential Rooftop Photovoltaic in Long-Term Energy and Climate Scenarios. Appl. Energy 2020, 279, 115705. [Google Scholar] [CrossRef]
- Joshi, S.; Mittal, S.; Holloway, P.; Shukla, P.R.; Ó Gallachóir, B.; Glynn, J. High Resolution Global Spatiotemporal Assessment of Rooftop Solar Photovoltaics Potential for Renewable Electricity Generation. Nat. Commun. 2021, 12, 5738. [Google Scholar] [CrossRef]
- Risch, S.; Maier, R.; Du, J.; Pflugradt, N.; Stenzel, P.; Kotzur, L.; Stolten, D. Potentials of Renewable Energy Sources in Germany and the Influence of Land Use Datasets. Energies 2022, 15, 5536. [Google Scholar] [CrossRef]
- Ren, H.; Sun, Y.; Zhang, Y. A Novel 3D-Geographic Information System and Deep Learning Integrated Approach for High-Accuracy Building Rooftop Solar Energy Potential Characterization of High-Density Cities. Build. Simul. Conf. Proc. 2023, 18, 3880–3887. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Yu, L.; Mao, J. What Really Influences the Development of Renewable Energy? A Systematic Review and Meta-Analysis. Environ. Sci. Pollut. Res. 2023, 30, 62213–62236. [Google Scholar] [CrossRef]
- Mehmood, U.; Agyekum, E.B.; Tariq, S.; Haq, Z.U.; Uhunamure, S.E.; Edokpayi, J.N.; Azhar, A. Socio-Economic Drivers of Renewable Energy: Empirical Evidence from BRICS. Int. J. Environ. Res. Public Health 2022, 19, 4614. [Google Scholar] [CrossRef]
- Bódis, K.; Kougias, I.; Jäger-Waldau, A.; Taylor, N.; Szabó, S. A High-Resolution Geospatial Assessment of the Rooftop Solar Photovoltaic Potential in the European Union. Renew. Sustain. Energy Rev. 2019, 114, 109309. [Google Scholar] [CrossRef]
- Kapsalis, V.; Maduta, C.; Skandalos, N.; Bhuvad, S.S.; D’Agostino, D.; Yang, R.J.; Udayraj; Parker, D.; Karamanis, D. Bottom-up Energy Transition through Rooftop PV Upscaling: Remaining Issues and Emerging Upgrades towards NZEBs at Different Climatic Conditions. Renew. Sustain. Energy Transit. 2024, 5, 100083. [Google Scholar] [CrossRef]
- Gagnon, P.; Margolis, R.; Melius, J.; Phillips, C.; Elmore, R. Rooftop Solar Photovoltaic Technical Potential in the United States: A Detailed Assessment; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2016. [Google Scholar]
- Masoom, A.; Kosmopoulos, P.; Bansal, A.; Kazadzis, S. Solar Energy Estimations in India Using Remote Sensing Technologies and Validation with Sun Photometers in Urban Areas. Remote Sens. 2020, 12, 254. [Google Scholar] [CrossRef]
- Kosmopoulos, P.; Dhake, H.; Kartoudi, D.; Tsavalos, A.; Koutsantoni, P.; Katranitsas, A.; Lavdakis, N.; Mengou, E.; Kashyap, Y. Ray-Tracing Modeling for Urban Photovoltaic Energy Planning and Management. Appl. Energy 2024, 369, 123516. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, B.; Zhu, R.; Dong, Z. City-Scale Solar PV Potential Estimation on 3D Buildings Using Multi-Source RS Data: A Case Study in Wuhan, China. Appl. Energy 2024, 359, 122720. [Google Scholar] [CrossRef]
- Singh, R.; Banerjee, R. Estimation of Rooftop Solar Photovoltaic Potential of a City. Sol. Energy 2015, 115, 589–602. [Google Scholar] [CrossRef]
- Kaleshwarwar, A.; Bahadure, S. Assessment of the Solar Energy Potential of Diverse Urban Built Forms in Nagpur, India. Sustain. Cities Soc. 2023, 96, 104681. [Google Scholar] [CrossRef]
- Singh, R. Approximate Rooftop Solar PV Potential of Indian Cities for High-Level Renewable Power Scenario Planning. Sustain. Energy Technol. Assess. 2020, 42, 100850. [Google Scholar] [CrossRef]
- Mishra, T.; Rabha, A.; Kumar, U.; Arunachalam, K.; Sridhar, V. Assessment of Solar Power Potential in a Hill State of India Using Remote Sensing and Geographic Information System. Remote Sens. Appl. Soc. Environ. 2020, 19, 100370. [Google Scholar] [CrossRef]
- Kumar, A.; Kosmopoulos, P.; Kashyap, Y.; Gautam, R. Rooftop Photovoltaic Energy Production Estimations in India Using Remotely Sensed Data and Methods. Remote Sens. 2023, 15, 3051. [Google Scholar] [CrossRef]
- Dumka, U.C.; Kosmopoulos, P.G.; Ningombam, S.S.; Masoom, A. Impact of Aerosol and Cloud on the Solar Energy Potential over the Central Gangetic Himalayan Region. Remote Sens. 2021, 13, 3248. [Google Scholar] [CrossRef]
- Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Forster, P.; Kerminen, V.-M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. IPCC AR5 Clouds and Aerosols. In Climate Change 2013: The Physical Science Basis; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 571–658. [Google Scholar] [CrossRef]
- Bergin, M.H.; Ghoroi, C.; Dixit, D.; Schauer, J.J.; Shindell, D.T. Large Reductions in Solar Energy Production Due to Dust and Particulate Air Pollution. Environ. Sci. Technol. Lett. 2017, 4, 339–344. [Google Scholar] [CrossRef]
- Ghosh, S.; Dey, S.; Ganguly, D.; Baidya Roy, S.; Bali, K. Cleaner Air Would Enhance India’s Annual Solar Energy Production by 6–28 TWh. Environ. Res. Lett. 2022, 17, 054007. [Google Scholar] [CrossRef]
- Ghosh, S.; Ganguly, D.; Dey, S.; Chowdhury, S.G. Future Photovoltaic Potential in India: Navigating the Interplay between Air Pollution Control and Climate Change Mitigation. Environ. Res. Lett. 2024, 19, 124030. [Google Scholar] [CrossRef]
- Copernicus Emergency Management Service. Human Settlement Data. Available online: https://human-settlement.emergency.copernicus.eu/ (accessed on 6 January 2025).
- Florczyk, A.J.; Corbane, C.; Ehrlich, D.; Freire, S.; Kemper, T.; Maffenini, L.; Melchiorri, M.; Pesaresi, M.; Politis, P.; Schiavina, M.; et al. GHSL Data Package 2019, EUR 29788 EN; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Giles, D.M.; Sinyuk, A.; Sorokin, M.G.; Schafer, J.S.; Smirnov, A.; Slutsker, I.; Eck, T.F.; Holben, B.N.; Lewis, J.R.; Campbell, J.R.; et al. Advancements in the Aerosol Robotic Network (AERONET) Version 3 Database—Automated near-Real-Time Quality Control Algorithm with Improved Cloud Screening for Sun Photometer Aerosol Optical Depth (AOD) Measurements. Atmos. Meas. Tech. 2019, 12, 169–209. [Google Scholar]
- Sethi, D.; Radhakrishnan, S.R.; Sharma, C.; Mishra, S.K.; Jaswant. Aerosol Optical Properties over Delhi during a Dust Event in Summer 2014: Plausible Implications. Indian J. Phys. 2021, 95, 2531–2540. [Google Scholar] [CrossRef]
- Government of India. Smart Cities Mission: A Step Towards Smart India. Available online: https://www.india.gov.in/spotlight/smart-cities-mission-step-towards-smart-india (accessed on 6 January 2025).
- Government of India. PMS Surya Ghar. Available online: https://www.pmsuryaghar.gov.in/ (accessed on 6 January 2025).
- Ministry of New and Renewable Energy, Government of India. Schemes and Guidelines. Available online: https://mnre.gov.in/en/policies-and-regulations/schemes-and-guidelines/schemes/ (accessed on 6 January 2025).
- Hünerbein, A.; Bley, S.; Deneke, H.; Meirink, J.F.; Van Zadelhoff, G.J.; Walther, A. Cloud Optical and Physical Properties Retrieval from EarthCARE Multi-Spectral Imager: The M-COP Products. Atmos. Meas. Tech. 2024, 17, 261–276. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical Note: The LibRadtran Software Package for Radiative Transfer Calculations—Description and Examples of Use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The LibRadtran Software Package for Radiative Transfer Calculations (Version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Kosmopoulos, P.; Dhake, H.; Melita, N.; Tagarakis, K.; Georgakis, A.; Stefas, A.; Vaggelis, O.; Korre, V.; Kashyap, Y. Multi-Layer Cloud Motion Vector Forecasting for Solar Energy Applications. Appl. Energy 2024, 353, 122144. [Google Scholar] [CrossRef]
- Kinne, S. The MACv2 Aerosol Climatology. Tellus Ser. B Chem. Phys. Meteorol. 2019, 71, 1–21. [Google Scholar] [CrossRef]
- Eskes, H.J.; Van Velthoven, P.F.J.; Valks, P.J.M.; Kelder, H.M. Assimilation of GOME Total-Ozone Satellite Observations in a Three-Dimensional Tracer-Transport Model. Q. J. R. Meteorol. Soc. 2003, 129, 1663–1681. [Google Scholar] [CrossRef]
- Kopeika, N.S. Optical Properties of the Atmosphere. In A System Engineering Approach to Imaging; SPIE Optical Engineering Press: Bellingham, WA, USA, 2017. [Google Scholar] [CrossRef]
- Sethi, D.; Kosmopoulos, P.G. Effect of Dust Events on Photovoltaics Electricity Production in the European and North African Regions. Environ. Sci. Proc. 2023, 26, 8. [Google Scholar] [CrossRef]
- Zsiborács, H.; Zentkó, L.; Pintér, G.; Vincze, A.; Baranyai, N.H. Assessing Shading Losses of Photovoltaic Power Plants Based on String Data. Energy Rep. 2021, 7, 3400–3409. [Google Scholar] [CrossRef]
- Batista, R.V.F. The Impact of Shadowing in Photovoltaic Systems and How to Minimizing It; Faculty of Engineering and Sustainable Development, University of Gävle: Gävle, Sweden, 2018. [Google Scholar]
- GRASS Development Team. Geographic Resources Analysis Support System (GRASS GIS); OSGeo Foundation: Beaverton, OR, USA, 2024. [Google Scholar]
- Liu, J.; Peng, C.; Zhang, J. Understanding the Relationship between Rural Morphology and Photovoltaic (PV) Potential in Traditional and Non-Traditional Building Clusters Using Shapley Additive ExPlanations (SHAP) Values. Appl. Energy 2025, 380, 125091. [Google Scholar] [CrossRef]
- Izquierdo, S.; Rodrigues, M.; Fueyo, N. A Method for Estimating the Geographical Distribution of the Available Roof Surface Area for Large-Scale Photovoltaic Energy-Potential Evaluations. Sol. Energy 2008, 82, 929–939. [Google Scholar] [CrossRef]
- Tröndle, T.; Pfenninger, S.; Lilliestam, J. Home-Made or Imported: On the Possibility for Renewable Electricity Autarky on All Scales in Europe. Energy Strateg. Rev. 2019, 26, 100388. [Google Scholar] [CrossRef]
- LONGi LR5-54HTH 445~455M Datasheet. Available online: https://static.longi.com/L_Gi_LE_PM_T_PMD_059_F131_LR_5_54_HTH_445_455_M_30_30_and_15_Frame_Scientist_V19_9e6db880ac.pdf (accessed on 15 February 2025).
- Mercom India Mercom India. Available online: https://www.mercomindia.com/ (accessed on 6 January 2025).
- Atia, D.M.; Hassan, A.A.; El-Madany, H.T.; Eliwa, A.Y.; Zahran, M.B. Degradation and Energy Performance Evaluation of Mono-Crystalline Photovoltaic Modules in Egypt. Sci. Rep. 2023, 13, 13066. [Google Scholar] [CrossRef]
- Saxena, A.K.; Saxena, S.; Sudhakar, K. Energy, Economic and Environmental Performance Assessment of a Grid-Tied Rooftop System in Different Cities of India Based on 3E Analysis. Clean Energy 2021, 5, 288–301. [Google Scholar] [CrossRef]
- Dumka, U.C.; Kosmopoulos, P.G.; Patel, P.N.; Sheoran, R. Can Forest Fires Be an Important Factor in the Reduction in Solar Power Production in India? Remote Sens. 2022, 14, 549. [Google Scholar] [CrossRef]
- Sarkar, S.; Chauhan, A.; Kumar, R. Impact of Deadly Dust Storms (May 2018) on Air Quality, Meteorological, and Atmospheric Parameters Over the Northern Parts of India. GeoHealth 2019, 3, 67–80. [Google Scholar] [CrossRef]
- Masoom, A.; Kosmopoulos, P.; Bansal, A.; Gkikas, A.; Proestakis, E.; Kazadzis, S.; Amiridis, V. Forecasting Dust Impact on Solar Energy Using Remote Sensing and Modeling Techniques. Sol. Energy 2021, 228, 317–332. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, W.; Zhang, G.J. What Rainfall Rates Are Most Important to Wet Removal of Different Aerosol Types? Atmos. Chem. Phys. 2021, 21, 16797–16816. [Google Scholar] [CrossRef]
- Mohan, M.; Kandya, A.; Battiprolu, A. Urban Heat Island Effect over National Capital Region of India: A Study Using the Temperature Trends. J. Environ. Prot. 2011, 02, 465–472. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Tripathi, S.N.; Dey, S.; Kanawade, V.P.; Tiwari, S. Inferring Aerosol Types over the Indo-Gangetic Basin from Ground Based Sunphotometer Measurements. Atmos. Res. 2012, 109–110, 64–75. [Google Scholar] [CrossRef]
- Sarangi, C.; Tripathi, S.N.; Mishra, A.K.; Goel, A.; Welton, E.J. Elevated Aerosol Layers and Their Radiative Impact over Kanpur during Monsoon Onset Period. J. Geophys. Res. 2016, 121, 7936–7957. [Google Scholar] [CrossRef]
- Bhadauria, N.; Chauhan, A.; Ranjan, R.; Jindal, T. An Assessment of Seasonal, Monthly and Diurnal Variations of Ambient Air Quality in the Gurugram City (Haryana). J. Appl. Nat. Sci. 2023, 15, 306–313. [Google Scholar] [CrossRef]
- Akanksha; Shukla, A.K.; Bhowmik, H.S.; Yadav, A.K.; Jain, V.; Murari, V.; Gaddamidi, S.; Lalchandani, V.; Tripathi, S.N. Comparative Analysis of Winter Composite-PM2.5 in Central Indo Gangetic Plain Cities: Combined Organic and Inorganic Source Apportionment and Characterization, with a Focus on the Photochemical Age Effect on Secondary Organic Aerosol Formation. Atmos. Environ. 2024, 338, 120827. [Google Scholar] [CrossRef]
- Mishra, S.K.; Ahlawat, A.; Khosla, D.; Sharma, C.; Prasad, M.V.S.N.; Singh, S.; Gupta, B.; Tulsi; Sethi, D.; Sinha, P.R.; et al. Experimental Investigation of Variations in Morphology, Composition and Mixing-State of Boundary Layer Aerosol: A Balloon Based Study over Urban Environment (New Delhi). Atmos. Environ. 2018, 185, 243–252. [Google Scholar] [CrossRef]
- Sethi, D.; Sharma, C.; Radhakrishnan, S.R. Physical Properties of Aerosols in Different Environments; Academy of Scientific and Innovative Research (AcSIR): Ghaziabad, India, 2022. [Google Scholar]
- Singh, T.; Ravindra, K.; Sreekanth, V.; Gupta, P.; Sembhi, H. Climatological Trends in Satellite-Derived Aerosol Optical Depth over North India and Its Relationship with Crop Residue Burning: Rural-Urban Contrast. Sci. Total Environ. 2020, 748, 140963. [Google Scholar]
- Saini, G.; Jagadeesh, P.; Saikumar, G. Trend Assessment of Rainfall Over Mumbai and Pune Cities. In River Dynamics and Flood Hazards. Disaster Resilience and Green Growth; Pandey, M., Azamathulla, H., Pu, J.H., Eds.; Springer: Singapore, 2023; pp. 587–606. ISBN 9789811971006. [Google Scholar]
- Sunil, S.; Padmakumari, B. Optical and Radiative Characteristics of the Lower Part of Cirrus Clouds Over a Rain Shadow Region in South Peninsular India. Pure Appl. Geophys. 2024, 181, 1697–1724. [Google Scholar] [CrossRef]
- Jain, N. Changing Monsoonal Rainfall Patterns in the Western Ghats. Available online: https://india.mongabay.com/2019/01/changing-monsoonal-rainfall-patterns-in-the-western-ghats/ (accessed on 6 January 2025).
- Agathangelidis, I.; Cartalis, C.; Santamouris, M. Urban Morphological Controls on Surface Thermal Dynamics: A Comparative Assessment of Major European Cities with a Focus on Athens, Greece. Climate 2020, 8, 131. [Google Scholar] [CrossRef]
- Singh, A.; Srivastava, A.K.; Pathak, V.; Shukla, A.K. Quantifying the Impact of Biomass Burning and Dust Storm Activities on Aerosol Characteristics over the Indo-Gangetic Basin. Atmosperic Environ. 2022, 270, 118893. [Google Scholar] [CrossRef]
- Kumar, A.; Pratap, V.; Kumar, S.; Singh, A.K. Atmospheric Aerosols Properties over Indo-Gangetic Plain: A Trend Analysis Using Ground—Truth AERONET Data for the Year 2009–2017. Adv. Sp. Res. 2022, 69, 2659–2670. [Google Scholar] [CrossRef]
- Tripathi, S.N.; Yadav, S.; Sharma, K. Air Pollution from Biomass Burning in India. Environ. Res. Lett. 2024, 19, 073007. [Google Scholar] [CrossRef]
- Kulshrestha, U.; Kumar, B. Airmass Trajectories and Long Range Transport of Pollutants: Review of Wet Deposition Scenario in South Asia. Adv. Meteorol. 2014, 2014, 596041. [Google Scholar] [CrossRef]
- Yang, J.; Yi, B.; Wang, S.; Liu, Y.; Li, Y. Diverse Cloud and Aerosol Impacts on Solar Photovoltaic Potential in Southern China and Northern India. Sci. Rep. 2022, 12, 19671. [Google Scholar] [CrossRef]
- Li, X.; Mauzerall, D.L.; Bergin, M.H. Global Reduction of Solar Power Generation Efficiency Due to Aerosols and Panel Soiling. Nat. Sustain. 2020, 3, 720–727. [Google Scholar] [CrossRef]
- Masoom, A.; Kosmopoulos, P.; Kashyap, Y.; Kumar, S.; Bansal, A. Rooftop Photovoltaic Energy Production Management in India Using Earth-Observation Data and Modeling Techniques. Remote Sens. 2020, 12, 1921. [Google Scholar] [CrossRef]
- Nayak, S.; Takemi, T.; Maity, S. Precipitation and Temperature Climatologies over India: A Study with AGCM Large Ensemble Climate Simulations. Atmosphere 2022, 13, 671. [Google Scholar] [CrossRef]
- Tyagi, A.P. Solar Radiant Energy Over India; India Meteorological Department Ministry of Earth Sciences: New Delhi, India, 2009. [Google Scholar]
- Lopez, A. India Direct Normal & Global Horizontal Irradiance Solar Resources; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2016. [Google Scholar]
- Ayua, T.J.; Camara, M. Modeling and Estimation of Solar Panel Tilting Angles and Orientations in the Gambia: A Case Study of Brikama, West Coast Region. Discov. Energy 2024, 4, 31. [Google Scholar] [CrossRef]
- Gedifew, A.; Benor, A.; Lu, Y. Evaluating the Impact of Tilt Angles and Tracking Mechanisms on Photovoltaic Modules in Ethiopia. Front. Energy Res. 2025, 12, 1519725. [Google Scholar] [CrossRef]
- Ali, M.; Kumar, N. Pulses in Indo-Gangetic Plains Status and Strategies for Area Expansion and Productivity Gain. Indian Farming 2016, 66, 6–10. [Google Scholar]
- Government of India, PM Suryaghar: Solar Energy Initiative, Government of India, New Delhi, India. Available online: https://www.pmsuryaghar.gov.in/ (accessed on 7 January 2025).
- Tyagi, B.; Kuldeep, N. Community Solar for Advancing Power Sector Reforms and the Net-Zero Goals. 2023. Available online: https://www.ceew.in/sites/default/files/scaling-community-solar-for-net-zero-electricty-and-power-sector-decarbonisation.pdf (accessed on 6 January 2025).
- Singh, R.; Banerjee, R. Impact of Solar Panel Orientation on Large Scale Rooftop Solar Photovoltaic Scenario for Mumbai. Energy Procedia 2016, 90, 401–411. [Google Scholar] [CrossRef]
- Raptis, I.P.; Moustaka, A.; Kosmopoulos, P.; Kazadzis, S. Selecting Surface Inclination for Maximum Solar Power. Energies 2022, 15, 4784. [Google Scholar] [CrossRef]
- Sun, J.; Zhi, G.; Hitzenberger, R.; Chen, Y.; Tian, C.; Zhang, Y.; Feng, Y.; Cheng, M.; Zhang, Y.; Cai, J.; et al. Emission Factors and Light Absorption Properties of Brown Carbon from Household Coal Combustion in China. Atmos. Chem. Phys. 2017, 17, 4769–4780. [Google Scholar] [CrossRef]
- Khan, A.; Anand, P.; Khatun, R.; Khorat, S.; Niyogi, D.; Santamouris, M. Rooftop Photovoltaic Solar Panels Warm up and Cool down Cities. Nat. Cities 2024, 1, 780–790. [Google Scholar] [CrossRef]
- Solar, V. Solar Power—The Most Effective Solution for Controlling Carbon Footprint. Available online: https://www.vikramsolar.com/solar-power-the-most-effective-solution-for-controlling-carbon-footprint/ (accessed on 14 February 2025).
- U.S. Environmental Protection Agency. AVoided Emissions and GeneRation Tool (AVERT) User Manual; Version1; U.S. Environmental Protection Agency: Washington, DC, USA, 2018.
- Prayas (Energy Group). Electricity Consumption Patterns. Available online: https://energy.prayaspune.org/our-work/article-and-blog/electricity-consumption-patterns (accessed on 6 January 2025).
- Statista Worldwide. CO2 Emissions from Coal. Available online: https://www.statista.com/statistics/784682/worldwide-co2-emissions-from-coal/ (accessed on 6 January 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).