Broadband SAR Imaging Based on Narrowband Dense False Target Jamming
Abstract
1. Introduction
- We designed a broadband SAR imaging signal based on narrowband DFTJSs, and provided the overall signal design process and signal processing methods to solve the problem of limited signal bandwidth in conventional secondary compression processing methods;
- We studied the system constraints and parameter design of the signal and processing method designed in this paper through a reasonable theoretical analysis;
- We validated and evaluated the feasibility of this method through simulation experiments, including the jamming and imaging capabilities of the joint signal.
2. Application Scenarios and Signal Model
2.1. Geometric Scenes
2.2. Narrowband DFTJS Model with Phase Modulation
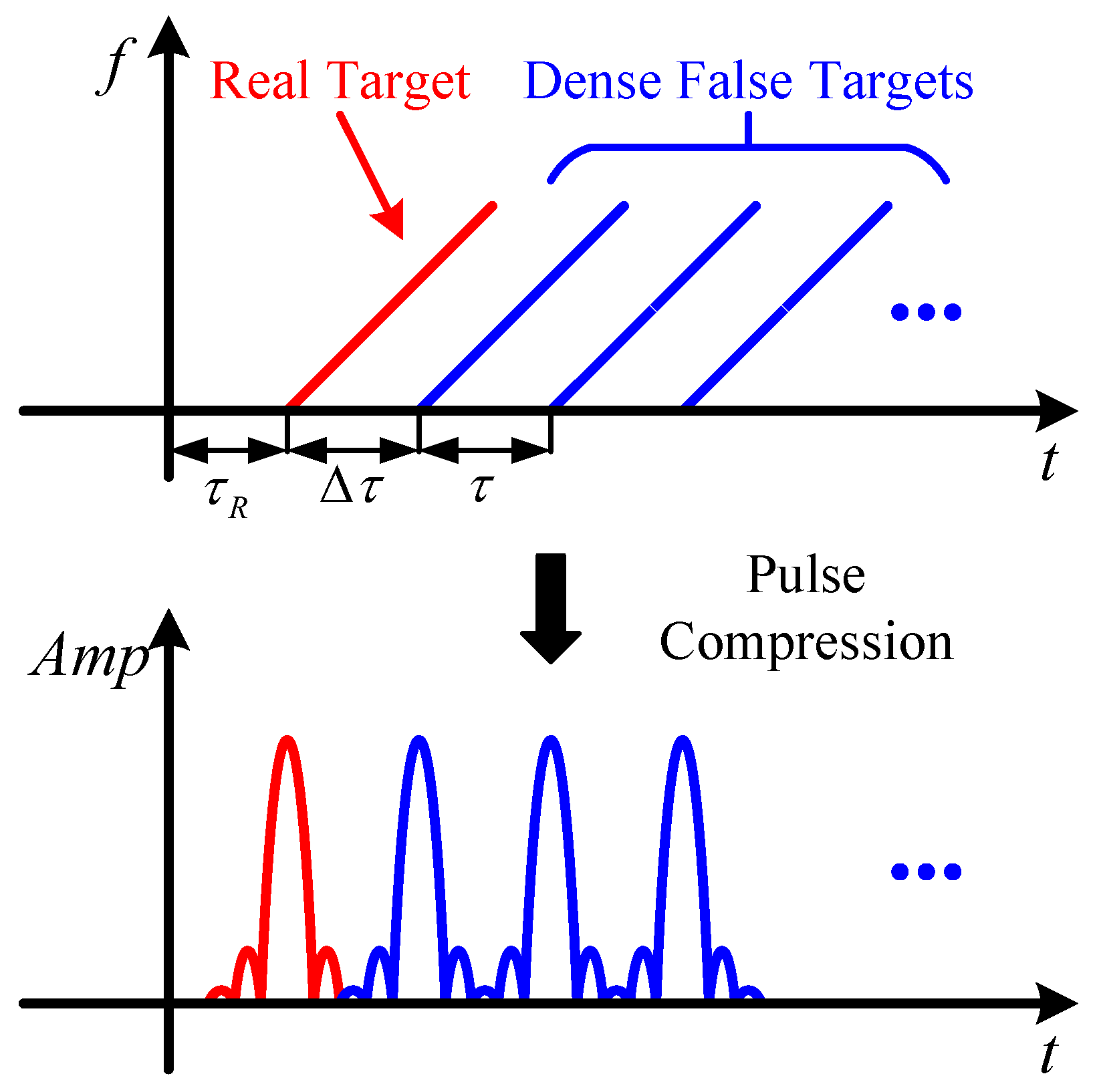
3. Jamming Effect Analysis
4. SAR Imaging Method
4.1. SAR Echo Signal Model
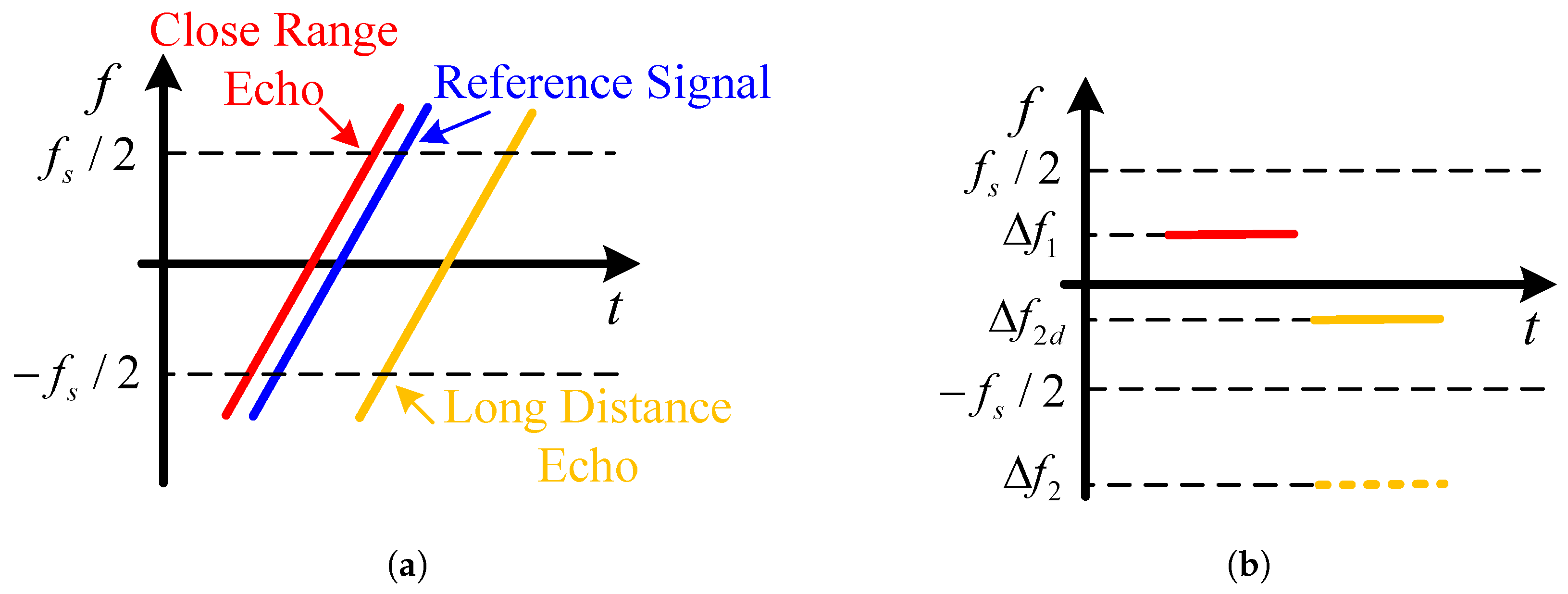
4.2. Range–Secondary Compression Based on Dechirping
4.3. Azimuth Compression
5. System Constraints
5.1. Jamming Constraints
5.2. Imaging Range Constraints
6. Simulation Results
6.1. Jamming Performance Analysis
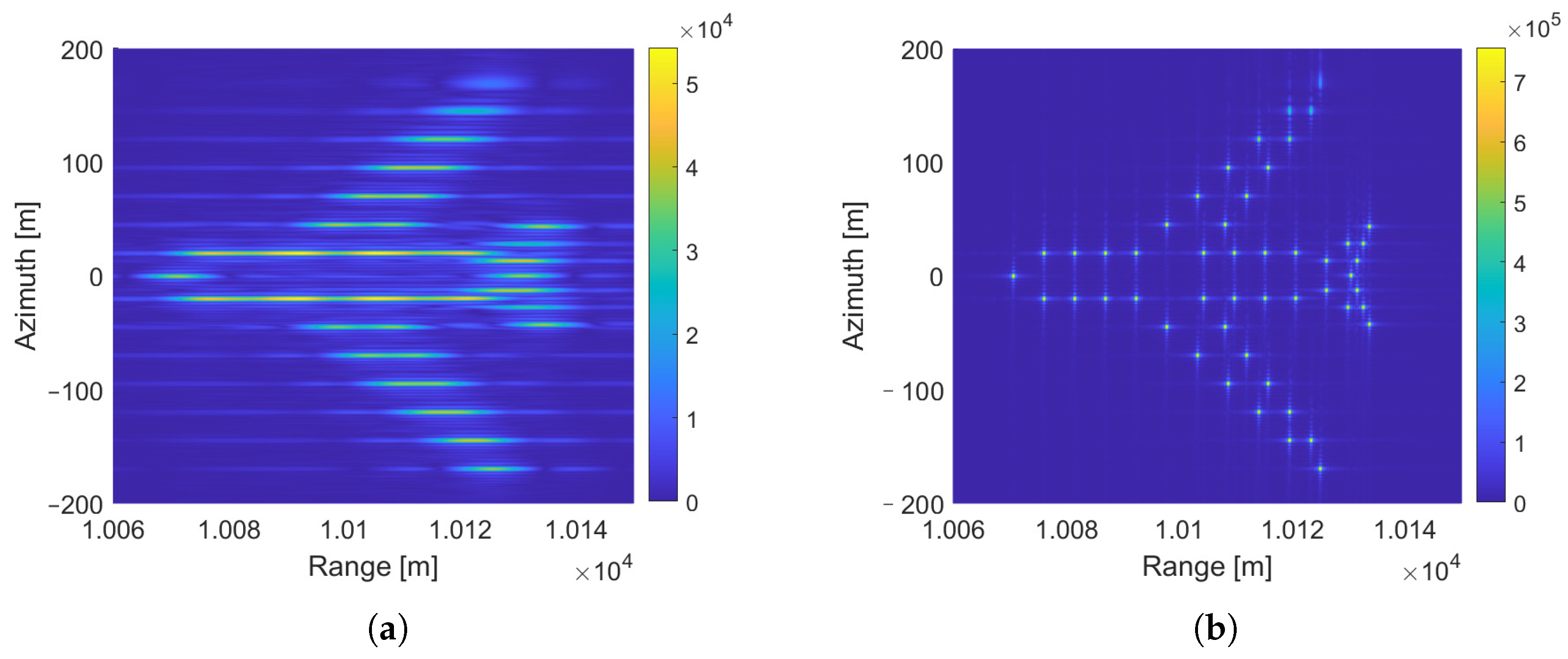
6.2. SAR Imaging Performance Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- James, R.J. A history of radar. IEE Rev. 1989, 35, 343–349. [Google Scholar] [CrossRef]
- Guarnieri, M. The Early History of Radar [Historical]. IEEE Ind. Electron. Mag. 2010, 4, 36–42. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, H. A CFAR algorithm based on Monte Carlo method for millimeter-wave radar road traffic target detection. Remote Sens. 2022, 14, 1779. [Google Scholar] [CrossRef]
- Sokol, Z.; Szturc, J.; Orellana-Alvear, J.; Popova, J.; Jurczyk, A.; Célleri, R. The role of weather radar in rainfall estimation and its application in meteorological and hydrological modelling—A review. Remote Sens. 2021, 13, 351. [Google Scholar] [CrossRef]
- Tagliaferri, D.; Rizzi, M.; Nicoli, M.; Tebaldini, S.; Russo, I.; Monti-Guarnieri, A.V.; Prati, C.M.; Spagnolini, U. Navigation-aided automotive SAR for high-resolution imaging of driving environments. IEEE Access 2021, 9, 35599–35615. [Google Scholar] [CrossRef]
- Piotrowsky, L.; Kueppers, S.; Jaeschke, T.; Pohl, N. Distance Measurement Using mmWave Radar: Micron Accuracy at Medium Range. IEEE Trans. Microw. Theory Tech. 2022, 70, 5259–5270. [Google Scholar] [CrossRef]
- Xu, Y.; Jin, T.; Chi, H.; Zheng, S.; Jin, X.; Zhang, X. Photonic generation of dual-chirp waveforms with improved time-bandwidth product. IEEE Photonics Technol. Lett. 2017, 29, 1253–1256. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Q.; Zhang, T.; Zhao, Q.; Fu, S. Research on interference coupling mechanism and test method of UAV in complex electromagnetic environment. In Proceedings of the 2021 13th International Symposium on Antennas, Propagation and EM Theory (ISAPE), Zhuhai, China, 1–4 December 2021; pp. 01–03. [Google Scholar] [CrossRef]
- Li, X.; Chen, B. An Effective Composite Jamming Method for Synthetic Aperture Radar in Practical Electronic Countermeasures. In Proceedings of the 2024 IEEE International Conference on Acoustics, Speech, and Signal Processing Workshops (ICASSPW), Seoul, Republic of Korea, 14–19 April 2024; pp. 370–373. [Google Scholar] [CrossRef]
- Han, X.; He, H.; Zhang, Q.; Yang, L.; He, Y. Suppression of deception-false-target jamming for active/passive netted radar based on position error. IEEE Sens. J. 2022, 22, 7902–7912. [Google Scholar] [CrossRef]
- Liu, G.; Li, L.; Ming, F.; Sun, X.; Hong, J. A controllable suppression jamming method against SAR based on active radar transponder. Remote Sens. 2022, 14, 3949. [Google Scholar] [CrossRef]
- Shi, Y.; Huang, H.; Ma, Z. An Inter-Pulse Non-Coherent Jamming Technology Against SAR Based on Stepped Time-Delay. In Proceedings of the 2021 7th International Conference on Systems and Informatics (ICSAI), Chongqing, China, 13–15 November 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Yang, K.; Ma, F.; Ran, D.; Ye, W.; Li, G. Fast generation of deceptive jamming signal against spaceborne SAR based on spatial frequency domain interpolation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhou, S.; Yang, L.; Ning, X.; Xing, M. Synthetic aperture radar interference based on scene fusion and active cancellation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10375–10382. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Tsokas, A.; Rysz, M.; Pardalos, P.M.; Dipple, K. SAR data applications in earth observation: An overview. Expert Syst. Appl. 2022, 205, 117342. [Google Scholar] [CrossRef]
- Jawak, S.D.; Bidawe, T.G.; Luis, A.J. A review on applications of imaging synthetic aperture radar with a special focus on cryospheric studies. Adv. Remote Sens. 2015, 4, 163–175. [Google Scholar] [CrossRef]
- Demirci, S.; Izumi, Y. Application of H/ Decomposition to Limited and Dual-Polarimetric 3D SAR Data of Civilian Vehicles. IEEE Access 2023, 11, 83589–83602. [Google Scholar] [CrossRef]
- Olsen, K.E.; Asen, W. Bridging the gap between civilian and military passive radar. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 4–12. [Google Scholar] [CrossRef]
- Almutiry, M. UAV tomographic synthetic aperture radar for landmine detection. Eng. Technol. Appl. Sci. Res. 2020, 10, 5933–5939. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Applications of lasers for tactical military operations. IEEE Access 2017, 5, 20736–20753. [Google Scholar] [CrossRef]
- Koo, V.; Chan, Y.K.; Vetharatnam, G.; Chua, M.Y.; Lim, C.H.; Lim, C.S.; Thum, C.; Lim, T.S.; bin Ahmad, Z.; Mahmood, K.A.; et al. A new unmanned aerial vehicle synthetic aperture radar for environmental monitoring. Prog. Electromagn. Res. 2012, 122, 245–268. [Google Scholar] [CrossRef]
- Liu, G.; Yang, W.; Wang, Y.; Bao, Y.; Wang, S.; Wu, H.; Li, P. MIMO FBMC-based joint radar imaging and electronic jamming. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, Q.; Huang, Z.; Chen, T.; Mu, B.; Guo, H. SAR Imaging of Dense False Target Jamming Based on Phase Modulation. IEEE Geosci. Remote Sens. Lett. 2024, 22, 4000105. [Google Scholar] [CrossRef]
- Richards, M.A.; Scheer, J.; Holm, W.A.; Melvin, W.L. Principles of Modern Radar; SciTech Publishing: Raleigh, NC, USA, 2010. [Google Scholar]
- Yang, X.; Wen, G.; Ma, C.; Hui, B.; Ding, B.; Zhang, Y. CFAR detection of moving range-spread target in white Gaussian noise using waveform contrast. IEEE Geosci. Remote Sens. Lett. 2016, 13, 282–286. [Google Scholar] [CrossRef]
- Chen, X.; Su, N.; Huang, Y.; Guan, J. False-alarm-controllable radar detection for marine target based on multi features fusion via CNNs. IEEE Sensors J. 2021, 21, 9099–9111. [Google Scholar] [CrossRef]
- Vaidyanathan, P. Generalizations of the sampling theorem: Seven decades after Nyquist. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2001, 48, 1094–1109. [Google Scholar] [CrossRef]
- Zhu, D.; Zhu, Z. Range resampling in the polar format algorithm for spotlight SAR image formation using the chirp z-transform. IEEE Trans. Signal Process. 2007, 55, 1011–1023. [Google Scholar] [CrossRef]
- Letsch, K.; Berens, P. PSLR estimation for SAR systems with consideration of clutter background. In Proceedings of the SAR Image Analysis, Modeling, and Techniques VII. SPIE, Bruges, Belgium, 19–20 September 2005; Volume 5980, pp. 13–22. [Google Scholar] [CrossRef]
- Xu, Z.; Li, H.C.; Shi, Q.; Wang, H.; Wei, M.; Shi, J.; Shao, Y. Effect analysis and spectral weighting optimization of sidelobe reduction on SAR image understanding. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3434–3444. [Google Scholar] [CrossRef]







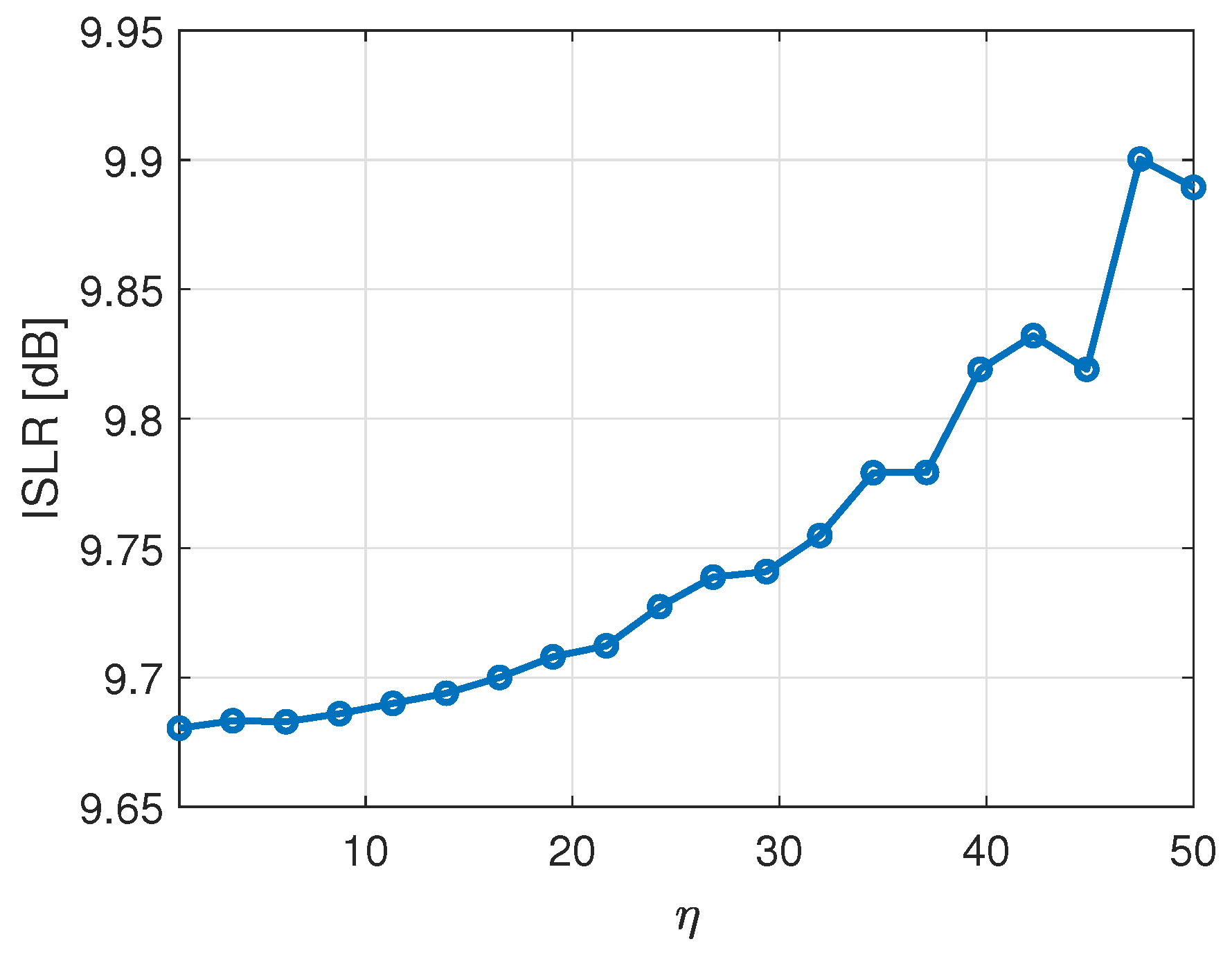
| Parameter | Value |
|---|---|
| Carrier frequency | 5 GHz |
| UAV velocity | 100 m/s |
| UAV altitude | 200 m |
| Central slant range | 10 km |
| Waveform bandwidth of P | 10 MHz |
| Pulse width of P | 10 us |
| Bandwidth of secondary phase signal | 200 MHz |
| Sampling rate | 400 MHz |
| SNR | 10 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Huang, Z.; Pan, H.; Zhang, Q.; Zhu, J. Broadband SAR Imaging Based on Narrowband Dense False Target Jamming. Remote Sens. 2025, 17, 1196. https://doi.org/10.3390/rs17071196
Liu G, Huang Z, Pan H, Zhang Q, Zhu J. Broadband SAR Imaging Based on Narrowband Dense False Target Jamming. Remote Sensing. 2025; 17(7):1196. https://doi.org/10.3390/rs17071196
Chicago/Turabian StyleLiu, Gaogao, Ziyu Huang, Haoran Pan, Qidong Zhang, and Jiangbo Zhu. 2025. "Broadband SAR Imaging Based on Narrowband Dense False Target Jamming" Remote Sensing 17, no. 7: 1196. https://doi.org/10.3390/rs17071196
APA StyleLiu, G., Huang, Z., Pan, H., Zhang, Q., & Zhu, J. (2025). Broadband SAR Imaging Based on Narrowband Dense False Target Jamming. Remote Sensing, 17(7), 1196. https://doi.org/10.3390/rs17071196






